| |
Figure 1:
Linear swing amplification of a density wave in the shearing sheet.
The wave is initialized as a delta like impulse in wave number space with an
initial wave vector
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{2657fig2.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg168.gif) |
Figure 2:
Initial set up of the 32 768 particles in the simulation of the
shearing sheet. The y-axis points into the direction of the shear flow.
The size is
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=16cm,clip]{2657fig3.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg169.gif) |
Figure 3: Dynamical evolution of the shearing sheet. Snapshots of particle positions are shown for t = 0.5, 1, ... 3.5, and 4, respectively. The y-axis is oriented in the direction of the shear flow. The size of each frame is the same as in Fig. 2. |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2657fig4.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg172.gif) |
Figure 4:
The rise of
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{2657fig5.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg180.gif) |
Figure 5: Same as Fig. 3, but the shearing sheet is dynamically cooled by accretion of particles during the simulation. |
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2657fig6.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg181.gif) |
Figure 6: Same as Fig. 4, but the shearing sheet is dynamically cooled by accretion of particles during the simulation. |
| Open with DEXTER | |
In the text
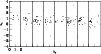 |
Figure 7:
Peaks of positive
|
| Open with DEXTER | |
In the text
 |
Figure 8:
Power spectrum
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{2657fig9.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg197.gif) |
Figure 9:
Response of the shearing sheet to an external impulsive potential
perturbation with an initial wave vector
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{2657fi10.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg199.gif) |
Figure 10:
Response of the shearing sheet to two external impulsive potential
perturbations with initial wave vectors
|
| Open with DEXTER | |
In the text
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{2657fi11.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg201.gif) |
Figure 11:
Same as Fig. 10, but with two external impulsive potential
perturbations with initial wave vectors
(kx, ky) = (-2, 0.5)
|
| Open with DEXTER | |
In the text