A&A 443, L29-L32 (2005)
DOI: 10.1051/0004-6361:200500199
UHE nuclei propagation and the interpretation of the ankle in the cosmic-ray spectrum
D. Allard1,2,3 - E. Parizot1 - A. V. Olinto2,3 - E. Khan1 - S. Goriely4
1 - Institut de Physique Nucléaire d'Orsay, IN2P3-CNRS/Université Paris-Sud, 91406 Orsay Cedex, France
2 -
Kavli Institute of Cosmological Physics, University of Chicago, 5640 S. Ellis, Chicago, IL 60637, USA
3 -
Department of Astronomy and Astrophysics, University of Chicago, 5640 S. Ellis, Chicago, IL 60637, USA
4 -
Institut d'Astronomie et d'Astrophysique, ULB, CP226, 1050 Brussels, Belgium
Received 27 May 2005 / Accepted 5 October 2005
Abstract
We consider the stochastic propagation of high-energy protons and nuclei in the cosmological microwave and infrared backgrounds, using revised photonuclear cross-sections and following primary and secondary nuclei in the full 2D nuclear chart. We confirm earlier results showing that the high-energy data can be fit with a pure proton extragalactic cosmic ray (EGCR) component if the source spectrum is 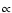 E-2.6. In this case the ankle in the CR spectrum may be interpreted as a pair-production dip associated with the propagation. We show that when heavier nuclei are included in the source with a composition similar to that of Galactic cosmic-rays (GCRs), the pair-production dip is not present unless the proton fraction is higher than 85%. In the mixed composition case, the ankle recovers the past interpretation as the transition from GCRs to EGCRs and the highest energy data can be explained by a harder source spectrum
E-2.6. In this case the ankle in the CR spectrum may be interpreted as a pair-production dip associated with the propagation. We show that when heavier nuclei are included in the source with a composition similar to that of Galactic cosmic-rays (GCRs), the pair-production dip is not present unless the proton fraction is higher than 85%. In the mixed composition case, the ankle recovers the past interpretation as the transition from GCRs to EGCRs and the highest energy data can be explained by a harder source spectrum 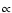 E-2.2-E-2.3, reminiscent of relativistic shock acceleration predictions, and in good agreement with the GCR data at low-energy and holistic scenarios.
E-2.2-E-2.3, reminiscent of relativistic shock acceleration predictions, and in good agreement with the GCR data at low-energy and holistic scenarios.
Key words: cosmic rays - abundances - nuclear reactions
1 Introduction
One of the keys to understanding the origin of cosmic-rays (CR) is the spectral shape of the transition from Galactic cosmic-rays (GCR) to extragalactic cosmic rays (EGCR). The Galactic origin of low-energy CRs is generally accepted, while the highest energy CRs (above 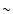 1019 eV) are no longer confined by Galactic magnetic fields and most probably originate from other galaxies. Thus, a transition between the two components has to occur in some energy range. The most natural location for this transition is around
1019 eV) are no longer confined by Galactic magnetic fields and most probably originate from other galaxies. Thus, a transition between the two components has to occur in some energy range. The most natural location for this transition is around 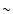
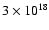 eV at a feature in the CR spectrum known as the ankle. This is the only energy range where the spectrum gets harder (i.e., its logarithmic slope gets smaller), offering a simple transition scheme to a harder CR component which is subdominant at lower energies.
eV at a feature in the CR spectrum known as the ankle. This is the only energy range where the spectrum gets harder (i.e., its logarithmic slope gets smaller), offering a simple transition scheme to a harder CR component which is subdominant at lower energies.
A different conclusion has recently been proposed on the basis of composition results from the HiRes Collaboration, tentatively showing a transition from heavy to light primary nuclei at an energy around
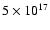 eV (Abbasi et al. 2005), which can be identified with a steepening in the spectrum around 1017.5 eV called the second knee. Such composition measurements rely on statistical determinations of the elongation rate of extensive air-showers and depend on shower development simulations which are still quite uncertain. One should thus remain cautious about such a result, but taken at face value it suggests a transition from a heavy GCR component to a light EGCR one at an energy below the ankle. A phenomenological class of models where the GCR/EGCR transition is around the second knee can be designed such that the extragalactic component accounts for CRs down to energies
eV (Abbasi et al. 2005), which can be identified with a steepening in the spectrum around 1017.5 eV called the second knee. Such composition measurements rely on statistical determinations of the elongation rate of extensive air-showers and depend on shower development simulations which are still quite uncertain. One should thus remain cautious about such a result, but taken at face value it suggests a transition from a heavy GCR component to a light EGCR one at an energy below the ankle. A phenomenological class of models where the GCR/EGCR transition is around the second knee can be designed such that the extragalactic component accounts for CRs down to energies 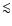 1018 eV (Berezinsky et al. 2002). In these models, the ankle is interpreted as an
1018 eV (Berezinsky et al. 2002). In these models, the ankle is interpreted as an
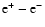 pair-production dip resulting from proton propagation over large distances in the cosmic microwave background (CMB). This effect is the pair production analog of the GZK flux suppression due to photo-pion production at higher proton energies (Greisen 1966; Zatsepin & Kuzmin 1966). While the composition measurements and the matching of GCRs to EGCRs at the second knee remain unclear, the main point to note is that the transition does not have to be at the ankle.
pair-production dip resulting from proton propagation over large distances in the cosmic microwave background (CMB). This effect is the pair production analog of the GZK flux suppression due to photo-pion production at higher proton energies (Greisen 1966; Zatsepin & Kuzmin 1966). While the composition measurements and the matching of GCRs to EGCRs at the second knee remain unclear, the main point to note is that the transition does not have to be at the ankle.
Phenomenological approaches are useful since the origin of neither the GCR nor the EGCR components are well understood (see, e.g., Parizot 2005). Concerning the EGCR component, although major uncertainties remain in the ultra-high-energy (UHE) range, where the expected GZK suppression of the flux may not be present in the data (e.g., the AGASA spectrum in Teshima et al. 2003), propagation studies find that the measured spectrum is best fitted by assuming a power-law source spectrum in
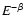 with
with
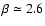 (De Marco et al. 2003). Except for the iron modification factor in Berezinsky et al. (2005), most studies assume that EGCRs are only protons.
(De Marco et al. 2003). Except for the iron modification factor in Berezinsky et al. (2005), most studies assume that EGCRs are only protons.
In this Letter, we investigate how these conclusions are modified when nuclei heavier than protons are also present in the source. We apply the revised scheme of photo-nuclear interactions described in Khan et al. (2005). Interestingly, we find that the two main aspects of EGCR phenomenology are jointly affected, namely the best fit slope of the source spectrum and the interpretation of the ankle. The interpretation of the ankle as a pair production dip is not viable in the mixed composition case, unless the fraction of protons is above 85%. When reasonable assumptions for the fraction of nuclei in the EGCR are introduced, the traditional interpretation of a GCR/EGCR transition at the ankle is recovered and the best fit spectral index for EGCR is 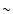 2.2-2.3, as expected from relativistic shock acceleration. Finally, the best fit EGCR spectrum occurs when both the GCR and EGCR component have the same spectral index, allowing for holistic approaches to the CR spectrum.
2.2-2.3, as expected from relativistic shock acceleration. Finally, the best fit EGCR spectrum occurs when both the GCR and EGCR component have the same spectral index, allowing for holistic approaches to the CR spectrum.
In the absence of a specific source model, the choice of CR composition at the source is somewhat arbitrary. Here, we consider a "generic composition'' assuming that EGCRs have the same relative abundances at the sources as the well knowns, low-energy GCRs, derived from Ulysses and HEAO 3 data (Duvernois & Thayer 1996). We convert the differential abundance ratios, xi, at a given energy per nucleon (E/A) into ratios at a given energy,
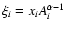 ,
where
,
where 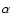 is the spectral index, so that the GCR source spectrum is:
is the spectral index, so that the GCR source spectrum is:
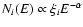 .
If EGCRs are accelerated out of the interstellar medium by a similar process as GCRs, it is not unreasonable to assume a similar composition as well. In this case
.
If EGCRs are accelerated out of the interstellar medium by a similar process as GCRs, it is not unreasonable to assume a similar composition as well. In this case
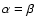 ,
where
,
where 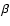 is the spectral index at injection, and
is the spectral index at injection, and
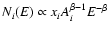 .
However, since our main goal is to investigate the difference between pure proton and mixed CR compositions, we also study the cases of
.
However, since our main goal is to investigate the difference between pure proton and mixed CR compositions, we also study the cases of
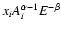 ,
where
,
where
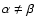 ,
specifically to investigate the viability of the second knee transition models when small fractions of nuclei are injected by the sources. Although we explore
,
specifically to investigate the viability of the second knee transition models when small fractions of nuclei are injected by the sources. Although we explore 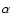 between 0 and 2.7, physically motived spectral indices are typically
between 0 and 2.7, physically motived spectral indices are typically
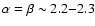 for the source spectrum.
for the source spectrum.
The injection spectra are exponentially cut with a rigidity dependent maximum energy for the various nuclear species
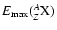 .
We assume that energy losses and photo-fragmentation inside the source can be neglected, so that all nuclei with the same gyroradius behave the same way. This implies
.
We assume that energy losses and photo-fragmentation inside the source can be neglected, so that all nuclei with the same gyroradius behave the same way. This implies
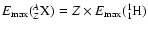 .
We find that, as long as
.
We find that, as long as
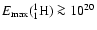 eV, changes in the maximum energy do not affect our results significantly.
eV, changes in the maximum energy do not affect our results significantly.
The main goal of the present study is to contrast the effect on the observed spectrum of a mixed composition against pure protons. Our main conclusions are not affected much by changes in source evolution with redshift (although specific injection indices need to be adjusted). In addition, extragalactic magnetic fields modify both the pure proton (see, Lemoine 2004) and the mixed composition spectrum, but relative effects remain similar for small enough magnetic fields (see e.g., Aloisio & Berezinsky 2004).
We compute the propagated spectrum of EGCRs for a uniform source distribution, using a Monte-Carlo technique. For protons, we take into account the energy losses due to the photo-production of pions and e+ - e- pairs, caused by the interaction with CMB photons. Photo-pair production is treated as a continuous process, as allowed by the short interaction length and small inelasticity, while pion production is treated stochastically: we first draw randomly the energy of the interacting photon in the proton rest frame, from the relevant boosted black-body distribution weighted by the interaction cross-section, and then calculate the inelasticity from the reaction kinematics after choosing randomly the interaction angle in the center-of-mass frame. We also include the evolution of the CMB temperature and energy losses due to the expansion of the universe.
The propagation of nuclei is also followed stochastically. In addition to e+ - e- pair production, nuclei are subject to photo-erosion, i.e., they lose nucleons through photo-nuclear interactions with the CMB and the infrared background (IRB). We use here for the first time a 2D scheme to follow the nuclei in the (A,Z) space, thanks to both revised and new cross-sections as described in Khan et al. (2005). Our code includes the following processes: i) the giant dipole resonance (GDR), with a loss of one or more nucleons, as well as 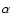 -particles (this process occurs with photons above a threshold of
-particles (this process occurs with photons above a threshold of 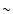 8 MeV in the nucleus rest frame), ii) the quasi-deuteron (QD) process, where a virtual pion interacts with a nucleon pair within the nucleus, leading to the ejection of the pair and possibly additional nucleons (this occurs with photons from 20 to 150 MeV), iii) baryonic resonances (BR), where a real pion is produced, ejecting a nucleon and possibly interacting further with a nucleon pair, eventually leading to the loss of an average of six nucleons for an Fe nucleus (this occurs above
8 MeV in the nucleus rest frame), ii) the quasi-deuteron (QD) process, where a virtual pion interacts with a nucleon pair within the nucleus, leading to the ejection of the pair and possibly additional nucleons (this occurs with photons from 20 to 150 MeV), iii) baryonic resonances (BR), where a real pion is produced, ejecting a nucleon and possibly interacting further with a nucleon pair, eventually leading to the loss of an average of six nucleons for an Fe nucleus (this occurs above 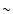 150 MeV), and iv) the photo-fragmentation (PF), occurring at very high energy (
150 MeV), and iv) the photo-fragmentation (PF), occurring at very high energy (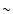 1 GeV) and breaking the nucleus into many fragments of much lower mass and energy.
1 GeV) and breaking the nucleus into many fragments of much lower mass and energy.
![\begin{figure}
\par\mbox{\includegraphics[height=5.5cm]{He272_f1a.eps}\hspace*{8mm}
\includegraphics[height=5.5cm]{He272_f1b.eps} }
\end{figure}](/articles/aa/full/2005/45/aahe272/Timg24.gif) |
Figure 1:
Left: mean-free-path of 56Fe nuclei against the various photo-nuclear processes in the CMB and IR background (see text), as a function of 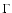 .
Right: energy loss length (including pair production) for various nuclei (labeled by their original A) as a function of E, with their dispersion. .
Right: energy loss length (including pair production) for various nuclei (labeled by their original A) as a function of E, with their dispersion. |
| Open with DEXTER |
The new GDR cross-sections are discussed in detail in Khan et al. (2005). For the higher-energy processes, we used the parameterisation of Rachen (1996). The QD cross-section is taken as
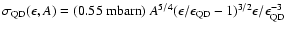 ,
where
,
where 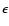 is the photon energy in the nucleus rest frame, A is the nucleon number and
is the photon energy in the nucleus rest frame, A is the nucleon number and
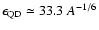 MeV is the interaction threshold. The number of emitted nucleons is obtained from the experimental branching ratios of Puget et al. (1976). The BR cross-section is modeled as the sum of four Lorentzians representing the four main resonances,
MeV is the interaction threshold. The number of emitted nucleons is obtained from the experimental branching ratios of Puget et al. (1976). The BR cross-section is modeled as the sum of four Lorentzians representing the four main resonances,
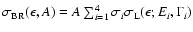 ,
with the following parameters (in GeV, GeV and
,
with the following parameters (in GeV, GeV and 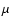 barn, respectively):
barn, respectively):
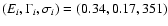 ,
(0.75,0.50,159),
(1.0,0.60,21) and
(1.5,0.80,26). Finally, the PF cross-section is modeled as
,
(0.75,0.50,159),
(1.0,0.60,21) and
(1.5,0.80,26). Finally, the PF cross-section is modeled as
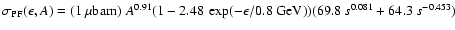 ,
where
,
where
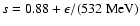 .
We also follow Rachen (1996) for the pair production cross-section, including corrections to the formulæ of Blumenthal (1970). The attenuation time of a AZX nucleus with Lorentz factor
.
We also follow Rachen (1996) for the pair production cross-section, including corrections to the formulæ of Blumenthal (1970). The attenuation time of a AZX nucleus with Lorentz factor 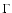 is related to that of the proton,
is related to that of the proton,
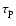 ,
as:
,
as:
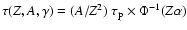 ,
where
,
where 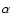 is the fine structure constant and
is the fine structure constant and
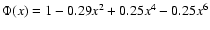 .
.
The propagation of all the nuclei (distributed in energy according to the source spectrum) is simulated with a Monte-Carlo code taking the above processes into account. We keep track of all secondary nuclei emitted and propagate them in the same way. It is assumed that each ejected fragment (or nucleon) takes away the same energy per nucleon as the parent nucleus, so that it has the same Lorentz factor. In addition to the CMB, we include the IRB as described in Malkan & Stecker (1998):
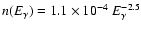 for
for
 eV. The resulting mean free path for a nucleus with Lorentz factor
eV. The resulting mean free path for a nucleus with Lorentz factor 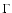 is given by:
is given by:
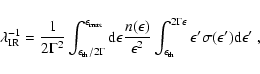 |
(1) |
where
 is the energy threshold of the process under consideration and
is the energy threshold of the process under consideration and
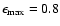 eV.
eV.
The total mean free path of 56Fe nuclei against the various photo-nuclear processes in the CMB and IRB is shown in Fig. 1a as a function of 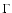 .
The GDR process clearly dominates up to
.
The GDR process clearly dominates up to
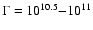 and is responsible for the main GZK effect for nuclei (sudden reduction of the flux). In Fig. 1b, we show the length scale of energy losses for protons, He, O and Fe nuclei at the source, defined as the propagation length,
and is responsible for the main GZK effect for nuclei (sudden reduction of the flux). In Fig. 1b, we show the length scale of energy losses for protons, He, O and Fe nuclei at the source, defined as the propagation length,
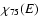 ,
after which a nucleus of initial energy E has lost 25% of its energy (including photo-pair production). The error bars indicate the dispersion due to the stochastic propagation, emphasizing the importance of a Monte-Carlo approach.
As can be seen, the drastic reduction of the propagation horizon, due to the GDR, occurs at different energies for different nuclei and is much more pronounced for heavy nuclei than for protons.
It should be stressed that, while the GZK effect appears stronger for nuclei than for protons, nuclei photoerosion products contribute to the EGCR flux at lower energies and substantially modify the shape of the spectrum. This leads to important changes in the global phenomenology of EGCRs, as we now discuss.
,
after which a nucleus of initial energy E has lost 25% of its energy (including photo-pair production). The error bars indicate the dispersion due to the stochastic propagation, emphasizing the importance of a Monte-Carlo approach.
As can be seen, the drastic reduction of the propagation horizon, due to the GDR, occurs at different energies for different nuclei and is much more pronounced for heavy nuclei than for protons.
It should be stressed that, while the GZK effect appears stronger for nuclei than for protons, nuclei photoerosion products contribute to the EGCR flux at lower energies and substantially modify the shape of the spectrum. This leads to important changes in the global phenomenology of EGCRs, as we now discuss.
![\begin{figure}
\par\mbox{\includegraphics[width=7.3cm,clip]{He272_f2a.eps}\hspace*{1cm}
\includegraphics[width=7.3cm,clip]{He272_f2b.eps} }
\end{figure}](/articles/aa/full/2005/45/aahe272/Timg43.gif) |
Figure 2:
Left: propagated spectra for sources with protons only and
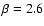 ,
and with mixed compositions and ,
and with mixed compositions and
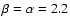 and 2.3. Data points from the main experiments are indicated, with an arbitrary downward shift of AGASA's energy scale by 20%. Right: evolution of the spectrum with the fraction of protons at the source, for an E-2.6 source spectrum.
and 2.3. Data points from the main experiments are indicated, with an arbitrary downward shift of AGASA's energy scale by 20%. Right: evolution of the spectrum with the fraction of protons at the source, for an E-2.6 source spectrum. |
| Open with DEXTER |
In Fig. 2a, we show the resulting propagated spectra obtained with the prescription described above where
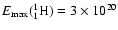 eV. The error bars represent the 1-
eV. The error bars represent the 1-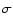 fluctuations of the flux in each energy bin, as expected for a data set with the statistics of the AGASA experiment, i.e., 866 events above 1019 eV (cf. De Marco et al. 2004). We compare our results with the data from HiRes (Abbasi et al. 2004) and AGASA (Takeda et al. 2003) experiments. In the pure proton case, we find again that the best fit spectrum has
fluctuations of the flux in each energy bin, as expected for a data set with the statistics of the AGASA experiment, i.e., 866 events above 1019 eV (cf. De Marco et al. 2004). We compare our results with the data from HiRes (Abbasi et al. 2004) and AGASA (Takeda et al. 2003) experiments. In the pure proton case, we find again that the best fit spectrum has
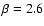 and a pair production dip, as in previous work. However, if the composition is mixed, the choice of
and a pair production dip, as in previous work. However, if the composition is mixed, the choice of
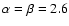 (corresponding to 24% of protons at the source above 1018 eV) provides a very poor fit to the data (cf. Fig. 2b, lower curve). Figure 2b shows how the spectrum around the ankle and the GZK bump evolves with the fraction of protons in the source composition (above 1018 eV). For fractions lower than 75%, the pair production dip is strongly attenuated and the ankle is actually reversed for fractions lower than
(corresponding to 24% of protons at the source above 1018 eV) provides a very poor fit to the data (cf. Fig. 2b, lower curve). Figure 2b shows how the spectrum around the ankle and the GZK bump evolves with the fraction of protons in the source composition (above 1018 eV). For fractions lower than 75%, the pair production dip is strongly attenuated and the ankle is actually reversed for fractions lower than 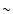 60%. Therefore, the interpretation of the ankle as an e+ - e- pair production dip requires a very large fraction of protons at the source (see also Berezinsky et al. 2005). In contrast, Fig. 2a shows two good fits to the highest energy data using mixed composition models with
60%. Therefore, the interpretation of the ankle as an e+ - e- pair production dip requires a very large fraction of protons at the source (see also Berezinsky et al. 2005). In contrast, Fig. 2a shows two good fits to the highest energy data using mixed composition models with
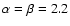 or 2.3, corresponding to 50% or 40% protons at the source, respectively. Note that the observed composition on Earth is much lighter than at the source, because of the massive production of secondary nucleons peaking around
or 2.3, corresponding to 50% or 40% protons at the source, respectively. Note that the observed composition on Earth is much lighter than at the source, because of the massive production of secondary nucleons peaking around
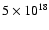 eV and the successive cut-offs of nuclei with increasing mass (Allard 2004).
For the mixed composition cases we studied in Fig. 2b, helium is the second most abundant element at the source (except in the case of
eV and the successive cut-offs of nuclei with increasing mass (Allard 2004).
For the mixed composition cases we studied in Fig. 2b, helium is the second most abundant element at the source (except in the case of
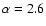 ). If a heavier nucleus, like iron, is the second most abundant observed nucleus, as claimed by the Hires Elongation rate (
). If a heavier nucleus, like iron, is the second most abundant observed nucleus, as claimed by the Hires Elongation rate (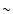 20% iron), the ankle cannot be explained solely by the proton pair production dip. In this case the ankle is partially due to the transition between CGR and ECGR and the proton pair production dip (Allard et al. 2005).
20% iron), the ankle cannot be explained solely by the proton pair production dip. In this case the ankle is partially due to the transition between CGR and ECGR and the proton pair production dip (Allard et al. 2005).
As can be seen in Fig. 2a, the pure proton model with
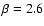 provides a good fit to the data down to
provides a good fit to the data down to 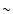 1018 eV (in a scenario with uniform source distribution and no magnetic field). In such a model, the transition from GCR to EGCR should occur at lower energies around the second knee (Berezinsky et al. 2004). However, most acceleration processes yield spectra harder than
1018 eV (in a scenario with uniform source distribution and no magnetic field). In such a model, the transition from GCR to EGCR should occur at lower energies around the second knee (Berezinsky et al. 2004). However, most acceleration processes yield spectra harder than
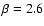 .
Analytical and numerical studies of particle acceleration in relativistic shocks give injection spectra with
.
Analytical and numerical studies of particle acceleration in relativistic shocks give injection spectra with
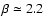 -2.3 (Bednarz & Ostrowski 1998; Kirk et al. 2000; Lemoine & Pelletier 2003). As shown in Fig. 2a, such spectral indices can provide equally good fits to the high energy data, assuming a realistic source model with a mixed composition and
-2.3 (Bednarz & Ostrowski 1998; Kirk et al. 2000; Lemoine & Pelletier 2003). As shown in Fig. 2a, such spectral indices can provide equally good fits to the high energy data, assuming a realistic source model with a mixed composition and
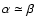 .
In such a scenario, the transition from GCRs to EGCRs occurs at the ankle, which thus keeps its "standard'' interpretation.
.
In such a scenario, the transition from GCRs to EGCRs occurs at the ankle, which thus keeps its "standard'' interpretation.
In conclusion, our calculations show that the phenomenological interpretation of the CR data at high energy strongly depends on the source composition. We confirm that pure proton sources require a steep spectrum 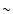 E-2.6 and can account for the ankle down to 1018 eV, interpreted as a pair production dip of the EGCR component. On the other hand, if the EGCRs are accelerated out of the interstellar medium with a source composition roughly similar to that of the GCRs, we find that a harder source spectrum
E-2.6 and can account for the ankle down to 1018 eV, interpreted as a pair production dip of the EGCR component. On the other hand, if the EGCRs are accelerated out of the interstellar medium with a source composition roughly similar to that of the GCRs, we find that a harder source spectrum 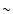 E-2.2 gives an equally good fit to the data, allowing the interpretation of the ankle as the transition from GCRs to EGCRs, with the GCR component extending up to
E-2.2 gives an equally good fit to the data, allowing the interpretation of the ankle as the transition from GCRs to EGCRs, with the GCR component extending up to 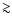 1018 eV.
1018 eV.
These results are interesting for several reasons. First, a source spectrum with
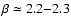 appears quite plausible from the theoretical point of view (relativistic shock acceleration). Second, a source spectrum
appears quite plausible from the theoretical point of view (relativistic shock acceleration). Second, a source spectrum 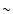 E-2.3 has also been considered as the best fit to the low-energy data for the GCR component (e.g. Strong & Moskalenko 2001; Ptuskin 1997). It is thus particularly interesting to note that assuming a similar composition for both the GCR and EGCR components is precisely what makes a similar source spectrum possible. In addition, it has been shown in Parizot (2005) that a source power-law index of
E-2.3 has also been considered as the best fit to the low-energy data for the GCR component (e.g. Strong & Moskalenko 2001; Ptuskin 1997). It is thus particularly interesting to note that assuming a similar composition for both the GCR and EGCR components is precisely what makes a similar source spectrum possible. In addition, it has been shown in Parizot (2005) that a source power-law index of 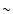 2.3 is a necessary condition for holistic models, in which the same sources produce the CRs at all energies. The results presented here show that a self-consistent model can be built for CRs with a similar composition and spectrum at all energies provided the GCR/EGCR transition is at the ankle.
2.3 is a necessary condition for holistic models, in which the same sources produce the CRs at all energies. The results presented here show that a self-consistent model can be built for CRs with a similar composition and spectrum at all energies provided the GCR/EGCR transition is at the ankle.
Acknowledgements
We thank Maximo Ave and Alan Watson for useful comments. This work was supported in part by the KICP under NSF PHY-0114422, by NSF AST-0071235, and DE-FG0291-ER40606 at the University of Chicago.
- Abbasi, R. U.,
Abu-Zayyad, T., Amann, J. F., et al. (HiRes) 2004, Phys. Rev.
Lett., 92, 151 101
(In the text)
- Abbasi, R. U.,
Abu-Zayyad, T., Archbold, G., et al. (HiRes) 2005, ApJ, 622,
910
(In the text)
- Allard, D.
2004, Ph.D. Thesis, Université Paris VI
(In the text)
- Allard et al.
2005, in preparation
(In the text)
- Aloisio, R.,
& Berezinsky, V. S. 2004,
[arXiv:astro-ph/0412578]
(In the text)
-
Berezinsky, V. S., Gazizov, A. Z., & Grigorieva S. I. 2002,
[arXiv:astro-ph/0204357]
(In the text)
-
Berezinsky, V. S., Gazizov, A. Z., & Grigorieva, S. I. 2005,
Phys. Lett. B, 612, 147 [NASA ADS] (In the text)
- Bednarz, J.,
& Ostrowski, M. 1998, Phys. Rev. Lett., 80, 3911 [NASA ADS] [CrossRef] (In the text)
-
Blumenthal, R. G. 1970, Phys. Rev. D, 1, 1596 [NASA ADS] [CrossRef] (In the text)
- De Marco,
D., Blasi, P., & Olinto, A. 2003, Astropart. Phys., 20, 53 [NASA ADS] [CrossRef]
-
Duvernois, M. A., & Thayer, M. R. 1996, ApJ, 465, 982 [NASA ADS] [CrossRef] (In the text)
- Greisen, K.
1966, Phys. Rev. Lett., 16, 748 [NASA ADS] [CrossRef] (In the text)
- Khan, E., Goriely,
S., & Allard, D., et al. 2005, Astropart. Phys., 23, 191 [NASA ADS] [CrossRef] (In the text)
- Kirk, J. G.,
Guthmann, A. W., Gallant, Y. A., & Achterberg, A. 2000, ApJ,
542, 235 [NASA ADS] [CrossRef] (In the text)
- Lemoine, M.,
& Pelletier, G. 2003, ApJ, 589, L73 [NASA ADS] [CrossRef] (In the text)
- Lemoine, M.
2005, Phys. Rev. D, 71, 083007 [NASA ADS] [CrossRef]
- Malkan, M. A.,
& Stecker, F. W. 1998, ApJ, 496, 982 (In the text)
- Parizot, E.
2005, in New Views on the Universe, Proc. of the Vth Rencontres du
Vietnam, Hanoi, 2004, [arXiv:astro-ph/0501274]
(In the text)
- Ptuskin, V.
S. 1997, Adv. in Space Res., 19, 697 [NASA ADS] (In the text)
- Puget, J. L.,
Stecker, F. W., & Bredekamp, J. H. 1976, ApJ, 205, 638 [NASA ADS] [CrossRef] (In the text)
- Rachen, J. P.
1996, Ph.D. Thesis of the Bonn University
(In the text)
- Strong, A.,
& Moskalenko, I. 2001, Adv. Space Res., 27, 717 [NASA ADS] (In the text)
- Takeda, M. et
al. (AGASA) 2003, in Proc. of the 28th ICRC (Tsukuba) 1, 381 and
Astroparticle Phys., 2003, 19, 447
(In the text)
- Zatsepin,
G. T., & Kuzmin, V. A. 1966, Sov. Phys. JETP Lett., 4, 78 (In the text)
Copyright ESO 2005
![\begin{figure}
\par\mbox{\includegraphics[height=5.5cm]{He272_f1a.eps}\hspace*{8mm}
\includegraphics[height=5.5cm]{He272_f1b.eps} }
\end{figure}](/articles/aa/full/2005/45/aahe272/Timg24.gif)
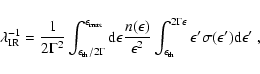
![\begin{figure}
\par\mbox{\includegraphics[width=7.3cm,clip]{He272_f2a.eps}\hspace*{1cm}
\includegraphics[width=7.3cm,clip]{He272_f2b.eps} }
\end{figure}](/articles/aa/full/2005/45/aahe272/Timg43.gif)