We study the relation between the mean effective surface temperature
A&A 443, 1025-1028 (2005)
DOI: 10.1051/0004-6361:20053628
A. Y. Potekhin1,2,3 - V. Urpin2,3 - G. Chabrier1
1 -
École Normale Supérieure de Lyon
(CRAL, CNRS UMR 5574),
46 allée d'Italie, 69364 Lyon Cedex 07, France
2 -
Ioffe Physico-Technical Institute,
Politekhnicheskaya 26, 194021 St. Petersburg, Russia
3 -
Isaac Newton Institute of Chile, St. Petersburg Branch, Russia
Received 14 June 2005 / Accepted 9 August 2005
Abstract
We study the relation between the mean effective surface
temperature
![]() and the internal temperature
and the internal temperature ![]() for magnetic
neutron stars, assuming that the magnetic field near the surface has
a small-scale structure. The heavy-element (iron) and
light-element (accreted) heat-blanketing envelopes are considered,
and the results are compared with the case of a dipole magnetic field.
We argue that the difference in the
for magnetic
neutron stars, assuming that the magnetic field near the surface has
a small-scale structure. The heavy-element (iron) and
light-element (accreted) heat-blanketing envelopes are considered,
and the results are compared with the case of a dipole magnetic field.
We argue that the difference in the
![]() -relation for
different magnetic configurations is always much smaller than the
possible difference caused by variations of the chemical composition
in the envelope.
-relation for
different magnetic configurations is always much smaller than the
possible difference caused by variations of the chemical composition
in the envelope.
Key words: stars: neutron - stars: magnetic fields - dense matter - conduction - pulsars: general
The most direct evidence for the nature of a poorly known
superdense matter in neutron stars is likely to emerge from
comparisons of surface thermal radiation measurements with
predictions of neutron star cooling models (e.g.,
Page 1997; Pethick 1992; Yakovlev & Pethick 2004; Page 1998).
Modeling of neutron
star cooling is a complex problem that, generally, requires
calculations of the temperature profile from the surface to the
core at various stages of the evolution. The temperature profile
for nonmagnetic neutron stars has been the subject of study for
many authors (e.g., Gudmundsson et al. 1983; Potekhin et al. 1997; Nomoto & Tsuruta 1987,
and references therein).
The key issue of these
studies is the so-called
![]() -relation used in cooling
models (
-relation used in cooling
models (![]() and
and ![]() are the surface and internal
temperature, respectively).
are the surface and internal
temperature, respectively).
Most of the neutron stars, however, possess surface magnetic
fields
![]() G, and some neutron stars are
possibly magnetars with
G, and some neutron stars are
possibly magnetars with
![]() G. The internal
magnetic field can be even higher. Such strong fields can
affect the properties of plasma in neutron stars and
alter the
G. The internal
magnetic field can be even higher. Such strong fields can
affect the properties of plasma in neutron stars and
alter the
![]() -relation.
In general, the magnetic field strength and direction varies over the
stellar surface, and hence
-relation.
In general, the magnetic field strength and direction varies over the
stellar surface, and hence ![]() may be different
for different surface points. In many applications (e.g., in the
neutron-star cooling theory) it is sufficient to know
the mean effective surface temperature
may be different
for different surface points. In many applications (e.g., in the
neutron-star cooling theory) it is sufficient to know
the mean effective surface temperature
![]() instead of
the position-dependent
instead of
the position-dependent ![]() .
The effective temperature is defined by the Stefan law,
.
The effective temperature is defined by the Stefan law,
![]() where
where ![]() is the Stefan-Boltzmann constant,
and L is the thermal luminosity in a local
neutron-star reference frame, integrated over the surface.
The apparent luminosity
measured by a distant observer is
is the Stefan-Boltzmann constant,
and L is the thermal luminosity in a local
neutron-star reference frame, integrated over the surface.
The apparent luminosity
measured by a distant observer is
![]() ,
and the apparent surface temperature inferred
by the observer from the radiation spectrum is
,
and the apparent surface temperature inferred
by the observer from the radiation spectrum is
![]() (e.g., Thorne 1977).
(e.g., Thorne 1977).
The effects of a strong
magnetic field on thermodynamic and kinetic properties of the
outer neutron star layers have been reviewed, for instance, by
Yakovlev & Kaminker (1994) and Ventura & Potekhin (2001).
The thermal structure of magnetized neutron stars has been
analyzed by a number of authors, often
adopting a simplified magnetic
geometry. For instance, much attention has been paid to the cases
of the radial magnetic field (e.g.,
Heyl & Hernquist 1998; Schaaf 1990; Van Riper 1988; Hernquist 1985) or
the tangential field (with the field lines parallel to the
surface; e.g.,
Heyl & Hernquist 1998; Schaaf 1990; Hernquist 1985).
The quantizing radial field field decreases
the difference between ![]() and
and ![]() ,
whereas
the tangential field increases this difference.
,
whereas
the tangential field increases this difference.
The case of an arbitrary inclination of the field lines has been
considered by Greenstein & Hartke (1983) and Page (1995) who
argued that the
![]() -relation for such a field can be
constructed in a simple way from the relations for the radial
and tangential magnetic fields. Numerical calculations
of the thermal structure (Potekhin & Yakovlev 2001; Potekhin et al. 2003) confirm an
accuracy of this approximation.
These calculations show that the
-relation for such a field can be
constructed in a simple way from the relations for the radial
and tangential magnetic fields. Numerical calculations
of the thermal structure (Potekhin & Yakovlev 2001; Potekhin et al. 2003) confirm an
accuracy of this approximation.
These calculations show that the
![]() -relation for the dipole magnetic
configuration is almost independent of the field
for
-relation for the dipole magnetic
configuration is almost independent of the field
for
![]() G.
The reason of such behaviour is the compensation of a decrease
in the thermal flux near the magnetic equator by an increase in the flux
near the pole.
G.
The reason of such behaviour is the compensation of a decrease
in the thermal flux near the magnetic equator by an increase in the flux
near the pole.
This result can essentially simplify the cooling
calculations for magnetized neutron stars
with dipole magnetic fields. It is likely, however, that the
surface magnetic field of neutron stars departs from a
dipole configuration.
Arons & Scharlemann (1979) and
Arons (1993,2000) noted that pulsars with long periods
require a more complex field configuration than a dipole if pair
creation is essential for the mechanism of radio emission.
Gil & Mitra (2001) and Gil & Melikidze (2002) also noted that radio
emission of many pulsars
can be explained if one adopts
the model with a strong (
![]() G) and complex surface field
with a small curvature of the field lines (
G) and complex surface field
with a small curvature of the field lines (
![]() cm).
Gil & Sendyk (2000) found that the behaviour
of drifting subpulses observed in many pulsars is
consistent with the vacuum gap maintained by a strong sunspot-like
magnetic field.
Recent observations of the X-ray spectra
of some pulsars provide an opportunity to estimate the
magnetic field near the neutron star surface. For example, a possible
interpretation of the feature observed in the spectrum of PSR B1821-24
as a cyclotron emission (Becker et al. 2003; see, however,
Mineo et al. 2004) indicates
that the local magnetic fields on the neutron
star surface can exceed the conventional dipole field
inferred from the spin-down data.
cm).
Gil & Sendyk (2000) found that the behaviour
of drifting subpulses observed in many pulsars is
consistent with the vacuum gap maintained by a strong sunspot-like
magnetic field.
Recent observations of the X-ray spectra
of some pulsars provide an opportunity to estimate the
magnetic field near the neutron star surface. For example, a possible
interpretation of the feature observed in the spectrum of PSR B1821-24
as a cyclotron emission (Becker et al. 2003; see, however,
Mineo et al. 2004) indicates
that the local magnetic fields on the neutron
star surface can exceed the conventional dipole field
inferred from the spin-down data.
The growing evidence for the distinction between the
local field strength at the stellar surface and the global
dipole field suggests that this can be a general phenomenon in
neutron stars. Several theoretical explanations of this
phenomenon were suggested.
Ruderman (1991) considered a "plate tectonics'' model,
in which a complex configuration of the surface magnetic field
of a neutron star is a result of neutron-star crust cracking
and platelet movements.
Ruderman et al. (1998) found that this model agrees with
observations of pulsar glitches.
Geppert et al. (2003) suggested a Hall-driven mechanism of
the formation of the sunspot-like magnetic-field structure
at the neutron-star surface.
The presence of
small scale field components can also be
generated during the initial convective stage of evolution, e.g.,
by the turbulent mean-field dynamo
(Bonanno et al. 2005,2003; Thompson & Duncan 1993).
The unstable stage in proto-neutron stars lasts
![]() -40 s, which is sufficient for a dynamo to reach a
saturation level.
The magnetic field generated
in proto-neutron stars will be frozen into the
crust that starts to form almost immediately after convection
stops. Since the crustal conductivity is high, both the large and
relatively small scale (
-40 s, which is sufficient for a dynamo to reach a
saturation level.
The magnetic field generated
in proto-neutron stars will be frozen into the
crust that starts to form almost immediately after convection
stops. Since the crustal conductivity is high, both the large and
relatively small scale (
![]() cm) fields can survive during a long time comparable to
the lifetime of pulsars,
cm) fields can survive during a long time comparable to
the lifetime of pulsars,
![]() yr (Urpin & Gil 2004).
yr (Urpin & Gil 2004).
If the dipole field in neutron stars is accompanied by a stronger
small-scale field, then the thermal structure of
the surface layers can be changed qualitatively.
For instance, the difference between the equator
and polar temperature should be much reduced.
The small-scale field can also affect the
total photon flux at given ![]() - that is the
- that is the
![]() relation.
In this paper, we consider the thermal structure
and calculate the
relation.
In this paper, we consider the thermal structure
and calculate the
![]() relation in the case of a neutron star
with a strong small-scale magnetic field in the envelope.
relation in the case of a neutron star
with a strong small-scale magnetic field in the envelope.
The thermal structure of the neutron star envelope is considered in
a steady state plane-parallel approximation.
We assume that ![]() is equal to the temperature at the
inner boundary of the envelope (taken at the neutron drip
density
is equal to the temperature at the
inner boundary of the envelope (taken at the neutron drip
density
![]() g cm-3) and does not
vary over this boundary.
g cm-3) and does not
vary over this boundary.
The statement of the problem for calculations of the temperature
profile in neutron star envelopes has been described in detail by
Potekhin et al. (2003). In the present study, the only difference
is the expression for the heat flux, that should
incorporate the effect of small-scale magnetic fields. In the
magnetic field ![]() ,
the heat flux is related to the
temperature gradient by
,
the heat flux is related to the
temperature gradient by
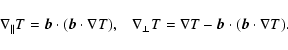 |
(2) |
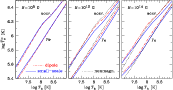 |
Figure 1:
The redshifted effective surface temperature
versus the internal temperature for a canonical neutron star
(
|
| Open with DEXTER | |
We calculate the thermal structure of a neutron star envelope by integrating Eq. (3) with the use of the numerical scheme developed previously (Potekhin et al. 2003,1997). We examine models of envelopes composed of iron and accreted material. The accreted envelope is assumed to be the same as described by Potekhin et al. (1997): the surface H layer is followed by He, C, O, and Fe layers. The physics input (equation of state, radiative opacities, and electron thermal conductivities) is described in Potekhin et al. (2003). Note some uncertainty of this input for the outermost layer of the iron envelope where Fe plasma is only partly ionized. In this case, the equation of state and opacities are based on the Thomas-Fermi and mean-ion approximations. For the accreted envelope, in contrast, we use the accurate equation of state and opacities for the partially ionized hydrogen plasma in a strong magnetic field (Potekhin & Chabrier 2004, and references therein).
The calculated temperature profiles and their dependences on Band ![]() are quite similar to those presented in Potekhin et al. (2003).
Therefore we will not describe the results in detail but focus on the
comparison of the
are quite similar to those presented in Potekhin et al. (2003).
Therefore we will not describe the results in detail but focus on the
comparison of the
![]() relation for the small-scale and
dipole fields.
relation for the small-scale and
dipole fields.
Examples of such a comparison are shown
in Figs. 1 and 2.
The panels (from left to right)
in Fig. 1
correspond to B=108 G, 1012 G, and 1014 G,
typical for millisecond pulsars, ordinary radio pulsars and
anomalous X-ray pulsars, respectively; B is the average field
strength in the case of a small-scale field and the field at the
magnetic pole in the dipole field model. For convenience, the
non-magnetic
![]() -relations are shown in the middle and right
panels of Fig. 1 by the dotted lines.
-relations are shown in the middle and right
panels of Fig. 1 by the dotted lines.
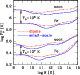 |
Figure 2:
The dependence of the mean effective temperature on B
for the dipole (dot-dash lines) and small-scale (solid lines)
fields. The curves are shown for the accreted and iron envelopes
and the internal temperature
|
| Open with DEXTER | |
Figure 2 shows the dependence of
![]() on B for different models and for two
on B for different models and for two ![]() values.
Independent of the field geometry, a weak field (
values.
Independent of the field geometry, a weak field (![]() G)
does
not affect the
G)
does
not affect the
![]() -relation for both the iron
and accreted envelopes.
With increasing B, the effective temperature
first decreases and then increases
nonmonotonically. This behaviour is explained as follows.
The value of
-relation for both the iron
and accreted envelopes.
With increasing B, the effective temperature
first decreases and then increases
nonmonotonically. This behaviour is explained as follows.
The value of ![]() at a given
at a given ![]() is controlled mainly
by the opacity values in the "sensitivity strip'' (Gudmundsson et al. 1983)
located typically at
is controlled mainly
by the opacity values in the "sensitivity strip'' (Gudmundsson et al. 1983)
located typically at
![]() -108 g cm-3,
where heat transport is provided by the electron conduction.
In a strong magnetic field, the electron thermal conductivity
as a function of
-108 g cm-3,
where heat transport is provided by the electron conduction.
In a strong magnetic field, the electron thermal conductivity
as a function of ![]() undergoes oscillations when
the electron Fermi energy crosses the magnetic Landau levels
(see, e.g., Ventura & Potekhin 2001; Yakovlev & Kaminker 1994).
The first oscillation at
undergoes oscillations when
the electron Fermi energy crosses the magnetic Landau levels
(see, e.g., Ventura & Potekhin 2001; Yakovlev & Kaminker 1994).
The first oscillation at
![]() g cm-3 is
the strongest one (here
g cm-3 is
the strongest one (here
![]() G and
A and Z are the atomic weight and charge numbers);
the classical (non-oscillating) magnetic electron conductivity
is recovered at
G and
A and Z are the atomic weight and charge numbers);
the classical (non-oscillating) magnetic electron conductivity
is recovered at
![]() .
In Fig. 2,
a decrease of
.
In Fig. 2,
a decrease of
![]() first occurs in the classical
regime, where the effect of the magnetic field amounts to
a suppression of
first occurs in the classical
regime, where the effect of the magnetic field amounts to
a suppression of
![]() in Eq. (3).
With further increase of B, the field becomes quantizing
in the sensitivity strip, leading to an increase of
in Eq. (3).
With further increase of B, the field becomes quantizing
in the sensitivity strip, leading to an increase of
![]() .
The increasing pieces of curves in Fig. 2
are wavy because of quantum oscillations
of
.
The increasing pieces of curves in Fig. 2
are wavy because of quantum oscillations
of
![]() ,
which are smoothed (but not entirely)
by the integration of Eq. (3) over the sensitivity strip.
,
which are smoothed (but not entirely)
by the integration of Eq. (3) over the sensitivity strip.
In the case of the dipole magnetic field,
the differences between the magnetic and
nonmagnetic
![]() -relations become appreciable only in a
very strong magnetic field,
-relations become appreciable only in a
very strong magnetic field,
![]() G, and if the internal
temperature is relatively low,
G, and if the internal
temperature is relatively low,
![]() K. In this case,
K. In this case,
![]() is noticeably increased by the magnetic field.
The increase of a
mean effective temperature is however quite moderate in
a comparison to the effect of such a strong field on the local
temperature value: a significant increase of
is noticeably increased by the magnetic field.
The increase of a
mean effective temperature is however quite moderate in
a comparison to the effect of such a strong field on the local
temperature value: a significant increase of ![]() at the magnetic pole
and a sharp decrease at the equator (see, e.g., Potekhin & Yakovlev 2001; Potekhin et al. 2003).
For lower magnetic field and higher temperature,
the difference in the magnetic geometry does not yield a considerable
departure in the
at the magnetic pole
and a sharp decrease at the equator (see, e.g., Potekhin & Yakovlev 2001; Potekhin et al. 2003).
For lower magnetic field and higher temperature,
the difference in the magnetic geometry does not yield a considerable
departure in the
![]() -relation.
-relation.
The difference
in a magnetic configuration can manifest itself
at
![]() G.
The small-scale field, as a rule, results in a lower
G.
The small-scale field, as a rule, results in a lower
![]() at a given B compared to the dipole field. The difference in
at a given B compared to the dipole field. The difference in
![]() for the small-scale and dipole fields depends generally
on
for the small-scale and dipole fields depends generally
on ![]() ,
B, and the mass of the accreted light-element material
(see Fig. 2), but never exceeds 20%.
However, this difference in
,
B, and the mass of the accreted light-element material
(see Fig. 2), but never exceeds 20%.
However, this difference in ![]() can result in a factor of
can result in a factor of ![]() in the luminosity. In all
considered models, the uncertainty in a chemical composition of
the envelope (light versus heavy elements) causes a much
larger difference in
in the luminosity. In all
considered models, the uncertainty in a chemical composition of
the envelope (light versus heavy elements) causes a much
larger difference in
![]() than the uncertainty in the magnetic
field geometry (dipole versus small-scale).
than the uncertainty in the magnetic
field geometry (dipole versus small-scale).
To estimate the effect of a small-scale magnetic field on the
![]() -relation, one can use the fitting formulae derived for
the dipole field (see the Appendix of Potekhin et al. 2003) where
-relation, one can use the fitting formulae derived for
the dipole field (see the Appendix of Potekhin et al. 2003) where
![]() and
and
![]() should be replaced
by 1/3 and 2/3, respectively. Such fit reproduces the
present numerical results with an accuracy
should be replaced
by 1/3 and 2/3, respectively. Such fit reproduces the
present numerical results with an accuracy ![]() %.
%.
We have considered the relation between the surface and internal
temperature in neutron stars in the case where small scale magnetic
fields near the surface are stronger than a large scale (e.g.,
dipole) field. Calculations show that the difference in the
![]() -relation between the stars
with small-scale and dipole fields is not very significant, although,
generally, it should be taken into account if highly accurate
thermal luminosity calculations are required.
This can be important for the interpretation of future
high-precision measurements of neutron star thermal
radiation.
-relation between the stars
with small-scale and dipole fields is not very significant, although,
generally, it should be taken into account if highly accurate
thermal luminosity calculations are required.
This can be important for the interpretation of future
high-precision measurements of neutron star thermal
radiation.
For both the small-scale and dipole fields, the departure from the thermal structure of a nonmagnetic neutron star is relatively small, if the typical field strength B<1014 G. This is caused by the fact that the increase of thermal insulation near the region where the field lines are tangential is well compensated by the decrease of the insulation in the region where the field is normal to the surface. As seen from Fig. 2, for the dipole field this compensation is generally more efficient than for the small-scale field.
For a stronger field, an increase of the thermal conductivity along the field lines due to the magnetic quantization effects turns out to be so strong that it cannot be fully compensated by a decrease of the conductivity in the perpendicular direction.
Our results indicate that the geometry and strength of
the magnetic field are likely unimportant for the average thermal
structure of neutron stars, if the field strength is moderate
(
![]() .
Therefore, a magnetic field of moderate
strength can affect the neutron star cooling via Joule heating
rather than via the
.
Therefore, a magnetic field of moderate
strength can affect the neutron star cooling via Joule heating
rather than via the
![]() -relation. Joule heating is of
particular importance at the late evolutionary stage and can
maintain a relatively high surface temperature
-relation. Joule heating is of
particular importance at the late evolutionary stage and can
maintain a relatively high surface temperature
![]() K
for a long time, comparable to the decay time of the
magnetic field (Miralles et al. 1998).
K
for a long time, comparable to the decay time of the
magnetic field (Miralles et al. 1998).
Acknowledgements
The work of A.Y.P. and G.C. was partially supported by the CNRS French-Russian grant PICS 3202. The work of A.Y.P. was also supported in part by the RLSS grant 1115.2003.2 and the RFBR grants 05-02-16245, 03-07-90200 and 05-02-22003.