A&A 443, 793-804 (2005)
DOI: 10.1051/0004-6361:20053166
R. Gavazzi1,2
1 - Institut d'Astrophysique de Paris, UMR 7095, 98bis Bd Arago,
75014 Paris, France
2 - Laboratoire d'Astrophysique, OMP, UMR
5572, 14 Av. Edouard Belin, 31400 Toulouse, France
Received 31 March 2005 / Accepted 28 June 2005
Abstract
We revisit the mass properties of the lensing cluster of galaxies
MS2137-23 and assess the mutual agreement between cluster mass
estimates based on strong/weak lensing, X-rays and stellar dynamics.
We perform a thorough elliptical lens modelling using arcs and their
counter-images in the range
![]() kpc and weak
lensing (
kpc and weak
lensing (
![]() kpc). We confirm that the dark
matter distribution is consistent with an NFW profile (Navarro et al. 1997, ApJ, 490, 493)
with high concentration
kpc). We confirm that the dark
matter distribution is consistent with an NFW profile (Navarro et al. 1997, ApJ, 490, 493)
with high concentration
![]() .
.
We further analyse stellar kinematics data with
a detailed modelling of the line-of-sight velocity distribution
(LOSVD) of stars in the cD galaxy and quantify the small bias due to
the non-Gaussian shape of the LOSVD. After correction, the NFW lens
model is unable to properly fit kinematical data and is a factor of
![]() 2 more massive than suggested by X-rays analysis.
2 more massive than suggested by X-rays analysis.
The discrepancy between projected (lensing) and tridimensional
(X-rays, dynamics) mass estimates is studied by assuming prolate (triaxial)
halos with the major axis oriented toward the line-of-sight. This model
well explains the high concentration and the misalignement between stellar
and dark matter components
![]() .
.
We then calculate the systematic and statistical uncertainties in the
relative normalization between the cylindric M2(<r) and spherical
M3(<r) mass estimates for triaxial halos. These uncertainties prevent any
attempt to couple 2D and 3D constraints without undertaking a complete
tridimensional analysis. Such asphericity/projection effects should be
a major concern for comparisons between lensing and X-rays/dynamics
mass estimates.
Key words: cosmology: dark matter - galaxies: clusters: individual: MS2137 - galaxies: elliptical and lenticular, cD - gravitational lensing - galaxies: kinematics and dynamics - galaxies: clusters: general
Most CDM simulations predict a universal profile of the general form:
The global agreement between observations and simulations is subject to
controversy. The inner slope of dark matter halos of low surface
brightness (LSB) dwarf galaxies as inferred from rotation curves tends
to favor soft cores with
![]() (e.g. Salucci 2001; de Blok et al. 2003; Gentile et al. 2004),
leading to the so-called cusp-core
debate. Many observations have focused on LSB galaxies because their
baryonic content can be neglected and the dark matter distribution in
the halo matches simulations. However, departures from axisymmetry
(triaxial halos) make the interpretation of rotation curves more
complex and could reconcile observations and CDM predictions
(Hayashi et al. 2004). The question of the very central mass profile on
dwarfs scales is still open.
(e.g. Salucci 2001; de Blok et al. 2003; Gentile et al. 2004),
leading to the so-called cusp-core
debate. Many observations have focused on LSB galaxies because their
baryonic content can be neglected and the dark matter distribution in
the halo matches simulations. However, departures from axisymmetry
(triaxial halos) make the interpretation of rotation curves more
complex and could reconcile observations and CDM predictions
(Hayashi et al. 2004). The question of the very central mass profile on
dwarfs scales is still open.
A similar discrepancy at clusters of galaxies scales
is claimed by Sand et al. (2004, hereafter Sa04,2002). Using HST
images (allowing the modelling of strong gravitational lensing
configurations) together with Keck spectroscopy (providing the radial
velocity dispersion of stars in the central cD galaxy of the cluster,
the BCG) on a sample of six clusters, these authors found that the
inner slope of the dark matter halo must be significantly flatter than
that measured in simulations. Typically, on a subsample of three
clusters with radial arcs, they found an inner slope
![]() (68%CL). This result takes advantage of the
joint constraints provided by lensing and stellar kinematics. However,
the lensing part of the analysis of Sa04 has been independently
discussed by Bartelmann & Meneghetti (2004) and Dalal & Keeton (2003) because they
did not take into account the lens ellipticity when using the
critical lines radii as a constraint on the density profile.
These two latter authors found that the mass profile is consistent
with an NFW model. The analysis of Sa04 couples 2D projected (from
lensing that deals with mass enclosed in the cylinder of radius R)
and 3D tridimensional (from stellar dynamics which give an indirect
information on the mass enclosed in the sphere of radius r) mass estimates.
(68%CL). This result takes advantage of the
joint constraints provided by lensing and stellar kinematics. However,
the lensing part of the analysis of Sa04 has been independently
discussed by Bartelmann & Meneghetti (2004) and Dalal & Keeton (2003) because they
did not take into account the lens ellipticity when using the
critical lines radii as a constraint on the density profile.
These two latter authors found that the mass profile is consistent
with an NFW model. The analysis of Sa04 couples 2D projected (from
lensing that deals with mass enclosed in the cylinder of radius R)
and 3D tridimensional (from stellar dynamics which give an indirect
information on the mass enclosed in the sphere of radius r) mass estimates.
Comparing lensing and X-rays cluster mass estimates is another way to
couple 2D and 3D mass constraints. The overall agreement between X mass
and the mass enclosed in the Einstein radius of clusters has been addressed
by various authors (Wu 2000; Smith et al. 2005; Miralda-Escude & Babul 1995; Allen 1998; Arabadjis et al. 2004).
In most cases, depending on the presence of cooling flows or
the degree of relaxation of the cluster, strong lensing mass estimates
are often larger by a factor ![]() 1.5. With better S/N data, there is
increasing evidence that the assumption of spherical symmetry is
oversimplistic and may play a important role in this systematic trend
(Piffaretti et al. 2003; De Filippis et al. 2005; Hennawi et al. 2005; Oguri et al. 2005).
1.5. With better S/N data, there is
increasing evidence that the assumption of spherical symmetry is
oversimplistic and may play a important role in this systematic trend
(Piffaretti et al. 2003; De Filippis et al. 2005; Hennawi et al. 2005; Oguri et al. 2005).
In this paper, we focus on the density profile of the cluster MS2137-21 which is part of the Sa04 sample and search for further evidence for triaxiality in this peculiar cluster. In Sect. 2 we present the strong and weak lensing modelling of MS2137 with a NFW model and show that it is consistent with all the lensing data at hand from 10 kiloparsec to 1 megaparsec. In Sect. 3 we develop a detailed method for the analysis of stellar kinematics and apply it to the best fit NFW model derived in the previous section. We then discuss the overall agreement between lensing mass estimates and the constraints from the stellar kinematics and X-rays observations of Allen et al. (2001). In Sect. 4 we investigate the origin of the systematic overerestimate of lensing mass estimates as compared to that of 3D analyses, and show that the tridimensional shape of halos (prolate, triaxial) is likely to explain such discrepancies. In Sect. 5 we calculate the statistical properties of the relative normalization between 2D and 3D mass estimates of triaxial halos. We discuss our results and conclude in Sect. 6.
Throughout this paper, we assume a
![]() ,
,
![]() and
and
![]() ,
leading to the scaling
,
leading to the scaling
![]() .
.
In this section we focus on the density profile modeling using lensing
constraints only. The lens properties of the cluster of galaxies have been
extensively studied (Gavazzi et al. 2003; Dalal & Keeton 2003; Bartelmann 1996; Miralda-Escudé 1995; Sand et al. 2004; Mellier et al. 1993; Hammer et al. 1997; Fort et al. 1992; Sand et al. 2002). The cluster's redshift is
zl=0.313 and both radial and tangential arcs lie at zs=1.501(Sand et al. 2002), leading to the critical surface density
![]() kpc-2.
kpc-2.
Our analysis builds on the previous work of Gavazzi et al. (2003, hereafter G03). We use 26 multiple conjugate knots in
the tangential and radial arcs systems. The method and the knot
locations are presented in G03.
Here, we inflate the uncertainties on knot positions in order to
account for possible bad associations. The mean positional error
is raised to the more realistic value
![]() .
After a more detailed analysis of images, the G03 value
.
After a more detailed analysis of images, the G03 value
![]() turns
out to be underestimated. Moreover there was a mistake in the calculation
of error bars for model parameters in this earlier paper.
The uncertainty on each knot location is increased by the same amount,
so we do not expect any change in the best fit model.
Dalal & Keeton (2003) proceeded in the same way by inflating the G03 errors to
a value of
turns
out to be underestimated. Moreover there was a mistake in the calculation
of error bars for model parameters in this earlier paper.
The uncertainty on each knot location is increased by the same amount,
so we do not expect any change in the best fit model.
Dalal & Keeton (2003) proceeded in the same way by inflating the G03 errors to
a value of
![]() which is far too much.
The error bars of G03 on the best fit parameters are larger
than the ones we present in the following although they assumed
smaller uncertainties on knots locations. This is clear evidence for
an error in the analysis. The present updated results should be considered
as correct. We also exclude constraints from the fifth
central demagnified image reported in G03 since its detection is
marginal and is not confirmed by Sa04. We use a personal ray-tracing
inversion code which includes many aspects of the lensmodel software
(Keeton 2001a,b). In particular, we adopt the same
source plane
which is far too much.
The error bars of G03 on the best fit parameters are larger
than the ones we present in the following although they assumed
smaller uncertainties on knots locations. This is clear evidence for
an error in the analysis. The present updated results should be considered
as correct. We also exclude constraints from the fifth
central demagnified image reported in G03 since its detection is
marginal and is not confirmed by Sa04. We use a personal ray-tracing
inversion code which includes many aspects of the lensmodel software
(Keeton 2001a,b). In particular, we adopt the same
source plane
![]() definition.
definition.
In addition, we simultaneously include weak lensing constraints also presented in
G03. The catalogue of background "weakly lensed'' galaxies comes from VLT/FORS
and VLT/ISAAC images for which we were able to derive a good estimate of
photometric redshifts using UBVRIJK bands. We fully compute the likelihood
as a function of model parameters (King & Schneider 2001; Schneider et al. 2000)
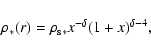 |
(5) |
Throughout the paper, we discuss the consequences of this particular choice. At this level, we expect the effect to be more important for stellar kinematics than for lensing. This can be understood because strong lensing constraints probe the total density profile well beyond the stellar scale radius where Hernquist, Jaffe or De Vaucouleur profiles are very similar (see Fig. 2 of Sa04).
| (SL) | (SL+WL) | (1) | Unit | |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
- |
|
| c |
|
|
|
|
| q |
|
|
- | |
|
|
|
- | deg | |
|
|
|
|
- |
|
The model requires a rest frame V band stellar mass-to-light ratio
![]() .
This value is in good agreement with
expectations of evolution of
.
This value is in good agreement with
expectations of evolution of
![]() Gyr old stellar
populations. The reason why the stellar mass content is so tightly
constrained is that the stellar and dark matter components are not aligned.
There is a position angle misalignment of
Gyr old stellar
populations. The reason why the stellar mass content is so tightly
constrained is that the stellar and dark matter components are not aligned.
There is a position angle misalignment of
![]() .
This was first pointed out by G03. Otherwise, there would be a degeneracy
between the relative contribution of dark matter and stars. Here the
degeneracy is broken although the contribution of stars is subdominant at all
scales (and a factor
.
This was first pointed out by G03. Otherwise, there would be a degeneracy
between the relative contribution of dark matter and stars. Here the
degeneracy is broken although the contribution of stars is subdominant at all
scales (and a factor ![]() 2 at the centre) as shown in
Fig. 3. This situation explains
the small inaccuracy in the radial arc modelling highlighted
in Sect. 4.2 of G03. By adding a small misaligned contribution of
stars at the center, one is able to twist to isopotentials and precisely
reproduce the radial arc and its counter-image. See Romanowsky & Kochanek (1998)
and Buote et al. (2002) for a similar example. We come back to this issue
in Sect. 4.4 and Appendix B.
Changing the stellar mass profile to a Jaffe model
does not make a difference. The total (misaligned) stellar mass is well fixed
by lensing.
2 at the centre) as shown in
Fig. 3. This situation explains
the small inaccuracy in the radial arc modelling highlighted
in Sect. 4.2 of G03. By adding a small misaligned contribution of
stars at the center, one is able to twist to isopotentials and precisely
reproduce the radial arc and its counter-image. See Romanowsky & Kochanek (1998)
and Buote et al. (2002) for a similar example. We come back to this issue
in Sect. 4.4 and Appendix B.
Changing the stellar mass profile to a Jaffe model
does not make a difference. The total (misaligned) stellar mass is well fixed
by lensing.
In Table 1 we present the best fit NFW model parameters
in terms of more physical quantities like the virial radius
![]() ,
the concentration parameter
,
the concentration parameter
![]() or the virial mass
or the virial mass
![]() that all derive from
that all derive from
![]() ,
,
![]() and q. At the best fit parameter
set, the minimum
and q. At the best fit parameter
set, the minimum ![]() value is
value is
![]() .
When considering strong lensing constraints only,
.
When considering strong lensing constraints only,
![]() showing that both
strong and weak lensing observations are well modeled
showing that both
strong and weak lensing observations are well modeled![]() .
The (SL) and (SL+WL) columns detail how the best fit model is changed whether
weak lensing constraints are added to the model or not. Basically, errors are
just reduced and no significant change in the best fit parameters value is
observed. Figure 2 shows the degeneracies between the
concentration parameter, virial mass, stellar mass-to-light ratio and
ellipticity (color-coded).
.
The (SL) and (SL+WL) columns detail how the best fit model is changed whether
weak lensing constraints are added to the model or not. Basically, errors are
just reduced and no significant change in the best fit parameters value is
observed. Figure 2 shows the degeneracies between the
concentration parameter, virial mass, stellar mass-to-light ratio and
ellipticity (color-coded).
Figure 3 shows the radial projected mass profile for the best
fit NFW+stellar components as well as a detail of the stellar component.
The thickness of the curves is representative of the 1![]() uncertainties.
This is done by considering many points of the MCMCs that lie within the
1-
uncertainties.
This is done by considering many points of the MCMCs that lie within the
1-![]() contour around the best fit model.
contour around the best fit model.
![\begin{figure}
\par\resizebox{12.6cm}{!}{\includegraphics[clip]{NEW/3166fg03.eps}} \end{figure}](/articles/aa/full/2005/45/aa3166-05/Timg115.gif) |
Figure 3:
Projected total mass (stars+DM) profile within
cylinder of radius R for the best fit NFW model (solid black), the
best fit general "gen'' model with
|
For the best fit model, we have
![]() ,
and
,
and
![]() .
Here again, the
.
Here again, the ![]() value
is satisfying
value
is satisfying![]() .
We found
.
We found
![]() also consistent with
stellar evolution models,
also consistent with
stellar evolution models,
![]() and
and
![]() .
The constraints on
.
The constraints on ![]() are very tight
and show that lensing is inconsistent with any soft core
are very tight
and show that lensing is inconsistent with any soft core
![]() .
However, it does not contradict the NFW behavior
.
However, it does not contradict the NFW behavior
![]() at
small scales because the fast transition 1+x2 in the "gen'' profile
differs from the NFW case (1+x). This can clearly be seen in
Fig. 3 where the projected NFW and "gen'' mass profiles
match over a broad radius range (
at
small scales because the fast transition 1+x2 in the "gen'' profile
differs from the NFW case (1+x). This can clearly be seen in
Fig. 3 where the projected NFW and "gen'' mass profiles
match over a broad radius range (
![]() ). The differences at
larger scales are still within the weak lensing uncertainties.
Consequently, we can trust the radial behavior of the lensing-deduced
mass profile of the NFW model between
). The differences at
larger scales are still within the weak lensing uncertainties.
Consequently, we can trust the radial behavior of the lensing-deduced
mass profile of the NFW model between
![]() .
Here again, changing the Hernquist stellar profile to a Jaffe model does
not change our results.
.
Here again, changing the Hernquist stellar profile to a Jaffe model does
not change our results.
Column (1) of Table 1 gives the NFW model parameters
deduced from Chandra X-ray observations of Allen et al. (2001, hereafter Al01).
The projected mass profile of their model is the orange thick curve on
Fig. 3. This NFW profile half the size of our NFW
and "gen'' models over a range
![]() (i.e. the factor 1/2 in
the value of
(i.e. the factor 1/2 in
the value of
![]() in Table 1).
At larger scales
in Table 1).
At larger scales
![]() ,
the Al01 mass profile becomes consistent
with weak lensing and our models. X-rays (Al01) and stellar dynamics (Sa04) mass
estimates agree at small scales
,
the Al01 mass profile becomes consistent
with weak lensing and our models. X-rays (Al01) and stellar dynamics (Sa04) mass
estimates agree at small scales
![]() .
.
The analysis presented in Appendix A shows that
departures from a Gaussian distribution are kept at a low level for
the lensing-deduced NFW mass model. For isotropic orbits a Gaussian
distribution is a fair assumption:
![]() at
at
![]() and then decreases whereas departures can reach
and then decreases whereas departures can reach ![]() 30%
for anisotropic orbits. With this mass model we plot
30%
for anisotropic orbits. With this mass model we plot
![]() and
and
![]() in the top panel of Fig. 5 for
different values of the anisotropy radius
in the top panel of Fig. 5 for
different values of the anisotropy radius
![]() and
and
![]() .
The agreement between the measurements of Sa04 and
.
The agreement between the measurements of Sa04 and
![]() is better than with
is better than with
![]() but introducing
anisotropy cannot improve the fit quality for
but introducing
anisotropy cannot improve the fit quality for
![]() :
the
:
the
![]() curve of the NFW model rises too fast whereas data indicate
a declining tendency. However, if kinematical data would extend to slighly
larger scales, we expect the profile to start rising and become closer
to the model beyond a few tens of kpc as observed in other cD galaxies
(Kelson et al. 2002; Dressler 1979).
curve of the NFW model rises too fast whereas data indicate
a declining tendency. However, if kinematical data would extend to slighly
larger scales, we expect the profile to start rising and become closer
to the model beyond a few tens of kpc as observed in other cD galaxies
(Kelson et al. 2002; Dressler 1979).
We attempted to couple lensing and kinematical constraints by minimizing
the merit function
![]() ,
with
,
with
Changing the Hernquist stellar light profile by a Jaffe model as proposed
by Sa04 slightly improves the fit of kinematical data without altering the
lens modelling (see Sect. 2.3). In this case, we have
![]() .
The velocity dispersion curve raises
more slowly compared to the Hernquist case. However, since the mass budget is
dominated by dark matter, there is not much improvement. Lensing constraints
are so tight that the allowed region in the parameter space is completely fixed.
.
The velocity dispersion curve raises
more slowly compared to the Hernquist case. However, since the mass budget is
dominated by dark matter, there is not much improvement. Lensing constraints
are so tight that the allowed region in the parameter space is completely fixed.
Likewise the "gen'' model also fails to reproduce kinematical data although it
has more free parameters. In this case, the inner slope
![]() is still fixed by lensing. The inferred stellar mass-to-light ratio is
is still fixed by lensing. The inferred stellar mass-to-light ratio is
![]() which is a rather low value. For the "gen'' profile
too, switching the stellar mass profile to a Jaffe model does not
significantly improve the fit to kinematical data.
which is a rather low value. For the "gen'' profile
too, switching the stellar mass profile to a Jaffe model does not
significantly improve the fit to kinematical data.
We have shown that departures from Gaussian absorption lines induce a small
bias which starts to be important for dynamical systems with radial orbits.
However this bias is unable to explain the discrepancy between lensing and
kinematical mass estimates. Furthermore, such a bias cannot be advocated to
explain the discrepancy between lensing and X-rays mass estimates.
We can see in the central and bottom panels of Fig. 5
that the mass model of Sa04 fairly reproduces the kinematical data, as well as
the Al01 model (provided one addes the contribution of a central cD galaxy
with
![]() ).
).
Since lensing is sensitive to the integrated mass contrast along the line
of sight, it is natural to expect overestimates due to fortuitous alignments
with mass concentrations which are not physically related to the main halo
of interest. Likewise, departures from spherical symmetry are observed
in N-body simulations (e.g. Jing & Suto 2002) and may bias
lensing estimates. This question has been addressed by various authors
(Cen 1997; Bartelmann 1995; Hennawi et al. 2005; Wambsganss et al. 2004; Reblinsky & Bartelmann 1999; Clowe et al. 2004).
Conclusions about the importance of unrelated structures
(large scale structure LSS) slightly differ from one author to another.
Hoekstra (2003) found LSS to add noise to mass estimates on large scales
but do not lead to biased estimates since on very large scales the skewness
of the density field is negligible and light rays cross overdense regions
as well as underdense ones. At smaller scales, this becomes obviously wrong
and one expects fortuitous alignments of halos to modify the properties of
halos. Wambsganss et al. (2004) claim that such effects can increase
the lensing mass of ![]()
![]() of halos by a factor of
of halos by a factor of
![]()
![]() whereas Hennawi et al. (2005) found this effect to change the
lensing cross-sections of clusters by a smaller amount (
whereas Hennawi et al. (2005) found this effect to change the
lensing cross-sections of clusters by a smaller amount (![]() 7%).
See also Hamana et al. (2004) and Hennawi & Spergel (2005) for a discussion of
projection effects on weak lensing cluster surveys.
7%).
See also Hamana et al. (2004) and Hennawi & Spergel (2005) for a discussion of
projection effects on weak lensing cluster surveys.
On smaller scales, Metzler et al. (2001) found the mass of surrounding (sub)structures like filaments to add a significant contribution to the total convergence of a cluster-size lens whereas Clowe et al. (2004) showed that triaxiality is an important issue for lensing mass estimates. In the following, we shall focus on this paticular aspect which has been found to be important for lensing Oguri et al. (2003); Oguri & Keeton (2004) and/or X-ray observations (Piffaretti et al. 2003; De Filippis et al. 2005; Hennawi et al. 2005).
For a triaxial or oblate/prolate halo, the ratio of the mass enclosed
in the cylinder of radius R to the mass enclosed in the sphere of same
radius will differ from that of a spherically symmetric situation.
In order to illustrate projection effects, we consider an axisymmetric
(either oblate or prolate) NFW density profile of the form:
Since we are interested in ratios between
mass estimates we pay no attention to normalization constants and write
the exact mass
![]() enclosed by the sphere of radius r as
enclosed by the sphere of radius r as
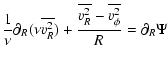 |
(12a) | ||
| (12b) |
| |
= |  |
(13a) |
| = | ![$\displaystyle -\int_z^\infty {\rm d}z'~\left[ \partial_R\nu\partial_z\Psi-\partial_z\nu\partial_R\Psi\right] .$](/articles/aa/full/2005/45/aa3166-05/img182.gif) |
(13b) |
We now calculate the observable luminosity-weighted line-of-light
velocity dispersion
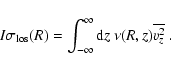 |
(15) |
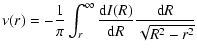 |
(16a) | ||
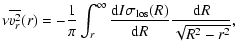 |
(16b) |
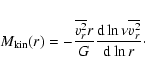 |
(17) |
We have
![]() with
with
![]() .
The X-rays surface brightness of the optically thin gas distribution is
.
The X-rays surface brightness of the optically thin gas distribution is
![\begin{displaymath}S_{\rm X}(R) \propto \int \exp\left[-2\Psi(R,z)/V_0^2\right] {\rm d}z,
\end{displaymath}](/articles/aa/full/2005/45/aa3166-05/img209.gif) |
(18) |
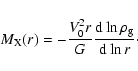 |
(19) |
Figure 6 clearly shows that moderate values of the axis ratio q can lead to strong discrepancies between 2D and 3D mass estimates or between lensing and X-rays or stellar kinematics.
It is difficult to fully characterize the ratio
![]() because it depends on the distribution of tracers
because it depends on the distribution of tracers ![]() and is very
sensitive to the orientation of the axis ratio relative to the line of sight.
Therefore a direct comparison between lensing and dynamical mass estimates
is hazardous.
and is very
sensitive to the orientation of the axis ratio relative to the line of sight.
Therefore a direct comparison between lensing and dynamical mass estimates
is hazardous.
![]() can have a different radial
behavior as a function of radius for a given axis ratio. It can be
either greater of less than unity.
can have a different radial
behavior as a function of radius for a given axis ratio. It can be
either greater of less than unity.
Comparing lensing and X-rays mass estimates is easier since the X-rays mass
estimate is less sensitive to projection effects. In this respect
![]() will systematically be >1 (resp. <1)
for prolate (resp. oblate) halos with a well known radial behavior.
will systematically be >1 (resp. <1)
for prolate (resp. oblate) halos with a well known radial behavior.
In the case of MS2137, a prolate halo with ![]() could well
explain most discrepancies between our best fit models and the results of
Sa04 and Al01. A prolate halo aligned toward the line of sight is a
natural explanation for the high concentration parameter we found
could well
explain most discrepancies between our best fit models and the results of
Sa04 and Al01. A prolate halo aligned toward the line of sight is a
natural explanation for the high concentration parameter we found
![]() and may also explain the high concentrations
and may also explain the high concentrations
![]() in CL0024 (Kneib et al. 2003) and
c=13.7+1.4-1.1 in A1689
(Broadhurst et al. 2005). Recently, Oguri et al. (2005) have investigated the effect
of triaxiality in A1689 and reached similar conclusions as did
Clowe et al. (2004) who studied numerical simulations
(see also Piffaretti et al. 2003).
in CL0024 (Kneib et al. 2003) and
c=13.7+1.4-1.1 in A1689
(Broadhurst et al. 2005). Recently, Oguri et al. (2005) have investigated the effect
of triaxiality in A1689 and reached similar conclusions as did
Clowe et al. (2004) who studied numerical simulations
(see also Piffaretti et al. 2003).
At this level, it is not possible to simply refine the modelling of
MS2137, since our prolate model is idealized. It should be triaxial
and/or not perfectly aligned with the line of sight because the
projected density profile is elliptical. However the hypothesis of a
projected triaxial halo also provides a direct explanation for the
misalignment between the projected diffuse stellar component of the cD
and the projected dark matter halo
![]() deg.
Binney (1985) and Romanowsky & Kochanek (1998) give the necessary formalism to
infer the position angle and projected ellipticity of both dark and
luminous halos from their tridimensional triaxial shape and orientation.
The information that can be derived from the geometry of projected light
and dark matter densities is detailed in Appendix B.
These independent constraints give the
following results for the orientation
deg.
Binney (1985) and Romanowsky & Kochanek (1998) give the necessary formalism to
infer the position angle and projected ellipticity of both dark and
luminous halos from their tridimensional triaxial shape and orientation.
The information that can be derived from the geometry of projected light
and dark matter densities is detailed in Appendix B.
These independent constraints give the
following results for the orientation ![]() (polar angle of the
major axis with respect to the line of sight), the minor axis ratios
(polar angle of the
major axis with respect to the line of sight), the minor axis ratios
![]() and c* of dark matter and stellar components
respectively:
and c* of dark matter and stellar components
respectively:
![]() ,
,
![]() ,
and
,
and
![]() .
This geometrical
information is fairly consistent with the value of
.
This geometrical
information is fairly consistent with the value of
![]() and the perfect alignement (
and the perfect alignement (![]() )
we assumed to explain the mass
discrepancies.
)
we assumed to explain the mass
discrepancies.
There is sufficient material to be convinced that no simple coupling between 2D and 3D mass estimates is possible. Consequently, we expect that most of the previous analyses based on such a coupling should be considered with caution, in terms of significance and of possibly biased results.
The mass within the sphere of radius r is independent of the halo
orientation and reads
The mass M2 within cylinder of radius r will depend on their axis
ratios and the orientation ![]() but the system is equivalent to
an elliptical projected mass distribution with axis ratio
but the system is equivalent to
an elliptical projected mass distribution with axis ratio ![]() and position
angle
and position
angle ![]() .
Thus we can express M2 as:
.
Thus we can express M2 as:
As before, an observer measuring the 3D mass profile within radius rwill find a different normalization as compared to an observer interested
in the cylindric mass of radius r. They will differ by a factor
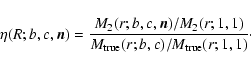 |
(22) |
We plot in the upper panel of Fig. 7 the distribution of ![]() for three fiducial values of
R=0.03,0.3 and 3 which are relevant
for strong lensing/stellar dynamics, strong lensing/X-rays and
weak lensing/X-rays comparisons respectively. We clearly see a broad,
shifted and skewed distribution that converges toward unity with increasing
radius. However, at small scales, the median value of
for three fiducial values of
R=0.03,0.3 and 3 which are relevant
for strong lensing/stellar dynamics, strong lensing/X-rays and
weak lensing/X-rays comparisons respectively. We clearly see a broad,
shifted and skewed distribution that converges toward unity with increasing
radius. However, at small scales, the median value of ![]() is not unity
and readily extends toward high values
is not unity
and readily extends toward high values
![]() .
Typically
.
Typically
![]() (resp.
1.19+0.17-0.14,
(resp.
1.19+0.17-0.14,
![]() )
for R=0.03 (resp. 0.3, 3.0). Thus, important departures between M2and
)
for R=0.03 (resp. 0.3, 3.0). Thus, important departures between M2and
![]() are naturally expected if halos are effectively triaxial.
are naturally expected if halos are effectively triaxial.
Moreover, there must be a correlation between the observed projected
axis ratio q and ![]() since the apparently rounder halos are
likely to be elongated along the line of sight. This effect can be
seen in Fig. 8 where we plot the conditional PDFs
since the apparently rounder halos are
likely to be elongated along the line of sight. This effect can be
seen in Fig. 8 where we plot the conditional PDFs
![]() ,
,
![]() ,
,
![]() and
and
![]() for a radius R=0.3. The highest values
of
for a radius R=0.3. The highest values
of ![]() are due to the roundest projected halos.
For instance, given q>0.7 we have
are due to the roundest projected halos.
For instance, given q>0.7 we have
![]() .
.
Projection effects of triaxial halos have the interesting property
to explain the fact that weak lensing and X-rays measurements generally match
since ![]() for
for ![]() a few
a few ![]() .
The same holds for the general
trend for strong lensing mass estimates to generally be greater
(by a factor of 1-3) than X-rays since they occur at scales
.
The same holds for the general
trend for strong lensing mass estimates to generally be greater
(by a factor of 1-3) than X-rays since they occur at scales
![]() (Wu 2000; Allen et al. 2001). The relative
normalization between lensing and stellar kinematics is more complex
and cannot be representated by the
(Wu 2000; Allen et al. 2001). The relative
normalization between lensing and stellar kinematics is more complex
and cannot be representated by the ![]() statistic. However we expect
a similar scatter and a strong dependence on the major axis orientation.
statistic. However we expect
a similar scatter and a strong dependence on the major axis orientation.
We have undertaken a thorough dynamical analysis of the line-of-sight
velocity distribution of stars in the cD in order to check whether
departures from a Gaussian distribution may explain the relative inconsistency
between our lens models and stellar kinematics. The effect of
non-Gaussian aborption lines is to slightly lower (![]() 15%)
the measured velocity dispersion estimates of Sa04 but does not greatly
improve the agreement between our lens model and the bias-corrected data.
Moreover such a bias cannot explain the disagreement between our lens
model and Al01 X-rays mass estimates. This 3D mass estimate turns
out to be consistent with stellar dynamics, showing that there must be
a problem in the relative normalization of 2D and 3D mass estimates.
15%)
the measured velocity dispersion estimates of Sa04 but does not greatly
improve the agreement between our lens model and the bias-corrected data.
Moreover such a bias cannot explain the disagreement between our lens
model and Al01 X-rays mass estimates. This 3D mass estimate turns
out to be consistent with stellar dynamics, showing that there must be
a problem in the relative normalization of 2D and 3D mass estimates.
These discrepancies can be alleviated if one considers the possibility
of departures from spherical symmetry for the dark matter and stellar
components. More precisely, we have shown that a prolate halo with its
major axis oriented close to the line of sight and an axis ratio ![]() 0.4
is likely to explain the discrepancies. This hypothesis is supported by
the misalignement (
0.4
is likely to explain the discrepancies. This hypothesis is supported by
the misalignement (
![]() )
between projected DM and
stellar distributions.
)
between projected DM and
stellar distributions.
Furthermore such a geometrical configuration well explains the concentration
parameter we infer from a lensing analysis
![]() .
A prefered
elongated halo toward the LOS boosts lensing efficiency
(Bartelmann 1995; Oguri et al. 2003; Clowe et al. 2004) and may explain the high
concentration of some strong lensing clusters
(Kneib et al. 2003; Hennawi et al. 2005; Broadhurst et al. 2005; Oguri et al. 2005).
.
A prefered
elongated halo toward the LOS boosts lensing efficiency
(Bartelmann 1995; Oguri et al. 2003; Clowe et al. 2004) and may explain the high
concentration of some strong lensing clusters
(Kneib et al. 2003; Hennawi et al. 2005; Broadhurst et al. 2005; Oguri et al. 2005).
We have shown that triaxiality is a general problem that hampers any
attempt to simply couple 2D and 3D mass estimates assuming spherical
symmetry. Once projected, triaxial halos are elliptical and lens modelling
is able to take ellipticity into account. Usually dynamical or X-rays
analyses do not fully incorporate such a complexity. This should be
done before comparison to (or coupling with) lensing.
In Sect. 5, we have assumed the statistical distribution
of axis ratios proposed by Jing & Suto (2002) in order to calculate the mass M2(r)
within a cylinder of radius r and the mass
![]() within
the sphere of the same radius. The difference is important and can lead to a
significant discrepancy in the relative normalization between 2D and 3D
mass estimates.
within
the sphere of the same radius. The difference is important and can lead to a
significant discrepancy in the relative normalization between 2D and 3D
mass estimates.
The statistics of ![]() shows that, at small scales R<1, on average
a systematic depart from unity is expected for
shows that, at small scales R<1, on average
a systematic depart from unity is expected for ![]() with an important
scatter and skewness toward high values of
with an important
scatter and skewness toward high values of ![]() .
Therefore the relative
normalization at small scales is biased and highly uncertain if one neglects
projection effects. At larger scales, the distribution of
.
Therefore the relative
normalization at small scales is biased and highly uncertain if one neglects
projection effects. At larger scales, the distribution of ![]() converges
to unity and explains why weak lensing mass estimates are generally in better
agreement with X-rays or dynamics of galaxies in clusters
(e.g. Wu 2000; Allen 1998; Arabadjis et al. 2004). Similarly, the coupling
between stellar kinematics and strong lensing at clusters scales
(Sand et al. 2004,2002) or at galaxies scales
(e.g. Rusin et al. 2003; Koopmans & Treu 2002; Treu & Koopmans 2004) may be oversimplistic
since they do not take asphericity into account. First, the mean value
converges
to unity and explains why weak lensing mass estimates are generally in better
agreement with X-rays or dynamics of galaxies in clusters
(e.g. Wu 2000; Allen 1998; Arabadjis et al. 2004). Similarly, the coupling
between stellar kinematics and strong lensing at clusters scales
(Sand et al. 2004,2002) or at galaxies scales
(e.g. Rusin et al. 2003; Koopmans & Treu 2002; Treu & Koopmans 2004) may be oversimplistic
since they do not take asphericity into account. First, the mean value
![]() for
for
![]() leads to an expected systematic bias,
but also the
leads to an expected systematic bias,
but also the ![]() 20% scatter in the distribution of
20% scatter in the distribution of ![]() will increase
the uncertainty in the mass normalization and prevent the temptation
to couple these independent mass estimates.
will increase
the uncertainty in the mass normalization and prevent the temptation
to couple these independent mass estimates.
Thus, the density profile of the dark matter halo of MS2137-23 is well consistent with NFW and previous claimed discrepancies may be due to the spherical symmetry assumption. Indeed, it turns out that when coupling lensing to other mass estimates we cannot avoid a detailed (and cumbersome) 3D triaxial modelling of X-rays and dynamical properties. Such a level of refinement is already achieved in lensing studies that assume elliptical symmetry. The triaxiality of dark matter halos (and stellar components) is a major concern for joint modelling and should systematically be taken into account for future analyses. As well, it is possible that X-rays or optically selected clusters are biased toward elongated configurations, leading to an overefficiency of lensing. The increasing precision of observations makes the assumption of spherical symmetry unlikely to be valid. Since clusters of galaxies are often seen as an important cosmological probe. It is important to better characterize their properties (mass, temperature, shape, abundance...) with realistic triaxial symmetries.
Acknowledgements
I would like to acknowledge J. Miralda-Escudé who helped me start this work, which greatly benefited from his insightful advice. I also thank B. Fort, Y. Mellier and G. Mamon for fruitful discussions, D. Sand who kindly made the velocity dispersion data available and I. Tereno for his help in the handling of MCMCs. Most of this work has benefited from the TERAPIX computing facilities at IAP.
For Osipkov-Merritt models, the DF f(Q) can directly be calculated,
through the Eddington formula (Binney & Tremaine 1987)
Once Eq. (A.2) his numerically integrated, it is
possible to derive the LOSVD
![]() as a function of the projected radius R by integrating over the line
of sight coordinate z and over the perpendicular velocity
as a function of the projected radius R by integrating over the line
of sight coordinate z and over the perpendicular velocity ![]() with
with
![]() .
.
The integration of Eq. (A.3) is done by randomly
sampling the distribution function with a large number N of stars.
Since the stellar density profile is known to a scaling mass-to-light
ratio, one can assign a radius r to each star according to the
cumulative Hernquist stellar mass profile
![]() .
Each radius ri can
be projected onto the plane of the sky yielding
.
Each radius ri can
be projected onto the plane of the sky yielding ![]() and zi,
the line of sight coordinate as before. At this point, it is trivial
to incorporate the smearing due to observational conditions like seeing
by adding a random displacement
and zi,
the line of sight coordinate as before. At this point, it is trivial
to incorporate the smearing due to observational conditions like seeing
by adding a random displacement
![]()
![]() . Similarly, if the slit width
. Similarly, if the slit width
![]() is negligible
is negligible
![]() can be identified to
the position along the slit, otherwise, it is straightforward to split
can be identified to
the position along the slit, otherwise, it is straightforward to split
![]() into (xi,yi), only considering those points satisfying
into (xi,yi), only considering those points satisfying
![]() and then identify xi as the position
along the slit. This is the situation we shall consider in the following.
and then identify xi as the position
along the slit. This is the situation we shall consider in the following.
This spatial sampling of the DF is thus independent of the potential
![]() or the anisotropy radius
or the anisotropy radius ![]() and can be stored for
further calculation. For a given
and can be stored for
further calculation. For a given ![]() and
and ![]() ,
one must solve
Eq. (A.2), assign a velocity v and a velocity
orientation
,
one must solve
Eq. (A.2), assign a velocity v and a velocity
orientation ![]() using the calculated DF f(Q). This sampling is
done with acceptance-rejection techniques (e.g. Press et al. 1992).
See also Kuijken & Dubinski (1994) or Kazantzidis et al. (2004) for similar
applications. We can write the conditional PDFs for the
polar angle
using the calculated DF f(Q). This sampling is
done with acceptance-rejection techniques (e.g. Press et al. 1992).
See also Kuijken & Dubinski (1994) or Kazantzidis et al. (2004) for similar
applications. We can write the conditional PDFs for the
polar angle ![]() and Q at radius r:
and Q at radius r:
We now compute the LOSVD deduced from the best fit NFW model of MS2137 and
compare the inferred velocity dispersion to the measurements of Sa04. We assume
the same observational conditions i.e. a slit width
![]() and a Gaussian seeing
and a Gaussian seeing
![]() FWHM. These data were obtained by assuming Gaussian absorption lines.
van der Marel & Franx (1993) showed that departures from a Gaussian distribution
imply a bias in any velocity dispersion measurement. To the first order,
the biased pseudo-velocity dispersion
FWHM. These data were obtained by assuming Gaussian absorption lines.
van der Marel & Franx (1993) showed that departures from a Gaussian distribution
imply a bias in any velocity dispersion measurement. To the first order,
the biased pseudo-velocity dispersion
![]() reads:
reads:
Figure A.1 shows the LOSVD as a function of the line-of-sight velocity
![]() for the innermost and outermost radial bins of
Sa04. Departures from a Gaussian case are visible close to the center and
decrease with increasing radius. Therefore, the velocity bias changes
with projected radius as can be seen on the top panel of
Fig. 5, in which we plot
for the innermost and outermost radial bins of
Sa04. Departures from a Gaussian case are visible close to the center and
decrease with increasing radius. Therefore, the velocity bias changes
with projected radius as can be seen on the top panel of
Fig. 5, in which we plot
![]() and
and
![]() for two values of the anisotropy radius
for two values of the anisotropy radius
![]() and
and
![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{NEW/3166fg13.eps}} \end{figure}](/articles/aa/full/2005/45/aa3166-05/Timg301.gif) |
Figure A.1:
Line-of-sight velocity probability distribution
for stars with a projected radius in the innermost
|
The projected distribution is elliptical with an axis ratio ![]() and a position angle
and a position angle ![]() given by:
given by: