A&A 443, 955-959 (2005)
DOI: 10.1051/0004-6361:20052853
G. Cassam-Chenaï1,2 - A. Decourchelle1 - J. Ballet1 - D. C. Ellison2
1 - Service d'Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
2 - Department of Physics, North Carolina State University, Box 8202, Raleigh, NC 27695,
USA
Received 9 February 2005 / Accepted 27 June 2005
Abstract
In the framework of test-particle and cosmic-ray
modified hydrodynamics, we calculate synchrotron emission radial
profiles in young ejecta-dominated supernova remnants (SNRs)
evolving in an ambient medium which is uniform in density and
magnetic field. We find that, even without any magnetic field
amplification by Raleigh-Taylor instabilities, the radio
synchrotron emission peaks at the contact discontinuity because
the magnetic field is compressed and is larger there than at the
forward shock. The X-ray synchrotron emission sharply drops behind
the forward shock as the highest energy electrons suffer severe
radiative losses.
Key words: acceleration of particles - ISM: supernova remnants - ISM: cosmic rays - X-rays: ISM
Shocks in supernova remnants (SNRs) are believed to produce the
majority of the Galactic cosmic-rays (CRs) at least up to the
"knee'' (![]()
![]() eV). The particle acceleration
mechanism most likely responsible for this is known as diffusive
shock acceleration (DSA) (e.g., Blandford & Eichler 1987; Drury 1983). This
mechanism may transfer a large fraction of the ram kinetic energy
(up to
eV). The particle acceleration
mechanism most likely responsible for this is known as diffusive
shock acceleration (DSA) (e.g., Blandford & Eichler 1987; Drury 1983). This
mechanism may transfer a large fraction of the ram kinetic energy
(up to ![]() )
into relativistic particles and remove it from the
thermal plasma (see, for example, Jones & Ellison 1991).
)
into relativistic particles and remove it from the
thermal plasma (see, for example, Jones & Ellison 1991).
Convincing observational support for the acceleration of particles
in shell-type SNRs comes from their nonthermal radio and X-ray
emissions due to synchrotron radiation from relativistic GeV and
at least TeV electrons, respectively. In radio and X-rays,
synchrotron-dominated SNRs display various morphologies: for
instance, the synchrotron emission dominates in two bright limbs
in SN 1006 (e.g., Rothenflug et al. 2004) whereas it is distorted and
complex in RX J1713.7-3946 (e.g., Cassam-Chenaï et al. 2004b). The detection
and imaging with the HESS telescopes of TeV ![]() -rays
in RX J1713.7-3946 provides unambiguous evidence for particle
acceleration to very high energies. The
-rays
in RX J1713.7-3946 provides unambiguous evidence for particle
acceleration to very high energies. The ![]() -ray morphology in
this remnant is similar to that seen in X-rays (Aharonian et al. 2004).
-ray morphology in
this remnant is similar to that seen in X-rays (Aharonian et al. 2004).
Recent works based on Chandra (Vink & Laming 2003, for Cas
A) and XMM-Newton (Cassam-Chenaï et al. 2004a, for Kepler's
SNR) observations have demonstrated that X-ray synchrotron
emission is also present in ejecta-dominated SNRs and largely
contributes to the continuum emission at the forward shock. This
X-ray emission arises from sharp filaments encircling the SNR's
outer boundary. The observed width of these filaments is a few
arcseconds, and has been used to constrain the magnetic field
intensity just behind the shock![]() (Berezhko & Völk 2004; Völk et al. 2005; Ballet 2005; Vink & Laming 2003; Berezhko et al. 2003).
(Berezhko & Völk 2004; Völk et al. 2005; Ballet 2005; Vink & Laming 2003; Berezhko et al. 2003).
A number of recent hydrodynamical models, including particle acceleration and photon emission, have been presented to explain various features of these observations. Reynolds (1998) has described the morphology and spectrum of the synchrotron X-ray emission from SNRs in the Sedov evolutionary phase. Similar work based on numerical simulations was done by van der Swaluw & Achterberg (2004) who take into account the diffusion of particles. CRs are treated as test-particles in these studies.
Here, we expand on the work of Reynolds (1998) by considering young (ejecta-dominated) SNRs. We investigate the synchrotron emission morphology, both in radio and X-rays, as well as how it can be modified by efficient particle acceleration. Our results show that the radio and X-ray profiles are very different due to the effects of the magnetic field evolution and synchrotron losses in the interaction region between the contact discontinuity and the forward shock. For typical parameters, the radio emission peaks at the contact discontinuity while the X-ray emission forms sheet-like structures at the forward shock.
The hydrodynamic evolution of young supernova remnants, including the backreaction from accelerated particles, can be described by self-similar solutions if the initial density profiles in the ejected material (ejecta) and in the ambient medium have power-law distributions (Chevalier 1983,1982), and if the acceleration efficiency (i.e. the fraction of total ram kinetic energy going into suprathermal particles) is independent of time.
Here, we use the self-similar model of Chevalier (1983) which
considers a thermal gas (
![]() )
and the cosmic-ray fluid
(
)
and the cosmic-ray fluid
(
![]() ), with the boundary conditions calculated from the
non-linear diffusive shock acceleration (DSA) model of
Berezhko & Ellison (1999) and Ellison et al. (2000) as described in Decourchelle et al. (2000).
This acceleration model is an approximate, semi-analytical model
that determines the shock modification and particle spectrum from
thermal to relativistic energies in the plane-wave, steady state
approximation as a function of an arbitrary injection parameter,
), with the boundary conditions calculated from the
non-linear diffusive shock acceleration (DSA) model of
Berezhko & Ellison (1999) and Ellison et al. (2000) as described in Decourchelle et al. (2000).
This acceleration model is an approximate, semi-analytical model
that determines the shock modification and particle spectrum from
thermal to relativistic energies in the plane-wave, steady state
approximation as a function of an arbitrary injection parameter,
![]() (i.e. the fraction of total particles
which end up with suprathermal energies). The validity of the
self-similar solutions has been discussed by Decourchelle et al. (2000) and
direct comparisons between this self-similar model and the more
general CR-hydro model of Ellison et al. (2004) showed good correspondence
for a range of input conditions.
(i.e. the fraction of total particles
which end up with suprathermal energies). The validity of the
self-similar solutions has been discussed by Decourchelle et al. (2000) and
direct comparisons between this self-similar model and the more
general CR-hydro model of Ellison et al. (2004) showed good correspondence
for a range of input conditions.
The hydrodynamic evolution provides the shock characteristics
necessary to calculate the particle spectrum at the forward
shock![]() , at any time. Once a particle
spectrum has been produced at the shock, it will evolve downstream
because of radiative and adiabatic expansion losses. We assume
that the accelerated particles remain confined to the fluid
element in which they were produced, so adiabatic losses are
determined directly from the fluid element expansion. The basic
power law spectrum produced by DSA, before losses are taken into
account, is modified at the highest energies with a exponential
cutoff,
, at any time. Once a particle
spectrum has been produced at the shock, it will evolve downstream
because of radiative and adiabatic expansion losses. We assume
that the accelerated particles remain confined to the fluid
element in which they were produced, so adiabatic losses are
determined directly from the fluid element expansion. The basic
power law spectrum produced by DSA, before losses are taken into
account, is modified at the highest energies with a exponential
cutoff,
![]() ,
where
,
where
![]() is
determined by matching either the acceleration time to the shock
age or the upstream diffusive length to some fraction of the shock
radius. In our simulation, the electron-to-proton density ratio at
relativistic energies,
is
determined by matching either the acceleration time to the shock
age or the upstream diffusive length to some fraction of the shock
radius. In our simulation, the electron-to-proton density ratio at
relativistic energies,
![]() ,
is set equal to
0.01 (see Ellison et al. 2000).
,
is set equal to
0.01 (see Ellison et al. 2000).
Unless explicitly stated, our numerical examples are given for the
following supernova parameters:
![]() for the ejected mass,
E51 = 1 where
E51 is the kinetic energy of the ejecta in units of 1051erg and n=9, where n is the index of the initial power-law
density profile in the ejecta (
for the ejected mass,
E51 = 1 where
E51 is the kinetic energy of the ejecta in units of 1051erg and n=9, where n is the index of the initial power-law
density profile in the ejecta (
![]() ). In our
simulations, the SNR age is
). In our
simulations, the SNR age is
![]() years and the shock
velocity at the forward shock is
years and the shock
velocity at the forward shock is
![]() .
For the ambient medium parameters, we take a
magnetic field
.
For the ambient medium parameters, we take a
magnetic field
![]() ,
a density
,
a density
![]() ,
an ambient gas pressure
,
an ambient gas pressure
![]() and s=0, where sis the index of its initial power-law density profile (
and s=0, where sis the index of its initial power-law density profile (
![]() ). The case s=0 corresponds to a uniform
interstellar medium (s=2 describes a stellar wind).
). The case s=0 corresponds to a uniform
interstellar medium (s=2 describes a stellar wind).
In the next section, we discuss the importance of the magnetic field for the synchrotron emission and particle acceleration. We do not, however, explicitly include the dynamical influence of the magnetic field on the hydrodynamics.
To track the synchrotron losses, we are interested in the temporal evolution of the magnetic field behind the shock. We assume the magnetic field to be simply compressed at the shock and passively carried by the flow, frozen in the plasma, so that it evolves conserving flux. In this simple 1-D approach, we do not consider any production of the SNR magnetic field, for instance, by hydrodynamical instabilities which is an additional effect. As for the magnetic field ahead of the forward shock, it is assumed to be isotropic and fully turbulent. Appendix A (see the on-line version) shows how to compute the magnetic field profile for self-similar solutions in both test-particle and nonlinear particle acceleration cases.
We first discuss the behavior of the normal and tangential components of the magnetic field in the test-particle case where the backreaction of the accelerated particles is neglected.
When the SNR evolves in an ambient medium which is uniform in density and magnetic field, the expansion and flux freezing generally cause the tangential component of the magnetic field to increase at the contact discontinuity whereas the normal component falls to zero (Fig. 1). As a result, the magnetic field profile is dominated by the tangential component.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2853_f1.eps}\end{figure}](/articles/aa/full/2005/45/aa2853-05/Timg28.gif) |
Figure 1:
Radial profile of the normal ( |
One has often invoked hydrodynamic instabilities to explain the magnetic field increase at the interface between the shocked ejecta and the shocked ambient medium (Jun et al. 1995). The numerical simulations of Jun & Norman (1996) have shown that the magnetic field could be amplified by a factor 60 by Rayleigh-Taylor and Kelvin-Helmholtz instabilities. Here, we note that simple advection of the magnetic field already predicts amplification by a factor 5 (Table A.1 top, n=9).
We note that, if the SNR evolves in a wind with a decreasing
initial density profile, advection goes the other way (diluting
the magnetic field instead of amplifying it). But when both the
ambient density and magnetic field decrease with radius, as would
be the case for a pre-supernova stellar wind, the magnetic field
is larger close to the contact discontinuity than at the forward
shock (by a factor of ![]() 1000 in some cases). This is because
the dilution of the advected magnetic field is negligible compared
to the fact that the ambient magnetic field was much larger at
early times.
1000 in some cases). This is because
the dilution of the advected magnetic field is negligible compared
to the fact that the ambient magnetic field was much larger at
early times.
We now consider the behavior of the normal and tangential components of the magnetic field in the nonlinear case where the backreaction of the accelerated particles on the shock is taken into account.
In the ideal non-linear case, where the acceleration is instantaneous, the magnetic field diverges at the contact discontinuity because of its tangential component, whatever the injection efficiency is, as in the test-particle case. However, the contrast between the magnetic field in a given fluid element and the one just behind the shock, will be always smaller than in the test-particle case (see Table A.1). Figure 2 shows the profile of the total downstream magnetic field for different values of the injection efficiency. Table 1 shows the associated compression ratio and immediate post-shock magnetic field.
|
|
10-3 |
|
10-4 | 10-5 |
|
|
8.5 | 7.5 | 5.9 | 4.1 |
| Bs (
|
69 | 61 | 49 | 34 |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2853_f3.eps}\par\includegraphics[width=8.5cm,clip]{2853_f4.eps}\end{figure}](/articles/aa/full/2005/45/aa2853-05/Timg33.gif) |
Figure 3:
Radio (top panel) and X-ray (bottom
panel) synchrotron volume emissivity,
|
Once the magnetic field structure and the particle spectrum
(attached to a fluid element) modified by the radiative and
adiabatic expansion losses as computed in Reynolds (1998) are known,
we compute the synchrotron emission (Rybicki & Lightman 1979), averaged over
the pitch-angle, in any energy band![]() .
.
Figure 3 shows the radial profiles of the
synchrotron emission in the radio (top panel) and X-ray (bottom
panel) domains for different injection efficiencies,
![]() .
An increase in the injection efficiency not
only provides a larger number of accelerated electrons, but also a
larger compression of the downstream magnetic field (see Table 1) and a narrower interaction region. These
effects combine to produce enhanced synchrotron emission as the
injection increases.
.
An increase in the injection efficiency not
only provides a larger number of accelerated electrons, but also a
larger compression of the downstream magnetic field (see Table 1) and a narrower interaction region. These
effects combine to produce enhanced synchrotron emission as the
injection increases.
The radio synchrotron emission is produced by GeV electrons which
are not affected by radiative losses. Consequently, the radio
synchrotron emission critically depends on the final magnetic
field profile (Fig. 2) and, therefore, peaks
at the contact discontinuity. In contrast, the X-ray synchrotron
emission is produced by the highest momentum electrons (![]()
![]() )
which, depending on the
downstream field strength, may suffer radiative losses. The high
energy electrons that have been accelerated at the earliest time
have suffered strong synchrotron losses as they were advected
behind the shock. Because of this, they are not numerous enough at
the end to radiate in the X-ray regime despite a strong magnetic
field. As a result, the X-ray synchrotron emission rapidly
decreases behind the shock. The X-ray profile becomes sharper when
the injection efficiency increases because it provides larger
compression of the downstream magnetic field and then stronger
synchrotron losses.
)
which, depending on the
downstream field strength, may suffer radiative losses. The high
energy electrons that have been accelerated at the earliest time
have suffered strong synchrotron losses as they were advected
behind the shock. Because of this, they are not numerous enough at
the end to radiate in the X-ray regime despite a strong magnetic
field. As a result, the X-ray synchrotron emission rapidly
decreases behind the shock. The X-ray profile becomes sharper when
the injection efficiency increases because it provides larger
compression of the downstream magnetic field and then stronger
synchrotron losses.
Figure 4 shows the synchrotron emission after integration along the line-of-sight. The radial profile of the radio emission (top panel) shows a peak at the contact discontinuity. The radial profile of the X-ray projected synchrotron emission (bottom panel) shows bright rims just behind the forward shock whose width decreases as the injection efficiency increases.
We have computed the radio and X-ray synchrotron emission in young ejecta-dominated SNRs. This has been done using a one dimensional, self-similar hydrodynamical calculation coupled with a non-linear diffusive shock acceleration model, and taking into account the adiabatic and radiative losses of the electron spectrum during its advection in the remnant.
We show that the morphology of the synchrotron emission in young ejecta-dominated SNRs is very different in radio and X-ray. This is the result of the increased magnetic field toward the contact discontinuity, to which only low energy electrons that emit radio are sensitive, while the high energy electrons emitting X-rays experience strong radiative losses and are mostly dependent on the post-shock magnetic field.
Briefly, the radio synchrotron emission increases as one moves from the forward shock toward the contact discontinuity due to a compression of the magnetic field (particularly its tangential component), assuming both uniform ambient density and upstream magnetic field. Such a compression naturally results from the dynamical evolution of the SNR. In contrast, because of the radiative losses, the X-ray synchrotron emission decreases behind the forward shock and forms sheet-like structures after line-of-sight projection. Their widths decrease as the acceleration becomes more efficient.
The morphology of the radio synchrotron emission obtained for the young ejecta-dominated stage of SNRs will differ from that of SNRs in the Sedov phase (but not in X-ray). Indeed, Reynolds (1998) has shown that both the normal and tangential components of the magnetic field decrease behind the forward shock in the Sedov phase and, as a result, we expect the radio synchrotron emission to decrease behind the shock (however, less rapidly than the X-ray synchrotron emission since the radio electrons do not experience radiative losses).
Our model qualitatively reproduces the main features of the radio and X-ray observations of emission in young ejecta-dominated SNRs (e.g., Tycho & Kepler), i.e. bright radio synchrotron emission at the interface between the shocked ejecta and ambient medium, and a narrow filament of X-ray emission at the forward shock. However, this model is unable to reproduce the thin radio filaments observed at the forward shock in some SNRs (for instance those seen in Tycho's SNR, Dickel et al. 1991).
We note that extensions of this work to cases with exponential ejecta profiles and/or SNRs evolving in a pre-supernova stellar wind with varying magnetic fields, cannot be done with self-similar solutions. These cases can be calculated in the numerical CR-modified hydrodynamical model described in Ellison et al. (2005) and this work is in progress (Ellison & Cassam-Chenaï 2005).
The evolution of the normal (subscript r) and tangential
(subscript t) components of the magnetic field at the downstream
position, B, is given by (Reynolds & Chevalier 1981):
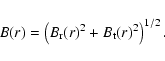 |
(A.3) |
We assume that the upstream magnetic field at time tj,
B0,j is isotropic and fully turbulent so that the components
of the immediate post-shock magnetic field Bj in Eqs.
(A.1) and (A.2) are given on average by
(Berezhko et al. 2002):
We consider that the current magnetic field upstream of the
forward shock,
![]() ,
can behave like:
,
can behave like:
We define the magnetic field contrast factor,
![]() ,
as the ratio between the current magnetic field in a
fluid element, B, and the current one just behind the shock,
,
as the ratio between the current magnetic field in a
fluid element, B, and the current one just behind the shock,
![]() .
We have:
.
We have:
Assuming adiabaticity of the thermal gas, the magnetic field
contrast factors of the normal and tangential components of the
field are given by:
In the framework of these self-similar solutions, the forward
shock velocity tends to infinity at early times, corresponding to
fluid elements close to the contact discontinuity at the current
time. To limit the maximum velocity to a realistic value, we look
at the value of
![]() for a shock velocity ratio
vj/vs = 10. For the typical forward shock velocity vsthat we have used for the numerical application, the initial
velocity corresponds to
for a shock velocity ratio
vj/vs = 10. For the typical forward shock velocity vsthat we have used for the numerical application, the initial
velocity corresponds to
![]() .
This shock velocity is the criterion used to
define the radial position of the oldest fluid element that is
currently located close to the contact discontinuity.
.
This shock velocity is the criterion used to
define the radial position of the oldest fluid element that is
currently located close to the contact discontinuity.
Here, we consider the case of both an uniform ambient medium
(s=0) and upstream magnetic field (q=0). Under this
assumption,
Bs=Bj, since
![]() is constant
with time. Then, the magnetic field contrast factor,
is constant
with time. Then, the magnetic field contrast factor,
![]() is equal to B/Bj and can be viewed as a compression or a
dilution factor. Table A.1 (top) gives the contrast
is equal to B/Bj and can be viewed as a compression or a
dilution factor. Table A.1 (top) gives the contrast
![]() for different values of n.
for different values of n.
| n | Rs/R |
|
|
vs(km s-1) | |||
| 7 | 1.181 | 0.964 | 0.95 | 4840 | |||
| Test-particle | 9 | 1.140 | 0.885 | 5.0 | 4850 | ||
| 12 | 1.121 | 0.836 | 54 | 4940 | |||
| n | Rs/R | Ps/P |
|
|
|
vs (km s-1) | |
| 7 | 1.080 | 1.135 | 0.806 | 0.50 | 0.66 | 4370 | |
| Nonlinear DSA | 9 | 1.060 | 1.045 | 0.754 | 2.6 | 3.4 | 4470 |
| 12 | 1.051 | 0.988 | 0.714 | 28 | 36 | 4610 | |
In the ideal non-linear case, where the acceleration is
instantaneous and efficient, the thermal gas pressure falls to
zero at the contact discontinuity while the relativistic gas
pressure goes to infinity. Hence, the contrast factor of the
tangential field component,
![]() ,
given by Eq.
(A.9), obtained in the test-particle limit, is not
defined when
vj/vs tends to infinity.
,
given by Eq.
(A.9), obtained in the test-particle limit, is not
defined when
vj/vs tends to infinity.
However, the contrast of the tangential component of the magnetic
field can also be found by using the adiabaticity of the
relativistic gas:
Because the thermal gas pressure vanishes as we approach the
contact discontinuity in the case of ideal particle acceleration,
i.e., when the acceleration is instantaneous and efficient, the
contrast of the tangential field component,
![]() ,
will
always be smaller than in the test-particle case where the thermal
gas pressure rapidly tends to a constant (see Eq. A.9).
Table A.1 (bottom) gives the lower and upper limits
on the magnetic field contrast factor,
,
will
always be smaller than in the test-particle case where the thermal
gas pressure rapidly tends to a constant (see Eq. A.9).
Table A.1 (bottom) gives the lower and upper limits
on the magnetic field contrast factor,
![]() ,
in the case
of ideal nonlinear particle acceleration for
,
in the case
of ideal nonlinear particle acceleration for
![]() and for different values of n when
both the ambient medium and upstream magnetic field areuniform
(s=0 and q=0). The lower and upper limits on
and for different values of n when
both the ambient medium and upstream magnetic field areuniform
(s=0 and q=0). The lower and upper limits on
![]() are
obtained by replacing in Eq. (A.12) the ratio of
the self-similar relativistic gas pressures,
are
obtained by replacing in Eq. (A.12) the ratio of
the self-similar relativistic gas pressures,
![]() ,
by the ratio of the
self-similar total gas pressures,
,
by the ratio of the
self-similar total gas pressures,
![]() ,
and by the ratio between the self-similar relativistic gas
pressure at the shock and the self-similar total gas pressure,
Pc,s/P, respectively.
,
and by the ratio between the self-similar relativistic gas
pressure at the shock and the self-similar total gas pressure,
Pc,s/P, respectively.
However, for an injection efficiency lower than ![]()
![]() ,
the acceleration is not efficient enough for the shock
to be modified at the beginning of the evolution. In that case,
the fluid elements that have been shocked at the earliest times
are still dominated by the thermal gas so that test-particle
solutions could still apply locally.
,
the acceleration is not efficient enough for the shock
to be modified at the beginning of the evolution. In that case,
the fluid elements that have been shocked at the earliest times
are still dominated by the thermal gas so that test-particle
solutions could still apply locally.