A&A 443, 851-861 (2005)
DOI: 10.1051/0004-6361:20042173

The IMF of the field population of 30 Doradus[*],[*],[*]

F. J. Selman - J. Melnick

European Southern Observatory, Alonso de Córdova 3107, Santiago, Chile

Received 14 October 2004 / Accepted 7 June 2005

Abstract
The star-formation history and IMF of the field population of the 30 Doradus super-association is determined using Wide Field Imager photometry. The cluster NGC 2070 and the OB association LH104 are also studied and used for comparison. The star-formation history of the 30 Doradus super-association appears to be characterized by a large increase in star-formation activity 10 Myr to 20 Myr ago. This seems to be the case across the whole eastern half of the LMC as demonstrated by the ages of stellar populations as far away as 30 Doradus and Shapley's Constellation III. Star-formation appears to be occurring at a constant rate in the field and in loose associations, and in bursts in the clusters. The field IMF is found to have almost the exact Salpeter slope in the range $7 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$, at odds with previous claims. We find that, for objects with more complex star-formation histories, Be stars and selective incompleteness strongly affect the determination of the IMF for $M > 40~ {M}_\odot$, naturally explaining the observed deviation of the high mass IMF slope from the Salpeter value. The present work supports the idea of a universal IMF.

Key words: stars: formation - galaxies: stellar content - galaxies: Magellanic Clouds - galaxies: star clusters - techniques: photometric - methods: statistical

1 Introduction

Precise knowledge of the stellar initial mass function, or IMF, and its properties is a pre-requisite for understanding a large variety of astrophysical phenomena ranging from the origin of elliptical galaxies to the energetics of starburst, and from the chemical enrichment history of open star clusters to the chemical enrichment of the intracluster medium of clusters of galaxies (Wyse 1998). A constant in many of these studies is the assumption of a universal IMF for the underlying stellar populations. Although this assumption has found ample observational and theoretical support (Kroupa 2002, and references therein), some valid observational evidence and compelling counter arguments remain. Foremost among the empirical evidence is the work of Massey (2002) in the field of the LMC which claims an IMF much steeper than in the cluster population where it is nearly Salpeter. Weaker is the case of the Arches cluster near the center of our galaxy which has been reported to have a flatter IMF in its central region (Stolte et al. 2002; Figer et al. 1999). Among the compelling arguments, there are two that are particularly troublesome for the hypothesis of universality: the apparent nonexistence of low mass stars with primordial chemical abundances (Cayrel 1996; Truran & Cameron 1971), supported by simulations of the collapse of primordial composition clouds which predict a top-heavy IMF (Abel et al. 2002), and the apparent consensus that most field stars were formed in clusters. If most field stars are indeed formed in clusters, then a steeper IMF is expected in the field because low mass clusters ( $5~{M}_\odot \le {M}_{\rm cl} \le 20 ~{M}_\odot$) are more numerous and incapable of forming very massive stars (Kroupa & Weidner 2003).

We report in this work the results of a recent investigation for the field IMF of the 30 Doradus super-association in the LMC. In Sect. 2 we give a brief summary of the data, their reduction, and analysis. The main claim of this section is that, contrary to conventional wisdom, it is possible to determine unbiased effective temperatures even for the most massive stars using UBV photometry. We will see at the end that this initial claim was overly optimistic, not for the reasons usually given, but because there are classes of stars whose spectral energy distributions (SEDs) depart from those described by the models, mimicking stars of higher masses. In Sect. 3 we compare the IMFs of NGC 2070 and LH104 obtained with our method with previous determinations from the literature. We next present our IMF for the field discordant with that found by Massey (2002) and discuss the origin of the discrepancy. In Sect. 4 we discuss the impact of this result within the context of the discussion of the universality of the IMF.

   
2 Observations and data analysis

The methodology of this study follows closely that of our previous work on NGC 2070 (Selman et al. 1999). We combined spectroscopy of selected stars in the region (Bosch et al. 1999) with UBV profile fitting photometry for a large number of stars over an area a half-degree on each side. We then applied a Bayesian analysis to the photometric data using the spectroscopy to calibrate the procedure. In this way we obtain unbiased masses, age, and reddenings for each star.


  \begin{figure} \par\includegraphics[width=17.4cm,clip]{2173fg1.eps} \end{figure} Figure 1: Colour rendition of the data used in this study. The nine UBV WFI frames have been combined to produce an RGB image of the field studied.
Open with DEXTER

   
2.1 Observational material and data reduction

The observations were carried out with the Wide Field Imager (WFI) mounted on the MPG/ESO 2.2-m telescope at La Silla. The telescope is an f/8 Ritchey-Chretien with a telescope-instrument scale of 0 $.\!\!^{\prime\prime}$238/15 $\mu$ pixel. The detector is a mosaic consisting of 8 main CCDs (plus an extra one for guiding) arranged in two rows of 4 CCDs each. All the CCDs are 2046k $\times$ 4098k EEV 44-82 CCDs. They have a readout noise of $\sim$4.5 e-, and an inverse gain of $\sim$2 e-/ADU. The maximum signal is limited to $\sim$65 000 ADU. The whole light path consists of two mirror reflections, a set of two triplets, a filter between the triplets, and the dewar window. For the whole system, a V=12.5 B1 V star, in ten second integrations in the B-band (the most sensitive of the UBV bands in the WFI system) is a factor of two below the limit of saturation, with a peak value of approximately $\sim$130 000 e-. For any star fainter than V=12.5 the non-linearities are less than 1.5% peak-to-valley. The whole mosaic lies behind a single disk shutter with a spatial uniformity better than 0.2% and overall accuracy better than 1% for integration times longer than 10 s.

Table 1 shows the actual ESO archive frames used which correspond to three dithered images each in the three standard UBV filters. Figure 1 shows a colour rendition of all these frames. The data was overscan corrected, bias subtracted, and flat-fielded with twilight sky flats using the standard techniques and the mscred package in IRAF (Valdes 1998).

One extra step was needed to obtain unbiased magnitudes across the field of the WFI mosaic: correcting the counts for the effect of light concentration. This effect, which has been studied in detail by several authors (Manfroid et al. 2001; Selman 2004; Andersen et al. 1995), causes field dependent photometric zero points which for the WFI are to first order colour independent. We determine a correction as a function of position in the mosaic and use observations of standard stars in several positions across the array to determine that the residuals of the photometry decrease from 0.034 to 0.009 in V, from 0.029 to 0.010 in B, and from 0.040 to 0.014 in U.

Extensive simulations of the WFI transformation equations showed that it is impossible to convert the instrumental magnitudes as the strong colour term for the WFI B band, and to a lesser extent for the WFI U band, induce a reddening related uncertainty[*] which can be as large as 8% in B and 5% in U. Because the effect is in opposite directions in U and B, the total effect becomes $\sim$13% in (U-B). Furthermore, our simulations show that the U filter colour equation has a many-valued dependence on spectral type which can be as large as 5%. For these reasons we decided to work in the WFI band-passes themselves. As part of the analysis processes we are able to use the subset of stars with spectroscopy to calibrate our conversion of magnitudes to physical parameters.

Finally we did chip-by-chip profile fitting photometry in each of the nine frames shown in Table 1. We used DAOPHOT II (Stetson 1997,1987) as implemented within IRAF (Massey & Davis 1992). Using an interactive interface we determined a linearly varying point spread function (PSF) for each chip for a total of 81 PSFs. With approximately 20 stars per PSF this required the examination and cleaning of over 1500 stars. As a result we obtained a catalogue with magnitudes for a large number of stars, most of them with three magnitudes in three colours.

One of the most negative aspects of not working in the standard system is the impossibility of comparing with previous work. To overcome this problem, and for comparison, we decided to do a transformation to the standard system using the equations for unreddened stars. We do this with the understanding that such a comparison can only uncover gross errors. The conversion equations from unreddened Johnson UBV to WFI ubvwill also be needed when we place each point of a theoretical isochrone on the observable WFI ubv colour-magnitude space. In doing this we are defining a native WFI photometric system which leaves us the freedom to assign arbitrary zero points. We do this by forcing the colours of the bluest unreddened main-sequence stars to be (u-b)0 = -1.229 and (b-v)0 = -0.33, the same as for Johnson UBV. Thus, the transformation equations for unreddened stars are

  \begin{eqnarray*}{v} & = & V + 0.08\times \{0.33 + (B-V)\} \\ [1mm] {b} & = & B... ... \\ [1mm] {u}-{b} & = & (U-B) + 0.30\times \{1.229 + (U-B)\}, \end{eqnarray*}


where the equation for u and (u-b) are only valid for dwarfs with (U-B)<0. In writing the above equations we have referred our zero points to the work of Selman et al. (1999), which in turn referred to the zero points of Parker (1993): v = v' + v0, b = b' + b0, and u = u' + u0, where prime quantities are the raw WFI instrumental magnitudes[*] and subscripted quantities are the zero point shifts required to bring our photometry to the system of Parker for the hottest stars: v0=24.29, b0=24.39, and u0=20.82. Figure 2 shows the residuals obtained if we subtract our UBV magnitudes from Parker's. The figure shows that in the three band-passes there are no major systematic effects.

There is one further check that we can make using stars with known spectroscopic types. Figure 3 shows the colour-colour diagrams for the Parker and WFI data for a set of dwarf stars with spectral types earlier than B2 near NGC 2070. The top panel shows the Johnson UBV colours measured by Parker for these stars and the bottom panel shows the WFI ubv colours. The parallel lines show the reddening vectors in the respective colour spaces for O3 and B0 stars for a galactic reddening law (described in the next section for the WFI ubv system). Two things are immediately evident in these figures: first, a systematic shift in colour is seen in the high quality WFI data, but masked by random errors in Parker's data. Second, the better quality of the WFI data which, apart from the systematic shift, is restricted to a band of comparable width of what is expected for these stars. The origin of this shift, which is almost 20%, is only partly due to the errors in the transformation equations for reddened stars, which our simulations show to be less than 13%. We use these stars with spectroscopy to determine this systematic colour shift. From their spectroscopy we determined physical parameters: effective temperatures and bolometric magnitudes. We then determined the shift that we have to apply to the colours so that the physical parameters determined with the method of the next section agree with the spectroscopic ones. We found that to predict spectroscopic types from the WFI photometry we need to subtract 0.08 to (b-v) and add 0.12 to (u-b).


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{2173fg2.eps} \end{figure} Figure 2: Comparison between the magnitudes of Parker (1993) and those of the present work, converted to the standard system. The differences are in the sense $m_{\rm parker} - m_{\rm wfi}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{2173fg3a.eps} \includegraphics[width=8cm,clip]{2173fg3b.eps} \end{figure} Figure 3: ( Top) The positions in the colour-colour diagram for stars of spectral types earlier than B2, according to Parker's (1993) photometry. ( Bottom) The WFI data, calibrated using Parker's photometry, for the same set of stars. The lines show the reddening trajectories for O3 and B0 stars. The typical errors are smaller than $\pm $0.01 for the brighter stars ( upper left-most stars), and approximately $\pm $0.04, about twice the size of the symbols for the fainter stars at the lower right.
Open with DEXTER

   
2.2 The Bayesian analysis

We use the techniques in Selman et al. (1999) modified to work with the non-standard band-pass to determine the physical parameters using our WFI ubv photometry.

The Geneva evolutionary models (Schaerer et al. 1993) are used to calculate effective temperatures ( $T_{\rm eff}$) and effective surface gravities ($\log~ g$) as a function of mass (M) and age (t) for a large grid of stars with a metallicity of Z=0.008 appropriate for the LMC. We then used the calibrations of Schmidt-Kaler (1982) for standard unreddened Johnson UBV colours, and Malagnini et al. (1986) or Vacca et al. (1996) for bolometric corrections as a function of $T_{\rm eff}$ and $\log~ g$.

The next step is to use the transformation equations from the previous section to determine the WFI ubv magnitudes as a function of M and t. These equations are only valid for dwarf stars and, although the correction for giants and super-giants is not large for the B and V band-passes, it can be up to 0.05 mag in U. We use simulations with the WFI band-passes and the models in Kurucz (2002) to determine these corrections.

At this point we have the position in ubv space for unreddened stars of mass M and age t. Next we need the reddening law to estimate the displacement of the star as a function of reddening. Selman et al. (1999) found that the extinction law in the area around NGC 2070 was, within the errors, similar to the normal galactic extinction. For the determination of the extinction law in the WFI ubv system we used the Fitzpatrick (1999) parametrization of the galactic extinction law and the Kurucz models (we validated the procedure reproducing the Johnson UBV extinction law). The result is given by

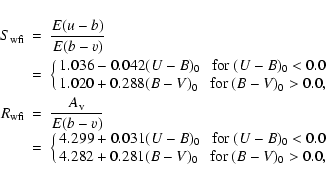
\begin{eqnarray*}S_{\rm wfi} & = & {E( {u}- {b})\over E( {b}- {v})} \\ & = & \... ... 0.281(B-V)_0 {{\rm\ \ \ for}\ (B-V)_0 > 0.0},\cr } \right. \\ \end{eqnarray*}


where the standard, unreddened, Johnson colours have been used as independent variables.

Thus, given physical parameters mass, age, and reddening we can calculate its WFI ubv magnitudes which, together with a model for the measurement errors, we transform into a distribution of probabilities to find a star in a given volume element in the stereogram defined by Selman et al. (1999). We then use Bayes' theorem to determine the most likely set of physical parameters for a given UBV observation. Formally, we construct a column vector with these magnitudes

\begin{displaymath}\vec{m_*} = \pmatrix{{u}_*\\ {b}_*\\ {v}_*}. \end{displaymath}

We next use a model of errors to assign to each physical model, now indexed with the vector of magnitudes, $\vec{m_*}$, the probability of observing a given set of WFI ubv magnitudes. Assuming Gaussian errors we can write

\begin{displaymath}p(\vec{m}\vert\vec{m_*},Q_{\rm m}^*) \propto {\rm e}^{-{1\ove... ...m m}[\vec{m}-\vec{m_*}]} \propto {\rm e}^{-{1\over 2} \chi^2}, \end{displaymath}

where $\vec{m_*}$ indexed the physical models, $Q_{\rm m}^*$ is the curvature matrix, and encapsulates our error model. It is given by $Q_{\rm m}^* = {\rm Diag}(\sigma_u^{-2},\sigma_b^{-2},\sigma_v^{-2})$, where we have assumed independent errors.

The use of Bayes theorem allows us to write

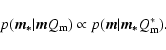
\begin{displaymath}p(\vec{m_*}\vert\vec{m}Q_{\rm m}) \propto p(\vec{m}\vert\vec{m_*}Q_{\rm m}^*). \end{displaymath}

This relation is the one that allows us to assign, to each observation $\vec{m}$, the most probable model, $\vec{m_*}$.

Because we believe that visualization of the whole process is vital to keep in check the multitude of systematic effects that can affect the data, we have decided to work in the color-magnitude stereogram space, CMS . In this space a measurement will be characterized by a vector given by $\vec{x} = (b-v,u-b,v)^{\rm T}$. Since $\vec{x}$ is related to $\vec{m}$ by a unitary transformation, the probability density of $\vec{x}$ is given by

\begin{displaymath}p(\vec{x}) = {\rm e}^{-{1\over 2} [\vec{x}-\vec{x_*}]^{\rm T}Q_x[\vec{x}-\vec{x_*}]}, \end{displaymath}

where $Q_x = O^{\rm T}Q_{\rm m}O,\ \ O\vec{x} = \vec{m}$. The price paid for working in color-magnitude space is that the covariance matrix, Cx = Qx-1is no longer diagonal.

Figure 4 shows the positions of the stars in the 3-D stereogram, together with the locus of the 4.5, 12, and 50 Myr isochrones. The 12 Myr isochrone has been extruded to show the effect of reddening. The Bayesian method could be understood as finding the minimum distance from the ubv point of a star to the reddening-extruded surfaces of each isochrone, the so-called theoretical surface.

  \begin{figure} \par\mbox{\includegraphics[width=7cm,clip]{2173fg4a.eps} \includegraphics[width=7cm,clip]{2173fg4b.eps} } \end{figure} Figure 4: ( Left) Observed stellar points, together with isochrones for 4.5, 12, and 50 Myr, in the 3-D colour-colour-magnitude stereogram. The theoretical surface is plotted for the 12 Myr isochrone. The tubes representing each isochrone is painted blue, yellow, or red depending on whether the star is of luminosity class V, III, or I respectively. ( Right) Evolutionary track for a 12 $M_\odot $ star. The color of the tube represents the luminosity class, while its width is proportional to the speed at which the star would move during its evolution, representing one measure of the observing probability. Both figures created with VTK (Schroeder et al. 1998).
Open with DEXTER


  \begin{figure} \par\includegraphics[width=9.7cm,clip]{2173fg5.eps} \end{figure} Figure 5: Comparison of $T_{\rm eff}$ obtained photometrically and spectroscopically. The circles correspond to stars from NGC 2070, the squares to LH104, and the triangles to Hodge 301. Filled symbols represent supergiants, while open symbols are used for all other luminosity classes. The thick line below the diagonal illustrates the effect of a 0.05 blueward shift in (u-b).
Open with DEXTER

The method so far presented, although it makes use of Baye's theorem, is just a Maximum Likelihood method. For it to be called Bayesian, in the sense currently given to that term (Loredo 1992), it should incorporate information on the prior probabilities, or priors. That is, the a priori probability distribution of the different reddening values, masses, and ages. One could think in terms of an iterative scheme, in which once a solution is found for all stars in the sample, we can construct the priors, and use them in a second solution.

One further issue should be taken in consideration: during the course of its evolution, a star transits on its evolutionary track at different rates making the probability of observing a star in a given volume of the stereogram inversely proportional to the speed with which it moves. Figure 4 shows this effect for the 12 $M_\odot $ track. The color of the tube represents the luminosity class of the star, but now its width represents the observing probability. We can see the well-known result that a star is most likely to be observed in the main sequence phase, in the ascent to the red giant branch (near the Hayashi edge), and at the bluest extremes of the blue loops.

In what follows we will only use the distribution of reddening values as a prior, and only to set limits to the maximum and minimum values allowed. This is done so that the method will not pick up stars with unreasonable reddening values forcing them to populate the physically permitted regions of the HR diagram. The minimum reddening value is thus selected to be 0.0, while, from the distribution of reddening values found in NGC 2070 in Selman et al. (1999), the maximum reddening value is chosen to be E(B-V)=2.0. For all the other variables we will let the data speak for itself.

Figure 5 and Table 3 compare the $T_{\rm eff}$obtained with this method with that obtained for a group of stars observed spectroscopically by several authors (Schild & Testor 1992; Walborn & Blades 1997; Bosch et al. 1999).

The stars used to draw this figure come from NGC 2070, LH104, and Hodge 301, a small cluster of stars to the north-west of NGC 2070. There are four outliers: 16000959 and 16000546 are foreground stars for which our analysis breaks down; for 16001150 our find algorithm erroneously selected a much fainter star; while 16000332 is a star with uncertain spectroscopic type. This figure shows that there is an unbiased correlation between spectroscopic and photometric temperatures for main sequence stars. Nevertheless, we see that there is a discrepancy for some stars which have been identified as giants and supergiant stars. Note particularly the set of points from LH104 with $T_{\rm eff}\sim4.3$: all these stars are B2 III stars, prime candidates for Be stars. The other LH104 stars, which are in the correlation line, are mostly of types B1 V and B2 V, with a few B0 V, B0.5 V, and two B1 III. The small triangles next to the supergiants come from the comparison stars in Hodge 301, and correspond to Be stars (Grebel & Chu 2000). Restricting our counts to main-sequence stars the bias in the supergiants does not affects us, but the Be stars cannot be singled out with broad-band photometry alone.

Be stars have SEDs that mimic stars of higher effective temperatures. Mendoza (1958) found that many Be stars have the Balmer jump in emission giving rise to a U excess. Redward of 500 nm, and extending into the infrared, there is excess emission affecting the V filter (Schild 1966). These two effects displace these stars to the upper right of the colour-colour diagram by as much as 0.3 mag (e.g. see Fig. 6 in Mermilliod 1982). The number of Be stars can be a considerable fraction of the early B-types. Grebel & Chu (2000) estimate this to be 60% for B0, 40% for B1, and 30% for B2 stars in Hodge 301. Keller et al. (1999) estimate that approximately 30% of the early B stars in clusters and 15% in the field are Be. We can expect an effect dependent on the age of the stellar population studied, as these stars are most frequent in clusters with ages between 10 Myr and 20 Myr (Fabregat & Torrejón 2000; Mermilliod 1982; Grebel 1997), even though they are observed in clusters as young as 2.6 Myr (Maeder et al. 1999).

We can estimate the effect of the distorted SEDs of Be stars in our determination of masses by noticing that the effective temperature is overestimated by $\sim$0.15 dex and thus the bolometric correction is overestimated by $\sim$1.5 mag, shifting the most massive of these stars, which typically have masses between 20 and 40 $M_\odot $, to the 60 to 85 $M_\odot $ mass bin. Because the fraction of Be stars in the field is small the effect in the source mass bin is also small, but the effect will be significant in the less populated upper mass bins where they migrate to[*]. This is exactly what is observed as we will see in the next section.

With the above calibration we have determined the physical parameters for the program stars (Full Table 2 is only available in electronic form at the CDS). Figure 6 shows the resulting HR diagram. The upper panel shows the stars alone and the lower one also shows several reference curves: the evolutionary tracks at the model masses and the isochrones corresponding to the main-sequence lifetimes for those masses - ZAMS, 2.9 Myr (120 $M_\odot $), 3.2 Myr (85 $M_\odot $), 3.8 Myr (60 $M_\odot $), 4.9 Myr (40 $M_\odot $), 7.2 Myr (25 $M_\odot $), 9.1 Myr (20 $M_\odot $), 12.9 Myr (15 $M_\odot $), 17.6 Myr (12 $M_\odot $), 24 Myr (10 $M_\odot $), and 47 Myr (7 $M_\odot $). The figure also shows lines of constant visual magnitude: V=12.5, above which nonlinearity affects the data; V=17.5, below which the catalogue becomes incomplete and V=16.0, below which differential reddening affects the completeness of the sample. We should only use data between the upper and the middle thick lines. We can see from Fig. 6 that this limits the range of unbiased mass bins to those between $\ga$12 $M_\odot $ and $\la$40 $M_\odot $.


  \begin{figure} \par\includegraphics[width=8cm,clip]{2173fg6.eps} \end{figure} Figure 6: Photometrically determined HR diagram of the whole region under study.
Open with DEXTER

Figure 6 shows real and spurious features. Among the real features are the apparent turnoff between 7 and 15 Myr (the whole eastern half of the LMC appears to be characterized by a large increase in star-formation activity 10 Myr to 20 Myr ago as demonstrated by the ages of stellar populations as far away as 30 Doradus and Shapley's Constellation III, Braun et al. 1997); the red supergiants corresponding to such a turnoff, and confirming it; contamination from disk stars between the MS and the red-giant branch somewhat filling the Hertzsprung gap[*]; and the tendency of the stars to populate extremes of the blue loops. We can also appreciate the completeness limit of the photometry at approximately V=17.5. Among the spurious features we can see an accumulation of points toward the ZAMS corresponding to stars with errors in their photometry either due to random measuring errors, or to real features such as emission lines; some structure in the red supergiant region probably due to the complicated topology of the isochrones there is also apparent.

   
3 The IMF of the field population

The determination of the IMF of a group of stars is intrinsically entangled with the determination of their ages. We will use b(t), the birth rate , to refer to the number of stars of any mass born per unit time, per unit area on the sky. The fraction of stars born at time t in a mass interval $(m,m+{\rm d}m)$, $f(m,t){\rm d}m$, is called the stellar mass spectrum  at birth. Consider a region which started to produce stars at a time t=0, but that we observe at a later time T. The number of stars per unit area, dN, observed in a mass interval $(m,m+{\rm d}m)$, is given by

 \begin{displaymath} {\rm d}N = \left[ \int\limits_{t={\rm max}(0,T-\tau(m))}^T b(t){\rm d}t\right] f(m){\rm d}m \end{displaymath} (1)

where we have introduced the lifetime function, $\tau(m)$, the lifetime of a star of mass m. In the present work we only count main-sequence stars, so $\tau(m)$ corresponds to their main-sequence lifetime. The term between brackets in Eq. (1) depends on the mass m only through the lifetime function. Therefore, if we know the star formation history of the region, we can find its mass spectrum at birth from the observed mass spectrum.

Here we will consider only two possible star-formation histories: single bursts of duration $\Delta t$ a time T ago, and a constant rate of duration T. Thus, in the first case

 \begin{displaymath} {\rm d}N = b(0)\Delta t f(m){\rm d}m {\rm\ \ \ \ for \ \ \ \ } m < m_{\rm max}, \end{displaymath} (2)

where $m_{\rm max}$ is the largest mass a star can have and survive for a time T. For for the constant case,

 \begin{displaymath} {\rm d}N = b_0 \min(T,\tau(m)) f(m){\rm d}m, \end{displaymath} (3)

which for the mass range defined by $\tau(m)<T$ becomes,

 \begin{displaymath} {\rm d}N = b_0 \tau(m) f(m){\rm d}m. \end{displaymath} (4)

In this case, therefore, the mass spectrum at birth is simply obtained from the observed mass spectrum dividing by $\tau(m)$. It is customary to count stars in logarithmic (base 10) bins,

 \begin{displaymath} {\rm d}N = b_0\tau(m)mf(m)(\ln 10){\rm d}\log m = b_0\tau(m) \xi(\log m){\rm d}\log m. \end{displaymath} (5)

It is the function $\xi(\log m)$ which is usually referred to as initial mass function (Scalo 1986). Fitting a power law function to the high mass end we write,

 \begin{displaymath} f(m){\rm d}m \sim m^\Gamma {\rm d}\log m, \end{displaymath} (6)

which for a Salpeter (1955) power law has $\Gamma = -1.35$.

3.1 Gauging the method with previous work

Figure 7a shows the IMF for NGC 2070. The result is almost identical with that determined in Selman et al. (1999), with a slope $\Gamma = -1.26\pm0.07$, consistent with the Salpeter value and with the results of other investigations (Massey & Hunter 1998; Hunter et al. 1995,1996). Comparing this IMF with that from the previous work shows that we are complete down to ${M}=12~{M}_{\odot}$. Being this the most crowded region it is safe to state that in the rest of the super-association we are complete down to at least the same mass. Notice also that, because this is such a very young cluster, there has not been enough time to develop a large population of Be stars so there is no apparent artifact from their presence.


  \begin{figure} \par\includegraphics[width=6.6cm,clip]{2173fg7a.eps} \includegraphics[width=6.6cm,clip]{2173fg7b.eps} \end{figure} Figure 7: a) IMF of NGC 2070. The solid and dotted lines represent the best fit to the IMF from Selman et al. (1999), and its 1$\sigma $ uncertainty. The IMF has been normalized to a 1 Myr burst. b) PDMF, open circles, and IMF, filled circles with error bars, for LH104. The dotted and solid lines represent the best fits to the PDMF in the $12 ~{M}_\odot \le {M} \le 120 ~{M}_\odot$, and the $12 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$ mass ranges, respectively. The triangles plot the IMF from Testor & Niemela (1998).
Open with DEXTER

Figure 7b shows the PDMF and IMF for LH104. We have analyzed the same area studied by Testor & Niemela (1998) which in our catalogue is defined by 4800 < xc < 5650 and 1376 < yc < 2047, corresponding approximately to the finding chart in Fig. 5 of Schild & Testor (1992). We can see that the counts in the high mass bins compare well thus establishing the reality of the observed minimum in the IMF at masses between 30 and 40 $M_\odot $, and the bump at 50 $M_\odot $, the kind of effects expected from the presence of Be stars.

The upper mass bins are also affected by stochastic variations. For example, the two top mass bins, absent in Testor & Niemela (1998), contain a single star each (a Wolf-Rayet star and an O8 I((f)) star to which these authors assign 40 $M_\odot $, while we assign 66 $M_\odot $). For lower masses our counts reveal a steeper PDMF, probably an effect of our better observational material (0 $.\!\!^{\prime\prime}$238/pix sampling and 0 $.\!\!^{\prime\prime}$8 seeing versus 0 $.\!\!^{\prime\prime}$63/pixel sampling and 1 $.\!\!^{\prime\prime}$3 seeing).

Uncertainties in the star-formation history are particularly troublesome for LH104. Testor & Niemela (1998) report the PDMF as the IMF despite the fact that they find a complex star-formation history: "LH 104 consists mainly of a young population spreading out between 2 and 6 Myr (Table 4). The HR diagrams also show ... a group of older and less massive stars.'' The PDMF we derive has a slope $\Gamma = -1.9\pm0.3$ over $12 ~{M}_\odot \le {M} \le 120 ~{M}_\odot$and $\Gamma = -3.0\pm0.6$ over $12 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$. The IMF obtained dividing by the MS lifetimes has a slightly shallower slope at $\Gamma = -1.1\pm0.3$ over the larger mass range. Testor & Niemela (1998) report a slope, $\Gamma = -1.05\pm0.12$, which should be compared with our value of $\Gamma = -1.9\pm0.3$. Considering the effect of Be stars, the low number counts in the upper mass bins, and the uncertain star formation history, we cannot say whether the present data is consistent with a Salpeter IMF.

3.2 Applying the method to the field


  \begin{figure} \par\includegraphics[width=6.33cm,clip]{2173fg8a.eps} \includegra... ...]{2173fg8b.eps} \includegraphics[width=6.33cm,clip]{2173fg8c.eps} \end{figure} Figure 8: a), ( Top) Field studied in this work identifying several of the OB associations and clusters. Our definition of field is the area outside the marked circles, and within the boundaries of the image. This area has a total size of 0.124 kpc2. b), ( Middle) The IMF of the full LMC area covered by Massey (2002), lower line (open triangles), and that obtained by restricting Massey's data to the area covered by this study, upper line (filled triangles). c), ( Bottom) PDMF, open circles, and IMF, filled circle, for the field obtained in this study. The filled triangles correspond to the IMF obtained using data from Massey (2002), restricted to the area of the present study (includes a division by the mass dependent life-time function). The error bars in this latter IMF should be almost the same as those in the IMF of this study, those around the filled circles.
Open with DEXTER

The main objective of this work is the investigation of the IMF in the field of 30 Doradus to check the steep IMF found by Massey (2002). The area covered in that work is 10.9 kpc2 while the area covered here corresponds to only 0.124 kpc2. Nevertheless, the point under contention is the steep nature of the IMF in regions of low density. Figure 8a shows the intersection between the areas covered by this study and the field defined in Massey et al. (1995); Massey (2002). Although we cover a much smaller area, there is a non-negligible region of overlap. Figure 8b shows the IMF of this region constructed using Massey's (2002, Table 8A) compared with his IMF for the whole area. Although the stellar number density is almost a factor of ten larger in the smaller region, the slope of the IMF does not change by much (-3.4 in the smaller region versus $-3.8\pm0.6$ in the larger region).

Table 4: Mass functions for the fiels stars.

Table 4 and Figure 8c show the PDMF and IMF for the field. We can see that between 7 and 40 $M_\odot $ the PDMF is well represented by a power-law with a characteristic fall-off for lower masses and a bump for $M > 40~{M}_\odot.$The data from Massey (2002) restricted to our field is shown as filled triangles in Fig. 8c without any vertical shift. We can see that the counts compare well with the exception of the lowest mass point. The break from the power-law for masses larger than 40 $M_\odot $appears thus to be real. Following the discussion in Sect. 2.2, this is what we expect from the presence of Be stars.

We can also see that the effect is not as pronounced as in the case of LH104, consistent with the lower fraction of Be stars expected in the field. To avoid the effect of the Be stars and the effect of selective bin depletion induced by the upper magnitude cut discussed below, we restrict the analysis to the range $7 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$. In this mass range the PDMF is well represented by a power-law with slope $\Gamma = -2.58\pm 0.05$, while the IMF has slope $\Gamma~=~-1.38~\pm~0.04$, significantly flatter than the $\Gamma~=~-3.8~\pm~0.6$ obtained by Massey in the range $25 ~M_\odot \le M \le 120 ~M_\odot$, and close to the Salpeter value.

   
4 Discussion

What is the origin of the discrepancy? There are several possible causes. (1) Massey's work is valid for $25 ~M_\odot \le M \le 120 ~M_\odot$ while ours is only valid in the range $7 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$. We do not believe this to be the main reason for the discrepancy since there are no good reasons to believe that there is a break in the IMF above 50 $M_\odot $. The Be effect also affects Massey's work, as revealed by the general agreement between the counts for $40 ~M_\odot \le M \le 120~ M_\odot$. (2) Massey's work is based on data obtained with the Curtis-Schmidt 0.6-m telescope at CTIO with a pixel size of 2.32 $^{\prime\prime}$. The upper limit at which the detector becomes non-linear is reported at V=12.0. Thus, out of the four mass bins used for the determination of the IMF, only the lowest one at $25 ~M_\odot \le M \le 40 ~M_\odot$ is free of non-linearity effects. (3) As illustrated in Fig. 9, the imposed cut-off at V=12.0 introduces a strong steepening bias on the IMF. This selective bin depletion is due to the rejection of stars still in the main sequence but above the V=12.0 line. If we correct the counts by the fraction of area of the mass bin above the V=12.0 line we obtain an IMF consistent with Salpeter within the reported errors. (4) Massey's work is based on aperture photometry with a 16 $^{\prime\prime}$ diameter aperture corresponding to 4 pc. In Selman (2004) we have shown that the two-point correlation function of the distribution of stars in the 30 Doradus super-association shows an excess of pairs with separations smaller than 4 pc. This excess is a factor of three to five over what is expected from a random distribution of points. Thus, Massey's lower mass bin can be significantly affected by the migration of lower mass multiple systems to higher mass bins.


  \begin{figure} \par\includegraphics[width=6.2cm,clip]{2173fg9.eps}\par \end{figure} Figure 9: HR diagram of the field of the 30 Doradus super-association. The open circles correspond to the values obtained in this work using the Bayesian technique. The filled circles correspond to the stars from Massey (2002) catalogue restricted to our field (his $T_{\rm eff}$ and $M_{\rm bol}$). The thick line corresponds to V=12.0.
Open with DEXTER

We started this research with the aim of determining unbiased masses for a sample containing the most massive stars known using only photometry. The method applied to dwarf stars works extremely well. Nevertheless, for a real sample of young stars this is not enough. Such a sample includes many varied stars, the most problematic being the Be stars. WR stars also have, by their mimicking of more massive stars, the ability to contaminate the upper mass bins. Because of this it becomes necessary to use other methods, such as spectroscopy, to identify and properly "weight'' these stars. Another possibility is to use H$_\alpha$ imaging to identify them and to either remove them from the sample altogether (and use simulations to determine the bias introduced by this), or to correct their photometry as recently done by Keller et al. (2000).

Is the IMF universal? It is perhaps too ambitious to address such an issue with the observational material at hand which pertain to a single region, but we are starting to understand the multitude of effects that can affect the determination of the IMF which, if not considered, mimic variations: variable reddening, Be stars, improper modeling of the stars themselves, variations in the reddening law, binaries, etc. Figure 5 in Kroupa (2002) shows that the $M>1~M_\odot$ IMF slopes for a large variety of objects cluster around the Salpeter value with a range of $\pm $0.5 units. This variation can naturally be accommodated by the empirical uncertainties in the IMF determination. Showing that the 30 Doradus field IMF is a Salpeter power law between $7 ~{M}_\odot \le {M} \le 40 ~{M}_\odot$, this work supports the hypothesis of universality[*].

  \begin{figure} \par\includegraphics[width=6.2cm,clip]{2173fg10.eps} \end{figure} Figure 10: The large open stars represent non-rotating stars of type B1 V, and B5 V. The open circles represent stars rotating at 80% of the critical speed, for several viewing angles. The reddest point corresponds to the equatorial view, while the bluest to the polar one. Filled circles represent stars rotating at the critical speed. The thick line represents E(U-B)=0.05 normal reddening (after Collins et al. 1991).
Open with DEXTER

The argument by Kroupa & Weidner (2003) for variations of the stellar IMF, namely the construction of the field population out of disrupted clusters, which produces a field population IMF which is steeper than the corresponding parent clusters IMF is interesting in the context of the present work. We can compare the IMF we derive for NGC 2070, with a slope $\Gamma = -1.26\pm0.07$, with the IMF we derive for the field, $\Gamma = -1.38\pm0.04$, both valid in the mass interval $25 ~M_\odot \le M \le 40 ~M_\odot$ (although the NGC 2070 slope is valid in a wider mass interval). Both slopes, derived here with exactly the same procedure and observational material, disagree only at the 2$\sigma $ level. Although the disagreement is small, it is in the direction predicted by (Kroupa & Weidner 2003). According to those authors (their Fig. 2), for a cluster IMF slope close to Salpeter, and for a cluster mass function with a slope $\beta\sim 2$, the IMF slope increases by approximately 0.2, while we observe a difference of 0.12 (close to the steepening they predict for $\beta\sim 1.9$). Nevertheless, the difference can be due to many other factors such as different fractions of Be stars, different rotational properties of stars, or different binary fractions, which have also been shown to affect the determination of IMF slopes (Sagar & Richtler 1991).

One could ask whether it is possible to determine the IMF of different objects with enough precision to be able to detect real variations. We have seen that Be stars affect the determination of IMF slopes of different objects to varying degrees: NGC 2070 probably has almost no Be stars while LH104 has a considerable fraction, and this is reflected in the IMF slopes. There are other subtleties which nevertheless become important if we want to reduce the magnitude of systematic errors. Figure 10 shows the effect in colours and magnitudes introduced by rotation, from Collins et al. (1991). The figure shows that we need photometry to an accuracy better than 0.5% in the colours if we expect the data to reflect and disentangle the effects of rotation and variable reddening (and this does not include the effect of rotation in the evolutionary models themselves). We do not only need higher quality data, both spectroscopically and photometrically, but also more realistic models.

The 30 Doradus super-association is the ideal laboratory for a thorough study of a young stellar population, and we should plan future observations keeping in mind what we have learned so far. To improve the quality of the photometry we need narrow or medium-band photometry, choosing the bands so as to minimize nebular contamination. A band around H$_\alpha$ should also be used to at least identify the Be stars, but this will be difficult in areas of strong nebulosity. The effect of reddening in the transformation equations is significant for broad-band photometry. The photometry should be done with telescopes with as little glass as possible in the light path: the zero-point variations across the field of the WFI introduced by the double triplet was a problem. Spectroscopic observations should be performed in a large number of stars to determine the value of v sini so that we can model the stars more realistically. To improve the current situation will be quite challenging.

Acknowledgements
This work was presented in partial fulfillment of the Ph.D. degree at Caltech by F.J.S., who thanks Nick Scoville, his thesis advisor, for the enormous support and many valuable suggestions which improved the final results. The authors would also like to thank the anonymous referee for many valuable suggestions, and specially for pointing out the work of Kroupa & Weidner (2003) about the effect on the slope of the IMF from constructing a field population out of clusters.

References

 

  
Online Material

Table 1: Log of data used in this work.

Table 2: Catalog of observed and physical parameters for the stars in the 30 Doradus super-association (The full catalog is only available at the CDS).

Table 3: Spectroscopic and photometric $T_{\rm eff}$ for stars in selected fields.


Copyright ESO 2005