A&A 443, 883-889 (2005)
DOI: 10.1051/0004-6361:20042144
G. Paturel1 - P. Teerikorpi2
1 -
CRAL-Observatoire de Lyon,
69561 Saint-Genis Laval Cedex, France
2 -
Tuorla Observatory, Turku University, Väisäläntie 20, SF21500 Piikkiö, SF, Finland
Received 8 October 2004 / Accepted 18 June 2005
Abstract
The unique measurements with the Hubble Space Telescope of Cepheid variable stars in nearby
galaxies led to extragalactic distances that made the HST Key Project conclude that the
Hubble constant is H0 = 72 km s-1 Mpc-1.
The idea that H0 is now known is widely spread among the astronomical community.
Some time ago, we suggested that a strong selection effect may still exist in the Cepheid method,
resulting in too short distances.
Using a model similar to traditional bias corrections, we deduce here new estimates of distances from HST and previous
ground-based observations which are both affected by this effect, showing the same trend which starts at different distances.
The recent measurement of M 83 with the VLT is unbiased.
Revisiting the calibration of HSTKP's with our new scale, makes long-range distance criteria
more concordant and reduces the value of H0 to
![]() 60 km s-1 Mpc-1.
Locally, the corrected Cepheid distances give
60 km s-1 Mpc-1.
Locally, the corrected Cepheid distances give
![]() km s-1 Mpc-1and reduce the velocity dispersion in the Hubble flow.
These numbers are indicative of the influence of the suggested Cepheid bias in the context
of the HSTKP studies and are not final values.
km s-1 Mpc-1and reduce the velocity dispersion in the Hubble flow.
These numbers are indicative of the influence of the suggested Cepheid bias in the context
of the HSTKP studies and are not final values.
Key words: stars: variables: Cepheids - cosmology: distance scale
The Hubble Space Telescope (HST) has provided astronomers with unprecedented high accuracy measurements free of atmospheric disturbance (Kennicutt et al. 1995). It can detect Cepheid stars in galaxies, up to the Virgo cluster. The determination of distances via the Period-Luminosity (PL) relation (Leavitt & Pickering 1912; Madore & Freedman 1991) made it possible to calibrate several secondary distance indicators (Freedman et al. 2001), which can be used to measure the distances to large numbers of more distant galaxies and to determine the global value of the Hubble constant.
At a given Cepheid period, the cosmic dispersion of the average
absolute magnitude is so small (![]() 0.2 mag) that the systematic errors in the
measured distances to the calibrator galaxies were
considered as negligible. Based on this premise, the analysis led several teams
(including us) to almost concordant Cepheid distances
(Freedman et al. 2001; Saha et al. 2001; Paturel et al. 2002b).
The Hubble constant finally derived by the HST Key Project was
0.2 mag) that the systematic errors in the
measured distances to the calibrator galaxies were
considered as negligible. Based on this premise, the analysis led several teams
(including us) to almost concordant Cepheid distances
(Freedman et al. 2001; Saha et al. 2001; Paturel et al. 2002b).
The Hubble constant finally derived by the HST Key Project was
![]() km s-1 Mpc-1.
It seemed to many that the dilemma between high and low H was resolved, especially after
the WMAP background radiation analysis led to a similar value. At the same time, the
"precision'' global cosmology from the WMAP and (future) PLANCK experiments has emphasized
the growing importance of an accurate local H determination
to test the physics of the standard cosmological model (Spergel et al. 2003;
Blanchard et al. 2003).
km s-1 Mpc-1.
It seemed to many that the dilemma between high and low H was resolved, especially after
the WMAP background radiation analysis led to a similar value. At the same time, the
"precision'' global cosmology from the WMAP and (future) PLANCK experiments has emphasized
the growing importance of an accurate local H determination
to test the physics of the standard cosmological model (Spergel et al. 2003;
Blanchard et al. 2003).
The distances from the HST data also confirmed that the Hubble law works at surprisingly small scales as observed in independent studies (Sandage & Tammann 1975; Ekholm et al. 2001; Karachentsev et al. 2002). The Hubble diagram (velocity vs. distance) directly shows the local expansion rate H as given by these remarkable HST observations.
Figure 1 shows an important ingredient of the bias: how a relevant limiting magnitude of Cepheid samples changes with the kinematical distance. Ideally, one would like to see this limit increase in step with distance. But Fig. 1 reveals that the magnitude limit no longer grows properly above a certain distance. We have suggest that the biased region starts there for the HST distance determinations.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6884F01.eps} %\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg9.gif) |
Figure 1:
Variation of the deepness of the Cepheid samples with distance.
The (normalized) apparent V magnitude limit of the Cepheid
samples first grows with distance (radial velocity |
| Open with DEXTER | |
Another clue that suggests the presence of the bias, in addition to those already discussed in our previous papers, is given by Fig. 7a. The local Hubble diagram shows a departure from the expected linearity above a distance of 10 Mpc.
Finaly, it should be possible to see the departure from a proper sampling directly on the raw PL relation. As an example we show the V-band PL relation in Figs. 2a and b, for an unbiased galaxy (NGC 3351) and a biased one (NGC 1425). The positions of these galaxies are shown in Figs. 1 and 6, where the bias effect is visible.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6884F02.eps} %
\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{6884F03.eps} %\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg10.gif) |
Figure 2: V-band period luminosity relation for NGC 3351, an unbiased galaxy ( top panel) and NGC 1425, a biased galaxy ( bottom panel). These galaxies are shown in Fig. 6, where we compare the corrected and uncorrected distance moduli. |
| Open with DEXTER | |
Thus, the absolute limiting magnitudes of the Cepheid samples are calculated either as:
| (1) |
| (2) |
As in TP02, we then improve the
![]() diagrams
with a normalization of the absolute limiting magnitude. It is made using the list of
limiting observational periods of Cepheid stars (TP02).
Its rationale is to put all individual bias curves on the same mean curve by
compressing or expanding the x-axis according to
each individual period. This method highlights the phenomenon
with less distortion, as shown by observations (TP02)
and simulations (PT04).
diagrams
with a normalization of the absolute limiting magnitude. It is made using the list of
limiting observational periods of Cepheid stars (TP02).
Its rationale is to put all individual bias curves on the same mean curve by
compressing or expanding the x-axis according to
each individual period. This method highlights the phenomenon
with less distortion, as shown by observations (TP02)
and simulations (PT04).
The normalized absolute limiting magnitude is calculated as:
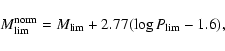 |
(3) |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6884F04.eps}\par\vspace*{2mm}
\includegraphics[width=8.5cm,clip]{6884F05.eps}
\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg21.gif) |
Figure 3:
Observed Hubble values in log scale against normal ( top panel) and normalized
( bottom panel) limiting absolute magnitude.
These absolute magnitudes are calculated from Eq. (1), using corrected radial velocity |
| Open with DEXTER | |
In our first paper TP02 we realized that the trend in the parameter
![]() could be due to a correlation of errors.
Indeed, in Fig. 3a, we calculate
the limiting absolute magnitude from the radial velocity, according to Eq. (1).
Thus, the radial velocity appears on both axes. If the observed velocity
of a given object is too large, due, for instance, to random velocity,
the corresponding point will be higher on the y-axis and lower on the x-axis.
The point will be displaced in a direction with a negative slope.
If the velocity is too small, the point will be displaced in the opposite direction,
i.e., along the same line. This effect could thus produce something like the effect
we have shown in Fig. 3a.
could be due to a correlation of errors.
Indeed, in Fig. 3a, we calculate
the limiting absolute magnitude from the radial velocity, according to Eq. (1).
Thus, the radial velocity appears on both axes. If the observed velocity
of a given object is too large, due, for instance, to random velocity,
the corresponding point will be higher on the y-axis and lower on the x-axis.
The point will be displaced in a direction with a negative slope.
If the velocity is too small, the point will be displaced in the opposite direction,
i.e., along the same line. This effect could thus produce something like the effect
we have shown in Fig. 3a.
In TP02, we
argued that the dispersion in the local Hubble law is small enough
so that the systematic distance error dominates in the
![]() diagram.
Indeed, at small distances, less than 5 to 10 Mpc, there is evidence for a low
dispersion
diagram.
Indeed, at small distances, less than 5 to 10 Mpc, there is evidence for a low
dispersion ![]() 50 km s-1 (e.g. Ekholm et al. 1999; Karachentsev et al. 2002, 2003;
Thim et al. 2003), as we discussed in TP02.
Also, we checked that the trend in the
50 km s-1 (e.g. Ekholm et al. 1999; Karachentsev et al. 2002, 2003;
Thim et al. 2003), as we discussed in TP02.
Also, we checked that the trend in the ![]() vs.
vs.
![]() diagram is
also visible for cluster members, when the cluster velocity is used for the members,
which should be at the same (cluster) distance.
diagram is
also visible for cluster members, when the cluster velocity is used for the members,
which should be at the same (cluster) distance.
If we repeat the test with
![]() (Eq. (2)), instead of
(Eq. (2)), instead of
![]() ,
there is also a correlation of errors but in the opposite direction.
We thus expect a positive slope. The result is shown in Fig. 4a.
There is no evidence of such a positive slope (on the contrary, the slope
still seems slightly
negative). The real trend is probably intermediate between these two extreme cases.
If a true bias exists, its signature is expected to diminish in the
,
there is also a correlation of errors but in the opposite direction.
We thus expect a positive slope. The result is shown in Fig. 4a.
There is no evidence of such a positive slope (on the contrary, the slope
still seems slightly
negative). The real trend is probably intermediate between these two extreme cases.
If a true bias exists, its signature is expected to diminish in the
![]() vs.
vs.
![]() diagram, when the kinematic distance is replaced by the biased
photometric distance. Figure 4b shows the same diagram, but with the normalization.
Thus, we conclude that the observed trend may well be real. Because such a trend can result
from a statistical bias (see the Appendix, and also PT04), we will apply the old precepts to analyze it,
by fitting a classical bias curve.
diagram, when the kinematic distance is replaced by the biased
photometric distance. Figure 4b shows the same diagram, but with the normalization.
Thus, we conclude that the observed trend may well be real. Because such a trend can result
from a statistical bias (see the Appendix, and also PT04), we will apply the old precepts to analyze it,
by fitting a classical bias curve.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6884F06.eps}\par\includegraphics[width=8.4cm,clip]{6884F07.eps}
\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg24.gif) |
Figure 4:
Observed Hubble values in log scale against normal ( top panel) and normalized
( bottom panel) limiting absolute magnitude.
These absolute magnitudes are calculated from Eq. (2), using observed distance moduli |
| Open with DEXTER | |
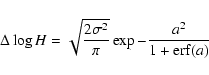 |
(4) |
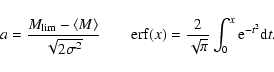 |
(5) |
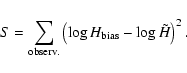 |
(6) |
We emphasize that this adopted value of the parameter ![]() for the bias curve
does not affect the global value of H0, as derived in
Sect. 5. Only the relative form
for the bias curve
does not affect the global value of H0, as derived in
Sect. 5. Only the relative form
![]() of the bias curve is important there,
giving an estimate of the distance bias for each calibrator galaxy.
of the bias curve is important there,
giving an estimate of the distance bias for each calibrator galaxy.
We have added in Figs. 5a and b (filled star) the measurement of
the galaxy M 83 (NGC5236) by Thim et al. (2003).
They used the 8.2 m Unit Telescope 1 of the ESO VLT under subarcsecond seeing
and could reach
![]() and
and
![]() d.
This very good ground observation puts M 83 at 4.5 Mpc, directly in the unbiased
plateau.
This demonstrates the capability of the Very Large Telescope to measure Cepheid distances
up to at least 5 Mpc.
d.
This very good ground observation puts M 83 at 4.5 Mpc, directly in the unbiased
plateau.
This demonstrates the capability of the Very Large Telescope to measure Cepheid distances
up to at least 5 Mpc.
In spite of the complexity of the bias, it is remarkable that
the simple bias curve represents quite well the behaviour of real data.
From the adopted bias curve we deduce the change
![]() and derive a new corrected distance for each calibrator galaxy.
and derive a new corrected distance for each calibrator galaxy.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{6884F08.eps}\par\vspace*{2mm}
\includegraphics[width=8.4cm,clip]{6884F09.eps}
\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg41.gif) |
Figure 5: Application of the cluster incompleteness bias curve fitting to the Cepheid bias. Top panel: the fit of Fig. 3b with the bias curve following the method described in the text. Bottom panel: the same figure as the previous one, when the bias fit is applied to Fig. 4b. We have added on both figures the recent measurement of the galaxy M 83 (filled star) by Thim et al. (2003). It is in the unbiased plateau. |
| Open with DEXTER | |
Only about twenty percent of galaxies can be considered as unbiased. This seems surprising, but in fact the fraction is similar to typical cases of galaxy cluster incompleteness or field galaxy Malmquist biases (Bottinelli et al. 1987; Theureau et al. 1997). Fortunately, most of the biased galaxies are still very valuable when corrected.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{6884F10.eps}
\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg44.gif) |
Figure 6: Comparison of corrected and uncorrected distance moduli for HST (light gray or red) and ground-based (dark gray or blue) observations. The ground-based (open circles) and HST observations (filled circles) show the same trend (dashed lines) at different distances as explained by the systematic error in Cepheid distances. From the ground, the bias starts soon beyond the closest galaxy (M 31), except for the new VLT result on M 83 (filled star). From space, the bias appears beyond the distance of closest galaxy groups (M 81). At the distance of the closest large galaxy cluster (Virgo) it has a large incidence. The identified galaxies (NGC 3351 and NGC 1425) were used above (Fig. 2) to show the PL relation for an unbiased and biased galaxy. |
| Open with DEXTER | |
The Hubble diagrams with uncorrected and corrected distances (Figs. 7a,b)
show that the correction improves the linearity of the Hubble relation
(the linear correlation coefficient increases from
![]() to
to
![]() )
and reduces the dispersion (from 120 to 84 km s-1). The local value of
)
and reduces the dispersion (from 120 to 84 km s-1). The local value of
![]() drops from 69 to 56 km s-1 Mpc-1.
It was surprising in Freedman et al. (2001) that
the local Hubble
diagram for Cepheids was quite scattered. Now we propose that this was due to the variable
distance bias.
drops from 69 to 56 km s-1 Mpc-1.
It was surprising in Freedman et al. (2001) that
the local Hubble
diagram for Cepheids was quite scattered. Now we propose that this was due to the variable
distance bias.
Even in the nearer distance range, for galaxies observed from the ground
with
![]() km s-1 (open circles in Fig. 7),
the dispersion decreases from 35 km s-1 to 31 km s-1. These numbers again highlight the
remarkable smoothness of the Hubble flow in the local inhomogeneous environment,
for long recognized
as a puzzle (e.g. Sandage 1999), but which has recently obtained theoretical
clarification from
km s-1 (open circles in Fig. 7),
the dispersion decreases from 35 km s-1 to 31 km s-1. These numbers again highlight the
remarkable smoothness of the Hubble flow in the local inhomogeneous environment,
for long recognized
as a puzzle (e.g. Sandage 1999), but which has recently obtained theoretical
clarification from ![]() CDM N-body simulations by Klypin et al. (2003) and Macciò et al.
(2005), and other considerations by Teerikorpi et al. (2005).
These studies support the suggestion by Chernin (2001) and Baryshev et al. (2001) that
the low velocity dispersion may be a local signature of the dominating cosmological vacuum
or dark energy.
CDM N-body simulations by Klypin et al. (2003) and Macciò et al.
(2005), and other considerations by Teerikorpi et al. (2005).
These studies support the suggestion by Chernin (2001) and Baryshev et al. (2001) that
the low velocity dispersion may be a local signature of the dominating cosmological vacuum
or dark energy.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{6884F11.eps}\par\vspace*{3mm}
\includegraphics[width=8.6cm,clip]{6884F12.eps}
\end{figure}](/articles/aa/full/2005/45/aa2144-04/Timg49.gif) |
Figure 7:
Local Hubble diagrams for uncorrected ( top) and corrected ( bottom) distances.
Top panel: the clear curvature in the uncorrected relation is now understood to be caused by the bias
that moves the galaxies up from the Hubble line. Open circles show the galaxies observed from the ground
with a velocity
|
| Open with DEXTER | |
Table 1 below summarizes the result.
The value of H0 from a given secondary distance indicator is
calculated as a
weighted mean (
![]() )
of the contribution of each calibrator.
The mean values of H0 are calculated by weighting individual values
according to the mean errors (
)
of the contribution of each calibrator.
The mean values of H0 are calculated by weighting individual values
according to the mean errors (
![]() ).
Two important facts are seen: i) the range of individual values is reduced.
In particular the Fundamental Plane method is no longer an enigmatic outlier, but is in good agreement
with the two main distance indicators (SNIa and Tully-Fisher). ii) The Hubble constant is
reduced by about 15 percent. The mean value from different distance indicators is H0=60 km s-1 Mpc-1.
).
Two important facts are seen: i) the range of individual values is reduced.
In particular the Fundamental Plane method is no longer an enigmatic outlier, but is in good agreement
with the two main distance indicators (SNIa and Tully-Fisher). ii) The Hubble constant is
reduced by about 15 percent. The mean value from different distance indicators is H0=60 km s-1 Mpc-1.
Table 1: Influence of the Cepheid bias on the Hubble constant from long-range distance criteria.
How some astronomers (most notably A. Sandage and G. Tammann) in the pre-HST era, consistently derived values of H0 of less than 60 km s-1 Mpc-1, even though the number of calibrator galaxies was much smaller. With hindsight, we see that the distances to those nearby calibrators were less biased, while efforts were made to avoid the selection biases in field and cluster galaxy samples (Sandage & Tamman 1975; Bottinelli et al. 1986).
We summarize the new results from this study:
Acknowledgements
This work has been supported by the Academy of Finland (the project ``Fundamental questions of observational cosmology''). We thank G. Tammann for proposing a test to see the influence of the correlation of errors. We thank the referee for reading the manuscript with extreme attention.
Table A.1: The sample used in this paper.
The true distances are derived from the radial velocity and an arbitrary Hubble constant.
Then, from a Gaussian distribution (
![]() )
of
)
of ![]() ,we obtain the absolute
magnitudes through realistic V- and I-band PL relations.
Then, from distances and absolute magnitudes we obtain apparent magnitudes V and I.
Each quantity is combined with realistic errors and an extinction is added to the apparent
magnitudes from random color excess and proper extinction coefficients.
Thus we constructed for true galaxies an artificial catalog of Cepheids with known
periods and apparent magnitudes, like a real one.
However, for these data we know the true distances and realistic observational limits for
periods and apparent magntiudes.
,we obtain the absolute
magnitudes through realistic V- and I-band PL relations.
Then, from distances and absolute magnitudes we obtain apparent magnitudes V and I.
Each quantity is combined with realistic errors and an extinction is added to the apparent
magnitudes from random color excess and proper extinction coefficients.
Thus we constructed for true galaxies an artificial catalog of Cepheids with known
periods and apparent magnitudes, like a real one.
However, for these data we know the true distances and realistic observational limits for
periods and apparent magntiudes.
Thus, making classical derivations of distances from the V and I Period-luminosity relations, we construct the bias diagram (as in Fig. 3), for two cases:
To see the effect of the velocity dispersion, we added to the simulated galaxies
a random velocity dispersion increasing with distance, in order to reproduce the
observations that show a very small velocity dispersion in the nearby universe.
The adopted velocity dispersion is:
![]() (in km s-1).
We obtained Fig. A.2a, b that reproduce quite well Figs. 5a, b based on
real data. This also confirms that the bias is visible, even when it should be cancelled
by an inverse correlation of errors (Bottom panel). The velocity
dispersion contributes to hide the bias. The bias being visible with real data, this
suggests again that the local velocity dispersion is very small.
(in km s-1).
We obtained Fig. A.2a, b that reproduce quite well Figs. 5a, b based on
real data. This also confirms that the bias is visible, even when it should be cancelled
by an inverse correlation of errors (Bottom panel). The velocity
dispersion contributes to hide the bias. The bias being visible with real data, this
suggests again that the local velocity dispersion is very small.