A&A 443, 747-752 (2005)
DOI: 10.1051/0004-6361:20041514

Gamma-ray bursts' spectra and synchro-curvature mechanism

X. L. Deng1 - T. S. Xia2 - J. Liu3


1 - University of Kentucky, USA
2 - University of Texas at Austin, USA
3 - University of Science and Technology of China, PR China

Received 23 June 2004 / Accepted 21 May 2005

Abstract
We apply the synchro-curvature mechanism instead of the synchrotron one to explain the spectra of gamma-ray bursts (hereafter, GRBs), especially those with both a turnoff point and high energy excess, which are often explained by combining with some other processes. We fit several spectra and get very good results. Our mechanism can give more detailed descriptions of the magnetic fields and strict constraints on the formation mechanism, thus it is helpful for understanding the physical processes in GRBs.

Key words: gamma rays: bursts - radiation mechanisms: non-thermal - magnetic fields

1 Introduction

It's very important to study the spectrum of a GRB to get information, such as the burst energy, the size of the event, the local magnetic field, the distribution of the particles, the acceleration mechanisms, the surroundings, the expanding fireball, and so on.

Though the light curves of GRBs are extremely variable, their spectra are fairly homogeneous. Most of their energy is released as photons with energies in the range of 30 keV to a few MeV, with a smaller fraction of the energy radiated in afterglows (van Paradijs et al. 2000). The spectra are fitted phenomenologically by Band et al. (1993), and Katz (1994) suggests that synchrotron emission is likely to be the radiation mechanism. The spectra of some GRBs can be well fitted by synchrotron radiation from relativistic particles with a power law distribution (Tavani 1996a,b). Some proposals are presented to solve the inconsistency in low energy (B. Zhang 2003, and references therein).

Observations of EGRET and COMPTEL onboard the Compton Gamma-Ray Observatory (CGRO) are consistent with the possibility that all bursts have high-energy tails (Piran 1999 and references therein). Many observational spectra showed turnoff points and energy excesses in the higher frequency parts. People like to solve this problem by adding other mechanisms including inverse-Compton (IC) scattering, synchrotron self-Compton (SSC), pair production, etc. But all these efforts are more artificial and have too many adjustable parameters. Evolution of the spectral indices have not yet been explained very well. Furthermore, IC and pair production is often used to explain the photons above GeV energies (Piran 1999; Mészáros 2002, and referenced therein), but not the energy band about MeV-100 MeV. SSC can explain this problem, but it has its own problem and may be examined in the future Swift and GLAST era (Guetta & Granot 2003).

We here offer a more convenient and more reasonable treatment for the spectra of GRBs with high energy excess, which is based on the synchro-curvature mechanism proposed by Zhang & Cheng (Zhang & Cheng 1995, 1996; Cheng & Zhang 1996). The synchro-curvature mechanism unifies the synchrotron and curvature mechanism, and is able to show a single particle's radiation in a non-uniform magnetic field, which means that the calculations are no longer bound in two special cases: uniform magnetic field and motion along the magnetic field lines. Lieu et al. (1997) pointed out that the synchro-curvature mechanism offers "more realistic treatments'' than Larmor's formula.

Zhang & Cheng (1997, 1998), Zhang et al. (2000b), and Cheng & Zhang (1998) applied synchro-curvature mechanism instead of curvature mechanism to restudy many important problems with $\gamma$-ray pulsars and fitted the newest observational results very well. Sobolev (2001) gave the more concrete formulae, and Harko et al. (2002) used a new way to expand it to the situation with fairly large transverse drift velocity. Hirotani et al. (2003) applied syhchro-curvature formulae to discussing some problems about the electrodynamics of an outer gap accelerator and expanded the formulae to the situation in which particles drift azimuthally. Zhang & Yuan gave general formulae for a single relativistic electron's radiation in classical and quantum situations (Zhang & Yuan 1998; Yuan & Zhang 1998). Using the synchro-curvature mechanism, X. W. Tang then presented a proposal to build a new kind of lamp-house in a ring magnetic field accelerator (Yang et al. 2003).

Assuming a power law energy distribution, Zhang et al. (2000a) also calculated the resulting spectra of relativistic particles by synchro-curvature mechanism. It was found that radiation spectra can be obviously different from the power-law shape, and can have turnoff points. The notion that "for relativistic electrons with a power-law energy distribution in magnetic field, the resulting spectrum is power-law'', which is widely accepted and in application, is now open to question. And as discussed below, we show that the synchro-curvature mechanism offers a better way to treat the spectra of GRBs with turnoff points than those explanations that include two or three mechanisms and require a lot of arbitrary adjusting parameters.

Some results of synchro-curvature mechanism are reviewed in Sect. 2, where we also consider parameters in concrete operations. We then present our models and interpret several observed spectra in Sect. 3, after which we introduce our results in Sect. 4.

2 The synchro-curvature mechanism

To consider the radiation problems of relativistic particles in a general magnetic field, the formulae of synchro-curvature mechanism are particularly useful.

The formulae for the power per unit frequency of synchro-curvature radiation in two polarizations are (Zhang & Cheng 1995, 1996; Cheng & Zhang 1996; Zhang et al. 2000a):

 
                               $\displaystyle \frac{{\rm d}P_\perp}{{\rm d}\omega}$ = $\displaystyle -\frac{\sqrt{3}e^2\left[(r_B+\rho)\Omega_0^2+r_B\omega_B^2\right]^2\gamma}{4\pi c^4 Q_2^2 r_{\rm c}} F_1\left(\frac{\omega}{\omega_{\rm c}}\right),$  
$\displaystyle \frac{{\rm d}P_\parallel}{{\rm d}\omega}$ = $\displaystyle -\frac{\sqrt{3}}{2}\frac{e^2\gamma}{2\pi}\frac{1}{r_{\rm c}} F_2\left(\frac{\omega}{\omega_{\rm c}}\right)$ (1)

and

 \begin{displaymath} \frac{{\rm d}P}{{\rm d}\omega}=\frac{{\rm d}P_\parallel}{{\rm d}\omega}+\frac{{\rm d}P_\perp}{{\rm d}\omega} \end{displaymath} (2)

where

 
$\displaystyle F_1(x) = x\left[\int^\infty_x K_{5/3}(z){\rm d}z+K_{2/3}\left(x\right)\right],$      
$\displaystyle F_2(x) = x\left[\int^\infty_x K_{5/3}(z){\rm d}z-K_{2/3}\left(x\right)\right]$     (3)

where the cyclotron frequency $\omega_B=eB/(\gamma m c)$, with $\gamma$ the Lorentz factor of a relativistic electron, m the electron mass, e the electron charge, c the velocity of light, B the magnetic field strength; and where the cyclotron radius $r_B=c\sin{\alpha}/\omega_B$, with $\omega_{\rm c}$ the characteristic frequency, $\Omega_0$ the angular velocity of the guiding center along the magnetic field line, $\rho $ and $r_{\rm c}$ are the curvature radius of the magnetic field line and the particle trajectory, respectively. We then have:
  
                                       $\displaystyle r_{\rm c}$ = $\displaystyle \frac{c^2}{(r_B+\rho)\Omega_0^2+r_B\omega_B^2},$ (4)
$\displaystyle \omega_{\rm c}$ = $\displaystyle \frac{3}{2}\gamma^3cQ_2$  
  $\textstyle \equiv$ $\displaystyle \frac{3}{2}\gamma^3c\frac{1}{\rho} \left[\frac{(r_B^3+\rho r_B^2-... ...frac{3\rho}{r_B}\cos^2\alpha+\frac{\rho^2}{r_B^2}\sin^4\alpha\right]^{1/2}\cdot$ (5)

Here $\alpha$ is the angle between direction of injected electron and magnetic field lines. It can easily prove that from the above formulae (1-5) we can deduce all the results of synchrotron and curvature mechanisms in two extreme situations. But for the synchro-curvature mechanism, the relation between $\frac{{\rm d}P}{{\rm d}\omega}$ and $\gamma$ is more complex. $\frac{{\rm d}P}{{\rm d}\omega}$ relates to $\gamma$, not only by $\omega_{\rm c}$ (no longer a simple power law function of $\gamma$), but also by $r_{\rm c}$. We can write (Zhang & Cheng 1995, 1996; Cheng & Zhang 1996):
 
$\displaystyle \frac{1}{r_{\rm c}}=\frac{mc^2\sin\alpha\cos^2\alpha}{eB\rho^2}\g... ...} +\frac{eB\sin\alpha}{mc^2\gamma} \equiv a_0\gamma+a_1+\frac{a_2}{\gamma}\cdot$     (6)

We assume a power law distribution of the relativistic electrons:

 \begin{displaymath} N(\gamma)= N_0 \gamma^{-n}, \gamma>\gamma_{\min} \end{displaymath} (7)

where $\gamma$ is the electron Lorentz factor. Thus we can get the spectral energy emissivity J as a function of the radiated photon frequency $\omega$:
  
$\displaystyle J_\perp(\omega) = -\frac{\sqrt{3}e^2}{4\pi}\frac{9c^2}{4}N_0 \int... ...a_{\rm c}}\right) \left[a_0\gamma+a_1+\frac{a_2}{\gamma}\right]^3{\rm d}\gamma,$     (8)
$\displaystyle J_\parallel(\omega) = -\frac{\sqrt{3}e^2}{4\pi}N_0\int^{\gamma_{\... ...mega_{\rm c}}\right) \left[a_0\gamma+a_1+\frac{a_2}{\gamma}\right]{\rm d}\gamma$     (9)

and

 \begin{displaymath} J(\omega)=J_\parallel(\omega)+J_\perp(\omega) \end{displaymath} (10)

where $\gamma_{\min}$ is related to $\epsilon_{\rm e}$ and to the total energy, and $\gamma_{\max}$ is determined by balancing acceleration and cooling losses (Piran 1999). We assume $\gamma_{\max}\gg\gamma_{\min}$ for convenience.

The above integrals usually need numerical calculations, but to analyze them physically, we can see that even if the electron energy distribution is power-law, the radiation spectrum isn't guaranteed to be purely power-law in a general situation. It is possible to present a more complex spectrum, such as holding turnoff points. Usually we assume an isotropic pitch angle distribution, and integrate $\alpha$ to get the fitting spectrum, but this won't change the above spectral character. Turnoff points could also be found, which could naturally give a spectrum with high-energy excess (Zhang et al. 2000a).

When considering the parameters in the concrete fitting processes, we choose for our model to begin with those previously used for the synchrotron mechanism and then adjust them with the properties of the turnoff point and some additional physical conditions. The parameters chosen for the fit, such as the magnetic field strength, are constrained to reasonable values.

Two approximate equations are quite useful in approximating the value of $\gamma_{\rm c}$, $\rho $, and $\alpha_{\rm c}$. To get a curved spectrum, we should have $a_0\gamma_{\rm c} \simeq a_2/\gamma_{\rm c}$, which leads to

 \begin{displaymath} eB\rho \simeq \gamma_{\rm c} m c^2 \cos \alpha_{\rm c} \end{displaymath} (11)

and we could even write $\omega_{\rm c}$ approximately as

 \begin{displaymath} \omega_{\rm c} \simeq \frac{3c}{2\rho}\gamma^3_{\rm c}. \end{displaymath} (12)


  \begin{figure} \par\epsfig{file=1514fig1.EPS,width=7.8cm,clip} \end{figure} Figure 1: Calculated synchro-curvature spectral power $\nu F_\nu $(arbitrary units) as a function of the energy (keV) for different $\rho $. Solid curve: $\rho =0.5\times 10^3$ cm, dashed curve: $\rho =1\times 10^3$ cm, dashdotted curve: $\rho =5\times 10^3$ cm, dotted curve: $\rho =50\times 10^3$ cm. The other parameters are: $\Gamma =1.0\times 10^3$, $B=1.0\times 10^4$ G, $\gamma_{\min}=1.0\times 10^3$, n=5.0.
Open with DEXTER

3 New explanations for GRB spectra

Before applying the model, we can give the probable range of the parameters $\Gamma$, $\gamma_{\min}$ and B. Typically, we take $\Gamma\sim10^2{-}10^3$, $\gamma_{\min}\sim10^2{-}10^3$, $B\sim10^4$, following the papers presented by Piran (1999) and Guetta & Granot (2003). $\gamma_{\min}$, $\rho $, B may be determined by the spectra and $\Gamma$, and related to each other, so there is only one free parameter. Where $\Gamma$ is the bulk Lorentz factor of the moving shock front, we merely take it to be 103 and conveniently ignore the effect of redshift. At first, we calculate some curves and fit spectra by using a single characteristic radius.

Figure 1 shows the calculated spectral shapes of the synchro-curvature model for different $\rho $ in $\nu F_\nu $-space. We can see that when $\rho $ is large enough, the spectrum is close to the shape of the Synchrotron Model. When $\rho $ is smaller, the turnoff point emerges and the high energy excess is larger. As a result, the low-energy part is similar in the two models, and ours can explain the turnoff points and high-energy excesses without adding more mechanisms and more parameters. There are other effects: e.g. the peak energy and the slope increase when $\rho $ decreases.

Figure 2 shows the calculated spectral shapes of the synchro-curvature model for different B in $\nu F_\nu $-space. From this figure, we can see that when the curvature radius is relatively small, the magnetic strength can affect the spectral shape markedly. When $\rho $ is fixed and the magnetic field is very strong, the shape tends to be like that of the Synchrotron Model, and when the magnetic field is weak, the high energy excess is obvious.


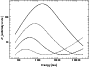  \begin{figure} \par\epsfig{file=1514fig2.EPS,width=7.8cm,clip} \end{figure} Figure 2: Calculated synchro-curvature spectral power $\nu F_\nu $(arbitrary units) as a function of the energy (keV) for different B. Solid curve: $B=5\times 10^4$ G, dashed curve: $B=2\times 10^4$ G, dashdotted curve: $B=1\times 10^4$ G, dotted curve: $B=0.5\times 10^4$ G. The other parameters are: $\Gamma =1\times 10^3$, $\rho =1\times 10^3$ cm, $\gamma_{\min}=1.0\times 10^3$, n=5.0.
Open with DEXTER

The spectrum of GRB 930131, one of the brightest bursts detected by CGRO, reached a peak flux of 105 photons s-1 cm-2 (Meegan et al. 1996) and has been called the "Superbowl Burst'' after its time of occurrence. Meegan (1996) and Ryan (1994) give its EGRET and COMPTEL spectra, respectively. Then Bromm & Schaefer (1999) constructed a broadband spectrum for GRB 930131, ranging from 20 keV to 200 MeV, by combining spectral information from the CGROs BATSE, COMPTEL, and EGRET instruments. Bromm & Schaefer (1999) found that the resulting spectrum is remarkably flat (in $\nu F_\nu $-space) up to high energies, fitted the spectral shape by synchrotron mechanism, and showed that the flatness of the spectrum at high energies is not due to spectral time variability.


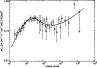  \begin{figure} \par\epsfig{file=1514fig3.ps,width=8.5cm,clip} \end{figure} Figure 3: Spectrum of GRB 930131 and the fitting result of the synchro-curvature radiation. Solid curve is the fitting line. The physical parameters can be found in Table 1, and for a Gaussian distribution of the radius of curvature, with $\sigma=\frac{1}{10}\bar{\rho}$, $\Gamma[\gamma_{\min}^3/\bar{\rho}]_{8}=12.0$; with $\sigma=\frac{1}{8}\bar{\rho}$, $\Gamma[\gamma_{\min}^3/\bar{\rho}]_{8}=11.7$.
Open with DEXTER

Table 1: Some characteristics of several composite GRB spectra.

Here, we use our model presented above to fit the spectum. In Fig. 3 (parameters in Table 1), it's obvious that our model fits the spectral much better, even to very high energy. And from our fitting, we can say that this spectrum is so strange just because of its weak magnetic field or its very small curvature radius. Figures 4-6 then show three time-averaged CGRO spectra of bright bursts extending 3-4 decades of photon energies (Schaefer et al. 1998, and references therein). In all these cases, we can fit the spectra well.


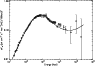  \begin{figure} \par\epsfig{file=1514fig4.ps,width=8.3cm,clip} \end{figure} Figure 4: Spectrum of GRB 910503 and the fitting result of the synchro-curvature radiation. Solid curve is the fitting line. The physical parameters can be found in Table 1.
Open with DEXTER


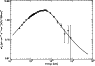  \begin{figure} \par\epsfig{file=1514fig5.ps,width=8.3cm,clip} \end{figure} Figure 5: Spectrum of GRB 910601 and the fitting result of the synchro-curvature radiation. Solid curve is the fitting line. The physical parameters can be found in Table 1.
Open with DEXTER


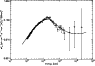  \begin{figure} \par\epsfig{file=1514fig6.ps,width=8.3cm,clip} \end{figure} Figure 6: Spectrum of GRB 910814 and the fitting result of the synchro-curvature radiation. Solid curve is the fitting line. The physical parameters can be found in Table 1.
Open with DEXTER

Furthermore, we introduce a Gaussian distribution to describe the radius of curvature, and use it to fit the spectra. We found that in order to get the same curve to fit the same spectrum well, when a Gaussian distribution is adopted, the expected value is only a little higher than the value of a single radius. And with different variances, the expected values are also somewhat different. However, these values are still in the above range, and the characters of curves are not changed. Detailed values are shown in Table 1 and in related figures.

We have the similar table as Tavani (1996a,b) (see Table 1), where our indices n are somewhat larger than that given by the synchrotron mechanism, because the small radiuses increase the slopes a little in our model. For example, for GRB 910601, Tavani (1996a,b) used the synchrotron mechanism to get the index 6, while our result is 6.1; for GRB 910814, his result is 5 and ours 5.2 (see Sect. 4).

4 Discussion

From the fitting above, we can see that in the low energy range, our model is similar to the synchrotron model, except that it cannot explain the turn-off point and the high energy excess. However, not only in low energy range, but also in very high energy range, our model works well. We now discuss the main consequences:
1.
Turnoff point and high-energy excess. The turnoff point and high-energy excess are natural results of the small curvature radius in our model. We need not artificially add any other mechanisms to get the "abnormal'' shape, so our model is more credible.

2.
Parameters. There is only one free parameter $\rho $ in our model. Given a $\Gamma$, $\rho $, $\gamma_{\min}$, and B can be obtained from the spectrum, thus we have not imported any more free parameters, which makes it both reliable and convenient.

3.
The curvature radius of the magnetic field. In our fitting, if we adopt characteristic values for $\Gamma$ and $\gamma_{\min}$, the curvature radius is much smaller than the scale of the emission area. For example, for GRB 930131, one set of possible parameters is: $\Gamma=10^3$, $\gamma_{\min} = 5.35\times 10^2$, $\rho = 1.25\times 10^2$ cm, $B = 1.72~\times~ 10^4$ G, $\bar{\rho}=1.43~\times~ 10^2$ cm with $\sigma=\frac{1}{5}\bar{\rho}$, n=5.3. It strictly restricts the formation mechanism of the magnetic field. For example, Medvedev & Loeb (1999) showed that the Weibel instability could naturally generate strong magnetic fields in the collisionless shocks of gamma-ray burst sources. The characteristic coherence scale of the magnetic fields generated by this mechanism is the order of the relativistic skin depth, i.e. $\sim $103 cm for internal shocks in the comoving frame of the shock. Maybe this mechanism can account for our results.

4.
In the above analysis, the magnetic field strength B is about 104 Gauss. We have $B=\sqrt{32\pi}c\epsilon^{1/2}_B\gamma_{\rm sh}m^{1/2}_{\rm p} n^{1/2}_1\sim 0.4\sqrt{\epsilon_B n_1}\gamma_{\rm sh}$, where $\gamma_{\rm sh}$ describes the shock's velocity, as well as the "thermal'' motion of the shocked particles (Piran 1999). Since $n_1\sim 3\times10^{10}$ cm-3 (Medvedev & Loeb 1999), it's easy to get 104 Gauss. A characteristic magnetic field of $\sim $104 Gauss is also shown in Guetta (2003). As for the indices of the distribution of electrons n, because synchro-curvature mechanism gives curves similar to what the synchrotron mechanism gives in the lower energy part of the spectra, we try to use the indices from the synchrotron mechanism (Tavani 1996a,b) and then adjust them slightly. These results are different from those of the simulations, which examined Fermi-type acceleration at relativistic shocks and got n=2.2-2.5 (Gallant 1999). Recently, Baring & Braby (2004) also show the apparent contradiction between standard Fermi acceleration and spectral observations of GRBs. Then Hededal et al. (2004) tried to solve this problem by getting a power-law distribution of accelerated electrons from an acceleration mechanism that is decidedly different from Fermi acceleration. With more studies, we should know the real mechanism in the near future.

5.
Determination of some properties. It has been found that the combination of Lorentz factor and postshock magnetic field of a GRB $\Gamma\gamma^2_{\min}B$ remains constant in fitting the spectrum and even the range of them in many GRBs is not large (Tavani 1996a,b). Our value is only a little lower than that given by the synchrotron mechanism. A greater difference of this value between the two models means a smaller curvature radius, and so the high-energy excess is more obvious. Our fittings can give another constraint, as $\Gamma\gamma_{\min}^3/\rho$ remains constant, too. This means that if the shapes of spectra are similar and we take a standard $\Gamma$, it can give the relation between the curvature radiuses of magnetic fields and the Lorentz factors of the electrons. We can explain the two relations simply: if $\epsilon_{\rm e}$ is larger, $\epsilon_B$ will be smaller, so the magnetic field will be weaker and looser, where $\epsilon_{\rm e}$ and $\epsilon_B$ are the ratio of the electron energy density and the ratio of the magnetic field energy to the total thermal energy, respectively.

6.
About IC, SSC, and other mechanisms. Tavani (1996a) show that a possible IC modification of GRB spectra does not change the overall shape of the continuum below 100 MeV. Guetta & Granot (2003) propose that the SSC component may become dominant above a certain energy ($\sim $100 MeV), if the $\nu F_\nu $ slope turns from negative to positive. Our results show that maybe the IC, SSC, and any other mechanisms do not affect the spectra very much or do not change the overall shape even to energy much higher than 100 MeV. In other words, we may need not to add any other mechanisms ro any other parameters to describe the spectra of most GRBs, where there may be a uniform mechanism to explain the spectrum from low to very high energy, which is synchro-curvature mechanism.

7.
Spectral evolution. Not only a decrease in B or an increase in n (Tavani 1996a), but also the evolution of curvature radius can affect the evolution of spectra, for fixed values of $\Gamma$, $\gamma_{\min}$. Especially in the high-energy range, $\rho $ affects (see Fig. 1) the shape much more. From the evolution of the high energy part of the spectra of GRBs, we can gain the evolution of $\rho $, then give the limitation on the formation mechanism of magnetic fields. Hence, we need more detailed observed spectra of GRBs, especially the evolutional spectra.

5 Conclusions

In this paper, we present a new mechanism to explain the spectra of GRBs and apply it to fitting several observed spectra. We propose that a synchro-curvature mechanism may be applicable to the spectra of GRBs, especially to analyze the turnoff point and high-energy excess, which are not explained well by synchrotron mechanism. It gives a strict constraint on the magnetic fields for both the intensity and the curvature radius, which can then restrict the formation mechanism of the magnetic fields. It can also give more information about the source. As new satellites (e.g. Swift, GLAST, AGILE) will provide ever more accurate spectra of GRBs, especially the evolutional spectra and the spectra in the extremely high-energy band in the near future, the application of this mechanism will offer even more accuracy.

Acknowledgements
It is pleasure to thank Dr. J. M. Yang for useful discussions. We are also grateful to the referee for comments and suggestions. This work was partly supported by the National Natural Science Foundation and the Doctoral Science Foundation of the Chinese Ministry of Education.

References

 
Copyright ESO 2005