A&A 443, 201-210 (2005)
DOI: 10.1051/0004-6361:20053236

On ion-ion correlation effects during stellar core collapse

A. Marek1 - H.-Th. Janka1 - R. Buras2 - M. Liebendörfer3 - M. Rampp1,[*]


1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
2 - Max-Planck-Institut für Physik (Werner-Heisenberg-Institut), Föhringer Ring 6, 80805 München, Germany
3 - CITA, University of Toronto, Toronto, Ontario M5S 3H8, Canada

Received 13 April 2005 / Accepted 19 June 2005

Abstract
The role of ion-ion correlations in suppressing neutrino-nucleus elastic scattering during stellar core collapse is reinvestigated, using two different equations of state. We test the improved description by Itoh et al. against the treatment suggested by Horowitz and find that the stronger cross-section reduction for small momentum transfer in the former case does not lead to noticeable changes of the core deleptonization and entropy increase during collapse, because the improvements are relevant below neutrino trapping conditions only for very low neutrino energies, corresponding to a very small phase-space volume. Treating screening effects for ionic mixtures by the linear mixing rule applied to the collection of representative heavy nucleus, $\alpha $ particles, and free nucleons, which is assumed to characterize the composition in nuclear statistical equilibrium, we cannot determine mentionable differences during stellar collapse, because $\alpha $ particles are not sufficiently abundant, and their coherent scattering opacity is too small.

Key words: stars: supernovae: general - neutrinos - radiative transfer - hydrodynamics

  
1 Introduction

Heavy (iron-group or more massive) nuclei dominate the composition in stellar iron cores until nuclear densities are reached in the inner core and the bounce shock raises the entropies in the outer core to values where free nucleons are favored in nuclear statistical equilibrium (NSE). During the infall phase, therefore, coherent, isoenergetic scattering off nuclei is the main source of opacity for the electron neutrinos produced by electron captures (cf., e.g., Bruenn 1989b,1985,1989a). Neutrino-nucleus scattering thus hampers the free escape of neutrinos, is responsible for neutrino trapping around a density of 1012 g cm-3, and regulates the deleptonization and increase of entropy during core collapse.

In the medium of the supernova core, nuclei are coupled strongly with each other by Coulomb forces. They thus form a highly correlated plasma, in which the interactions of neutrinos with wavelengths larger than the average ion-ion separation $a_{{\rm ion}}$ (corresponding to neutrino energies $\epsilon_\nu \la 2\hbar c/a_{{\rm ion}} \sim 20~$MeV) are reduced by phase interference effects (Itoh 1975). The corresponding ion screening was more recently calculated by Horowitz (1997) and Itoh et al. (2004), and investigated in its effects on stellar core collapse by Bruenn & Mezzacappa (1997). The last authors employed the correction factor for neutrino-nucleus scattering cross sections as given by Horowitz (1997).

Itoh et al. (2004), however, pointed out that the Monte Carlo calculations, which Horowitz's fit was based on, did not allow him to accurately represent the cross-section reduction for low neutrino energies, i.e., for energies $\epsilon_\nu \la \hbar c/a_{{\rm ion}}\sim 10~$MeV, thereby underestimating the importance of ion-ion correlation effects. Itoh et al. (2004) provided a more accurate analytic fitting formula by using the correct behavior of the liquid structure factor for small momentum transfer in neutrino-nucleus scattering.

The investigations presented in this work have two goals. On the one hand, we aim at studying the differences in stellar core collapse and the formation of the supernova shock, which arise from the improved description of ion screening as suggested by Itoh et al. (2004), compared to a treatment using the formulae of Horowitz (1997). On the other hand, we intend to explore the sensitivity of the evolution to ion screening effects associated with the ionic mixture of nuclei and nucleons that are present during core collapse. In accordance with the treatment of NSE in current equations of state (EoSs) for supernova simulations, we consider the nuclear components to be free neutrons, free protons, $\alpha $ particles, and one kind of heavy nucleus which is considered as representative of the NSE distribution of nuclei beyond 4He. Two different nuclear EoSs with largely different $\alpha $ mass fractions during core collapse are employed. The first EoS ("L&S''), provided by Lattimer & Swesty (1991), is based on a compressible liquid drop model and uses a Skyrme force for the nucleon interaction (Lattimer et al. 1985). Our choice of the compressibility modulus of bulk nuclear matter is 180 MeV, and the symmetry energy parameter 29.3 MeV, but the differences in the supernova evolution caused by other values of the compressibility were shown to be minor (Thompson et al. 2003; Swesty et al. 1994). The second EoS used here ("Shen'') is the new relativistic mean field EoS of Shen et al. (1998a,b) with a compressibility of nuclear matter of 281 MeV and a symmetry energy of 36.9 MeV.

The paper is organized as follows. In Sect. 2 the prescriptions for the ion-ion correlation factor provided by Horowitz (1997) and Itoh et al. (2004) are briefly summarized. In Sect. 3 the input (code, initial stellar model) in our simulations is described, while in Sect. 4 the results are presented and finish with conclusions in Sect. 5.

  
2 Ion-ion correlation factor

In this study we make use of two different fitting formulae for the angle-averaged correlation factor $\left\langle S_{\rm ion} \right\rangle$, which describes the reduction of the neutral-current scattering of neutrinos off nuclei by ion-ion correlation effects. It is used as a multiplicative correction to the neutrino-nucleus isoenergetic scattering opacity (cf. Bruenn & Mezzacappa 1997; Rampp & Janka 2002; Horowitz 1997). The first formula is provided by Horowitz (1997) and is based on Monte Carlo results. The second one is given by Itoh et al. (2004) and was obtained from data calculated with the improved hypernetted-chain method (see Itoh et al. 1983, and references therein) for a classical one-component plasma. In all simulations with ion screening, we also take into account (the rather small) electron screening effects according to Horowitz (1997) by applying the additional correction factor of his Eq. (19) to the rates of coherent neutrino-nucleus scattering.


  \begin{figure} \par\includegraphics[width=8cm,clip]{3236f1.eps} \end{figure} Figure 1: The ratio of the angle-averaged ion-ion correlation factor as calculated with the fitting formula of Horowitz (1997) (see Fig. 9 in Bruenn & Mezzacappa 1997) relative to the one obtained from the prescription provided by Itoh et al. (2004, see their Fig. 2) as a function of the variable $\xi $for different values of the dimensionless parameter $\Gamma $.
Open with DEXTER

   
2.1 One-component plasma

If the stellar plasma consists of only one nuclear species of ions $(Z_{\rm ion},A_{\rm ion})$, the ion sphere radius which gives the mean interion distance is defined as

 \begin{displaymath}a_{\rm ion}=\left(\frac{3}{4\pi n_{\rm ion}}\right)^{1/3} , \end{displaymath} (1)

where $n_{\rm ion}= n_{\rm b} X_{\rm ion}/A_{\rm ion}$ is the number density of the ions with mass number $A_{\rm ion}$, charge $Z_{\rm ion}e$and mass fraction $X_{\rm ion}$ ($n_{\rm b}$ is the number density of baryons). The strength of the ion-ion correlations is characterized by the dimensionless parameter

 \begin{displaymath}\Gamma = \frac{Z_{\rm ion}^2 e^2}{a_{\rm ion} k_{\rm B} T} =... ...\left(\rho_{12}~{X_{\rm ion} \over A_{\rm ion}}\right)^{1/3} , \end{displaymath} (2)

which is the ratio of the unshielded electrostatic potential energy between the neighbouring ions to the thermal energy. Here T10 denotes the temperature in units of 1010 K, and $\rho_{12}$ the mass density in 1012 g cm-3. Note that the definition of $\Gamma $ in Horowitz (1997) differs from the ones used here, and in Bruenn & Mezzacappa (1997) and Itoh et al. (2004) by a factor $(4\pi)$ in the denominator of Eq. (2). In Horowitz's notation this factor is absorbed in the employed value of e2.

Horowitz (1997) provided the following fitting formula for the angle-averaged suppression factor $\langle S_{\rm ion}(\xi,\Gamma) \rangle_{\rm Hor}$

 \begin{displaymath}\langle S_{\rm ion}(\xi,\Gamma) \rangle _{\rm Hor} = \frac{1}... ...i \right)} \ , {\rm for} \ \ \ \xi < 3+{4\over \Gamma^{1/2}} , \end{displaymath} (3)

and

 \begin{displaymath}\langle S_{\rm ion}(\xi,\Gamma) \rangle _{\rm Hor} = 1 , \end{displaymath} (4)

otherwise, to be applied for $1 \le \Gamma \le 150$; for values of $\Gamma < 1$or $\Gamma > 150$, Horowitz (1997) recommends simply setting $\Gamma $ to 1 or 150, respectively. The $\beta_i$ are coefficient functions of $\Gamma $ determined from fits to Monte Carlo data. In Eq. (3) the variable $\xi $ is the ratio of the mean ion-ion separation $a_{{\rm ion}}$to the wavelength for neutrinos (during core collapse primarily electron neutrinos with energy $\epsilon_\nu$), i.e.,

 \begin{displaymath}\xi=a_{\rm ion}\frac{\epsilon_\nu}{\hbar c} \cdot \end{displaymath} (5)

Itoh et al. (2004) provide a different fitting formula (see Eqs. (23)-(26) in their paper), which is restricted to the case of a strongly degenerate electron gas, a usually well-fulfilled condition during stellar core collapse. Their treatment gives different results for the ion-ion correlation factor, $\langle S_{\rm ion}(\xi,\Gamma)\rangle$, in the limit of low neutrino energies ($\xi \la 1$). This can be seen in Fig. 1. Itoh et al. (2004) argue that the reason for this difference compared to the description by Horowitz (1997) is their correct calculation of the liquid structure factor S(k) for small momentum transfer k. This makes the suppression of neutrino-nucleus scattering by ion-ion correlations greater than estimated by Horowitz (1997) and Bruenn & Mezzacappa (1997).

The simulations presented here intend to study the dynamical consequences of these differences during supernova core collapse. Up to now we have considered a stellar medium consisting of only one nuclear species and referred to formulae derived for a classical one-component plasma. However, in the collapsing core of a massive star a mixture of nuclei besides free neutrons and protons is present, usually approximated by $\alpha $ particles plus one representative, heavy nucleus. To deal with that we decided, in the simplest approach, to calculate the suppression factor $\langle S_{\rm ion}(\xi,\Gamma)\rangle$ for $\alpha $ particles and for the heavy nucleus independently, using the values for the average distance $a_{{\rm ion}}$ between ions of the same kind, derived from the number densities $n_\alpha$ or nA, respectively. This assumes that different ionic components coexist without collectively affecting the screening of neutrino-nucleus interactions. Alpha particles thus change the ion screening for heavy nuclei only by the fact that their presence may reduce the number density of heavier nuclei.

  
2.2 Ionic mixtures

For a liquid mixture of different ions (Zj,Aj) including free protons, Itoh et al. (2004) suggest a modified treatment, referring to earlier work by Itoh et al. (1979). Employing the so-called linear mixing rule, one can extend the calculations of neutrino-nucleus scattering cross sections, obtained for a one-component ion liquid, to the case of multi-component fluids.

The ion sphere radius for an ion j in the mix is now given by

 \begin{displaymath}a_j = a_{\rm e}~Z_j^{1/3} \end{displaymath} (6)

with $a_{\rm e}$ being the electron sphere radius,

 \begin{displaymath}a_{\rm e}=\left(\frac{3}{4\pi \sum_i Z_i n_i}\right)^{1/3} , \end{displaymath} (7)

where the sum extends over free protons and all nuclei with number densities ni. The dimensionless variable $\xi_j$ then becomes

 \begin{displaymath}\xi_j = a_j ~{\epsilon_\nu \over \hbar c} \cdot \end{displaymath} (8)

The ion-ion correlations of nuclear species j depend on the dimensionless parameter $\Gamma_{\! j}$ defined as
 
                             $\displaystyle \Gamma_{\! j}$ = $\displaystyle \frac{{Z_j}^{5/3}e^2}{a_{\rm e}k_{\rm B}T} = {Z_j^2 e^2\over k_{\rm B}T} \left( {4\pi\over 3}\sum_i {Z_i\over Z_j}n_i\right)^{1/3}$  
  = $\displaystyle 0.2275~{Z_j^{5/3}\over T_{10}} \left(\rho_{12} \sum_i {X_i Z_i \over A_i} \right)^{1/3} \cdot$ (9)

The angle-averaged ion-ion correlation factor $\langle S_{{\rm ion}}(\xi_j,\Gamma_{\! j})\rangle$ is now evaluated for $\alpha $ particles and heavy nuclei with the fitting formula provided by Itoh et al. (2004), using $\xi_j$and $\Gamma_{\! j}$ as given in Eqs. (8) and (9), respectively.

Applying the naive procedure of Sect. 2.1 for the conditions in a supernova core shows that usually $\xi \gg 1$for $\alpha $ particles, because $\alpha $'s are less abundant than heavy nuclei in the central part of the core and during most phases of the collapse. Their $\Gamma $ is then less than unity. Both factors diminish ion screening for $\alpha $'s to a negligible level. In contrast, following the description in this section, the presence of $\alpha $'s can also affect the ion screening of heavy nuclei by reducing the interion separation (Eq. (6)) and thus $\xi_j$ (Eq. (8)). Moreover, $\Gamma_j$for heavy nuclei according to Eq. (9) might become larger than in Eq. (2). Therefore the presence of $\alpha $'s has an indirect influence on neutrino scattering off heavy nuclei and thus on ion-ion correlations during stellar core collapse, despite the fact that the screening effects for $\alpha $ particles are still small because their $\Gamma $ is usually below unity; following Horowitz (1997), $\Gamma $ is then set to unity for evaluating the angle-averaged cross section suppression factor.

While our procedure for treating the effects of $\alpha $particles in an ionic mixture with heavy nuclei and free nucleons adopts the recipe of Itoh et al. (2004), Sawyer (2005) has recently discussed an alternative approach to the problem of multi-component fluids by applying the Debye-Hückel approximation. He points out that in multi-component plasmas the ion-ion correlation effects might be greatly reduced, leading to much larger neutrino opacities than for a one-component plasma, even if the constituent ions have only a small range of N/Z ratios. Electron density fluctuations for an ionic mixture enhance this tendency. Sawyer's calculations therefore yield a result which is opposite to our application of the linear mixing rule for calculating multi-component plasma parameters. They tend to bring one back closer to the case with ion-ion correlations being ignored, simulations of which will be presented below, too. Thus we provide a set of models with the intention of encompassing and bracketing the "extreme'' possibilities discussed in the literature.

  
3 Numerical simulations

The core collapse simulations performed in this work were carried out with the neutrino-hydrodynamics code VERTEX in spherical symmetry. This code is described in detail in Rampp & Janka (2002).

VERTEX employs the PROMETHEUS hydrodynamics code (Fryxell et al. 1989), which is a direct Eulerian implementation of the Piecewise Parabolic Method. It uses an explicit Godunov-type scheme with second-order temporal and third-order spatial accuracy, which allows for the simulation of high Mach number, self-gravitating flows with discontinuities, and it can handle complicated equations of state. The VERTEX transport solver employs a variable Eddington factor algorithm in spherical coordinates. Angular moments of the O(v/c) comoving frame transport equation form a system of lower-dimensional moment equations, which is closed with a variable Eddington factor. The latter is determined from a (simplified) "model'' Boltzmann equation. General relativistic gravity and corresponding effects in the transport are approximately taken into account. Details about this can be found in Rampp & Janka (2002) and Marek et al. (2005). A comparison with fully relativistic calculations reveals excellent agreement during core collapse and shock formation (Liebendöerfer et al. 2005).

Table 1: Overview of neutrino-matter and neutrino-neutrino interactions included in our simulations. For each process, we provide reference(s) where more information can be found about physics and approximations employed in the rate calculations. The numerical implementation is described in detail in Rampp & Janka (2002) and Buras et al. (2003). The symbol $\nu $ represents any of the neutrinos $\ensuremath{\nu_{\rm e}} ,\bar{\nu}_{\rm e},\nu_\mu,\bar\nu_\mu,\nu_\tau,\bar\nu_\tau$, the symbols e-, e+, n, p, and A denote electrons, positrons, free neutrons and protons, and heavy nuclei, respectively. The symbol N means neutrons or protons.

The neutrino interactions used in the simulations of the present work are summarized in Table 1. Note that neutral-current scatterings of neutrinos off nucleons and charged-current $\beta$-processes include the effects of nucleon recoil, thermal motions, phase space blocking, nucleon correlations in dense media (Burrows & Sawyer 1999,1998), corrections due to the weak magnetism of nucleons (Horowitz 2002), the possible quenching of the axial-vector coupling in nuclear matter (Carter & Prakash 2002), and the reduction of the effective nucleon mass at high densities (Reddy et al. 1999). Electron captures on nuclei are implemented according to the improved treatment of Langanke et al. (2003) in regions where NSE holds, taking into account the collective e-captures of a large sample of nuclei in NSE with rates determined from shell model Monte Carlo calculations; the prescription of Bruenn (1985) is used in regions which are out of NSE. With this input, the production of $\nu_{\rm e}$ by nuclei dominates the one by protons during core collapse (Langanke et al. 2003).

The core collapse simulations presented in this paper were started from the 15 $~M_{\odot}$ progenitor s15a28 from Heger et al. (2001).

For describing the thermodynamics and composition of the stellar plasma, the EoS of Lattimer & Swesty (1991) and the one of Shen et al. (1998a,b) are applied at high densities ( $\rho > 6.7\times 10^7~$g cm-3 or $\rho > 2.7\times 10^8~$g cm-3, respectively). At lower densities the EoS contains a mixture of electrons, positrons, photons, nucleons, and nuclei, with the nuclear composition described by a simple approximation to a four-species NSE for temperatures above about 0.5 MeV. Below that temperature, the composition is adopted from the progenitor star and modified if nuclear burning plays a role during collapse (for details, see Appendix B in Rampp & Janka 2002). The two EoSs show major differences in the abundances of $\alpha $ particles, which can be larger by up to a factor of $\sim$10 in the case of the Shen et al. (1998a,b) EoS. This is visible in Fig. 2, where the number fractions of free neutrons, protons, $\alpha $'s, and of the representative heavy nucleus (whose mass and charge numbers typically grow with density until nuclei disappear at the phase transition to nuclear matter) are displayed as functions of increasing density during collapse both at the stellar center and at an enclosed mass of 0.5 $~M_{\odot}$. Although their mass fraction is much lower, $\alpha $ particles in the Shen et al. (1998a,b) EoS can become equally or even more abundant (by a factor up to about two) than heavy nuclei in the outer layers of the collapsing core, in particular outside of $M(r)\ga 0.5$-0.6 $~M_{\odot}$.


  \begin{figure} \par\includegraphics[width=14cm,clip]{3236f2.eps} \end{figure} Figure 2: Composition as a function of density at the center ( top) and at an enclosed mass of 0.5$~M_{\odot}$ ( bottom) for the evolution during core collapse with the EoSs of Lattimer & Swesty (1991, left) and Shen et al. (1998a,b, right). The plots show the evolution of the number fractions Y for free neutrons, protons, $\alpha $-particles, and the representative heavy nucleus until shock formation. The results were obtained with ion-ion screening treated according to case "EoS_ion_Itoh'' (see text).
Open with DEXTER

For each of the employed EoSs, four core collapse simulations were performed, all starting from the onset of gravitational instability and carried on until the moment of shock formation. Calculations with ion-ion correlation (and electron screening) effects in neutrino-nucleus scattering switched off, i.e. for $\langle S_{\rm ion} \rangle \equiv 1$ (and $R_{\rm e} \equiv 1$, instead of Eq. (19) of Horowitz 1997), are denoted with "EoS_ion_off'', where EoS stands for "L&S'' or "Shen''. They are compared to (i) simulations (models "EoS_ion_Hor'') where the ion-ion correlation factor of Horowitz (1997, Eqs. (3), (4)) is used and (ii) models in which ion-ion correlations are described according to Itoh et al. (2004) (models "EoS_ion_Itoh''). Finally, the sensitivity of stellar core collapse to the treatment of ion screening for ionic mixtures is investigated by simulations (models "EoS_ion_mix'') in which the correction factors $\langle S_{\rm ion}(\xi_j,\Gamma_j)\rangle$ are calculated from the Itoh et al. (2004) formulae with $\xi_j$ and $\Gamma_j$, as given in Sect. 2.2.

  
4 Results

Figures 3 and 4 show electron fraction $Y_{\rm e}$, lepton fraction $Y_{\rm lep}$, and (gas) entropy s, respectively, at the core center during collapse simulations with the Shen et al. (1998a,b) EoS. For both EoSs employed in this work, the same relative changes are found when models without ion screening are compared with calculations with ion-ion correlations according to Horowitz (1997) (see Models Shen_ion_Hor and Shen_ion_off in Figs. 3 and 4). We shall concentrate here mostly on the results obtained with the Shen et al. (1998a,b) EoS, because $\alpha $ particles are much more abundant there (see Fig. 2) and many aspects of ion screening in simulations with the EoS of Lattimer & Swesty (1991) have already been discussed by Bruenn & Mezzacappa (1997). Our results agree qualitatively with those of the latter paper. Quantitative differences compared to Bruenn & Mezzacappa (1997) are caused by the inclusion of improved electron capture rates on nuclei in our work, which significantly increases electron captures above a few 1010 g cm-3so that lower values of $Y_{\rm lep}$ and s result after trapping (cf. Martínez-Pinedo et al. 2005; Langanke et al. 2003).

  \begin{figure} \par\includegraphics[width=7.4cm,clip]{3236f3.eps} \end{figure} Figure 3: Central electron fraction $Y_{\rm e}$ and lepton fraction $Y_{\rm lep}$ as functions of central density for core collapse calculations with the EoS of Shen et al. (1998a,b). Model Shen_ion_off does not include the effects of ion-ion correlations, Model Shen_ion_Hor uses the description of ion screening according to Horowitz (1997), Model Shen_ion_Itoh employs the Itoh et al. (2004) treatment for a one-component plasma, and Model Shen_ion_mix their treatment of ionic mixtures.
Open with DEXTER

As explained in detail by Bruenn & Mezzacappa (1997), the screened cross section for neutrino-nucleus scattering reduces the transport optical depth of low-energy neutrinos (cf. Fig. 3 in Bruenn & Mezzacappa 1997) and allows them to escape from the core more easily. This is obvious from a flux enhancement of neutrinos at energies $\epsilon_\nu \la 10~$MeV in Fig. 6, where the situation is displayed at a density of $\rho = 10^{12}~$g cm-3. Ion-ion correlations thus cause a decrease in $Y_{\rm e}$ and $Y_{\rm lep}$ that is stronger by about 0.02 until neutrino trapping sets in (Fig. 3). The homologously collapsing stellar core correspondingly shrinks, and the shock forms at a somewhat smaller enclosed mass (Fig. 5). The shock formation is defined by the moment when the postshock entropy first reaches a value of 3 $~k_{\rm B}$ per nucleon. A part of the effect visible in Fig. 5 might, therefore, be a consequence of the slightly higher core entropy after neutrino trapping in models with ion screening (see Figs. 4 and 7).


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{3236f4.eps} \end{figure} Figure 4: Same as Fig. 3 but for the central (matter) entropy s.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{3236f5.eps} \end{figure} Figure 5: Gas entropy vs. enclosed mass at the moment of shock formation in the models of Figs. 3 and 4. The shock formation is defined by the instant when the entropy in the core first reaches a value of 3 $~k_{\rm B}$per nucleon.
Open with DEXTER

Neutrino-electron scattering is very efficient in downscattering neutrinos from the high energies, where they are created mostly by electron captures, to lower energy states. Therefore the phase space at low energies is quickly refilled. Figure 8 shows the source term for energy redistribution by neutrino scatterings off electrons for two density values below trapping conditions. The downscattering of high-energy neutrinos explains why the local energy spectra, ${\rm d}E_\nu/{\rm d}\epsilon_\nu$with $E_\nu$ being the neutrino energy density, are essentially the same in Models Shen_ion_off and Shen_ion_Hor, despite clear differences between the energy flux spectra of both runs (Fig. 6).

On their way out, escaping neutrinos transfer a part of their energy to electrons in collisions, thus heating the stellar medium (Bruenn 1986). Since ion screening of neutrino-nucleus scatterings reduces the transport opacity and, therefore, the effective optical depth for energy exchange with the stellar background mainly for low-energy neutrinos, but hardly changes the downscattering probability of high-energy neutrinos (Fig. 9); the larger loss of lepton number leads to an increase of the central entropy by about 0.12 $~k_{\rm B}$ per nucleon (Fig. 4). In Fig. 9 the optical depth $\tau$ at the center is calculated as

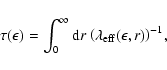\begin{displaymath}\tau(\epsilon)=\int_0^\infty {\rm d}r~ {\left(\lambda_{\rm eff}(\epsilon,r)\right)^{-1}} , \end{displaymath} (10)

where ${\lambda_{\rm eff}(\epsilon,r)}$ is the effective mean path for energy exchange, i.e., the average displacement between two reactions with energy exchange between neutrinos and target particles (see Rybicki & Lightman 1979). It can be expressed as

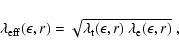\begin{displaymath}{\lambda_{\rm eff}(\epsilon,r)}=\sqrt{\lambda_{\rm t}(\epsilon,r)~ \lambda_{\rm e}(\epsilon,r)} \mbox{ ,} \end{displaymath} (11)

when $\lambda_{\rm e}$ is the mean free path for reactions with energy exchange, i.e. neutrino absorption and neutrino-electron scattering in the present context; and $\lambda_{\rm t}$ is the total mean free path for momentum transfer ("transport mean free path''), which includes all processes by which neutrinos interact with the stellar fluid.

Figure 10 displays the ion screening factors $\langle S_{\rm ion}\rangle$superimposed on the normalized neutrino energy spectra ${\rm d}E_\nu/{\rm d}\epsilon_\nu$at the stellar center for densities of 1011 g cm-3, 1012 g cm-3, 1013 g cm-3, and 1014 g cm-3. Figure 10 once more demonstrates that the reduction of neutrino-nucleus scattering mostly affects neutrinos at energies below the spectral maximum for all plotted cases. In combination with Fig. 9, it also shows that the trapping conditions for the bulk of the neutrino spectrum are not influenced strongly by ion screening. This was identified by Bruenn & Mezzacappa (1997) as the reason ion-ion correlations have no dramatic effect on the core deleptonization.

From Fig. 1 it is clear that differences between the treatments of ion-ion correlations by Horowitz (1997) and Itoh et al. (2004) are largest for $\xi \la 0.5$. The improvements by Itoh et al. (2004) are, therefore, most important for the lowest neutrino energies in the energy window affected by ion screening. Since the phase space available at such low energies is small, one cannot expect large quantitative consequences for stellar core collapse. This is confirmed by Figs. 3-5 and 7. Itoh et al.'s (2004) description (in Model Shen_ion_Itoh) leads to values of $Y_{\rm e}$, $Y_{\rm lep}$, and s after trapping which are essentially indistinguishable from those obtained with Horowitz's (1997) formulae, consistent with the insignificant differences between Models Shen_ion_Hor and Shen_ion_Itoh seen in the other plots. Note that the crossing of the $Y_{\rm e}$-, $Y_{\rm lep}$- and s-profiles for simulations with and without ion screening at 0.45$~M_{\odot}$ (Fig. 7) was also present in the results of Bruenn & Mezzacappa (1997). Finally testing the sensitivity of the core collapse evolution to the treatment of ion screening for the ionic mixture of free protons, $\alpha $ particles, and a representative heavy nucleus, we also could not discover any differences in relevance.

A more detailed analysis reveals the reasons for this insensitivity, which are valid for both employed EoSs. Below the neutrino trapping regime (i.e., for $\rho \la 10^{12}~$g cm-3) even for low-energy neutrinos ( $\epsilon_\nu \approx 5~$MeV), the parameter $\xi $is larger than unity or around unity, except for neutrinos interacting with $\alpha $ particles in an ionic mix when $\xi_\alpha$ is computed from Eqs. (6)-(8). Moreover, $\Gamma \la 50$ holds at the same time, implying that the ion-ion correlation factors $\langle S_{\rm ion}(\xi,\Gamma) \rangle_{\rm Hor}$and $\langle S_{\rm ion}(\xi,\Gamma) \rangle_{\rm Itoh}$for neutrino scattering off heavy nuclei are essentially the same (see Fig. 1). Only at densities above the trapping density, the value of $\xi $drops significantly below unity and $\Gamma $ exceeds 50, causing visible (typically, factors 2-3 for $\epsilon_\nu \la 5~$MeV; Fig. 10) differences in the ion-ion suppression factors $\langle S_{\rm ion}\rangle$. At these densities, however, the exact value of the neutrino-nucleus scattering cross section has no noticeable influence on the evolution of the core properties and on the neutrino transport.

  \begin{figure} \par\includegraphics[width=8.4cm,clip]{3236f6a.eps}\hspace*{4mm} \includegraphics[width=8.4cm,clip]{3236f6b.eps} \end{figure} Figure 6: Spectra of neutrino energy density (solid line) and energy flux (dashed) for Model Shen_ion_off ( left) and Model Shen_ion_Hor ( right), when a density of 1012 g cm-3 is reached at an enclosed mass of 0.3$~M_{\odot}$.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{3236f7a.eps}\hspace*{3mm} \includegraphics[width=8.4cm,clip]{3236f7b.eps} \end{figure} Figure 7: Profiles of electron fraction $Y_{\rm e}$, lepton fraction $Y_{\rm lep}$ ( left), and (gas) entropy s ( right) versus enclosed mass for Models Shen_ion_off (dotted), Shen_ion_Hor (solid), Shen_ion_Itoh (dashed), and Shen_ion_mix (dash-dotted) at the time when the central density has reached a value of 1014 g cm-3.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.4cm,clip]{3236f8a.eps}\hspace*{3mm} \includegraphics[width=8.4cm,clip]{3236f8b.eps} \end{figure} Figure 8: The energy source term for neutrino-electron scattering for densities of a) 1011 g cm-3 and b) 1012 g cm-3at the stellar center in the collapse models with the Shen et al. (1998a,b) EoS. Negative values mean that neutrino energy is "absorbed'' (net scattering out of the corresponding energy bin), and positive values mean "emission'' of neutrino energy (i.e., net scattering of neutrinos into the energy bin).
Open with DEXTER


  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=8cm,clip]{3236f9a.e... ...s} } \subfigure[]{\includegraphics[width=8cm,clip]{3236f9d.eps} }}\end{figure} Figure 9: The optical depth for energy exchange between neutrinos and stellar plasma as a function of the neutrino energy at the center of the iron core for densities of a) 1011 g cm-3, b) 1012 g  cm-3, c) 1013 g cm-3, and d) 1014 g  cm-3. The results were taken from collapse calculations with the Shen et al. (1998a,b) EoS. The left panels show enlargements of the low-energy window where ion-ion correlations have the largest effect.
Open with DEXTER


  \begin{figure} \par\mbox{\subfigure[]{\includegraphics[width=8cm,clip]{3236f10a.... ...} } \subfigure[]{\includegraphics[width=8cm,clip]{3236f10d.eps} }}\end{figure} Figure 10: The cross-section suppression factor $\langle S_{\rm ion}\rangle$ for neutrino scattering off heavy nuclei (bold lines) as function of neutrino energy at the center of the iron core for densities of: a) 1011 g cm-3, b) 1012 g cm-3, c) 1013 g cm-3, and d) 1014 g cm-3. The results are taken from collapse simulations with the Shen et al. (1998a,b) EoS. Also plotted (thin solid lines with crosses) are the local spectra of the neutrino energy density (normalized to the spectral maximum), which are practically identical for all simulations.
Open with DEXTER

Alpha particles in the inner core do not become sufficiently abundant to cause mentionable differences. Their indirect effect on ion-ion correlations of heavy nuclei in an ion mixture by reducing aj (and thus $\xi_j$) and increasing $\Gamma_j$ (Sect. 2.2) for the heavier nuclei is essentially negligible, because their contribution to the sum in Eq. (7) is diminished by their number density being multiplied with a factor $Z_\alpha/Z_j \ll 1$. Moreover, $\alpha $ particles do not account for a significant contribution to the total neutral-current scattering opacity, because the opacity for coherent scattering of neutrinos by nuclei (Z,N,A) scales roughly with N2/A and, therefore, is much smaller for $\alpha $ particles than for heavy nuclei. For this reason, the direct influence of $\alpha $ particles, and thus of the suppression of their coherent (elastic) scattering cross section for low neutrino energies, is miniscule, despite the fact that $\xi_\alpha$ drops below unity already at densities $\rho \la 10^{11}~$g cm-3in a mixture with heavy nuclei. On the other hand, $\Gamma_\alpha$ turns out to be always less than unity and, following Horowitz (1997), is therefore set to $\Gamma_\alpha = 1$ for evaluating the angle-averaged ion screening correction factor.

   
5 Conclusions

In this paper we presented results from simulations of stellar core collapse with the aim of investigating the consequences of ion-ion correlations in neutrino-nucleus scattering, comparing the improved description of Itoh et al. (2004) with an older one by Horowitz (1997). We employed the EoS of Shen et al. (1998a,b), in addition to Lattimer & Swesty's (1991) EoS, and treated electron captures on heavy nuclei according to Langanke et al. (2003), making nuclei dominant over protons in producing neutrinos up to the density of the phase transition to nuclear matter.

Despite these differences in the input physics, our models essentially confirmed the previous calculations by Bruenn & Mezzacappa (1997), who followed Horowitz (1997) in their description of ion screening. Because ion screening is effective only in a low-energy window where the available phase space is rather small, the influence of ion-ion correlations during stellar core collapse and on the formation of the supernova shock is moderate (Bruenn & Mezzacappa 1997).

We found that the improvement by Itoh et al. (2004) does not lead to any noticeable differences, because it affects only neutrinos of very low energies ($\la$5 MeV) before trapping densities ( $\rho \approx 10^{12}~$g cm-3) are reached. Differences at larger neutrino energies occur only at higher densities and thus do not affect the deleptonization and entropy evolution. Effects due to the ionic mixture of free protons, $\alpha $particles, and a representative heavy nucleus - using the linear mixing rule as suggested by Itoh et al. (2004) - were found to be negligibly small, too, mainly because the abundance of $\alpha $ particles in the inner regions of the collapsing stellar core is too low to affect the ion screening of heavy nuclei indirectly (see Sect. 2.2). Alpha particles do not contribute to the total opacity for elastic neutrino-nucleus scattering on a level where their ion screening, which becomes sizable only when the mixture effects of Sect. 2.2 are accounted for, might be relevant.

Improving the description of ion-ion correlations for the complex mix of heavy nuclei with a large variety of components, alpha particles, and free nucleons in the supernova core, however, is desirable. Referring to multi-component calculations based on the Debye-Hückel approximation in the limit of small momentum transfer, Sawyer (2005) argues that a range of N/Z ratios in ionic mixtures can protect against the strong ion screening suppression of neutrino-nuclei scattering predicted by the effective averages of one-component plasma parameters applied in the current literature and in this work. Moreover, the description of nearly free nucleons and nuclei in NSE is expected to hold only up to a density of about 1013 g cm-3. Above this density and below the normal nuclear matter saturation density, a pasta phase may develop with nucleons clustered in subtle and complex shapes. Correlation effects for coherent neutrino scattering can then not be treated within the single heavy nucleus approximation (e.g., Watanabe et al. 2004; Horowitz et al. 2004b,a).

Acknowledgements
We thank Naoki Itoh for providing us with a subroutine to compute his ion-ion correlation factor and for helpful discussions about the treatment of ionic mixtures. We are grateful to the anonymous referee for pointing out an inaccurate use of an average ion sphere radius in the case of ionic mixtures. We also thank K. Langanke, G. Martínez-Pinedo and J. M. Sampaio for their table of electron capture rates on nuclei, which was calculated by employing a Saha-like NSE code for the abundances written by W. R. Hix. Support by the Sonderforschungsbereich 375 "Astro-Particle Physics'' of the Deutsche Forschungsgemeinschaft is acknowledged.

References

 
Copyright ESO 2005