A&A 443, 185-194 (2005)
DOI: 10.1051/0004-6361:20042249
L. Barrière-Fouchet1 - J.-F. Gonzalez1 - J. R. Murray2 - R. J. Humble3 - S. T. Maddison2
1 - Centre de Recherche Astronomique de Lyon (CNRS-UMR 5574),
École Normale Supérieure de Lyon, 46 allée d'Italie,
69364 Lyon Cedex 07, France
2 -
Centre for Astrophysics and Supercomputing, Swinburne University
of Technology, PO Box 218, Hawthorn, VIC 3122, Australia
3 -
Canadian Institute for Theoretical Astrophysics, University of Toronto,
60, St. George Street, Toronto, ON M5S 3H8, Canada
Received 25 October 2004 / Accepted 3 August 2005
Abstract
We present the results of a three dimensional, locally isothermal,
non-self-gravitating SPH code which models protoplanetary disks with two
fluids: gas and dust. We ran simulations of a 1 ![]() star surrounded
by a 0.01
star surrounded
by a 0.01 ![]() disk comprising 99% gas and 1% dust in mass and extending from
0.5 to
disk comprising 99% gas and 1% dust in mass and extending from
0.5 to ![]() AU. The grain size ranges from 10-6 m to 10 m for the
low resolution (
AU. The grain size ranges from 10-6 m to 10 m for the
low resolution (
![]() SPH particles) simulations and from 10-4 m
to 10 cm for the high resolution (
SPH particles) simulations and from 10-4 m
to 10 cm for the high resolution (
![]() SPH particles) simulations.
Dust grains are slowed down by the sub-Keplerian gas and lose angular
momentum, forcing them to migrate towards the central star and settle to
the midplane. The gas drag efficiency varies according to the grain size,
with the larger bodies being weakly influenced and following marginally
perturbed Keplerian orbits, while smaller grains are strongly coupled
to the gas. For intermediate sized grains, the drag
force decouples the dust and gas, allowing the dust to preferentially
migrate radially and efficiently settle to the midplane.
The resulting dust distributions for each grain size will indicate, when
grain growth is added, the regions when planets are likely to form.
SPH particles) simulations.
Dust grains are slowed down by the sub-Keplerian gas and lose angular
momentum, forcing them to migrate towards the central star and settle to
the midplane. The gas drag efficiency varies according to the grain size,
with the larger bodies being weakly influenced and following marginally
perturbed Keplerian orbits, while smaller grains are strongly coupled
to the gas. For intermediate sized grains, the drag
force decouples the dust and gas, allowing the dust to preferentially
migrate radially and efficiently settle to the midplane.
The resulting dust distributions for each grain size will indicate, when
grain growth is added, the regions when planets are likely to form.
Key words: stars: planetary systems: protoplanetary disks - hydrodynamics - methods: numerical
Protoplanetary disks are by definition where we expect planets to
form, with micron to millimetre size grains characteristic of the
interstellar medium collecting and aggregating to form bodies
thousands of kilometres in diameter. Grain growth initially occurs via
individual grains sticking via collisions. However, once grains
reach millimetre size, their collision velocities are sufficiently large
to shatter the grains upon impact (Jones et al. 1996).
One way of reducing the relative velocity of colliding grains is to increase
their number density. Until recently, the dust dynamics of protoplanetary
disks has mostly been studied from the viewpoint of calculating rates of
radial migration into the central star. Classical work in this field was done
by Weidenschilling (1977), who investigated the nature of the drag force
between the dust and gas components of a non-turbulent protostellar disk
and then derived equations describing the radial motions of individual
dust particles. Weidenschilling concluded that the maximum
radial velocity was independent of the drag law and was also insensitive
to the nebula mass. Radial migration was fastest for meter sized
objects with a velocity of
![]() cm s-1.
cm s-1.
Stepinski & Valageas (1997,1996) added turbulence
and grain coagulation and stressed the idea that the dust
motion is decoupled from the gas for a given range of particle size.
They found that grains with sizes 0.1 to 104 cm have inward
radial velocities larger than that of the gas, while larger particles
have smaller velocities. Stepinski & Valageas (1997) modelled a Minimum
Mass Solar Nebula (0.24 ![]() )
with radial extent 15 AU in which
all the solids migrated onto the star, whereas a nebula of 0.002
)
with radial extent 15 AU in which
all the solids migrated onto the star, whereas a nebula of 0.002 ![]() and
extending over 250 AU (which is close to our disk parameters) resulted in
a distribution of solids close to that of our solar system. They did
not investigate vertical settling to the midplane.
and
extending over 250 AU (which is close to our disk parameters) resulted in
a distribution of solids close to that of our solar system. They did
not investigate vertical settling to the midplane.
Rice et al. (2004) studied the concentration of dust in the spiral arms of marginally stable, self-gravitating protoplanetary disks. They followed the evolution of dust test particles added into their existing SPH code which models gas accretion disks. The test particles feel the gravitational effects of the star and gas disk, as well as gas drag, but do not influence the gas disk. They found that the dust density enhancement was significant only for particle sizes between 10 and 100 cm with their nebula parameters, suggesting that grain growth was possible due to the increased density in the dust layer and the decrease in the relative velocities of the dust grains to each other. Vertical settling was found to be insignificant inside the spiral arms.
The case of vertical settling was investigated by Garaud et al. (2004), who analytically derive fluid equations for the average motion of particles in a non-turbulent nebula. Starting from the momentum equation of a single particle in either Stokes or Epstein drag regime (for respectively large and small particles), a Boltzmann distribution is used to obtain the collective behaviour of dust particles which is consistent as dust particles do not interact with each other and the action of dust on the gas is neglected. Garaud et al. (2004) found that small particles move smoothly to the midplane, while large bodies oscillate about the midplane with decreasing amplitude.
It should be noted that the grain sizes discussed here are larger than those found in the interstellar medium. This is consistent with the spectral signature recently observed in the disk of CQ Tau (Testi et al. 2003) suggesting the presence of large grains (a few centimetres), as well as evidence of dust processing and grain growth found in other disks (e.g. Apai et al. 2004; Meeus et al. 2003).
In this article, we present our new three dimensional gas + dust code and compare the results of disk simulations briefly to the work of Weidenschilling (1977) and more extensively with Garaud et al. (2004) and Garaud & Lin (2004). The code allows us to follow both the radial migration and vertical settling of dust in high resolution, and the possibility of including additional physical processes such as turbulence, grain evolution, and radiative transfer in a simple approximation or detailed equation of state. It has already been applied in a preliminary study which uses scattered light as a diagnosis of dust settling (Barrière-Fouchet et al. 2004).
In a separate project, we incorporate dust physics into a parallel N-body +SPH code which calculates self-gravitational forces using a tree based data structure (Humble et al. 2005; Maddison et al. 2003). The data tree adds considerably to the algorithmic complexity of the code, but means we can consider gravitational stability problems.
In Sect. 2, we present the basic equations for dust hydrodynamics and in Sect. 3 we describe our code. In Sect. 4 we describe our simulations: the physical hypotheses, units and initial state, as well as the results. Finally in Sect. 5 we discuss our results in the light of the afore-mentioned references.
A single particle in circular orbit of radius r about a central body of
mass ![]() will move with the Keplerian velocity
will move with the Keplerian velocity
![]() ,
where G is the gravitational
constant. Gas moving in a disk around the same central body will typically
orbit at a slower velocity due to the radial pressure gradient, which solid
bodies moving in the gas disk do not experience and so orbit
at a velocity different than that of the gas. The two phases interact
via a drag which slows down the dust and forces it to migrate
inwards to conserve angular momentum.
,
where G is the gravitational
constant. Gas moving in a disk around the same central body will typically
orbit at a slower velocity due to the radial pressure gradient, which solid
bodies moving in the gas disk do not experience and so orbit
at a velocity different than that of the gas. The two phases interact
via a drag which slows down the dust and forces it to migrate
inwards to conserve angular momentum.
According to Whipple (1972,1973) and Weidenschilling (1977), small bodies are strongly coupled to the gas and have about the same velocity field, whereas large bodies follow marginally perturbed Keplerian orbits. Medium size particles experience the strongest perturbation to their movement, with increased accretion to the central object and vertical settling.
Before describing the equation of motion, we must explain the notations we
have adopted for densities. We use the subscripts d and g to denote dust and
gas respectively. We then define the intrinsic density
(
![]() ,
,
![]() )
of a fluid and the void fraction
(
)
of a fluid and the void fraction
(
![]() ,
,
![]() )
as the fraction of the volume
occupied by a given phase, such that
)
as the fraction of the volume
occupied by a given phase, such that
![]() .
The density (
.
The density (
![]() ,
,
![]() )
of a phase in
a given volume of fluid is then given by
)
of a phase in
a given volume of fluid is then given by
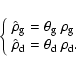 |
(1) |
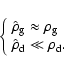 |
(2) |
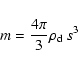 |
(4) |
The functional form of the drag force is determined by the Reynolds number,
Re, and by the ratio of the mean free path of gas molecules, ![]() ,
to the radius of the grains, s(see Stepinski & Valageas 1996; Weidenschilling 1977). The Reynolds number
is given by
,
to the radius of the grains, s(see Stepinski & Valageas 1996; Weidenschilling 1977). The Reynolds number
is given by
![]() where
where
![]() is the gas molecular viscosity
and
is the gas molecular viscosity
and ![]() the sound speed. Thus
the sound speed. Thus
![]() .
.
If
![]() ,
we are in the Stokes regime and the drag is due to the
wake created by dust particles moving through the gas. The expression for the
drag force varies according to the Reynolds number:
,
we are in the Stokes regime and the drag is due to the
wake created by dust particles moving through the gas. The expression for the
drag force varies according to the Reynolds number:
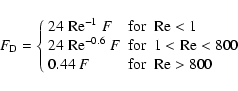 |
(5) |
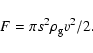 |
(6) |
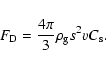 |
(7) |
We use the Smoothed Particles Hydrodynamics (SPH) algorithm, a Lagrangian technique described by Monaghan (1992). The SPH equations and approximations have been rigorously established by Bicknell (1991).
Our code was based on that of Murray (1996), originally developed to study tidally unstable accretion disks in cataclysmic variables. We have made several major changes: the configuration is for that of a protoplanetary disk rather than a binary disk and we have modified the algorithm for finding near neighbours so that the code can better handle variable spatial resolution. Following the work of Monaghan & Kocharyan (1995) and Maddison (1998), we have added a second "dust'' phase in a full, self-consistent, fluid approach, contrary to other studies using only test particles to describe the dust phase (e.g. Rice et al. 2004). We take into account the pressure exerted by gas on dust and by dust on gas, as well as the drag force of gas on dust. In the results presented in this paper, we did not calculate the drag force of dust on gas because it is negligible in magnitude and computationally time consuming, but it is implemented into the code and can be turned on if required. We do not review the SPH method as it has been extensively described (see, for example, Monaghan 1992), but stress the changes made to the code written by Murray (1996) in the following subsections.
As we are following the evolution of two fluids, we therefore have two
independent density equations. The
gas density is obtained by summation over only the gas neighbours
and the dust density is obtained through summation over the dust
neighbours. Using the subscripts a and b to refer to gas particles and
i and j for dust particles, we find:
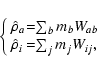 |
(8) |
The SPH smoothing length is usually given by
In order to calculate the number density and subsequently the smoothing
length, we need
to find all the close neighbours of a given particle. As our code does not
include self gravity, rather that using a tree code to find neighbours
(see Hernquist & Katz 1989), we use a less time consuming link list.
In the original implementation of the code, the cells in the linked list
were
![]() in size, where
in size, where
![]() was the maximum value
of the smoothing length over the entire simulation (Murray 1996).
With such a cell size,
a given particle's neighbours laid either in the same link cell or in one
immediately neighbouring it. However, with h varying by as much as
a factor 1000, the number of particles in some cells became very large
and the searches became inefficient.
We implemented an alternative link-list scheme due to Speith (private
communication) in which the size of the link cell is chosen to be
sufficiently small so that each cell only contains a few particles. This means
that, in order to find all the neighbours, the search has to be run over
a large number of cells. We nevertheless find this to be efficient compared
to the traditionally used link cell algorithm without introducing the
programming complexity of a tree structure.
was the maximum value
of the smoothing length over the entire simulation (Murray 1996).
With such a cell size,
a given particle's neighbours laid either in the same link cell or in one
immediately neighbouring it. However, with h varying by as much as
a factor 1000, the number of particles in some cells became very large
and the searches became inefficient.
We implemented an alternative link-list scheme due to Speith (private
communication) in which the size of the link cell is chosen to be
sufficiently small so that each cell only contains a few particles. This means
that, in order to find all the neighbours, the search has to be run over
a large number of cells. We nevertheless find this to be efficient compared
to the traditionally used link cell algorithm without introducing the
programming complexity of a tree structure.
For the gas, the equation of motion is given by:
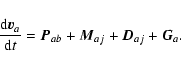 |
(10) |
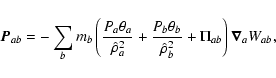 |
(11) |
The mixed pressure term,
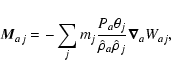 |
(12) |
The drag force term is given by:
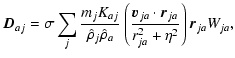 |
|||
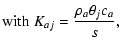 |
(13) |
Finally,
![]() is the gravity exerted by the central star only,
as we do not take self gravity into account. The derivation of the
is the gravity exerted by the central star only,
as we do not take self gravity into account. The derivation of the
![]() and
and
![]() terms can be found in Maddison (1998).
terms can be found in Maddison (1998).
The dust equations are slightly different. The internal pressure
term disappears because the dust fluid is made of large bodies (compared to
gas molecules) that hardly ever encounter each other. These encounters are
better described by an SPH shock treatment than by an internal pressure. Thus
the dust equation of motion is given by:
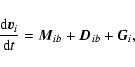 |
(14) |
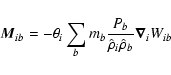 |
(15) |
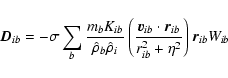 |
(16) |
We use an implicit scheme which is iterative and hence a matrix inversion is not necessary to derive the drag force. The equations are given by Monaghan (1997) and can be found in Appendix A. Note that we use the simpler implicit scheme of Monaghan (1997), since our tests of the Tischer algorithm were very slow and did not give much better results.
A timestep is defined for each physical force: the pressure
(
![]() ), gravity (
), gravity (
![]() ), and drag
(
), and drag
(
![]() )
timesteps. The pressure timestep is defined so as to
verify the Courant condition and includes the viscosity timestep
(see Maddison 1998):
)
timesteps. The pressure timestep is defined so as to
verify the Courant condition and includes the viscosity timestep
(see Maddison 1998):
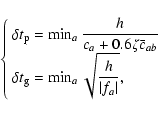 |
(17) |
We also use operator splitting for the drag force because
![]() but
but
![]() can get
much smaller than
can get
much smaller than
![]() in case of strong drag (which happens
close to the central object where the gas density is highest and for the
smaller grain sizes). We choose "by hand'' the number of times the drag
routine is run after a single run of the pressure routine:
in case of strong drag (which happens
close to the central object where the gas density is highest and for the
smaller grain sizes). We choose "by hand'' the number of times the drag
routine is run after a single run of the pressure routine:
![]() decreases with the grain size and we find that, down to
1 mm, we just need to run it once and then 5 times for 100
decreases with the grain size and we find that, down to
1 mm, we just need to run it once and then 5 times for 100 ![]() m, 25 times
for 10
m, 25 times
for 10 ![]() m and 100 times for 1
m and 100 times for 1 ![]() m grains.
m grains.
The code treats turbulence in a very limited manner. The dissipation term in the equation of motion was chosen to reproduce the level of dissipation characteristic of the Shakura-Sunyaev turbulence model. However, the length scale on which dissipation occurs is of the order of the smoothing length and so a full turbulent cascade does not develop.
The resolution of the inner edge of the disk is also limited.
In the calculations, the disk scale height, which is defined by
![]() ,
where
,
where
![]() is the angular
velocity,
has to be larger than the smoothing length h otherwise the disk is not
resolved. However, H<h at small radii and we therefore must set
is the angular
velocity,
has to be larger than the smoothing length h otherwise the disk is not
resolved. However, H<h at small radii and we therefore must set
![]() to be able to carry on the calculations.
It should be noted therefore that the disk is unresolved
for r < 6 AU in our high resolution simulations and
r< 20-40 AU in the low resolution simulations.
Indeed, our disk extends over more than 2 orders of magnitude in radius
making it difficult to resolve both the small and large radii.
The solution is not, however, to simply truncate the disk at 6 AU (in the
high resolution case) because this would result in boundary layer problems.
Instead we know that we can trust the results from 6 AU.
Hereafter, what we call the inner parts of the disk refer to the regions
immediately outside the unresolved parts and not the actual disk inner edge.
to be able to carry on the calculations.
It should be noted therefore that the disk is unresolved
for r < 6 AU in our high resolution simulations and
r< 20-40 AU in the low resolution simulations.
Indeed, our disk extends over more than 2 orders of magnitude in radius
making it difficult to resolve both the small and large radii.
The solution is not, however, to simply truncate the disk at 6 AU (in the
high resolution case) because this would result in boundary layer problems.
Instead we know that we can trust the results from 6 AU.
Hereafter, what we call the inner parts of the disk refer to the regions
immediately outside the unresolved parts and not the actual disk inner edge.
We model a protoplanetary disk of mass 0.01 ![]() with 1% of dust by mass
around a 1
with 1% of dust by mass
around a 1 ![]() star. We consider dust particles ranging from 1
star. We consider dust particles ranging from 1 ![]() m
to 10 m and run a series of simulations that include only one grain size at a
time. Our disk is vertically isothermal which means that the temperature is
constant in the vertical direction but follows a radial power law
(
m
to 10 m and run a series of simulations that include only one grain size at a
time. Our disk is vertically isothermal which means that the temperature is
constant in the vertical direction but follows a radial power law
(
![]() ). We implicitly assume that whatever heating process is
acting within the disk, the subsequent heat is immediately radiated away.
). We implicitly assume that whatever heating process is
acting within the disk, the subsequent heat is immediately radiated away.
We do not include the effects of photoevaporation, radiation pressure, Poynting Robertson flux, magnetic fields or grain coagulation, sublimation or condensation.
We scale our model so as to have numbers close to unity. The mass unit is
one solar mass, the length unit 100 AU and the
time unit is the orbital period of a particle at 100 AU around a 1 ![]() object divided by
object divided by ![]() (1000 yr/
(1000 yr/![]() ). This choice of units leads
to a gravitational constant set to 1.
). This choice of units leads
to a gravitational constant set to 1.
We choose an initial state in near equilibrium conditions. In the
following simulations, we let a gaseous non dusty disk relax from an
initial distribution given by
![]() and
and
![]() .
The initial velocity is Keplerian, given by
.
The initial velocity is Keplerian, given by
![]() .
For the power laws of the temperature and initial surface density, we take the
parameters of the Minimum Mass Solar Nebula (Hayashi et al. 1985).
.
For the power laws of the temperature and initial surface density, we take the
parameters of the Minimum Mass Solar Nebula (Hayashi et al. 1985).
Starting from that initial distribution, we let the disk relax for
![]() 8000 years, i.e. 8 orbits at 100 AU, which allows the pressure and
artificial viscosity time to smooth out the velocity field. The gas velocity
becomes slightly sub-Keplerian because of the pressure gradient. Once the gas
disk has relaxed, we then add the dust particles on top of the gas particles
with the same velocity and let the disk evolve for a further 8000 years.
8000 years, i.e. 8 orbits at 100 AU, which allows the pressure and
artificial viscosity time to smooth out the velocity field. The gas velocity
becomes slightly sub-Keplerian because of the pressure gradient. Once the gas
disk has relaxed, we then add the dust particles on top of the gas particles
with the same velocity and let the disk evolve for a further 8000 years.
We checked that the Reynolds number is always less than
unity since the velocity difference between dust and gas particles stays
subsonic. The mean free path is given by
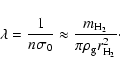 |
(18) |
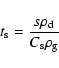 |
(19) |
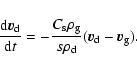 |
(20) |
Table 1: Simulation parameters.
A high resolution single grain size computation requires an average of
15 000 CPU hours shared over 64 processors with OpenMP parallelisation
on the SGI Origin 3800 of the French national computing centre CINES
based in Montpellier. As the grain size decreases, the drag timestep gets
smaller and the computation time increases. The 100 ![]() m simulation required
22 400 CPU hours.
m simulation required
22 400 CPU hours.
Our simulations show that the dust in the solar nebula behaves qualitatively
in the way of the analysis of Whipple (1972,1973) and
Weidenschilling (1977). For example, the larger bodies (![]() m) are
weakly
coupled to the gas and follow marginally perturbed Keplerian orbits and the
dust disk is flared except near the centre where the gas drag is the most
efficient because of the high gas density. On the other hand, the smaller
bodies (
m) are
weakly
coupled to the gas and follow marginally perturbed Keplerian orbits and the
dust disk is flared except near the centre where the gas drag is the most
efficient because of the high gas density. On the other hand, the smaller
bodies (
![]() m) are so strongly coupled to the gas that they follow
its motion and again the dust disk is flared.
m) are so strongly coupled to the gas that they follow
its motion and again the dust disk is flared.
But for intermediate size particles (100 ![]() m
m ![]() 10 cm), the drag
strongly influences the dust
dynamics and induces a motion that is very different from that of the gas. We
first see a rapid stopping phase, where the dust settles into a region where
the drag force dominates. This region is shown in Fig. 3 as the
interior of the
10 cm), the drag
strongly influences the dust
dynamics and induces a motion that is very different from that of the gas. We
first see a rapid stopping phase, where the dust settles into a region where
the drag force dominates. This region is shown in Fig. 3 as the
interior of the ![]() contours. This parameter
contours. This parameter ![]() was characterised
by Garaud et al. (2004) as the ratio of the orbital time to the
stopping time:
was characterised
by Garaud et al. (2004) as the ratio of the orbital time to the
stopping time:
![\begin{figure}
\par\includegraphics[width=15cm]{2249fig1.eps}\end{figure}](/articles/aa/full/2005/43/aa2249-04/Timg105.gif) |
Figure 1:
Density contours for dust particles for the disk seen face on
at the end of the low resolution simulations, each quadrant representing a
different size of particles. The vertical bar gives |
| Open with DEXTER | |
![\begin{figure}
\includegraphics[width=12cm]{2249fig2.eps}\end{figure}](/articles/aa/full/2005/43/aa2249-04/Timg106.gif) |
Figure 2:
Density contours for dust particles of different sizes for the disk
seen edge on at the end of the low resolution simulations. The outermost
contour is the
|
| Open with DEXTER | |
Figure 1 also shows the transition between regimes of weak and
strong vertical settling, as well as weak and strong radial migration. The 10 m
particles do not show any particular increase in density because the
settling is weak, and their distribution stays very close to their initial
configuration, which is that of the gas (as one can see in the edge-on plots in
Fig. 2). Then for 1 m particles, the settling becomes efficient
in the inner regions of the disk, but the radial migration is still weak.
The particles therefore pile up towards the inner edge of the disk and the
density increases. For 10 cm particles, the settling is even stronger and
extends to larger radii, but then the radial migration becomes efficient and
the particles are lost to the star and hence the density enhancement is
weaker than for larger grains. For 1 cm
particles, the settling is now so efficient that it extends over even larger
radii and despite efficient accretion, too many particles arrive at the
inner part of the disk at the same time and thus they pile up and we see a
strong density enhancement. For 1 mm
particles, the combined effects of settling and migration have proven so
efficient that the outer parts of the disk are depleted of dust.
Then the efficiency of the vertical settling decreases together with the
radial migration, up to the point where particles are completely
coupled to the gas as for 1 ![]() m particles, for which the distribution is
undistinguishable from their inital configuration.
m particles, for which the distribution is
undistinguishable from their inital configuration.
In Fig. 4, one can see a large increase in the volume density ratio between dust and gas, rising from 10-2 to 10-1 for some radii. This increase is not as striking when we look at the surface density because the effect of the settling is hidden by the summation over the vertical scale height of the disk. Therefore 2D simulations will underestimate the density enhancement. The meaningful quantity to study is in fact the volumetric density, which has the potential to sufficiently damp the dust velocities to allow the grains to stick together via collisions instead of being shattered. It should be noted, however, that while we do not consider the drag of the dust on the gas because it is negligible when the dust to gas ratio is small, as this ratio approach one the dust could drag the gas with it into high density regions, thus resulting in a self regulation of the dust to gas density ratio.
![\begin{figure}
\par\resizebox{\hsize}{!}{\includegraphics[angle=-90]{2249fig3.eps}}\end{figure}](/articles/aa/full/2005/43/aa2249-04/Timg107.gif) |
Figure 3:
|
| Open with DEXTER | |
 |
Figure 4:
Surface density |
| Open with DEXTER | |
Humble et al. (2005) show that, for values typical of the solar nebula, the distribution of solid particles evolves to an essentially stationary state and that the final radius of the dust disk can be characterised in terms of the particle size.
As in Weidenschilling (1977), we find that the radial migration rate is highest for a given grain size and drops quickly for larger and smaller particle sizes. We find this maximum is reached for 1 cm size particles, whereas Weidenschilling (1977) found it to be 1 m. This discrepancy comes from the difference in the parameters we use for the nebula and Weidenschilling (1977) showed that the gas density and dust intrinsic density have an impact on this maximum grain size.
To check the vertical evolution, we first compare our results with the self-similar behaviour of the dust phase during settling as described by Garaud & Lin (2004) and shown in their Figs. 1b and 2. Despite the noise due to the SPH technique, our results indeed show the same kind of behaviour, shown in Fig. 5. Note that our density increase is orders of magnitudes smaller than theirs because the computation is too time consuming to be run for as long an evolutionary time as given in Garaud & Lin (2004).
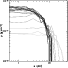 |
Figure 5:
Volume density versus z at r=150 AU for the 100 |
| Open with DEXTER | |
We next validate the formula derived by Garaud et al. (2004) in the
Epstein regime and reproduce their Fig. 5 with our conditions
(see Fig. 6). Starting from the trajectory of a single
particle and then using a Boltzmann averaging, Garaud et al. (2004)
derived an analytical formula for the vertical velocity
![\begin{figure}
\includegraphics[width=10.5cm,clip]{2249fig6.eps}\end{figure}](/articles/aa/full/2005/43/aa2249-04/Timg111.gif) |
Figure 6:
Contours of the vertical velocity for 1 mm ( top panels) and 100 |
| Open with DEXTER | |
The proportionality between vertical velocity and vertical position is most striking at the very beginning of the simulation when the vertical extension is maximal and the particle velocities towards the midplane are largest. The plots are shown 400 yr (0.4 orbits at 100 AU) after the addition of dust.
We can easily see the vertical stratification of the velocity for the 1 mm
grains. It is less obvious for the 100 ![]() m grains because the dust
is more strongly coupled to the gas and settles more slowly towards the
midplane. Furthermore, the noise from the simulation makes the structure more
difficult to detect. At the beginning of the simulations for the 10 cm and
1 cm particles, the grains oscillate about the midplane
following perturbed Keplerian orbits before
the gas damps these oscillations efficiently as shown in Fig. 2 of
Garaud et al. (2004).
m grains because the dust
is more strongly coupled to the gas and settles more slowly towards the
midplane. Furthermore, the noise from the simulation makes the structure more
difficult to detect. At the beginning of the simulations for the 10 cm and
1 cm particles, the grains oscillate about the midplane
following perturbed Keplerian orbits before
the gas damps these oscillations efficiently as shown in Fig. 2 of
Garaud et al. (2004).
Finally, looking at the sequence of edge-on images in Fig. 2, we see qualitatively the behaviour discussed by Garaud et al. (2004) that at a given height the region will be depleted of intermediate size particles.
In this article, we have shown the importance of the vertical settling of
intermediate size grains (10 cm to 100 ![]() m) in a protoplanetary disk
with a central object of
m) in a protoplanetary disk
with a central object of ![]() =
=
![]() ,
a gas disk mass of
,
a gas disk mass of
![]() and a dust disk mass of
and a dust disk mass of
![]() .
.
We find that the dust distribution is completely different from the gas and the general approximation that the dust to gas ratio is constant throughout the disk is wrong for grains in this size range. This has an impact on the interpretation of observations made in the millimetre domain, for instance, as the opacity of millimetre size grains dominates. It is thus important to understand the specific behaviour of the dust to avoid misinterpretations such as an underestimate or overestimate of the gas density.
Our simulation results compare well with the radial migration seen in Weidenschilling (1977), the analytical work of Garaud et al. (2004) and the vertical settling of Garaud & Lin (2004).
The Shakura & Sunyaev (1973) turbulence modelling has been extensively used in the domain of protoplanetary disks and has proven to give consistent results. It should, however, be used cautiously and ideally a better prescription for turbulence should be used. Indeed, turbulence will likely reduce the dust settling velocities and lessen the density enhancements we observe in our simulations (see, e.g., Weidenschilling & Cuzzi 1993). The magneto-rotational instability has been consistently described by Balbus & Hawley (1991) and global numerical simulations for this instability are becoming more accurate (Fromang et al. 2004). It is now possible to have a consistent description of this kind of turbulence in a numerical simulation and a first step towards this goal was given by Monaghan (2002), who derived an SPH prescription of turbulence. We plan to incorpate SPH turbulence into our code in order to investigate how turbulence affects the dust settling.
While the locally isothermal approximation is roughly consistent with the temperature distribution in a protoplanetary disk, a lot of effort is currently going into the domain of radiative transfer in protoplanetary disks (e.g. Dullemond & Dominik 2004), suggesting that the energetics in such an object deserve a better treatment. Unfortunately, including full radiative transfer in our SPH code is not feasible because of the increased computation it would require. Nevertheless, we will be able to achieve a better description by implementing an adiabatic equation of state with cooling functions as one of the improvements we plan to add in our code.
This consistent description of the dust distribution in a protoplanetary disk is a first step towards planet formation. By implementing a consistent treatment of the grain growth, coagulation, and shattering, we will be able to better understand planetesimal formation and their distribution in the disk.
Acknowledgements
This work was funded by the French PNPS and L.B.-F. would like to thank the French CINES for the important amount of computing time that made these simulations possible. The authors are grateful to the French-Australian PICS for financial support for travel to Australia. L.B.-F. is also deeply grateful to Eduardo Delgado for comments and suggestions as well as to Roland Speith for the idea of the new link list routine.
All the following equations are derived from Monaghan (1997).
The momentum equations for gas and dust in Epstein regime read
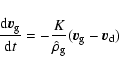 |
(A.1) |
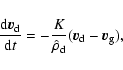 |
(A.2) |
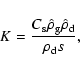 |
(A.3) |
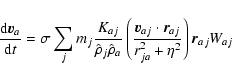 |
(A.4) |
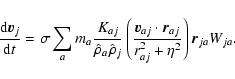 |
(A.5) |
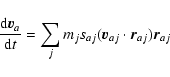 |
(A.6) |
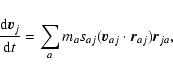 |
(A.7) |
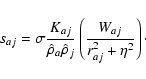 |
(A.8) |
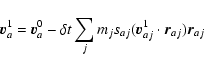 |
(A.9) |
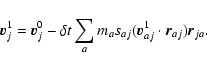 |
(A.10) |
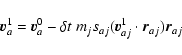 |
(A.11) |
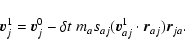 |
(A.12) |
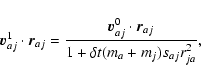 |
(A.13) |
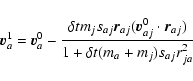 |
(A.14) |
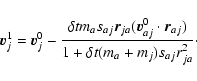 |
(A.15) |
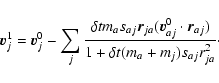 |
(A.16) |
Now, we subdivide each timestep into two, and we note
![]() the velocity at
the velocity at
![]() :
:
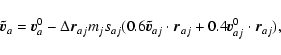 |
(A.17) |
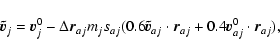 |
(A.18) |
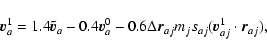 |
(A.19) |
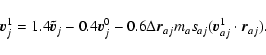 |
(A.20) |
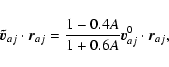 |
(A.21) |
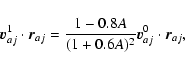 |
(A.22) |
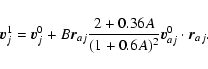 |
(A.23) |