A&A 442, 331-343 (2005)
DOI: 10.1051/0004-6361:20053360
Prominence fine structures in a magnetic equilibrium
II. A grid of two-dimensional models
P. Heinzel
1,2 -
U. Anzer2 - S. Gunár1,3
1 - Astronomical Institute,
Academy of Sciences of the Czech Republic,
25165 Ondrejov, Czech Republic
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Strasse 1, 85740 Garching, Germany
3 -
Astronomical Institute, Faculty of Mathematics and
Physics,
Charles University,
Prague, Czech Republic
Received 3 May 2005 / Accepted 1 July 2005
Abstract
We construct a grid of 2D vertical-thread models for
prominence fine structures which are in magnetohydrostatic (MHS)
equilibrium. Such thread models have been described in a previous paper
by Heinzel & Anzer (2001), but here we use a modified 2D transfer code
with an adaptive MHS grid. Multilevel non-LTE transfer calculations
are now performed for a 12-level plus continuum hydrogen model atom,
in order to study the behaviour of the Lyman-series lines observed
by SOHO/SUMER. Our grid consists of 18 models which cover a range
of central column masses, magnetic-field intensities and two
parameters characterising the 2D temperature structure of the
thread. Since different Lyman lines and their parts (line center,
peak, wings) are formed at different places within the thread, the
Lyman series may serve as a good diagnostic tool for thermodynamic
conditions varying from central cool parts to a prominence-corona
transition region. We demonstrate this behaviour for various lines,
showing their synthetic profiles as seen from two perpendicular
directions along and across the magnetic field lines, respectively,
and displaying the respective contribution functions. This
study confirms our earlier conclusion that the Lyman line profiles
are much more reversed when seen across the field lines, compared
to those seen along the lines. The latter can be even unreversed.
We also show the geometrical cross-section (shape) of all 18
models. Their thread-like shape with a considerable aspect ratio
resembles recent high-resolution H images. Finally, we discuss the relation of our thread models
to the vertical threads studied by Fontenla et al. (1996, ApJ, 466, 496).
images. Finally, we discuss the relation of our thread models
to the vertical threads studied by Fontenla et al. (1996, ApJ, 466, 496).
Key words: Sun: prominences -
magnetohydrodynamics (MHD) -
radiative transfer - line: profiles
During almost one decade of observations SOHO (SOlar and
Heliospheric Observatory) has collected a large amount of UV and
EUV data on prominences and filaments. Among them, spectral
observations of hydrogen Lyman lines and continuum obtained by the
SUMER UV-spectrograph represent an important constraint on
prominence modelling. Various examples of such data and their
analysis can be found in Schmieder et al. (1998, 1999, 2003) and
Heinzel et al. (2001); see also a review of SOHO prominence
observations by Patsourakos & Vial (2002). The formation depths of
these optically-thick lines span the whole prominence structure
and thus the line profiles of the Lyman series can provide us with
a reliable diagnostics of prominence/filament thermodynamic
conditions. The fact that SUMER is capable of observing the
whole Lyman series is quite unique.
In order to interpret properly the Lyman-line profiles, one has to
perform rather complex non-LTE radiative transfer computations
using sophisticated models. Important steps towards this goal were
the following: magnetohydrostatic (MHS) and radiative-transfer
models developed by Heasley & Mihalas (1976), first 2D prominence
models by Mihalas et al. (1978) and Vial (1982), demonstration of
importance of the partial frequency redistribution (PRD) for
hydrogen Lyman lines (Heinzel et al. 1987), a grid of 1D models by
Gouttebroze et al. (1993), 2D models with PRD (Paletou et al.
1993; Paletou 1995), multi-thread models in energy balance by
Fontenla et al. (1996). Recently, Heinzel & Anzer (2001)
(hereafter referred to as Paper I) have generalised the 1D MHS
models of Heasley & Mihalas (1976) to the 2D case and have given
examples of 2D diagnostics of vertical fine-structure threads in
MHS equilibrium. Three important aspects play a role in the
spectral-line formation: the pressure structure, the temperature
variation in the prominence-corona transition region (PCTR)
and the depth variations of the line source functions. The
pressure structure is described by 2D MHS equilibria (for details
see also Heinzel & Anzer 2005). The temperature profile is in
principle determined by the energy balance, but here we model it
by an ad hoc spatial variation and for the calculation of the
source function we perform the consistent 2D radiative transfer.
Moreover, PRD plays an important role for the ionisation of
hydrogen and affects the line intensities. The results of Paper I
support the conclusions of Heinzel et al. (2001) that when looking
along the magnetic-field lines the Lyman-line profiles
appear as unreversed or only weakly reversed emission profiles,
while when looking across the field lines, the profiles may
exhibit rather strong reversals. This behaviour is due to the
temperature structure of the PCTR.
However, so far no detailed quantitative fit of all observed Lyman
lines (e.g. those presented for three different prominences in
Heinzel et al. 2001) was achieved. It is the purpose of this
paper to make further steps in our understanding of the behaviour
of the Lyman spectrum formation. We construct here a grid of 18
fine-structure thread models, which are in 2D MHS equilibrium and
have an infinite vertical extension. Selecting a set of input
parameters allows us to demonstrate the sensitivity of individual
models to various physical conditions. This experience will be
used in the future to obtain a quantitative fitting of SOHO/SUMER
Lyman spectra.
The paper is organised as follows. Section 2 summarizes the basic
physical conditions inside the fine-structure thread and presents
our 18 models. Section 3 describes the non-LTE radiative transfer
in two dimensions, together with a new MHS adaptive-grid
scheme. Section 4 explains how the so-called contribution
functions can be used to visualize the line-formation regions.
Section 5 gives a detailed discussion of our
results obtained for individual models.
Section 6 shows how the fine-structure dips can be
seen in projection against the disk.
Finally, Sect. 7 presents the discussion and the conclusions.
For our modelling of prominence threads we use the form of
vertically infinite 2D threads hanging in a horizontal magnetic field.
The exact
mathematical formulation of the equations of the MHS equilibrium
was published in Paper I, here we give only an overview.
The pressure equation has the form
![\begin{displaymath}
p(m,y)=4p_{{\rm c}}(y)\frac{m}{M(y)}\left[1-\frac{m}{M(y)}\right]+p_{0},
\end{displaymath}](/articles/aa/full/2005/40/aa3360-05/img8.gif) |
(1) |
with the definition of the magnetic pressure
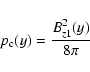 |
(2) |
and with M(y) (the column mass integrated over x-direction)
given by
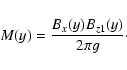 |
(3) |
Here p0 is the boundary coronal pressure, Bx(y) is
the horizontal field-component (constant along a given field line),
Bz1(y) is the vertical field-component at the boundary and g the
gravitational acceleration at the solar surface. Because of the
requirement of MHS equilibrium we have the relation
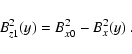 |
(4) |
Here Bx0 is the horizontal field between individual
threads.
As in Paper I, we use the column-mass coordinate
m instead of the cartesian coordinate x, which is more
useful in the case of non-uniform temperature and ionisation structure.
Then the transformation from
the mass coordinate m to the spatial coordinate x requires the
following integration
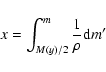 |
(5) |
at each value of the coordinate y, where  is the density.
is the density.
The temperature profile with an empirically described
PCTR first used by Anzer & Heinzel (1999) has the form
![\begin{displaymath}
T(m,y)=T_{{\rm cen}}(y)+[T_{{\rm tr}}-T_{{\rm
cen}}(y)]\le...
...}\left[1\!-\!\frac{m}
{M(y)}\right]\right\}^{\gamma_{1}}\!,~
\end{displaymath}](/articles/aa/full/2005/40/aa3360-05/img14.gif) |
(6) |
where
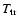 represents the temperature at the
boundary and the exponent
represents the temperature at the
boundary and the exponent
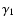 has to be chosen properly.
The temperature at x=0,
has to be chosen properly.
The temperature at x=0,
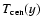 ,
is
given by
,
is
given by
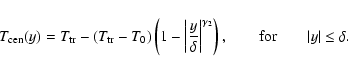 |
(7) |
T0 is the (minimum) central temperature, 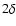 represents
the width of the thread in y-direction (perpendicularly to the field
lines) and the exponent
represents
the width of the thread in y-direction (perpendicularly to the field
lines) and the exponent
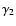 is again a free parameter.
The 2D temperature structure is then fully
determined by the exponents
is again a free parameter.
The 2D temperature structure is then fully
determined by the exponents
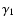 and
and
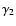 .
.
The shape of synthetic spectral-line profiles obtained by
radiative transfer modelling depends on the set of input
parameters which describe the MHS equilibrium, the form of
temperature structure, and on the incident radiation.
The set of input MHS-parameters fully determines the shape of the magnetic
dips and will influence the shape of the calculated synthetic
profiles. The full description of all input MHS-parameters
has been presented in
Paper I. The first parameter which is varied in our calculations is the maximum
column density M0 appearing in the mass function
M(y)
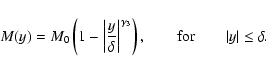 |
(8) |
Once we have prescribed M0 we can use Bx(0) (horizontal
field in the middle of the thread) instead of Bx0 (horizontal
field between threads), where the former one represents a
measurable quantity for prominences. The values of Bx0 and
Bx(0) are simply related through Eqs. (3) and
(4).
In order to describe the dependence of the synthetic profiles on
given input parameters we have constructed a grid of 18 prominence
models. Within this grid of models we varied M0, Bx(0)and the exponents
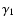 and
and
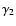 .
The other input
parameters have been fixed for all our models, with the values:
.
The other input
parameters have been fixed for all our models, with the values:
T0=8000 K;
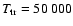 K;
K;
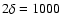 km;
km;
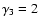 ;
p0=0.03 dyn cm-2.
;
p0=0.03 dyn cm-2.
The model grid consists of three series with 6 models for each of
them. The series differ only in the value of one of the
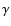 -parameters. The models in each series have different
values of M0 and Bx(0). The full list of our model grid
is summarised in Table 1. Geometrically all these models
represent structures with a width of 1000 km and their lengths
vary between 2000 km and 25 000 km which partially depends on the
solution of the radiative-transfer problem (see below). An example
of the 2D variation (in the x-y plane) of the temperature, gas pressure
and density and of the magnetic structure is shown in Paper I.
-parameters. The models in each series have different
values of M0 and Bx(0). The full list of our model grid
is summarised in Table 1. Geometrically all these models
represent structures with a width of 1000 km and their lengths
vary between 2000 km and 25 000 km which partially depends on the
solution of the radiative-transfer problem (see below). An example
of the 2D variation (in the x-y plane) of the temperature, gas pressure
and density and of the magnetic structure is shown in Paper I.
Table 1:
Parameters for the model grid.
For the solution of the 2D radiative transfer problem we used the
Accelerated Lambda Iteration (ALI) technique (Auer & Paletou
1994) with the short characteristics (SC) method to obtain the
formal solution along individual rays. A detailed description of
the method is given in Paper I.
In contrast to our previous paper we use here a 12-level plus
continuum hydrogen model atom (see e.g. Heinzel et al. 1997), in
order to obtain higher members of the Lyman series as they are
observed by SOHO/SUMER. The 12-level model also ensures a higher
accuracy as compared to the 5-level model (at least of lower Lyman
lines) because of more precisely computed level
populations.
In Figs. 1 and 2 we show averaged profiles of
the L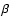 and L
and L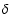 lines, in order to compare the 5-level
and 12-level solutions. Full lines result from averaging along the
dip thickness 2
lines, in order to compare the 5-level
and 12-level solutions. Full lines result from averaging along the
dip thickness 2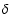 ,
dashed lines represent averaging along
the whole dip length (i.e. in the x-direction). The difference
in intensities is given by the different level populations, while
the ionisation is almost the same for the two cases.
,
dashed lines represent averaging along
the whole dip length (i.e. in the x-direction). The difference
in intensities is given by the different level populations, while
the ionisation is almost the same for the two cases.
Lyman-line profiles of the incident radiation are taken from the
SOHO/SUMER disk observations made by Warren et al. (1998). The
observed profiles show an asymmetry due to flows in the solar
atmosphere, however, for our purposes we used quiet-Sun profiles
symmetrised by averaging the red and blue parts. Since Warren et al. (1998) data do not include the L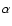 line (this line was
difficult to detect with SUMER), we still use the same incident
profiles as in the previous Paper I. The averaged incident
radiation was computed at height of 10 000 km above the solar
surface.
line (this line was
difficult to detect with SUMER), we still use the same incident
profiles as in the previous Paper I. The averaged incident
radiation was computed at height of 10 000 km above the solar
surface.
A new feature of the present models is that we use here an adaptive MHS grid. In the y-direction the grid is fixed and we
use the logarithmic spacing in order to properly describe a steep
PCTR at the boundary. However, in the x-direction, i.e. along
the field lines, the geometrical extension of the magnetic dip
follows from the MHS equilibrium - for a given field strength, the
larger M0 the deeper the dip will be (and thus the structures
are effectively less extended). Moreover, the conversion from the
column-mass coordinate m as used to express the MHS equilibrium
(Paper I) to geometrical one needed for 2D radiative transfer,
depends on the local gas density which in turn depends on the
ionisation degree. In Paper I we just used an initial estimate of
the ionisation degree (see Eq. (17) in Paper I) and kept the
x-grid fixed. In this paper we follow the procedure described in
Heinzel & Anzer (2003). After the converged non-LTE solution is
obtained for a given 2D model, and thus 2D distribution of the
ionisation degree, a new grid is constructed along the field lines
which is consistent with the current ionisation degree. Then the
2D transfer is solved again to get a new ionisation degree and
this procedure is repeated until the changes between two
subsequent grids are negligible. Typically 5 iterations are
sufficient. For more details see Heinzel & Anzer (2003)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig1.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg32.gif) |
Figure 1:
L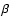 profiles for the 5-level model ( left-hand side)
and for the 12-level model ( right-hand side). Full lines represent
averages
over y, dashed lines are mean profiles over x.
profiles for the 5-level model ( left-hand side)
and for the 12-level model ( right-hand side). Full lines represent
averages
over y, dashed lines are mean profiles over x. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig2.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg33.gif) |
Figure 2:
L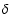 profiles for the 5-level model ( left-hand side)
and for the 12-level model ( right-hand side). Full lines represent
averages over y, dashed lines are mean profiles over x.
profiles for the 5-level model ( left-hand side)
and for the 12-level model ( right-hand side). Full lines represent
averages over y, dashed lines are mean profiles over x. |
| Open with DEXTER |
For the analysis of the diagnostic properties of the Lyman lines
we need to know the corresponding formation depths. For this
purpose we use the contribution function C. This function for
the emergent specific intensity is defined by the integral
relation
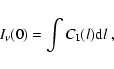 |
(9) |
where l is the geometrical length (depth) which we take here
either in x or y-direction.
In terms of the optical depth
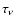 the contribution function is defined as
the contribution function is defined as
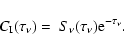 |
(10) |
The transformation between optical depth
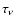 and geometrical depth
l is given by
and geometrical depth
l is given by
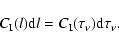 |
(11) |
Then the contribution function has the form
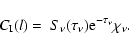 |
(12) |
Here
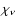 represents the absorbtion coefficient. Since the
source function is given by
represents the absorbtion coefficient. Since the
source function is given by
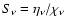 ,
we obtain
,
we obtain
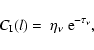 |
(13) |
with
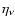 being the emission coefficient.
being the emission coefficient.
The contribution to the specific intensity on the surface from a
given point of the geometrical grid depends on the direction of
the line-of-sight. In this paper we display the contributions as
functions of x and y for two perpendicular directions of view:
along x-coordinate (along the field lines) and along
y-coordinate (across the field lines). 2D plots of computed
contribution functions, for all considered Lyman lines, are
available on the web site http://www.asu.cas.cz/~radtrans. Examples are shown below
for selected models, lines and positions in the line profile (line
center, peaks, wings). These plots show the spatial variation of
the contribution to the specific intensity as a function of the
position in the structure of the prominence (x-y dimensions are
in cm). White regions represent places with major contribution to
the specific intensity (for a given frequency), black regions
indicate minor contributions. The contours in the figures are
iso-lines of the temperature structure. Isothermal contours are
plotted in steps of 10 000 K. Note that these figures are not drawn
to the true scale.
In this section we discus the dependence of our synthetic profiles on
the values of the input parameters defining individual models, as well as
their variation with the viewing direction. All line-profile plots
are also available at
http://www.asu.cas.cz/~radtrans.
As was shown in Heinzel et al. (2001), the computed Lyman-line
profiles of prominences strongly depend on the viewing angle with
respect to the magnetic-field orientation. Paper I contains one
example of a synthetic profile computed for a specific model with
a 5-level atom. Here we show synthetic profiles obtained for our
grid of models using an extended 12-level hydrogen atom.
In Fig. 3 we show L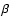 ,
L
,
L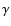 and L6
line profiles. Full lines again represent profiles averaged over
y, dashed lines are profiles averaged over x. The intensity
plots (Fig. 4) show the variation of the line
intensity as a function of x and wavelength. Each profile
there represents a mean profile averaged locally over 1000 km in
x-direction.
and L6
line profiles. Full lines again represent profiles averaged over
y, dashed lines are profiles averaged over x. The intensity
plots (Fig. 4) show the variation of the line
intensity as a function of x and wavelength. Each profile
there represents a mean profile averaged locally over 1000 km in
x-direction.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig3.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg44.gif) |
Figure 3:
The profiles of lines L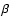 ,
L ,
L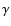 and L6. Full
lines are y-mean profiles, dashed lines are x-mean profiles.
and L6. Full
lines are y-mean profiles, dashed lines are x-mean profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3360fig4.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg45.gif) |
Figure 4:
The intensity plots for the lines of L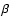 ( pair of plots at the top),
L
( pair of plots at the top),
L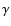 ( middle plots) and L6
( pair of plots at the bottom). On the left-hand side the structure is
shown from the front,
on the right-hand side from the rear.
( middle plots) and L6
( pair of plots at the bottom). On the left-hand side the structure is
shown from the front,
on the right-hand side from the rear. |
| Open with DEXTER |
The field orientation has a two-fold effect on the Lyman-line shapes.
First, the density distribution along the field lines
is given by the MHS equations, while across the field lines the
column mass M(y) can vary in a rather arbitrary way because the individual
flux tubes are magnetically separated. For the variation of M(y) we use
an ad hoc form described by Eq. (8).
Second, along the field lines the temperature variation is supposed to be
relatively smooth because of efficient heat conduction - we describe this
variation by an empirical formula (6). On the other hand, the heat
conduction across the field lines is strongly inhibited and thus we assume
a schematic temperature profile (7) which exhibits a rather steep
rise at the boundaries.
From our grid of models we conclude that the L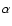 profiles
are rather similar when one looks along the x-axis and when one
looks in y-direction. But for all higher lines we see that in
general the line profiles are much more reversed when we look
along the y-axis (i.e. across the field lines). This trend
becomes more pronounced when one goes to higher lines. The
x-variation of the line intensity is shown for three different
lines in Fig. 3. We can see that in the center of the structure
(at x=0) the reversal is not very pronounced, but it strongly
increases outside the central parts. Finally, approaching the
boundaries where
profiles
are rather similar when one looks along the x-axis and when one
looks in y-direction. But for all higher lines we see that in
general the line profiles are much more reversed when we look
along the y-axis (i.e. across the field lines). This trend
becomes more pronounced when one goes to higher lines. The
x-variation of the line intensity is shown for three different
lines in Fig. 3. We can see that in the center of the structure
(at x=0) the reversal is not very pronounced, but it strongly
increases outside the central parts. Finally, approaching the
boundaries where
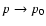 ,
the profiles become
unreversed with a central emission peak. This behaviour can be
understood as follows. First, we have to realize that the
temperature structure across the field lines is rather flat in the
inner parts and only very near to the boundaries the temperature
steeply increases to values of the surrounding corona - see Eq.
(4) and the contours in the plots of the contribution functions).
On the other hand, along the field lines (along the
x-direction), the central temperature increases much more
gradually (Eq. (3)). Let us now assume that looking across the
field lines, we see different "slabs'' of thickness of 1000 km,
having temperatures gradually increasing from T0=8000 K to
,
the profiles become
unreversed with a central emission peak. This behaviour can be
understood as follows. First, we have to realize that the
temperature structure across the field lines is rather flat in the
inner parts and only very near to the boundaries the temperature
steeply increases to values of the surrounding corona - see Eq.
(4) and the contours in the plots of the contribution functions).
On the other hand, along the field lines (along the
x-direction), the central temperature increases much more
gradually (Eq. (3)). Let us now assume that looking across the
field lines, we see different "slabs'' of thickness of 1000 km,
having temperatures gradually increasing from T0=8000 K to
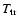 .
At the same time, the gas pressure decreases. It was
demonstrated already by Gouttebroze et al. (1993) that in the case
of isothermal-isobaric finite prominence slabs, the Lyman-line
reversals strongly increase when the temperature starts to exceed
.
At the same time, the gas pressure decreases. It was
demonstrated already by Gouttebroze et al. (1993) that in the case
of isothermal-isobaric finite prominence slabs, the Lyman-line
reversals strongly increase when the temperature starts to exceed
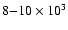 K and if also the pressure is sufficiently
high. This is exactly what we observe outside the innermost parts
of our 2D configurations. This behaviour can be understood by
looking at the line source-function variations along the
line-of-sight. The slabs are strongly irradiated from the solar
surface and if the corresponding radiation temperature is
comparable to the slab temperature, the line source function is
only weakly decreasing towards the irradiated slab surface.
However, by increasing the slab temperature, the source function
starts to increase in the slab interior and decreases towards to
surface. This naturally produces a strong reversal in Lyman lines,
unless the gas pressure is so low that the whole line goes into
emission (i.e. when it becomes optically thin).
K and if also the pressure is sufficiently
high. This is exactly what we observe outside the innermost parts
of our 2D configurations. This behaviour can be understood by
looking at the line source-function variations along the
line-of-sight. The slabs are strongly irradiated from the solar
surface and if the corresponding radiation temperature is
comparable to the slab temperature, the line source function is
only weakly decreasing towards the irradiated slab surface.
However, by increasing the slab temperature, the source function
starts to increase in the slab interior and decreases towards to
surface. This naturally produces a strong reversal in Lyman lines,
unless the gas pressure is so low that the whole line goes into
emission (i.e. when it becomes optically thin).
The shape of the temperature structure is fully described by the
exponents
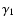 and
and
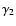 .
For the discussion of effects of
the temperature structure
on the line profiles it is useful to compare two
models which differ only in one of these parameters.
.
For the discussion of effects of
the temperature structure
on the line profiles it is useful to compare two
models which differ only in one of these parameters.
Here we compare models A1 and
C1 which differ in 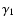 (
(
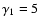 for
A1 and
for
A1 and
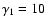 for
C1). We demonstrate the effect of changes of the
exponent
for
C1). We demonstrate the effect of changes of the
exponent
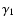 on various lines.
on various lines.
L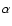 and L
and L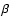
The center of these spectral lines for both directions of view
forms at the boundary of the prominence structure (Fig. 8), in areas with a high temperature rising up to the
boundary value of 50 000 K where p goes to coronal pressure
p0. The value of the L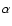 central intensity is almost the
same for both directions of view and for both models. Model
A1 gives the higher value of a specific
intensity in the line peak (more than 40%) compared to model
C1 (Fig. 5). This is due to a
higher temperature in the region of the peak formation (Fig. 8). The temperature is higher because we keep the
boundary temperature fixed and have a lower temperature gradient
close to the boundary for A1, given by the
lower value of the parameter
central intensity is almost the
same for both directions of view and for both models. Model
A1 gives the higher value of a specific
intensity in the line peak (more than 40%) compared to model
C1 (Fig. 5). This is due to a
higher temperature in the region of the peak formation (Fig. 8). The temperature is higher because we keep the
boundary temperature fixed and have a lower temperature gradient
close to the boundary for A1, given by the
lower value of the parameter
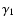 .
The wings of spectral
lines are mostly optically thin and originate in the center of the
thread (Fig. 8), the place with a low temperature,
high density and negligible influence of the parameter
.
The wings of spectral
lines are mostly optically thin and originate in the center of the
thread (Fig. 8), the place with a low temperature,
high density and negligible influence of the parameter
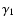 .
.
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{3360fig5.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg48.gif) |
Figure 5:
Profiles of L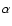 and L
and L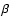 for
model A1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles.
for
model A1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fig6.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg49.gif) |
Figure 6:
Profiles of L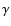 for
model A1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles.
for
model A1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fig7.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg50.gif) |
Figure 7:
Profiles of L7 for
model A1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
L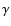
The region of formation of the line center is now deeper inside the
structure
. This leads to a higher value of the specific intensity in the
center of L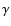 for A1 (up to 20%) in
comparison to C1 (Fig. 6) which is
due to higher temperature in the region of origin of the line center
(similarly as for L
for A1 (up to 20%) in
comparison to C1 (Fig. 6) which is
due to higher temperature in the region of origin of the line center
(similarly as for L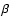 ). The mean profile over y for
the model A1 has a weak self-reversal, while for
C1 the y-averaged profile is in emission
(Fig. 6). This is again due to temperature differences.
The mean profiles over x for both models still have a self-reversed
shape (see discussion in Sect. 5.1), however the value of the specific
intensity for A1 is higher by some 20% than
for model C1. The line wings are formed in
the prominence center with negligible influence of
the parameter
). The mean profile over y for
the model A1 has a weak self-reversal, while for
C1 the y-averaged profile is in emission
(Fig. 6). This is again due to temperature differences.
The mean profiles over x for both models still have a self-reversed
shape (see discussion in Sect. 5.1), however the value of the specific
intensity for A1 is higher by some 20% than
for model C1. The line wings are formed in
the prominence center with negligible influence of
the parameter
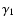 .
.
L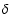 -L11
-L11
The mean-profiles over y are in emission while the mean profiles over xshow self-reversal for both models (Fig. 7). This is
again consistent with our interpretation given in Sect. 5.1.
The central and peak-intensities of the model A1 are
higher by some 40%. The line wings of lines L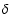 -L7 originate in the central part with
the lowest temperature. The place of origin of the spectral lines
L8-L11 is
however shifted into regions with higher temperature which is
required for the formation of these high-frequency lines (Fig. 9).
-L7 originate in the central part with
the lowest temperature. The place of origin of the spectral lines
L8-L11 is
however shifted into regions with higher temperature which is
required for the formation of these high-frequency lines (Fig. 9).
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{3360fig8.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg51.gif) |
Figure 8:
L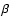 contributions as functions of x and y. The first
six panels are for model A1, the other six
for model C1. On the left-hand side the
viewing is in the direction
along the x-axis ( from the left side), on the right-hand side
in the
y-direction ( from the bottom). The upper pairs of each model are
for the
central frequency, the middle pairs are for the peak frequency and
the lower ones represent
contributions in the line wings. x-y dimensions are in cm.
contributions as functions of x and y. The first
six panels are for model A1, the other six
for model C1. On the left-hand side the
viewing is in the direction
along the x-axis ( from the left side), on the right-hand side
in the
y-direction ( from the bottom). The upper pairs of each model are
for the
central frequency, the middle pairs are for the peak frequency and
the lower ones represent
contributions in the line wings. x-y dimensions are in cm. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3360fig9.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg52.gif) |
Figure 9:
L9 contributions as functions of x and y. The first
six panels are for model A1, the other six
for model C1. The figure is arranged in the same
way as Fig. 8. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=15.94cm,clip]{3360fg10.eps}\end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg53.gif) |
Figure 10:
Depth-variations of the line-center contribution function
for the Lyman series (L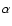 to L10), as viewed along the field
lines. The model A1 was used.
to L10), as viewed along the field
lines. The model A1 was used. |
| Open with DEXTER |
Now we compare models B1 (
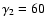 )
and
C1 (
)
and
C1 (
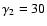 ).
).
L
The line center originates from the boundary for both models and
the values of the central intensity are identical. The place of
formation of the peak intensity is shifted into the structure and
the value of the specific intensity for model
C1 is higher (up to 30%) compared to the
model B1 (Fig. 11). It is due to the
shape of the temperature structure (Fig. 12). The
profiles for both models and for each direction of view have a
self-reversal. The line wings, formed in the center of the thread,
are not
affected by the parameter
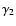 .
.
L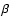
The central intensity is again influenced by the shape of the temperature
structure and for C1 is higher by about 20%. The
C1 profile has a deeper self reversal while for
B1 the self reversal is quite negligible
(Fig. 13). This is due to the formation of the peak in
model C1 in places with higher temperature
than in model B1 (Fig. 14). The line
wings again form in the central regions.
L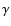 -L11
-L11
The mean profiles over y are in emission for both models.
For model C1, the x-averaged profiles show
a self-reversal, but B1 profiles averaged over
x are in emission.
In order to demonstrate how the Lyman series can be used to
diagnose the thread structure, we plot in Fig. 10 the
contribution functions at the line center of L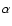 to L10, as
viewed along the magnetic-field lines. This clearly shows that
higher members of the Lyman series do form deeper and thus their
line-center intensity reflects the temperature and density
variations through the structure.
to L10, as
viewed along the magnetic-field lines. This clearly shows that
higher members of the Lyman series do form deeper and thus their
line-center intensity reflects the temperature and density
variations through the structure.
Figure 10 shows that the L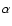 line center
is formed at rather high temperatures, around 50 000 K or even more.
We have made some test simulations with
line center
is formed at rather high temperatures, around 50 000 K or even more.
We have made some test simulations with
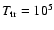 K and for such
models the L
K and for such
models the L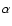 line-center formation region is entirely between
50 000 and 105 K. However, the actual mechanism of the line
formation at these regions largely depends on the density.
At the boundary where the gas pressure reaches values p0=0.03 dyn cm-2 in our models, the particle number density is almost
two orders of magnitude lower than at the central cool regions.
Therefore, the scattering of incident radiation can still play a role
in determining the line source function, together with collisional
excitations. According to our plots of L
line-center formation region is entirely between
50 000 and 105 K. However, the actual mechanism of the line
formation at these regions largely depends on the density.
At the boundary where the gas pressure reaches values p0=0.03 dyn cm-2 in our models, the particle number density is almost
two orders of magnitude lower than at the central cool regions.
Therefore, the scattering of incident radiation can still play a role
in determining the line source function, together with collisional
excitations. According to our plots of L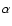 profiles, the
central intensity is roughly a factor of two larger than that
of the diluted quiet-Sun intensity.
profiles, the
central intensity is roughly a factor of two larger than that
of the diluted quiet-Sun intensity.
The value of the magnetic-field intensity has an essential effect on the
shape of the prominence structure. We show the effect of field
intensity variation for models A3
(
Bx(0)=2 Gauss) and A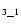 (
Bx(0)=10Gauss). Due to the lower value of the field intensity the model
A3 has a length around 5000 km while model
A
(
Bx(0)=10Gauss). Due to the lower value of the field intensity the model
A3 has a length around 5000 km while model
A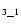 is 10 000 km long. Changes of the
x-dimension cause different distributions of density inside the
prominence structure.
is 10 000 km long. Changes of the
x-dimension cause different distributions of density inside the
prominence structure.
L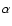
The line profile for model A3 has a sharp self-reversal
shape for both directions of view, different from model
A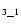 (Fig. 15). A higher
value of the peak intensity (up to 30%) for model A3
is due to the higher temperature in the place of origin of the
peak (Fig. 16).
(Fig. 15). A higher
value of the peak intensity (up to 30%) for model A3
is due to the higher temperature in the place of origin of the
peak (Fig. 16).
Other spectral lines
The other line profiles are not reversed, for both models and
directions of view (when averaged over x-direction).
A3 profiles have higher
values of the specific intensity due to higher temperatures.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg11.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg55.gif) |
Figure 11:
Profiles of L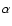 for
model B1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles.
for
model B1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg12.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg56.gif) |
Figure 12:
L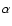 contribution functions for model
B1
( top) and C1 ( bottom), showing the
contributions for the peak frequency for observation in y-direction.
contribution functions for model
B1
( top) and C1 ( bottom), showing the
contributions for the peak frequency for observation in y-direction. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg13.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg57.gif) |
Figure 13:
Profiles of L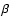 for
model B1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles.
for
model B1 ( left-hand side) and
C1 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fg14.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg58.gif) |
Figure 14:
L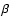 contribution functions for model B1
( top) and C1 ( bottom), showing the
contributions for the peak frequency for observation in y-direction.
contribution functions for model B1
( top) and C1 ( bottom), showing the
contributions for the peak frequency for observation in y-direction. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg15.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg59.gif) |
Figure 15:
Profiles of L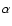 for
models A3 ( left-hand side) and
A
for
models A3 ( left-hand side) and
A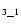 ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. ( right-hand side).
Full lines are y-mean profiles, dashed lines are x-mean
profiles. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg16.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg60.gif) |
Figure 16:
L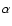 contribution functions for model A3
( top) and A
contribution functions for model A3
( top) and A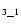 ( bottom), showing the
contributions for the peak frequency for observation in y-direction. ( bottom), showing the
contributions for the peak frequency for observation in y-direction. |
| Open with DEXTER |
The geometrical shape of the prominence fine structure, i.e. its
horizontal cross-section, is determined mainly
by the magnetic field strength and the column mass, and to some extent
also by the temperature structure. Variations of the input
parameters for our 18 models
have an essential effect on the magnetic field structure (dip)
and therefore lead to different extensions in x-direction.
In Fig. 17 the geometrical shape of all
models is shown. Each of these models has a fixed width of 1000 km
in y-direction.
The extension in x-direction (along magnetic field
lines) is for each model represented by the length of the black bars.
Now we shall briefly analyse the effect of each input parameter on
the geometrical length of the threads. The higher values of
Bx(0) give more extended thread structure due to larger
magnetic tension force (dips can be less deep). This is clear from
a comparison of the models with labels 3 and
3_1 and those labelled 4 and
4_1. Models with labels 1 and
3_1 have comparable values of Bx(0) but
different values of M0. The larger extension of models
1 is due to the larger amount of mass in the
structure. The temperature structure described by the 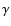 parameters has also an influence on the density distribution in
the thread. The shallower the increase of temperature, the more
extended is the structure of the thread.
parameters has also an influence on the density distribution in
the thread. The shallower the increase of temperature, the more
extended is the structure of the thread.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3360fg17.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg61.gif) |
Figure 17:
The geometrical shape of all models. Each bar has a
width of
1000 km. |
| Open with DEXTER |
The actual shape of the structure as it would be projected onto
the solar disk is somewhat more complex, but it retains features
from Fig. 17. Restricting the thread to a finite
vertical extension, one can use the 2D horizontal distribution of
the vertical opacity (optical thickness) to compute e.g. the
H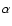 line contrast against the solar disk. For this a simple
cloud model with the constant source function can be applied (see
e.g. Heinzel & Anzer 2005). The resulting dark fibrils are
rather long, their aspect ratio depends on the fixed thickness in
y-direction which we took here to be 1000 km. In reality,
however, this thickness can be smaller and thus the fibrils could
appear long. This situation resembles recent high-resolution (up
to about 0.2 arcsec) H
line contrast against the solar disk. For this a simple
cloud model with the constant source function can be applied (see
e.g. Heinzel & Anzer 2005). The resulting dark fibrils are
rather long, their aspect ratio depends on the fixed thickness in
y-direction which we took here to be 1000 km. In reality,
however, this thickness can be smaller and thus the fibrils could
appear long. This situation resembles recent high-resolution (up
to about 0.2 arcsec) H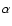 images obtained either with the new
SVST or with DOT on La Palma (see Engvold 2005; or DOT website).
We interpret the central parts of quiescent filaments as
being composed of shorter, densely packed fibrils which are in
fact the magnetic dips projected onto the disk - see also Aulanier
& Démoulin (1998, 2003). Very long individual fibrils which
extend out of the filament body may have different nature, they
can correspond to low-lying extended fluxtubes with significant
horizontal flows (Engvold 2005).
images obtained either with the new
SVST or with DOT on La Palma (see Engvold 2005; or DOT website).
We interpret the central parts of quiescent filaments as
being composed of shorter, densely packed fibrils which are in
fact the magnetic dips projected onto the disk - see also Aulanier
& Démoulin (1998, 2003). Very long individual fibrils which
extend out of the filament body may have different nature, they
can correspond to low-lying extended fluxtubes with significant
horizontal flows (Engvold 2005).
Let us now comment briefly on the models of Fontenla et al. (1996).
These models were aimed, as ours here, to represent the vertical
fine-structure threads of quiescent prominences.
But in contrast to our models they consider 1D isobaric slab
configurations.
Their approach is in some respect complementary to ours: they
determine the temperature structure in the slab from the condition
of energy balance (assuming some kind of heating function and
taking the energy transport by ambipolar diffusion into account).
But they do not solve the MHS equilibrium equations. In contrast
to this we solve the 2D MHS equilibrium, but prescribe ad hoc
temperature profiles ignoring the energetics. Also the geometries
of the two sets of models are very different: Fontenla et al. (1996)
take a very large number of extremely thin slabs (just a few tens
km each)
which are perpendicular to the magnetic field
(see also discussion by Anzer & Heinzel 1999), while we study individual
2D threads aligned with the magnetic field.
Fontenla et al. (1996) considered several 1D slabs (threads) along the
line-of-sight and the emergent synthetic intesities were computed for
Lyman lines (also using PRD for L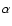 and L
and L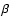 ). Comparing this
to our 2D models, two problems arise. First, in our MHS scenario, only
one thread (dip) is allowed along the given field line, others being formed
along nearby lines. This then means that looking strictly along the field
lines, we can see only one thread, not a multithread structure. However,
our 2D approach allows us to look also across the field lines and then we
can see several threads along the line-of-sight. Considering the energy balance
in the way similar to Fontenla et al. (1996), in 2D one could compute
the ambipolar diffusion along the field lines, but look through several
threads perpendicularly. The second problem is that the models of Fontenla
et al. (1996) are very narrow along the magnetic field, while ours
show a rather long extension in this direction (see Fig. 17).
This is a direct consequence of the MHS
equilibrium and the empirical temperature structure.
). Comparing this
to our 2D models, two problems arise. First, in our MHS scenario, only
one thread (dip) is allowed along the given field line, others being formed
along nearby lines. This then means that looking strictly along the field
lines, we can see only one thread, not a multithread structure. However,
our 2D approach allows us to look also across the field lines and then we
can see several threads along the line-of-sight. Considering the energy balance
in the way similar to Fontenla et al. (1996), in 2D one could compute
the ambipolar diffusion along the field lines, but look through several
threads perpendicularly. The second problem is that the models of Fontenla
et al. (1996) are very narrow along the magnetic field, while ours
show a rather long extension in this direction (see Fig. 17).
This is a direct consequence of the MHS
equilibrium and the empirical temperature structure.
Another comment concerns the assumption that the threads are very
extended vertically, in fact we take them as vertically infinite
in our 2D approach. The idea comes from Poland & Mariska (1988)
who suggested that when a dip is formed locally the field below
becomes compressed and that above diluted. Therefore the dip
region grows in height, by vertical propagation and thus forms a
thread filled by cool plasma. However, the real vertical extension
is difficult to estimate. From the observational point-of-view,
one should try to derive the vertical extension from
high-resolution disk observations of filaments (see discussion in
Sect. 6), from the theoretical side a 3D MHS configuration
should be constructed and then used for fully 3D transfer
modelling.
We discuss how the magnetic field configuration of a vertical
prominence thread can influence the structure of the
prominence-corona transition region. As we show, depending on
this structure one obtains different line profiles for the series
of Lyman lines, namely when looking, respectively, along and
across the magnetic-field lines. Studying these lines can
give us important information on the physical conditions in the
prominence threads. In the next paper we intend to apply this
modelling to sets of Lyman-line profiles observed in prominences
by SOHO/SUMER. By searching for the best fit simultaneously to all
observed Lyman profiles one should be able to determine in detail
the physical structure of prominence threads. However, this may
require a more complex modelling based on multi-thread
configurations - several threads seen along the line-of-sight
which passes across the magnetic-field lines.
Acknowledgements
P.H. acknowledges the support from MPA Garching, U.A. thanks for
support of the Ondrejov Observatory. This work was done in the
frame of grant No. IAA 3003203 of the Grant Agency of the Academy
of Sciences of the Czech Republic, ESA-PECS project No. 98030
and the research project AVOZ10030501.
SOHO is a space mission of international cooperation between ESA
and NASA. The authors thank to P. Gouttebroze and J.-C. Vial for their
valuable comments.
- Anzer, U., &
Heinzel, P. 1999, A&A, 349, 974 [NASA ADS] (In the text)
- Auer, L. H., &
Paletou, F. 1994, A&A, 285, 675 [NASA ADS] (In the text)
- Aulanier,
G., & Démoulin, P. 1998, A&A, 329, 1125 [NASA ADS] (In the text)
- Aulanier,
G., & Démoulin, P. 2003, A&A, 402, 769 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Engvold, O.
2005, in Multiwavelength Investigations of Solar Activity, ed. A.
V. Stepanov, E. F. Benevolenskaya, & A. G. Kosovichev
(Cambridge Univ. Press), Proc. IAU Symp., 223, 187
(In the text)
- Fontenla, J.
M., Rovira, M., Vial, J.-C., & Gouttebroze, P. 1996, ApJ, 466,
496 [NASA ADS] [CrossRef] (In the text)
- Gouttebroze, P., Heinzel, P., &
Vial, J.-C. 1993, A&AS, 99, 513 [NASA ADS] (In the text)
- Heasley, J.
N., & Mihalas, D. 1976, ApJ, 205, 273 [NASA ADS] [CrossRef] (In the text)
- Heinzel, P., & Anzer, U. 2001,
A&A, 375, 1082 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I)
(In the text)
- Heinzel, P.,
& Anzer, U. 2003, in Stellar Atmosphere Modeling, ed. I.
Hubeny, D. Mihalas, & K. Werner, ASP Conf. Ser., 288, 441
(In the text)
- Heinzel, P.,
& Anzer, U. 2005, in Solar Magnetic Phenomena, ed. A.
Hanslmeier, A. Veronig, & M. Messerotti, Astron. Astrophys.
Space Sci. Lib., 320 (Dordrecht: Springer), 115
(In the text)
- Heinzel, P.,
Gouttebroze, P., & Vial, J.-C. 1987, A&A, 183, 351 [NASA ADS] (In the text)
- Heinzel, P.,
Schmieder, B., & Vial, J.-C. 1997, in Proc. Fifth SOHO
Workshop, ESA SP-404, 427
(In the text)
- Heinzel, P.,
Schmieder, B., Vial, J. C., & Kotrc, P. 2001, A&A, 370,
281 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Mihalas, D.,
Auer, L. H., & Mihalas, B. 1978, ApJ, 220, 1001 [NASA ADS] [CrossRef] (In the text)
- Paletou, F.
1995, A&A, 302, 587 [NASA ADS] (In the text)
- Paletou, F.,
Vial, J.-C., & Auer, L. H. 1993, A&A, 274, 571 [NASA ADS] (In the text)
- Patsourakos, S., & Vial, J.-C.
2002, Sol. Phys., 208, 253 [NASA ADS] [CrossRef] (In the text)
- Poland, A. I.,
& Mariska, J. T. 1988, in Dynamics and Structure of Solar
Prominences, Proc. of a Workshop held at Palma de Mallorca, ed. J.
L. Ballester, & E. R. Priest, Universitat de les Illes Balears,
133
(In the text)
- Schmieder,
B., Heinzel, P., Kucera, T., & Vial, J.-C. 1998, Sol. Phys.,
181, 309 [NASA ADS] [CrossRef] (In the text)
- Schmieder,
B., Heinzel, P., Vial, J.-C., & Rudawy, P. 1999, Sol. Phys.,
189, 109 [NASA ADS] [CrossRef] (In the text)
- Schmieder,
B., Tziotziou, K., & Heinzel, P. 2003, A&A, 401, 361 [EDP Sciences] [NASA ADS] (In the text)
- Vial, J.-C. 1982,
ApJ, 254, 780 [NASA ADS] [CrossRef] (In the text)
- Warren, H. P.,
Mariska, J. T., & Wilhelm, K. 1998, ApJ, 119, 105 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{displaymath}
p(m,y)=4p_{{\rm c}}(y)\frac{m}{M(y)}\left[1-\frac{m}{M(y)}\right]+p_{0},
\end{displaymath}](/articles/aa/full/2005/40/aa3360-05/img8.gif)
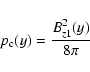
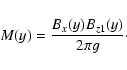
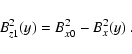
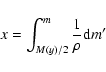
![\begin{displaymath}
T(m,y)=T_{{\rm cen}}(y)+[T_{{\rm tr}}-T_{{\rm
cen}}(y)]\le...
...}\left[1\!-\!\frac{m}
{M(y)}\right]\right\}^{\gamma_{1}}\!,~
\end{displaymath}](/articles/aa/full/2005/40/aa3360-05/img14.gif)
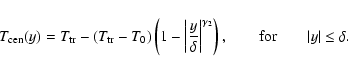
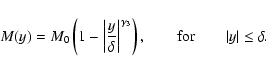
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig1.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg32.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig2.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg33.gif)
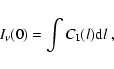
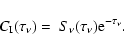
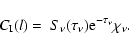
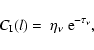
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fig3.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg44.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3360fig4.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg45.gif)
![\begin{figure}
\par\includegraphics[width=8.7cm,clip]{3360fig5.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fig6.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg49.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fig7.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg50.gif)
![\begin{figure}
\par\includegraphics[width=15.3cm,clip]{3360fig8.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg51.gif)
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3360fig9.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg52.gif)
![\begin{figure}
\par\includegraphics[width=15.94cm,clip]{3360fg10.eps}\end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg53.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg11.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg12.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg13.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg57.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3360fg14.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg15.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg59.gif)
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{3360fg16.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg60.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3360fg17.eps} \end{figure}](/articles/aa/full/2005/40/aa3360-05/Timg61.gif)