A&A 441, 791-806 (2005)
DOI: 10.1051/0004-6361:20053453

Oligarchic and giant impact growth of terrestrial planets in the presence of gas giant planet migration

M. J. Fogg - R. P. Nelson

Astronomy Unit, Queen Mary, University of London, Mile End Road, London E1 4NS, UK

Received 17 May 2005 / Accepted 24 June 2005

Abstract
Giant planets found orbiting close to their central stars, the so-called "hot Jupiters'', are thought to have originally formed in the cooler outer regions of a protoplanetary disk and then to have migrated inward via tidal interactions with the nebula gas. We present the results of N-body simulations which examine the effect such gas giant planet migration has on the formation of terrestrial planets. The models incorporate a 0.5 Jupiter mass planet undergoing type II migration through an inner protoplanet-planetesimal disk, with gas drag included. Each model is initiated with the inner disk being at successively increased levels of maturity, so that it is undergoing either oligarchic or giant impact style growth as the gas giant migrates.

In all cases, a large fraction of the disk mass survives the passage of the giant, either by accreting into massive terrestrial planets shepherded inward of the giant, or by being scattered into external orbits. Shepherding is favored in younger disks where there is strong dynamical friction from planetesimals and gas drag is more influential, whereas scattering dominates in more mature disks where dissipation is weaker. In each scenario, sufficient mass is scattered outward to provide for the eventual accretion of a set of terrestrial planets in external orbits, including within the system's habitable zone. This scattering, however, significantly reduces the density of solid material, indicating that further accretion will occur over very long time scales. A particularly interesting result is the generation of massive, short period, terrestrial planets from compacted material pushed ahead of the giant. These planets are reminiscent of the short period Neptune-mass planets discovered recently, suggesting that such "hot Neptunes'' could form locally as a by-product of giant planet migration.

Key words: planets and satellites: formation - methods: N-body simulations - astrobiology

  
1 Introduction.

Over the last ten years the radial velocity technique has been successfully employed in the detection of giant planets orbiting nearby main sequence stars (e.g. Butler et al. 2004; Mayor & Queloz 1995; Marcy et al. 2000). To date, 136 extra-solar planetary systems have been discovered, 14 of them multiple, leading to a total of 155 giant planets[*]. Even though radial velocity observations are more sensitive to short period orbits, a surprising discovery has been the substantial population of giant planets orbiting close to their central star at distances $\la$0.1 AU. Twenty nine such objects are known (3 of them sited in multiple systems) comprising $\sim $20% of the total sample. These so-called "hot Jupiters'' are mostly sub-jovian in mass, with low eccentricity orbits, and are often found associated with stars more metal rich than the Sun (Udry et al. 2003; Fischer & Valenti 2005; Santos et al. 2003).

The most likely scenario for the origin of hot Jupiters involves initial formation further out in the nebula beyond the "snowline'' as per conventional formation theories (e.g. Pollack et al. 1996), followed by an episode of inward orbital migration, propelled by tidal interactions between the planet and gas disk. A variety of orbital migration phenomena have been proposed for protoplanets as they grow in mass, but the one most likely to operate in this case is type II migration where the planet has become sufficiently massive ($\ga$ $100~{M}_\oplus$) to open up a gap in the gas, thereby migrating inward at a rate controlled by the disk viscous time scale (Lin et al. 1996; Nelson et al. 2000; Lin & Papaloizou 1986). This time scale is typically on the order of a few $\times 10^5$ years. What finally stops the inward drift of these planets at such small radial distances, other than fortuitous disk dispersal, is presently unknown and it may be that some migrating planets are accreted by the central star.

It appears therefore that hot Jupiter systems are not uncommon and possibly represent an extreme rearrangement of planetary mass during formation as compared with the Solar System. This comparison raises an interesting set of questions. What effect would hot Jupiter migration have on terrestrial planet formation? Might accretion of terrestrial planets be interrupted or prevented altogether? Can we have any realistic expectation of ever discovering Earth-like planets in these systems, or is it probable their habitable zones are empty of significant material, having been swept clean by the passage of the giant? The assumption that hot Jupiter systems are barren are among those advanced to support such speculative concepts as the "Rare Earth'' hypothesis (Ward & Brownlee 2000) and the Galactic Habitable Zone (Lineweaver et al. 2004; Lineweaver 2001), both of which argue for a large number of special circumstances required to form an Earth-like planet. From their standpoint, any significant difference in planetary system architecture from that of the solar system is likely to preclude the formation or survival of planets that are habitable for multi-cellular life.

These issues were examined by Armitage (2003) with a simple time-dependent disk model of the evolution of gas, dust and planetesimals. He assumed that the effect of giant planet migration is to first sweep the inner disk clear of planetesimals, and then looked at whether a new generation of planetesimals could be formed in the terrestrial planet region by the subsequent resupply of dust from outer regions by advection and diffusion. His conclusion was that resupply of solid material into the inner disk would be inefficient and terrestrial planet formation would be unlikely. In contrast, Mandell & Sigurdsson (2003) consider a late migration scenario and use N-body simulations to model the migration of a Jupiter mass planet through a fully formed terrestrial planet system. The typical pattern of evolution observed included: 1) excitation of planetary orbits by sweeping resonances with the inward migrating giant; 2) close encounters between the planets resulting in collisions or mutual scattering; and 3) slingshot encounters with the giant as it passed through the inner system, leading to ejection, collision with the central star, or scattering into bound exterior orbits with increased semi-major axis, eccentricity and inclination. Short migration times allowed a larger fraction of planets to survive rather than being ejected whereas the trend was reversed for long migration times. Overall, $\sim $25% of the planets survived in a wide variety of orbits exterior to the giant, orbits which, they speculated, might subsequently become circularized as a result of dynamical friction with outer system planetesimals or interaction with the remnant gas disk. They concluded therefore that inward migration of a giant planet does not invariably eliminate pre-formed terrestrial planets and that, given an initial layout of bodies similar to that of the Solar System, between $\sim $1-4% of systems in which migration occurred could still possess a planet in the habitable zone. Actual formation of terrestrial planets in the presence of a hot Jupiter has been modelled by Raymond et al. (2004). They assume a previous rapid migration of the giant into its final close orbit and then model the later stages of terrestrial planet accretion from an exterior protoplanet disk using N-body methods. Their conclusion is that the presence of a hot Jupiter does little to interfere with terrestrial planet formation outside of an annulus that is within a factor of three in period to the giant (about a factor of two in semi-major axis). Planet formation in the habitable zone is not adversely affected.

The conclusions of these three papers span the widest possible range of outcome, from the occurrance of terrestrial planets in hot Jupiter systems being highly unlikely, through possible but rare, to commonplace. This variation originates from the very different assumptions and initial conditions in each case. Armitage (2003) does not model the dynamic effects of the migrating giant on planetesimals and instead assumes total loss of planetary building blocks from within the swept zone. This may be unrealistic especially as, by the time a giant planet has grown large enough to start type II migration, considerable accretion into larger planetary embryos could have already occurred in the inner system, bodies which might not be so readily accreted or bulldozed into the central star. The picture of Mandell & Sigurdsson (2003) of a giant migrating through a mature terrestrial planet system may suffer from unrealistic timing as giant planet formation and migration is constrained to occur within the $\sim $ 106-107 year lifetime of the gas disk whereas the terminal "giant impacts'' phase of terrestrial planet formation is thought to last $\sim $108 years (e.g. Chambers 2001). The optimistic conclusions of Raymond et al. (2004) are a function of their initial condition of placing the hot Jupiter in its final, post migration, orbit and then modelling terrestrial planet formation in an essentially undisturbed, unmixed, exterior disk. This requires rapid giant planet formation and migration followed by the formation of a new terrestrial disk from the remaining debris which must somehow be reduced back to a more unevolved, damped, and chemically differentiated state.

Timing issues are therefore important in the study of this problem, involving initially isolated sequences of events inside and beyond the nebula snowline. Whilst there remains much uncertainty over detail, one fairly certain constraint which gives an upper limit to the time available is that giant planets must both form and complete migration in considerably less than 107 years, before the dispersal of the nebular gas. Observations suggest that 50% of stars in clusters have lost their disks by an age of $\sim $ $3\times 10^6$ years (Haisch et al. 2001). Estimation of a lower age limit is more problematic as it must rely on our incomplete theories of giant planet formation. If the core-accretion model is to be preferred, favorable conditions would allow giants to form in $\ga$106 years (Alibert et al. 2004; Pollack et al. 1996; Papaloizou & Nelson 2004). In the meantime, accretion will be ongoing within the planetesimal swarm in the terrestrial planet region. According to the current picture, an early phase of runaway growth will give way to a more lengthy phase of oligarchic growth where similar sized protoplanets emerge from the swarm in well-spaced orbits which remain near circular due to dynamical friction from the surrounding sea of planetesimals (Kokubo & Ida 1998). Oligarchic growth ends when planetesimal numbers decline to the extent that their damping effect on protoplanet orbits becomes insufficient to prevent orbit crossing. This inaugurates the last phase of terrestrial planet formation, that of so-called "giant impacts'', involving the mutual accretion of protoplanets and thinning down of their number to the point where the final planets emerge, positioned in stable non-crossing orbits. Simulations of this final stage of terrestrial planet growth suggest that it would take $\sim $108 years to complete (Chambers 2001), long after the disappearance of the nebular gas. Oligarchic growth however starts much earlier, whilst gas is still present: simulations by Kokubo & Ida (2000) have shown that it takes only $\sim $ $5\times10^5$ years to generate $\sim $ $0.01{-}0.03~M_\oplus$planetary embryos from a planetesimal disk at 1 AU. Thus, in the case of a giant planet migrating through the terrestrial planet zone, it seems most probable that this would occur at some time within, or towards the end of the phase of oligarchic growth in that region.

In order to better satisfy these timing constraints, we present below a set of N-body simulations of giant planet migration through progressively evolved inner system protoplanet-planetesimal disks undergoing either late oligarchic or early giant impact style growth. In Sect. 2 we outline our model and its initial conditions; in Sect. 3 the results are presented and discussed; in Sect. 4 we consider some caveats and future model improvements, and in Sect. 5 we offer our conclusions.

  
2 Description of the model

  
2.1 Forces

We choose to model planet growth and migration using the hybrid-symplectic N-body simulation package Mercury 6 (Chambers 1999), modified to include the effect of gas drag on planetesimals and type II migration on a single giant planet. The ingredients required for the simulations are thus one migrating giant planet, and an interior disk of small protoplanets embedded within a swarm of planetesimals. However, due to the huge number of particles involved, the realization of a realistic planetesimal disk, with every body treated as fully interacting, is well beyond the current state of the art. We proceed therefore by following the so-called N + N' approach of Thommes et al. (2003) where we have N protoplanets embedded in a disk of N' "super-planetesimals'', particles that represent an idealized ensemble of a much larger number of real planetesimals. The giant and the protoplanets feel all the modeled gravitational forces, whereas the super-planetesimals feel gravitational forces from the central star, protoplanets, and giant planet, but are otherwise non self-interacting. This prevents their relatively high masses from unrealistically auto-exciting the disk. Super-planetesimals alone also experience gas drag with the drag being calculated using a defined physically realistic planetesimal radius. The issue of the mass of the super-planetesimals was addressed by Thommes et al. (2003) who found in test runs that protoplanets undergo effective dynamical friction if super-planetesimal masses are $\la$0.1 times the initial protoplanet masses.

The coordinate origin is based on the central star. The acceleration experienced by each of the super-planetesimals is given by:

 
$\displaystyle \frac{{\rm d}^2\vec{r}_i}{{\rm d}t^2} = - \frac{GM_\ast\vec{r}_i}... ...N'}_{k=1} \frac{Gm_k\vec{r}_k}{\vert\vec{r}_{k}\vert^3} + \vec{a}_{{\rm drag}},$     (1)

where $M_\ast$ is the stellar mass, mj and $\vec{r}_j$ are particle masses and position vectors, and $\vec{r}_{ij}=\vec{r}_i-\vec{r}_j$. The first term on the right hand side represents the acceleration from the central star, the second term the accelerations from the protoplanet and giant planet, the third and fourth terms are the indirect terms arising from the acceleration of the coordinate system, and $\vec{a}_{{\rm drag}}$ is the acceleration due to gas drag.

The acceleration experienced by the protoplanets and gas giant planet is given by:

 
$\displaystyle \frac{{\rm d}^2\vec{r}_i}{{\rm d}t^2} = - \frac{GM_\ast\vec{r}_i}... ..._{k=1} \frac{Gm_k\vec{r}_k}{\vert\vec{r}_{k}\vert^3} + \vec{a}_{{\rm type~II}}.$     (2)

The first term again represents the acceleration due to the central star, the second and third terms represent the accelerations due to the protoplanets/giant planet and super-planetesimals, respectively, and $\delta_{ij}$ is the Kronecker delta function. The fourth and fifth terms are indirect terms, and $\vec{a}_{{\rm type~II}}$ is the acceleration driving type II migration of the gas giant planet alone.

Planetesimals are small enough to experience a drag force from moving through the nebula gas. This acceleration, which acts both to cause an inward radial drift and a damping of eccentricities and inclinations, takes the form:

 \begin{displaymath} \vec{a}_{{\rm drag}}=-\frac{1}{2m_{{\rm pl}}} C_{{\rm D}} \pi r^2_{{\rm pl}} \rho_{{\rm g}} \vert\vec{u}\vert\vec{u} , \end{displaymath} (3)

where $m_{{\rm pl}}$ and $r_{{\rm pl}}$ are the physical mass and radius of a single planetesimal respectively, $C_{{\rm D}}$is the drag coefficient (taken here to be $C_{{\rm D}} = 1$) and $\vec{u}=\vec{v}_{{\rm p}} - \vec{v}_{{\rm g}}$ is the velocity of the planetesimal with respect to the gas. The gas is assumed to move in a circular orbit which, due to pressure support, revolves at slightly less than Keplerian speed. The relation is:

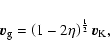\begin{displaymath}\vec{v}_{{\rm g}} = \left(1-2\eta\right)^{\frac{1}{2}}\vec{v}_{{\rm K}} , \end{displaymath} (4)

where $\vec{v}_{{\rm K}}$ is the local Keplerian velocity and $\eta=0.0019(a/1~\mbox{AU})^{1/2} $, given the nebula scale height introduced later in Eq. (9) (Adachi et al. 1976).

In order to model type II migration of a giant planet, we adopt a simple prescription and assume that this occurs at a rate controlled by a local viscous disk evolution timescale that is proportional to orbital period. Assuming an alpha viscosity model, this is roughly:

 \begin{displaymath} \tau_{\nu} = \frac{2}{3}\left(\frac{r}{h}\right)^2\left(\alpha\Omega \right)^{-1}, \end{displaymath} (5)

where r is the radial distance, h is the disk scale height, $\alpha$ is the alpha parameter and $\Omega$ is the orbital frequency. Given $\alpha = 2 \times 10^{-3}$, h/r = 0.05 and $r = 5\ \mbox{AU}$ then $\tau_\nu \approx 0.25\ \mbox{Myr}$. Since $\tau_\nu \propto a^{1.5}$, where a is the semi-major axis, $\dot{a} \propto a^{-0.5}$ so inward migration speeds up as it proceeds. (Note that this value of h/r differs slightly from that obtained from Eq. (9).)

The type II migration process is also assumed to exert strong eccentricity and inclination damping which is taken here to operate over a timescale $\ = \tau_\nu/50$. The acceleration $\vec{a}_{{\rm type~II}}$ is therefore implemented as:

\begin{displaymath}\vec{a}_{{\rm type~II}} = - \frac{\vec{v}}{2\tau_\nu} - 25 \l... ..._\nu} +\frac{2(\vec{v}\cdot\vec{k})\vec{k}}{\tau_\nu} \right], \end{displaymath} (6)

where $\vec{v}$ is the giant planet's velocity vector and $\vec{k}$ is a unit vector in the vertical direction. Note that the factor of 2 appearing in the the first term on the right hand side arises because the migration time is half the angular momentum removal time.

  
2.2 The nebula

The nebula model used for this study is based on the minimum mass solar nebula (MMSN) of Hayashi (1981) and is defined as follows.

The surface density of solids is:

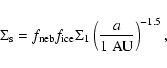\begin{displaymath}\Sigma_{{\rm s}} = f_{{\rm neb}} f_{{\rm ice}} \Sigma_1 \left( \frac{a}{1~{\rm AU}}\right)^{-1.5} , \end{displaymath} (7)

where $f_{{\rm neb}} $ is a nebular mass scaling factor, $\Sigma_1 = 7~\mbox{g~cm}^{-2} $ and the ice condensation coefficient $f_{{\rm ice}}=1$ for $a< 2.7\ \mbox{AU} $ (the distance chosen for the nebula "snowline'') and $f_{{\rm ice}}=4.2$ for  $a \ge 2.7\ \mbox{AU} $.

The volume density of gas is:

\begin{displaymath}\rho_{{\rm g}} = f_{{\rm neb}} \rho_1 \left(\frac{a}{1~{\rm AU}}\right)^{-\frac{11}{4}} \exp\left[-z^2/h^2\right] , \end{displaymath} (8)

where $\rho_1 = 2.0\times10^{-9}(f_{{\rm gas}}/240)(\Sigma_1/10)~\mbox{g~cm}^{-3} $, $f_{{\rm gas}} $ is the gas to dust ratio, z is the height from the midplane of the nebula and the disk scale height h is taken to be:

 \begin{displaymath} h = 0.045\left(\frac{a}{{\rm AU}}\right)^{\frac{5}{4}} \cdot \end{displaymath} (9)

In the context of the core-accretion model of giant planet formation, a significant additional mass of solids seems to be required in order to form a core quick enough to initiate gas accretion before the loss of the gaseous component of the nebula (Lissauer 1987; Thommes et al. 2003; Pollack et al. 1996). Moreover, since hot Jupiters are usually found around stars more metal-rich than the Sun, a greater solids content might reasonably be expected within their protoplanetary nebulae. Thus, for this study we assume an equivalent mass of $3\times\mbox{MMSN}$ of solids. However, as the nebula is taken to be somewhat evolved at our starting point, considerable gas could already have been lost so we assume a smaller equivalent mass of $2\times\mbox{MMSN}$ of gas. The relevant parameters are therefore set to $f_{{\rm neb}} = 3$ and $f_{{\rm gas}} = 160$.

  
2.3 Initial conditions and running of the simulations

The interior disk of protoplanets and planetesimals is modeled initially from 0.4-4 AU which, given the nebula parameters already described in Sect. 2.2, amounts to $M_{{\rm solid}} = 24.8~{M}_{\oplus}$ of solid (rocky or icy) material. Adopting the oligarchic growth picture advanced by Kokubo & Ida (2000), we set a nominal age for the disk of 0.5 Myr, by which point protoplanets in the inner disk may have grown to a few percent of an Earth mass and perhaps to greater than this beyond the snowline. Initial protoplanet masses of $m_{{\rm proto}} = 0.025\ {M}_{\oplus}$ and $m_{{\rm proto}} = 0.1\ {M}_{\oplus}$ are therefore chosen to represent bodies interior and exterior to the snowline respectively. The number Nof protoplanets was calculated based on an assumption that the average radial spacing between them is 8 mutual Hill radii. Semi-major axes for this number of protoplanets are then generated randomly with probabilities weighted in order to reproduce the disk surface density profile. Eccentricities and inclinations are randomized from a Rayleigh distribution with rms values of 0.01 and 0.005 respectively. Additional orbital elements required are randomized uniformly from within their range. The total mass of protoplanets is then subtracted from the total mass of the disk annulus and the mass that remains is divided into N'super-planetesimals with a mass ( $m_{{\rm s-pl}}$) one tenth that of the protoplanets in their zone. The orbital elements of the super-planetesimals are then generated in the same manner. Note that the super-planetesimal mass  $m_{{\rm s-pl}}$ is distinct from the physical planetesimal mass  $m_{{\rm pl}}$ which is used solely for the purpose of calculating gas drag (see Eq. (3)).

Data for this initial disk model are shown in Table 1. The overall values are N = 75 and N' = 4278 and the mass fraction of the disk contained in protoplanets $f_{{\rm proto}} \approx 0.1$. The parameter $f_{{\rm proto}}$ is used here as a rough measure of the evolution of the disk and we take $f_{{\rm proto}} = 0.5$, the point where the total mass in protoplanets exceeds that in planetesimals, to denote the transition between oligarchic and giant impact growth regimes.

Mercury 6 models accretion as inelastic collisions between objects whose radii are calculated from an input density, values of 1, 2 and 3 $\mbox{g~cm}^{-3}$ for giant, icy and rocky masses respectively being chosen here. All collision permutations are enabled, except that between super-planetesimals, and a physically realistic planetesimal radius of $r_{{\rm pl}} = 10~{\rm km}$is imposed both for calculating drag and collisions. The mass of the central star is taken to be $M_\ast = 1~{M}_\odot$.

Table 1: Initial disk set-up.

Before the giant is added to the picture, five instances of this disk were allowed to evolve by being run for 0.1, 0.25, 0.5, 1.0 and 3.0 Myr, the purpose being to provide the basis for five type II migration scenarios through progressively evolved inner system material. In these runs, the timestep for the symplectic part of Mercury's hybrid integrator was set to 8 days and all mass straying inward of 0.1 AU was eliminated and added to the mass of the central star. Data for these evolved disks are given in Table 2. It can be seen that the amount of mass lost to the central star, principally via gas drag-induced orbital decay of planetesimals, remains modest (except in the case of Scenario V) but that as the disk ages the maximum protoplanet mass $m_{{\rm max}}$ increases and particle numbers decrease. As would be expected, $f_{{\rm proto}}$ increases with time until by 1 Myr $f_{{\rm proto}} > 0.5$ and giant impact style growth has begun.

Table 2: Overall disk data: after 0.1-3.0 Myr of evolution.


  \begin{figure} \par\includegraphics[width=14cm,clip]{3453fig1.EPS} \end{figure} Figure 1: Scenario I at 20 000 years after the start of giant planet migration, showing the mass, inclination and eccentricity of objects. Small black dots represent super-planetesimals; white filled circles are rocky protoplanets; grey filled circles are icy protoplanets and the large highlighted grey filled circle is the giant. The dotted line in the upper panel shows the eccentricity at which the pericentre of an exterior object intersects the orbit of the giant. The location of the 2:1, 3:2 and 4:3 resonances with the giant are indicated.
Open with DEXTER

The five type II migration scenarios studied here are constructed from these five evolved disks. A giant planet of mass  $0.5~M_{\rm J}$ is placed into each simulation at 5 AU and allowed to migrate inward with $\tau_{\nu}(5~{\rm AU}) = 237~000\ {\rm years}$ (see Eq. (5)). The giant migrates down to 0.1 AU in $\ga$160 000 years, the exact time depending on the amount of mass remaining interior to its orbit. All simulations therefore were run for 170 000 years, with the type II migration algorithm being switched off once the giant reached 0.1 AU. In order to better model processes when the giant migrates down to small radial distances, collision with the central star is computed when  $r < 0.014\ {\rm AU} \cong 3~{R}_{\odot}$, the approximate radius of a T-Tauri star. The initial timestep chosen for the symplectic integrator was 1 day; but as dynamical spreading and the effects of migration and drag drives some material into closer orbits, the timestep was reduced as the simulation progressed. The position of the inner edge of the swarm was therefore monitored at intervals during each run keeping the timestep close to one tenth the orbital period of the innermost object. This considerably increased the run times of these simulations, especially those based on younger disks, requiring about a month of processor time for completion.

  
3 Results

  
3.1 Typical features of a run


  \begin{figure} \par\includegraphics[width=14cm,clip]{3453fig2.EPS} \end{figure} Figure 2: Scenario I at 100 000 years after the start of giant planet migration. The giant has now moved inward to 2.68 AU and has scattered a significant amount of mass into exterior orbits.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=14cm,clip]{3453fig3.EPS} \end{figure} Figure 3: Scenario I at 160 000 years after the start of giant planet migration. The giant has now moved inward to 0.52 AU. The scattered exterior disk has grown, but a substantial amount of mass in planetesimals and six rapidly accreting protoplanets remain interior to the giant. The outer three of these six are in first order resonances with the giant.
Open with DEXTER

The character of the planetary systems formed from these runs was found to vary systematically with the age of the inner disk. However, all scenarios also exhibited a number of behavioral features in common. We discuss these first by describing one of the scenarios in detail.

Five snapshots of the evolution of Scenario I are illustrated in Figs. 1-5 showing the mass, inclination and eccentricity of objects vs. semi-major axis. The original provenance of the protoplanets (interior or exterior to the snowline) is denoted by the shading of its symbol as described in the caption to Fig. 1. In the case of a merger between rocky and icy protoplanets, this shading is determined by that of the most massive of the pair.

A juncture early in the simulation is illustrated in Fig. 1, 20 000 years after the start of migration when the giant has moved inward to 4.58 AU. Several prominent features have developed. The outer edge of the disk has been pushed inward at the 4:3 resonance with the giant - a shepherding process that acts primarily on planetesimals that are damped by gas drag (Tanaka & Ida 1999). In addition, sweeping resonances have captured a substantial population of planetesimals and some protoplanets at 3:2 and 2:1, increasing their concentration at these locations and exciting their orbits. The overall effect is a compaction and excitation of the outermost annulus of the disk between the 4:3 and 2:1 resonances. Inwards of this zone, the presence of the approaching giant has had little influence.

The state of play some time later at 100 000 years is shown in Fig. 2. The giant has now moved inward to 2.68 AU, continuing to push the outer edge of the disk ahead of it at the 4:3 resonance. An increased amount of mass has been entrained in the region between 4:3 and 2:1 and resonant pumping and mutual scattering has raised the eccentricities of some protoplanets to high values. This has allowed some objects to cross the gap between the disk and giant whereupon a close slingshot encounter causes expulsion into an exterior orbit. A diffuse and excited exterior disk is now in the process of formation, composed predominantly of the more weakly damped protoplanet material.

At 160 000 years the giant has moved inward to 0.52 AU as shown in Fig. 3. The most prominent feature now appears to be the scattered exterior disk made up of numerous protoplanets with large a and e and a diffuse population of planetesimals with a $\Sigma_{\rm s}$ of only a few percent of the original disk. This however still represents the minority of solids mass. Two thirds of the disk mass remains interior to the giant in the form of remaining planetesimals and six protoplanets. A blow-up of the interior regions of the system at this juncture is shown in Fig. 4. A total of $\sim $ $15~{M}_\oplus$ of solid material has been compacted interior to the giant, most of which lies between 0.32-0.39 AU. Two massive protoplanets of 3.57 and 1.14  ${M}_\oplus $ are captured at the 3:2 resonance with the giant and a smaller 0.48  ${M}_\oplus $ protoplanet is found at the 2:1 resonance. The majority of the mass however remains in super-planetesimals entrained at these resonances (and mostly over-plotted in the figure) and in a ring of matter between them. Protoplanetary eccentricities therefore remain low, even at resonances, due to strong dynamical friction. In addition, accretion rates onto these objects have now become so high that collisional damping is also acting to control the growth of their eccentricities.

The final snapshot of Scenario I at 170 000 years is shown in Fig. 5. The giant has stopped its migration at 0.1 AU and, whilst the character of the exterior disk is unchanged, evolution has proceeded rapidly to $f_{{\rm proto}} = 1$ within the compacted interior material. No planetesimals remain, having either been swept up by protoplanets or accreted by the central star. An intense episode of runaway accretion and giant impacts has ended in the assembly of a single $15.65~{M}_{\oplus}$ planet out of resonance with the giant at 0.055 AU. This arrangement of close orbiting giant and an inner Neptune-mass planet has a striking similarity to the two innermost planets in the 55 Cancri system (McArthur et al. 2004).

  \begin{figure} \par\includegraphics[width=8cm,clip]{3453fig4.EPS} \end{figure} Figure 4: Detail of the interior regions of Scenario I at 160 000 years after the start of giant planet migration, showing e vs. a for objects $\leq $2 AU. Planetary masses are indicated in units of  ${M}_\oplus $. A total of $\sim $ $15~{M}_\oplus$ of material has been pushed inward by the giant, $\sim $ two thirds of it remaining in super-planetesimals, many of which do not show individually in this diagram as they are over-plotted in the vicinity of the 3:2 and 2:1 resonances.
Open with DEXTER

To reinforce the above interpretation of processes at work in Scenario I, the surface density evolution of the disk and its accretion rate are shown in Fig. 6. The left hand panel shows the disk surface density profile (obtained by summing all protoplanets and super-planetesimals in 0.1 AU width bins) at 20 000, 60 000, 120 000 and 160 000 years after the start of migration; the right hand panel plots the amount of mass accreted onto protoplanets only (including giant impacts) every 1000 years for the duration of the run. In the $\Sigma_{\rm s}$ plot, two surface density enhancements are clearly visible as spikes at the 3:2 and 2:1 resonances and are seen to grow whilst moving inward. At 120 000 years, these have merged into one: the outer half of the original disk having by now been squeezed into a dense ring. By 160 000 years, most of this mass is now confined within 0.5 AU and  $\Sigma_{\rm s}$ here has risen to $\sim $ $10^3~{\rm g~cm}^{-2}$ (an increase by a factor of $\ga$10 over the previous, undisturbed, disk surface density) which is off the vertical scale in the figure. The effect of this disk compaction process is seen clearly in the accretion rate plot. Mass accretion rises significantly after 120 000 years due to both the resultant high values of  $\Sigma_{\rm s}$ and the fact that much of this mass now resides in a zone where dynamical times are shorter. Growth interior to the giant ends in a short-lived and dramatic phase of runaway planetesimal accumulation and giant impacts within the material pushed into the small volume inside 0.1 AU from the central star.


  \begin{figure} \par\includegraphics[width=14cm,clip]{3453fig5.EPS} \end{figure} Figure 5: Scenario I at 170 000 years after the start of giant planet migration. The giant has now stopped at 0.1 AU. All interior mass has accreted into a single $\sim $ $16~{M}_\oplus$ object after an intense episode of runaway accretion and giant impacts.
Open with DEXTER

The behavioral features seen to a greater or lesser extent in all the runs summarize as follows.

1.
Shepherding of planetesimals. As planetesimal random velocities are continuously damped by gas drag, their tendency is to be pushed inward, ahead of the giant. Shepherding of protoplanets also results as a weaker secondary effect as they are, to a varying extent, coupled to the planetesimal disk by dynamical friction.
2.
Resonant capture. First order resonances with the giant gather an increasing amount of mass as they sweep inward. This, in addition to the shepherding effect eventually results in the compacting of some of the disk mass into a zone close to the central star.
3.
Acceleration of planetary growth interior to the giant. Accretion speeds up within the compacted interior disk. This is particularly rapid within the disk remnant squeezed inside 0.1 AU, where the final evolutionary phases of accretion are rushed through in mere thousands rather than millions of years. Typically, 1-3 massive close orbiting planets are the end result. Where there is one survivor, its mass and configuration can be reminiscent of the "hot Neptune'' type of planet identified recently.
4.
Creation of a scattered exterior disk. Pumping of eccentricities at resonances and by mutual perturbations permit some disk material to undergo a close encounter with the giant where it is scattered into an external orbit. Protoplanets, being less strongly damped, are more likely to have this happen than planetesimals. The result is a dynamically excited and widely dispersed external disk of material where accretion rates are greatly reduced. Leaving aside the issue of interaction of this ejecta with the disk of gas and solids outside the giant's original formation orbit (not simulated here), it seems likely from the result shown in Fig. 5 that further giant impact style evolution ending with a set of planets in non-crossing orbits would take much longer than the $\sim $108 years estimated for the solar system.

  \begin{figure} \par\includegraphics[width=14cm,clip]{3453fig6.EPS} \end{figure} Figure 6: Surface density evolution ( left hand panel) and accretion rates ( right hand panel) for Scenario I. Growing surface density peaks at the 2:1 and 3:2 resonances sweep through the inner system ahead of the giant. Accretion rates increase after $\sim $120 000 years and the final intense accretion spike represents clear up of remaining material shepherded within 0.1 AU.
Open with DEXTER

  
3.2 Dependence on the maturity of the inner disk

The purpose of running five scenarios through a progressively more mature inner disk is to explore the issue of whether the timing of migration has any systematic effect on the results. This is possible because when a disk evolves and small objects accumulate onto larger ones, both dynamical friction and gas drag become less effective overall, influencing both the shepherding and scattering behaviors previously described.

In all the simulations there were five possible fates awaiting all the modeled disk particles: 1) survival in a body orbiting interior to the giant; 2) survival in a body orbiting exterior to the giant; 3) accretion by the central star; 4) accretion by the giant; and 5) ejection from the system. These data are shown in Table 3 which lists the fate of the disk mass at the end of the simulations: the total surviving solids and the five end points being shown as a percentage of the total initial solids. It is noticeable from Table 3 that systematic trends in the fractionation of solids between some of these end points do appear.

The most obvious trends are that the percentage of the original disk mass that ends up surviving interior to the giant falls with disk maturity whereas that expelled into exterior orbits rises with disk maturity (see Fig. 7). The protoplanet mass fraction $f_{{\rm proto}} = 1$ for the inner material is indicative of its rapid evolution, whereas the values of $f_{{\rm proto}} \approx 0.6{-}0.9$ for the outer material are as much influenced by the preferential tendency for protoplanets to be widely scattered as it is by their previous growth. The implication is that scattering is noticeably more effective in older, less dissipative disks. Giant planet migration through a protoplanet/planetesimal disk rapidly advances its evolution (as measured by  $f_{{\rm proto}}$), both by speeding up accretion and by fractionating objects according to the magnitude of their damping, but disks in an oligarchic stage of growth have more of a tendency to push material ahead of the giant and disks undergoing giant impact type growth allow a greater amount of mass to escape into external orbits.

The amount of mass accreted by the giant or ejected are minor in all cases but the picture is complicated by the statistics of mass accreted by the central star. In the last three scenarios, this is significant. However, the high values in Scenarios III and IV result mainly from the impact of a single massive protoplanet during the final energetic phase of accretion within 0.1 AU. The loss of mass to the star in Scenario V resulted from the orbital decay of a substantial annulus of super-planetesimals in the absence of any remaining interior protoplanet which could accrete them. The stochastic fate of large individual bodies at late times can therefore overwrite and partially obscure systematic trends in the data. In Scenario III, for example, if a single close encounter near the end of the simulation had resulted in a giant impact rather than a scattering into the star, a single interior planet of ($\sim $ $12.5~{M}_\oplus$) would have formed instead - another hot Neptune analogue.

Table 3: Fate of the disk mass at 170 000 years.

There are, however, many examples of hot Jupiters that have migrated further inward than 0.1 AU. Orbits at $\sim $0.05 AU are common and some objects have been found as close as $\sim $0.02 AU. It is less likely that interior planets would survive in such systems. If we assume that all remaining interior mass is accreted by the star (which is not always true, as demonstrated below) then the total surviving mass reduces to the exterior surviving mass which, as illustrated in Fig. 7, shows a clear trend with disk maturity. The later the migration episode the more disk mass will remain: from $\sim $$30\%$ for our earliest scenario to $\sim $$70\%$for our latest. None of our simulations support the conjecture of a near-complete loss of solids from the swept zone.

  
3.3 The interior planets

In all scenarios, barring the latest, giant planet migration was found to stimulate accretion within the portion of the disk shepherded inward. By the end of the simulations, this mass had accumulated into one or more massive planets within 0.1 AU. Details of these planets and the giant, including their simulation ID, mass, a, e, and the presence of resonances are given in Table 4.


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{3453fig7.EPS} \end{figure} Figure 7: Interior and exterior surviving solids as a percentage of initial disk mass at 170 000 years.
Open with DEXTER

A single interior planet was the most common result, but in one case there were three survivors. Their masses ranged between $\sim $ $2{-}16~{M}_{\oplus}$ with semi-major axes between $\sim $0.02-0.07 AU. None of them remained in resonance with the giant even though some of their precursor bodies would have been originally been pushed inward at first order resonances (see Fig. 4). These resonances were broken during the final accretion phase within 0.1 AU. In Scenario II however, the three planets that remain are all in resonant relation with each other. The inner planet is in the 5:4 resonance with the middle planet and the 5:3 resonance with the outer planet. The middle planet is in the 4:3 resonance with the outer planet, giving a 5:4:3 commensurability overall. It is possible that such a relationship could act to stabilize the orbits of these planets, but they are closely spaced, the orbits of OLI9 and ICE9 cross, and the giant acts to perturb the system, so we suspected accretion here to be incomplete. Running the inner system of Scenario II for an additional 1.0 Myr resulted in a prompt giant impact between the inner pair (ICE9 and OLI9, see Table 4), followed by a longer phase of interaction of the two 9.02 and 5.58  ${M}_\oplus $ survivors. Their orbits gradually became more elliptical, especially that of the lighter outer planet (ICE1). Seven close encounters followed causing an outward scattering and a further excitation of the outer planet's eccentricity. Just before the million years was up, ICE1 encountered the giant for the first time and 18 close encounters later they collided. Thus, the final outcome for Scenario II was a single remaining inner planet, separated from the giant by 12.9 mutual Hill radii with a mass of 9.02  ${M}_\oplus $, a = 0.0465 AU, e = 0.132.

Generation of these massive interior planets by these simulations is particularly interesting as three examples of short period Neptune-mass objects have been recently discovered in the systems GJ 436 (Butler et al. 2004), 55 Cancri (McArthur et al. 2004) and $\mu$ Arae (Santos et al. 2004) and a short period planet about half as massive may also have been detected in the GJ 876 system (Rivera et al. 2005). These systems are compared with those generated here in Table 4 and Fig. 8. In three of these natural systems the inner Neptune-mass planet is accompanied by more than one outer giant and, in the cases of 55 Cancri and GJ 876, the innermost giant is placed close to where our simulated giant ends its migration. The results of the simulations do have a particular resemblance to reality in these two cases. The best matches are given by Scenario I, where the mass and orbital radius of the interior planet are similar to the $m\sin i$ and a of 55 Cnc e, and Scenario III where the resemblance is closer to the configuration of GJ 876 d and c. One might speculate therefore that, rather than hot Neptune type planets forming far out in the disk and migrating inward to their present location, they might, as illustrated here, form at these locations from disk material shepherded and compacted by a migrating giant.

Table 4: Interior surviving planets at 170 000 years compared with the four currently known "hot Neptune'' systems. Data include the closest giant planet.

Against this proposition is the case of GJ 436 where the hot Neptune appears unaccompanied by an exterior giant; although Butler et al. (2004) did detect a linear velocity trend in their data implying the possible existence of a more distant companion. The primary of this system is a $\sim $ $0.4~{M}_{\odot}$ red dwarf star which might affect the comparison. Giant planets appear to be rare in red dwarf systems and it may be that they do not form efficiently from the lower mass protoplanetary disks expected around low mass stars (Laughlin et al. 2004). GJ 436 b may therefore be this system's largest planet, rather than a secondary object, which could indeed have formed at large radius before migrating in. However, not all red dwarf stars lack giant planets. In the one known case where giants are present (GJ 876) and past migration may have played a role in their current configuration (e.g. Snellgrove et al. 2001), an interior half-hot Neptune appears to be present. The hot Neptune in the $\mu$ Arae system is accompanied by a giant, but it is situated much further out (at 1.5 AU) than the final location of the giant in the simulations. No simulations have yet been performed to evaluate the outcome of stopping the giant migration at 1.5 AU, but at the point in the runs where the giant passes through 1.5 AU (at $\sim $140 000 years) about 60% of the original mass of the disk is compacted within $\sim $1 AU. This is enough mass to assemble a $\ga$ $13~{M}_{\oplus}$ hot Neptune over a longer period although, since $\mu$ Arae d and $\mu$ Arae b are separated by $\sim $22 mutual Hill radii, one might expect some additional smaller planets to have formed and perhaps to have survived to the present. Less massive interior planets of $\sim $ $2{-}7~{M}_{\oplus}$ are produced in the simulations and may exist in nature as smaller versions of the hot Neptunes already discovered. GJ 876 d may represent the first discovery of a planet in this mass range. However, such objects would only produce a $\sim $ $1{-}3~{\rm m~s}^{-1}$ stellar radial velocity at $\sin i = 1$, a value that is close to the observation limit, so others will have escaped detection so far.

  \begin{figure} \par\includegraphics[width=7.4cm,clip]{3453fig8.EPS} \end{figure} Figure 8: Comparison of computer generated interior planets with the interior regions of four known "hot Neptune'' systems.
Open with DEXTER

Another reason for the apparent rarity of hot Nepture type objects could be that many hot Jupiter systems are more compact than 0.1 AU; a typical example being 51 Pegasi b: $m \sin i \approx 0.5~M_{\rm J}$, $a \approx 0.05$ AU (Mayor & Queloz 1995). For a planet shepherded well within this distance, significant eccentricity excitation by the giant companion may cause it to impact the star.

To examine this possibility, Scenarios I-IV were run for an extra 300 years, allowing the giant in each case to migrate further in to stop at 0.05 AU. In Scenarios I and II all the interior planets were driven into the central star. The mechanism at work is illustrated for the case of Scenario I in Fig. 9 where the semi major axis, periastron and apastron distances, for both the giant and terrestrial planet, and the resonant angles for the 2:1 resonance, are all plotted against time. The orbit of the interior planet is initially undisturbed, but when the giant has moved inward to 0.087 AU the planet is captured into the 2:1 resonance as can be seen from the libration of the resonant angles. From this point the planet is pushed in ahead of the giant at the 2:1 resonance, its eccentricity increasing progressively. By the time the planet has reached $a \approx 0.035$ AU, its eccentricity has increased to $e \approx 0.6$ and impact with the star occurs at periastron. The events in Scenario II were similar: the migrating giant in this case caused the three interior planets present to accrete each other, capturing the single 14.6  ${M}_\oplus $ survivor into the 2:1 resonance. From here, evolution proceeded as in Fig. 9, the planet eventually hitting the star through having been forced into a tighter, more elongated, orbit.


  \begin{figure} \par\includegraphics[width=10cm,clip]{3453fig9.EPS} \end{figure} Figure 9: Scenario I: collision of the inner planet with the central star as the giant moves inward to 0.05 AU. Resonant angles for the 2:1 resonance are read on the left hand axis: light grey symbols plot the angle $\phi _1 = 2\lambda '-\lambda -\varpi '$ and dark grey symbols plot the angle  $\phi _2 = 2\lambda '-\lambda -\varpi $ where  $\lambda ',\varpi '$ and  $\lambda ,\varpi $ are the mean longitudes and longitudes of periastron for the outer and inner planet respectively. The semi major axis, periastron and apastron for both the giant and the inner planet are plotted as black lines and are read on the right hand axis.
Open with DEXTER

In Scenarios III and IV, both the interior planets survived this additional migration by the giant. This is because their initial orbits were closer to the star (see Table 4) so the planet only becomes captured at the 2:1 resonance much later, or not at all. The interior planet in Scenario III remained stable as the 2:1 resonance did not reach its location and sweeping higher order resonances had no apparent effect. Survival of such a planet for the long term is therefore probable, since orbital decay due to tidal interaction with the star is expected to be very slow (see below). In Scenario IV, the interior planet was captured into the 2:1 resonance late: at the point where the giant reached 0.057 AU. Its orbit was compressed and elongated to a = 0.032 AU and e = 0.35but the progressive increase in eccentricity ceased when the giant finished migrating and impact with the star was avoided (see Fig. 10).

The effect of tidal interactions with a slowly rotating star will cause the lower mass planet obtained in Scenarios III and IV to migrate inward slowly. For a circular orbit tidal dissipation occurs within the star only, with turbulent convection in the stellar envelope being responsible for dissipating the tidally induced motions. The estimated orbital evolution time in this case is given by (Terquem et al. 1998):

 \begin{displaymath} t_{\rm orb} \simeq 2.8 \times 10^{-4} \left(\frac{M_{\odot}}... ...(\frac{P}{1 \; {\rm day}} \right)^{\frac{13}{3}} \; {\rm Gyr}, \end{displaymath} (10)

where P is the orbital period and $m_{\rm p}$ is the mass of the planet. For a 15  ${M}_\oplus $ planet with an orbital period of 1.5 days this gives a orbital decay time of $\sim $36 Gyr - i.e. comfortably longer than the age of the universe. For a planet on an eccentric orbit, tidal dissipation within the planet becomes important due to more effective dissipation within the solid body (e.g. Goldreich & Soter 1966). The raising and dissipation of tides within the planet leads to eccentricity damping, and the low moment of inertia of the planet ensures that it maintains near-synchronous rotation. This also means that effective removal of orbital angular momentum can only be achieved through tidal dissipation in the star. We therefore expect that a planetary system consisting of an exterior gas giant planet and an interior rocky planet, orbiting in close proximity to a solar type star, will evolve such that the rocky planet orbit decays on a time scale on the order of that given by Eq. (10). The inner planet will have an eccentricity determined by a balance between tidal dissipation originating in the planet itself and eccentricity excitation caused by the exterior giant. In general, the long term effects of this will be to make the orbits of both the inner terrestrial and outer giant planet more circular. This will be enhanced by the tidal interaction between the gas giant and the central star which will also tend to circularize its orbit (e.g. Rasio et al. 1996), though we note that this effect is not particularly relevant for our simulations as the giant planet is assumed to maintain a near-circular orbit through tidal interaction with the gas disk. For the specific case of Scenario IV, where the inner planet is in 2:1 resonance with the gas giant, tidal dissipation will cause the rocky planet orbit to circularize at a smaller semi major axis, probably removing the inner planet from the 2:1 resonance in the process. Using Eq. (10) we estimate that the rocky planet formed in Scenario III will spiral into its host star on a time scale of $\sim $54 Gyr, and that formed in Scenario IV on a time scale of $\la$700 Gyr, again both comfortably longer than the age of the universe.
  \begin{figure} \par\includegraphics[width=10cm,clip]{3453fig10.EPS} \end{figure} Figure 10: Scenario IV: survival of the inner planet as the giant moves inward to 0.05 AU. Resonant angles for the 2:1 resonance are read on the left hand axis: light grey symbols plot the angle $\phi _1 = 2\lambda '-\lambda -\varpi '$ and dark grey symbols plot the angle $\phi _2 = 2\lambda '-\lambda -\varpi $. The semi major axis, periastron and apastron for both the giant and the inner planet are plotted as black lines and are read on the right hand axis.
Open with DEXTER

Table 5: External surviving protoplanets at 170 000 years.

If the disk shepherding and compaction scenario advanced here has some validity, then it suggests the formation of hot Neptunes or lesser massive terrestrial planets as a by-product of giant planet migration. However, if the giant comes to rest too close to the star ($\la$0.05 AU) then the effects of mean motion resonances may cause interior planets to hit the star. The best prospect therefore of detecting close orbiting terrestrial type planets of $\ga$ ${M}_\oplus $ might be in systems with a circumscribing giant at $a \sim 0.05{-}1.5$ AU.

  
3.4 The exterior scattered disk

As the giant migrated through the inner disk it scattered $\sim $30-70% of the disk mass into external orbits (see Figs. 5 and 7 and Table 3). In each case, a diffuse and dynamically excited external disk was generated, composed predominantly of protoplanet material ( $f_{{\rm proto}} \approx 0.7{-}0.9$): individual protoplanets having a wide range of mass and orbital parameters. Data for the external protoplanets are presented in Table 5, giving their number, mean and maximum masses and orbital inclinations, and their mean, minimum and maximum semi major axes and eccentricities. It can be seen from the data that the number of external protoplanets reduced and their masses increased with disk maturity. Similarly, there is a tendency for protoplanets from a more mature disk to be more widely scattered. The former trend is primarily due to previous accretion, whereas the latter is a result of the decreased dynamical friction operating at later times.

The ejecta that comprised the scattered disk were spread over a much wider volume than their original location at <4 AU. Planetesimal orbits were damped quite rapidly by gas drag to form a thin ($\sim $ $1{-}2~{M}_{\oplus}$) external disk with a surface density $\la$ a few percent of the pre-existing $\Sigma_{\rm s}$. Protoplanets were often in highly eccentric orbits, passing well beyond the confines of the original disk but with their periastra still located close to the location of their scattering within 4 AU. Mean orbital inclinations were comparable to the solar system planets, but with a larger number of outliers as high as $i \approx 25\hbox{$^\circ$ }$ (see Fig. 5). Thus, by selectively pushing planetesimals inward and widely scattering its external ejecta, the migrating giant partially evacuates a cavity within its swept zone.

Further accretion in this disk will therefore be characterized by low $\Sigma_{\rm s}$ and high random velocities, reducing both the mass available and the effect of gravitational focussing. In some collisions, impact velocities could be high enough to cause disruption of the protoplanets rather than accretion and a reversal of growth (Agnor & Asphaug 2004). Long evolution times are implied for the mass contained in the scattered disk to rearrange itself into a smaller number of planets in stable orbits. This final configuration cannot be predicted from the juvenile stage illustrated in Fig. 5.

No original matter more distant than the giant's starting position was modeled here. Objects in the external scattered disk traverse more widely than this and so could interact with matter in the outer disk beyond $\sim $6 AU. A fresh supply of planetesimals would be encountered which could act to circularize and contract protoplanet orbits via dynamical friction (Thommes et al. 2002). Alternatively, encounters with other giant planets remaining in the outer system could have a role to play in clearing material via ejection. The long term end product of the mass scattered by the migrating giant therefore depends partially on the nature of the outer disk: what other planets have formed there and its remaining population of small bodies. In a hot Jupiter system where no other gas giants have formed, we might speculate over the resulting planetary configuration at $\sim $1 Gyr: a hot Neptune, or lesser massive terrestrial planet at $\sim $0.05 AU, the giant at $\sim $0.1 AU, then from $\sim $0.5 AU a succession of Mars to Earth-mass planets, some still in eccentric or inclined orbits, extending as far out as $\sim $5 AU. Beyond this, the content of the original outer disk would determine what is to be found.

The ejection of low mass planets to large ($\sim $30 AU) semi-major axes may have some influence on the observed morphology of the system in its debris disk phase. Systems such as Fomalhaut and $\varepsilon$ Eridani (Quillen & Thorndike 2002; Wyatt & Dent 2002) have observational features that have been explained by resonant trapping of planetesimals (Wyatt & Dent 2002) or dust grains in mean motion resonances with a planet. We suspect that the dust trapping proposed by Quillen & Thorndike (2002) will also occur for lower mass planets (they considered $m_{\rm planet} \approx 30~{M}_\oplus$), but is likely to occur for resonances that lie closer to the planet than the 3:2 resonance that was dominant in their study.

Table 6: Total mass and number of protoplanets orbiting within, or crossing, the habitable zone (0.84-1.67 AU) at the end of the simulation.

What of the probability of one of these surviving planets residing in the system's habitable zone? Habitable zones are dynamically stable in hot Jupiter systems (Menou & Tabachnik 2003) so a planet forming there would have a stable orbit if sufficiently well-spaced from neighbors. The simulations presented here cannot provide any numerical estimate that might address this question: the simulations have not been run for long enough and, in any case, ignore the strong potential influence of an outer disk. However, protoplanets are found within, or with their orbits passing though, the habitable zone (taken to be 0.84-1.67 AU; Kasting et al. 1993) at the end of each run (see Table 6). Thus, some mass is available for forming a completed planet in the right place, especially in view of the fact that damping of the protoplanet's orbits from interaction with outer disk material, collisional damping during ensuing accretion, destructive collisions, and gas drag on remaining planetesimals and debris could act to return some material into closer orbits. Assuming eventual re-circularization of orbits with conservation of angular momentum, the data in Table 6 convert to those illustrated in Fig. 11 which shows, for each scenario, the number of protoplanets and their total mass predicted in the habitable zone. Protoplanets occupy the habitable zone in three out of the five cases and, in two scenarios, more than an Earth-mass of material is present. Thus, since there is dynamical room available within the habitable zone of a hot Jupiter system, it is perhaps more likely than not that long term evolution of the scattered external disk could result in a terrestrial planet being located there.


  \begin{figure} \par\includegraphics[width=7.4cm,clip]{3453fig11.EPS} \end{figure} Figure 11: Number and total mass of protoplanets predicted in the habitable zone assuming orbital re-circularization with conservation of angular momentum.
Open with DEXTER

  
4 Caveats and future model improvements

Inevitably a number of assumptions have been used in constructing the models presented in this paper, with the consequence that potentially important physical processes have been omitted. Here we discuss the possible implications of these for our results, whilst noting that work is underway to include them in future models:
(i) Gap formation & cavity clearing: a giant planet is expected to form an annular gap in the gas disk centred around its orbit. As a Jupiter mass planet migrates inward, hydrodynamic simulations indicate that the inner disk becomes depleted of gas, forming a low density cavity there (e.g. Nelson et al. 2000). This arises in part because the viscous time scale in the inner disk is shorter than the migration time. The depletion is probably enhanced artificially by the use of an outflow boundary condition at the disk inner edge, which for computational reasons is located at a radius much larger than the expected surface of the central star. At this time it is not known accurately to what degree the inner disk is depleted. We have assumed an undepleted disk, and the effects of this will be the subject of future investigation. We note that our use of a 0.5 $M_{\rm J}$ planet will lead to significantly less gas depletion than obtained in hydrodynamic simulations performed using more massive planets.
The effect of depleting the gas disk interior to the giant planet will be to reduce the gas drag experienced by the planetesimals. Reducing the dissipation level is likely to lead to greater scattering of bodies into the outer disk by the giant planet, which may reduce the efficiency of planet formation in the inner disk. We note, however, that the loss of planetesimals into the central star due to gas drag will also diminish. Models similar to those presented here, but coupled to an evolving gas disk model, will be the subject of a future publication.
(ii) Gas disk removal: implicit within our models is a mechansim for preventing the gas giant planet from migrating all the way into the central star. While the presence of a magnetospheric cavity has been cited as a possible stopping mechanism for hot Jupiters (Lin et al. 1996), we note that planets are found to exist with a range of semi major axes for which this mechanism cannot be invoked. A more plausible reason for migration halting is the removal of the gas disk during migration. The removal of the outer gas disk would remove a source of dissipation for the scattered protoplanets and planetesimals, increasing the accretion time scale for any planets forming exterior to the giant.
(iii) Giant planet eccentricity evolution: our model assumes that type II migration is associated with an eccentricity damping which maintains a near-circular orbit. However the question of whether a giant planet has its eccentricity damped or excited by the protoplanetary disk remains a point of ongoing debate (Ogilvie & Lubow 2003; Goldreich & Sari 2003; Papaloizou et al. 2001). In the absence of eccentricity damping, interaction of the giant with the solids disk may cause modest excitation, but not at a level to significantly effect our results. If the gas disk was to drive significant eccentricity increase then this would probably lead to a stronger interaction between the giant and the solids disk resulting in greater scattering and a more efficient clearing of material.
(iv) Planetesimals exterior to the gas giant: there will be a population of planetesimals exterior to the giant planet whose size distribution is unknown. Planetesimals with radii <1 km will migrate in behind the gas giant due to gas drag, providing a source of material that may be accreted by outwardly scattered protoplanets that reside interior to 5 AU, and which may contribute to the damping of their inclination and eccentricity.
(v) Planetesimal size evolution: the model we have used assumes that a population of 10 km sized planetesimals coexists with a population of larger protoplanets at the beginning of gas giant migration. Collisions between planetesimals may lead to both their growth and fragmentation, with a range of sizes developing. At present these processes are not included in our model, and their effect on the outcome of our calculations is unclear. We simply note that smaller bodies produced by fragmentation will experience larger gas drag forces, leading to a more rapid in-spiral toward the central star, and reduced eccentricity that assists rapid accretion by the protoplanets. The build-up of larger bodies will lead to reduced effectiveness of gas drag, and a greater probability of scattering.
(vi) Type I migration: we have neglected the effects of type I migration which operates for non-gap forming sub-Jovian planets (Ward 1997). This may become important for bodies more massive than $\sim $ $1~M_{\oplus}$, causing inward migration and strong eccentricity damping. For our model disk parameters type I migration proceeds faster than the gas giant migration for bodies more massive than $\sim $ $5~M_{\oplus}$. We note that such bodies usually form during a rapid burst of accretion as the planet approaches the star, so their formation is unlikely to be greatly affected by type I migration. Their subsequent evolution will depend on the gas density in the inner disk, which at present is unknown, as discussed in point (i) above.
We further comment that a consistent model of giant planet formation via the core-instability model is difficult to achieve if type I migration operates as efficiently as current calculations suggest. Our model of a gas-giant forming and then slowly migrating inward implicitly contains the assumption that type I migration does not operate efficiently. We note that recent simulations of low mass planets in turbulent disks suggest that some low mass planets may avoid rapid inward migration (e.g. Nelson 2005; Nelson & Papaloizou 2004), so the role played by type I migration during planet formation is unclear at present.

Type I disk-planet interactions are also thought to include significant eccentricity damping on a timescale $\sim $100 times shorter than the migration timescale (Papaloizou & Larwood 2000), an effect that could be relevant to the picture we have presented. The influence of this in simulations would be to exert additional dissipation on the protoplanets and hence increase their probability of being shepherded by the giant. Such behavior would have its greatest impact in more evolved systems where dissipation is weaker, such as our Scenarios IV and V. Type I damping would also effect the evolution of the scattered external disc and would be an additional influence acting to return some planet-forming material into closer orbits. Its integrated effect however would depend on how much of the nebula's gas remains and how much longer it lasts for. Eccentricity damping from a thin residual gas disk could act to circularize the orbits of any final planetary configuration (Kominami & Ida 2002), whereas if ample gas persists and type I migration is also in force, a pileup of mass could also occur exterior to the giant as migrating protoplanets are entrained in its exterior mean-motion resonances (Thommes 2005). It is possible therefore that a modest degree of type I eccentricity damping could promote, rather than hinder, the accretion of a planetary system external to the orbit of the giant planet.

  
5 Conclusions

Whilst this study has addressed the effect of giant planet migration through inner disks of varying maturity, we have not examined the effect of changing some of the basic parameters that could influence accretion, shepherding and scattering behavior. These might include varying the giant's mass, its migration time ( $\tau_{\nu}$) and the mass of the nebula ( $f_{{\rm neb}} $). Such a study will be the subject of future work, which will also address some of the issues raised in Sect. 4 concerning extensions to the basic physical model. It is likely that varying the mass of the nebula would result in a change in accretion time scales and a corresponding increase or decrease in the mass of the surviving planets, but not in their elimination entirely. It would also affect the level of dissipation in the disk which influences the dynamical partitioning of disk mass brought about by the migration. Increasing the mass of the giant would raise the overall effect of scattering, as would extending the migration time which increases opportunities for repeated and incremental scatterings (Mandell & Sigurdsson 2003). It seems reasonable to speculate that varying any of these parameters within reasonable limits would still produce a result that, whilst varying in detail, remains consistent with our established picture.

There are three principal conclusions that arise from this work.

1.
Migration of a giant planet through an inner disk partitions the mass of that disk into internal and external remnants. The fraction of disk mass in either remnant is dependent on the level of dissipation and is thus sensitive to the maturity of the disk material at the time of the migration episode. Late migration favors the escape of more material into external orbits. The survival of an inner remnant is also sensitive to the final position of the giant at the end of migration, this becoming increasingly unlikely in hot Jupiter systems with $a \la 0.05$ AU. The concept that giant planet migration would eliminate all the mass in its swept zone is not supported by our results.
2.
Hot Neptunes and lesser massive terrestrial planets are a possible by-product of type II migration, being formed from an inner system disk compacted by a migrating giant. Future searches of hot Jupiter systems for radial velocity signals close to the current detection limit might uncover more examples of these planets.
3.
Our results are supportive of the eventual accumulation of a number of terrestrial planets orbiting exterior to the giant, including within the system's habitable zone. Thus, the early evolution and the final architecture of Hot Jupiter systems does necessarily eliminate their possibility of hosting Earth-like planets.

References

 
Copyright ESO 2005