A&A 441, 815-818 (2005)
DOI: 10.1051/0004-6361:20053160
K. Aksnes 1 - T. Grav2
1 - Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029, Blindern 0315 Oslo, Norway
2 -
Institute for Astronomy, University of Hawaii,
2680 Woodlawn Drive, Honolulu, HI 96822, USA
Received 30 March 2005 / Accepted 20 June 2005
Abstract
Differential orbit correction is performed by computing
an osculating orbit from observations from which the perturbations
have been subtracted. No variational equations need to be integrated
except to solve for non-gravitational forces.
The perturbations in the observations are obtained by subtracting a
two-body orbit from an integrated, perturbed orbit. The method is
used to update the orbits of the Uranian satellite Caliban and of
the comets 46P/Wirtanen and 67P/Churyumov-Gerasimenko with recent
observations. The method is shown to agree very well with, but is
considerably faster than, the conventional method based entirely on
variational equations. Algorithms are given for both methods.
Key words: celestial mechanics - comets: general - planets and satellites: general
This paper deals with orbit correction of solar system objects (comets, asteroids, satellites). Usually orbit correction is done by matching a perturbed orbit directly to the available observations, starting from an osculating orbit or state vector whose six elements are adjusted by least squares. This requires numerical integration of one orbit and six variational equations to derive the partial derivatives needed in the least squares solution. This method may be referred to as the coordinate perturbation method.
We present here a simpler and faster method which we shall call the observation perturbation method. The perturbations are first removed from the observations to obtain a set of unperturbed fictitious observations from which the osculating orbit is derived as a pure two-body orbit using analytic partial derivatives. The perturbations in the observations are obtained by subtraction between a numerically integrated, perturbed orbit and an analytic, unperturbed orbit in an iterative procedure. No variational equations need to be integrated except to solve for non-gravitational forces. The method was introduced by the first author who used it to compute the orbits of Jupiters's satellite Leda (Aksnes 1978) and Uranus' satellites Caliban and Sycorax (Marsden et al. 2000). The second author (Grav 2001) then applied the method to the comet 46P/Wirtanen and extended it by the inclusion of non-gravitational forces.
In the following we will give an exposition of the observation perturbation method and demonstrate its use through some examples. We will also compare the results with the corresponding ones obtained with the conventional coordinate perturbation method for which an algorithm is also given.
The equations of motion for a body of mass m attracted by a central mass
m0 and N perturbing masses m1, m2, ....mN take the form
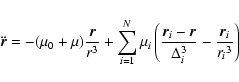 |
(1) |
| (2) |
![\begin{displaymath}G = \left[ \begin{array}{cccc}
\frac{\partial x}{\partial x_...
... & \frac{\partial z}{\partial \dot{z_0}} \end{array} \right] .
\end{displaymath}](/articles/aa/full/2005/38/aa3160-05/img10.gif) |
(3) |
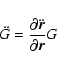 |
(4) |
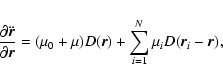 |
(5) |
![\begin{displaymath}D(\vec{r})= -\nabla(\frac{\vec{r}}{r^3})= \frac{3}{r^5}\left[...
...^2-r^2/3 & yz\\
zx & zy & z^2-r^2/3 \end{array} \right] \cdot
\end{displaymath}](/articles/aa/full/2005/38/aa3160-05/img13.gif) |
(6) |
![\begin{displaymath}\left[\begin{array}{c}\Delta\alpha\cos{\delta}\\ \Delta\delta...
...& \cos{\delta}
\end{array}\right]\frac{\Delta\vec{r}}{r} \cdot
\end{displaymath}](/articles/aa/full/2005/38/aa3160-05/img18.gif) |
(7) |
| (8) |
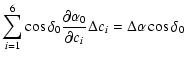 |
|||
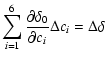 |
(9) |
The above equations of condition also apply for the coordinate
perturbation method if the unperturbed
![]() are replaced
by the perturbed
are replaced
by the perturbed
![]() .
This then requires the partials in
the G matrix obtained through numerical integration.
.
This then requires the partials in
the G matrix obtained through numerical integration.
When dealing with comets, one frequently has to include forces due to
outgassing from the nucleus. We here adopt a model due to Marsden et
al. (1973). To Eq. (1) is added an acceleration decomposed in a
radial, transverse and normal direction:
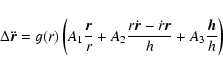 |
(10) |
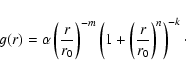 |
(11) |
The parameters A1, A2 and A3 are assumed to be solved for
along with the state vector or orbital elements of the comet at some
epoch. We then need the partial derivatives of the observables w.r.t.
these parameters. We define a column vector
![\begin{displaymath}\vec{p}_i = \frac{\partial\vec{r}}{\partial A_i} =
\left[\be...
...al A_i \\
\partial z/\partial A_i \end{array}\right], i=1,2,3
\end{displaymath}](/articles/aa/full/2005/38/aa3160-05/img38.gif) |
(12) |
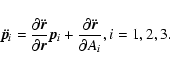 |
(13) |
The preceding formulas have been implemented in two FORTRAN programs which we shall refer to as Model 1, the coordinate perturbation method, and Model 2, the observation perturbation method. Both programs use the same input:
The integration is done with the Bulirsch-Stoer (1980) first-order method and adaptive step size control. This is a very efficient scheme of numerical integration. No additional interpolations are required to match the output to the times of observation.
In both models the state vector is integrated in accordance with Eq. (1) and, for comets, Eq. (10), and the 9 components of the non-gravitational partial derivatives pi are obtained by integrating Eqs. (13) with the aid of Eq. (5). Model 1 requires the additional integrations of the variational Eqs. (4) for the 18 elements of G. This sums up to the integration of 30 s-order differential equations in Model 1 but only 12 in Model 2. Without non-gravitational perturbations, these numbers are reduced to 21 and 3 respectively. Model 2 thus offers a very substantial savings of integration time, especially if non-gravitational forces are excluded, although to some extent this savings will be offset by the need to compute two-body partials. Model 2 also appears to converge somewhat faster and be more stable, but this may be due to solving for corrections to the orbital elements instead of to the state vector, as in Model 1.
We will illustrate the use of both models for one satellite and two comets.
Our first example is orbit improvement for the Uranian satellite Caliban based on 47 observations between June 1984 and November 1998, covering a little over 9 revolutions of the satellite which has a period of 579 days. Perturbations were included due to the Sun, Jupiter and Saturn. We started from an orbit with an average rms residual of 104 arcsec. Note that this is a rather large relative error because the orbit spans only about 17 arcmin in the sky. Model 1 diverged, while Model 2 converged with an rms residual of 0.63 arcsec after 4 integrations. With a more accurate starting orbit (rms = 37 arcsec), Model 1 converged on very nearly the same orbit, but it took 6 integrations. Thus the observation perturbation method appears to be more robust and stable than the coordinate perturbation method.
Table 1 lists the orbital elements of the satellite according to both solutions. The differences between the two sets of elements are well within the standard errors of the fits.
Table 1: Orbit of Caliban from 47 obs. 1984-1998.
Our second example involves the comet 46P/Wirtanen which was the original
target of ESA's Rosetta mission. The orbit of this comet has been studied
by several authors. Grav (2001) used the observation perturbation
method to analyze observations between 1948 and 1999. He tried several
models for the non-gravitational forces: (1) Marsden's model with and
without a time shift ![]() making g(r) in Eq. (11) peak after perihelion
if
making g(r) in Eq. (11) peak after perihelion
if ![]() ,
(2) Sitarski's rotating nucleus model (Sitarski 1990), and
(3) Sekanina's forced precession model as implemented by Krolikowska &
Szutowicz (1999).
,
(2) Sitarski's rotating nucleus model (Sitarski 1990), and
(3) Sekanina's forced precession model as implemented by Krolikowska &
Szutowicz (1999).
This comet is affected rather strongly by non-gravitational forces which have undergone substantial changes during the 50-year interval considered, probably mainly due to close approaches to Jupiter in 1971 and 1984. Just prior to the 1971 approach the comet's period was 6.7 years which was reduced to about 5.5 years after the 1984 approach. The same set of non-gravitational parameters gives satisfactory residuals for at most three apparitions of the comet.
Table 2 gives some results obtained by several authors for the non- gravitational parameters A1, A2 and A3 for different observation intervals.
Table 2: Non-gravitational parameters in units of 10-8 AU/day2 for 46P/Wirtanen.
The best result (Grav 2001) was obtained with the use of the forced
precession model with a rotating nucleus, as introduced by Krolikowska &
Szutowicz (1999) for 46P/Wirtanen; see Table 3. It was necessarry
to use two different values for the main parameter A: ![]() before 1971
and
before 1971
and
![]() after 1971. The inclusion of a time shift
after 1971. The inclusion of a time shift ![]() in the
second run did not have a noticeable effect on the residuals. The non-
gravitational parameters are in rough agreement with those obtained by
Krolikowska and Szutowicz, except that they found a much larger negative
value for
in the
second run did not have a noticeable effect on the residuals. The non-
gravitational parameters are in rough agreement with those obtained by
Krolikowska and Szutowicz, except that they found a much larger negative
value for ![]() (-23.476). However, they used observations only up to
1995 and a different epoch (Jan. 27 1998), so the two sets of results are
not directly comparable.
(-23.476). However, they used observations only up to
1995 and a different epoch (Jan. 27 1998), so the two sets of results are
not directly comparable.
In all of Grav's calculations, the available observations were screened using the the Bielicki criterion for rejecting and weighting observations, as outlined by Bielicki & Sitarski (1991). Note that in the examples that follow (Tables 4 and 5), the observations are all given equal weight and are rejected if they produce residuals larger than 4 arcsec. The rms values of the fits can therefore be expected to be somewhat larger than if the Bielicki selection criterion had been used.
The orbital elements in Table 3 are in good agreement with the orbital elements in Table 4 derived from 555 observations between July 8 1991 and April 10 2003, using both model 1 and model 2 with the three Marsden parameters. Perturbations were included from all the nine planets and the Moon. The very good internal agreement of the two models again shows that the observation perturbation method works equally well as the coordinate perturbation method.
Table 3: Forced precession model for 46P/Wirtanen 1948-1999.
Table 4: Results for 46P/Wirtanen from 555 obs. 1991-2003.
Our last example is orbit computation for the comet 67P/Churyumov- Gerasimenko which has a period of 6.6 yr. This comet is of special interest since the Rosetta spacecraft is scheduled to rendezvous with the comet in 2014. Table 5 gives the orbital elements and the non-gravitational parameters obtained for this comet by means of model 1 and model 2 based on 1301 observations between Sep. 9, 1969 and June 20, 2004. Again all nine planets and the Moon were included as perturbers (inclusion of the Moon reduced the rms residual by 0.2 arcsec). For comparison, we also show the corresponding results obtained by Krolikowska (2003) based on 1169 observations between Sep. 9, 1969 and March 13, 2003. The fact that the 1.16 arcsec rms residual obtained by Krolikowska is smaller than the 1.57 arcsec in model 1 and model 2, is probably due to Krolikowska's use of the Bielicki observation selection criterion. Even so, the three sets of orbital elements and non-gravitational parameters are in excellent agreement.
The small values for A1, A2 and A3 show that this comet is much less affected by non-gravitational forces than is 46P/Wirtanen. For a discussion of the orbital evolution of this comet, the reader is referred to the article by Krolikowska (2003).
Table 5: Results for 67P/Churyumov-Gerasimenko.
Our results show that the observation perturbation method is fully compatible with the conventional coordinate perturbation method. The former method is simpler and requires less computer time; it also seems to have better convergence when applied to satellites. One might suspect that this method will handle very strongly perturbed orbits less well than the conventional method, but this is not borne out in the case of 46P/Wirtanen which had two close approahes to Jupiter, although both methods had problems satisfying the observations near those times.
Acknowledgements
We wish to thank Gareth V. Williams, Associate Director of the Minor Planet Center, Cambridge, Mass., for providing the observations on which this paper is based.
Let
![]() be the orbital elements, referred to the
ecliptic, of an object in an elliptic orbit. The object's Earth-equatorial
coordinates x,y,z centered on the primary may then be expressed as
be the orbital elements, referred to the
ecliptic, of an object in an elliptic orbit. The object's Earth-equatorial
coordinates x,y,z centered on the primary may then be expressed as
![\begin{displaymath}\left[\begin{array}{c} x\\ y\\ z\\ \end{array}\right] =
\left...
...
\left[\begin{array}{c} \bar{x}\\ \bar{y}\\ \end{array}\right]
\end{displaymath}](/articles/aa/full/2005/38/aa3160-05/img85.gif) |
(14) |
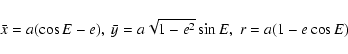 |
(15) |
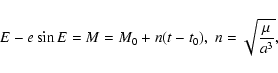 |
(16) |
| R11 | = | ||
| R12 | = | ||
| R21 | = | ||
| R22 | = | ||
| R31 | = | ||
| R32 | = | (17) |
where
![]() (J2000) is the obliquity of the ecliptic.
We need the partial derivatives of x,y,z w.r.t.
(J2000) is the obliquity of the ecliptic.
We need the partial derivatives of x,y,z w.r.t.
![]() :
:
| |
= | 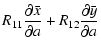 |
|
| (18) | |||
| = | 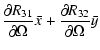 |
| |
= | ||
| = | 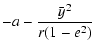 |
||
| = | (19) | ||
| = | |||
| = | |||
| = |