A&A 441, 573-588 (2005)
DOI: 10.1051/0004-6361:20053108

The evolution of planetary nebulae

III. Internal kinematics and expansion parallaxes^,

D. Schönberner - R. Jacob - M. Steffen

Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany

Received 22 March 2005 / Accepted 11 July 2005

Abstract
A detailed theoretical study of the basic internal kinematics of planetary nebulae is presented, based on 1D radiation-hydrodynamics simulations of circumstellar envelopes around central stars of 0.595 and 0.696 $M_{\odot }$. By means of observable quantities like radial surface-brightness distributions and emission-line profiles computed from the models, a comparison with real objects was performed and revealed a reasonable agreement. This allowed to draw important conclusions by investigating the kinematics of these models in detail.
Firstly, it is shown that the determination of kinematical ages, normally considered to be simple if size and expansion rate of an object are given, can seriously be flawed. Secondly, the expansion law of a planetary nebula is different from what is assumed for deriving spatio-kinematical models. Thirdly and most importantly, our hydrodynamical models help to correctly use existing angular expansion measurements for distance determinations. The mere combination of the angular expansion rates with the spectroscopic expansion velocities leads always to a serious underestimate of the distance, the degree of which depends on the evolutionary state of the object. The necessary correction factor varies between 3 and 1.3. Individual correction factors can be estimated with an accuracy of about 10% by matching our hydrodynamical models to real objects. As a result, revised distances for a few objects with reliable angular expansion rates are presented. But even these corrected distances are not always satisfying: they still appear to be inconsistent with other distance determinations and, even more disturbing, with the accepted theory of post-asymptotic giant branch evolution.
As a byproduct of the angular expansion measurements, the transition times from the vicinity of the asymptotic giant branch to the planetary-nebula regime could be estimated. They appear to be shorter than assumed in the present evolutionary calculations.

Key words: hydrodynamics - radiative transfer - planetary nebulae: general - stars: AGB and post-AGB

   
1 Introduction

Our understanding of the final evolution of low and intermediate-mass stars is severely hampered by the fact that the distances to planetary nebulae (PNe) are only poorly known, a fact that leads to only a limited accuracy of fundamental distant-dependent quantities like central-star luminosity and nebular mass which are so important for the theory of the late asymptotic-giant branch (AGB) evolution and for the quantitative description of the circuit of matter. Distances derived statistically may be useful for large samples of PNe, but are often subject to large errors when applied to individual objects. Moreover, the underlying assumptions are calibrated by means of a rather small sample of objects, the distances of which are believed to be known to an acceptable degree of accuracy. The need for relatively direct and straightforward methods to determine distances to a larger number of individual planetary nebulae is very pressing.

To date the success of trigonometric parallaxes is rather limited because only few objects are close enough. More promising are the spectroscopic and expansion parallaxes. The first method needs very sophisticated model atmospheres to analyze the photospheric spectrum of the central stars and has successfully been applied to a number of objects (cf. Méndez et al. 1992). The second method uses the observed nebular expansion rates and is much simpler: it relates the radial angular expansion on the sky, $\dot{\theta}$, to a spectroscopically measured expansion velocity along the line-of-sight, V. From the geometry of expansion, the distance to the nebula follows as

$$D = V/\dot{\theta} ,$$

or $D = 211 (V/\dot{\theta})$ , if D in pc, V in km s^-1, and $\dot{\theta}$ in mas yr^-1. A summary of the distances based on the expansion parallax method and a comparison with other results has been presented by Terzian (1997).

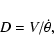
The implicit assumption is that spectroscopy and imaging are sampling the same physical regime within the object, so that it appears justified to use the (small angle) relation $D~\dot{\theta} = V$. This assumption, however, cannot be taken for granted because it is well known that measured Doppler splits do often depend on the ion considered, indicative of velocity gradients within the expanding shell. The question is which velocity to take, a question difficult to answer without detailed knowledge of the velocity field and the ionization stratification of the PN under consideration.

The determination of expansion parallaxes is, of course, only meaningful for objects with a spherical or ellipsoidal shape, allowing to relate the expansions in the plane of the sky and along the line-of-sight at the position of the central star (cf. Palen et al. 2002). But even in this case assumptions about the internal expansion law have to be made that are not verified.

The most severe drawback of this method, not considered at all in previous applications, is the fact that the measured edges of the expanding shells are either ionization or shock fronts, the expansion speeds of which are not measurable by spectroscopy. In both cases one compares pattern with matter velocity, where the latter is always less than the former, leading to a systematic underestimate of the distance. This fact has been mentioned at several occasions in the past but did not find proper attention (cf. Marten et al. 1993; Steffen et al. 1997).

Very recently Mellema (2004) investigated the expansion properties of the shell edges of PNe by applying the jump conditions across shock and ionization fronts. Assuming that the spectroscopically measured expansion speeds refer to the material immediately behind the shock front, he estimated that correction factors between 1.3 and 1.5 need to be applied to the distances.

In the present work we utilize detailed 1D-radiation-hydrodynamics simulations of planetary nebulae to give a more realistic estimate of the correction factors to be expected. Selecting models that have a very close similarity to real objects, we demonstrate that, due to the density and velocity structure typical of PNe, material velocities do not refer usually to regions immediately behind the shock fronts. This fact increases the disparity between pattern and material velocity, and distance corrections up to a factor of two and more are easily possible (cf. Perinotto et al. 2004, hereafter Paper I, Fig. 22 therein).

The present paper is organized as follows: we first introduce in Sect. 2 our method of modelling the PN evolution and discuss to some extent the properties of our hydrodynamical models, in particular their kinematical ages and expansion laws. We verify in Sect. 3 the usefulness of our models by comparing observable quantities like surface brightnesses and emission-line profiles computed from the models with those observed. Section 4 deals then with the important issue of the expansion parallaxes. The paper closes in Sect. 5 with a short summary and discussion.

   
2 The hydrodynamical model

   
2.1 Method and assumptions

Our method of calculating 1D radiation-hydrodynamics models of planetary nebulae has been extensively described in Perinotto et al. (1998) and in Paper I. In the latter work an extensive grid of evolutionary nebula sequences was presented and their structures and expansion properties studied.

Figure 1: Top: evolutionary path for the 0.595  $M_{\hbox {$\odot $ }}$ post-AGB model with ages indicated (left), and the corresponding photon and wind luminosity, $L_{\rm wind}=\dot{M}\cdot V^2/2$ (dashed line) vs. time (right). Bottom: mass-loss rate (left) and wind velocity (right). The end of the strong AGB wind sets the zero point of the post-AGB evolution and the beginning of the much weaker post-AGB winds.

Open with DEXTER

In the present paper we employed again the 0.595 $M_{\odot }$ post-AGB model introduced in Schönberner et al. (2005, hereafter Paper II) as the typical representative of central stars. This model was generated by interpolation between the 0.605 $M_{\odot }$ track of Blöcker (1995b) and the 0.565 $M_{\odot }$ track of Schönberner (1983). Its general properties are repeated in Fig. 1 showing the evolution in the Hertzsprung-Russell diagram and the corresponding temporal evolution of the photon and wind luminosities, and the mass-loss rate and the wind speed. We followed the recommendations of Pauldrach et al. (1988) for the parameters of the central-star wind, while we assumed a Reimers' wind (Reimers 1975) during the transition from the vicinity of the AGB to higher effective temperatures where the wind becomes line driven. For more details, the reader is again referred to Paper I.

We computed with this central-star model a new sequence with an initial AGB envelope model which had been used earlier in conjunction with a 0.605 $M_{\odot }$ central-star model (Paper I, T YPE C initial model of sequence No. 6 from Table 1). This model which is shown in Fig. 2 has an initial density and velocity structure based on consistent radiation-hydrodynamics simulations along the upper AGB using the mass-loss prescription of Blöcker (1995a). The important property of this model is that the radial density distribution falls off much steeper than obtained under the assumption of stationary winds: at larger distances from the star we have $\rho(r)\propto r^{-3}$. This is the consequence of the luminosity increase after the the last thermal pulse on the AGB whose signature in the wind envelope is seen at a distance of 10¹⁸ cm, corresponding to $t\simeq -30~000$ yr. Further details are given in Steffen et al. (1998) and in Paper I.

We followed the hydrodynamical evolution of the nebular envelope along the central-star's track across the HR diagram and down along the white-dwarf cooling path until the model nebula reached the outer boundary of the computational domain after 22 000 yr. The morphology of the model PN turned out to be very similar to that of sequence No. 6 discussed in Paper I. The only noticeable difference is the consequence of the lower evolutionary speed of the central-star: the nebular model has more time to expand and becomes optically thin at a lower effective temperature, viz. at $\approx$48 000 K instead of at $\approx$60 000 K in the case of the faster 0.605 $M_{\odot }$ central star, which is more consistent with the observations.

	Figure 2: Initial model used in this paper. Plotted are the density of the heavy particles (thick), of the electrons (dotted), and the flow velocity (thin) against the distance from the central star.
Open with DEXTER

In order to facilitate the comparison with observed quantities, several supplementary codes were used for the computation of surface brightnesses and especially the emission-line profiles along preselected lines-of-sight with different spatial resolutions. For the line profiles we employed an updated version of the code used by Gesicki et al. (1996). We always assumed infinite spectral resolution, although it is possible to broaden the theoretical profiles by prescribed functions in order to simulate finite spectral resolutions. Additionally, several IDL routines were developed for the automatic determination of shock front positions from the model structures and of the flow variables immediately before and behind these shocks. Furthermore, we fitted the computed line profiles by multi-component Gaussians (usually four) in order to determine the bulk motions within the individual nebular shells. In general, the determination of bulk velocities within the respective shells by decomposition into Gaussians worked very well.

By decomposition of the line profile into individual components we are able to "measure'' expansion velocities of models in the same manner as one would do for a real objects, with the important difference that we know the true expansion rate. The latter is given by the speed of the shocks which can not be measured spectroscopically. By comparing both velocities we can estimate the systematic error inherent in the expansion parallax method. We preferred in our analysis of the model properties the strong lines [N  II] 6583 Å and [O  III] 5007 Å, computed for the central line-of-sight through the model nebulae. These lines are usually easy to observe with sufficiently high resolution and signal-to-noise ratio.

Figure 3: Heavy-particle density (thick), electron density (dotted), and velocity field (thin) together with the [O  III] and [N  II] surface brightnesses and emission-line profiles of hydrodynamical models at selected positions along the horizontal part of the 0.595 $M_{\odot }$ post-AGB evolutionary track shown in Fig. 1. The line profiles are computed for the central line-of-sight with infinite spectral resolution and are normalized to their maximum value. The circular aperture has a radius of $1\times 10^{16}$ cm. In the structure and surface-brightness panels, the positions of the leading shock fronts of rim and shell are indicated by thick vertical lines, while the thin horizontal lines (solid and dashed) correspond to the thin vertical lines in the profile panels. They indicate the typical flow velocities within the individual shells as the result of the Gaussian decomposition of the total emission-line profiles. The stellar parameters along the 0.595 $M_{\odot }$ track from Fig. 1 are as follows: t=3 364 yr, $T_{\rm eff}=39~297$ K, L=5 545 $L_{\odot }$ (top); t=4 538 yr, $T_{\rm eff}=54~526$ K, L=5 417 $L_{\odot }$ (next to top); t=7 027 yr, $T_{\rm eff}=98~393$ K, L=4 650 $L_{\odot }$ (next to bottom); t=9 104 yr, $T_{\rm eff}=139~923$ K, L=2 844 $L_{\odot }$ (bottom). Note the different radial extents of the structure and surface-brightness plots.

Open with DEXTER

   
2.2 General properties of the nebular model

We start this section with an overview of the general behaviour of our new simulation. Figure 3 illustrates in four "snapshots'' how the nebular structures evolve as the central star crosses the Hertzsprung-Russell diagram. The figure shows the density and velocity structures of the model nebula with the radial positions of the leading shocks indicated, together with the surface brightness distributions and corresponding emission-line profiles for [N  II] 6583 Å and [O  III] 5007 Å. Thin lines mark the typical velocities within the shells as measured by the decomposition of the line profiles into individual Gaussian components.

These snapshots illustrate the important phases in the life of a PN. The top panel shows the early, optically thick stage when the ionization front is still trapped and the high pressure of the ionized gas is driving a shock into the neutral ambient AGB wind (D-type ionization front). The ionized shell is highly stratified as can be seen by the shapes of the surface brightnesses in the lines of [N  II] and [O  III]. The peak at $0.65\times10^{17}$ cm, only seen in [O  III], delineates the inner edge of the model, i.e. the position of the contact surface or discontinuity.

Consequently, the [N  II] and [O  III] lines monitor completely different regions of the H  II region with their different gas velocities. Gas close to the outer edge is expanding with large speed, (v=26.5 km s^-1), as indicated by the outer components of the [N  II] line, whereas it is streaming only very slowly near the the contact surface (v=5.0 km s^-1 from [O  III]). At $r=1.1\times10^{17}$ cm the gas is weakly shocked because the slowly moving shell gas is being abruptly swept up by faster gas accelerated by the contact discontinuity. One recognizes also from the top panel of Fig. 3 that only the [O  III] line probes the kinematics of the developing rim. The strong inner components of the [N  II] line monitor the region behind the ionization front where the gas velocities are still quite large. In the rim, nitrogen is mainly in the second ionization stage.

The next panel gives the moment shortly after the beginning of the optically thin stage: the ionization front left the shock behind, and the latter constitutes now the outer edge of the PN proper. The velocity profile behind the shock front becomes nearly linear with a positive gradient. The ionization stratification is still persistent, as the different profiles of [N  II] and [O  III] show. Because of the now more vigorous stellar wind, the contact surface moves faster and compresses the gas of the inner regions into the "rim'' bounded at $r=1.6\times10^{17}$ cm by a weak shock.

The PN has now entered its main evolutionary phase where it consists of two independently expanding shells. The (outer) shell, driven by the thermal pressure maintained by heating from the ionizing photons emitted from the central star, expands supersonically into the ionized AGB flow, and its shock (at $r=3.3\times10^{17}$ cm) accelerates the gas from 15 to 27 km s^-1. From the strong outer [N  II] components we deduce 25.6 km s^-1. The rim is a "bubble'' blown into the shell by the pressure of the thermalized stellar wind gas and is steadily accelerated. The [O  III] line indicates a velocity of 7.8 km s^-1, intermediate between the postshock value of 5.5 km s^-1and that at the contact surface of 9.5 km s^-1.

The last two panels illustrate more advanced phases of the double-shell stage. The rim is now always the most dense and prominent part of the PN, the shell is faint and sometimes called "attached'' (Chu et al. 1987). Rim and shell continue to expand independently of each other: the expansion speed of the shell is mainly determined by the radial slope of the AGB density distribution, whereas the rim is accelerated by the steadily increasing wind power of the central star (Schönberner et al. 2004; Paper I). The surface brightness of the shell turns into one with a nearly (negative) linear slope which is typical for AGB envelopes with radial density profiles significantly steeper than $n(r)\propto r^{-2}$.

In these advanced stages with very hot central stars the ionization degrees depend smoothly on distance from the star. The [N  II] and [O  III] line profiles are similar, but the [N  II] line intensities are very low since all nitrogen atoms are mainly in their second and third ionization stage.

   
2.3 The kinematics of the nebular model

Figure 4: Detailed illustration of how the kinematical properties of our model PN from Fig. 3 develop with time while the central star evolves across the HR diagram as shown in Fig. 1. Material velocities are indicated by V, motions of structures by $\dot{R}$, with R indicating their radial position. All velocities are measured in the rest frame of the central star. The dotted vertical lines correspond to the models selected for the presentation in Fig. 3. On the left, the properties of the shell are given, on the right those of the rim. The following variables are displayed: Top, left: for the shell, the velocities (in the stellar rest frame) of the shock front, $\dot{R}_{\rm shell}$, the postshock flow, $V_{\rm post}$, and those as measured by decomposition of the synthetic line profiles of [N  II] and [O  III] resp., are given. The subscript "post'' refers to the maximum velocity reached after the passage of the shell's shock front, corresponding to the end of the shock's relaxation zone (see also Fig. 3). However, during the optically-thick stage, t < 4000 yr, shock and ionization front are so close that the electron temperature immediately behind the shock front is fully determined by photo-ionization, and the shock relaxation zone does not exists. Also in this case "post'' refers to the maximum speed of the flow behind the shock front. Top, right: corresponding velocities for the rim, except that instead of the post-shock velocity we plotted its pre-shock velocity, $V_{\rm pre}$, and added also the speed of the contact discontinuity, $\dot{R}_{\rm cd}$. Middle: mach numbers of the resp. shocks, $M=(\dot{R}-V_{\rm pre})/C_{\rm s}$, with $C_{\rm s}$ being the (isothermal) sound speed ahead of the shock, and the ratios between shock speed and corresponding gas velocity as measured by means of a "Doppler'' split emission line, $F = \dot{R}/V$. Bottom: kinematic ages, $t_{\rm kin}$, determined from various combinations of shock positions and velocities vs. the "true'' evolutionary age. The dashed line is the 1:1 relation.

Open with DEXTER

We now take a closer look into the characteristic expansion properties of our nebular models. In particular, we discuss shell and rim separately, investigate their expansion laws, and comment on the usefulness of kinematical ages. We emphasize that all velocities are relative to the star if not noted otherwise.

   
2.3.1 The shell

The shell is being formed when the central star becomes hot enough to ionize and heat the AGB-wind matter after 2000 yr of post-AGB evolution, and its evolution is illustrated in the left panels of Fig. 4. The top panel shows, as a function of time, the following velocities: the leading shock-front speed, $\dot{R}_{\rm shell}$, the post-shock gas velocity, $V_{\rm post}$, and the Doppler velocities measured from emission-line profiles. Due to the positive velocity gradient within the shell these spectroscopic expansion velocities are always smaller than $V_{\rm post}$ (cf. also Fig. 3).

During the optically-thick phase which lasts till t = 4000 yr, the leading shock of the shell is steadily accelerated. Its speed is highly supersonic (middle panel) and reaches finally 38 km s^-1 when the transition to the optically-thin stage occurs. During the following "champagne'' phase of expansion, the shocks resumes its acceleration until the star fades at $t\approx 9500$ yr, causing the electron temperature in the shell to drop. The main cause of the shocks acceleration during this "champagne'' phase of expansion is the steepening of the density slope of the AGB wind with distance from the star (cf. Fig. 2), but also the slowly increasing electron temperature as the star becomes hotter contributes to a lesser degree (for a comprehensive discussion see Paper II). The shock's Mach number with respect to the upstream flow, $M=(\dot{R}-V_{\rm pre})/C_{\rm s}$, with $C_{\rm s}$ being the isothermal sound speed, and $V_{\rm pre}$ the pre-shock flow speed, is always a little bit below 2.

Concerning the spectroscopic expansion speed of the shell, both ions give similar results, except during the optically-thick stage (more precisely for $t\la 4000$ yr) where the shell is highly ionization stratified. The [O  III] lines probe only the inner more highly ionized region where the gas velocity is quite small (Fig. 3, top panel). Using [N  II] only, the real expansion speed of the PN, as given by the motion of the shell's shock front, will be underestimated by a factor F that depends on the evolutionary stage and may amount up to a factor of 1.4 (middle panel). Using proper motion measurements of the shell, $\dot{\theta}_{\rm shell}$, the distance would then be given by $D=F \cdot V/\dot{\theta}_{\rm shell}$.

The left bottom panel of Fig. 4 contains the important information how kinematic ages of PNe, as determined by the radial position of the shock front, i.e. the outer edge of a PN, divided by an expansion velocity, compare with the true post-AGB ages. It turns out that, using lower ionized species like [N  II], the agreement between both ages is not too bad during the whole course of evolution shown in the figure. Using higher ionized elements like [O  III] gives, as expected, poor agreement only during the early, optically thick period. We have here obviously two effects that compensate each other to a certain degree: the lower expansion speed as determined from the emission lines makes up for the fact that due to the shock's acceleration the kinematical age of the shell falls well behind the true age, as is evident from the time behaviour of $R_{\rm shell}/\dot{R}_{\rm shell}$.

   
2.3.2 The rim

The rim is formed later than the shell, at $t\approx 3000$ yr, because earlier the central-star wind is not powerful enough to compete with the high pressure of the ionized gas (cf. Fig. 1 for the time evolution of the post-AGB wind). The expansion behaviour of the rim is different since it constitutes a bubble driven into the ambient shell by the action of the very hot shocked wind gas from the star, and is illustrated in the right panels of Fig. 4.

Once formed, the speed of the rim's leading shock, $\dot{R}_{\rm rim}$, is steadily increasing from a rather low value, $\simeq$10 km s^-1, to over 35 km s^-1, driven by the expansion of the bubble, $\dot{R}_{\rm cd}$. However, the shock's relative speed to the ambient shell gas stays close to the (isothermal) sound speed since $V_{\rm pre}$ increases as well with time. Thus the shock remains always very weak, with Mach numbers close to unity, with one exception (middle panel). Shortly after t=6000 yr the He  II ionization front is approaching the shock, leading to an additional acceleration because of the larger electron temperature behind the ionization front. After the passage of the He  II ionization front the rim's acceleration and speed return to the normal values.

The top panel contains also information about the Doppler speeds, measured from the split strong line components (cf. Fig. 3). As we have found for the shell, the expansion velocities based on line-profile analyses are significantly below $\dot{R}_{\rm rim}$. Actually they are close to the speed of the contact surface because the highest rim density is there.

The discrepancy between the rim's motion and the matter flow within the rim is quite large and invalidates all attempts to combine both velocities for a distance determination. We will come back to this point in Sect. 4. We mention here only that the mismatch between shock and matter speed, as expressed by $F = \dot{R}/V$, is $\approx$3 during the early phase, declining later to more modest values around 1.4 (right middle panel of Fig. 4). This behaviour is consistent with Mellema's analysis of weak isothermal shocks (Mellema 2004, Fig. 3 therein).

For weak isothermal shocks, $\gamma=1$ and $M\simeq 1$, one gets from the jump conditions in the stellar frame (cf. Eq. (4) in Mellema 2004),

$$F = \dot{R}_{\rm rim}/V_{\rm rim} \simeq \dot{R}_{\rm rim}/V_{\rm post} = 1 + C_{\rm s}/V_{\rm pre},$$

with the isothermal sound speed, $C_{\rm s}$, and $V_{\rm rim}\simeq V_{\rm post}$. Early on when the material around the contact discontinuity is nearly stalling, the very small pre-shock velocity leads to a large factor F. Later $V_{\rm pre}$ is increasing, and F decreases accordingly. This general trend is temporarily interrupted during the passage of the He  II ionization front when the electron temperatures are different on both sides of the front (Fig. 4, right top panel).

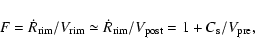
The bottom panel of Fig. 4 contains again information about the relations between derived kinematical ages and the true evolutionary age. As it turns out, the rim of a PN is not at all suited to determine the object's age. Using size and Doppler expansion, the kinematical age is not indicative for the real age. Instead, the kinematical age may even decrease with time if one uses the splitting of the [O  III] line. Using the rim's proper motion instead is not very useful either: because of the roughly constant acceleration of the rim's front the kinematical age falls well behind the real age (see also the discussion in Sect. 3.2).

The difficulties of determining realistic ages from sizes and spectroscopic measurements have already be noted earlier (cf. Marten et al. 1993; Mellema 1994; Schönberner et al. 1997). Especially Mellema discussed this problem in some detail, and we confirm his conclusions. We defer a more extensive discussion on kinematical ages to Sect. 2.3.4.

   
2.3.3 Expansion laws

Our hydrodynamical models can also be used to investigate the general expansion laws relevant for the construction of spatio-kinematical models from imaging and spectroscopy. Usually one assumes isotropic expansion, $\dot{\theta} \propto \theta$, without any proof, or very similarly $v\propto r$, when observed Doppler shifts are related to distances from the central star along the line of sight. Assuming further a radial expansion with the nebula's outer radius increasing linearly with time, a unique expansion age, $R/\dot{R} = r/\dot{r} = {\rm const.}$, follows.

Real planetary nebulae are, however, ruled by hydrodynamics instead of ballistics, and their expansion properties can be checked by means of the hydrodynamical models displayed in Fig. 3. We see clearly that, although the shell as a thermally-driven shock wave develops a velocity field with a nearly constant and positive slope, $\dot{r} \propto r$ does not really hold because the velocity is not vanishing at the origin, i.e. at the position of the central star. The rim's velocity field is not similar to $\dot{r} \propto r$ at all because the rim matter is being compressed by the expanding bubble of wind-heated gas and the confining shell. Based on the wind model used here, the flow is fastest close to the contact discontinuity (cf. Fig. 3).

The expansion of our hydrodynamical model is illustrated in Fig. 5. Plotted are the radial positions of the outer edges, i.e. the shock fronts, of the shell and the rim, and also the position of the contact discontinuity. It is evident from this figure that none of the plotted structures expand ballistically! Instead, the expansion is accelerated: that of the shell by the increase of the circumstellar density gradient with distance from the star, and that of the rim mainly by the increase of the stellar wind power with time.

Figure 5: Radial displacements of shell, rim and contact surface of a model PN as a function of time. Plotted are $R_{\rm shell}$, $R_{\rm rim}$, and $R_{\rm cd}$ from Fig. 4. The dotted curves represent fits to $R_{\rm rim}$ and $R_{\rm cd}$ of the form R=R0+c (t-t0)b (see text). The parameters for $R_{\rm rim}$ are R0= 0.031 pc, t0=3016 yr, $c=6.70\times10^{-7}~ {\rm pc}/{\rm yr}^b$, and b=1.40, and those for $R_{\rm cd}$ are R0=0.016 pc, t0=2039 yr, $c=2.93\times10^{-9}~ {\rm pc}/{\rm yr}^b$, and b=1.95.

Open with DEXTER

For the rim, the expansion law is of the form

R=R₀+c (t-t₀)^b ,

with t₀ being the time lapse between the departure from the AGB and the formation of the rim, and R₀ the corresponding distance from the star where the rim forms, $R_0 \simeq V_{\rm agb}~t_0$. Fits using appropriate constants for c and b are shown in Fig. 5 for the rim shock and the contact discontinuity.

The sizes of the exponents, b=1.40 and 1.95, reflect the fact that the rim is driven by increasing stellar wind power (cf. Fig. 1) into an expanding confining medium. The shell disturbs the original circumstellar density profile to such an extent that the density decrease ahead of the rim is different from the original one. In fact, we derived from the model that the gas density in front of the rim decreases roughly with $\rho\propto r^{-2}$, although the original radial density decline of the wind envelope was close to $\rho\propto r^{-2.5}$.

We note that similarity solutions for adiabatic wind-driven bubbles predict b=1.0 if $\rho\propto r^{-2.0}$ and b=1.2 if $\rho\propto r^{-2.5}$ for the rim shock (Koo & McKee 1992), well below the result of our hydrodynamic simulation, b=1.4. Note that these similarity solutions assume expansion into a static medium under the influence of constant wind power. We conclude that analytical solutions based on simplified conditions are not suited to describe the expansion of planetary nebulae.

We investigated also the rim expansion laws for the simpler models with initial power-law density profiles, $\rho\propto r^{-\alpha}$, used in Paper II. For fixed $\alpha = 2$, we found b to vary slightly between 1.2 and 1.4, but virtually independently of central-star mass and initial envelope density. The dependence on $\alpha$ is, however, significant: we found $b\simeq 1.8$ for $\alpha=3$.

For elliptical objects it is generally assumed that the equatorial (e) and polar (p) radii and (spectroscopic) expansion velocities behave like $V_{\rm e}/V_{\rm p} = R_{\rm e}/R_{\rm p}$. This implies $V=\dot{R}$ and uniform acceleration starting in the origin. Both assumptions are not supported by our hydrodynamical models. However, considering the weak dependence of b on the environment conditions as follows from our spherical models, a relation $\dot{R}_{\rm e}/\dot{R}_{\rm p} \simeq R_{\rm e}/R_{\rm p}$ is very likely to hold provided R is substantially larger than $R_{\rm0}$.

More problematic is the fact that we found, as long as the shock-heated wind gas continues to expand, $V_{\rm rim} \simeq \dot{R}_{\rm cd} < \dot{R}_{\rm rim}$ (cf. Fig. 4, right upper panel). This offset in velocity results in $V_{\rm e}/V_{\rm p} < R_{\rm e}/R_{\rm p}$, but the error introduced thereby cannot be estimated without realistic 2D hydrodynamics simulations.

   
2.3.4 Kinematical ages

The kinematical properties of our PN model can also be used to comment on the common practice to determine nebular ages from sizes and expansion velocities. One notices immediately from the bottom panels of Fig. 4 that the rim and the shell have quite different expansion time scales, $R/\dot{R}$. The rim, although it forms after the shell and closer to the star, appears to be older than the shell during the early evolution. Only later the opposite is true. The reason is the low initial value of $\dot{R}_{\rm rim}$. In practice $\dot{R}$ is not known, and one has to rely on the expansion velocities, V, as measured by a Doppler-split line profile, but the discrepancy of the kinematical ages is qualitatively the same.

The expansion velocities of PNe listed in existing catalogues are usually measured from the bright nebular parts, i.e. they belong to the rim in the case of double shell objects, while the radii are exclusively those of the shell. Using our model sequence, we thus combined shell radii, $R_{\rm shell}$, with the corresponding spectroscopic expansion velocities, $V_{\rm rim}$, and the result is plotted in Fig. 6. The models appear to be very old right from the beginning: the kinematical ages vary between 10 000 and 15 000 years, depending on the line used, and are virtually independent of the real evolutionary age! Only for a very advanced stage of evolution when the central star is approaching its maximum temperature ( $t \ga 8000$ yr) we find a reasonable agreement between the real post-AGB age and $t_{\rm kin}$.

	Figure 6: Comparison of different kinematical ages derived from the shell radius. They are computed from our hydrodynamical models and plotted as a function of their real evolutionary age. The curves for $R_{\rm shell}/V_{\rm shell}$ are the same as in Fig. 4 and are given for comparison. The dashed line indicates the 1:1 correspondence.
Open with DEXTER

Judging from this very disappointing result it appears to be not straightforward at all to determine empirically ages for planetaries even if the distances and hence the dimensions are known. According to the model sequence presented here, reasonable results for the whole range of evolutionary times considered are in principle only to be expected if the radius of the shell is combined with the shell's spectroscopic expansion speed (see Fig. 6, $R_{\rm shell}/V_{\rm shell}$). For this purpose, the [O  III] lines should not be used for young, optically thick objects because of their ionization stratification. We thus caution here that extreme care should be taken when interpreting kinematical ages of double shell PNe since the spectroscopic velocities of shells are usually not known.

In this context we would like to mention the work of McCarthy et al. (1990) where kinematical ages of PNe, most of which are double shell objects, were compared to evolutionary ages, the latter being determined from positions of the central stars in a $\log g - \log T_{\rm eff}$ diagram of post-AGB evolutionary tracks. These authors found systematic discrepancies in the sense that in general the empirical ages are larger than the evolutionary ones. This has been interpreted in the sense that the residual envelope masses of the AGB remnants are in most cases larger than used in the evolutionary calculations.

Not considering the fact that the determination of evolutionary ages demands a very accurate evaluation of the surface parameters of the central stars, it is clear from the above results that this method is not able to provide results useful for such a study. For instance, although McCarthy et al. (1990) do not provide the radii and velocities used for their age determination, the only possible combinations for the double shell objects they could have used are either $R_{\rm shell}/V_{\rm rim}$, since the shell velocities were not known, or $R_{\rm rim}/V_{\rm rim}$, both of which are unsuited for estimating kinematical ages (cf. Figs. 4 and 6).

Another illuminating example is the case study performed for M 1-46 by Guerrero et al. (1996). This PN appears to be a young double shell object with a rather cool central star of $T_{\rm eff} = 45~000$ K. The [N  II] spectroscopic velocities of rim and shell are 11.5 and 26.0 km s^-1, respectively (Guerrero et al. 1996; Paper II). Adopting a distance of 4.4 kpc, Guerrero et al. found ages of 12 650 and 5700 years, depending on whether the rim or the shell velocity is combined with the outer radius, i.e. with the shell radius.

Our models offer a simple explanation for this discrepancy: M 1-46 is still close to the optically thick/thin transition phase, and based on our hydrodynamical models we have shown that a large discrepancy between $R_{\rm shell}/V_{\rm shell}$ and $R_{\rm shell}/V_{\rm rim}$ exists, which in the case depicted in Fig. 6 are about 4000 and 12 000 yr, i.e. a difference of about 8000 yr, in astonishing agreement with what has been found for M 1-46. Considering that only $R_{\rm shell}/V_{\rm shell}$ provides a reasonable age estimate, it follows that the real age of M 1-46 is close to 5700 years (for the assumed distance), and that there is no reason to assume two distinct mass-loss episodes separated by several thousands of years.

It may also happen that the kinematical age, based on $R_{\rm shell}/V_{\rm rim}$, becomes smaller during later stages than that based on $R_{\rm shell}/V_{\rm shell}$ if $V_{\rm rim}$ increases sufficiently faster than $V_{\rm shell}$. The corresponding curves in Fig. 6 would then intersect at larger ages. Candidates are NGC 7662 (Guerrero et al. 2004) and other evolved PNe with very hot central stars and similar expansion rates for shell and rim.

   
3 The models in comparison with observations

Before we continue discussing the expansion properties of our nebular models in the context of distance determinations, it appears necessary to have a closer look at how these models compare with the observations. Useful criteria for any comparisons are the surface brightness distribution, i.e. the morphology, and the expansion behaviour.

For this purpose, we selected three planetaries with rather well-defined double shell structures not too much deviating from sphericity: NGC 6826, IC 2448, and NGC 3242, which cover a certain range of evolutionary stages as is evident from the different effective temperatures of their central stars (Table 1). We also discuss in some detail NGC 7027 which is a young but evolved PN around a massive central star.

Table 1: Objects selected for comparison with our hydrodynamical models. The effective temperatures of the central stars are from Méndez et al. (1992), and the spectroscopic expansion velocities from the decomposition of [O  III] line profiles (Paper II, Table 4 therein).

   
3.1 Surface brightness and expansion speed

Figure 7: Top: normalized surface brightness distributions in [O  III] of three selected planetary nebulae from HST monochromatic images (F502N), with effective temperatures of their central stars increasing from left to right (cf. Table 1). For NGC 3242 the He  II image (F469N) is added. The cuts are taken along or close to the minor axes and scaled to the model sizes. Bottom: normalized surface-brightness distributions in [O  III] 5007 Å (and additionally in He  II 4686 Å in the case of NGC 3242) for selected hydrodynamical models that match the observations as closely as possible. The positions of the models along the track shown in Fig. 1 are ( from left to right) at $T_{\rm eff} = 67~250, 74~287, \mbox{and}\ 88~628$ K.

Open with DEXTER

NGC 6826, IC 2448, NGC 3242

Figure 7 (top panels) presents surface-brightness distributions of these objects, arranged according to increasing effective temperatures of their central stars. The surface brightnesses are based on monochromatic images retrieved from the HST archive and represent cuts along, or close to, the minor axes. In the case of NGC 3242, the [O  III] image is supplemented by the He  II image which constrains the evolutionary stage of NGC 3242 quite well: the He  II ionization front is still trapped within the rim.

The models along the evolutionary path shown in Fig. 1 are selected such as to provide a reasonable match to the observations (bottom panels of Fig. 7). As it turned out, the models follow also a sequence with increasing stellar temperatures, although these temperatures are generally somewhat larger than those of the observed objects. The agreement of our models with these objects is astonishing, especially if one considers that we have not aimed at fitting particular objects from the outset: relative sizes and brightnesses of the shells and rims are remarkably well matched.

There are, however, differences to be noted: the "cavities'' enclosed by the rim appear deeper than the models predict, NGC 6826 excepted. Also the observed brightness profiles of the shells are somewhat flatter (e.g. in IC 2448). We have shown in Paper II that the shape of the shell's surface brightness depend on the radial density profile of the initial configuration set up during the final AGB mass-loss phase. From the small mismatch between the models and the observation that is evident from Fig. 7 we conclude that the original density gradient should be a little bit steeper than the one in our initial model (see Fig. 2).

The density gradient in the wind envelope rules also the expansion speed (see Paper II), hence we expect also a small mismatch between modelled and observed expansion speeds. This is shown in Fig. 8 where the spectroscopic velocities listed in Table 1 are compared with the model predictions. It is evident from the figure that the spectroscopic velocities of the shells and the rims of the models are falling behind the observations for the two more evolved objects. A larger density gradient of the initial model would be needed to accelerate the expansion of the models.

In any case, the relative speeds between shell and rim are rather well matched by our models. We conclude therefore that also the shock properties, especially that of the rim, are adequately described by our models.

We found already in Paper II that most likely all double shell PNe have very similar properties concerning morphology and expansion properties. Obviously they form an evolutionary sequence, and their evolutionary status can be inferred from their morphology, expansion property, and temperature of the central star. The combination of a post-AGB model of about 0.6 $M_{\odot }$ with an appropriate model for the AGB-wind envelope enables obviously a successful hydrodynamical modelling of the planetary-nebula evolution.

NGC 7027

We added NGC 7027 to the list of comparison objects although it is not a typical double shell PN. Its central star is very hot, very luminous, and hence more massive ($\approx$0.7 $M_{\odot }$) than the others from the sample listed in Table 1 (e.g. Volk & Kwok 1997). From the evolutionary point of view the nebular envelope is in a very advanced stage, although it is still optically thick and of low kinematical age. This is the consequence of the fast evolution of massive central stars which cross the HR diagram in a few 100 years or even less instead of some 1000 years as is typical for the standard central star.

	Figure 8: Spectroscopic expansion velocities of the objects from Table 1 compared with predictions from the models used in Fig. 7. The dashed line is the 1:1 relation.
Open with DEXTER

Morphologically, NGC 7027 consist of a bright rim-like structure with an attached faint shell, surrounded by a molecular shell seen in emission from H₂ (Latter et al. 2000, Fig. 7 therein). We have shown in Paper I that envelopes around massive, very fast evolving central stars remain optically thick and that most likely the interface between the neutral and the ionized domains, i.e. the photo-dissociation region, is a place where all sorts of molecules, including H₂, are being formed and destroyed (cf. Hasegawa et al. 2000).

For the case of NGC 7027 we employed sequence No. 10 from Paper I which combines a simple AGB-wind envelope with a rapidly evolving post-AGB object of 0.696 $M_{\odot }$. A detailed description of the evolutionary properties of this hydrodynamical model sequence is presented in the Appendix. Here we show in Fig. 9 (top panel) a number of normalized H$\beta$ surface-brightness profiles computed from this hydrodynamical sequence and selected at positions along the high-temperature part of the evolutionary track, as shown in Fig. A.1, which embrace the estimated position of NGC 7027 at $T_{\rm eff}\simeq 200~000$ K and $L\simeq 7700$ $L_{\odot }$ (Latter et al. 2000).

Figure 9: Top: radial H$\beta$ surface-brightness profiles, normalized to maximum emission, of selected hydrodynamical models with a massive central star of 0.696 $M_{\odot }$ (sequence No. 10 in Paper I) plotted as a double logarithmic presentation. The corresponding model structures (except that with t= 900 yr) are shown in Fig. A.2. Bottom: normalized cut of the HST P$\alpha$ image (F187N) along the large semi-major axis (orientation "OA'' of Latter et al. 2000, thick line) compared with the scaled H$\beta$ surface-brightness profile of the 584 yr old model from the top panel (dotted line). The stellar parameters of this particular model are $M = 0.696~\mbox{$M_{\odot}$ },\ L = 9875~\mbox{$L_{\odot}$ },\ T_{\rm eff}= 155~504~{\rm K}$. We have not corrected for the small effects caused by the different temperature dependence of the Balmer and Paschen line emissivities.

Open with DEXTER

The H$\beta$ brightness profiles displayed in the top panel of Fig. 9 are reflecting the underlying nebular structures as illustrated in Fig. A.2: development of a very bright and (geometrically) thick rim due to the action of the powerful stellar wind while the central star crosses the HR diagram within about 700 years, surrounded by a much fainter shell. The morphology resembles indeed that of the double-shell objects discussed earlier, with the difference that the outer edge of the shell appears to be sharp due to the D-type ionization front typically for optical thick conditions (t=304 and 450 yr).

As the stellar temperature exceeds 100 000 K, the number of hydrogen-ionizing photons decreases to such an extent that recombination begins to dominate, leading to a smoothing of the ionization front (t=584 yr). Recombination increases further in the shell as the central star approaches and passes its maximum effective temperature, and the emission from the shell disappears quickly (t>584 yr).

We selected the model with t=584 yr and compared in the bottom panel of Fig. 9 its (scaled) H$\beta$ surface-brightness profile with a cut along the semi-major axis of the HST P$\alpha$ image of NGC 2027 from the observations of Latter et al. (2000). The model matches astonishingly well the relative sizes and brightnesses of rim and shell. The rather smooth outer edge of NGC 2027's brightness profile indicates that recombination has already started there, just as in the model. We note further that the model's electron densities and temperatures are $\approx$10⁵ cm^-3 and 16 000 K in the rim, and $\approx$10⁴ cm^-3 and 13 000 K in the shell, values that are consistent with those reported in the literature, viz. $7\times10^4$ cm^-3 (Basart & Daub 1987) and 14 000 K (Masson 1989). The total mass of the ionized region is 0.015 $M_{\odot }$.

With 155 000 K, the central star of our selected model is cooler than usually inferred for NGC 7027 from recent observational analyses which suggest effective temperatures of 200 000 K or more (see Latter et al. 2000; Volk & Kwok 1997). However, the exact position along an evolutionary track where recombination starts depends on the local density and stellar luminosity, and may thus differ considerably from object to object. There appears also some hydrogen-line emission beyond the edge of the shell (at $r \ga 7\hbox{$^{\prime\prime}$ }$) not accounted for by our models. Obviously the real object is not as homogeneous as our (spherical) model, and we suggest some leakage of ionizing photons to be responsible for this weak emission.

In any case, our hydrodynamical model provides an overall better fit to the observed Paschen brightness profile than the rather sophisticated kinematic model of Latter et al. (2000, Fig. 4 therein) which does not account for the shell emission (ibid. Fig. 7). We can not provide a comparison with the H₂ molecular emission which occurs just at the outskirts of the recombining shell where the excitation conditions appear to be most favorable (Hasegawa et al. 2000). The reason is that our radiation-hydrodynamics code does not include formation and destruction of molecules.

Table 2: Expansion time scales from proper-motion measurements. The data are either from Palen et al. (2002), optical measurements, or from the compilation of Terzian (1997), radio measurements. The angular radii, $\theta _{\rm rim}$, and their expansion rate, $\dot{\theta}_{\rm rim}$, refer to the semi-minor axes. The effective temperatures are spectroscopic values (Méndez 1992) or He  II Zanstra temperatures (Gorny, priv. comm.)

   
3.2 Expansion time scales

Another test for the reliability of our models follows directly from the proper-motion measurements of the rim itself. We collected in Table 2 only good angular expansion measurements based on recent optical observations using HST (Palen et al. 2002) and radio observations, compiled by Terzian (1997). Note that the angular radii listed in Table 4 of Terzian (1997) are based on rather old measurements of unknown sources and quality. We thus redetermined these radii as carefully as possible from the HST images at our disposal. The angular size was determined at the rim's outer edge in order to locate the position of the shock front as closely as possible. We included in Table 2 only objects which are known to have a double-shell structure. We used again the effective temperatures of the central stars as a distance-independent proxy for the evolutionary state or age, and compare in Fig. 10 the observed expansion time scales with the predictions of model PNe with different central stars.

Although the studied sample is too small as to allow definitive conclusions, it appears from Fig. 10 that, within the errors, and again with the assumption that all objects from the plotted sample (with the exception of NGC 7027) have very similar evolutionary histories, the time scale of the rim's expansion does not depend on the effective temperature, i.e. the time scale remains virtually constant with evolution, at least in the temperature range between 60 000 and 100 000 K. With other words, size and proper motion of the rim does not appear to be a good age indicator either, a fact stated already in Sect. 2.3.2. Based on the rim expansion properties found from our model simulation (Fig. 4, right bottom), the true ages are substantially larger than the observed expansion times listed in Table 2.

The observations are, qualitatively, supported by our model simulations. From Fig. 10 it is evident that indeed the kinematical time scale of the rim increases only slowly with effective temperature and falls significantly behind the true age for all sequences shown in the figure. The reason is, of course, the steady acceleration of the rim with time (see Fig. 4, right top).

Figure 10: Kinematic expansion time scales, $t_{\rm kin} = R_{\rm rim}/\dot{R}_{\rm rim}$, as defined by the motion of the rim shocks of evolving model PNe, against the effective temperatures of their central stars. The sequence with the the 0.595 $M_{\odot }$ model used throughout this paper is supplemented by sequences with other central stars taken from Paper I (Table 1 therein): 0.605 $M_{\odot }$ (No. 6), 0.625 $M_{\odot }$ (No. 8), and 0.696 $M_{\odot }$ (No. 10). Dotted portions belong to the cooling part of the stellar tracks. Selected post-AGB ages (in 103 yr) are indicated along the curves by small circles. The observational data points, $\theta_{\rm rim}/\dot{\theta}_{\rm rim}$, are those listed in Table 2.

Open with DEXTER

However, assuming that all the objects plotted in Fig. 10, (except NGC 7027), have typical masses of about 0.6 $M_{\odot }$, it is also evident that the two low-mass sequences have kinematical ages which are definitively too large. It is easy to remedy this discrepancy: reducing the transition time needed for the models to evolve from the vicinity of the AGB to, say, 30 000 K, by about 1000 years, leaving the further evolution unaltered, would shift the sequences downwards to such an extent that a reasonable agreement with the observations could be achieved. Thus it appears that, as a byproduct of the proper-motion measurements, one can pose limits on the duration of the transition from the AGB to the PN regime.

Two of the objects from Table 2 deserve additional comments: NGC 3242 and NGC 7027, both of which have very small kinematical ages. The angular expansion of NGC 3242 is the largest of all objects listed in Table 2, and its expansion time of 700 yr implies a relatively large central-star mass of >0.65 $M_{\odot }$, similar to what is assumed for NGC 7027. This is in sharp contrast to our finding in Sect. 3.1 where NGC 3242 appears as an ordinary double shell PN of intermediate age, representing simply a more evolved stage of, e.g., IC 2448 or NGC 6826. All these 3 objects have electron densities of about $3\times 10^3$ cm^-3 which correspond perfectly with the densities of the hydrodynamical models illustrated in Fig. 3. A real young object like NGC 7027 has much larger electron densities exceeding 10⁴ cm^-3, and is most likely still optically thick. In view of these evidences for a substantially larger age of NGC 3242 we consider the proper motion measurements of Hajian et et al. (1995) as problematic, and new measurements, preferably with the HST, are urgently needed.

NGC 7027 is the object with the hottest central star for which angular expansion measurements exist. Its low age, combined with its very hot central star, is consistent with the theoretical expectation for more massive, rapidly evolving post-AGB stars. Since the expansion time is the upper limit of the transition time needed for post-AGB stars to reach the PN regime, this transition must have been very short for NGC 7027, and most likely also for other PNe with massive central stars as well. For the 0.696 $M_{\odot }$ sequence shown in Fig. 10 this transition time amounts to about 100 yr (cf. Fig. A.1).

   
4 The expansion parallaxes

Although a direct quantitative agreement of the predictions of our new hydrodynamics simulations with the observations could not be achieved, the models are close enough to the observations as to allow a detailed assessment of the expansion parallax method and the determination of correction factors. We begin with a detailed discussion for the objects shown in Fig. 7 and continue then more generally with other objects. Please note that in any case the correction factors for the distances deduced from our models are always larger than unity! This is a consequence of the jump conditions for shocks, as emphasized by Mellema (2004). Additional corrections may be necessary if departures from sphericity exist (cf. Palen et al. 2002), which, however, are not addressed here.

Figure 11: Detailed illustration of the different possible correction factors $F = \dot{R}/V$ already presented in the middle panels of Fig. 4 and explained in the legend, but now plotted over effective temperature. The corresponding post-AGB ages are given for comparison, too. The thick vertical mark indicates the moment when the ionization front passes the shock, i.e. of the thick/thin transition. The [N  II] and [O  III] lines give quite different results only below 50 000 K, i.e. during the optically-thick stage of evolution.

Open with DEXTER

In Fig. 11 the various combinations of shock and matter speeds based on our 0.595 $M_{\odot }$ model sequence are collected and their variations during the course of evolution plotted. The effective temperature of the central star is used again as an indicator for the evolutionary stage in order to facilitate the comparison with real objects. We repeat here that the ratio $F = \dot{R}/V$ is the factor by which the distance to an object in question has to be enlarged to correct for the assumption that shock and matter speed are equal.

Figure 11 illustrates in more detail what is already seen in the middle panels of Fig. 4. We have already noted in Sect. 2.3 that shell and rim have different expansion properties and hence different correction factors F. That of the rim is generally larger and begins with about 3 when the rim is forming during the optically-thick stage. It decreases later until it approaches the value of F for the shell. After the passage of the He  II ionization, both factors vary only slowly between 1.4 and 1.3. The correction factor for the shell remains always rather modest: It remains close to unity during the optically-thick stage, and does not exceed 1.4 later on. Mellema (2004) proposed a smaller correction factor, $F\approx 1.2$, since he used the post-shock velocity ( $V_{\rm post}$ in Fig.  4) which is always larger than the spectroscopic velocity used here.

From this discussion we conclude that proper motion measurements of the shell are more promising since the necessary correction is small and virtually independent of the evolutionary state of the object in question for a rather long period of evolution. Further advantages are that the shell's asphericity is usually small and that it expands faster than the rim. A disadvantage is that the shells are much fainter than the rims. Hence most existing proper motion measurements relied on the bright rims, making a thorough check of the object's evolutionary state necessary.

As a first guess, the evolutionary state of an object can be determined from the effective temperature of its central star, and the corresponding value of F can then be read of from Fig. 11. More relevant, however, is the dynamical state of the nebular envelope, which depends mainly on the initial envelope configuration, viz. AGB-wind velocity and radial density distribution. We therefore preferred to use the models shown in Fig. 7 with their larger central-star temperatures to estimate the correction factors F for the PNe shown there.

The errors of the F determinations based on our still simple spherical models are difficult to quantify. We implicitly assume in the following, if not otherwise stated, that our 0.595 $M_{\odot }$ central-star model sequence describes real objects sufficiently well. Considering then the rather smooth variation of F with temperature during the optically thin stage, we estimate uncertainties between 10 and 20%. Because they are smaller than the present errors of the angular expansion determinations, we will neglect them in the following considerations.

We can also not quantify the error caused by assuming ballistic expansion to estimate $V_{\rm eq}$ for elliptical rims. The accelerated expansion begins at a certain distance from the star and will lead to a $V_{\rm p}/V_{\rm eq}$ not consistent with the assumption of ballistic expansion (Sect. 2.3.3). Although 2D simulations are necessary to quantify the error, we estimate from the expansion properties of our models that $V_{\rm eq}$ will most likely be somewhat underestimated.

In the following detailed discussion of individual objects ballistic expansion is always assumed for deriving equatorial expansion velocities.

NGC 6826

This is obviously the least evolved object from Table 1 with a relatively cool central star. The structure of the nebular envelope in terms of surface-brightness profile and expansion velocities is well described by a model which just became optically thin (cf. Figs. 7 and 8). With the model's central-star temperature of $T_{\rm eff}\simeq 67~000$ K one derives from Fig. 11 the rather large correction factor of 1.8 for the rim. Unfortunately reliable angular expansion measurements are not yet available.

IC 2448

This is a middle-aged PN for which the angular expansion of the rim has recently been measured by Palen et al. (2002). Taking ellipsoidal corrections into account, these authors find a distance of $1.4\pm 0.4$ kpc. Our correction factor is F=1.5, giving a new distance to IC 2448 of $2.1\pm 0.6$ kpc which is, within the errors, nearly consistent with the spectroscopic distance of 3.5 kpc (Méndez et al. 1992) and ensures that the luminosity of the central star is well above 10³ $L_{\odot }$. Mellema 2004 gives the same correction, i.e. $F=1.5\pm0.1$.

NGC 3242

Hajian et al. (1995) measured the angular expansion for the rim of NGC 3242 and derived a distance of $0.42\pm 0.16$ kpc. They used an expansion velocity of 26 km s^-1  but our high-resolution Echelle data presented in Paper II and in Table 1 give $V_{\rm rim} = 19.5$ km s^-1, leading to an even smaller distance of only 0.32 kpc.

The central star is hotter than those of the two objects discussed above. Helium is doubly ionized in the rim, but not in the shell (Balick et al. 1987), and possible values for F are between 1.6 and 1.9, larger than Mellema's estimate, $F=1.3\pm0.2$. Our selected model with its He  II profile shown in Fig. 7, in conjunction with Fig. 11, suggests F=1.7. In any case, the distance to NGC 3242 would then be between 0.5 and 0.6 kpc, a still rather small distance, considering that the luminosity of the central star would be just marginally about 10³ $L_{\odot }$.

The spectroscopic distance to NGC 3242 has recently been revised downwards to 1.1 kpc by Pauldrach, Hoffmann, & Méndez (2004). But even this new spectroscopic distance is well above our corrected expansion distance. A significantly smaller angular proper motion would bring the expansion distance into better agreement with other distance determinations and would also increase the expansion age to values found for similar objects.

NGC 7662

The central star is also hot enough to have all the helium in the rim fully ionized. Also a large part of the shell is visible in He  II (Guerrero et al. 2004, Fig. 3 therein). A reasonable value to correct the expansion parallax would then be F=1.4, in fair agreement with Mellema's (2004) estimate, $F=1.5\pm0.3$. We refrain from recommending a new distance since the error of the angular expansion rate is of the same size as the measurement itself.

NGC 7027

We have shown that a nebular model with a massive and fast evolving very hot central star is able to reproduce qualitatively the morphology of a PN like NGC 7027. Although this model is optically thick, it shows nevertheless a double-shell structure with a rim that dominates the emission. Consequently, all the measured angular expansion rates refer to this rim.

We analyzed the expansion behaviour of the shock fronts of the nebular envelope around the 0.696 $M_{\odot }$ post-AGB model (see Appendix) in the same way as we did for the 0.595 $M_{\odot }$ sequence, and the corresponding correction factors are plotted in Fig. 12 for both the rim and the shell. Because the model remains always highly ionization stratified, we can use for the shell only [N  II] and for the rim only [O  III]. Note that the overall behaviour of F is very similar to that of the models with the less massive central-star shown in Fig. 11. During the high-temperature phase of evolution the rim's correction factor varies only slowly from 1.5 to 1.3. Mellema (2004) proposes a larger correction factor of $1.75\pm0.15$, which, according to our models, is not consistent with the high temperature of the central star (cf. Fig. 12).

	Figure 12: Same as in Fig. 11, but now for hydrodynamical models with a central star of 0.696 $M_{\odot }$ (sequence No. 10 of Paper I). In this particular case, [N  II] traces only the shell, and [O  III] only the rim (see also detailed discussion in the Appendix).
Open with DEXTER

An equatorial expansion velocity of 13 km s^-1, based on [O  III] 4959 Å, has been measured recently by Bains et al. (2003). Together with the angular expansion listed in Table 2 and a correction factor of 1.4 as read of from Fig. 12 a new distance to NGC 7027 of $580 \times 1.4 = 800$ pc follows, with an error of $\pm130$ pc.

4.1 Other objects

For the objects of Table 2 not discussed above in detail we can simply estimate the correction factors from the effective temperatures of their central stars. Using Fig. 11 $F \simeq 1.6\dots 1.8$ follows. Other objects not listed in the table are NGC 6543 and BD  $+30\hbox{$^\circ$ }~3639$ which are discussed in more detail in the following.

NGC 6543

The "cat's eye'', or NGC 6543, has a structure that is too complicated as to allow detailed comparisons with simple 1D radiation-hydrodynamics models used in this study. However, Balick & Hajian (2004) showed that the nebular "core'' (rim in our notation) expands quite uniformly with a time scale of 1 300 yr, a value which is consistent with the range typical for the objects listed in Table 2.

BD +30$^\circ$3639

This object is the only PN discussed here with a [WC] central star. Morphologically it is a single-shell, optically thick PN whose central star has an effective temperature of 47 000 K according to Leuenhagen et al. (1996). Li et al. (2002) measured the angular expansion and arrived at a mean kinematical age of 800 yr, at the outer edge of only 580 yr. Together with the spectroscopic radial expansion of 36 km s^-1, and considering the ellipsoidal shape of the nebular shell, these authors arrive at a distance of 1.2 kpc.

Because of the different spectral type of its central star, it does not appear to be wise to apply the results of our hydrodynamical simulation directly to BD +30$^\circ$3639 . The evolutionary properties and also the wind power of its central star are certainly too different. The nebular shell has, however, a single-shell morphology and is still optically thick with a corresponding ionization stratification, i.e. low-ionization stages are expected to be located close to the ionization front, higher ones closer to the star (Harrington et al. 1997; Bryce & Mellema 1999).

In this respect, the measurements of Bryce & Mellema (1999) are interesting. They found expansion velocities along the central line of sight of 28 km s^-1 from [N  II] profiles and 35.5 km s^-1 from [O  III] profiles. From our optically-thick models (top panels of Fig. 3) we would expect the larger velocity from [N  II]. Thus the measurements of Bryce & Mellema (1999) hint to a very powerful wind from the [WC] central star which has already compressed and considerably accelerated the innermost parts of the ionized shell.

For a distance estimate we proceed as follows. Because of the ionization stratification, the outer regions of the shell are better probed by ions of lower ionization. We used the Doppler split of the [N  II] lines, 28 km s^-1, and combined this spectroscopic radial expansion with the angular expansion of 4.25 mas yr^-1 measured by Li et al. (2002), yielding a distance of 1.4 kpc.

The factor necessary to correct for the improper use of a spectroscopic velocity can be read of from Fig. 11, viz. $F\simeq 1.3$ for the shell at $T_{\rm eff}= 47~000$ K, consistent with Mellema (2004) who gives $F=1.2\pm0.2$. We have thereby implicitly assumed that the D-type ionization front of BD +30$^\circ$3639 behaves in a similar fashion as our models predict . The distance would then be 1.8 kpc. If we correct for the axial ratio of 1.5 as Li et al. (2002) recommend, the final distance to BD +30$^\circ$3639 is then back to the Li et al. value of 1.2 kpc. The error is difficult to quantify, but we estimate it close to 20 %, i.e. $\pm 0.2$ kpc.

   
5 Summary and discussion

We presented a comprehensive interpretation of the expansion properties of planetary nebulae, based on radiation-hydrodynamics simulations from the birth of the nebula in the vicinity of the tip of the AGB down to the realm of white dwarfs. Although we employed spherical models, the agreement between computed and observed quantities turned out to be very good, making us confident about the predictive power of these models.

We found that an evolving central star model of 0.6 $M_{\odot }$, coupled to a AGB wind envelope which accounts fully for the final mass-loss history on the AGB and which consequently has a radial density profile much steeper than the usually assumed r^-2 law, appears to be an acceptable choice for interpreting the properties of typical double shell PNe if the full radiation-hydrodynamics is considered. Mellema (1994) has also pointed out that his model sequence with a r^-3 initial density distribution gives a better agreement with the observations than the sequences based on $\rho\propto r^{-2}$. A more massive central-star model of, say 0.7 $M_{\odot }$, which evolves very quickly across the HR diagram, is necessary to explain the structure of objects like NGC 7027.

Further conclusions drawn from this work and other detailed radiation-hydrodynamics parameter studies (e.g. Mellema 1994; Paper I; Paper II) concerning the internal kinematics of PNe are as follows:

• The two principal constituents of a "standard'' planetary nebula, the rim and the shell, expand independently of each other. The shell is driven by thermal pressure, and its velocity reflects the density gradient of the ambient matter and the sound speed. The rim is driven into the shell by the power of the central-star wind. Both the rim and the shell are bounded by shock fronts, and one has to distinguish carefully between pattern and matter velocities.

• We emphasized here that PNe do not expand ballistically as is usually assumed for deriving spatio-kinematical models from detailed spectroscopic observations. Instead, their expansion is generally accelerated, starting at some distance from the position of the central star. Analytical expressions based on the properties of wind-driven bubbles are not valid because (i) the wind parameters change considerably with time, and (ii) the density distribution of the confining gas is modified as the the outer shock ploughs through the AGB-wind material.

• The determination of kinematical ages is not as straightforward as usually believed since (i) the expansion is accelerated, and (ii) $V\not= \dot{R}$ (see also Marten et al. 1993; Mellema 1994). Furthermore, one has to consider carefully the underlying structure of the object in question, i.e. in the case of double shell PNe only outer radius and spectroscopic velocity of the shell appear to give acceptable results (cf. Schönberner et al. 1997). We note, however, that the velocity of the shell is difficult to measure spectroscopically and thus is not available in many cases.

• Because of the difference between pattern and matter velocity it is principally not possible to derive distances by simply combining measured angular expansion rates with spectroscopic expansion velocities. It is, however, possible to correct these so-called expansion parallaxes by means of hydrodynamical models. The correction to be applied depends on the evolutionary stage of the object in question and is at least a factor of 1.3. For the young rim the correction may even exceed a factor of 2.

  From the theoretical side, the situation appears to be better for the shell where the correction factor does not exceed 1.4. The shell's edge is, however, difficult to observe properly because of its often rather low contrast to the halo emission.

  We note that the correction factors estimated by Mellema (2004) using the jump conditions of shocks and reasonable assumptions for the flow velocities are, with exceptions, in good agreement with our more elaborate determinations based on radiation-hydrodynamics simulations.

• A further important result of the present work is that, according to hydrodynamical model sequences with different stellar masses, the existing proper-motion measurements of nebular rims hint to faster transitions from the tip of the AGB towards the PN regime than has been presumed for our models.

Despite the obvious success of our hydrodynamical models we have to admit that our corrected distances based on the best proper motion measurements are still not always satisfactory. As a matter of fact, the distances to the well-known objects IC 2448 and NGC 3242 are just at the limit what one would accept for a post-AGB object, and they are (in the case of NGC 3242) well below the spectroscopically derived distances. We can not offer an explanation for this annoying discrepancy. Any adjustment of the models that can be thought of can certainly not produce an additional correction factor of at least 1.5 that is necessary to reconcile the expansion distance to NGC 3242 with what is demanded by the post-AGB theory.

We believe that further proper motion studies with a longer time base are needed before any definite conclusion on this matter can be drawn. Equally important is the fact that different epoch observations must be taken with exactly the same instrument and filter setting in order to avoid possible systematic errors.

References

• Bains, I., Bryce, M., Mellema, G., Redman, M. P., & Thomasson, P. 2003, MNRAS, 340, 381 [NASA ADS] [CrossRef] (In the text)
• Balick, B., & Hajian, A. 2004, AJ, 127, 2269 [NASA ADS] [CrossRef] (In the text)
• Balick, B., Preston, H. L., & Icke, V. 1987, AJ, 94, 1641 [NASA ADS] [CrossRef] (In the text)
• Basart, J. P., & Daub, C. T. 1987, ApJ, 317, 412 [NASA ADS] [CrossRef] (In the text)
• Blöcker, T. 1995a, A&A, 297, 727 [NASA ADS] (In the text)
• Blöcker, T. 1995b, A&A, 299, 755 [NASA ADS] (In the text)
• Bryce, M., & Mellema, G. 1999, MNRAS, 309, 731 [NASA ADS] [CrossRef] (In the text)
• Chu, Y.-H., Jacoby, G. H., & Arendt, R. 1987, ApJS, 64, 529 [NASA ADS] [CrossRef] (In the text)
• Gesicki, K., Acker, A., & Szczerba, R. 1996, A&A, 309, 907 [NASA ADS] (In the text)
• Guerrero, M. A., Manchado, A., Stanghellini, L., & Herrero, A. 1996, ApJ, 464, 847 [NASA ADS] [CrossRef] (In the text)
• Guerrero, M. A., Jaxon, E. J., & Chu, Y.-H. 2004, AJ, 128, 1705 [NASA ADS] [CrossRef] (In the text)
• Hajian, A. R., & Terzian, Y. 1996, PASP, 108, 419 [NASA ADS] [CrossRef]
• Hajian, A. R., Terzian, Y., & Bignell, C. 1993, AJ, 106, 1965 [NASA ADS] [CrossRef]
• Hajian, A. R., Terzian, Y., & Bignell, C. 1995, AJ, 109, 2600 [NASA ADS] [CrossRef] (In the text)
• Harrington, J. P., Lame, N. J., White, S. M., & Borkowski, K. J. 1997, AJ, 113, 2147 [NASA ADS] [CrossRef] (In the text)
• Hasegawa, T., & Kwok, S. 2001, ApJ, 562, 824 [NASA ADS] [CrossRef] (In the text)
• Hasegawa, T., Volk, K., & Kwok, S. 2000, ApJ, 532, 994 [NASA ADS] [CrossRef] (In the text)
• Jaminet, P. A., Danchi, W. C., Sutton, E. C., et al. 1991, ApJ, 380, 461 [NASA ADS] [CrossRef] (In the text)
• Koo, B.-C., & McKee, C. F. 1992, ApJ, 388, 103 [NASA ADS] [CrossRef] (In the text)
• Latter, W. B., Dayal, A., Bieging, J. H., et al. 2000, ApJ, 539, 783 [NASA ADS] [CrossRef] (In the text)
• Li, J., Harrington, J. P., & Borkowski, K. 2002, AJ, 123, 2676 [NASA ADS] [CrossRef] (In the text)
• Leuenhagen,U., Hamann, W.-R., & Jeffrey, C. S. 1996, A&A, 312, 167 [NASA ADS] (In the text)
• Marten, H., Gesicki, K., & Szczerba, R. 1993, in Planetary Nebulae, ed. R. Weinberger, & A. Acker (Kluwer Acad. Publ.), IAU Symp., 155, 315 (In the text)
• Masson, C. R. 1989, ApJ, 336, 294 [NASA ADS] [CrossRef] (In the text)
• McCarthy, J. K., Mould, J. R., Méndez, R. H., et al. 1990, ApJ, 351, 230 [NASA ADS] [CrossRef] (In the text)
• Mellema, G. 1994, A&A, 290, 915 [NASA ADS] (In the text)
• Mellema, G. 2004, A&A, 416, 623 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Méndez, R. H., Kudritzki, R. P., & Herrero, A. 1992, A&A, 260, 329 [NASA ADS] (In the text)
• Palen, S., Balick, B., Hajian, A. R., et al. 2002, AJ, 123, 2666 [NASA ADS] [CrossRef] (In the text)
• Pauldrach, A., Puls, J., Kudritzki, R. P., Méndez, R. H., & Heap, S. H. 1988, A&A, 207, 123 [NASA ADS] (In the text)
• Pauldrach, A. W. A., Hoffmann, T. L., & Méndez, R. H. 2004, A&A, 419, 1111 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Perinotto, M., Kifonidis, K., Schönberner, D., & Marten, H. 1998, A&A, 332, 1044 [NASA ADS] (In the text)
• Perinotto, M., Schönberner, D., Steffen, M., & Calonaci, C. 2004, A&A, 414, 993 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I) (In the text)
• Reimers, D. 1975, in Problems in Stellar Atmospheres and Envelopes, ed. B. Baschek, W. H. Kegel, & G. Traving (Berlin: Springer), 229 (In the text)
• Schönberner, D. 1983, ApJ, 273, 708 [NASA ADS] [CrossRef] (In the text)
• Schönberner, D., Steffen, M., Stahlberg, J., Kifonides, K., & Blöcker, T. 1997, in Advances of Stellar Evolution, ed. R. T. Rood, & A. Renzini (Cambridge Univ. Press), 146 (In the text)
• Schönberner, D., Steffen, M., & Jacob, R. 2004, in Asymmetric Planetary Nebulae III, ed. M. Meixner, J. Kastner, B. Balick, & N. Soker, ASP Con. Ser., 313, 283 (In the text)
• Schönberner, D., Jacob, R., Steffen, M., et al. 2005, A&A, 431, 963 [EDP Sciences] [NASA ADS] [CrossRef] (Paper II) (In the text)
• Steffen, M., Schönberner, D., Kifonidis, K., & Stahlberg, J. 1997, in Planetary Nebulae, ed. H. J. Habing, & H. J. G. L. M. Lamers, Kluwer Acad. Publ., IAU Symp., 180, 368 (In the text)
• Steffen, M., Szczerba, R., & Schönberner, D. 1998, A&A, 337, 149 [NASA ADS] (In the text)
• Terzian, Y. 1997, in Planetary Nebulae, ed. H. J. Habing, & H. J. G. L. M. Lamers (Kluwer Acad. Publ.), IAU Symp., 180, 29 (In the text)
• Volk, K., & Kwok, S. 1997, A&A, 477, 722 [NASA ADS] (In the text)

 

  
Online Material

Appendix A: Hydrodynamical PNe sequence with a 0.696 M$_{\odot }$ central-star

Figure A.1: Same as in Fig. 1 but for a 0.696 $M_{\odot }$ hydrogen-burning post-AGB model from Blöcker (1995b). Note that in this diagram the ages are given in 100 yr instead of 1000 yr!

In this appendix we present the details of a radiation-hydrodynamics simulation of a planetary nebula with a star of 0.696 $M_{\odot }$ used in this article to interprete the angular expansion of NGC 7027. The gross properties of this model have already been explained in Paper I (cf. sequence no. 10 from Table 1 therein). The initial nebular model is of T YPE A, which means constant mass-loss rate and wind speed during the end of the AGB evolution. Specifically, we have selected for this sequence $\dot{M}_{\rm agb} = 10^{-4}$ $M_{\odot }$ yr^-1 and $V_{\rm agb} = 15$ km s^-1.

A.1 General properties

The stellar properties relevant for the hydrodynamical simulation are shown in Fig. A.1. They are very similar to those of the 0.595 $M_{\odot }$ model in Fig. 1, but the time scale is reduced by about a factor of ten: in only 700 years the 0.696 $M_{\odot }$ model reaches the turn-around point to the white-dwarf cooling path. For such a short period of time the assumption of a constant AGB mass-loss rate appears to be a reasonable assumption. For illustrating the variations of observable quantities we selected again 4 positions along the horizontal part of the stellar track, computed observable quantities like surface-brightnesses and emission-line profiles and displayed them in Fig. A.2.

Figure A.2: Same as in Fig. 3 but for a 0.696 $M_{\odot }$ hydrogen-burning post-AGB model from Blöcker (1995b) whose evolutionary properties are illustrated in Fig. A.1. The snapshots are arranged with increasing post-AGB ages, and the corresponding stellar parameters are as follows (from top to bottom): $t=304~{\rm yr},\ T_{\rm eff}= 71~292~{\rm K},\ L = 11~384~\mbox{$L_{\odot}$ }$; $t=450~\mbox{yr},\ T_{\rm eff}= 110~618~\mbox{K},\ L= 10~857~\mbox{$L_{\odot}$ }$; $t=584~\mbox{yr},\ T_{\rm eff}= 155~504~\mbox{K},\ L= 9~875~\mbox{$L_{\odot}$ }$; $t=752~\mbox{yr},\ T_{\rm eff}= 220~105~\mbox{K},\ L= 7~238~\mbox{$L_{\odot}$ }$. Note the different radial extents of the structure and surface-brightness plots.

During the early ionization phase (top panel) the model develops a structure similar to the one seen for less massive stars, except that its size is ten times smaller and its density about hundred times larger than for a less massive and more slowly evolving post-AGB star (cf. Fig. 3). However, because of the very rapid evolution of the central star, the circumstellar matter remains so dense during the high-luminosity part of the star's evolution that the ionization front is always bounded by neutral (or molecular) material (D-type ionization front). The shock is nearly isothermal and compresses the AGB matter into a very thin, dense shell.

Nevertheless, a double-shell structure develops, with a rather dense and thick rim consisting of wind-compressed and accelerated shell material (middle panels). Contrary to the optically-thin models of Fig. 3, an important property of the models with a massive central star is their extreme ionization stratification, with species of low ionization close to the ionization front and those with high ionization in the rim close to the hot star. This stratification is evident from the surface-brightness profiles shown in Fig. A.2: in the light of [O  III] both rim and shell are visible, but not in [N  II]. The N  II zone behind the ionization front is so narrow that the model appears as a ring structure with an extreme center-to-limb brightness variation (top panels). This stratification is responsible for the different expansion velocities measured by the Doppler splits of the [O  III] and [N  II] profiles.

Later on the ionization front cannot advance further (in mass), and recombination weakens its steepness (panels next to bottom). Consequently, the shell fades in the light of [O  III] (and hydrogen as well), while the N  II zone extends somewhat inwards, leading to a less extreme ring structure.

With the continuing luminosity drop of the central star, recombination dominates until only the rim remains fully ionized and the shell is not visible anymore (bottom panels). The outer leading shock, at $r=0.7\times10^{17}$ cm, which is decelerating because of the decreasing post-shock electron temperature, is nevertheless still travelling with a relatively high speed of about 25 km s^-1 (stellar frame). It is isothermal and compresses and accelerates the neutral/molecular AGB matter considerably: the density inside the geometrically thin shell is with a few 10⁵ cm^-3 substantially larger than the density of the ionized region, and the gas velocity is increased from 15 to about 25 km s^-1 across the shock. The rim travels much faster and is approaching the outer shock.

During the approach of the central star to its maximum effective temperature, the whole circumstellar structure is changing from the double-shell morphology into one which is very similar to the empirical model constructed by Volk & Kwok (1997) and Hasegawa et al. (2000) for NGC 7027: a very compact H  II region of high density and temperature, $n_{\rm H}\approx n_{\rm e} \simeq 1\times10^4$ cm^-3 and $T_{\rm e} > 12~000$ K, is surrounded by a high-density, geometrically very thin shell of neutral material compressed by the outer shock, and in which the (electron) temperature falls off rapidly over a distance of less than 10¹⁶ cm to the low values of the still undisturbed AGB wind. The total size of the ionized/neutral shells is a few hundredth of parsecs in diameter, well within the range estimated for NGC 7027.

The partially ionized and neutral shells embracing the PN proper are, as a photon-dominated region (PDR), a site of active circumstellar chemistry (cf. Latter et al. 2000; Hasegawa & Kwok 2001). The detailed study of the CO molecular lines by Jaminet et al. (1991) revealed that there exists, in addition to the main molecular flow of the AGB wind with 15 km s^-1, a region where the gas expands faster, i.e. with 23 km s^-1. Jaminet et al. argue that this faster expanding gas comes from a thin high-density shell which, as an interface between the AGB wind and the H  II region, is being compressed and accelerated by the thermal pressure of the ionized gas.

This interpretation is in accordance with our model, although it is, for the particular evolutionary stage of NGC 7027 considered here, the outer shock set up earlier during the ionization phase which compresses and accelerates the neutral/molecular AGB gas. The post-shock speed decreases with the shock speed: at the beginning of the recombination phase we found (in the stellar frame) $V_{\rm post} \simeq35$ km s^-1 which then later decreases to 25 km s^-1 (bottom panel of Fig. A.2).

Figure A.3: Same as in Fig. 4 but now for the sequence with the 0.696 $M_{\odot }$ central star illustrated in the two previous figures. The vertical lines indicate the ages of the models shown in Fig. A.2.

We should mention that the hydrodynamical models used here were not intended to describe properly the PDRs which obviously form in the circumstellar envelopes around fast evolving central stars since our code does not contains all the physical processes necessary to describe formation and destruction of molecules, including H₂. However, since the basic structure forming processes are photo-ionization and wind interaction we are confident about the usefulness of our models also for the dense envelopes around massive central stars.

A.2 Kinematics

The detailed expansion properties of the nebular model with the 0.696 $M_{\odot }$ central star are illustrated in Fig. A.3. The qualitative expansion behaviour is quite similar to that of the 0.595 $M_{\odot }$ sequence from Fig. 4, although the time scale is only one tenth.

There are, however, also differences, mainly caused by the fact that the nebular shell becomes never optically thin, i.e. the shell is always bounded by an D-type ionization front whose associated shock moves highly supersonically through the neutral AGB wind (left middle). This shock is accelerated during the early ionization phase ($t \la 250$ yr), proceeds with roughly constant speed for another 150 years until it decelerates when the ionization front weakens and detaches slowly from the shock because of the increasing recombination rate. Because of the slower shock speed the now neutral matter behind the shock becomes even more compressed into a (geometrically) thin shell (bottom panel of Fig. A.2).

Because of recombination the shell disappears completely as an ionized structure at about t=630 yr and is not plotted any further (cf. also Fig. A.2). Like in the 0.595 $M_{\odot }$ case of Fig. 4 the kinematic age can be estimated quite reliably from size and spectroscopic velocity of the shell (left bottom).

The evolution of the rim is illustrated in the right panels of Fig. A.3. Driven by the expanding contact surface, the weak rim shock is steadily accelerated (top) and "snowploughes'' the shell matter. Once the shell's temperature and pressure is reduced because of recombination, the shock speed and Mach number increases somewhat $(t \ga 650$ yr). After 750 years the outer edges of the rim start to recombine as well, and the shock position becomes difficult to determine. Like in the case with the low-mass central star, the correction factor between shock and matter speed can be large (middle), and also the determination of kinematic ages from the rim's size and expansion speed is problematic (bottom).

Figure A.4: Same as in Fig. 5 but now for the sequence with the 0.696 $M_{\odot }$ central star. The dotted curves represent again fits to $R_{\rm rim}$ and $R_{\rm cd}$ of the form R=R0+c (t-t0)b (the fit for $R_{\rm rim}$ is indistinguishable). The parameters for $R_{\rm rim}$ (for $t\le 400$ yr only, see text), are R0= 0.0021 pc, t0=153 yr, $c=1.05\times10^{-5}~{\rm pc}/{\rm yr}^b$, and b=1.13. For $R_{\rm cd}$ we have R0=0.0013 pc, t0=130 yr, $c=1.51\times10^{-6}~{\rm pc}/{\rm yr}^b$, and b=1.42.

As Fig. A.4 shows, the expansion laws are qualitatively the same as those for the low-mass sequence from Fig. 5. A fit to the rim has only be done for the first 400 years since the physical environment changes later substantially due to recombination.