A&A 441, 615-629 (2005)
DOI: 10.1051/0004-6361:20052988
A. Miglio - J. Montalbán
Institut d'Astrophysique et de Géophysique de l'Université de Liège, Allée du 6 Août 17, 4000 Liège, Belgium
Received 4 March 2005 / Accepted 1 June 2005
Abstract
We apply the Levenberg-Marquardt minimization algorithm to seismic and classical observables of the
![]() Cen binary system in order to derive the fundamental parameters of
Cen binary system in order to derive the fundamental parameters of ![]() CenA+B, and to analyze the
dependence of these parameters on the chosen observables,
on their uncertainty, and on the physics used in stellar modelling.
We show that while the fundamental stellar parameters do not depend on the treatment of convection adopted
(Mixing Length Theory - MLT - or "Full Spectrum of Turbulence'' - FST), the age of the system depends
on the inclusion of gravitational settling, and is
deeply biased by the small frequency separation of component B.
We try to answer the question of the universality of the mixing length parameter, and we find a
statistically reliable dependence of the
CenA+B, and to analyze the
dependence of these parameters on the chosen observables,
on their uncertainty, and on the physics used in stellar modelling.
We show that while the fundamental stellar parameters do not depend on the treatment of convection adopted
(Mixing Length Theory - MLT - or "Full Spectrum of Turbulence'' - FST), the age of the system depends
on the inclusion of gravitational settling, and is
deeply biased by the small frequency separation of component B.
We try to answer the question of the universality of the mixing length parameter, and we find a
statistically reliable dependence of the ![]() -parameter on the HR diagram location
(with a trend similar to the predictions based on 2-D simulations).
We propose the frequency separation ratios as better observables to determine the fundamental stellar parameters, and to use the large frequency
separation and
frequencies to extract information about the stellar structure. The effects of diffusion and equation of state
on the oscillation frequencies are also studied, but present seismic data do not allow their determination.
-parameter on the HR diagram location
(with a trend similar to the predictions based on 2-D simulations).
We propose the frequency separation ratios as better observables to determine the fundamental stellar parameters, and to use the large frequency
separation and
frequencies to extract information about the stellar structure. The effects of diffusion and equation of state
on the oscillation frequencies are also studied, but present seismic data do not allow their determination.
Key words: stars: oscillations - stars: interiors - stars: fundamental parameters - stars: individual:
![]() Cen
Cen
As a consequence, a great number of theoretical studies dealing with ![]() Cen has been published since
the one by Flannery & Ayres (1978) (see Eggenberger et al. 2004, for a comprehensive review).
Before the definitive identification of p-mode frequencies in the
Cen has been published since
the one by Flannery & Ayres (1978) (see Eggenberger et al. 2004, for a comprehensive review).
Before the definitive identification of p-mode frequencies in the ![]() Cen A power spectrum by
Bouchy & Carrier (2002), the uncertainty in the parallax (and therefore in the masses) and in the chemical
composition did not allow an unambiguous determination of stellar parameters. Some controversial results
came up concerning, for instance, the universality or not of the mixing-length parameter (
Cen A power spectrum by
Bouchy & Carrier (2002), the uncertainty in the parallax (and therefore in the masses) and in the chemical
composition did not allow an unambiguous determination of stellar parameters. Some controversial results
came up concerning, for instance, the universality or not of the mixing-length parameter (![]() )
describing the stellar convection (Edmonds et al. 1992; Guenther & Demarque 2000; Fernandes & Neuforge 1995; Morel et al. 2000; Noels et al. 1991; Neuforge 1993; Lydon et al. 1993);
the role of the chemical composition on discriminating between
these two possibilities (Fernandes & Neuforge 1995), and on the presence or not of a convective core,
and its effect on the age of the system (Guenther & Demarque 2000). Some efforts (Guenther & Demarque 2000; Brown et al. 1994; Morel et al. 2000)
were also devoted to study the capability of solar-like
oscillations expected in
)
describing the stellar convection (Edmonds et al. 1992; Guenther & Demarque 2000; Fernandes & Neuforge 1995; Morel et al. 2000; Noels et al. 1991; Neuforge 1993; Lydon et al. 1993);
the role of the chemical composition on discriminating between
these two possibilities (Fernandes & Neuforge 1995), and on the presence or not of a convective core,
and its effect on the age of the system (Guenther & Demarque 2000). Some efforts (Guenther & Demarque 2000; Brown et al. 1994; Morel et al. 2000)
were also devoted to study the capability of solar-like
oscillations expected in ![]() Cen (Kjeldsen & Bedding 1995) to constrain the fundamental stellar
parameters and the physics included in stellar models.
Cen (Kjeldsen & Bedding 1995) to constrain the fundamental stellar
parameters and the physics included in stellar models.
In addition to the p-mode identification by Bouchy & Carrier (2002), Pourbaix et al. (2002)
improved the precision of the orbital parameters and, adopting the parallax derived by
Söderhjelm (1999), provided very precise masses for ![]() Cen A and B.
These high quality data stimulated new calibrations of the system by Thévenin et al. (2002) and
Thoul et al. (2003). The two teams reached different results. While Thévenin et al. (2002) could not
fit the seismic data without changing the masses more than 4
Cen A and B.
These high quality data stimulated new calibrations of the system by Thévenin et al. (2002) and
Thoul et al. (2003). The two teams reached different results. While Thévenin et al. (2002) could not
fit the seismic data without changing the masses more than 4![]() with respect to Pourbaix's data,
the second group fitted the
with respect to Pourbaix's data,
the second group fitted the ![]() Cen A p-mode spectrum and the spectroscopic constraints
using a single value of mixing length parameter, and
with the new values for the masses.
Cen A p-mode spectrum and the spectroscopic constraints
using a single value of mixing length parameter, and
with the new values for the masses.
Interferometric measurements with VINCI/VLTI by Kervella et al. (2003) have provided high
precision values of the angular diameter of ![]() Cen A and B,
and new observations by Carrier & Bourban (2003) have allowed to identify p-mode frequencies
also in the B component. These new constraints have been used by Eggenberger et al. (2004).
Their calibration, based on a grid of models obtained by varying the
mixing-length parameters, the chemical composition, and the age, leads to a stellar model in good agreement with
the astrometric, photometric, spectroscopic and asteroseismic data, and they assert that "the global
parameters of the
Cen A and B,
and new observations by Carrier & Bourban (2003) have allowed to identify p-mode frequencies
also in the B component. These new constraints have been used by Eggenberger et al. (2004).
Their calibration, based on a grid of models obtained by varying the
mixing-length parameters, the chemical composition, and the age, leads to a stellar model in good agreement with
the astrometric, photometric, spectroscopic and asteroseismic data, and they assert that "the global
parameters of the ![]() Cen system are now firmly constrained to an age of
Cen system are now firmly constrained to an age of
![]() Gyr, an initial
helium mass fraction
Gyr, an initial
helium mass fraction
![]() and an initial metallicity
and an initial metallicity
![]() '' and that "the mixing length parameter
'' and that "the mixing length parameter ![]() of the B component is larger than the one of the A component''.
These results are quantitatively consistent with those obtained by Thoul et al. (2003), nevertheless,
both groups have performed the calibration assuming a given, but different, "physics''.
of the B component is larger than the one of the A component''.
These results are quantitatively consistent with those obtained by Thoul et al. (2003), nevertheless,
both groups have performed the calibration assuming a given, but different, "physics''.
The aim of this work is to study, following the theoretical analysis of the utility of seismology
to constrain fundamental parameters made by Brown et al. (1994), the dependence of the
set of parameters obtained by fitting the observables, on the details of the fitting procedure.
That is:
i) the kind of constraints included in the
![]() functional that drives the fitting procedure, as well as other effects of their uncertainties, and
ii) the physics included in the stellar evolution theory.
Only in this way we will be able to provide an estimation of the uncertainty in the obtained set of
stellar parameters, and to evaluate the degree at which the present data precision
can constrain the physics in stellar evolution models.
functional that drives the fitting procedure, as well as other effects of their uncertainties, and
ii) the physics included in the stellar evolution theory.
Only in this way we will be able to provide an estimation of the uncertainty in the obtained set of
stellar parameters, and to evaluate the degree at which the present data precision
can constrain the physics in stellar evolution models.
To do that, and also with the prospect of dealing with a great quantity of seismic data from spatial missions such as MOST (Matthews 1998) and COROT (Baglin & The COROT Team 1998) and from new generation spectrograph such as HARPS (Bouchy 2002), we have implemented a non-linear fitting algorithm that performs a simultaneous least-square adjustment of all the observable characteristics, the classical and the seismic features.
The fitting method is described in Sect. 2.
In Sect. 3 we
discuss the different sets of classical and seismic observables that will be included in our
![]() quality function.
The physics included in the stellar evolutionary code is summarized in Sect. 4.
The results of these different combinations of observables and
of different physics are presented and discussed in Sect. 5.
A special effort has been devoted to the problem of stellar convection (Sect. 5.2).
We will try to answer to the question about the universality of the mixing-length parameter, and to study
the effect of different convection treatments. With respect to
the convection modelling, a controversial result was obtained by Morel et al. (2000);
they reached different ages depending on whether they used the classical MLT theory (Böhm-Vitense 1958), or
the FST theory by Canuto & Mazzitelli (1991,1992).
Hence, we
performed different calibrations changing the convection treatment (FST or MLT), as well as
different MLT
calibrations either with a unique or different
quality function.
The physics included in the stellar evolutionary code is summarized in Sect. 4.
The results of these different combinations of observables and
of different physics are presented and discussed in Sect. 5.
A special effort has been devoted to the problem of stellar convection (Sect. 5.2).
We will try to answer to the question about the universality of the mixing-length parameter, and to study
the effect of different convection treatments. With respect to
the convection modelling, a controversial result was obtained by Morel et al. (2000);
they reached different ages depending on whether they used the classical MLT theory (Böhm-Vitense 1958), or
the FST theory by Canuto & Mazzitelli (1991,1992).
Hence, we
performed different calibrations changing the convection treatment (FST or MLT), as well as
different MLT
calibrations either with a unique or different ![]() values for each component.
The effects of using different equation of state, including gravitational settling or not, and adopting a
different solar mixture are discussed in
Sect. 5.3.
Finally, results and conclusions are summarized in Sect. 6.
values for each component.
The effects of using different equation of state, including gravitational settling or not, and adopting a
different solar mixture are discussed in
Sect. 5.3.
Finally, results and conclusions are summarized in Sect. 6.
Usually the approach to analyze stellar oscillation data is standard: i) several stellar models that bracket the known observational constraints (typically composition, mass, luminosity, and effective temperature) are computed; ii) p-mode oscillation frequencies are calculated for the models; and iii) the model oscillation spectra are compared with the observed one. We believe that a different approach is needed, so that asteroseismology is directly included in the calibration procedure and the results are not biased by a limited/subjective exploration of the parameter space or strongly depent on an initial guess of the model parameters.
The development and use of objective and efficient procedures to fit stellar models to observations has become of evident utility in particular since seismic constraints are included in the modelling (see e.g. Brown et al. 1994).
Guenther & Brown (2004) have proposed a method that quantifies at which degree
the oscillation spectra as obtained from a grid of models
parametrised in mass, age and composition reproduce the
observations. Models providing a minimum in the ![]() ,
defined
by the differences between the theoretical and observational
frequencies, are selected for an additional inspection in a finer
grid. As noted by Guenther & Brown (2004) the first problem in
this kind of approach is its computational cost. Moreover the direct fit of
the oscillation spectra implies a good
knowledge of the surface layers of the star, as that strongly affects
the exact frequency values. Guenther & Brown (2004) quantify
the uncertainty in the theoretical frequencies due to our poor
modelling of the external layers by using the discrepancies between observed and
theoretical solar frequencies. But, how good is this estimation
for stars with different superficial gravity, chemical composition
and age? On the other hand, Eggenberger et al. (2004) use the
aforementioned conventional approach, and only in a second and a
third phase take into account
the asteroseismic data, first the large and small frequency separations
(
,
defined
by the differences between the theoretical and observational
frequencies, are selected for an additional inspection in a finer
grid. As noted by Guenther & Brown (2004) the first problem in
this kind of approach is its computational cost. Moreover the direct fit of
the oscillation spectra implies a good
knowledge of the surface layers of the star, as that strongly affects
the exact frequency values. Guenther & Brown (2004) quantify
the uncertainty in the theoretical frequencies due to our poor
modelling of the external layers by using the discrepancies between observed and
theoretical solar frequencies. But, how good is this estimation
for stars with different superficial gravity, chemical composition
and age? On the other hand, Eggenberger et al. (2004) use the
aforementioned conventional approach, and only in a second and a
third phase take into account
the asteroseismic data, first the large and small frequency separations
(![]() ,
,
![]() ), and then the frequencies.
), and then the frequencies.
Here we propose a calibration method that finds the parameters of
the system by the minimization of a ![]() functional including
at the same time classical and asteroseismic observables. The
parameters of the models are, as usual, the mass, initial chemical
composition, age, parameter(s) of
convection
functional including
at the same time classical and asteroseismic observables. The
parameters of the models are, as usual, the mass, initial chemical
composition, age, parameter(s) of
convection ![]() .
The observables could be chosen among the masses,
.
The observables could be chosen among the masses,
![]() ,
L, R, [Fe/H],
,
L, R, [Fe/H],
![]() ,
,
![]() (or combinations of these frequency differences). Of
course,
(or combinations of these frequency differences). Of
course, ![]() Cen being a binary system, the same initial
chemical composition and age have to be assumed when calibrating
components A and B.
Cen being a binary system, the same initial
chemical composition and age have to be assumed when calibrating
components A and B.
We define a quality function measuring the distance between models and observations, that is, a
goodness-of-fit measurement by:
The choice of the observables included in the objective function is thoroughly described in Sect. 3.
In the general case of a binary system the model that generates
the observables and their derivatives has seven free parameters (or six
if
![]() ). The most substantial part of
the model consists of a stellar evolution code (CLES, see Sect.
4) which takes as inputs the masses of each
component (
). The most substantial part of
the model consists of a stellar evolution code (CLES, see Sect.
4) which takes as inputs the masses of each
component (![]() ,
,
![]() ), the initial chemical
composition of the system (Y, Z), the age and the convection
mixing-length parameters (
), the initial chemical
composition of the system (Y, Z), the age and the convection
mixing-length parameters (
![]() ), that
in general are assumed to be different for the two stars.
), that
in general are assumed to be different for the two stars.
We compute oscillation frequencies for the models by solving the
equations of adiabatic oscillations (OSC), and determine
![]() and
and
![]() for the degrees
for the degrees
![]() .
This is not done by
a least square fit to the computed frequencies, based on
the asymptotic properties of low degree modes, but by making the
average of the theoretical separations in the domain of observed
radial order n (n=15-25, for
.
This is not done by
a least square fit to the computed frequencies, based on
the asymptotic properties of low degree modes, but by making the
average of the theoretical separations in the domain of observed
radial order n (n=15-25, for ![]() Cen A, and n=17-27 for
Cen A, and n=17-27 for
![]() Cen B). The observed average separations have been
determined from observed frequencies in the same way.
Cen B). The observed average separations have been
determined from observed frequencies in the same way.
For each component the evolution code provides the stellar luminosity, the radius and the effective
temperature, as well as the model quantities required in the subsequent calculations of the oscillation
frequencies. In the calibration process, the derivatives of the observable quantities
are obtained varying each of the parameters (![]() ,
,
![]() ,
Z, Y,
,
Z, Y,
![]() ,
,
![]() ,
and the age).
We do not derive colors or visual magnitudes, and we do not
include orbital elements
such as apparent semi-major axis (a'), orbital period (
,
and the age).
We do not derive colors or visual magnitudes, and we do not
include orbital elements
such as apparent semi-major axis (a'), orbital period (
![]() )
or parallax. We assume
the parallax as determined by Söderhjelm (1999) and the values of observables based on it.
The masses, however, are considered as parameters and also as observable
quantities in our calibrations.
)
or parallax. We assume
the parallax as determined by Söderhjelm (1999) and the values of observables based on it.
The masses, however, are considered as parameters and also as observable
quantities in our calibrations.
In the calibration of a binary system the large number of variables involved, both in terms of model parameters and observables, suggests the use of a least-squares based fitting procedure. This is particularly useful in this kind of calibration as we fit at the same time classical and seismological observables without first making a selection based on the HR location of the system.
As shown in Brown et al. (1994) the observable quantities depend on the parameters in a complex way: stellar evolution is not a linear problem. Most of the observables are influenced by several parameters, and hence the connection between observables and parameters that could conceptually seem to us the simplest one will not always provide the correct results.
We use the gradient-expansion algorithm known as Levenberg-Marquardt method. This algorithm combines the advantages of an expansion method, i.e. rapid convergence close to the minima, with those of the gradient-search, that is, a rapid approach to a far away minimum. This method has as well the strong advantage of being reasonably insensitive to the starting values of the parameters.
At each step the fitting function is linearized calculating
numerical derivatives (centered differences) of the observables
with respect to each model parameter. The displacement in the
parameter space, leading to a lower value of ![]() ,
is
calculated following the prescription of Bevington & Robinson (2003), pp. 161-164 and the iterative procedure is ended when
,
is
calculated following the prescription of Bevington & Robinson (2003), pp. 161-164 and the iterative procedure is ended when ![]() no
longer changes more than 2%.
In calibrations with
no
longer changes more than 2%.
In calibrations with ![]() ,
,
![]() ,
Z, Y,
,
Z, Y,
![]() ,
,
![]() ,
and the age as model parameters, convergence is typically achieved in 3-4 iterations and at each of them
the computation of 16 evolutionary tracks is needed to evaluate centered derivatives.
The result of such a local minimization could be sensitive to the
initial guess of the parameters; therefore, in order to get a more reliable
final solution we perform several runs starting from
different points in the parameter space. The effect we
find is limited to a variation of the number of iterations needed
to reach the minimum
,
and the age as model parameters, convergence is typically achieved in 3-4 iterations and at each of them
the computation of 16 evolutionary tracks is needed to evaluate centered derivatives.
The result of such a local minimization could be sensitive to the
initial guess of the parameters; therefore, in order to get a more reliable
final solution we perform several runs starting from
different points in the parameter space. The effect we
find is limited to a variation of the number of iterations needed
to reach the minimum ![]() ,
whereas the final parameters of the
system differ much less than their uncertainty.
On the other hand, building
a 6-dimensional dense grid of models seems impractical considering
the aim of evaluating the effects
of using different physical prescriptions in our models (e.g.
different equation of state, different metal mixture etc.).
,
whereas the final parameters of the
system differ much less than their uncertainty.
On the other hand, building
a 6-dimensional dense grid of models seems impractical considering
the aim of evaluating the effects
of using different physical prescriptions in our models (e.g.
different equation of state, different metal mixture etc.).
It is sometimes nonetheless possible to make fairly direct connections between the observables and the
parameters, particularly when one observable is much better determined than the rest.
The solution is determined by the parameter that is known with very small
uncertainty.
The uncertainties in the parameters for these fits are calculated
from the diagonal terms in the error matrix (inverse of curvature
matrix in the parameter space) and are, in general considerably
larger than the uncertainties obtained in the grid- and
gradient-search methods. The latter are obtained by finding the
change in each parameter to produce as change of ![]() of 1
from the minimum values, without re-optimizing the fit, while there
is a strong suggestion that correlations among the parameters play
an important role in fitting (see e.g. Bevington & Robinson 2003).
of 1
from the minimum values, without re-optimizing the fit, while there
is a strong suggestion that correlations among the parameters play
an important role in fitting (see e.g. Bevington & Robinson 2003).
Due to the proximity of the ![]() Cen binary system, the
precision on the measurement of its trigonometric parallax is
potentially very high. Unfortunately, some discrepancies have
appeared among the most recent published values
(see Table 10 in Kervella et al. 2003). Guenther & Demarque (2000) studied
the uncertainty in the stellar
parameters due to the different parallax values. This, indeed affects the determination of mass,
luminosity and radius. Following Eggenberger et al. (2004) we adopt
Cen binary system, the
precision on the measurement of its trigonometric parallax is
potentially very high. Unfortunately, some discrepancies have
appeared among the most recent published values
(see Table 10 in Kervella et al. 2003). Guenther & Demarque (2000) studied
the uncertainty in the stellar
parameters due to the different parallax values. This, indeed affects the determination of mass,
luminosity and radius. Following Eggenberger et al. (2004) we adopt
![]() mas (Söderhjelm 1999)
and, therefore, the corresponding mass values determined by Pourbaix et al. (2002): (
mas (Söderhjelm 1999)
and, therefore, the corresponding mass values determined by Pourbaix et al. (2002): (
![]()
![]() ,
,
![]()
![]() )
and the radii: (
)
and the radii: (
![]()
![]() ;
;
![]()
![]() )
(Kervella et al. 2003).
)
(Kervella et al. 2003).
Table 1: Non-asteroseismic constraints. References(1): Eggenberger et al. (2004); (2): Thoul et al. (2003).
As in the case of the parallax, there is a large scatter in the
published values of other quantities, such as
![]() ,
luminosity,
and metallicity. We decided to use the same values adopted by
Eggenberger et al. (2004) in order to have a reference
model. Eggenberger et al. (2004) took as
,
luminosity,
and metallicity. We decided to use the same values adopted by
Eggenberger et al. (2004) in order to have a reference
model. Eggenberger et al. (2004) took as
![]() for the component
A a value to encompass those given by two spectroscopic
determinations, the one from Neuforge-Verheecke & Magain (1997)
(
for the component
A a value to encompass those given by two spectroscopic
determinations, the one from Neuforge-Verheecke & Magain (1997)
(
![]()
![]() K,
K,
![]()
![]() K), and the one
by Morel et al. (2000) based on a re-analysis of Chmielewski et al. (1992)
spectra (
K), and the one
by Morel et al. (2000) based on a re-analysis of Chmielewski et al. (1992)
spectra (
![]()
![]() K,
K,
![]()
![]() K), used respectively in the
K), used respectively in the ![]() Cen
calibrations by Thoul et al. (2003) and Thévenin et al. (2002).
We will use the effective temperature as constraint in our
minimization method only in one of the calibrations (A1t, B1t, in
Table 2), since the precise determination of the
radius provides a narrower
domain in the space of observable quantities.
The luminosity values adopted by Eggenberger et al. (2004) come
from a new and weighted calibration of previous Geneva photometric
data, where they have also coherently taken into account the
effective temperatures and the parallax. These values cover the
domain considered by Thévenin et al. (2002) that considered an
error bar twice smaller, and a lower luminosity for the component
B. The luminosity values, directly determined from the
adopted radius and effective temperature, are in very good
agreement with the those determined by Eggenberger et al. (2004):
Cen
calibrations by Thoul et al. (2003) and Thévenin et al. (2002).
We will use the effective temperature as constraint in our
minimization method only in one of the calibrations (A1t, B1t, in
Table 2), since the precise determination of the
radius provides a narrower
domain in the space of observable quantities.
The luminosity values adopted by Eggenberger et al. (2004) come
from a new and weighted calibration of previous Geneva photometric
data, where they have also coherently taken into account the
effective temperatures and the parallax. These values cover the
domain considered by Thévenin et al. (2002) that considered an
error bar twice smaller, and a lower luminosity for the component
B. The luminosity values, directly determined from the
adopted radius and effective temperature, are in very good
agreement with the those determined by Eggenberger et al. (2004):
![]() ,
,
![]() .
On the other hand, the values determined by Pijpers (2003)
for
.
On the other hand, the values determined by Pijpers (2003)
for ![]() are much larger and only marginally
overlap the values considered here.
are much larger and only marginally
overlap the values considered here.
The precise values of masses and radius provide also precise
values of the surface gravity for both stars:
![]() and
and
![]() ,
while the
spectroscopic values determined by Neuforge-Verheecke & Magain (1997)
are
,
while the
spectroscopic values determined by Neuforge-Verheecke & Magain (1997)
are
![]() and
and
![]() .
These values were used by Thoul et al. (2003) to fix
the luminosity domain, leading to higher central values and
to larger error bars with respect to those determined by
Eggenberger et al. (2004) and Thévenin et al. (2002).
.
These values were used by Thoul et al. (2003) to fix
the luminosity domain, leading to higher central values and
to larger error bars with respect to those determined by
Eggenberger et al. (2004) and Thévenin et al. (2002).
For the metallicity of both components there is also no complete
agreement in the literature: [Fe/H]
![]() ,
and
[Fe/H]
,
and
[Fe/H]
![]() from Morel et al. (2000), and
[Fe/H]
from Morel et al. (2000), and
[Fe/H]
![]() ,
and [Fe/H]
,
and [Fe/H]
![]() from Neuforge-Verheecke & Magain (1997). The uncertainty in the
observable Z/X is quite large, if we take into account also the
10% in the
from Neuforge-Verheecke & Magain (1997). The uncertainty in the
observable Z/X is quite large, if we take into account also the
10% in the
![]() .
We have taken
the value adopted by Thoul et al. (2003), that is
.
We have taken
the value adopted by Thoul et al. (2003), that is
![]() ,
the same for both stars. The detailed abundance analysis
of
,
the same for both stars. The detailed abundance analysis
of ![]() Cen A and B carried out in Neuforge-Verheecke & Magain (1997) suggested
no evidence for a different metal mixture relative to the sun,
therefore all our models were computed assuming the solar mixture
by Grevesse & Noels (1993), except for the calibration (A5, B5) in
which we have considered the recently determined solar metal
abundances (Asplund et al. 2004,2005) that implies
Cen A and B carried out in Neuforge-Verheecke & Magain (1997) suggested
no evidence for a different metal mixture relative to the sun,
therefore all our models were computed assuming the solar mixture
by Grevesse & Noels (1993), except for the calibration (A5, B5) in
which we have considered the recently determined solar metal
abundances (Asplund et al. 2004,2005) that implies
![]() .
.
The non-asteroseismic constraints used in this work are summarized in Table 1.
Solar-like oscillations generate periodic motions of the stellar
surface with periods in the range of 3-30 min
and with extremely small amplitudes. The frequency and amplitude of each oscillation mode depend on the physical
condition prevailing in the layers crossed by the waves and provide a powerful seismological tool.
Helioseismology led to major improvements in the knowledge of solar structure and to revision of the "standard
solar
model''. The potential utility of seismology applied to other stars, in particular ![]() Cen,
to constrain the stellar parameters was extensively studied in Brown et al. (1994),
and also by Guenther & Demarque (2000).
Cen,
to constrain the stellar parameters was extensively studied in Brown et al. (1994),
and also by Guenther & Demarque (2000).
Several groups have made thorough attempts to detect the signature of p-mode oscillations in ![]() Cen A, but
their
results were not confirmed. Only recently Bouchy & Carrier (2002), from high precision radial velocity
measurements with the CORALIE echelle spectrograph have reported a clear detection of p-mode oscillation, and
identified several modes between 1800 and 2900
Cen A, but
their
results were not confirmed. Only recently Bouchy & Carrier (2002), from high precision radial velocity
measurements with the CORALIE echelle spectrograph have reported a clear detection of p-mode oscillation, and
identified several modes between 1800 and 2900 ![]() Hz, and with an envelope amplitude of about
Hz, and with an envelope amplitude of about
![]() .
Assuming that frequency modes
.
Assuming that frequency modes
![]() satisfy the
simplified asymptotic relation (Tassoul 1980):
satisfy the
simplified asymptotic relation (Tassoul 1980):
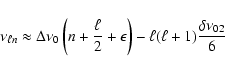 |
(2) |
Notice that the given errors come from the autocorrelation
algorithm, but we must keep in mind that their frequency
resolution is only 0.93
![]() ,
and that they derive an
uncertainty in the frequency determination equal to 0.46
,
and that they derive an
uncertainty in the frequency determination equal to 0.46
![]() .
They also point out that an error of
.
They also point out that an error of
![]() could have been introduced at some identified mode frequency, that
could explain the dispersion of mode frequency around the
asymptotic relation. In particular, higher observational uncertainty could affect mainly the
could have been introduced at some identified mode frequency, that
could explain the dispersion of mode frequency around the
asymptotic relation. In particular, higher observational uncertainty could affect mainly the ![]() modes that
determine the value of
modes that
determine the value of
![]() for the lower and higher
frequency
for the lower and higher
frequency
![]() (n=16 and 25).
(n=16 and 25).
Carrier & Bourban (2003) have also detected solar-like oscillations in the fainter component, ![]() Cen B.
Only twelve frequencies,
between 3000 and 4600
Cen B.
Only twelve frequencies,
between 3000 and 4600
![]() ,
have been kept in the final
list of identified p-modes, four of them with a detection level
lower than 3
,
have been kept in the final
list of identified p-modes, four of them with a detection level
lower than 3![]() ,
and it is
recommended to take them with caution. As for component A the
frequency resolution is 0.93
,
and it is
recommended to take them with caution. As for component A the
frequency resolution is 0.93
![]() .
The large and small
separations, determined by autocorrelation of the asymptotic
relation, are respectively
.
The large and small
separations, determined by autocorrelation of the asymptotic
relation, are respectively
![]()
![]() and
and
![]()
![]() .
The value derived for
.
The value derived for
![]() comes from only few
p-modes. In fact, from their frequency table is only possible to
obtain two values:
comes from only few
p-modes. In fact, from their frequency table is only possible to
obtain two values:
![]() and
and
![]() .
Carrier & Bourban (2003)
expect a rotational splitting
.
Carrier & Bourban (2003)
expect a rotational splitting ![]()
![]() that, given
the frequency resolution, could imply an increase of the
uncertainty of frequencies for modes of degree
that, given
the frequency resolution, could imply an increase of the
uncertainty of frequencies for modes of degree ![]() and
and
![]() .
.
New observations of this system by Kjeldsen & Bedding (2004) have confirmed the values determined
by Bouchy & Carrier (2002) concerning the frequency separations of component A. However, component B with
this new more precise data shows
![]() and
and
![]() .
Our computations were done before these values were available, therefore, we will not take them into
account in our calibration. Nevertheless, those values are reached and imposed
by the other observables used in some of our calibrations (A3, B3), see Sect. 5.
.
Our computations were done before these values were available, therefore, we will not take them into
account in our calibration. Nevertheless, those values are reached and imposed
by the other observables used in some of our calibrations (A3, B3), see Sect. 5.
How should these seismological observations be used to constrain our stellar models?
The classical way is to use the large and small separations to characterize
the power spectrum of solar-like oscillations.
The standard asymptotic theory of stellar oscillations (Tassoul 1980) relates the averages
values of high-radial order/low-degree small and large separations to conditions
in the stellar core (![]() )
and to the mean density of the star (
)
and to the mean density of the star (![]() ).
Recently Guenther & Brown (2004) and Metcalfe (2005) have proposed to use directly the
p-mode frequencies as observables to constrain the stellar models.
).
Recently Guenther & Brown (2004) and Metcalfe (2005) have proposed to use directly the
p-mode frequencies as observables to constrain the stellar models.
Brown et al. (1994) theoretically analyzed the case in which the individual frequencies are included as observables. Their purpose was to illustrate the potential loss of information resulting from representing the spectra in terms of the large and small separations derived from the expected asymptotic behavior. The dominant source of frequency changes is very close to the stellar surface. It could be difficult to disentangle these effects from the uncertainties in the treatment of the physics of the outer layers, where non-adiabaticity and dynamics effects of convection have to be taken into account.
The oscillation frequencies, the large and small separations depend on the structure of both the inner and the
outer
layers of a star, so model fitting and testing techniques to probe the interior structure
of the stars are dependent on our having a good understanding of the structure of the outer
layers. But these are just the layers where our ignorance is greatest; non-adiabatic convection
is important but not understood, the oscillations are non-adiabatic in the surface
layers and the structure of real stellar atmosphere is poorly understood.
For example the oscillation frequencies predicted by the reference solar models (S96)
(Christensen-Dalsgaard et al. 1996) differ from
the observed values up to 10
![]() at the higher end of the observed frequency range.
at the higher end of the observed frequency range.
In a first step, we will include as seismic constraints in our fitting algorithm
the combinations of frequencies: the large
As discussed in Christensen-Dalsgaard et al. (1995) and Di Mauro et al. (2003), care has to be taken when considering as a constraint in
the modelling the large separation, as its averaged value at high frequencies could be influenced by
near-surface effects as well. This is in fact the case when comparing the observed and the predicted
low-degree large separations of the Sun (see Fig. 1), where the disagreement of the order of
a ![]() Hz is related to a simplified treatment of the model outer layers.
Hz is related to a simplified treatment of the model outer layers.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{2988fig0.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg81.gif) |
Figure 1:
Solar large frequency difference
|
| Open with DEXTER | |
With the aim of checking whether the calibration we perform considering
![]() and
and
![]() is
not biased by a simplified treatment of the outer structure in our models, we considered the effect on
the calibration of choosing as seismic constraint r02, the ratio between the small and large frequency
separations defined by:
is
not biased by a simplified treatment of the outer structure in our models, we considered the effect on
the calibration of choosing as seismic constraint r02, the ratio between the small and large frequency
separations defined by:
Table 2:
Sets of parameters of fitted models. Meaning of numeric labels:
1 (fixed masses and ![]() ,
,
![]() as seismic constraints);
2 (as 1 but with variable masses); 3 (as 2 but using r02(n) as seismic constraint);
4 (as 3 but including convective overshooting) and
5 (as 3 but using Asplund et al. 2005 instead of Grevese & Noels 1993).
Meaning of alphabetic labels: nd (non diffusion models); f (FST convection treatment);
e (CEFF EoS instead of OPAL01 one);
c (a unique mixing-length parameter);
ns (fit without seismic constraints); only for the case 1, t refers to effective temperature as constraint, and
r to radius as constraint.
as seismic constraints);
2 (as 1 but with variable masses); 3 (as 2 but using r02(n) as seismic constraint);
4 (as 3 but including convective overshooting) and
5 (as 3 but using Asplund et al. 2005 instead of Grevese & Noels 1993).
Meaning of alphabetic labels: nd (non diffusion models); f (FST convection treatment);
e (CEFF EoS instead of OPAL01 one);
c (a unique mixing-length parameter);
ns (fit without seismic constraints); only for the case 1, t refers to effective temperature as constraint, and
r to radius as constraint.
All our stellar models were obtained from evolutionary tracks including the pre-main sequence
phase, and ending at ![]() 9 Gyr.
The stellar models have approximately 1200 shells,
the last one corresponding to
9 Gyr.
The stellar models have approximately 1200 shells,
the last one corresponding to
![]() as determined using
as boundary conditions those given by the Kurucz (1998)
atmosphere models. Furthermore, for the computation of
oscillations we have added atmospheric layers from
as determined using
as boundary conditions those given by the Kurucz (1998)
atmosphere models. Furthermore, for the computation of
oscillations we have added atmospheric layers from
![]() up to
up to
![]() .
.
We have computed models where the convection is treated both using
the Mixing Length Theory (MLT Böhm-Vitense 1958) with the formalism
described in Cox & Giuli (1968), and the Full Spectrum of Turbulence
(FST Canuto et al. 1996) with a formalism similar to the one
used by Morel et al. (2000) or Bernkopf (1998). That means
convective fluxes as given by Canuto et al. (1996), but another
prescription of the scale length. The parameter ![]() of the
MLT and the corresponding in the FST are considered as free
parameters of the model calibration, and the values obtained are
compared with the values required in the solar calibration for the
same physics.
of the
MLT and the corresponding in the FST are considered as free
parameters of the model calibration, and the values obtained are
compared with the values required in the solar calibration for the
same physics.
Finally we have computed stellar models with and without gravitational settling of helium and metals. The microscopic diffusion formulation is that given by Thoul et al. (1994), solving the Burgers (1969) equations for H, He and Z and thus considering diffusion due both to thermal and concentration gradients. We also assume complete ionization and the effect of radiative acceleration is ignored. This assumption is completely justified for the precision of the models and for the masses considered (Turcotte et al. 1998).
Table 3: Observable quantities predicted from the sets of parameters in Table 2.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.7cm,clip]{2988fig1.ps}\par\includegraphics[angle=-90,width=7.8cm,clip]{2988fig2.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg96.gif) |
Figure 2:
HR diagram location of models with stellar parameters from
differing fits. Labels corresponds to those in Tables 2, and 3.
Upper and lower panel correspond respectively to components A and B. The error boxes for
|
| Open with DEXTER | |
In the three following subsections we shall analyze the effect of changing the non-seismic constraints, the seismic constraints and finally the physics used in the models, that is, a different treatment of convection, different equation of state, different solar mixture, models including or not gravitational settling, and the effect of considering overshooting in our models.
Figure 2 shows the HR location of each of these fitted models. We have indicated the
error boxes in
![]()
![]() ,
and radius, corresponding to 1
,
and radius, corresponding to 1![]() (solid line), and
2
(solid line), and
2![]() (dashed-line).
(dashed-line).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.2cm,clip]{2988fig3.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg99.gif) |
Figure 3:
Large ( upper panels) and small ( lower panels) separations for the A ( left) and B ( right)
components
of |
| Open with DEXTER | |
A first calibration (A1r, B1r) was performed including in the
![]() function the luminosity, the radii and the
actual
function the luminosity, the radii and the
actual
![]() ,
as well as the average large and small
frequency separations (computed as described in
Sect. 2) for each component. The model parameters
are the initial chemical composition
(Y0, Z0), the mixing length parameters (
,
as well as the average large and small
frequency separations (computed as described in
Sect. 2) for each component. The model parameters
are the initial chemical composition
(Y0, Z0), the mixing length parameters (
![]() ,
,
![]() )
and the age (
)
and the age (![]() ). In this calibration we
consider, following Eggenberger et al. (2004), that the masses are
perfectly determined, and we assume the mass of each component to be
fixed to its observational central value, as given
Pourbaix et al. (2002). The parameters providing the
minimum
). In this calibration we
consider, following Eggenberger et al. (2004), that the masses are
perfectly determined, and we assume the mass of each component to be
fixed to its observational central value, as given
Pourbaix et al. (2002). The parameters providing the
minimum ![]() are:
are:
![]() Gyr,
Gyr,
![]() ,
,
![]() ,
Y0=0.276 and
Z0=0.0325. We
note that these results are in complete agreement with those
obtained by Eggenberger et al. (2004):
,
Y0=0.276 and
Z0=0.0325. We
note that these results are in complete agreement with those
obtained by Eggenberger et al. (2004):
![]() Gyr,
Z0=0.0302, Y0=0.275, and also their value for the
mixing-length parameter of
Gyr,
Z0=0.0302, Y0=0.275, and also their value for the
mixing-length parameter of ![]() Cen B is
Cen B is ![]() 10% larger
than
10% larger
than
![]() .
.
This agreement is not surprising, as similar observational constraints were considered. It strengthens the results obtained, since a different calibration procedure and different stellar evolution codes (with different equation of state, treatment of diffusion and treatment of sub-photospheric boundary conditions) were used, and it provides us with a good reference model to study the dependence of the calibrated stellar parameters on the choice of observable quantities and of the physics.
The observational values of the masses given by Pourbaix et al. (2002), though precisely determined, should be
treated as observables and therefore introduced, with their error bars, in the definition of the ![]() and allowed to be changed during the calibration.
and allowed to be changed during the calibration.
![]() and
and ![]() are considered both as parameters and observables in a second set of fittings
(A2, B2; A2f, B2f). The readjustment of parameters leads to a decrease of
are considered both as parameters and observables in a second set of fittings
(A2, B2; A2f, B2f). The readjustment of parameters leads to a decrease of ![]() which is 1.5
which is 1.5![]() smaller than the value determined by Pourbaix et al. (2002), and to a decrease of age
(
smaller than the value determined by Pourbaix et al. (2002), and to a decrease of age
(
![]() Gyr instead of
Gyr instead of
![]() Gyr). The location of
Gyr). The location of ![]() Cen B in the HR diagram
has significantly improved compared with (A1r, B1r) (Fig. 2) and
Cen B in the HR diagram
has significantly improved compared with (A1r, B1r) (Fig. 2) and
![]() is also better reproduced (Fig. 3), leading to an overall lower
is also better reproduced (Fig. 3), leading to an overall lower
![]() compared with
the equivalent fitting with fixed masses.
compared with
the equivalent fitting with fixed masses.
Even including the stellar masses among the parameters, we are not
able to improve significantly the fit of radii and large
separations. Actually the large separation is strongly dependent
on radius (
![]() ), and, given the high
precision of radius data, the procedure privileges sets of
parameters providing the radii within 1
), and, given the high
precision of radius data, the procedure privileges sets of
parameters providing the radii within 1![]() (for A), and
1.5
(for A), and
1.5![]() (for B) to detriment of a too high large
separation:
(for B) to detriment of a too high large
separation:
![]() is always around 106.6
is always around 106.6 ![]() Hz
instead of 105.5
Hz
instead of 105.5
![]() .
In order to relax the
constraints, we have performed a fitting including
.
In order to relax the
constraints, we have performed a fitting including
![]() among
the observables instead of the radii (A1t, B1t). This fitting
provided a small
among
the observables instead of the radii (A1t, B1t). This fitting
provided a small
![]() thanks to the good match of
large separation values. However, the radii (not included in the
thanks to the good match of
large separation values. However, the radii (not included in the
![]() function) are systematically larger (by more than 2
function) are systematically larger (by more than 2![]() )
than Kervella et al. (2003) ones. The large separation is very much
affected by the external layers properties, such as either the
description of the super-adiabatic region in the upper boundary of
the convective zone, or the non-adiabatic processes (not taken
into account either in the stellar models or in the oscillation
code). An inspection of frequencies predicted for these models
(Fig. 6) shows that even if the fit of
)
than Kervella et al. (2003) ones. The large separation is very much
affected by the external layers properties, such as either the
description of the super-adiabatic region in the upper boundary of
the convective zone, or the non-adiabatic processes (not taken
into account either in the stellar models or in the oscillation
code). An inspection of frequencies predicted for these models
(Fig. 6) shows that even if the fit of
![]() is almost perfect, the frequencies show a
shift of 25
is almost perfect, the frequencies show a
shift of 25
![]() with respect to the values determined by
Bouchy & Carrier (2002). On the other hand, sets of parameters
with a better fit of the radii reduce significantly the shift
of frequencies.
with respect to the values determined by
Bouchy & Carrier (2002). On the other hand, sets of parameters
with a better fit of the radii reduce significantly the shift
of frequencies.
The small separation for the A component (Fig. 3) suggest that
seismic observables would privilege younger models, whereas one of the two values of
![]() (n=23)
and the classical observables tend to a high value of the age.
In fact, in
our calibration (Ans, Bns) where only classical observable have
been taken into account for the fit, we obtain a very good
agreement for masses, radii, luminosity and effective temperature
(not taken as observable) for both components, and the age is
(n=23)
and the classical observables tend to a high value of the age.
In fact, in
our calibration (Ans, Bns) where only classical observable have
been taken into account for the fit, we obtain a very good
agreement for masses, radii, luminosity and effective temperature
(not taken as observable) for both components, and the age is
![]() Gyr.
Gyr.
Although the small separation averaged value of component A is well reproduced by our models, the
slope of ![]() as a function of
as a function of ![]() differs from the theoretical prediction.
One could argue that this could be a consequence of taking as observable the average value of
differs from the theoretical prediction.
One could argue that this could be a consequence of taking as observable the average value of ![]() .
Roxburgh & Vorontsov (2003, and references therein), show that the
Tassoul asymptotic result gives a poor fit both to the small
separations of stellar models
and to the observed values for the Sun, and that a better fit is
obtained by using the ratios of small and the large separations
(r02(n)). This ratio depends only on the inner phase shifts
which are determined solely by the interior structure of the star
and are uninfluenced by the unknown structure of the outer layers.
.
Roxburgh & Vorontsov (2003, and references therein), show that the
Tassoul asymptotic result gives a poor fit both to the small
separations of stellar models
and to the observed values for the Sun, and that a better fit is
obtained by using the ratios of small and the large separations
(r02(n)). This ratio depends only on the inner phase shifts
which are determined solely by the interior structure of the star
and are uninfluenced by the unknown structure of the outer layers.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{2988fig4.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg113.gif) |
Figure 4:
As Fig. 3 but for models computed using different approach for convection:
MLT with two mixing length parameters (solid line); FST (dashed lines); MLT with
|
| Open with DEXTER | |
We have performed a similar fitting using six observational values of
the ratio r02 as seismic constraints for the A component. Unfortunately, the p-modes identified for
B component do not allow us to define any value of r02; we decided, therefore,
to take as the seismic constraint the average large separation.
The first thing to be noticed, when comparing the new set of parameters (A3, B3) with the one
based on average large and small separation for both components (A2, B2), is a difference in the
resulting age of about 1 Gyr.
We also see that by fitting r02, we get a good fit of
![]() for both stars (Fig. 4). The large separation is slightly
higher than the observational one, as we obtained in (A2, B2) and
(A1r, B1r).
for both stars (Fig. 4). The large separation is slightly
higher than the observational one, as we obtained in (A2, B2) and
(A1r, B1r).
In Fig. 6 we can see also the effect on the p-mode frequencies, the model (A3, B3) providing a better fit to the observational ones than the model (A2, B2).
Notice that the parameter set (A3, B3) was determined without
taking into account the small separation for the
B component. Theoretical
![]() is
is ![]()
![]() ,
that is close to the new observational value (
,
that is close to the new observational value (
![]() )
by
Kjeldsen & Bedding (2004). We wonder whether the high age obtained by
taking
)
by
Kjeldsen & Bedding (2004). We wonder whether the high age obtained by
taking
![]() as given by the average of two points
(Carrier & Bourban 2003) is only a consequence of the low value
imposed to
as given by the average of two points
(Carrier & Bourban 2003) is only a consequence of the low value
imposed to
![]() .
In fact, a different calibration
performed using the small
and large separations as observables, but taking only
.
In fact, a different calibration
performed using the small
and large separations as observables, but taking only
![]() instead of the average of two available values, provides an age of 6.0 Gyr, in
good agreement with r02 (A3, B3) fittings, and quite younger
than (A2, B2) models.
instead of the average of two available values, provides an age of 6.0 Gyr, in
good agreement with r02 (A3, B3) fittings, and quite younger
than (A2, B2) models.
Finally, we have also used r02 but without varying the masses. Again, the age is of the order of 6.0 Gyr, but now, the mixing-length parameters needed for both stars are quite different (by 17%).
The fits reported in Table 3 could indicate an inconsistency
between the seismic
and classical observables. Actually for component B the resulting
radii are larger than the observed ones by more than ![]()
![]() or
or ![]()
![]() and
the masses are smaller by more than
and
the masses are smaller by more than ![]()
![]() or
or ![]()
![]() with respect
to the values observationally derived.
These results could be interpreted as a systematic error in the radii and/or in
the mass determination.
A calibration performed with a free
with respect
to the values observationally derived.
These results could be interpreted as a systematic error in the radii and/or in
the mass determination.
A calibration performed with a free ![]() parameter/observable, leads to
parameter/observable, leads to
![]()
![]() and
and
![]()
![]() .
The other parameters do not significantly change. This mass value would imply a systematic
error of
.
The other parameters do not significantly change. This mass value would imply a systematic
error of ![]()
![]() that, given the available high precision data, does not seem reliable.
On the other hand, if
that, given the available high precision data, does not seem reliable.
On the other hand, if ![]() is left free, the fit of the other observables provides
is left free, the fit of the other observables provides
![]()
![]() instead
of 0.863
instead
of 0.863
![]() ,
and a
,
and a ![]() value within
value within ![]() from the observed one.
However, these fits have
from the observed one.
However, these fits have
![]() included in the
included in the ![]() functional.
To check if the large radius is only a consequence of
functional.
To check if the large radius is only a consequence of
![]() ,
we calibrate the system adopting as seismic
constraints r02(n) for component A, and
,
we calibrate the system adopting as seismic
constraints r02(n) for component A, and
![]() for component B. In this case we are able to fit
the radii and masses of both components within
for component B. In this case we are able to fit
the radii and masses of both components within ![]() ,
but
,
but
![]() is more than +3-
is more than +3-![]() away
from the observational value, and the predicted frequencies are
away
from the observational value, and the predicted frequencies are ![]() 40
40
![]() larger than observed ones.
A priori, we cannot rule out a larger uncertainty in the observed radius. In the observational radius determination there is an implicit definition of stellar radius (that is not
necessarily the same as the one used in stellar modelling) and an assumption about the limb darkening law and the atmosphere models.
How much is the stellar radius affected by these assumptions? Kervella (2005, private communication) claims that these effects
are much smaller than other errors intrinsic to the measurement method and already taken into account.
So, more precise seismic data for
larger than observed ones.
A priori, we cannot rule out a larger uncertainty in the observed radius. In the observational radius determination there is an implicit definition of stellar radius (that is not
necessarily the same as the one used in stellar modelling) and an assumption about the limb darkening law and the atmosphere models.
How much is the stellar radius affected by these assumptions? Kervella (2005, private communication) claims that these effects
are much smaller than other errors intrinsic to the measurement method and already taken into account.
So, more precise seismic data for ![]() CenB are needed to understand this apparent inconsistency.
CenB are needed to understand this apparent inconsistency.
![]() Cen offers a unique opportunity of testing our
assumption about
Cen offers a unique opportunity of testing our
assumption about ![]() and, therefore, our simplified way of overcoming
the complex problem of convection in stars. The question of
the universality of the mixing-length parameter has been approached
many times in the past (Edmonds et al. 1992; Guenther & Demarque 2000; Fernandes & Neuforge 1995; Morel et al. 2000; Noels et al. 1991; Neuforge 1993; Lydon et al. 1993). Some
attempts of calibrating
and, therefore, our simplified way of overcoming
the complex problem of convection in stars. The question of
the universality of the mixing-length parameter has been approached
many times in the past (Edmonds et al. 1992; Guenther & Demarque 2000; Fernandes & Neuforge 1995; Morel et al. 2000; Noels et al. 1991; Neuforge 1993; Lydon et al. 1993). Some
attempts of calibrating ![]() Cen A and B in luminosity and radii
using MLT theory suggest different values of
Cen A and B in luminosity and radii
using MLT theory suggest different values of
![]() for each component and different from the
for each component and different from the
![]() ,
while others favor similar values for both
components, or conclude that the uncertainties in masses and radii
as well as the chemical composition should be reduced
significantly before being able to draw firm a conclusion on
whether the MLT parameter is unique or not (Andersen 1991; Guenther & Demarque 2000; Lydon et al. 1993). Nowadays, the high
precision with which we know masses and radii for
,
while others favor similar values for both
components, or conclude that the uncertainties in masses and radii
as well as the chemical composition should be reduced
significantly before being able to draw firm a conclusion on
whether the MLT parameter is unique or not (Andersen 1991; Guenther & Demarque 2000; Lydon et al. 1993). Nowadays, the high
precision with which we know masses and radii for ![]() Cen A and B
allows to analyze again this problem. The frequencies are very
sensitive to R and therefore to
Cen A and B
allows to analyze again this problem. The frequencies are very
sensitive to R and therefore to ![]() ,
and
the difference between the observed frequencies (
,
and
the difference between the observed frequencies (
![]() )
and the theoretical ones
(
)
and the theoretical ones
(
![]() )
is highly affected by how the super-adiabatic zone is described
(see e.g. Schlattl et al. 1997).
)
is highly affected by how the super-adiabatic zone is described
(see e.g. Schlattl et al. 1997).
In order to analyze these questions we have made several fits of the ![]() Cen observable quantities
by using MLT with i)
Cen observable quantities
by using MLT with i)
![]() as free parameters; ii)
as free parameters; ii)
![]() free parameter; and iii)
free parameter; and iii)
![]() fixed; and iv) since Morel et al. (2000) presented also controversial results when
comparing calibrations for
fixed; and iv) since Morel et al. (2000) presented also controversial results when
comparing calibrations for ![]() Cen using MLT or FST, we shall analyze as well
the effect of using the FST treatment of convection.
Cen using MLT or FST, we shall analyze as well
the effect of using the FST treatment of convection.
The convection parameters that result from our fits are,
as in the case of the calibration with MLT,
close to the parameter needed to calibrate the Sun (0.753). Furthermore,
in comparing the models (A3, B3) with (A3f, B3f) ones, we
do not observe any difference in the parameters of the models fitting the system ![]() Cen using
MLT or FST. In principle this is a logical behavior since we considered as the seismological observable
the r02(n) (Roxburgh & Vorontsov 2003) ratio, and this quantity
is independent of surface properties of the model.
However, also the sets of parameters (A2, B2) and (A2f, B2f) determined
by using large and small frequency separations as constraints
are in fact the same, independent of the convection description used.
Cen using
MLT or FST. In principle this is a logical behavior since we considered as the seismological observable
the r02(n) (Roxburgh & Vorontsov 2003) ratio, and this quantity
is independent of surface properties of the model.
However, also the sets of parameters (A2, B2) and (A2f, B2f) determined
by using large and small frequency separations as constraints
are in fact the same, independent of the convection description used.
We would expect, as in the Sun, a decrease of the difference between theoretical and observational frequencies in the high frequency domain when FST is used. However, for our binary system, the improvement provided by FST treatment with respect to MLT is quite small.
For ![]() Cen A the improvement is of the order of 4
Cen A the improvement is of the order of 4 ![]() Hz at 3000
Hz at 3000 ![]() Hz, while
for the B component, this effect does not appear clearly (Fig. 6).
In fact, the
difference between MLT and FST frequencies is due to a different
radius and mass. If we adopt for
Hz, while
for the B component, this effect does not appear clearly (Fig. 6).
In fact, the
difference between MLT and FST frequencies is due to a different
radius and mass. If we adopt for ![]() and
and ![]() the values determined in the
calibration B3 as the real ones, and compute a new FST calibration,
we
find that the difference between the MLT and FST frequencies in the observational
domain (3000-4600
the values determined in the
calibration B3 as the real ones, and compute a new FST calibration,
we
find that the difference between the MLT and FST frequencies in the observational
domain (3000-4600 ![]() Hz) goes from 0 to 3
Hz) goes from 0 to 3 ![]() Hz, while the difference in frequencies
between B3 and B3f introduced by the different mass and radius is of the order of 8
Hz, while the difference in frequencies
between B3 and B3f introduced by the different mass and radius is of the order of 8 ![]() Hz.
Hz.
Several times in the literature the question has been addressed of whether convection
in the two components of ![]() Centauri should
be described with distinct mixing-length parameters and, if, given the observational uncertainties,
the inferred difference between mixing length parameters is significant
(see e.g. Eggenberger et al. (2004), where an exhaustive review
of previous calibrations is also presented).
It was, in fact, already suggested in Guenther & Demarque (2000) that a reduction in the observational uncertainties
and the inclusion of seismic constraints in the modelling would allow a more robust inference on the
mixing-length parameters of
Centauri should
be described with distinct mixing-length parameters and, if, given the observational uncertainties,
the inferred difference between mixing length parameters is significant
(see e.g. Eggenberger et al. (2004), where an exhaustive review
of previous calibrations is also presented).
It was, in fact, already suggested in Guenther & Demarque (2000) that a reduction in the observational uncertainties
and the inclusion of seismic constraints in the modelling would allow a more robust inference on the
mixing-length parameters of ![]() Cen A and B.
This is now the case, thanks to the detection of solar-like oscillations and to the precise determination
of radii. These are compatible with effective temperatures spectroscopically determined and significantly
reduce the error box in the HR diagram.
As a general result of the calibrations presented in the previous sections we find that the mixing-length
parameter of the calibrated model A (
Cen A and B.
This is now the case, thanks to the detection of solar-like oscillations and to the precise determination
of radii. These are compatible with effective temperatures spectroscopically determined and significantly
reduce the error box in the HR diagram.
As a general result of the calibrations presented in the previous sections we find that the mixing-length
parameter of the calibrated model A (
![]() )
is approximately 5-10% smaller than
)
is approximately 5-10% smaller than
![]() .
.
Numerical simulations of convection have permitted us to
carry out a calibration of the mixing-length parameter
through the HR diagram.
A function
![]() is determined to reproduce the step
of the specific entropy provided by the atmosphere hydrodynamic models.
Both calibrations,
the one by Ludwig et al. (1999) (based on 2-D simulations) and
the one by Trampedach (2004) (based on 3-D simulations) show slight
variations of
is determined to reproduce the step
of the specific entropy provided by the atmosphere hydrodynamic models.
Both calibrations,
the one by Ludwig et al. (1999) (based on 2-D simulations) and
the one by Trampedach (2004) (based on 3-D simulations) show slight
variations of ![]() with the position in the HR diagram, and
suggest that the mixing parameter should be represented as a
function of
with the position in the HR diagram, and
suggest that the mixing parameter should be represented as a
function of
![]() ,
,
![]() and chemical composition.
and chemical composition.
Actually, comparing our results with these theoretical predictions, we see that the difference
between the
value determined for
![]() and
and
![]() is in good agreement with the
predictions by numerical simulations of convection. Moreover, our
is in good agreement with the
predictions by numerical simulations of convection. Moreover, our ![]() values for the two
components bracket that
obtained by calibrating the Sun (
values for the two
components bracket that
obtained by calibrating the Sun (
![]() )
with the same
physics (see for instance the model A3, B3). This is what one
expects from their HR location and from the calibrations by
Ludwig et al. (1999) and Trampedach (2004).
We note, however, that
in the fits obtained by using
)
with the same
physics (see for instance the model A3, B3). This is what one
expects from their HR location and from the calibrations by
Ludwig et al. (1999) and Trampedach (2004).
We note, however, that
in the fits obtained by using
![]() and
and
![]() we find
we find
![]() ,
but also
,
but also
![]() larger than the solar one. The difference with respect to the solar
value is even larger when the masses of the components are assumed to be fixed.
The same effect is present in
Eggenberger et al. (2004): they find
larger than the solar one. The difference with respect to the solar
value is even larger when the masses of the components are assumed to be fixed.
The same effect is present in
Eggenberger et al. (2004): they find
![]() ,
but their
values are far
from their solar one.
,
but their
values are far
from their solar one.
In order to determine whether the addition of an extra free parameter leads to a significant improvement
of the fit, we performed a calibration assuming a single mixing-length parameter for both components,
and including the
![]() ratios in the quality function
(A3c, B3c). The value of
ratios in the quality function
(A3c, B3c). The value of ![]() for this calibration is
for this calibration is
![]() (quite close to the solar one),
but the masses now are slightly larger for the component A, and slightly smaller for the component B. The same happens if we decide to fix
(quite close to the solar one),
but the masses now are slightly larger for the component A, and slightly smaller for the component B. The same happens if we decide to fix
![]() .
The masses are within 2
.
The masses are within 2![]() of the observed value, and the age is the same,
of the observed value, and the age is the same,
![]() Gyr.
Gyr.
A different result is obtained if the small and large differences are considered in the
quality function (A2c, B2c), and the mixing-length parameter is assumed to be the same for both
stars. In this case, the value reached (
![]() )
is not so close to the solar one,
)
is not so close to the solar one,
![]() must decrease to 0.919
must decrease to 0.919
![]() ,
and the age of the system decreases with respect to
the value obtained allowing two different mixing-length parameters. This result recalls that
obtained by Thévenin et al. (2002), who using a unique
,
and the age of the system decreases with respect to
the value obtained allowing two different mixing-length parameters. This result recalls that
obtained by Thévenin et al. (2002), who using a unique ![]() had to decrease the
had to decrease the
![]() to 0.907
to 0.907
![]() .
.
Since adding a free parameter would naturally lead to a better fit
(a lower ![]() as defined in Eq.(1)), for a
quantitative comparison between the quality of the fit obtained
with a different
number of model parameters, it is more meaningful to compare the so-called "reduced''
as defined in Eq.(1)), for a
quantitative comparison between the quality of the fit obtained
with a different
number of model parameters, it is more meaningful to compare the so-called "reduced''
![]() (Eq. (4)).
As can be seen in Table 3 the value of
(Eq. (4)).
As can be seen in Table 3 the value of ![]() is
lower if two distinct mixing length parameters are used in the
modelling (both comparing A3, B3 with A3c, B3c and A2, B2 with A2c, B2c):
this suggests that, with the adopted observational constraints,
the addition of another free mixing-length parameter is justified.
In fact, comparing the fits obtained with one or two mixing-length parameters, the F-test gives a confidence of
85-90% that the inclusion of two different parameters for convection is significant. We should however recall
that such a statistical test, and generally the
is
lower if two distinct mixing length parameters are used in the
modelling (both comparing A3, B3 with A3c, B3c and A2, B2 with A2c, B2c):
this suggests that, with the adopted observational constraints,
the addition of another free mixing-length parameter is justified.
In fact, comparing the fits obtained with one or two mixing-length parameters, the F-test gives a confidence of
85-90% that the inclusion of two different parameters for convection is significant. We should however recall
that such a statistical test, and generally the ![]() statistics, assumes that the observational errors are
distributed about the mean following a Gaussian distribution. This is not necessarily true as systematic shifts
in the observed quantities and inaccuracies in the models cannot be excluded.
As could also be expected, the uncertainties adopted with the observational
constraints are crucial. For instance, we find that if the observational error in the mass of the component B
is doubled, the addition of a second free parameter for convection is no longer justified.
statistics, assumes that the observational errors are
distributed about the mean following a Gaussian distribution. This is not necessarily true as systematic shifts
in the observed quantities and inaccuracies in the models cannot be excluded.
As could also be expected, the uncertainties adopted with the observational
constraints are crucial. For instance, we find that if the observational error in the mass of the component B
is doubled, the addition of a second free parameter for convection is no longer justified.
The central question is whether the residual errors are observationally significant. If the residuals are all small compared to the observational errors, it is not possible to distinguish parameter changes from changes in physical assumptions. In general, we find that stars obeying different physics succeed remarkably well in masquerading as stars that merely have different parameters (Brown et al. 1994).
Concerning the equation of state, the calibration assuming CEFF (A3e, B3e)
leads to a result in agreement with the fit
(A3, B3) computed adopting OPAL01, both in terms of
![]() (either the total one or that
corresponding at each observable quantity), and of the fitted parameters.
This is expected for stars with an internal structure similar to
the sun: as shown by Miglio (2004) the differences
between the sound speed and the first adiabatic exponent (
(either the total one or that
corresponding at each observable quantity), and of the fitted parameters.
This is expected for stars with an internal structure similar to
the sun: as shown by Miglio (2004) the differences
between the sound speed and the first adiabatic exponent (![]() ), due solely to
the use of a different EOS (CEFF and OPAL01), are smaller than 1% except
in outer regions with radii larger than 0.95 R*, that is
of the same order of those predicted in solar models (see e.g. Basu & Christensen-Dalsgaard 1997).
The differences appear to be larger in the lower-mass model B than in model A,
and are mainly located in the hydrogen and helium ionization
regions. In that study, the differences in
), due solely to
the use of a different EOS (CEFF and OPAL01), are smaller than 1% except
in outer regions with radii larger than 0.95 R*, that is
of the same order of those predicted in solar models (see e.g. Basu & Christensen-Dalsgaard 1997).
The differences appear to be larger in the lower-mass model B than in model A,
and are mainly located in the hydrogen and helium ionization
regions. In that study, the differences in ![]() came from the application
of CEFF or OPAL01 to a given stellar structure (
came from the application
of CEFF or OPAL01 to a given stellar structure (
![]() )
and chemical
composition.
In the calibration procedure, such small differences in the internal structure of a
model propagate in a variation of the observables of each model
that could be easily compensated by a re-adjustment of the free
parameters.
)
and chemical
composition.
In the calibration procedure, such small differences in the internal structure of a
model propagate in a variation of the observables of each model
that could be easily compensated by a re-adjustment of the free
parameters.
![\begin{figure}
\par\includegraphics[angle=-90,width=8.1cm,clip]{2988fig5.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg148.gif) |
Figure 5: As Fig. 4 but with different curves corresponding to different physics included in the stellar computation: convective overshooting (dashed lines); solar mixture from Asplund et al. (2004) instead of Grevesse & Noels (1993)(dash-dotted lines); no gravitational settling (solid lines); CEFF equation of state instead of OPAL01 (dotted lines). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2988fig6.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg149.gif) |
Figure 6:
Difference between theoretical and observed frequencies for the sets of parameters whose
separations have been plotted in Fig. 3 ( upper panel); in Fig. 4 ( middle panel);
and Fig 5 ( lower panel). Left side corresponding to |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2988fig7.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg150.gif) |
Figure 7: Difference of frequencies between a reference calibration (A3, B3), and both, that with a different EoS (A3e, B3e) (solid lines), and without microscopic diffussion (A3nd, B3nd) (dahsed lines). Upper panel corresponds to component A, and lower panel to component B. |
| Open with DEXTER | |
The models calibrated by using different equations of state are very similar.
There is, nevertheless, a difference in the frequencies. In Fig. 7 (solid lines)
we plot the difference between (A3, B3) and (A3e, B3e) frequencies.
The upper panel corresponds to the A component, and the lower panel to the B one.
This difference in frequencies shows a behavior depending on ![]() with an oscillatory signature.
This is expected for instance, when the models have either different locations of the
convective region boundaries, or a different behaviour of
with an oscillatory signature.
This is expected for instance, when the models have either different locations of the
convective region boundaries, or a different behaviour of ![]() .
The bottom of the convective zone in
.
The bottom of the convective zone in ![]() Cen A is located at
Cen A is located at
![]() for
A3 calibration, and
for
A3 calibration, and
![]() for A3e model.
Therefore, the oscillatory signature is probably related to the changes in
the second helium ionization zone. The amplitude of this oscillation is linked to
the difference in depth of the
for A3e model.
Therefore, the oscillatory signature is probably related to the changes in
the second helium ionization zone. The amplitude of this oscillation is linked to
the difference in depth of the ![]() bump, and the period
contains information about the location of the difference in stellar structure.
For star A, the amplitude of the oscillation between the order n=10 and 15 is
around 0.7
bump, and the period
contains information about the location of the difference in stellar structure.
For star A, the amplitude of the oscillation between the order n=10 and 15 is
around 0.7
![]() ,
while for the B component that is almost 2
,
while for the B component that is almost 2
![]() .
.
The calibrations without diffusion
(A1nd, B1nd) and (A3nd, B3nd) provide fits of similar quality with respect to the
corresponding calibrations including gravitational settling, respectively
(A1r, B1r) and (A3, B3).
As reported in Table 2 the parameters resulting from the
calibrations differ, as expected, in the initial chemical composition.
The smaller mass fraction of He required in these calibrations implies also
a slight increase in the age of the system: ![]() Gyr for (A3nd, B3nd) versus
Gyr for (A3nd, B3nd) versus
![]() Gyr for (A3, B3) (and
Gyr for (A3, B3) (and ![]() Gyr for (A1nd, B1nd) versus
Gyr for (A1nd, B1nd) versus
![]() Gyr for (A1r, B1r)).
The (A3nd, B3nd) calibration is consistent with the one obtained by Thoul et al. (2003). Since they use
only
Gyr for (A1r, B1r)).
The (A3nd, B3nd) calibration is consistent with the one obtained by Thoul et al. (2003). Since they use
only ![]() Cen A frequencies, their age estimation is not affected by the low
Cen A frequencies, their age estimation is not affected by the low ![]() (B) value.
(B) value.
The mixing-length parameters are also re-adjusted to fit the stellar radius, and
also in this case
![]() is almost 8% larger than
is almost 8% larger than
![]() ,
and both
bracket the mixing length parameter obtained for a Sun calibrated without microscopic diffusion
(
,
and both
bracket the mixing length parameter obtained for a Sun calibrated without microscopic diffusion
(
![]() ).
).
In Fig. 7 (dashed-line) we show how diffusion affects the frequencies.
We plot the residuals
defined as
![]() (upper panel) and
(upper panel) and
![]() (lower panel).
For component A the residuals as function of the order n show an oscillatory behavior,
reflecting the changes in envelope He abundance (
(lower panel).
For component A the residuals as function of the order n show an oscillatory behavior,
reflecting the changes in envelope He abundance (![]() ). Actually the calibrated model including
diffusion has a superficial He abundance
). Actually the calibrated model including
diffusion has a superficial He abundance
![]() ,
while model A3nd, without
gravitational settling has
,
while model A3nd, without
gravitational settling has
![]() .This difference implies
as well a different opacity and, therefore, a different location of the boundary of the convective zone
(
.This difference implies
as well a different opacity and, therefore, a different location of the boundary of the convective zone
(
![]() ). To avoid changing the figure scale,
the curve of residuals in the upper panel has been shifted down by 2.5
). To avoid changing the figure scale,
the curve of residuals in the upper panel has been shifted down by 2.5
![]() ;
we see that the
amplitude of the oscillatory signal is around 0.5
;
we see that the
amplitude of the oscillatory signal is around 0.5
![]() between n=10 and n=20.
between n=10 and n=20.
For component B the curve of residuals shows a completely different behavior. Since ![]() Cen B is less
massive than its companion,
the mass contained in its convective zone is much larger and, therefore, the effect of
microscopic diffusion is much smaller. The value of
Cen B is less
massive than its companion,
the mass contained in its convective zone is much larger and, therefore, the effect of
microscopic diffusion is much smaller. The value of ![]() for B3 is less than 4%
smaller than that for B3nd, while for the component A, the difference in
for B3 is less than 4%
smaller than that for B3nd, while for the component A, the difference in ![]() between both calibrations
(A3 and A3nd) is around 10%.
between both calibrations
(A3 and A3nd) is around 10%.
An additional consequence of our simple way of describing
convection in stellar models is the need to parameterize
convective overshooting.
In general (see e.g. Schaller et al. 1992) convective core overshooting is necessary
to fit isochrones of open clusters for masses larger than a given critical mass. The problem
is to determine this critical mass
and to describe the transition between no-overshooting
mass domain and overshooting mass domain. On the one hand, the mass
and effective temperature of ![]() Cen A are quite close to
solar values, and one could think that no overshooting should be
introduced. Nevertheless the chemical composition of
Cen A are quite close to
solar values, and one could think that no overshooting should be
introduced. Nevertheless the chemical composition of ![]() Cen A
is different from the solar one and the evolution of a
convective core does not necessarily show the same
behaviour. The mass of
Cen A
is different from the solar one and the evolution of a
convective core does not necessarily show the same
behaviour. The mass of ![]() Cen places it in the boundary
region between models with and without a convective core. We have
made several calibrations varying the thickness of the
overshooting layer
Cen places it in the boundary
region between models with and without a convective core. We have
made several calibrations varying the thickness of the
overshooting layer
![]() (where
(where
![]() is the radius of the convective core)
with
is the radius of the convective core)
with ![]() from 0.0, 0.1, 0.15 and 0.2. In fact, for values of
from 0.0, 0.1, 0.15 and 0.2. In fact, for values of
![]() no convective core remains after the PMS, therefore the
parameters resulting from the fitting are not changed.
no convective core remains after the PMS, therefore the
parameters resulting from the fitting are not changed.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.6cm,clip]{2988fig8.ps}\end{figure}](/articles/aa/full/2005/38/aa2988-05/Timg169.gif) |
Figure 8:
r10(n) ratios for A component. Points represent the observational values with their
error bars assuming an error in frequencies equal to |
| Open with DEXTER | |
In Tables 2 and 3 we report the set of
parameters and observables corresponding to models (A4, B4)
calibrated with ![]() .
As should be expected, including
overshooting reduces the age of the system.
Figure 5 shows the large and small separations.
We find a possible direct indicator
of a convective core in the behavior of the small separation of
component A at high frequencies (
.
As should be expected, including
overshooting reduces the age of the system.
Figure 5 shows the large and small separations.
We find a possible direct indicator
of a convective core in the behavior of the small separation of
component A at high frequencies (
![]()
![]() ).
That is even more evident in the signature left in
).
That is even more evident in the signature left in ![]() .
However, given the uncertainty (1.3
.
However, given the uncertainty (1.3
![]() )
affecting the p-modes
involved in the highest frequency r02(n) (or
)
affecting the p-modes
involved in the highest frequency r02(n) (or
![]() ),
it is not possible, based only on r02(n) or
),
it is not possible, based only on r02(n) or
![]() ,
to rule out a convective core in
,
to rule out a convective core in ![]() Cen A.
The ratio
Cen A.
The ratio
![]() ,
however,
is much more eloquent, as shown in Fig. 8,
and allows us to reject model A4: current observational constraints seem not to be
in favour of a convective core in
,
however,
is much more eloquent, as shown in Fig. 8,
and allows us to reject model A4: current observational constraints seem not to be
in favour of a convective core in ![]() Cen A.
Cen A.
We propose a calibration of the binary system ![]() Cen by means of the Levenberg-Marquardt minimization
algorithm applying it simultaneously to classical (photometric, spectroscopic and astrometric) and
seismic observables. The main features of this sort of algorithm make it an ideal tool for the aim of
this work: to practically analyze the effectiveness of oscillation frequencies in constraining stellar model
parameters and stellar evolution physics, by using the p-modes identified by Bouchy & Carrier (2002) (
Cen by means of the Levenberg-Marquardt minimization
algorithm applying it simultaneously to classical (photometric, spectroscopic and astrometric) and
seismic observables. The main features of this sort of algorithm make it an ideal tool for the aim of
this work: to practically analyze the effectiveness of oscillation frequencies in constraining stellar model
parameters and stellar evolution physics, by using the p-modes identified by Bouchy & Carrier (2002) (![]() Cen A) and
by Carrier & Bourban (2003)(
Cen A) and
by Carrier & Bourban (2003)(![]() Cen B).
Actually thanks to its low computational cost, this algorithm allows one to search for the best model in the full
7-dimensional parameter space describing the binary system, varying both the set of stellar observables and the
physics included in stellar modelling.
Cen B).
Actually thanks to its low computational cost, this algorithm allows one to search for the best model in the full
7-dimensional parameter space describing the binary system, varying both the set of stellar observables and the
physics included in stellar modelling.
As a starting point we assumed the same observables as Eggenberger et al. (2004). In spite of the different EoS (MHD), diffusion treatment (Richard et al. 1996, for five elements separately), cross section of nuclear reactions (NACRE) and atmospheric boundary conditions, we derive a set of stellar parameters (A1r, B1r) in complete agreement with theirs.
By comparison between calibrations with different observables we make clear that care has to be taken when using
![]() to constrain fundamental stellar parameters.
Given the strong dependence of
to constrain fundamental stellar parameters.
Given the strong dependence of
![]() on surface layers, and our poor understanding of the physics
describing
outer stellar regions, seeking a perfect agreement between observed and predicted
on surface layers, and our poor understanding of the physics
describing
outer stellar regions, seeking a perfect agreement between observed and predicted
![]() ,
may bias our
results toward, for instance, inaccurate radii.
This is clear when comparing the models A1t and A1r;
in the former a perfect agreement with the observed
,
may bias our
results toward, for instance, inaccurate radii.
This is clear when comparing the models A1t and A1r;
in the former a perfect agreement with the observed
![]() is reached but the radii (and the frequencies, see Fig.
6) deviate significantly from their observational values.
is reached but the radii (and the frequencies, see Fig.
6) deviate significantly from their observational values.
An additional source of systematic error in the calibrations
concerns the value of the small frequency separation of component
B. Since the observational data are still rather poor one of the
two measured values,
![]() leads to
a higher age than suggested by
leads to
a higher age than suggested by
![]() .
.
The value of
![]() predicted in our calibration
(A3, B3) (where
predicted in our calibration
(A3, B3) (where
![]() is not included in the
is not included in the
![]() )
is in agreement with
)
is in agreement with
![]() and with
the very recent value published by Kjeldsen & Bedding (2004). This also suggests that sufficiently precise seismic
data of one star are sufficient to determine fundamental
parameters of the system. In fact additional calibrations, not
shown in Table 2, where no seismic constraints of component B are
included, lead to fitted parameters compatible with e.g. (A3, B3)
even though a large discrepancy between predicted and observed
frequencies of
and with
the very recent value published by Kjeldsen & Bedding (2004). This also suggests that sufficiently precise seismic
data of one star are sufficient to determine fundamental
parameters of the system. In fact additional calibrations, not
shown in Table 2, where no seismic constraints of component B are
included, lead to fitted parameters compatible with e.g. (A3, B3)
even though a large discrepancy between predicted and observed
frequencies of ![]() Cen B is observed.
Cen B is observed.
We therefore propose to use ![]() as a reliable seismic
constraint to determine fundamental parameters of a star. The large
frequency separation could, nonetheless, provide a first estimate
of the mean density and, as shown e.g. in Gough (1990), an
useful information on localized features in stellar interior once
more accurate determinations of solar-like oscillations will be
available.
as a reliable seismic
constraint to determine fundamental parameters of a star. The large
frequency separation could, nonetheless, provide a first estimate
of the mean density and, as shown e.g. in Gough (1990), an
useful information on localized features in stellar interior once
more accurate determinations of solar-like oscillations will be
available.
Section 5.2 was devoted to the study of the
effects on the calibration of our uncertainties concerning stellar
convection. If the calibrations, e.g. (A3, B3), are performed
considering a free parameter describing convection in each
component (
![]() ,
,
![]() )
we find, as
Eggenberger et al. (2004),
)
we find, as
Eggenberger et al. (2004),
![]() 5-11%
higher than
5-11%
higher than
![]() .
Differently from Eggenberger et al.
(2004) we find that
.
Differently from Eggenberger et al.
(2004) we find that
![]() :
this is of primary relevance when making statements
concerning the difference between
:
this is of primary relevance when making statements
concerning the difference between
![]() and
and
![]() ,
otherwise we would also have to justify an even
bigger (not expected) difference between
,
otherwise we would also have to justify an even
bigger (not expected) difference between
![]() and
and
![]() .
We notice also that our inferred values of
.
We notice also that our inferred values of
![]() follow the same trend predicted by MLT parameter calibration based on
2D (Ludwig et al. 1999) and 3D (Trampedach 2004) hydrodynamic atmosphere models.
follow the same trend predicted by MLT parameter calibration based on
2D (Ludwig et al. 1999) and 3D (Trampedach 2004) hydrodynamic atmosphere models.
In order to draw more firm conclusions on the significance of
considering
![]() and
and
![]() as free
parameters we repeated our calibrations (A3, B3) and (A2, B2)
assuming a single parameter for both components ((A3c, B3c) and
(A2c, B2c)). The fit necessarily improves when an
additional free parameter is introduced in the calibration,
nevertheless we
find, with the observational constraints we adopted, the
difference between
as free
parameters we repeated our calibrations (A3, B3) and (A2, B2)
assuming a single parameter for both components ((A3c, B3c) and
(A2c, B2c)). The fit necessarily improves when an
additional free parameter is introduced in the calibration,
nevertheless we
find, with the observational constraints we adopted, the
difference between
![]() and
and
![]() significant.
We note also that the value of
significant.
We note also that the value of ![]() obtained in (A3c, B3c) and (A2c, B2c) calibrations
is quite close to the corresponding
obtained in (A3c, B3c) and (A2c, B2c) calibrations
is quite close to the corresponding
![]() .
.
We also find that, contrary to what was obtained by Morel et al. (2000), the use of a different theory of convection (MLT or FST) in our models does not change the set of parameters derived from the fitting. The only effect of convection model is a slight improvement in the fit of high frequencies when using FST (in particular for A component).
The available seismic data are not in favour of a convective
core in ![]() Cen A, moreover, the overshooting parameter needed for a convective core to
persist after the PMS (
Cen A, moreover, the overshooting parameter needed for a convective core to
persist after the PMS (![]() )
appears to be too large for a
model of the mass and chemical composition of
)
appears to be too large for a
model of the mass and chemical composition of ![]() Cen A (see
e.g. Demarque et al. 2004).
Cen A (see
e.g. Demarque et al. 2004).
Finally, we find that stars obeying different physics provide similar fits to those obtained with stars that merely have different parameters. As a consequence, we are not able from present data to discriminate either between different EoS, or between diffusion or diffusion-free models. Figure 7 shows, however, that expected precision from space missions would allow us to apply inversion techniques to frequency data. Adding seismic observables has significantly improved the determination of the system fundamental parameters, but more precise observations are needed to be able to extract information about the internal structure of the stars.
Acknowledgements
A.M. and J.M. acknowledge financial support from the Prodex-ESA Contract 15448/01/NL/Sfe(IC). A.M. is also thankful to Teresa Teixeira for her useful suggestions.