A&A 441, 23-39 (2005)
DOI: 10.1051/0004-6361:20053544
Equilibrium of large astrophysical structures in the Newton-Hooke spacetime
A. Balaguera-Antolínez - M. Nowakowski
Departamento de Fisica, Universidad de los Andes. A.A. 4976, Santafe de Bogota, DC, Colombia
Received 31 May 2005 / Accepted 13 July 2005
Abstract
Using the scalar and tensor virial equations, the Lane-Emden equation
expressing the hydrostatic equilibrium and small oscillations around the equilibrium, we show
how the cosmological constant  affects various astrophysical quantities important
for large matter conglomeration in the universe.
Among others we examine the effect of
affects various astrophysical quantities important
for large matter conglomeration in the universe.
Among others we examine the effect of  on the polytropic equation of state
for spherically symmetric objects and find non-negligible results in certain realistic cases.
We calculate the angular velocity for non-spherical oblate
configurations which demonstrates a clear effect of
on the polytropic equation of state
for spherically symmetric objects and find non-negligible results in certain realistic cases.
We calculate the angular velocity for non-spherical oblate
configurations which demonstrates a clear effect of  on high eccentricity objects.
We show that for oblate as well as prolate ellipsoids the cosmological constant
influences the critical mass and the temperature of the astrophysical object.
These and other results show that the effect of
on high eccentricity objects.
We show that for oblate as well as prolate ellipsoids the cosmological constant
influences the critical mass and the temperature of the astrophysical object.
These and other results show that the effect of  is large for
flat astrophysical bodies.
is large for
flat astrophysical bodies.
Key words: cosmology: large-scale structure of Universe - galaxies: clusters: general - instabilities
It is by now an established fact that the universe
accelerates faster than previously anticipated (Krauss 1998, 2003; Perlmutter et al. 1998, 1999;
Riess et al. 2004; Allen et al. 2004). Hence some hitherto neglected
ingredient (in general called Dark Energy) has to be responsible for this new phenomenon.
To account for this phenomenon we can introduce new physics in terms of a scalar field (Ratra & Peebles 1988)
or
modify three expressions in Einstein's equations which are often equivalent
to a specific model with a scalar field.
The three possibilities to account for the new physics are: the Einstein tensor, the energy-momentum
tensor (this is to say, the energy momentum tensor of a fluid
gets modified by the inclusion of other components, Kremer 2003) or the
equation of state (Kamenshchik et al. 2001).
The first possibility encompasses
a positive cosmological constant  and higher order gravity
with a more complicated Einstein-Hilbert action (Nojiri & Odintsov 2003). In the the present work we choose to work
with the cosmological constant as the simplest explanation for the acceleration of the universe.
We shall put forward the question if such a cosmological model has an influence
on astrophysical structures. We shall use equilibria concepts like hydrostatic
equilibrium and virial equations to see how relatively low density astrophysical matter
of different shapes behaves in a fast expanding universe. Anticipating the results, we can say that
indeed there are some interesting effects.
and higher order gravity
with a more complicated Einstein-Hilbert action (Nojiri & Odintsov 2003). In the the present work we choose to work
with the cosmological constant as the simplest explanation for the acceleration of the universe.
We shall put forward the question if such a cosmological model has an influence
on astrophysical structures. We shall use equilibria concepts like hydrostatic
equilibrium and virial equations to see how relatively low density astrophysical matter
of different shapes behaves in a fast expanding universe. Anticipating the results, we can say that
indeed there are some interesting effects.
Often it is assumed that  does not have any effect on
astrophysical processes which take place at scales different from the
cosmological ones.
Indeed, looking at the scales set by
does not have any effect on
astrophysical processes which take place at scales different from the
cosmological ones.
Indeed, looking at the scales set by  ,
this assumption seems to be
justified at the first glance. The scales set by the cosmological constant
are of truly cosmological order of magnitude (Nowakowski 2001; Balaguera-Antolínez et al. 2004).
The density scale is set by
,
this assumption seems to be
justified at the first glance. The scales set by the cosmological constant
are of truly cosmological order of magnitude (Nowakowski 2001; Balaguera-Antolínez et al. 2004).
The density scale is set by
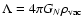 with
with
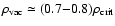 .
The length scale,
.
The length scale,
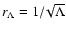 is of the order of the Hubble
radius while the mass scale
is of the order of the Hubble
radius while the mass scale
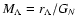 reaches up to the value of the
mass of the universe. These scales constitute the so-called coincidence
problem, namely the question as to why we should live exactly at an epoch where
the scales of the cosmological constant are also the scales of the universe.
Neither was it so in the past nor will it be so in the future when the universe expands further.
The only astrophysical structures which match these scales are superclusters whose
densities
are indeed of the order of magnitude of
reaches up to the value of the
mass of the universe. These scales constitute the so-called coincidence
problem, namely the question as to why we should live exactly at an epoch where
the scales of the cosmological constant are also the scales of the universe.
Neither was it so in the past nor will it be so in the future when the universe expands further.
The only astrophysical structures which match these scales are superclusters whose
densities
are indeed of the order of magnitude of
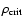 .
Indeed, here we can almost be sure that
the cosmological constant is of relevance (Nowakowski 2001; Sussman &
Hernandez 2003).
However, probing into astrophysical consequences of the cosmological constant of other, smaller and denser
structures
like clusters of galaxies or even galaxies themselves, would look a hopeless undertaking
unless we find circumstances where the effect of
.
Indeed, here we can almost be sure that
the cosmological constant is of relevance (Nowakowski 2001; Sussman &
Hernandez 2003).
However, probing into astrophysical consequences of the cosmological constant of other, smaller and denser
structures
like clusters of galaxies or even galaxies themselves, would look a hopeless undertaking
unless we find circumstances where the effect of  (which in the very principle is present)
gets enhanced. This can indeed happen through various mechanisms.
For instance, in a problem where
(which in the very principle is present)
gets enhanced. This can indeed happen through various mechanisms.
For instance, in a problem where
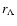 combines with a much smaller length scale,
say r0,
the effects can be sometimes expressed as
combines with a much smaller length scale,
say r0,
the effects can be sometimes expressed as
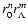 .
In consequence, the observable in which this expression enters gets affected
by
.
In consequence, the observable in which this expression enters gets affected
by  in a way which is important at much smaller scales
than
in a way which is important at much smaller scales
than
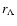 .
A concrete example is the Schwarzschild-de Sitter metric where
we find the parameter
.
A concrete example is the Schwarzschild-de Sitter metric where
we find the parameter
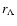 together with the much smaller length scale of the
Schwarzschild radius
together with the much smaller length scale of the
Schwarzschild radius 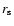 .
These two conspire in the form
.
These two conspire in the form
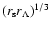 to define the largest
extension of bound orbits as explained in the text and in
Balaguera-Antolínez et al. (2005
to define the largest
extension of bound orbits as explained in the text and in
Balaguera-Antolínez et al. (2005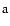 ).
We will discuss a very similar combination which emerges from the virial theorem defining
the largest possible virialized structure with a given mass.
Another possibility to enhance the effect of the
cosmological constant is to consider non-spherical objects. It then often happens
that the effect of
).
We will discuss a very similar combination which emerges from the virial theorem defining
the largest possible virialized structure with a given mass.
Another possibility to enhance the effect of the
cosmological constant is to consider non-spherical objects. It then often happens
that the effect of  becomes
becomes
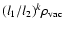 where liare two different length scales of a flattened object like a disk or an ellipsoid (Nowakowski et al. 2002).
This indeed happens for many astrophysical quantities, among other the critical mass,
the angular velocity and the temperature (mean velocity of the components
of the large structure) which we will discuss in the present paper.
Finally, we can vary a dimensional variable
to see if this enhances the effect of the cosmological constant.
As an example let us quote the polytropic index n in the equation of state
entering also the Lane-Emden equation. It is known that with growing n (
where liare two different length scales of a flattened object like a disk or an ellipsoid (Nowakowski et al. 2002).
This indeed happens for many astrophysical quantities, among other the critical mass,
the angular velocity and the temperature (mean velocity of the components
of the large structure) which we will discuss in the present paper.
Finally, we can vary a dimensional variable
to see if this enhances the effect of the cosmological constant.
As an example let us quote the polytropic index n in the equation of state
entering also the Lane-Emden equation. It is known that with growing n (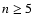 )
the object described by this equation of state does not have a well-defined radius
as the density goes only asymptotically to zero. We will show that this pattern of behavior
becomes more dominant with
)
the object described by this equation of state does not have a well-defined radius
as the density goes only asymptotically to zero. We will show that this pattern of behavior
becomes more dominant with
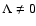 .
.
Of course, all these effects become stronger the more diluted the mass
conglomeration is. The superclusters are certainly the best candidates if we look
for astrophysical effects of the cosmological constant. As a matter of fact,
they do not seem to be virialized due to the extreme low density and their
pancake structure (Jaaniste et al. 1998) where the effect of flatness mentioned above becomes
powerful (Nowakowski et al. 2002; Sussman & Hernandez 2003).
For the next structure, the clusters of galaxies (or groups of galaxies)
with densities between one and three orders of magnitude above the critical density (see Padmanabhan 1993),
we would need one of the enhancing factors discussed above to see an appreciable effect of  .
This is possible in various ways as shown below. Galaxy clusters can have various forms, among others oblate and
prolate (Cooray 2000; Kalinkov et al. 2005).
And what is more, they can even rotate (Kalinkov et al. 2005).
We will show an explicit effect of
.
This is possible in various ways as shown below. Galaxy clusters can have various forms, among others oblate and
prolate (Cooray 2000; Kalinkov et al. 2005).
And what is more, they can even rotate (Kalinkov et al. 2005).
We will show an explicit effect of  on their
angular velocity and temperature in case the angular velocity is zero. Since the effect
of large eccentricity is larger for prolate than for oblate ellipsoids, it is
comforting to know that clusters can assume a prolate shape.
For low-density galaxies like the Low Surface Brightness (LSB) galaxies whose density
is roughly four orders of magnitude above the critical density (Blok & McGaugh 1996;
Blok et al. 2004) we still find some
effects. For n=5 and
on their
angular velocity and temperature in case the angular velocity is zero. Since the effect
of large eccentricity is larger for prolate than for oblate ellipsoids, it is
comforting to know that clusters can assume a prolate shape.
For low-density galaxies like the Low Surface Brightness (LSB) galaxies whose density
is roughly four orders of magnitude above the critical density (Blok & McGaugh 1996;
Blok et al. 2004) we still find some
effects. For n=5 and 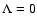 the solution of the Lane-Emden equation (Chandrasekhar 1967)
is very often used as a phenomenologically valid description of the density profile (called also
Plummer's law (Plummer 1911)). This is still possible as
the solution of the Lane-Emden equation (Chandrasekhar 1967)
is very often used as a phenomenologically valid description of the density profile (called also
Plummer's law (Plummer 1911)). This is still possible as
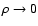 as
as
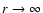 .
However, this
property vanishes for low-density galaxies and the n=5 case not only does not have a well-defined radius,
its solution does not vanish asymptotically which thus rendering it unphysical.
.
However, this
property vanishes for low-density galaxies and the n=5 case not only does not have a well-defined radius,
its solution does not vanish asymptotically which thus rendering it unphysical.
The paper is organized as follows. In the second section we will briefly review
the general form of virial theorem including pressure, magnetic fields and, of course, the cosmological constant.
Here we will also discuss some general results regarding  .
In the third section we will
specialize on spherical configurations. We will show how
.
In the third section we will
specialize on spherical configurations. We will show how  sets the scale of a maximal virial radius
and compare it to a result from the Schwarzschild-de Sitter metric. We will also solve the Lane-Emden
equation numerically and analytically (for the polytropic index n=2). In the fourth section we will
discuss non-spherical configurations. First, we will show how
sets the scale of a maximal virial radius
and compare it to a result from the Schwarzschild-de Sitter metric. We will also solve the Lane-Emden
equation numerically and analytically (for the polytropic index n=2). In the fourth section we will
discuss non-spherical configurations. First, we will show how  affects the
angular velocity of spheroids. In addition, we will discuss the
effects of
affects the
angular velocity of spheroids. In addition, we will discuss the
effects of  for the critical mass, mean velocity and mean rotational velocity too.
The fifth section is devoted to small oscillations around equilibrium.
for the critical mass, mean velocity and mean rotational velocity too.
The fifth section is devoted to small oscillations around equilibrium.
The cosmological constant enters the equations of Newtonian limit as a consequence of its appearance in the Einstein field equations.
It is through this weak field limit approximation that  enters also in the equations describing the structure of astrophysical configurations. It is interesting to note that all variables to be found in the
virial equations, are also present in the Poisson equation of the Newtonian limit. However, this is not always
the reason why these terms enter the virial equations, at least in the first order. The Poisson equation for a self-gravitating system modeled as an ideal fluid is written as
enters also in the equations describing the structure of astrophysical configurations. It is interesting to note that all variables to be found in the
virial equations, are also present in the Poisson equation of the Newtonian limit. However, this is not always
the reason why these terms enter the virial equations, at least in the first order. The Poisson equation for a self-gravitating system modeled as an ideal fluid is written as
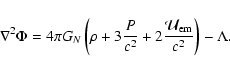 |
(1) |
where P is the pressure and
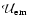 is the electromagnetic energy density.
The solution of (1) at the zeroth order of v/c (from now on we set c=1) is written as
is the electromagnetic energy density.
The solution of (1) at the zeroth order of v/c (from now on we set c=1) is written as
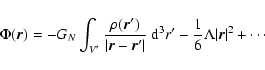 |
(2) |
where the dots stand for the correction terms that appear because the boundary conditions are now set at a
finite distance (Nowakowski 2001). These terms can be usually neglected.
The cosmological constant
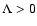 contributes to the expansion of the universe. This fact remains partly valid in the Newtonian limit
where
contributes to the expansion of the universe. This fact remains partly valid in the Newtonian limit
where  gives us an external force. This defines the
so-called (non-relativistic) Newton-Hooke spacetime (Bacry & Levy-Leblond 1967;
Derome & Dubois 1972; Aldrovandi et al. 1999).
gives us an external force. This defines the
so-called (non-relativistic) Newton-Hooke spacetime (Bacry & Levy-Leblond 1967;
Derome & Dubois 1972; Aldrovandi et al. 1999).
The second order tensor virial equation can be derived in different ways:
from a statistical point of view through the collisionless Boltzmann equation, from a variational principle or
by direct differentiation of the moment of inertia tensor
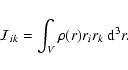 |
(3) |
In the following we use the statistical approach (Chandrasekhar 1961)
which also allows to derive higher order virial equations
(for instance, the first order virial equation refers to the motion of the center of mass). In this context,
from Boltzmann's equation ones can derive the equation for momentum conservation (Euler's equation) written for
a self gravitating system influenced by a magnetic field as
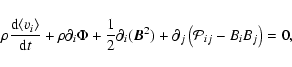 |
(4) |
where 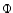 is the gravitational potential given by (2) (which includes
is the gravitational potential given by (2) (which includes  )
and
)
and
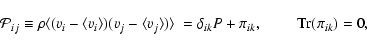 |
(5) |
is the pressure tensor, P is the pressure and 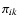 its traceless part. Equations (1)
and (4)
together with an equation of state
its traceless part. Equations (1)
and (4)
together with an equation of state
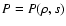 (s is the entropy) complete the description of a self gravitating fluid.
By taking exterior products of rk with Euler's equation and integrating over the volume of the system one obtains
the second order virial equation as
(s is the entropy) complete the description of a self gravitating fluid.
By taking exterior products of rk with Euler's equation and integrating over the volume of the system one obtains
the second order virial equation as
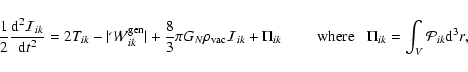 |
(6) |
where Tik is the kinetic energy tensor and
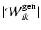 is a generalized potential energy tensor which contains the contribution
from the gravitational potential energy tensor
is a generalized potential energy tensor which contains the contribution
from the gravitational potential energy tensor
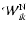 and
the contributions of magnetic field through
and
the contributions of magnetic field through
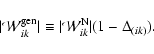 |
(7) |
The other quantities are defined as follows
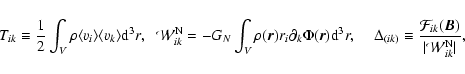 |
(8) |
together with
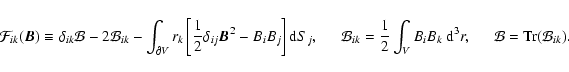 |
(9) |
A very useful version of the virial equation can be derived by assuming an isotropic pressure
tensor and taking the trace in Eq. (6). This way we get the scalar  -virial equation
-virial equation
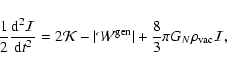 |
(10) |
where the total kinetic energy is written as
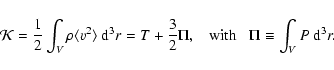 |
(11) |
The equilibrium condition is reached for
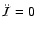 .
This gives us the general
.
This gives us the general  -virial theorem
-virial theorem
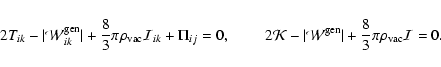 |
(12) |
For rotating configurations with constant angular velocity, the kinetic
term is modified as in the standard way as
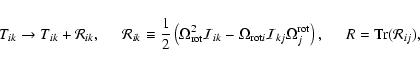 |
(13) |
with
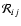 the rotational kinetic energy tensor and Tik is referred to motions observed from the rotating reference frame.
the rotational kinetic energy tensor and Tik is referred to motions observed from the rotating reference frame.
The  -virial theorem has been used in different contexts in Barrow (1989),
Wang & Steinhardt (1998), Nowakowski et al. (2002) and
Balaguera-Antolínez et al. (2004). In the present work we will extend these studies.
-virial theorem has been used in different contexts in Barrow (1989),
Wang & Steinhardt (1998), Nowakowski et al. (2002) and
Balaguera-Antolínez et al. (2004). In the present work we will extend these studies.
The tensor virial equation is widely used in many astrophysical applications.
The inclusion of  provides a new way to study effects of the cosmological constant
(parameters, in general) on astrophysical objects. The outcome depends essentially on two factors:
the geometry of the configuration and the density profile.
We will explore the spherical geometry for both constant and varying density profiles
and study some effects for non spherical geometry with constant density.
The consequences that can be derived from the
provides a new way to study effects of the cosmological constant
(parameters, in general) on astrophysical objects. The outcome depends essentially on two factors:
the geometry of the configuration and the density profile.
We will explore the spherical geometry for both constant and varying density profiles
and study some effects for non spherical geometry with constant density.
The consequences that can be derived from the  -virial theorem can be classified
in two categories. The first one puts an upper bound on the cosmological constant
or alternatively a lower bound on density of objects in gravitational
equilibrium. Provided these bounds are satisfied, we can also study in the second step
the effects of
-virial theorem can be classified
in two categories. The first one puts an upper bound on the cosmological constant
or alternatively a lower bound on density of objects in gravitational
equilibrium. Provided these bounds are satisfied, we can also study in the second step
the effects of  on other properties of the astrophysical configurations like rotation, small oscillations etc.
on other properties of the astrophysical configurations like rotation, small oscillations etc.
The first simple consequence of the virial equation emerges if we require the system to satisfy Eq. (12).
The fact that
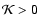 implies an upper bound on the vacuum energy density
implies an upper bound on the vacuum energy density
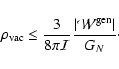 |
(14) |
All systems in equilibrium have to satisfy Eq. (14).
Note that the right hand side of this expression is a function of both the density and the geometry of the system.
Hence, we must expect different bounds for different geometries and density profiles.
For instance, if we assume a constant density and 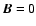 ,
we can define
,
we can define
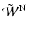 and
and
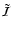 through
through
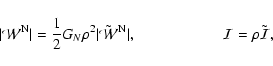 |
(15) |
such that the bound written in Eq. (14) becomes
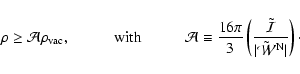 |
(16) |
The factor
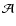 which is only a function of the geometry (if we neglect the contribution of magnetic fields),
will appear in many places in the paper.
Its relevance lies in the fact that it enhances the effect of the cosmological constant for
geometries far from spherical symmetry when
which is only a function of the geometry (if we neglect the contribution of magnetic fields),
will appear in many places in the paper.
Its relevance lies in the fact that it enhances the effect of the cosmological constant for
geometries far from spherical symmetry when 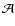 is large. A useful generalization
can be done for situations in which we use the tensor form of the virial equation, namely
is large. A useful generalization
can be done for situations in which we use the tensor form of the virial equation, namely
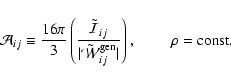 |
(17) |
Finally, a curious equation can be derived by eliminating  from the tensor virial equations:
from the tensor virial equations:
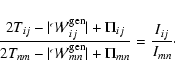 |
(18) |
Although  does not enter this equation, (18) is only valid if the denominator is non-zero as is the case
with
does not enter this equation, (18) is only valid if the denominator is non-zero as is the case
with
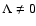 .
In Sect. 4 we will use this equality to infer a relation between the geometry and rotational velocity of
an ellipsoid.
Having discussed the general form of the virial theorem, we will discuss now the effects of
.
In Sect. 4 we will use this equality to infer a relation between the geometry and rotational velocity of
an ellipsoid.
Having discussed the general form of the virial theorem, we will discuss now the effects of  and set
and set 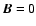 .
The tensor virial equation is trivially satisfied for spherically symmetric configuration without a magnetic field,
since
.
The tensor virial equation is trivially satisfied for spherically symmetric configuration without a magnetic field,
since
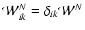 and
and
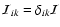 .
Therefore, in this section we use only the scalar form of Eq. (6).
.
Therefore, in this section we use only the scalar form of Eq. (6).
Explicit expressions can be derived in the spherical case with constant density, with
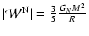 and
and
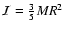 ,
so that
,
so that
 .
In this case the ratio
.
In this case the ratio
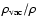 does not get enhanced much by the
geometrical factor
does not get enhanced much by the
geometrical factor
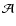 .
.
Worth mentioning is the result from general relativity.
There the upper bound for the cosmological constant comes out as
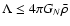 (Böhmer 2002, 2003)
where
(Böhmer 2002, 2003)
where
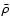 is the mean density defined by
is the mean density defined by
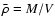 .
This bound is derived not only from Newtonian astrophysics,
but also from a general relativistic context via the Tolmann-Oppenheimer-Volkoff equation (Oppenheimer & Volkoff 1939)
for hydrostatic equilibrium of compact objects (Böhmer 2003; Balaguera-Antolínez et al. 2004).
.
This bound is derived not only from Newtonian astrophysics,
but also from a general relativistic context via the Tolmann-Oppenheimer-Volkoff equation (Oppenheimer & Volkoff 1939)
for hydrostatic equilibrium of compact objects (Böhmer 2003; Balaguera-Antolínez et al. 2004).
Another relevant effect of the cosmological constant is the existence of a maximal virial radius of a
spherical configuration which can be
calculated
from the  -virial equation. Using the expressions for
-virial equation. Using the expressions for
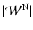 and
and
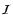 given before, Eq. (10) yields as a cubic equation for the virial radius
given before, Eq. (10) yields as a cubic equation for the virial radius
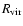
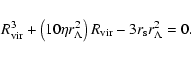 |
(19) |
Here we introduced the dimensionless temperature 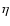 as
as
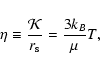 |
(20) |
where 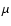 is the mass of the average member of the configuration,
is the mass of the average member of the configuration, 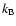 is the Boltzmann constant,
T is the temperature and
is the Boltzmann constant,
T is the temperature and 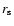 is defined by
is defined by
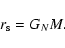 |
(21) |
The length scale
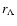 is set by the the cosmological constant as
is set by the the cosmological constant as
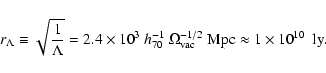 |
(22) |
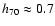 is the dimensionless Hubble parameter (Rich 2001) and
is the dimensionless Hubble parameter (Rich 2001) and
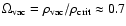 is the density parameter at the present time.
The positive real root of Eq. (19) is given by
is the density parameter at the present time.
The positive real root of Eq. (19) is given by
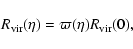 |
(23) |
where
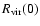 is radius for the configuration at
is radius for the configuration at 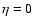 is given by
is given by
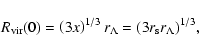 |
(24) |
and the dimensionless parameter x is defined as
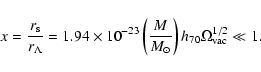 |
(25) |
The radius
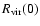 is the largest radius that a spherical homogeneous cloud may have in virial equilibrium
(i.e., satisfying Eq. (12)). The function
is the largest radius that a spherical homogeneous cloud may have in virial equilibrium
(i.e., satisfying Eq. (12)). The function
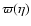 can be obtained from the solution of the cubic equation and reads
(clarified in the Appendix A)
can be obtained from the solution of the cubic equation and reads
(clarified in the Appendix A)
![\begin{displaymath}
\varpi(\eta)=2.53 x^{-1/3}\eta^{1/2}\sinh\left[\frac{1}{3}{\rm arcsinh}\left(0.24 x\eta^{-3/2}\right)\right].
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img92.gif) |
(26) |
Figure 1 shows the behavior of
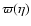 for different values of x.
We see that the increase of the temperature implies a decrease of the effects of
for different values of x.
We see that the increase of the temperature implies a decrease of the effects of  which can be easily checked if we solve
which can be easily checked if we solve
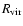 from the virial theorem with
from the virial theorem with 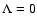 and
compare it to the approximation
and
compare it to the approximation
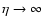 in (23):
in (23):
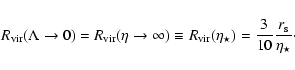 |
(27) |
We can consider Eq. (23) as a radius-temperature relation for a fixed mass applied on astrophysical structures in a single state of equilibrium
in the presence of  .
That is, given x and
.
That is, given x and 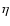 we calculate the radius.
But we can adopt another point of view for this relation.
Imagine a spherical configuration characterized by a constant mass M. In analogy to a thermodynamical reversible process, the configuration may pass from one state of virial equilibrium to another following the curve
we calculate the radius.
But we can adopt another point of view for this relation.
Imagine a spherical configuration characterized by a constant mass M. In analogy to a thermodynamical reversible process, the configuration may pass from one state of virial equilibrium to another following the curve
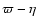 ,
that is, satisfying the condition
,
that is, satisfying the condition
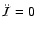 .
Clearly, there must be some final temperature
.
Clearly, there must be some final temperature
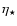 when this process ends since the temperature cannot increase indefinitely. But of course since the virial equations are not dynamical we cannot know which stage is the final one. If we assume that the effects of
when this process ends since the temperature cannot increase indefinitely. But of course since the virial equations are not dynamical we cannot know which stage is the final one. If we assume that the effects of  are negligible when
are negligible when
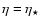 ,
then using Eqs. (26) and (27) we get
,
then using Eqs. (26) and (27) we get
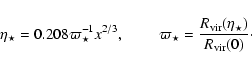 |
(28) |
This is an equation for the temperature 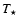
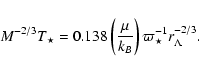 |
(29) |
For a hydrogen cloud (
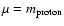 ), we then write the mass-temperature relation using Eqs. (22) and (25) as
), we then write the mass-temperature relation using Eqs. (22) and (25) as
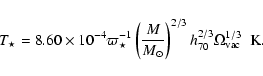 |
(30) |
Note that this expression maintains the same dependence of the standard mass-temperature relation derived
from the virial theorem, i.e.,
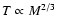 (see Wang & Steinhardt 1998, or Eq. (71) of this paper).
However the meaning of Eq. (30) is different from that of typical mass temperature relations
since (30)
is associated to the temperature that a system acquires in the final stage
after going through some reversible processes
which took the system through successive states of virial equilibrium
with constant mass from a radius
(see Wang & Steinhardt 1998, or Eq. (71) of this paper).
However the meaning of Eq. (30) is different from that of typical mass temperature relations
since (30)
is associated to the temperature that a system acquires in the final stage
after going through some reversible processes
which took the system through successive states of virial equilibrium
with constant mass from a radius
 to a radius
to a radius
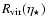 or vice versa. On the other hand, the
mass-temperature relation like Eq. (71) of this paper relates the temperature of any configuration in equilibrium with its observed mass at constant density. In that context one considers only one equilibrium state and the cosmological constant enters just as corrections.
or vice versa. On the other hand, the
mass-temperature relation like Eq. (71) of this paper relates the temperature of any configuration in equilibrium with its observed mass at constant density. In that context one considers only one equilibrium state and the cosmological constant enters just as corrections.
![\begin{figure}
\par\includegraphics[width=8cm,height=6.5cm,clip]{3544f1.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg105.gif) |
Figure 1:
Ratio between
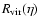 and
and
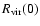 for different values of x as a function of
for different values of x as a function of
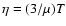 ,
where ,
where 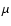 is the mass of the main average components of the system.
is the mass of the main average components of the system. |
| Open with DEXTER |
As a final remark on Eq. (23), we discuss a result which formally coincides with the
virial radius
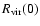 derived from the Schwarszchild de-Sitter
spacetime (Balaguera-Antolínez et al. 2005
derived from the Schwarszchild de-Sitter
spacetime (Balaguera-Antolínez et al. 2005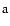 ),
but whose physical meaning is quite different.
The Schwarzschild-de Sitter metric takes the form
),
but whose physical meaning is quite different.
The Schwarzschild-de Sitter metric takes the form
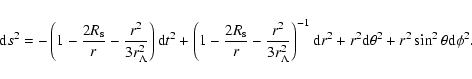 |
(31) |
Now in contrast to Eq. (21) we have
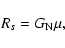 |
(32) |
with 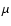 the mass of the object giving rise to the
Schwarzschild-de Sitter metric (in Eq. (21) M is the mass of the total conglomeration whereas
here we consider
the mass of the object giving rise to the
Schwarzschild-de Sitter metric (in Eq. (21) M is the mass of the total conglomeration whereas
here we consider 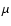 as the mass of its average member).
Choosing the affine parameter as the proper time
as the mass of its average member).
Choosing the affine parameter as the proper time 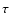 the equation of motion of a test-body
can be cast in a form similar to the corresponding equations from non-relativistic classical
mechanics.
the equation of motion of a test-body
can be cast in a form similar to the corresponding equations from non-relativistic classical
mechanics.
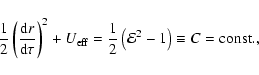 |
(33) |
where
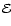 is a conserved quantity and
is a conserved quantity and
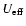 is the effective potential, defined by
is the effective potential, defined by
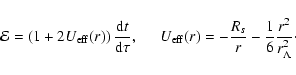 |
(34) |
For simplicity we are have chosen here the angular momentum L to be zero. With
L zero or not,
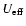 displays a local maximum below zero due
to
displays a local maximum below zero due
to
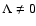 forming a potential barrier. This is to say, the standard local minimum where we find all the the bound orbits is now followed by a local maximum after which
forming a potential barrier. This is to say, the standard local minimum where we find all the the bound orbits is now followed by a local maximum after which
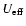 goes to
goes to 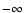 .
With
.
With 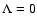 this function approaches zero asymptotically. One is immediately tempted to say that this barrier will occur at
cosmological distances. This is not the case and one calculates
this function approaches zero asymptotically. One is immediately tempted to say that this barrier will occur at
cosmological distances. This is not the case and one calculates
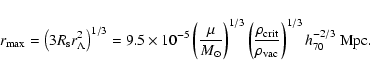 |
(35) |
In other words, the combination of the large scale
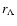 with the small
scale Rs gives us a distance of astrophysical relevance, namely
with the small
scale Rs gives us a distance of astrophysical relevance, namely
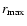 .
Its relevance lies in the fact that
beyond
.
Its relevance lies in the fact that
beyond
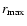 there are no bound orbits. Indeed, with
there are no bound orbits. Indeed, with 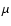 the solar mass,
the solar mass,
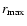 is of the order of a globular cluster extension;
with
is of the order of a globular cluster extension;
with 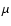 as the mass of globular cluster (70 pc),
as the mass of globular cluster (70 pc),
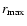 comes out to be of the order
of the size of a galaxy (10 kpc), and finally taking
comes out to be of the order
of the size of a galaxy (10 kpc), and finally taking 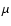 to be the mass of a galaxy,
to be the mass of a galaxy,
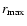 gives the right length scale of a galaxy cluster (1 Mpc). Certainly, the value of the extension of a large astrophysical body is the result of a multi-body interaction. But with the actual values of
gives the right length scale of a galaxy cluster (1 Mpc). Certainly, the value of the extension of a large astrophysical body is the result of a multi-body interaction. But with the actual values of
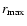 ,
it appears as if the length scale (we emphasize that we are concerned here about scales and not precise numbers) of an astrophysical conglomeration is approximately
,
it appears as if the length scale (we emphasize that we are concerned here about scales and not precise numbers) of an astrophysical conglomeration is approximately
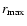 which apparently means that this scale does not change drastically when going from a two body problem to a multi-body calculation. This makes sense if the object under consideration is not too dense.
We can now say that whereas M in
which apparently means that this scale does not change drastically when going from a two body problem to a multi-body calculation. This makes sense if the object under consideration is not too dense.
We can now say that whereas M in
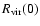 (via
(via 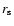 )
is the mass of the object,
)
is the mass of the object,
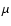 in Eq. (33) is the mass of its members. Clearly, we have
in Eq. (33) is the mass of its members. Clearly, we have
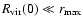 ,
but both scales are of astrophysical order of magnitude.
A result related to Eq. (24) derived in the framework of general
relativity can be found in Mak et al. (2000).
The examination of configurations with non-constant densities can be done in two directions.
Knowing the density profile
,
but both scales are of astrophysical order of magnitude.
A result related to Eq. (24) derived in the framework of general
relativity can be found in Mak et al. (2000).
The examination of configurations with non-constant densities can be done in two directions.
Knowing the density profile 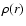 ,
we can set up the virial equation and evaluate
the equilibrium conditions from the inequality (14).
In this picture, the effects of
,
we can set up the virial equation and evaluate
the equilibrium conditions from the inequality (14).
In this picture, the effects of  are included in the solution for the potential
are included in the solution for the potential 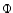 as
in Eq. (2)
and the resulting term acts like an external force, as mentioned before.
as
in Eq. (2)
and the resulting term acts like an external force, as mentioned before.
The second option is to combine the Eqs. (1), (4) and an equation of state (e.o.s)
for which we can take a polytropic form
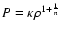 .
Then we obtain the Lane-Emden equation
with
.
Then we obtain the Lane-Emden equation
with  (Balaquera-Antolínez et al. 2004)
(Balaquera-Antolínez et al. 2004)
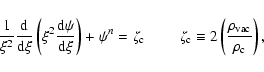 |
(36) |
where
 is the central density,
is the central density,  ,
,
 with
with 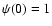 ,
,
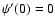 and a is the associated Jeans length defined as
and a is the associated Jeans length defined as
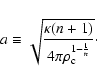 |
(37) |
It is important to notice that in this picture the expected effects of  are to be found in the behavior of the density profile
since now Eq. (36) implies that its solution is also function of the parameter
are to be found in the behavior of the density profile
since now Eq. (36) implies that its solution is also function of the parameter
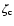 .
Some effects of
.
Some effects of  are contained in the total mass and the radius of the configuration
which is reached when
are contained in the total mass and the radius of the configuration
which is reached when
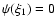 .
Hence Eq. (36) implies
.
Hence Eq. (36) implies
![\begin{displaymath}
\xi_{1}=\left[\frac{1}{\zeta_{\rm c}}\left\vert\frac{{\rm d}...
...i}{{\rm d}\xi} \right)_{\xi_{1}} \right\vert\right]^{1/2}\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img127.gif) |
(38) |
Note that the radius of the configuration is now proportional to
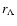 .
This is due to the fact that
.
This is due to the fact that  sets a scale for length.
However, this does not mean that R will be always of the order
sets a scale for length.
However, this does not mean that R will be always of the order
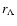 as
as  is also contained in
the expression in the square brackets in Eq. (38). We will show this below in a concrete example.
Since
is also contained in
the expression in the square brackets in Eq. (38). We will show this below in a concrete example.
Since  is a new constant scale the Lane-Emden equation loses some of its scaling properties as explained
in Balaguera-Antolínez et al. (2004).
The mass of the configuration can be determined as usual with,
is a new constant scale the Lane-Emden equation loses some of its scaling properties as explained
in Balaguera-Antolínez et al. (2004).
The mass of the configuration can be determined as usual with,
![\begin{displaymath}
M(\xi)=4\pi a^{3}\rho_{\rm c}\int_{0}^{\xi}\xi^{2}\psi^{n}~{...
...ta_{\rm c}-\frac{3}{\xi}\frac{{\rm d}\psi}{{\rm d}\xi}\right],
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img128.gif) |
(39) |
where we used Eq. (36) for the second equality.
The total mass is then obtained by evaluating the last expression at
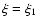 .
As expected, the mass increases because the Newtonian gravity has to be stronger in order for the configuration to be in equilibrium
with
.
As expected, the mass increases because the Newtonian gravity has to be stronger in order for the configuration to be in equilibrium
with
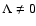 .
Figure 2 shows the numerical solutions
for n=1 to n=5. We expect that the radius of the configuration is increased by the contribution of
.
Figure 2 shows the numerical solutions
for n=1 to n=5. We expect that the radius of the configuration is increased by the contribution of
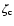 and find it confirmed in the figures.
However, not always is the radius of the configuration well defined, even if n<5.
For sizable values of
and find it confirmed in the figures.
However, not always is the radius of the configuration well defined, even if n<5.
For sizable values of
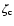 (black line) we cannot find physical solutions of
Eq. (36)
as the function
(black line) we cannot find physical solutions of
Eq. (36)
as the function 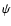 acquires a positive slope.
One might be tempted to claim that the radius of the configuration could be defined in these situations as the position
where
acquires a positive slope.
One might be tempted to claim that the radius of the configuration could be defined in these situations as the position
where 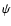 has its first minimum, but as can be seen for n=3such a radius would be smaller than the radius with
has its first minimum, but as can be seen for n=3such a radius would be smaller than the radius with
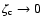 which contradicts the behavior shown for the other solutions where
which contradicts the behavior shown for the other solutions where
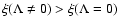 .
As already mentioned above this is the correct hierarchy between the radii because large
.
As already mentioned above this is the correct hierarchy between the radii because large
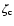 gives rise to
a large external force pulling at the matter.
The numerical solutions show that for relatively large values of
gives rise to
a large external force pulling at the matter.
The numerical solutions show that for relatively large values of
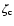 ,
only n=1 has a well defined radius.
In this case the
effect of
,
only n=1 has a well defined radius.
In this case the
effect of  is a
is a 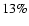 increase of the matter extension as compared to
increase of the matter extension as compared to
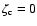 .
As we increase the polytropic index,
.
As we increase the polytropic index,
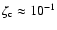 leads to non-physical solutions
while the effect with bigger values of
leads to non-physical solutions
while the effect with bigger values of
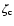 becomes visible only for n=3.
For instance,
becomes visible only for n=3.
For instance,
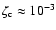 results in a radius which is
results in a radius which is 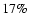 bigger than the corresponding value with
bigger than the corresponding value with
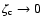 .
The combination n=4 and
.
The combination n=4 and
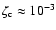 also leads to a non-physical solution,
whereas the radius of the case
also leads to a non-physical solution,
whereas the radius of the case
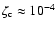 displays a difference of
displays a difference of 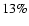 as compared to
as compared to
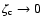 .
Finally, for n=5, the only physical solutions are obtained for the lowest values of
.
Finally, for n=5, the only physical solutions are obtained for the lowest values of
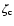 where
where 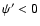 This case is particularly interesting as with
This case is particularly interesting as with
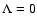 it is often used as a viable phenomenological
parametrization of densities (Plummer 1911; Binney & Tremaine 1987). The solution has an asymptotic behavior as r-awhich has been also found in LSB galaxies de Blok et al. 2004). With
it is often used as a viable phenomenological
parametrization of densities (Plummer 1911; Binney & Tremaine 1987). The solution has an asymptotic behavior as r-awhich has been also found in LSB galaxies de Blok et al. 2004). With
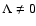 the n=5 seems less appealing is the matter
is diluted.
For all values of n, the difference between
the n=5 seems less appealing is the matter
is diluted.
For all values of n, the difference between
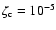 and 10-7 is negligible.
and 10-7 is negligible.
![\begin{figure}
\par\includegraphics[angle=270,width=14cm]{3544f2.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg141.gif) |
Figure 2:
Effects of  on the behavior of the density of a polytropic configuration for different ratios
on the behavior of the density of a polytropic configuration for different ratios
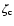 and different polytropic indices. The radius of the configuration is not always defined, even for n<5.
For higher values of
and different polytropic indices. The radius of the configuration is not always defined, even for n<5.
For higher values of
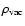 ,
only the n=1 case has a definite radius for these values
of ,
only the n=1 case has a definite radius for these values
of
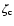 .
For other cases, the configuration is defined only for small .
For other cases, the configuration is defined only for small
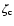 . . |
| Open with DEXTER |
Analytical solutions of (36) can be found for n=0,1 and n=5 if 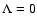 .
For
.
For
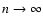 ,
the polytropic equation of state reduces to the equation of state
of the isothermal sphere
,
the polytropic equation of state reduces to the equation of state
of the isothermal sphere
 .
As an example, for
.
As an example, for
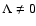 ,
we can write the analytical solution in the case n=1 as
,
we can write the analytical solution in the case n=1 as
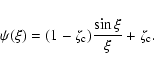 |
(40) |
The radius is
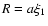 ,
where
,
where 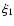 is the solution of the transcendental equation
is the solution of the transcendental equation
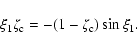 |
(41) |
In the first order of
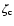 one finds
one finds
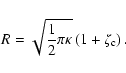 |
(42) |
Equation (41) also implies that there exists some
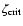 such that for
such that for
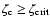 ,
we cannot find a real solution for
,
we cannot find a real solution for 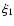 .
Approximately this gives
.
Approximately this gives
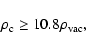 |
(43) |
which, provided the overall density is not too big, is better that
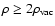 which is a result from
the general inequality (16) for
which is a result from
the general inequality (16) for
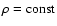 and spherical symmetry.
Finally, we can calculate the contribution of
and spherical symmetry.
Finally, we can calculate the contribution of  to the total energy of the object. Generalizing
the results found in (Chandrasekhar 1967) we obtain
to the total energy of the object. Generalizing
the results found in (Chandrasekhar 1967) we obtain
![\begin{displaymath}
E=\frac{1}{3}(3-n)\mathcal{W}^{\rm N}, \hspace{0.5cm} \mathc...
...ght)
\left[1
+\left(\frac{R}{r_{\rm max}}\right)^3\right]\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img154.gif) |
(44) |
from which we infer that the correction is very small in this case.
At the end of this section we would like to summarize
the findings from Fig. 2. In Table 1 we write the ratio
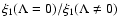 for the same ratios
for the same ratios
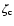 and polytropic index as in Fig. 2. The horizontal line represents a non-defined radius. The symbol
and polytropic index as in Fig. 2. The horizontal line represents a non-defined radius. The symbol  indicates that the radius is defined only asymptotically in case of
indicates that the radius is defined only asymptotically in case of 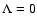 .
.
Table 1:
Values of the fraction
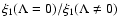 for different values of the ratio
for different values of the ratio
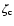 and the polytropic index. The horizontal lines represents the non well defined radius.
and the polytropic index. The horizontal lines represents the non well defined radius.
As emphasized already before, the effect of  can get enhanced for non-spherical objects. This happens when the vacuum energy gets multiplied
by a ratio of two length scales l1 and l2 and we end up with expressions like
can get enhanced for non-spherical objects. This happens when the vacuum energy gets multiplied
by a ratio of two length scales l1 and l2 and we end up with expressions like
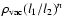 .
For ellipsoidal configurations the geometrical parameter
.
For ellipsoidal configurations the geometrical parameter 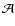 entering among others the inequality (16) can be calculated from its definition (17) with
entering among others the inequality (16) can be calculated from its definition (17) with
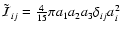 and
and
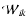 given in Binney & Tremaine (1987, p. 57). We have (Nowakowski et al. 2002)
given in Binney & Tremaine (1987, p. 57). We have (Nowakowski et al. 2002)
where the eccentricity![[*]](/icons/foot_motif.gif) e is
e2=1-a32/a12 for the oblate and
e2=1-a12/a32 for the prolate case.
The behavior of
e is
e2=1-a32/a12 for the oblate and
e2=1-a12/a32 for the prolate case.
The behavior of
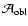 and
and
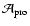 is shown in Fig. 3.
It is clear that for very flat astrophysical objects we can gain in this way several orders of magnitude of enhancement
of the effect of
is shown in Fig. 3.
It is clear that for very flat astrophysical objects we can gain in this way several orders of magnitude of enhancement
of the effect of  if
if 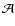 is a factor of attached to
is a factor of attached to
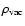 .
Needless to say that we often encounter in the universe flat objects like elliptical galaxies,
spiral disk galaxies, clusters of galaxies of different forms and finally
superclusters which can have the forms
of pancakes.
Of course, the more dilute the system is, the bigger the effect of
.
Needless to say that we often encounter in the universe flat objects like elliptical galaxies,
spiral disk galaxies, clusters of galaxies of different forms and finally
superclusters which can have the forms
of pancakes.
Of course, the more dilute the system is, the bigger the effect of  .
We can expect sizable effects for clusters and superclusters,
even for very flat galaxies.
Regarding the latter, low density galaxies like the nearly invisible galaxies are among other the best candidates.
.
We can expect sizable effects for clusters and superclusters,
even for very flat galaxies.
Regarding the latter, low density galaxies like the nearly invisible galaxies are among other the best candidates.
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f3.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg171.gif) |
Figure 3:
Function g(e) and geometrical factor
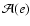 for prolate and oblate ellipsoids.
These functions have their largest values for flat oblates and large prolates.
for prolate and oblate ellipsoids.
These functions have their largest values for flat oblates and large prolates. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f4.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg172.gif) |
Figure 4:
Effects of  on the angular velocity
on the angular velocity
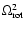 and the ratio
and the ratio 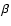 for
for
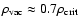 . .
|
| Open with DEXTER |
A convenient way to model almost all flat shaped objects is to consider ellipsoids which in the limit of
flattened spheroids can be considered as disks.
There are three different kinds of elliptical configurations, characterized by three semi-axes
a1=a, a2=b and a3=c: oblate, with a=b<c, prolate with a=b>c and triaxial systems with a> b > c.
Here the tensor virial equation provides a tool to determine which of these geometries are compatible with the
virial equilibrium. Considering the case
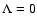 and
and 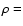 constant,
or spheroids with confocal density
distribution whose isodensity surfaces are similar concentric ellipsoids (Roberts 1962; Binney & Tremaine 1987) i.e.
constant,
or spheroids with confocal density
distribution whose isodensity surfaces are similar concentric ellipsoids (Roberts 1962; Binney & Tremaine 1987) i.e.
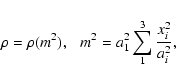 |
(46) |
the oblate ellipsoid (MacLaurin) emerges as a solution of the virial equations with a bifurcation point to a triaxial
Jacobi ellipsoid (Chandrasekhar 1969). We can view the virial equation without  as a homogeneous
equation. Switching on
as a homogeneous
equation. Switching on
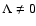 this
becomes an inhomogeneous equation whose right hand side is proportional to
this
becomes an inhomogeneous equation whose right hand side is proportional to
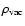 .
It is therefore a priori not clear
if in the case of
.
It is therefore a priori not clear
if in the case of
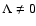 we can draw the same conclusions as with
we can draw the same conclusions as with 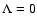 .
.
Let us assume a configuration which is rotating with constant angular velocity around the z axis. Neglecting the internal motions, the  -tensor virial Eq. (6) for such a configuration is
-tensor virial Eq. (6) for such a configuration is
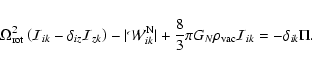 |
(47) |
The equations with diagonal elements yield the following identities
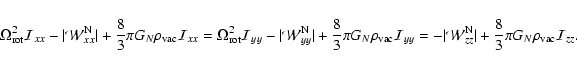 |
(48) |
This set of equations can be resolved for the angular velocity:
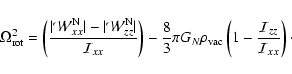 |
(49) |
The same expression holds if we make the replacement
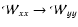 and
and
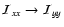 on the right hand side of Eq. (49).
We can also eliminate
on the right hand side of Eq. (49).
We can also eliminate
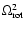 from these expressions to arrive at the condition
from these expressions to arrive at the condition
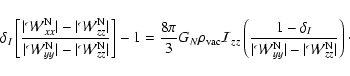 |
(50) |
With
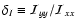 .
This expression determines the possible ellipsoidal configurations. One solution is obvious:
.
This expression determines the possible ellipsoidal configurations. One solution is obvious:
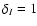 together with
together with
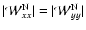 .
This happens if the density is constant or for a
confocal ellipsoid with the density given in Eq. (46). Hence this is not different from the
.
This happens if the density is constant or for a
confocal ellipsoid with the density given in Eq. (46). Hence this is not different from the
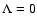 case. However, the bifurcation point to a triaxial system will get affected by
case. However, the bifurcation point to a triaxial system will get affected by  (Balaguera-Antolínez et al. 2005
(Balaguera-Antolínez et al. 2005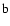 ).
Furthermore, the explicit calculation of this bifurcation point will now depend also on the details
of the density profile even if we take the latter to be as in Eq. (46). This is a direct consequence
of a ``pre-existing'' density scale
).
Furthermore, the explicit calculation of this bifurcation point will now depend also on the details
of the density profile even if we take the latter to be as in Eq. (46). This is a direct consequence
of a ``pre-existing'' density scale
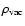 .
For a homogeneous configuration we have
.
For a homogeneous configuration we have
| |
|
![$\displaystyle \frac{\Omega_{\rm rot}^{2}}{8\pi G_N\rho}=\frac{1}{3}\mathcal{A}_...
...left(\frac{\mathcal{A}_{xx}-\eta_{x}\mathcal{A}_{zz}}{1-\eta_{x}}\right)\right]$](/articles/aa/full/2005/37/aa3544-05/img185.gif) |
(51) |
| |
|
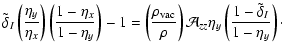 |
|
Where
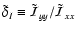 ,
,
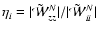 and
and
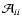 are defined in
Eq. (17).
For an oblate configuration they can be calculated in terms of the eccentricity
are defined in
Eq. (17).
For an oblate configuration they can be calculated in terms of the eccentricity
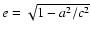 to give (Binney & Tremaine 1987)
to give (Binney & Tremaine 1987)
![\begin{displaymath}
\mathcal{A}_{xx}=\mathcal{A}_{yy}=\frac{4}{3}\frac{e^{2}}{\s...
...[\frac{1}{\sqrt{1-e^{2}}}-\frac{\arcsin e}{e}\right]^{-1}\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img191.gif) |
(52) |
Furthermore we have
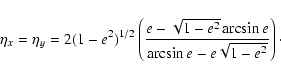 |
(53) |
Using these expressions, we write the constant angular velocity for an oblate ellipsoid from the first line of Eq. (51) as
![\begin{displaymath}
\Omega_{\rm rot}^{2}=\Omega_{0}^{2}\left[1-\left(\frac{\rho_{\rm vac}}{\rho}\right)g(e)\right],
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img193.gif) |
(54) |
where
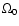 corresponding to the angular velocity when
corresponding to the angular velocity when 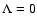 is given by the MacLaurin formula
is given by the MacLaurin formula
![\begin{displaymath}
\Omega_{0}^{2}=\frac{8}{3}\pi\mathcal{A}_{xx}^{-1}\left(1-\e...
...2}\right)\arcsin e-\frac{3}{e^{2}}\left(1-e^{2}\right)\right].
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img195.gif) |
(55) |
The function g(e) defined through Eq. (51) can also be calculated with explicit
dependence on the eccentricity as
![\begin{displaymath}
g(e)\equiv \frac{\mathcal{A}_{xx}-\eta_{x}\mathcal{A}_{zz}}{...
...t(3-2e^{2}\right)\arcsin e-3e\left(1-e^{2}\right)\right]^{-1}.
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img196.gif) |
(56) |
As is evident from the above equations,  has a twofold effect on the angular velocity.
Firstly, it reduces the angular velocity with respect to the value
has a twofold effect on the angular velocity.
Firstly, it reduces the angular velocity with respect to the value
 especially at the local maximum (see Fig. 3).
This is not a small effect and can affect even galaxies.
Secondly, we see from Eq. (55) that
especially at the local maximum (see Fig. 3).
This is not a small effect and can affect even galaxies.
Secondly, we see from Eq. (55) that
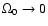 for
for 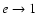 .
On the other hand
.
On the other hand
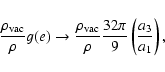 |
(57) |
approaching 1 for a very flat oblate configuration and not too dense matter. Therefore, beyond the local maximum in
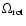 the cosmological constant causes a steeper fall of
the cosmological constant causes a steeper fall of
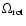 towards 0.
Another relevant interesting quantity which can be calculated in this context is the ratio of the rotational over
the gravitational energy contributions to the scalar virial equations, i.e.,
towards 0.
Another relevant interesting quantity which can be calculated in this context is the ratio of the rotational over
the gravitational energy contributions to the scalar virial equations, i.e.,
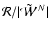 .
In accordance with Eq. (55) the latter can be written as
.
In accordance with Eq. (55) the latter can be written as
![\begin{displaymath}
\beta\equiv \mathcal{R}/\vert\mathcal{W}^N\vert, \hspace{0.8...
...3}{2e^{2}}\left[1-\frac{e(1-e^{2})^{1/2}}{\arcsin e}\right]-1.
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img201.gif) |
(58) |
The effects on 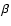 are therefore similar to the the ones encountered in
are therefore similar to the the ones encountered in
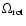 (see also Figs. 3).
Finally, on account of P >0 we can infer from the virial equations with
(see also Figs. 3).
Finally, on account of P >0 we can infer from the virial equations with
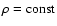 .
the following inequality
.
the following inequality
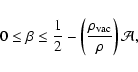 |
(59) |
which together with Eq. (58) results in an inequality for the density of an ellipsoidal configuration:
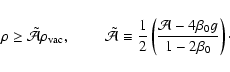 |
(60) |
For 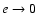 ,
we have
,
we have
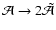 ,
while for
,
while for 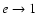 ,
,
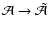 ,
and
,
and
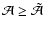 .
Therefore the above inequality is slightly weaker than the bound given in Eq. (16). Nevertheless it is useful since it it derived
directly from a different starting point (P>0) than Eq. (16) which is based on
.
Therefore the above inequality is slightly weaker than the bound given in Eq. (16). Nevertheless it is useful since it it derived
directly from a different starting point (P>0) than Eq. (16) which is based on
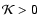 .
.
Not always the deviation from spherical symmetry guarantees that the effect of  on observables is
sizable. This depends which observable we calculate and, in particular, which scales we compare. If we compare
on observables is
sizable. This depends which observable we calculate and, in particular, which scales we compare. If we compare
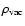 to densities,
the quantities
to densities,
the quantities 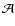 and
and
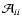 defined in Eq. (16)
are for flattened objects large enough to enhance the effect of
defined in Eq. (16)
are for flattened objects large enough to enhance the effect of  .
If
.
If
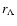 is combined with the
Schwarzschild radius
is combined with the
Schwarzschild radius 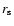 to give
to give
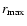 as in Eq. (24), the result is still of astrophysical relevance.
But if we had to compare one of the axes of an ellipsoid to
as in Eq. (24), the result is still of astrophysical relevance.
But if we had to compare one of the axes of an ellipsoid to
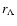 (i.e.
(i.e.
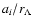 )
the effect would be
negligible unless the extension ai is bigger than Mpc (clusters and superclusters) and the small ratio
)
the effect would be
negligible unless the extension ai is bigger than Mpc (clusters and superclusters) and the small ratio
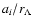 is comparable to another small quantity of the same order of magnitude entering the equation under
consideration.
This happens for instance if we generalize a result (discussed in Binney & Tremaine 1987, Chap. 4)
on a mass-weighted mean-square rotation speed v0 of an ellipsoidal object to include
is comparable to another small quantity of the same order of magnitude entering the equation under
consideration.
This happens for instance if we generalize a result (discussed in Binney & Tremaine 1987, Chap. 4)
on a mass-weighted mean-square rotation speed v0 of an ellipsoidal object to include  .
Assume that due to symmetry properties of the object
the only relevant components of the tensors in the tensor virial equations are xx and zz. We then
obtain
.
Assume that due to symmetry properties of the object
the only relevant components of the tensors in the tensor virial equations are xx and zz. We then
obtain
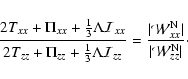 |
(61) |
If the only motion is a rotation about the z axis we have Tzz=0 and we can solve for Txx as
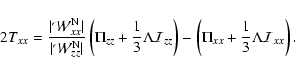 |
(62) |
Using Eqs. (5), (6) and (8), the quantities entering our equation can be parametrized
in the following way
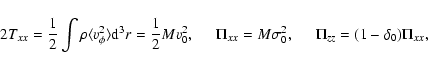 |
(63) |
where v02 is the mass weighted mean angular velocity, 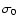 is the mass-weighted mean-square random velocity in the x direction and
is the mass-weighted mean-square random velocity in the x direction and 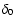 measures the anisotropy in
measures the anisotropy in 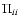 .
If
.
If 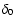 is of the order of one, it suffices to compare
is of the order of one, it suffices to compare
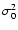 with
with
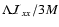 .
If both are
of the same order of magnitude, the effect of
.
If both are
of the same order of magnitude, the effect of  is non-negligible. Since v0 and
is non-negligible. Since v0 and 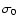 are of
the same order of magnitude and v0 is non-relativistic, we can assume that
are of
the same order of magnitude and v0 is non-relativistic, we can assume that
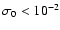 .
The
quantity
.
The
quantity
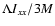 can be estimated to be
can be estimated to be
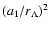 .
Hence if
.
Hence if
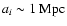 ,
v0 (
,
v0 (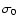 )
has to be truly non-relativistic and of the the order of 10-6 to gain an appreciable effect of
)
has to be truly non-relativistic and of the the order of 10-6 to gain an appreciable effect of  .
This
improves if ai is one order of magnitude bigger which is possible for large galaxy clusters. The velocities have to be then at most
10-4. In these cases we have to keep
.
This
improves if ai is one order of magnitude bigger which is possible for large galaxy clusters. The velocities have to be then at most
10-4. In these cases we have to keep  and while solving Eq. (63) for v02 one has
and while solving Eq. (63) for v02 one has
![\begin{displaymath}
\frac{1}{2}\frac{v_0^2}{\sigma_0^2}=\left(1-\delta_0\right)\...
...x}^{\rm N}\vert}{\vert\mathcal{W}_{zz}^{\rm N}\vert}-1\right].
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img222.gif) |
(64) |
Note that if  cannot be neglected
cannot be neglected
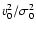 is not only a function of the eccentricity for
ellipsoids with the density give in Eq. (46), but depends also on the details of the matter density as the latter does not cancel.
is not only a function of the eccentricity for
ellipsoids with the density give in Eq. (46), but depends also on the details of the matter density as the latter does not cancel.
Using almost the same set-up as above, we can use Eq. (18) to establish a relation between
v0, the mass M and the geometry of the object which we choose below to be oblate. After straightforward
algebra we obtain
![\begin{displaymath}
\frac{v_0^2}{2\sigma_{0}^{2}}=\frac{3}{10}\frac{G_NM}{\sigma...
...}\right]+(1-\delta_{0})\left(\frac{a_{1}}{a_{3}}\right)^{2}-1.
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img224.gif) |
(65) |
Since this relation is derived from Eq. (18) which in turn is based on the assumption
of
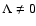 it is only valid for non-zero cosmological constant albeit the latter does not enter
the expression. Note the enhancement factor
(a1/a3)2.
it is only valid for non-zero cosmological constant albeit the latter does not enter
the expression. Note the enhancement factor
(a1/a3)2.
We can now derive other relevant quantities from the scalar  -virial theorem applied
to homogeneous ellipsoidal configurations. In this section we will not consider rotating configurations,
but systems with kinetic energy coming from internal motions. We will focus again on ellipsoidal, oblate and prolate, geometries.
As in the
preceding section the relevant quantity here is the function
-virial theorem applied
to homogeneous ellipsoidal configurations. In this section we will not consider rotating configurations,
but systems with kinetic energy coming from internal motions. We will focus again on ellipsoidal, oblate and prolate, geometries.
As in the
preceding section the relevant quantity here is the function
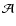 written for both configurations in Eq. (45).
written for both configurations in Eq. (45).
Critical mass: consider the stability criteria for a homogeneous cloud with mass
M and internal mean velocity
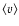 in mechanical equilibrium with the background with pressure P
(see Padmannabhan 2000, Chap. 8).
The system will collapse under it's own gravity (P<0) if its mass is greater than a critical mass
in mechanical equilibrium with the background with pressure P
(see Padmannabhan 2000, Chap. 8).
The system will collapse under it's own gravity (P<0) if its mass is greater than a critical mass 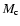 .
With cosmological constant, this critical mass is increased with respect to its value
.
With cosmological constant, this critical mass is increased with respect to its value
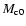 when
when 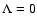 ,
which is expected,
since now there is an external force associated to
,
which is expected,
since now there is an external force associated to  that acts against Newtonian gravity
and hence the collapse can be postponed. By using the scalar virial theorem (12) and setting P=0
as the criterion for the onset of instability, we can write for arbitrary geometry
that acts against Newtonian gravity
and hence the collapse can be postponed. By using the scalar virial theorem (12) and setting P=0
as the criterion for the onset of instability, we can write for arbitrary geometry
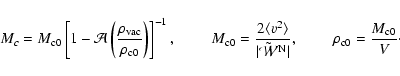 |
(66) |
This expression is valid for any geometry.
However, we pointed out already that spherical symmetry implies
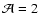 and the effect is suppressed. Some numerical values can be considered
by writing
and the effect is suppressed. Some numerical values can be considered
by writing
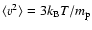 for a hydrogen cloud with
for a hydrogen cloud with
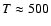 K and radius
K and radius
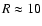 pc. One then has
pc. One then has
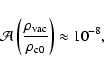 |
(67) |
which represents a very tiny correction to the critical mass
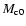 for a spherically symmetric object.
On the other hand, for ellipsoidal configurations with the same temperature, we have
for a spherically symmetric object.
On the other hand, for ellipsoidal configurations with the same temperature, we have
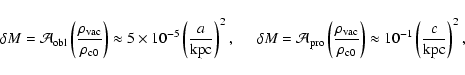 |
(68) |
in the 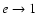 approximation for oblate and prolate configurations, respectively.
We have set c=10a for the prolate case and
approximation for oblate and prolate configurations, respectively.
We have set c=10a for the prolate case and
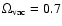 .
For an oblate ellipsoid with
.
For an oblate ellipsoid with
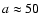 kpc, one has
kpc, one has
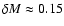 while for the prolate ellipsoid with
while for the prolate ellipsoid with
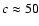 ,
,
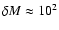 .
.
Mean velocity and Mass-Temperature relation.
By virtue of the scalar  -virial theorem, we can also write down the mass-temperature relation for an astrophysical structure.
Note first that using
-virial theorem, we can also write down the mass-temperature relation for an astrophysical structure.
Note first that using
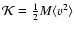 in Eq. (12) we have for
in Eq. (12) we have for 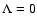 the standard expression for
the mean velocity
the standard expression for
the mean velocity
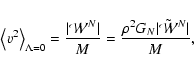 |
(69) |
where the second equality applies to the constant density case. Clearly, with 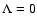 the mean velocity cannot become zero. Let us
contrast it to the case with
the mean velocity cannot become zero. Let us
contrast it to the case with
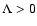 .
One obtains
.
One obtains
![\begin{displaymath}
\left\langle v^{2} \right\rangle =\frac{\rho^{2}G_{\rm N}\ve...
...mathcal{A}\left(\frac{\rho_{\rm vac}}{\rho}\right)\right]\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img242.gif) |
(70) |
As can been seen from Eq. (70) the mean velocity in the ellipsoidal configurations is decreased because of the
 -external force, in the same way the critical mass is affected in
Eq. (66).
-external force, in the same way the critical mass is affected in
Eq. (66).
A drastic effect of the cosmological constant could be reached
for the geometrical factor
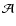 approaching the critical value
approaching the critical value
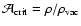 which is possible for very flat objects. In the extreme the mean velocity can go to zero
which is possible for very flat objects. In the extreme the mean velocity can go to zero![[*]](/icons/foot_motif.gif) . Together with inequality (16) the result in Eq. (70) tells us that the temperature,
. Together with inequality (16) the result in Eq. (70) tells us that the temperature,
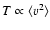 of the objects is very small if the object is just above the limit to reach equilibrium (the square bracket in Eq. (70) is then very small). This is a qualitative conclusion based on the
the presence of non-zero cosmological constant. For ellipsoidal configurations, this defines also a maximum value for the eccentricity
of the objects is very small if the object is just above the limit to reach equilibrium (the square bracket in Eq. (70) is then very small). This is a qualitative conclusion based on the
the presence of non-zero cosmological constant. For ellipsoidal configurations, this defines also a maximum value for the eccentricity
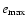 given
given 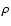 or vice versa, i.e. a minimum value for the density
or vice versa, i.e. a minimum value for the density
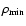 given e, through the relation
given e, through the relation
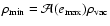 .
The behavior of
.
The behavior of
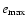 is shown in Fig. 5 as a function of
is shown in Fig. 5 as a function of
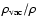 .
Galactic clusters with
.
Galactic clusters with
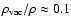 may have a vanishing mean velocity for
may have a vanishing mean velocity for
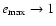 in the oblate case and
in the oblate case and
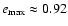 in the prolate case. If the density is smaller, a vanishing mean velocity can be reached for non so flat objects. Spherical configurations have
in the prolate case. If the density is smaller, a vanishing mean velocity can be reached for non so flat objects. Spherical configurations have
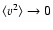 for
for
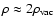 .
.
Since the mean velocity is proportional to the temperature, with 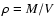 ,
Eq. (70) represents also a mass-temperature relation. Hence, the results for the mean velocity squared are also applicable to the temperature of the configuration. For instance, we can write the
Eq. (70) for a cosmological structure, say a galactic cluster, by writing its density as resulting from a perturbation
,
Eq. (70) represents also a mass-temperature relation. Hence, the results for the mean velocity squared are also applicable to the temperature of the configuration. For instance, we can write the
Eq. (70) for a cosmological structure, say a galactic cluster, by writing its density as resulting from a perturbation
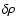 from the background matter density of the universe
from the background matter density of the universe
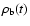 as
as
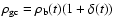 ,
where
,
where
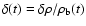 .
Equation (70) then allows us to determine the temperature of the cluster at a given cosmic time t as
.
Equation (70) then allows us to determine the temperature of the cluster at a given cosmic time t as
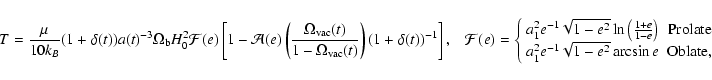 |
(71) |
where a(t) is the scale factor and 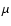 is the mass of average components of the cluster. Equation (71) assumes a flat universe
is the mass of average components of the cluster. Equation (71) assumes a flat universe
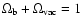 .
This result is a generalization of
a result derived in Wang & Steinhardt (1998) valid for spherical
geometry. In that case one recovers the typical mass temperature relation
.
This result is a generalization of
a result derived in Wang & Steinhardt (1998) valid for spherical
geometry. In that case one recovers the typical mass temperature relation
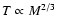 maintaining
maintaining 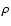 constant. Although this has the same dependence as in Eq. (30), the meaning is different
since (71) for
constant. Although this has the same dependence as in Eq. (30), the meaning is different
since (71) for
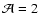 computes the temperature of a certain galactic cluster at some redshift given its mass while Eq. (30) is associated to a reversible process where a configuration passes from T=0 to some final
computes the temperature of a certain galactic cluster at some redshift given its mass while Eq. (30) is associated to a reversible process where a configuration passes from T=0 to some final 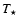 through states of virial equilibrium maintaining a constant mass.
through states of virial equilibrium maintaining a constant mass.
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f5.eps}\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg260.gif) |
Figure 5:
Behavior of
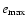 as function of the ratio
as function of the ratio
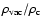 for oblate (solid line) and prolate (dashed line). In the left hand side we show the complete range. In the right hand side, the same plot for
for oblate (solid line) and prolate (dashed line). In the left hand side we show the complete range. In the right hand side, the same plot for 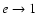 and
and
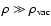 . . |
| Open with DEXTER |
The stability condition of Newtonian configurations against oscillations can be also derived from
the second order virial equation by
expanding the periodic Lagrangian perturbations
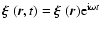 with oscillation frequency
with oscillation frequency 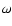 .
For simplicity, we will consider a rotational configuration without internal motions.
By assuming adiabatic perturbations, the variational form of the second order virial
Eq. (6) is written as (see Chandrasekhar 1961; Friedman & Schutz 1978; Shapiro & Teukolsky 1983)
.
For simplicity, we will consider a rotational configuration without internal motions.
By assuming adiabatic perturbations, the variational form of the second order virial
Eq. (6) is written as (see Chandrasekhar 1961; Friedman & Schutz 1978; Shapiro & Teukolsky 1983)
where
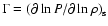 is the adiabatic index governing the adiabatic perturbations.
For polytropic e.o.s we have
is the adiabatic index governing the adiabatic perturbations.
For polytropic e.o.s we have
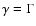 ,
of course.
The Lagrangian displacement is constrained with the boundary conditions i),
,
of course.
The Lagrangian displacement is constrained with the boundary conditions i),
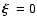 at r=0 and ii)
at r=0 and ii)
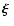 must be finite at the surface.
The boundary conditions are required to solve the equation of motion for
must be finite at the surface.
The boundary conditions are required to solve the equation of motion for
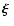 resulting from perturbing Euler's equation (the Sturm-Liouville eigenvalue equation).
resulting from perturbing Euler's equation (the Sturm-Liouville eigenvalue equation).
Let us consider radial oscillations which are adequate for spherical systems and for small deviation from spherical symmetry.
By assuming a general trial function for the Lagrangian displacement
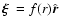 satisfying the boundary conditions and taking the trace in Eq. (72), we can solve for frequency
of the oscillation about equilibrium
satisfying the boundary conditions and taking the trace in Eq. (72), we can solve for frequency
of the oscillation about equilibrium
![\begin{displaymath}
\omega^{2}=\frac{8\pi \varrho}{A}\left[\Gamma-\frac{4}{3} -2...
...frac{2}{3}A\left(\frac{\rho_{\rm vac}}{\varrho}\right)\right],
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img271.gif) |
(73) |
where we have assumed 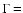 constant throughout the configuration and we have defined in analogy to Eq. (16) the quantities
constant throughout the configuration and we have defined in analogy to Eq. (16) the quantities
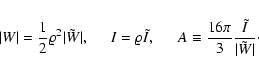 |
(74) |
In Eq. (74) 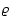 is a parameter with units of density, and
is a parameter with units of density, and
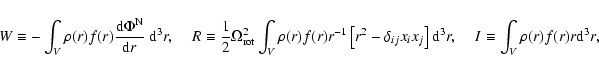 |
(75) |
together with
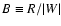 .
The critical adiabatic index is written as
.
The critical adiabatic index is written as
![\begin{displaymath}
\Gamma_{\rm crit}=\frac{4}{3}\left(1-2B\right)^{-1}\left[1+\frac{1}{2}A\frac{\rho_{\rm vac}}{\varrho}-\frac{5}{2}B \right],
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img277.gif) |
(76) |
such that for
 instability sets in and the system
becomes unstable while perturbed.
From Eq. (73),
we see that through the inclusion of the cosmological constant
we (the system) are forced to choose a bigger adiabatic index.
In the simplest case, when f(r)=r, we have
instability sets in and the system
becomes unstable while perturbed.
From Eq. (73),
we see that through the inclusion of the cosmological constant
we (the system) are forced to choose a bigger adiabatic index.
In the simplest case, when f(r)=r, we have
 ,
,
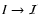 ,
,
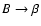 .
Furthermore, for
.
Furthermore, for
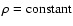 ,
we get
,
we get
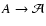 and
and
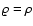 .
The stability condition then becomes
.
The stability condition then becomes
![\begin{displaymath}
\Gamma>\frac{4}{3}\left(1-2\beta\right)^{-1}\left[1+\frac{1}...
...athcal{A}\frac{\rho_{\rm vac}}{\rho}-\frac{5}{2}\beta \right].
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img285.gif) |
(77) |
The spherical symmetry which we assumed compels us to write the ratio 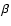 for low eccentricities
or to parametrize it in terms of the total angular momentum of the configuration.
In the first approximation, at low eccentricities the ratio
for low eccentricities
or to parametrize it in terms of the total angular momentum of the configuration.
In the first approximation, at low eccentricities the ratio 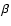 given in (58) takes the form
given in (58) takes the form
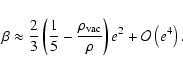 |
(78) |
This equation is useful if we want to calculate a small, but peculiar effect. Insisting
that 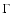 is very close to 4/3 we can convert the stability condition
is very close to 4/3 we can convert the stability condition
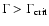 into a condition on eccentricity, namely
into a condition on eccentricity, namely
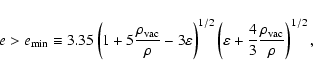 |
(79) |
where
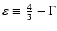 measures a small departure from the critical value 4/3.
For the specific case
measures a small departure from the critical value 4/3.
For the specific case
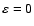 ,
we conclude that stability under quasi-radial oscillations is reached if the eccentricity is such that
,
we conclude that stability under quasi-radial oscillations is reached if the eccentricity is such that
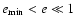 with
with
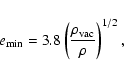 |
(80) |
which is clearly valid only for large values of 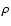 compared with
compared with
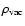 ,
say,
,
say,
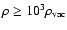 .
.
For completely spherical configurations with constant density, we can write
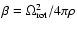 .
Figure 6 shows the behavior of the critical adiabatic index
as
a function of
.
Figure 6 shows the behavior of the critical adiabatic index
as
a function of 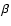 for different values of
for different values of
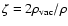 .
The largest deviation is for low densities as
expected.
.
The largest deviation is for low densities as
expected.
![\begin{figure}
\par\includegraphics[width=6.5cm,height=6cm,clip]{3544f6.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg296.gif) |
Figure 6:
Critical adiabatic index as a function of
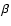 for a homogeneous spherical configuration for different values of
for a homogeneous spherical configuration for different values of
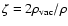 . . |
| Open with DEXTER |
Finally for non rotating configurations the stability criteria is
simply given by
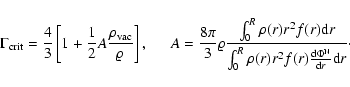 |
(81) |
If we work with a constant density profile,
the choice of another trial function satisfying the boundary conditions mentioned before
will not play a role in the above expressions since
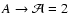 for any f(r).
for any f(r).
Related results regarding the adiabatic index in cosmologies with non-zero  have been obtained in the relativistic frame work in Böhmer & Harko (2005).
have been obtained in the relativistic frame work in Böhmer & Harko (2005).
In the present work we investigated in detail the astrophysical relevance of the
cosmological constant for equilibrium configurations. Using the tensor and scalar virial equations and the
Lane-Emden equation we could show that many astrophysical facets get modified by  .
The second aspect concerns the fact that
.
The second aspect concerns the fact that  introduces new relevant scales (these scales
would be zero if
introduces new relevant scales (these scales
would be zero if 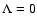 )
like the maximal
virial volume defined by the maximal virial radius (24) and the maximal extension of bound orbits given
in Eq. (35).
)
like the maximal
virial volume defined by the maximal virial radius (24) and the maximal extension of bound orbits given
in Eq. (35).
It is often assumed that superclusters with densities
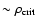 are not in equilibrium. With the inequality (16) we have a precise tool to quantify this statement. Indeed, the pancake structure of the superclusters lead us to the conclusion that they are even far away from the equilibrium state due to the factor
are not in equilibrium. With the inequality (16) we have a precise tool to quantify this statement. Indeed, the pancake structure of the superclusters lead us to the conclusion that they are even far away from the equilibrium state due to the factor
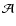 which grows with the object's flatness. On the other hand relatively low density objects can still reach equilibrium (even if
which grows with the object's flatness. On the other hand relatively low density objects can still reach equilibrium (even if
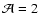 for the spherical case, the density of the object has to be only twice as large as
for the spherical case, the density of the object has to be only twice as large as
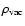 i.e.
i.e. 
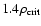 ).
There is nothing which could, in principle, prevent a relatively
low density object to be in equilibrium. This is not only a result
obtained from virial equations with
).
There is nothing which could, in principle, prevent a relatively
low density object to be in equilibrium. This is not only a result
obtained from virial equations with  ,
but follows also from hydrostatic equilibrium with the inclusion of
,
but follows also from hydrostatic equilibrium with the inclusion of  (Balaguera-Antolínez et al. 2004). It is then natural to put forward the question how the shape of such objects affect their properties as compared to the case without
(Balaguera-Antolínez et al. 2004). It is then natural to put forward the question how the shape of such objects affect their properties as compared to the case without  .
For instance, if
.
For instance, if
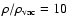 and
and 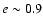 ,
the angular velocity is reduced approximately
,
the angular velocity is reduced approximately 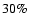 with respect to its value with
with respect to its value with 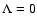 (
(
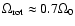 ). Other effects discussed in the text are the mean velocity (see Fig. 5) and the adiabatic index (see Fig. 6). To be specific let us take an example of a very low density object,
). Other effects discussed in the text are the mean velocity (see Fig. 5) and the adiabatic index (see Fig. 6). To be specific let us take an example of a very low density object,
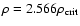 .
This object is still virialized as long as its eccentricty is e<0.5. Approaching
.
This object is still virialized as long as its eccentricty is e<0.5. Approaching 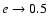 the mean velocity (temperature) goes to zero until finally
beyond 0.5 the object ceases to be in equilibrium.
the mean velocity (temperature) goes to zero until finally
beyond 0.5 the object ceases to be in equilibrium.
To highlight some other quantities which get affected let us mention the polytropic index n and the angular velocity.
Low-density objects with
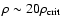 an index n > 1.5
becomes unphysical as the the conglomeration of matter does not have a definite finite radius. Taken together
with the results of section five on stability against small oscillations this implies that
the adiabatic index
an index n > 1.5
becomes unphysical as the the conglomeration of matter does not have a definite finite radius. Taken together
with the results of section five on stability against small oscillations this implies that
the adiabatic index 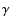 from the equation of state
from the equation of state
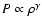 gets
restricted for these densities in a rather strong way, namely by
gets
restricted for these densities in a rather strong way, namely by
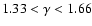 .
For higher densities the effect grows with n. For instance, for
.
For higher densities the effect grows with n. For instance, for
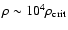 ,
n=5 is an unacceptable solution due to the lack of a finite extension.
For non-spherical configurations we could show an effect of
,
n=5 is an unacceptable solution due to the lack of a finite extension.
For non-spherical configurations we could show an effect of  on angular velocities,
the mean velocity of the component of the astrophysical object and on the critical mass, again
for densities one and two orders of magnitude above the critical one. We think that
the work can be generalized in various ways. For instance, to generalize
the virial equations to be able to differentiate between different models
of dark energy mentioned at the beginning. Another aspect is to look into
the Lane-Emden equation for non-spherical geometries (Lombardi & Bertin
2001; Balaguera-Antolínez et al. 2004). Here we concentrated on the equilibrium condition of already virialized matter. The collapse
of matter in an accelerated universe with dark energy has been considered in Mota & van de Bruck (2004).
on angular velocities,
the mean velocity of the component of the astrophysical object and on the critical mass, again
for densities one and two orders of magnitude above the critical one. We think that
the work can be generalized in various ways. For instance, to generalize
the virial equations to be able to differentiate between different models
of dark energy mentioned at the beginning. Another aspect is to look into
the Lane-Emden equation for non-spherical geometries (Lombardi & Bertin
2001; Balaguera-Antolínez et al. 2004). Here we concentrated on the equilibrium condition of already virialized matter. The collapse
of matter in an accelerated universe with dark energy has been considered in Mota & van de Bruck (2004).
Here we briefly show the solution for the cubic Eq. (19). Let us write that expression as
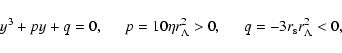 |
(A.1) |
corresponding to a positive cosmological constant. Associated with this expression one defines a discriminant and a quantity R defined as
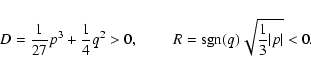 |
(A.2) |
Since p>0, the roots of Eq. (A.1) are given in term of the auxiliary angle  defined as
defined as
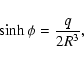 |
(A.3) |
so that the only real solution for Eq. (A.1) is written as
![\begin{displaymath}
y=-2R\sinh
\left(\frac{\phi}{3}\right)=\sqrt{\frac{4}{3}\ve...
...ac{1}{3}{\rm arcsinh}\left(\frac{q}{2R^{3}}\right)\right]\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img316.gif) |
(A.4) |
The other two roots are complex numbers whose real part are negative. If p<0 and q>0 the roots depend whether D is bigger or smaller than zero. If 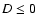 ,
the three roots are real and negative, while D>0 yields one real negative root and two complex roots which real parts are given as
,
the three roots are real and negative, while D>0 yields one real negative root and two complex roots which real parts are given as
![\begin{displaymath}
y=\sqrt{\frac{1}{3}\vert p\vert}\cosh\left[\frac{1}{3}{\rm
arccosh}\left(\frac{q}{2R^{3}}\right)\right]\cdot
\end{displaymath}](/articles/aa/full/2005/37/aa3544-05/img318.gif) |
(A.5) |
- Aldrovandi,
R., Barbosa, A. L., Crispino, L. C., & Pereira, J. G. 1999,
Class. Quantum Grav., 16, 495 [NASA ADS] [CrossRef] (In the text)
- Allen, S. W.,
Schmidt, R. W, Ebeling, H., Fabian, A. C., & van Speybroeck, L.
2004, MNRAS, 353, 457 [NASA ADS] [CrossRef]
- Bacry, H., &
Levy-Leblond, J. M. 1967, J. Math. Phys., 9, 1605 (In the text)
- Balaguera-Antolínez, A.,
Böhmer, C. G., & Nowakowski, M. 2005
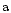 , Scales Set by the Cosmological Constant, in
preparation
(In the text)
, Scales Set by the Cosmological Constant, in
preparation
(In the text) - Balaguera-Antolínez, A.,
& Nowakowski, M. 2005
 , Ellipsoidal configurations with cosmological constant,
in preperation
, Ellipsoidal configurations with cosmological constant,
in preperation
- Balaguera-Antolínez, A.,
Böhmer, C. G., & Nowakowski, M. 2004, On Astrophysical
Bounds of the Cosmological Constant, [gr-qc/0409004]
(In the text)
- Barrow, J. D.,
& Gotz, G. 1989, Class. Quant. Grav., 6, 1253 [NASA ADS] (In the text)
- Binney, J., &
Tremaine, S. 1987, Galactic Dynamics (Princeton University
Press)
(In the text)
- de Blok, W. J. G.,
& McGaugh, S. S. 1996, ApJ, 469, L103 [NASA ADS] [CrossRef] (In the text)
- de Blok, W. J. G.,
McGaugh, S. S., Bosma, A., & Rubin, V. C. 2004, Mass Density
Profiles of LSB Galaxies [arXiv:astro-ph/0103102]
(In the text)
- Böhmer, C. G.
2002, General Relativistic Static Fluid Solutions with Cosmological
Constant, [gr-qc/0308057], unpublished Diploma Thesis
- Böhmer, C.
G. 2003, Gen. Rel. Grav., 36, 1039 [NASA ADS]
- Böhmer, C.
G., & Harko, T. 2005, Dynamical Instability of Fluid Spheres in
the Presence of a Cosmological Constant, Phys. Rev. D., 71,
084026
-
Chandrasekhar, S. 1961, Hydrodynamic and Hydromagnetic Stability
(Dover Publications Inc.)
(In the text)
-
Chandrasekhar, S. 1967, An Introduction to the Study of Stellar
Structure (Dover Publications)
(In the text)
-
Chandrasekhar, S. 1969, Ellipsoidal Figures of Equilibrium (New
Haven and London: Yale University Press)
(In the text)
- Cooray, A. R. 2000,
MNRAS, 313, 783 [NASA ADS] [CrossRef] (In the text)
- Derom, J.-R., &
Dubois, J.-G. 1972, Hooke's Symmetries and Non-Relativistic
Cosmological Kinematics, Nouvo Cimento, 9B, 351
(In the text)
- Friedman, J.,
& Schutz, B. 1978, ApJ, 221, 937 [NASA ADS] [CrossRef] (In the text)
- Jaaniste, J.,
Tago, E., Einasto, M., et al. 1998, A&A, 336, 35 [NASA ADS] (In the text)
- Kalinkov, M.,
Valchanov, T., Valtchanov, I., Kuneva, I., & Dissanska, M.
2005, MNRAS, 359, 1491 [NASA ADS] [CrossRef] (In the text)
-
Kamenshchik, A. Yu., Moschella, U., & Pasquier, V. 2001, Phys.
Lett., B511, 265 [NASA ADS] (In the text)
- Krauss, L. M. 1998,
ApJ, 501, 1998 (In the text)
- Krauss, L. M. 2003,
The State of the Universe: Cosmological Parameters 2002. ESO-CERN
Symposium on Astronomy, Cosmology and Fundamental Physics, March
2003
(In the text)
- Kremer, G. M. 2003,
Gen. Rel. Grav., 35, 1459 [NASA ADS] [CrossRef] (In the text)
- Lombardi, M.,
& Bertin, G. 2001, A&A, 375, 1091 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Mak, M. K., Jr. Dobson,
P. N., & Harko, T. 2001, Mod. Phys. Lett., A15, 2153 [NASA ADS]
- Mota, D. F., & van
de Bruck, C. 2004, A&A, 421, 71 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Nojiri, S., &
Odintsov, S. D. 2003, Phys. Rev. D, 68, 123512 [NASA ADS] [CrossRef] (In the text)
- Nowakowski,
M. 2001, Int. J. Mod. Phys. D, 10, 649 [NASA ADS] (In the text)
- Nowakowski,
M., Sanabria, J.-C., & Garcia, A. 2002, Phys. Rev. D, 66,
023003 [NASA ADS] [CrossRef] (In the text)
-
Oppenheimer, J. R., & Volkoff, G. M. 1939, Phys. Rev., 55,
374 [NASA ADS] [CrossRef] (In the text)
-
Padmananbhan, T. 1993, Structure Formation in the Universe
(Cambridge University Press)
-
Padmanabhan T. 2000, Theoretical Astrophysics, Vol. I:
Astrophysical Processes (Cambridge University Press)
- Perlmutter,
S., Aldering, G., della Valle, M., et al. 1998, Nature, 391,
51 [NASA ADS] [CrossRef] (In the text)
- Perlmutter,
S., Turner, M. S., & White, M. J. 1999, Phys. Rev. Lett., 83,
670 [NASA ADS] [CrossRef] (In the text)
- Plummer, H. C.
1911, MNRAS, 71, 460 [NASA ADS] (In the text)
- Ratra, B., &
Peebles, P. J. E. 1987, Phys. Rev. D, 37, 3406 [NASA ADS]
- Rich, J. 2001,
Fundamentals of Cosmology (Springer Verlag)
(In the text)
- Riess, A. G.,
Strolger, L.-G., Tonry, Y., et al. 2004, ApJ, 607, 665 [NASA ADS] [CrossRef] (In the text)
- Roberts, P. H.
1962, ApJ, 136, 1108 [NASA ADS] [CrossRef] (In the text)
- Shapiro, S., &
Teokolsky, S. 1983, Black Holes, White Dwarfs and Neutron Stars
(Wiley-Interscience Publications)
- Sussman, R. A.,
& Hernandez, X. 2003, MNRAS, 345, 871 [NASA ADS] [CrossRef] (In the text)
- Wang, L., &
Steinhardt, P. J. 1998, ApJ, 508, 483 [NASA ADS] [CrossRef] (In the text)
- Wetterich, C.
1987, Nucl. Phys., B302, 668 [NASA ADS]
Copyright ESO 2005
![]() affects various astrophysical quantities important
for large matter conglomeration in the universe.
Among others we examine the effect of
affects various astrophysical quantities important
for large matter conglomeration in the universe.
Among others we examine the effect of ![]() on the polytropic equation of state
for spherically symmetric objects and find non-negligible results in certain realistic cases.
We calculate the angular velocity for non-spherical oblate
configurations which demonstrates a clear effect of
on the polytropic equation of state
for spherically symmetric objects and find non-negligible results in certain realistic cases.
We calculate the angular velocity for non-spherical oblate
configurations which demonstrates a clear effect of ![]() on high eccentricity objects.
We show that for oblate as well as prolate ellipsoids the cosmological constant
influences the critical mass and the temperature of the astrophysical object.
These and other results show that the effect of
on high eccentricity objects.
We show that for oblate as well as prolate ellipsoids the cosmological constant
influences the critical mass and the temperature of the astrophysical object.
These and other results show that the effect of ![]() is large for
flat astrophysical bodies.
is large for
flat astrophysical bodies.
![]() does not have any effect on
astrophysical processes which take place at scales different from the
cosmological ones.
Indeed, looking at the scales set by
does not have any effect on
astrophysical processes which take place at scales different from the
cosmological ones.
Indeed, looking at the scales set by ![]() ,
this assumption seems to be
justified at the first glance. The scales set by the cosmological constant
are of truly cosmological order of magnitude (Nowakowski 2001; Balaguera-Antolínez et al. 2004).
The density scale is set by
,
this assumption seems to be
justified at the first glance. The scales set by the cosmological constant
are of truly cosmological order of magnitude (Nowakowski 2001; Balaguera-Antolínez et al. 2004).
The density scale is set by
![]() with
with
![]() .
The length scale,
.
The length scale,
![]() is of the order of the Hubble
radius while the mass scale
is of the order of the Hubble
radius while the mass scale
![]() reaches up to the value of the
mass of the universe. These scales constitute the so-called coincidence
problem, namely the question as to why we should live exactly at an epoch where
the scales of the cosmological constant are also the scales of the universe.
Neither was it so in the past nor will it be so in the future when the universe expands further.
The only astrophysical structures which match these scales are superclusters whose
densities
are indeed of the order of magnitude of
reaches up to the value of the
mass of the universe. These scales constitute the so-called coincidence
problem, namely the question as to why we should live exactly at an epoch where
the scales of the cosmological constant are also the scales of the universe.
Neither was it so in the past nor will it be so in the future when the universe expands further.
The only astrophysical structures which match these scales are superclusters whose
densities
are indeed of the order of magnitude of
![]() .
Indeed, here we can almost be sure that
the cosmological constant is of relevance (Nowakowski 2001; Sussman &
Hernandez 2003).
However, probing into astrophysical consequences of the cosmological constant of other, smaller and denser
structures
like clusters of galaxies or even galaxies themselves, would look a hopeless undertaking
unless we find circumstances where the effect of
.
Indeed, here we can almost be sure that
the cosmological constant is of relevance (Nowakowski 2001; Sussman &
Hernandez 2003).
However, probing into astrophysical consequences of the cosmological constant of other, smaller and denser
structures
like clusters of galaxies or even galaxies themselves, would look a hopeless undertaking
unless we find circumstances where the effect of ![]() (which in the very principle is present)
gets enhanced. This can indeed happen through various mechanisms.
For instance, in a problem where
(which in the very principle is present)
gets enhanced. This can indeed happen through various mechanisms.
For instance, in a problem where
![]() combines with a much smaller length scale,
say r0,
the effects can be sometimes expressed as
combines with a much smaller length scale,
say r0,
the effects can be sometimes expressed as
![]() .
In consequence, the observable in which this expression enters gets affected
by
.
In consequence, the observable in which this expression enters gets affected
by ![]() in a way which is important at much smaller scales
than
in a way which is important at much smaller scales
than
![]() .
A concrete example is the Schwarzschild-de Sitter metric where
we find the parameter
.
A concrete example is the Schwarzschild-de Sitter metric where
we find the parameter
![]() together with the much smaller length scale of the
Schwarzschild radius
together with the much smaller length scale of the
Schwarzschild radius ![]() .
These two conspire in the form
.
These two conspire in the form
![]() to define the largest
extension of bound orbits as explained in the text and in
Balaguera-Antolínez et al. (2005
to define the largest
extension of bound orbits as explained in the text and in
Balaguera-Antolínez et al. (2005![]() ).
We will discuss a very similar combination which emerges from the virial theorem defining
the largest possible virialized structure with a given mass.
Another possibility to enhance the effect of the
cosmological constant is to consider non-spherical objects. It then often happens
that the effect of
).
We will discuss a very similar combination which emerges from the virial theorem defining
the largest possible virialized structure with a given mass.
Another possibility to enhance the effect of the
cosmological constant is to consider non-spherical objects. It then often happens
that the effect of ![]() becomes
becomes
![]() where liare two different length scales of a flattened object like a disk or an ellipsoid (Nowakowski et al. 2002).
This indeed happens for many astrophysical quantities, among other the critical mass,
the angular velocity and the temperature (mean velocity of the components
of the large structure) which we will discuss in the present paper.
Finally, we can vary a dimensional variable
to see if this enhances the effect of the cosmological constant.
As an example let us quote the polytropic index n in the equation of state
entering also the Lane-Emden equation. It is known that with growing n (
where liare two different length scales of a flattened object like a disk or an ellipsoid (Nowakowski et al. 2002).
This indeed happens for many astrophysical quantities, among other the critical mass,
the angular velocity and the temperature (mean velocity of the components
of the large structure) which we will discuss in the present paper.
Finally, we can vary a dimensional variable
to see if this enhances the effect of the cosmological constant.
As an example let us quote the polytropic index n in the equation of state
entering also the Lane-Emden equation. It is known that with growing n (![]() )
the object described by this equation of state does not have a well-defined radius
as the density goes only asymptotically to zero. We will show that this pattern of behavior
becomes more dominant with
)
the object described by this equation of state does not have a well-defined radius
as the density goes only asymptotically to zero. We will show that this pattern of behavior
becomes more dominant with
![]() .
.
![]() .
This is possible in various ways as shown below. Galaxy clusters can have various forms, among others oblate and
prolate (Cooray 2000; Kalinkov et al. 2005).
And what is more, they can even rotate (Kalinkov et al. 2005).
We will show an explicit effect of
.
This is possible in various ways as shown below. Galaxy clusters can have various forms, among others oblate and
prolate (Cooray 2000; Kalinkov et al. 2005).
And what is more, they can even rotate (Kalinkov et al. 2005).
We will show an explicit effect of ![]() on their
angular velocity and temperature in case the angular velocity is zero. Since the effect
of large eccentricity is larger for prolate than for oblate ellipsoids, it is
comforting to know that clusters can assume a prolate shape.
For low-density galaxies like the Low Surface Brightness (LSB) galaxies whose density
is roughly four orders of magnitude above the critical density (Blok & McGaugh 1996;
Blok et al. 2004) we still find some
effects. For n=5 and
on their
angular velocity and temperature in case the angular velocity is zero. Since the effect
of large eccentricity is larger for prolate than for oblate ellipsoids, it is
comforting to know that clusters can assume a prolate shape.
For low-density galaxies like the Low Surface Brightness (LSB) galaxies whose density
is roughly four orders of magnitude above the critical density (Blok & McGaugh 1996;
Blok et al. 2004) we still find some
effects. For n=5 and ![]() the solution of the Lane-Emden equation (Chandrasekhar 1967)
is very often used as a phenomenologically valid description of the density profile (called also
Plummer's law (Plummer 1911)). This is still possible as
the solution of the Lane-Emden equation (Chandrasekhar 1967)
is very often used as a phenomenologically valid description of the density profile (called also
Plummer's law (Plummer 1911)). This is still possible as
![]() as
as
![]() .
However, this
property vanishes for low-density galaxies and the n=5 case not only does not have a well-defined radius,
its solution does not vanish asymptotically which thus rendering it unphysical.
.
However, this
property vanishes for low-density galaxies and the n=5 case not only does not have a well-defined radius,
its solution does not vanish asymptotically which thus rendering it unphysical.
![]() .
In the third section we will
specialize on spherical configurations. We will show how
.
In the third section we will
specialize on spherical configurations. We will show how ![]() sets the scale of a maximal virial radius
and compare it to a result from the Schwarzschild-de Sitter metric. We will also solve the Lane-Emden
equation numerically and analytically (for the polytropic index n=2). In the fourth section we will
discuss non-spherical configurations. First, we will show how
sets the scale of a maximal virial radius
and compare it to a result from the Schwarzschild-de Sitter metric. We will also solve the Lane-Emden
equation numerically and analytically (for the polytropic index n=2). In the fourth section we will
discuss non-spherical configurations. First, we will show how ![]() affects the
angular velocity of spheroids. In addition, we will discuss the
effects of
affects the
angular velocity of spheroids. In addition, we will discuss the
effects of ![]() for the critical mass, mean velocity and mean rotational velocity too.
The fifth section is devoted to small oscillations around equilibrium.
for the critical mass, mean velocity and mean rotational velocity too.
The fifth section is devoted to small oscillations around equilibrium.
![]() -virial theorem has been used in different contexts in Barrow (1989),
Wang & Steinhardt (1998), Nowakowski et al. (2002) and
Balaguera-Antolínez et al. (2004). In the present work we will extend these studies.
-virial theorem has been used in different contexts in Barrow (1989),
Wang & Steinhardt (1998), Nowakowski et al. (2002) and
Balaguera-Antolínez et al. (2004). In the present work we will extend these studies.
![]() implies an upper bound on the vacuum energy density
implies an upper bound on the vacuum energy density
![]() (Böhmer 2002, 2003)
where
(Böhmer 2002, 2003)
where
![]() is the mean density defined by
is the mean density defined by
![]() .
This bound is derived not only from Newtonian astrophysics,
but also from a general relativistic context via the Tolmann-Oppenheimer-Volkoff equation (Oppenheimer & Volkoff 1939)
for hydrostatic equilibrium of compact objects (Böhmer 2003; Balaguera-Antolínez et al. 2004).
.
This bound is derived not only from Newtonian astrophysics,
but also from a general relativistic context via the Tolmann-Oppenheimer-Volkoff equation (Oppenheimer & Volkoff 1939)
for hydrostatic equilibrium of compact objects (Böhmer 2003; Balaguera-Antolínez et al. 2004).
![]() -virial equation. Using the expressions for
-virial equation. Using the expressions for
![]() and
and
![]() given before, Eq. (10) yields as a cubic equation for the virial radius
given before, Eq. (10) yields as a cubic equation for the virial radius
![]()
![\begin{figure}
\par\includegraphics[width=8cm,height=6.5cm,clip]{3544f1.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg105.gif)
![]() derived from the Schwarszchild de-Sitter
spacetime (Balaguera-Antolínez et al. 2005
derived from the Schwarszchild de-Sitter
spacetime (Balaguera-Antolínez et al. 2005![]() ),
but whose physical meaning is quite different.
The Schwarzschild-de Sitter metric takes the form
),
but whose physical meaning is quite different.
The Schwarzschild-de Sitter metric takes the form
![]() .
Then we obtain the Lane-Emden equation
with
.
Then we obtain the Lane-Emden equation
with ![]() (Balaquera-Antolínez et al. 2004)
(Balaquera-Antolínez et al. 2004)
![\begin{figure}
\par\includegraphics[angle=270,width=14cm]{3544f2.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg141.gif)
![]() for the same ratios
for the same ratios
![]() and polytropic index as in Fig. 2. The horizontal line represents a non-defined radius. The symbol
and polytropic index as in Fig. 2. The horizontal line represents a non-defined radius. The symbol ![]() indicates that the radius is defined only asymptotically in case of
indicates that the radius is defined only asymptotically in case of ![]() .
.
![]() for different values of the ratio
for different values of the ratio
![]() and the polytropic index. The horizontal lines represents the non well defined radius.
and the polytropic index. The horizontal lines represents the non well defined radius.![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f3.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg171.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f4.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg172.gif)
![]() and
and ![]() constant,
or spheroids with confocal density
distribution whose isodensity surfaces are similar concentric ellipsoids (Roberts 1962; Binney & Tremaine 1987) i.e.
constant,
or spheroids with confocal density
distribution whose isodensity surfaces are similar concentric ellipsoids (Roberts 1962; Binney & Tremaine 1987) i.e.
![]() -tensor virial Eq. (6) for such a configuration is
-tensor virial Eq. (6) for such a configuration is
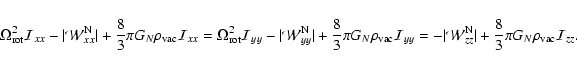
![]() in mechanical equilibrium with the background with pressure P
(see Padmannabhan 2000, Chap. 8).
The system will collapse under it's own gravity (P<0) if its mass is greater than a critical mass
in mechanical equilibrium with the background with pressure P
(see Padmannabhan 2000, Chap. 8).
The system will collapse under it's own gravity (P<0) if its mass is greater than a critical mass ![]() .
With cosmological constant, this critical mass is increased with respect to its value
.
With cosmological constant, this critical mass is increased with respect to its value
![]() when
when ![]() ,
which is expected,
since now there is an external force associated to
,
which is expected,
since now there is an external force associated to ![]() that acts against Newtonian gravity
and hence the collapse can be postponed. By using the scalar virial theorem (12) and setting P=0
as the criterion for the onset of instability, we can write for arbitrary geometry
that acts against Newtonian gravity
and hence the collapse can be postponed. By using the scalar virial theorem (12) and setting P=0
as the criterion for the onset of instability, we can write for arbitrary geometry
![]() -virial theorem, we can also write down the mass-temperature relation for an astrophysical structure.
Note first that using
-virial theorem, we can also write down the mass-temperature relation for an astrophysical structure.
Note first that using
![]() in Eq. (12) we have for
in Eq. (12) we have for ![]() the standard expression for
the mean velocity
the standard expression for
the mean velocity
![]() -external force, in the same way the critical mass is affected in
Eq. (66).
-external force, in the same way the critical mass is affected in
Eq. (66).
![]() approaching the critical value
approaching the critical value
![]() which is possible for very flat objects. In the extreme the mean velocity can go to zero
which is possible for very flat objects. In the extreme the mean velocity can go to zero![]() . Together with inequality (16) the result in Eq. (70) tells us that the temperature,
. Together with inequality (16) the result in Eq. (70) tells us that the temperature,
![]() of the objects is very small if the object is just above the limit to reach equilibrium (the square bracket in Eq. (70) is then very small). This is a qualitative conclusion based on the
the presence of non-zero cosmological constant. For ellipsoidal configurations, this defines also a maximum value for the eccentricity
of the objects is very small if the object is just above the limit to reach equilibrium (the square bracket in Eq. (70) is then very small). This is a qualitative conclusion based on the
the presence of non-zero cosmological constant. For ellipsoidal configurations, this defines also a maximum value for the eccentricity
![]() given
given ![]() or vice versa, i.e. a minimum value for the density
or vice versa, i.e. a minimum value for the density
![]() given e, through the relation
given e, through the relation
![]() .
The behavior of
.
The behavior of
![]() is shown in Fig. 5 as a function of
is shown in Fig. 5 as a function of
![]() .
Galactic clusters with
.
Galactic clusters with
![]() may have a vanishing mean velocity for
may have a vanishing mean velocity for
![]() in the oblate case and
in the oblate case and
![]() in the prolate case. If the density is smaller, a vanishing mean velocity can be reached for non so flat objects. Spherical configurations have
in the prolate case. If the density is smaller, a vanishing mean velocity can be reached for non so flat objects. Spherical configurations have
![]() for
for
![]() .
.
![]() ,
Eq. (70) represents also a mass-temperature relation. Hence, the results for the mean velocity squared are also applicable to the temperature of the configuration. For instance, we can write the
Eq. (70) for a cosmological structure, say a galactic cluster, by writing its density as resulting from a perturbation
,
Eq. (70) represents also a mass-temperature relation. Hence, the results for the mean velocity squared are also applicable to the temperature of the configuration. For instance, we can write the
Eq. (70) for a cosmological structure, say a galactic cluster, by writing its density as resulting from a perturbation
![]() from the background matter density of the universe
from the background matter density of the universe
![]() as
as
![]() ,
where
,
where
![]() .
Equation (70) then allows us to determine the temperature of the cluster at a given cosmic time t as
.
Equation (70) then allows us to determine the temperature of the cluster at a given cosmic time t as
![\begin{figure}
\par\includegraphics[angle=270,width=10cm,clip]{3544f5.eps}\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg260.gif)
![]() satisfying the boundary conditions and taking the trace in Eq. (72), we can solve for frequency
of the oscillation about equilibrium
satisfying the boundary conditions and taking the trace in Eq. (72), we can solve for frequency
of the oscillation about equilibrium
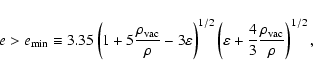
![]() .
Figure 6 shows the behavior of the critical adiabatic index
as
a function of
.
Figure 6 shows the behavior of the critical adiabatic index
as
a function of ![]() for different values of
for different values of
![]() .
The largest deviation is for low densities as
expected.
.
The largest deviation is for low densities as
expected.
![\begin{figure}
\par\includegraphics[width=6.5cm,height=6cm,clip]{3544f6.eps}
\end{figure}](/articles/aa/full/2005/37/aa3544-05/Timg296.gif)
![]() have been obtained in the relativistic frame work in Böhmer & Harko (2005).
have been obtained in the relativistic frame work in Böhmer & Harko (2005).
![]() are not in equilibrium. With the inequality (16) we have a precise tool to quantify this statement. Indeed, the pancake structure of the superclusters lead us to the conclusion that they are even far away from the equilibrium state due to the factor
are not in equilibrium. With the inequality (16) we have a precise tool to quantify this statement. Indeed, the pancake structure of the superclusters lead us to the conclusion that they are even far away from the equilibrium state due to the factor
![]() which grows with the object's flatness. On the other hand relatively low density objects can still reach equilibrium (even if
which grows with the object's flatness. On the other hand relatively low density objects can still reach equilibrium (even if
![]() for the spherical case, the density of the object has to be only twice as large as
for the spherical case, the density of the object has to be only twice as large as
![]() i.e.
i.e. ![]()
![]() ).
There is nothing which could, in principle, prevent a relatively
low density object to be in equilibrium. This is not only a result
obtained from virial equations with
).
There is nothing which could, in principle, prevent a relatively
low density object to be in equilibrium. This is not only a result
obtained from virial equations with ![]() ,
but follows also from hydrostatic equilibrium with the inclusion of
,
but follows also from hydrostatic equilibrium with the inclusion of ![]() (Balaguera-Antolínez et al. 2004). It is then natural to put forward the question how the shape of such objects affect their properties as compared to the case without
(Balaguera-Antolínez et al. 2004). It is then natural to put forward the question how the shape of such objects affect their properties as compared to the case without ![]() .
For instance, if
.
For instance, if
![]() and
and ![]() ,
the angular velocity is reduced approximately
,
the angular velocity is reduced approximately ![]() with respect to its value with
with respect to its value with ![]() (
(
![]() ). Other effects discussed in the text are the mean velocity (see Fig. 5) and the adiabatic index (see Fig. 6). To be specific let us take an example of a very low density object,
). Other effects discussed in the text are the mean velocity (see Fig. 5) and the adiabatic index (see Fig. 6). To be specific let us take an example of a very low density object,
![]() .
This object is still virialized as long as its eccentricty is e<0.5. Approaching
.
This object is still virialized as long as its eccentricty is e<0.5. Approaching ![]() the mean velocity (temperature) goes to zero until finally
beyond 0.5 the object ceases to be in equilibrium.
the mean velocity (temperature) goes to zero until finally
beyond 0.5 the object ceases to be in equilibrium.
![]() an index n > 1.5
becomes unphysical as the the conglomeration of matter does not have a definite finite radius. Taken together
with the results of section five on stability against small oscillations this implies that
the adiabatic index
an index n > 1.5
becomes unphysical as the the conglomeration of matter does not have a definite finite radius. Taken together
with the results of section five on stability against small oscillations this implies that
the adiabatic index ![]() from the equation of state
from the equation of state
![]() gets
restricted for these densities in a rather strong way, namely by
gets
restricted for these densities in a rather strong way, namely by
![]() .
For higher densities the effect grows with n. For instance, for
.
For higher densities the effect grows with n. For instance, for
![]() ,
n=5 is an unacceptable solution due to the lack of a finite extension.
For non-spherical configurations we could show an effect of
,
n=5 is an unacceptable solution due to the lack of a finite extension.
For non-spherical configurations we could show an effect of ![]() on angular velocities,
the mean velocity of the component of the astrophysical object and on the critical mass, again
for densities one and two orders of magnitude above the critical one. We think that
the work can be generalized in various ways. For instance, to generalize
the virial equations to be able to differentiate between different models
of dark energy mentioned at the beginning. Another aspect is to look into
the Lane-Emden equation for non-spherical geometries (Lombardi & Bertin
2001; Balaguera-Antolínez et al. 2004). Here we concentrated on the equilibrium condition of already virialized matter. The collapse
of matter in an accelerated universe with dark energy has been considered in Mota & van de Bruck (2004).
on angular velocities,
the mean velocity of the component of the astrophysical object and on the critical mass, again
for densities one and two orders of magnitude above the critical one. We think that
the work can be generalized in various ways. For instance, to generalize
the virial equations to be able to differentiate between different models
of dark energy mentioned at the beginning. Another aspect is to look into
the Lane-Emden equation for non-spherical geometries (Lombardi & Bertin
2001; Balaguera-Antolínez et al. 2004). Here we concentrated on the equilibrium condition of already virialized matter. The collapse
of matter in an accelerated universe with dark energy has been considered in Mota & van de Bruck (2004).