A&A 441, 337-346 (2005)
DOI: 10.1051/0004-6361:20052962
M. Schüssler 1 - M. Rempel 2
1 - Max-Planck-Institut für
Sonnensystemforschung,
Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
2 -
High Altitude Observatory,
NCAR, PO Box 3000, Boulder, Colorado 80307, USA
Received 1 March 2005 / Accepted 13 June 2005
Abstract
After a dynamically active
emergence phase, magnetic flux at the solar surface soon ceases to show
strong signs of the subsurface dynamics of its parent magnetic
structure. This indicates that some kind of disconnection of the
emerged flux from its roots in the deep convection zone should take
place. We propose a mechanism for the dynamical disconnection of the
surface flux based upon the buoyant upflow of plasma along the field
lines. Such flows arise in the upper part of a rising flux loop during
the final phases of its buoyant ascent towards the surface. The
combination of the pressure buildup by the upflow and the cooling of the
upper layers of an emerged flux tube by radiative losses at the surface
lead to a progressive weakening of the magnetic field in several Mm
depth. When the field strength has become sufficiently low, convective
motions and the fluting instability disrupt the flux tube into thin,
passively advected flux fragments, thus providing a dynamical
disconnection of the emerged part from its roots. We substantiate this
scenario by considering the quasi-static evolution of a sunspot model
under the effects of radiative cooling, convective energy transport, and
pressure buildup by a prescribed inflow at the bottom of the model. For
inflow speeds in the range shown by simulations of thin flux tubes, we
find that the disconnection takes place in a depth between 2 and 6 Mm
for disconnection times up to 3 days.
Key words: magnetohydrodynamics (MHD) - Sun: activity - Sun: magnetic fields - Sun: sunspots
Until the advent of local helioseismology, very little was known about the subsurface structure of sunspots and active regions. Differences in the measured rotation rates of the nonmagnetic plasma and the magnetic "tracers'' were taken as evidence that the latter are somehow "anchored'' in deeper layers, but no consensus could be reached as to where and how this anchoring should precisely take place (e.g., D'Silva & Howard 1994; Javaraiah & Gokhale 1997; Beck 2000; Schüssler 1984, 1987). The recent results from local helioseismology indicate significant changes of the thermodynamic and/or magnetic properties as well as of the flow field at a depth of less than 10 Mm below sunspots (Kosovichev et al. 2000; Couvidat et al. 2004; Zhao et al. 2001) and active regions (Hindman et al. 2004; Basu et al. 2004). These findings are consistent with the model of a sunspot as a shallow object, which breaks apart into a large number of flux tubes not far below the surface (Parker 1979; Spruit 1981; Choudhuri 1992), rather than that of a monolithic plug of magnetic flux extending deep into the convection zone (see also the detailed discussion of sunspot models by Thomas & Weiss 1992).
From the theoretical side, analytical studies and numerical simulations of magnetic flux tubes have provided a consistent picture of the formation of active regions and sunspot groups, comprising the storage and amplification of magnetic flux near the bottom of the convection zone as well as the formation of unstable loops and their rise through most of the convection zone. Given a strongly super-equipartition initial field of the order of 105 G (10 Tesla) at the bottom of the convection zone, large-scale properties of newly-emerged active regions and sunspot groups, like low emergence latitudes, systematic tilt angles (Joy's law), and asymmetric proper motions of the two polarities, can be quantitatively explained (see reviews by Fisher et al. 2000; Fan 2004; Moreno-Insertis 1997, and further references therein).
Numerical studies following the evolution of an unstable flux loop from
its origin at the bottom of the convection zone only reach until about
10 Mm from the surface, where the thin-flux-tube approximation breaks
down. Realistic simulations of the subsequent phases are still too
demanding in view of the computing power available today. Therefore, the
actual emergence of flux in the photosphere and the evolution thereafter
has not been covered by such simulations (except for rather
idealized situations aiming at describing the effects on the coronal
magnetic structure,
e.g., Archontis et al. 2004; Magara 2004; Fan & Gibson 2004). On the other
hand, a wealth of observational evidence indicates a remarkable change
in the dynamical properties of sunspots and active regions from "active''
to "passive'' evolution shortly after their emergence
(Schüssler 1987; Schrijver & Title 1999). The emerging flux
initially displays the clear signature of a rising, fragmented flux tube
and evolves according to its internal large-scale dynamics
(e.g., McIntosh 1981; Strous et al. 1996). However, the expansion
of the bipolar region and the proper motion of the sunspots with respect
to the surrounding plasma decays within a few days after emergence and
larger magnetic structures start to fragment into small-scale flux
bundles, which are largely dominated by the local near-surface flows
(granulation, supergranulation, differential rotation, meridional
circulation). The magnetic flux is then passively transported by these
velocity fields and becomes dispersed over wide areas![]() , a process well represented by
the so-called surface transport models
(e.g., van Ballegooijen et al. 1998; Baumann et al. 2004; Wang et al. 1989; Schrijver 2001). This behavior is in striking contrast to what would
be expected if the emerged flux would follow the evolution of its
magnetic roots at the bottom of the convection zone:
, a process well represented by
the so-called surface transport models
(e.g., van Ballegooijen et al. 1998; Baumann et al. 2004; Wang et al. 1989; Schrijver 2001). This behavior is in striking contrast to what would
be expected if the emerged flux would follow the evolution of its
magnetic roots at the bottom of the convection zone:
Longitudinal drift: the size range of bipolar magnetic regions corresponds to azimuthal wavenumbers between m=10 and 60, while the magnetic instabilities leading to loop formation favor values of m=1 or 2 (Spruit & van Ballegooijen 1982; Schüssler et al. 1994; Ferriz-Mas & Schüssler 1995). Consequently, the two polarities of an active region should move apart in longitudinal direction much further than actually observed. Moreover, there is no static equilibrium of the subsurface vertical "legs'' of an emerged bipolar region that is connected to an azimuthal field of 105 G at the bottom of the convection zone (van Ballegooijen 1982). The horizontal component of the magnetic tension force resulting from the bends of the flux tube where it turns horizontal sustains the drift of the two legs (and their associated poles at the surface) in opposite azimuthal directions. Thin-tube simulations in fact clearly show that the two poles drift apart unrestrained and even move around the whole circumference of the Sun within a few months. Clearly, no such systematic motion is observed.
Poleward drift: the emergence of a loop cuts off the azimuthal flow neccessary for mechanical equilibrium of the submerged field (Moreno-Insertis et al. 1992). As a result, the magnetic structure starts to drift poleward in response to the unbalanced latitudinal component of the magnetic tension force. No such systematic poleward drift is observed in bipolar regions or sunspot groups.
Tilt angle: the tilt angle of sunspot groups with respect to the East-West direction arises through the action of the Coriolis force on a rising and horizontally expanding flux loop (e.g., D'Silva & Choudhuri 1993). After emergence, the expansion stops and the flux tube should relax back to its original East-West orientation during the lifetime of a large bipolar region (Fan et al. 1994). No such relaxation is observed (Tóth & Gerlei 2004).
The observed change of the dynamics of magnetic structures from "active'' to "passive'' and the points listed above clearly indicate that bipolar magnetic regions somehow become disconnected from their deeper roots within a few days after emergence. Moreover, since the expected motions of sunspots would otherwise be quite marked, the complete absence of such behaviour indicates that the disconnection process must reliably work, virtually without exception. This represents an important constraint.
To our knowledge, two mechanisms for the disconnection of emerged flux have been proposed so far. Schrijver & Title (1999) have suggested subsurface reconnection of the two opposite polarities leading to disconnected U-loops in the upper layers. It does not seem obvious how this mechanism can achieve the required perfect reliability in view of the strong tendency of the poles to move apart in the longitudinal direction (see Sect. 2). Earlier, Fan et al. (1994) had given arguments for the necessity of disconnection and proposed a mechanism for the "dynamical disconnection'' of emerged flux by a local loss of lateral total pressure balance following the establishment of an isentropic hydrostatic equilibrium along magnetic field lines. As discussed in Sect. 2, the process sketched by Fan et al. (1994) does not seem to operate sufficiently rapidly to provide disconnection within the first few days after emergence. Here we propose a variation of the dynamical disconnection scenario, which is based upon the strong, buoyancy-driven upflow associated with the final phase of the rise of a flux loop through the convection zone. We discuss the various scenarios for disconnection in Sect. 2 and provide an illustrative quantitative elaboration of our model in Sect. 3. The results are discussed and put into a broader perspective in Sect. 4.
Schrijver & Title (1999) have suggested that active regions literally become disconnected from their roots by a subsurface reconnection between the opposite polarities in their (fragmented) legs; this would create shallow O- or U-loops, which then could float freely with the near-surface velocity fields. The problem with this concept is that, as explained above, the two legs of a bipolar region tend to rapidly move apart from each other owing to the geometry of the rising loop and as a result of the unbalanced tension force in the very deep part. Thus is would require a rather organized and converging flow to bring the opposite fluxes together to reconnect. Furthermore, the more separated the two legs already are, the more difficult is it to bring the opposite-polarity flux together. Consequently, once reconnection has failed to occur in time for whatever reason and the two poles continue to drift further apart, they cannot be disconnected any more and separate indefinitely. To our knowledge, not a single example of such a behaviour of a larger active region has been reported by observers.
Fan et al. (1994) have suggested that the establishment of hydrostatic equilibrium along a flux tube could lead to a dynamical disconnection of the emerged part from its deeper magnetic roots, which does not explicitely require a change of the magnetic topology (i.e., reconnection): as the subsurface part of the emerged flux tube approaches hydrostatic equilibrium, it eventually loses lateral pressure equilibrium at a certain height. This leads to a region of weak, passive magnetic field that effectively decouples the parts of the flux tube above and below this height.
This mechanism is closely related to the "explosion'' of magnetic flux tubes discussed by Moreno-Insertis et al. (1995): a slowly rising flux loop that maintains approximate hydrostatic equilibrium along the field lines experiences a sudden catastrophic weakening of the field strength at its apex when it reaches a critical height. This explosion height depends on the field strength in the part of the flux tube that remains at the bottom of the convection zone. The plasma is nearly isentropic within the adiabatically rising flux loop whereas the entropy decreases with height in the surrounding superadiabatically stratified convection zone. As a consequence of the higher entropy within the magnetic flux tube, the internal pressure decreases more slowly with height than the external pressure and thus eventually both become equal at a certain height above the bottom of the convection zone (Schüssler & Rempel 2002). When the loop apex approaches this "explosion height'', it expands drastically since pressure balance forces the magnetic field to become very small, so that it is no longer dynamically relevant (Rempel & Schüssler 2001). From mixing-length models of the solar convection zone one finds that a hydrostatic flux tube with a field strength of O(105) G at the base of the convection zone should explode at a depth of less than 10 Mm below the surface. On the other hand, dynamical simulations show that rising flux loops with such initial field strengths actually traverse this height range without exploding because a flow along the field lines keeps them sufficiently far away from hydrostatic equilibrium (e.g., Caligari et al. 1995).
The problem with the scenario of Fan et al. (1994) is the timescale for the establishment of the "global'' hydrostatic equilibrium required for the disconnection. The associated time scale if of the order of the Alfvén travel time along the circumference of the flux tube: taking an Alfvén speed of 1 km s-1 (corresponding to 105 G at the bottom of the convection zone), this corresponds to about a month, much too long to avoid an unrealistic evolution of the emerged part.
However, a more detailed consideration of the development in the upper parts of an emerged flux tube reveals a much faster and more local route towards dynamical disconnection, avoiding the requirement of a global hydrostatic equilibrium. Consider the following situation. A rising flux loop has emerged at the surface to form a bipolar magnetic region. The subsurface part of the loop has not exploded at its formal explosion height because the strongly buoyant and rapidly rising plasma in the loop maintains a super-hydrostatic gradient of the gas pressure (i.e., a steeper upward decline of the pressure than in the hydrostatic case) connected with an accelerated upflow (Caligari et al. 1995). After emergence, the near-surface parts of the sunspots, pores, and other flux concentrations are rapidly cooled by radiative losses, which gives rise to an inward propagating cooling front accompanied by a local downflow. This leads to a decrease of the gas pressure and a concomitant intensification of the magnetic field in the upper layers of the flux tube, while the upflow from below and the downflow from above increase the gas pressure below the first few Mm depth. After a few days, the gas pressure has increased sufficiently to approach the ambient pressure somewhere between 2 and 10 Mm depth. A thin flux tube (requiring lateral balance of total pressure) would then lose its equilibrium and explode. A more general magnetostatic equilibrium could possibly be maintained for some time but, in any case, the magnetic field becomes strongly weakened. Once the field strength falls below the equipartition value with respect to the external convective motions, the field becomes largely passive in that height range and progressively fragments, so that the upper, magnetostatic part becomes dynamically disconnected from its roots.
In order to evaluate the explanatory potential of the scenario sketched above and to provide an illustrative example, we study the quasi-static evolution of a sunspot model very similar to that of Deinzer (1965).
We basically follow the approach of Deinzer (1965) and consider a similarity solution (Schlüter & Temesváry 1958) for an axisymmetric magnetostatic configuration with hydrostatic equilibrium along the field lines and a mixing-length model of the convection zone (Kiefer et al. 2000) representing the (fixed) external stratification.
The similarity model assumes an axisymmetric magnetic structure
with a self-similar profile of the magnetic field as a function of the
radial coordinate, r, in cylindric coordinates.The two components
of the (untwisted) magnetic field are written in the form
We solve Eq. (5) through an iterative relaxation
procedure,
![\begin{displaymath}y_{n+1}=y_n+\frac{\varepsilon}{y_n^3}\left[\frac{\Phi}{2\pi}
...
...\rm d}z^2}
-y_n^3 y_{n+1}+8\pi(p_{\rm e}-p_{{\rm i}})\right],
\end{displaymath}](/articles/aa/full/2005/37/aa2962-05/img31.gif) |
(7) |
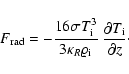 |
(9) |
The convective energy flux along the flux tube is determined following
Spruit (1974),
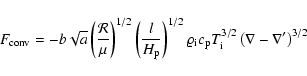 |
(10) |
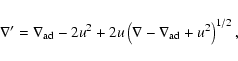 |
(11) |
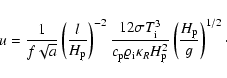 |
(12) |
In the case of a very strong systematic vertical flow with a time scale comparable to the turnover time of the convective motions, the mixing-length approach may be invalidated and, in addition, the advective entropy transport by the large-scale flow may become relevant. In our simulations, such a situation occurs only during the initial cooling phase when a rather strong transient downflow develops in the first 1-2 Mm depth (see the subsection on the implied vertical velocity below). For the later evolution of the configuration, the mixing length model appears to be adequate for the purposes of an illustrative model.
For solving Eqs. (6) and (5) we specify a boundary
condition for
![]() at the bottom of the integration domain and
values for y at the bottom and at the top, respectively. The magnetic
field strength is fixed at the upper boundary (typically at a value of
2000 G), while the thin flux tube relation,
at the bottom of the integration domain and
values for y at the bottom and at the top, respectively. The magnetic
field strength is fixed at the upper boundary (typically at a value of
2000 G), while the thin flux tube relation,
![]() ,
is assumed to hold at the bottom.
,
is assumed to hold at the bottom.
We integrate the hydrostatic balance upward from the lower boundary, specifying the value of the base pressure for each time step according to the influx of mass due to the assumed upflow. The effect of lateral expansion or contraction of the configuration is taken into account in the calculation of the base pressure. We can alternatively specify a constant upflow velocity, v0, or a constant total mass flux through the lower boundary of our integration domain.
In the thin flux tube approximation, the total mass within a flux tube
containing the (constant) magnetic flux ![]() is given by
is given by
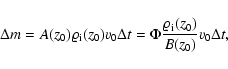 |
(14) |
A change of the pressure at the base,
![]() ,
alters the mass
within the flux tube through a change of
,
alters the mass
within the flux tube through a change of
![]() and B (the
latter is the dominant contribution since
and B (the
latter is the dominant contribution since
![]() except for the uppermost layers), which can be written formally as
except for the uppermost layers), which can be written formally as
![]() .
The adjustment of the base pressure
.
The adjustment of the base pressure
![]() has to be determined such that
has to be determined such that
For reasons of consistency with the self-similar solution it is required that the flow velocity has no variation over the cross section of the flux tube. This ensures that the magnetic field profiles remain self similar at all times.
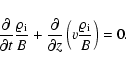 |
(16) |
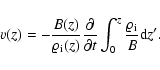 |
(17) |
We have not considered the advection effects from the implied vertical velocity in the energy equation. In the deeper, homentropic part of the flux tube, such effects are irrelevant for the (adiabatic) temperature structure, while the downflow in the upper part could be temporarily important, but rapidly diminishes to less than 20 m s-1 after the first phase of radiative cooling. The advection of low entropy by the downflow probably enhances the intensification of the magnetic field in the upper part (in effect, this is the convective collapse mechanism). A quantitative evaluation of these effects requires a fully dynamic simulation, which is beyond the scope of this paper.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2962fig1.ps}
\end{figure}](/articles/aa/full/2005/37/aa2962-05/Timg66.gif) |
Figure 1: Sequence of temperature profiles as a function of depth in the upper part of the model, showing the rapid inward propagation of a cooling front and the establishment of a largely stationary profile after a few hours. Zero depth corresponds to optical depth unity in the external stratification. The uppermost (thick full) curve shows the (time-independent) external temperature. The other curves show the temperature on the sunspot axis after 0.5 h (dotted curve), 1 h (dashed curve), 4 h (dash-dotted curve), 15 h (dash-triple-dotted curve), and 30 h (full curve), respectively, from the onset of radiative cooling (corresponding to the emergence of the flux tube at the surface). |
| Open with DEXTER | |
As an illustration of a typical evolution in the framework of our
quasi-static model, Figs. 1-3
show snapshots of temperature, magnetic field strength, and convective
energy flux, respectively, along the axis of the flux tube. In this
case we have assumed a total magnetic flux of 1021 Mx and a
constant mass flux at the bottom (located at 12.5 Mm depth)
corresponding to an initial inflow velocity of
700 m s-1. Simulations of thin flux tubes give rising
speeds of that order at the same depth (Caligari et al. 1995). The
spacing of the numerical grid is 25 km. The temperature at the upper
boundary (at optical depth unity of the external stratification) has
been fixed at a value of 3500 K and the magnetic field strength at
2000 G. The ratio
![]() of the mixing length, l, to the
local pressure scale height,
of the mixing length, l, to the
local pressure scale height, ![]() ,
determines the total energy flux in
the flux tube, which is rather well constrained by sunspot observations
at 20-25% of the undisturbed solar flux. A value of
,
determines the total energy flux in
the flux tube, which is rather well constrained by sunspot observations
at 20-25% of the undisturbed solar flux. A value of
![]() leads to an energy flux of about 22% of the undisturbed solar value at
the top of the model. About 40 h after the start of radiative
cooling and bottom inflow, the field strength has fallen below the
equipartition value (with respect to the convective velocity in the
exterior) at at depth of 4.7 Mm, implying the dynamical disconnection of
the upper part from its roots. At the same time, the inflow velocity has
decreased to less than 50 m s-1 owing to the strong
weakening of the field and the assumed constant mass flux.
leads to an energy flux of about 22% of the undisturbed solar value at
the top of the model. About 40 h after the start of radiative
cooling and bottom inflow, the field strength has fallen below the
equipartition value (with respect to the convective velocity in the
exterior) at at depth of 4.7 Mm, implying the dynamical disconnection of
the upper part from its roots. At the same time, the inflow velocity has
decreased to less than 50 m s-1 owing to the strong
weakening of the field and the assumed constant mass flux.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{2962fig2.ps}
\end{figure}](/articles/aa/full/2005/37/aa2962-05/Timg70.gif) |
Figure 2: Snapshots from the time evolution of the magnetic field strength along the tube axis as a function of depth for the same case as shown in Fig. 1 (note the different depth range). The curves correspond to about 1 h (upper full curve), 10 h (dotted curve), 20 h (short-dashed curve), 30 h (dash-dotted curve), 35 h (dash-triple-dotted curve), and 40 h (long-dashed curve) after the start of radiative cooling (emergence). The lower, thick full curve gives the equipartition field strength with respect to the convective velocities from the mixing length model of the external stratification (Kiefer et al. 2000). After an initial general drop, the field strength increases again down to a depth of about 4 Mm while a local minimum of the field strength develops and moves downward until, after about 40 h, the field strength falls below the local equipartition value at at depth of 4.7 Mm. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2962fig3.ps}
\end{figure}](/articles/aa/full/2005/37/aa2962-05/Timg71.gif) |
Figure 3: Profiles of the convective energy flux density (normalized by the undisturbed solar value) along the sunspot axis for the same instants of time as shown in Fig. 2 (note the different depth range). Above the Wilson depression, the energy transport is taken over by the radiative flux (not shown here). The convective transport affects progressively deeper layers in order to supply the (almost constant) surface energy flux density of about 22% of the undisturbed solar value. The corresponding downward extension of the superadiabatic stratification leads to a growth of the region that is stabilized against disconnection through the resulting increase of the magnetic field (cf. Fig. 2. |
| Open with DEXTER | |
Figure 1 shows the fixed external temperature stratification (thick full line) and five profiles of the temperature in the upper part of the model at various instants of time. After the emergence of the flux tube at the photosphere (start of the calculation), radiative cooling leads to the development of a cooling front, which rapidly progresses inward. Already after about 30 min, the level of optical depth unity in the flux tube (the Wilson depression) has reached a depth of about 375 km and after a few hours the inward propagation of the profile has become very slow (dash-dotted curve, after 4 h). The last curve (thin full line) shows the largely stationary temperature profile about 30 h after the start of radiative cooling. The Wilson depression has reached a value of about 550 km with a temperature of about 4100 K at (Rosseland) optical depth unity.
For the same case, Fig. 2 shows snapshots of the magnetic field profiles along the tube axis. The full curve shows the situation after about 1 h with a steep inward rise of the field strength that reflects the not quite realistic initial condition. As time progresses, the depth gradient of the magnetic field strength flattens and a local minimum develops, which becomes deeper and moves downward while, at the same time, there is a slow increase of the field strength in the upper layers. Both effects are connected to the development of a superadiabatic stratification in the sunspot model, which results from the growth of the region with convective energy transport. This is illustrated in Fig. 3, which shows depth profiles of the convective energy flux density (normalized by the undisturbed solar value) for the same instants as the magnetic field profiles in Fig. 2 (note the different depth scale). The superadiabatic stratification in the region with significant convective energy flux leads to a decrease of the pressure scale height and an associated increase of the field strength and thus prevents the field from becoming weak in the upper layers. As the superadiabatic region grows downward, the position of the field strength minimum also is shifted downward until the field strength eventually falls below the local equipartition level at a depth of about 4.7 Mm. The field strength at the bottom of the model has then reached about 10 kG, which is consistent with the results of thin flux tube simulations. The observable layers above the Wilson depression (optical depth unity, where the field strength remains around 2500 G) are largely unaffected by this whole development.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2962fig4a.ps}\par\vspace*{3mm}
\includegraphics[width=8cm,clip]{2962fig4b.ps}
\end{figure}](/articles/aa/full/2005/37/aa2962-05/Timg72.gif) |
Figure 4: Disconnection time ( upper panel) and disconnection depth ( lower panel) as functions of the initial upflow velocity at the lower boundary. The mass influx is kept constant in time in the individual simulation runs (indicated by asterisks). The connecting curves represent spline interpolations. |
| Open with DEXTER | |
The simulation run presented in the previous subsection yields values for the time scale and the depth of the disconnection that appear to be reasonable in view of what is indicated by observations of solar magnetic regions. How do these results depend on the various parameters and assumptions entering the model?
The most important parameter of the model is the inflow velocity at the bottom, which determines the rate of pressure buildup at the base. For the case of constant mass flux through the bottom, Fig. 4 gives the disconnection time and depth (determined as time and depth for which the field strength first equals the external equipartition value) as functions of the initial inflow velocity, all other parameters being the same as those of the reference run discussed above. The plots show that that smaller values of the mass flux (smaller initial inflow velocity) lead to later and deeper disconnection. In the alternative case with constant inflow velocity (as opposed to constant mass influx), even much smaller inflow speeds of the order of 100 m s-1 lead to disconnection within few days and in a few Mm depth.
For high initial inflow speeds, the disconnection depth and time become largely independent of speed and reach values around 9 h and 2.3 Mm, respectively. This saturation results from the low entropy of the gas in the upper layers of the model due to the strong surface cooling, so that a strong field is always maintained in these layers. In fact, switching off the radiative losses invariably leads to a dramatic weakening of the magnetic field at the very top of the integration domain (depth zero).
We have varied a number of other parameters as well as initial and
boundary conditions in order to evaluate their effects on the
disconnection depth (![]() )
and disconnection time (
)
and disconnection time (![]() ).
We find that the results are rather insensitive to the choice of
temperature and magnetic field at the top (z=0). The same is true for
the (constant) value of the entropy in the initial stratification. In
most cases we have taken the initial entropy equal to that of the
external medium at the bottom of the model (12.5 Mm depth). Since the
plasma in the flux tube originates from deeper layers zone, its entropy
could be somewhat larger. However, since nearly all of the entropy drop
through the convection zone takes place above 12.5 Mm, even taking the
entropy value corresponding to the bottom of the convection zone has
almost no effect on the results.
).
We find that the results are rather insensitive to the choice of
temperature and magnetic field at the top (z=0). The same is true for
the (constant) value of the entropy in the initial stratification. In
most cases we have taken the initial entropy equal to that of the
external medium at the bottom of the model (12.5 Mm depth). Since the
plasma in the flux tube originates from deeper layers zone, its entropy
could be somewhat larger. However, since nearly all of the entropy drop
through the convection zone takes place above 12.5 Mm, even taking the
entropy value corresponding to the bottom of the convection zone has
almost no effect on the results.
However, other parameters and conditions have a significant effect on
the disconnection. It turns out that ![]() and
and ![]() decrease
decrease
- with decreasing depth of the lower boundary;
- with decreasing total magnetic flux;
- with increasing initial mass content;
- and also by keeping the inflow velocity (in contrast to the mass influx)
constant in time.
Likewise, determining the magnetic field by replacing the similarity
solution by the thin flux approximation (taking the limit ![]() in
Eq. (5)) leads to more shallow and earlier disconnection.
in
Eq. (5)) leads to more shallow and earlier disconnection.
The quantitative results are combined in Fig. 5, which
gives ![]() as a function of
as a function of ![]() for a number of cases.
Although the various simulation runs represent quite different
conditions and assumptions, the results suggest a universal relationship
between disconnection time and disconnection depth. The curve drawn in
the figure is not a fit but gives, as a function of time, the depth at
which the convective energy flux density equals 10% of the undisturbed
solar value, about half of the emergent surface flux density. This curve
therefore reflects the downward progression of the region of convective
cooling as a result of the radiative losses at the surface (see
Fig. 3).
for a number of cases.
Although the various simulation runs represent quite different
conditions and assumptions, the results suggest a universal relationship
between disconnection time and disconnection depth. The curve drawn in
the figure is not a fit but gives, as a function of time, the depth at
which the convective energy flux density equals 10% of the undisturbed
solar value, about half of the emergent surface flux density. This curve
therefore reflects the downward progression of the region of convective
cooling as a result of the radiative losses at the surface (see
Fig. 3).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2962fig5.ps}
\end{figure}](/articles/aa/full/2005/37/aa2962-05/Timg77.gif) |
Figure 5:
Disconnection depth vs. disconnection time for various model
runs. Plus signs: runs with constant mass influx (the same runs as in
Fig. 4); asterisks: runs with constant inflow velocity
in the range 75-400 m s-1; diamonds: runs with different
values for the initial pressure at the top, changing the initial mass
in the flux tube by about |
| Open with DEXTER | |
The relationship between the disconnection depth and the downward
progressing convective "cooling front'' is in accordance with our
interpretation of the disconnection depth in the case discussed in the
previous subsection. Without surface cooling, the strongest weakening
of the field would occur near to the top of the model. The cooling
leads to the development of a superadiabatically stratified layer
connected with a strengthening of the magnetic field in the upper part
of the tube, which grows downward as the surface flux has to be
supplied by the thermal energy stored in the deeper layers. This
prevents the field in the upper layers from being weakened by the
pressure buildup due to the inflow from below. The disconnection then
takes place somewhere in the flank of the downward progressing
convective flux profiles shown in Fig. 3,
leading to the relation between ![]() and
and ![]() apparent
from Fig. 5. In the absence of convective energy
transport, the cool region would only extend down to the Wilson
depression and the sunspot would be disconnected and disrupted
immediately below that level, making it difficult to imagine that it
could survive as a coherent entity thereafter.
apparent
from Fig. 5. In the absence of convective energy
transport, the cool region would only extend down to the Wilson
depression and the sunspot would be disconnected and disrupted
immediately below that level, making it difficult to imagine that it
could survive as a coherent entity thereafter.
This interpretation is further supported by runs with varied efficiency
of convection, which affects the downward progression speed of the
region of convective cooling. For the case shown in
Figs. 1-3, we have
![]() ,
which gives a heat flux density ratio of 22%. Larger (smaller) values of
,
which gives a heat flux density ratio of 22%. Larger (smaller) values of ![]() lead to a faster (slower)
downward extension of the convectively cooled region and to deeper
(shallower) explosion: for
lead to a faster (slower)
downward extension of the convectively cooled region and to deeper
(shallower) explosion: for
![]() we find an explosion depth of
about 6 Mm and a flux of 30% of the undisturbed solar flux density,
while a tube model with
we find an explosion depth of
about 6 Mm and a flux of 30% of the undisturbed solar flux density,
while a tube model with
![]() explodes at a depth of 2.3 Mm and
shows only 14% of the undisturbed solar energy flux density. In both
cases, the corresponding explosion depths and times are consistent with
the downward propagation speed of the cooling flank.
explodes at a depth of 2.3 Mm and
shows only 14% of the undisturbed solar energy flux density. In both
cases, the corresponding explosion depths and times are consistent with
the downward propagation speed of the cooling flank.
The results from our illustrative model indicate that dynamical disconnection of emerged magnetic flux is possible at a depth of less than about 10 Mm and within a few days after emergence if upflow velocities as shown by simulations of thin flux tubes are considered (of the order of a km s-1 at 10 Mm depth). However, we have to keep in mind that the assumption of a quasi-static state in the model forces us to use a too strong initial magnetic field in the deeper layers, so that the time evolution as shown here may not correctly represent what is actually happening below a sunspot. A more realistic time evolution of the disconnection process requires a full MHD simulation. On the other hand, the disconnected state represents a fully self-consistent solution with realistic surface properties and a hydrostatic stratification as indicated by observations (e.g., Beckers 1977). Our results show that a disconnected magneto-static sunspot model can be consistently constructed.
We have taken the equipartition field strength with respect to the convective velocities in the mixing-length model of the (non-magnetic) external medium as the limit for the onset of disconnection. This is only a rough indicator and the detailed disconnection process certainly is more complex. For instance, we have not considered the possible effect of fragmentation by the interchange (fluting) instability at the periphery of a flux tube bounded by a current sheet (Parker 1975). Meyer et al. (1977) have shown that buoyancy may stabilize a sunspot only down to a few Mm depth below the solar surface. Deeper down the destabilizing effect of the curvature of the surface bounding the flux tube dominates. In our case, the weakening of the field by the upflow leads to a hourglass-like shape of the sunspot, so that buoyancy effects in the lower part actually promote the instability. This could lead to fragmentation even before the equipartition limit has been reached.
The requirement for disconnection of emerged flux does not only apply to sunspots but covers all magnetic flux in bipolar regions. We suggest that the smaller flux tubes which form the plage and network regions are dynamically disconnected by the same process that affects the sunspots. In fact, using the thin flux tube approximation we find a shallow disconnection depth (of about 2 Mm) for such structures. This could be even smaller since a large part of the radiative energy loss of a small tube is provided by lateral radiative heating in the surface layers, so that the cooling of the subsurface layers proceeds more slowly than in sunspots, leading to a more shallow disconnection. It is well conceivable that the weakening of the field by the upflow in small flux fragments extends up to the surface, so that all initial connectivity is lost already during emergence or shortly thereafter. The formation of intense fields and the patterns of flux distribution in plages then results from the interaction with the local velocity fields at the solar surface (e.g., Vögler et al. 2005).
In which way does the fragmented flux below the disconnected surface flux evolve further? Since the flux fragments are passive with respect to convection, they will be deformed and stretched by the convective motions, probably keeping the field strength at about the equipartion value. However, this must not lead to a dynamical "re-connection'' of the emerged part with its magnetic roots. We conjecture that this could be prevented by progressing fragmentation into ever thinner filaments, owing to various instabilities and dynamical processes (e.g., Schüssler 1984; Vishniac 1995). The fragmentation proceeds until the resistive length scale is reached, for which flux freezing is no longer valid and efficient exchange of mass and heat (by radiation) is provided (Schüssler 1987). The magnetic flux then has become truly passive and is kinematically transported by the motions of the plasma, providing no further possibility for restoring the dynamical link between the emerged flux and its the deep-lying parent flux tube. Such a transition to passive, weak field after the explosion of a flux tube has also been found in the numerical simulations of Rempel & Schüssler (2001). Sustained outflow of buoyant plasma from the "stumps'' of the disconnected parent flux tube and the horizontal motion driven by the curvature force until a narrow U-loop remains could also provide a mechanism for the removal of the parent flux tube from its storage region at the bottom of the convection zone. These processes can actually be observed in thin-tube simulations (Caligari et al., in preparation).
Acknowledgements
This work has immensely benefited from numerous discussions and much exchange of ideas over the years with Fernando Moreno Insertis. Helpful comments by Yuhong Fan on a draft version of this paper are gratefully acknowledged. The National Center for Atmospheric Research (NCAR) is sponsored by the National Science Foundation.