A&A 441, 41-45 (2005)
DOI: 10.1051/0004-6361:20052941

Astrophysical consequences of extended cosmology

P. S. Wesson 1,2


1 - Astronomy Group, Department of Physics, University of Waterloo, Waterloo, Ontario N2L 3G1, Canada
2 - Gravity-Probe B, Hansen Physics Labs, Stanford University, Stanford, California 94305, USA

Received 27 February 2005 / Accepted 13 June 2005

Abstract
We outline astrophysical implications of a cosmological model based on the popular view that gravity should be extended from four to more dimensions to unify the forces of physics. At early times the model is inflationary, galaxies form easier, and their peculiar velocities are damped to produce a universal energy field. At late times the model is close to standard, but the dynamics of field galaxies and those in clusters are modified. It is possible to further test the model using a high-velocity radially-moving spacecraft in the solar system. These consequences provide a good way to look for extra dimensions.

Key words: cosmology: diffuse radiation - galaxy: formation - cosmology: miscellaneous

1 Introduction

Presently, the preferred way to unify gravity with the interactions of particle physics is to extend the dimensionality of Einstein's theory of general relativity. There are many ways to do this, but five dimensions is the basic extension and the low-energy limit of theories with even more dimensions. How are we to test such accounts? A conservative but profitable approach is to take a 5D manifold with an unconstrained extra part, derive a class of 4D cosmological models that incorporates known facts, and look for new effects.

In following this approach below, we will draw on technical results in the literature, but concentrate on astrophysical consequences that are open to test. The technical starting point is a class of 5D cosmological models found recently by Mashhoon & Wesson (2004). These models are inflationary at early times (Linde 1991), but include the standard Friedmann-Robertson-Walker models at late times (Synge 1960; Hoyle & Narlikar 1974; Wesson 1999). The new class of 5D models smoothly embeds the 4D ones because of Campbell's theorem, which we will use below (Campbell 1926; Seahra & Wesson 2003; Abolghasem et al. 1996; Wesson 1994). The new class of models is characterized by an irremoveable cosmological "constant'', which may however decay with time and whose size agrees with astrophysical data (Lineweaver 1998; Overduin & Cooperstock 1998; Overduin 1999). The models are also characterized by an intrinsic extra force, which is the signature in 4D spacetime of 5D laws of dynamics (Mashhoon et al. 1998; Wesson 1999; Youm 2000, 2001; Barvinsky et al. 2002; Mukohyama 2003; Maartens 2003; Dahia et al. 2003; Bertolami & Paramos 2004; Belayev 2004; Bini et al. 2004). This so-called fifth force is common to both the current versions of 5D gravity, namely membrane and induced-matter theory, and will form the basis for much of the discussion below. It should be noted that the two just-mentioned theories are technically equivalent, both in terms of their field equations and dynamics (Ponce de Leon 1988, 2001, 2004). Our results should therefore be general. They complement others which have appeared recently in the literature, which explore observational aspects of higher-dimensional cosmology (Alcaniz 2005; Deffayet et al. 2002; Sahni & Shtanov 2002; Maia et al. 2005). Some of these cosmologies involve a decaying cosmological constant coupled with particle production, but there are constraints on such models from data to do with the age of the universe and data to do with background radiation (Lineweaver 1998; Overduin & Cooperstock 1998; Overduin 1999; Overduin & Wesson 2004). Our model will concentrate on dynamical effects, which are most important in the early universe, for galaxies, and leave the late universe to be described by standard solutions. However, we will also briefly consider the solar system, since while 5D gravity is in agreement with the classical tests of relativity (Kalligas et al. 1995), we see the opportunity for a new experiment involving a high-velocity, radially-moving spacecraft. Our aim is to bring higher-dimensional cosmology into the range of meaningful test.

2 Consequences of 5D cosmology

Current interest in higher-dimensional gravitational theory is largely driven by particle physics, but in constructing realistic cosmological models we have to be guided by astrophysical concerns. Thus we would like to have a model which is inflationary at early times but goes over to a standard Friedmann-Roberston-Walker (FRW) one at late times. An approach which includes both the deSitter and Einstein-deSitter models is due to Ponce de Leon (1988), who embedded the 4D metrics for these models in a 5D metric that is separable in the extra coordinate. (We use time and space coordinates t, $r\theta \phi $ with ${\rm d}\Omega ^{2}\equiv {\rm d}\theta ^{2}+\sin ^{2}\theta {\rm d}\phi ^{2}$, and x4=l as the extra coordinate.) That such an embedding is possible is guaranteed by Campbell's theorem (Campbell 1926; Seahra & Wesson 2003). This says for our purposes that a solution of the Einstein field equations

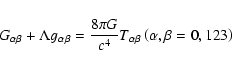\begin{displaymath}G_{\alpha \beta }+\Lambda g_{\alpha \beta }=\frac{8\pi G}{c^{4}}T_{\alpha \beta }\left( \alpha ,\beta =0,123\right) \end{displaymath} (1)

can be embedded in a solution of the Ricci-flat 5D field equations

\begin{displaymath}R_{AB}=0\;\;\;\left( A,B=0,123,4\right) . \end{displaymath} (2)

That is, the 5D Ricci tensor $\left( R_{AB}\right) $ for an apparently empty space contains the information normally encoded in the 4D Einstein tensor $% \left( G_{\alpha \beta }\right) $ and the 4D energy-momentum tensor $\left( T_{\alpha \beta }\right) $. The mechanism for going from (2) to (1) is by now well known (see e.g. Wesson 1999; we retain physical units for the speed of light c, the gravitational constant G and the cosmological constant $% \Lambda $). However, while the Ponce de Leon solutions are often regarded as the "standard'' 5D cosmological ones, they are piecemeal in that the deSitter (inflation) and Einstein-deSitter (dust) solutions are recovered as sub-solutions on different hypersurfaces (l= constants). To follow the evolution of the universe from early to late times in a more consistent manner, we would prefer to have a continuous class of solutions.

In this regard, it has been known for many years that the deSitter solution can be written in a form where the 4D metric is conformally flat, so the metric tensor is $g_{\alpha \beta }=f\left( t\right) \eta _{\alpha \beta }$and $\eta _{\alpha \beta }=\left( +1-1-1-1\right) $ is the Minkowski tensor for flat spacetime (Synge 1960). Also, though it is not so widely known, all of the 4D FRW models can be written in a conformally-flat form with $% g_{\alpha \beta }=f\left( t,r\right) \eta _{\alpha \beta }$ (Hoyle & Narlikar 1974). We are therefore interested in a class of 5D models whose metric has a 4D part that can be written ${\rm d}s^{2}=f\left( x^{\gamma }\right) \eta _{\alpha \beta }{\rm d}x^{\alpha }{\rm d}x^{\beta }$, where $f\left( x^{\gamma }\right) $ describes the FRW models which are supported by astrophysical data. Also for physical reasons, the 5D metric should not contain electromagnetic terms (so we set the metric coefficients $g_{0\alpha }$ that represent the electromagnetic potentials to 0), but should contain a scalar field that may relate to dark energy (so we set the coefficient g44 that represents the scalar potential to -1). Even with these practical constraints, we still have the theoretical problem of solving the field Eq. (2) and interpreting the results in terms of Eq. (1).

The details of this are tedious, and we refer the reader elsewhere for them (Mashhoon & Wesson 2004). The upshot is a class of exact solutions with

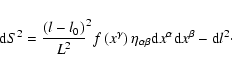\begin{displaymath}{\rm d}S^{2}=\frac{\left( l-l_{0}\right) }{L^{2}}^{2}f\left( ... ...a \beta }{\rm d}x^{\alpha }{\rm d}x^{\beta }-{\rm d}l^{2}\cdot \end{displaymath} (3)

Here l is the value of the extra coordinate which can vary away from some fiducial value l0 as the model evolves, and L is a constant length introduced for dimensional consistency. The latter is related to the effective 4D cosmological constant $\Lambda $, which has the physical dimensions of an inverse length squared. This parameter is fixed by the vacuum limit of the field Eq. (1), which then read $% R_{\alpha \beta }=\Lambda g_{\alpha \beta }$ (in terms of the Ricci tensor) and imply $R=4\Lambda $ (in terms of the Ricci scalar). Calculating the geometric quantities using Eqs. (2) and (3), the effective cosmological "constant'' is found to be

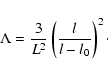\begin{displaymath}\Lambda =\frac{3}{L^{2}}\left( \frac{l}{l-l_{0}}\right) ^{2}\cdot \end{displaymath} (4)

This is large for $l\sim l_{0}$ and small for $l\gg l_{0}$ if L is a cosmological length, which astrophysical data indicate to be $L\simeq 1\times 10^{18}$ cm (Lineweaver 1998; Overduin & Cooperstock 1998; Overduin 1999). Its variation over cosmological proper time s can be specified given $l=l\left( s\right) $, which can be obtained by solving the 5D equations of motion. Again, we can apply a physical constraint to this problem, concentrating on null 5D geodesics because they are the analogs of the 4D paths of photons (Seahra & Wesson 2001; Youm 2001). Then we find that (4) gives

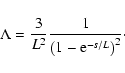\begin{displaymath}\Lambda =\frac{3}{L^{2}}\frac{1}{\left( 1-{\rm e}^{-s/ L}\right) ^{2}}% \cdot \end{displaymath} (5)

Here s=0 represents the big bang; and for velocities small compared to that of light and at late times $s\simeq ct$, where t is the ordinary time. We now proceed to examine the astrophysical consequences of Eq. (5) and related properties of the class of solutions (3).

(a) These 5D models are like 4D inflationary ones, insofar as they are dominated by $\Lambda $ near the big bang. The cosmological "constant'' is large at early times (formally infinite at the big bang), and decreases to 3/ L2 at late times (of order 10-56 cm<tex2htmlcommentmark> -2). To illustrate the potency of this effect, we note that according to (5), over the period 108 to 1010 yr the value of $\Lambda $ decreases by a factor of approximately 4000. Now (5) is the effective 4D value of this parameter, and in standard general relativity $\Lambda $ is usually related to a force (per unit mass) $\Lambda rc^2/3$, or an energy density for the vacuum $\left( c^{4}/ G\right) \left( \Lambda / 8\pi \right) $. Thus on the basis of a 4D interpretation, both the $\Lambda $-force and the vacuum decay. It may be possible to test for these effects using high-redshift sources at epochs of order 108 yr, such as QSOs.

(b) Galaxy formation is augmented in these models, because there is a velocity-dependent force associated with them. This is characteristic of most 5D theories, and exists for both induced-matter theory (Mashhoon et al. 1998) and membrane theory (Youm 2000). It also exists for other higher-dimensional theories, though its form depends on the nature of the line element (Barvinsky et al. 2002; Mukohyama 2003; Maartens 2003; Dahia et al. 2003; Bertolami & Paramos 2004; Belayev 2004; Bini et al. 2004). That such an extra force must exist in principle when the world is extended from 4D to 5D can be most quickly appreciated when we consider metric-based theories like those of Einstein for gravity and Maxwell for electromagnetism. The metric implies an orthogonality condition for the forces and velocites of the form $f^{\alpha}u_{\alpha}=0$ ( ${\alpha}=0,123$; see Rindler 2001). But extended to 5D, the corresponding condition is fAUA=0 (A=0,123,4). Thus $f^{\alpha}u_{\alpha}=-f^4U_4\neq 0$, and there is necessarily an extra force if we use 4D parameters such as the proper time s to describe a 5D world. This extra force should not be confused with the $\Lambda $ -force mentioned in the preceding paragraph, which is positive for $\Lambda >0$ but is only significant for large r. It should also not be confused with the short-range non-Newtonian forces predicted by certain other non-compactified theories, since the present approach gives back Newton's law in the weak-field limit of the one-body problem. (See Kalligas et al. 1995; and Wesson 1999, where the 1-body problem is studied in detail, but where there is no singular surface of the type found in certain versions of membrane theory and so no departure of the field lines from their standard form.) By contrast, the fifth force (per unit mass) that is characteristic of higher-dimensional gravity is range-independent, but because of the structure of the 5D geodesic equation normally involves a product of velocities and a length scale associated with the extended geometry. It should be noted that while such an extra force is required by the extension from 4D to 5D, in cosmological applications we expect it to be independent of the rest mass of the test object, so as to conform to the (weak) principle of equivalence. For our cosmological metric (3), all of the noted conditions of the fifth force are met, and its precise form can be derived by solving the radial component of the 5D equations of motion (Mashhoon & Wesson 2004). It is given by

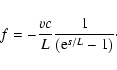\begin{displaymath}f=-\frac{vc}{L}\frac{1}{\left( {\rm e}^{s/ L}-1\right) }\cdot \end{displaymath} (6)

This describes a force (per unit mass) or acceleration which acts in addition to that associated with normal gravity, and in an expanding universe tends to pull matter back towards a local origin. The solution of (6) for the velocity is

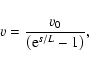\begin{displaymath}v=\frac{v_{0}}{\left( {\rm e}^{s/ L}-1\right) }, \end{displaymath} (7)

where v0 is the value when the proper time is $s=L\;\ln(2)$. The existence of the fifth force (6) has significant implications for galaxy formation. This process, in the usual 4D scheme, is presumed to occur when an over-dense region attracts more material than its surroundings, so that the density perturbation grows with time. Unfortunately, it does not do so fast enough in most models to account for the observed galaxies or other structures (Padmanabhan 1993). And while there are ways out of this dilemma (for example by using seed perturbations due to quantum effects or pregalactic stars), the fifth force naturally augments galaxy formation and deserves in-depth study.

(c) Peculiar velocities are naturally damped by the fifth force noted above. It is standard in modern cosmology to break the velocities of galaxies into two components, the (regular) Hubble flow and (random) departures from it. In theoretical work, the former component is often removed by a choice of coordinates, defining a comoving frame where the regular velocities of the galaxies are zero and to which their peculiar velocities can be referred. A practical definition of the comoving frame is the one in which the 3K microwave background looks completely homogeneous. At the present epoch, the peculiar velocities of field galaxies do not exceed a few 100 km s-1; and while there are other ways to account for this, the fifth force (6) and the velocity law (7) provide a natural mechanism. Put another way: the comoving frame which is assumed in most 4D work on cosmology is a natural equilibrium state of 5D gravity.

(d) The damping mechanism outlined above can lead to a cosmological energy field which is significant. We can calculate an approximate upper limit to this as follows. By (6), the magnitude of the force on an object of mass <tex2htmlcommentmark> m is $\left( mvc/ L\right) \left( {\rm e}^{s/ L}-1\right) ^{-1}$. The product of this with v gives the associated rate of change of energy or power, which by (7) is $\left( mcv_{0}^{\;\;2}/ L\right) \left( {\rm e}^{s/ L}-1\right) ^{-3}$. The integral of this over proper time from s1 to s2 gives the total energy change, and if we assume $s_{1}\ll s_{2}$ and $s_{1}\ll L$ this is approximately $\left( mv_{0}^{\;\;2}/ 2\right) \left( L/ s_{1}\right) ^{2}$. This is the energy lost by one object through the damping of its kinetic energy by the fifth force, and is sharply peaked at early epochs. If the objects concerned form a uniform distribution, and presently have a mean distance d from each other, the energy density of the field produced by the damping is $\epsilon \simeq \left( mv_{0}^{\;\;2}/ 2d^{3}\right) \left( L/ s_{1}\right) ^{2}$. We can write this in a more instructive form if we introduce the mass density $\left( \rho _{\rm m}\right) $, the epoch when the damping was severe $% \left( t_{\ast }\right) $ and the epoch now $\left( t_{0}\right) $. Then a rough estimate of the present energy density of the field that results from the damping is

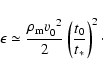\begin{displaymath}\epsilon \simeq \frac{\rho _{\rm m}v_{0}^{\;\;2}}{2}\left( \frac{t_{0}}{t_{\ast }% }\right) ^{2}\cdot \end{displaymath} (8)

This is a theoretical upper limit because of the approximations made, but of course the parameters in it are themselves highly uncertain. For the purpose of illustration, let us substitute $\rho _{\rm m}=2\times 10^{-31}$ g cm<tex2htmlcommentmark> -3, v0=100 km s-1, $t_{0}=1\times 10^{10}$ yr and $t_{\ast }=1\times 10^{8}$ yr. Then (8) gives $\epsilon =1\times 10^{-13}$ erg cm-3. This is a significant fraction of the energy density of the cosmic microwave background, and comparable to the energy densities of other components of the intergalactic photon field (Henry 1991). However, the physics which leads to (8) is different from that involved in the production of the CMB and the electromagnetic fields at other wavelengths such as the extragalactic background light (Wesson 1991). Indeed, the energy field (8) may not be electromagnetic in nature (this would require that the damping act on plasma protogalaxies or young galaxies with a significant content of ionized material). It could have a different nature, such as thermal energy or gravitational waves. We should recall, though, that while the nature of the energy field (8) is open to discussion, its existence follows necessarily from currently popular accounts of 5D gravity. In view of this, we suggest that it would be wise to use observations of known fields and their isotropy to constrain the underlying theory.

(e) The extra force associated with 5D strengthens local gravity and can therefore have dynamical effects on field galaxies and galaxies in clusters. This is because in the local limit, Newton's law is modified so that the force (per unit mass) is

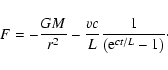\begin{displaymath}F=-\frac{GM}{r^{2}}-\frac{vc}{L}\frac{1}{\left( {\rm e}^{ct/ L}-1\right) }% \cdot \end{displaymath} (9)

Here $M=M\left( r\right) $ is the mass interior to radius r for a system with approximately spherical symmetry and we have put s=ct in (6). We have investigated (9) for several astrophysical systems in detail, but would like to present the results in a form which is generic. One way to do this is to rewrite (9) as if the system was Newtonian and redefine the gravitational "constant'' to be

\begin{displaymath}G^{\prime }=G\left[ 1+\frac{vr^{2}}{GM}\left( \frac{c}{L}\right) \frac{1}{% \left( {\rm e}^{ct/ L}-1\right) }\right] \cdot \end{displaymath} (10)

In this, vr2/ GM has the dimensions of a time and would conventionally define a dynamical timescale $\left( t_{\rm d}\right) $, while <tex2htmlcommentmark> L/ c is a timescale associated with the cosmology which we expect to be approximately equal to the present epoch $\left( t_{0}\right) $. Both this and the remaining factor in (10) are uncertain, so to be general we write the latter relation as

\begin{displaymath}G^{\prime }=G\left[ 1+\alpha \left( \frac{t_{\rm d}}{t_{0}}\right) \right] \cdot \end{displaymath} (11)

Here $\alpha $ is a dimensionless factor which depends on parameters to do with both the cosmology and the system, but which at present is of order of magnitude unity. In adopting this approach, it should be emphasised that we are not suggesting that the Newtonian "constant'' is really a variable parameter, as in 4D gravitational theories of the type proposed by Brans/Dicke, Dirac, Hoyle/Narlikar, Canuto and others, or in certain $% N( \geq$5)D theories of the Kaluza/Klein type. Rather, we are taking a pragmatic approach to see how a new effect fits into a framework of existing data. In this respect, the parametization (11) also has the advantage that we can use limits set on departures from Newtonian gravity in other contexts (Will 1993, 2001). Since the relations (9)-(11) will require detailed future study, we content ourselves here with noting the results for two situations of interest:

(i) Field galaxies which obey (9) and (11) do not show departures from Hubble's law, since $M\left( r\right) / r^{2}$ varies as r for a uniform distribution and so does v=Hr. However, there is a modification in the <tex2htmlcommentmark> t-behaviour of the dynamics of unclustered galaxies, and for the Einstein-deSitter model at early times the effect corresponds to a value of <tex2htmlcommentmark> G that is four times the conventional one. This means that young galaxies interacted more strongly than is usually assumed. It is widely believed that spiral galaxies acquired their angular momenta through gravitational quadrupole interactions in the early universe, as first proposed by Hoyle (1949). But models of this process have long been known to give values for the spins of spirals which are less than those observed (Wesson 1982). The new force being discussed here can resolve this discrepancy and give insight to other problems involving tidal interactions.

(ii) Galaxies in clusters are expected to be modelled by (11) with $t_{\rm d}$given by the crossing time. It should be noted, in this context, that (11) is based on (9) which in turn is based on (6). The last refers to an extra force in the radial direction, so we are here discussing an effect on galaxies whose orbits pass through or near the centres of their host clusters. This situation actually applies to the majority of clusters of galaxies, since it is now generally acknowledged that many clusters are not spherical or Abell-like, but indeed more elongated that other dynamical systems such as elliptical galaxies, with velocity distributions that are significantly anisotropic. The effect for galaxy clusters embodied in (11) is in the direction of helping to resolve the virial discrepancy which is apparently encountered for most of them. But the modification is modest, so we infer that most clusters harbour large amounts of dark matter/energy, as usually assumed.

(f) The observed solar system is believed to be dynamically in agreement with 4D gravitational theory, with the possible exception of one situation to which we will return below. Before proceeding to an outline of how 5D gravity might be tested in the solar system, it is instructive to review the status of higher-dimensional dynamics. Campbell's theorem, to which we have already alluded, guarantees that any solution of the equations of 4D general relativity (1) can be embedded in a solution of the (Ricci-flat) equations of 5D gravity (2). But it does not guarantee that the 4D Birkhoff theorem carries over to 5D. Since Birkhoff's theorem, which ensures the uniqueness of the Schwarzschild solution (up to coordinate transformations) depends not only on the assumption of (3D) spherical symmetry but also on boundary conditions at infinity, it is perhaps not surprising that it breaks down when the theory is extended to 5D. This is why there are (at least) two solutions of the 5D theory, both of which agree with the observed dynamics of the solar system. One of these, which is called the 5D canonical Schwarzschild solution, has exactly the same dynamics as the 4D solution (Wesson 1999). The other, which is nowadays called the 5D soliton solution, has unmeasurably small departures from the 4D solution (Kalligas et al. 1995). Both of these solutions are spherically symmetric in the three dimensions of ordinary space, and also static. By comparison, the class of cosmological models (3) which we are considering here is non-static, principally by virtue of the time-dependent cosmological "constant'' (5). This leads to the extra force (6), which affects the radial motion and depends critically on the ordinary velocity v in that direction. Clearly, if we have any prospect of seeing a cosmological 5D effect in the solar system, we have to look towards a situation where a test body has a large radial velocity. The planets, in their slow elliptical orbits, do not satisfy this criterion, and are expected to show insignificant departures from standard motion. Other objects in the solar system, such as the particles of the solar wind or comets on parabolic orbits, do meet the criterion but are not well studied. By contrast, the Pioneer spacecraft are suitable (Anderson et al. 1998, 2002). These two craft, launched more than thirty years ago, have approximately radial orbits: Pioneer 10 is on a path just 3$^{\circ}$ out of the ecliptic, while Pioneer 11 is moving out of the ecliptic at about 17$^{\circ}$ inclination. At a distance of over 20 AU from the Sun, they are indicating an anomalous acceleration of negative sign of about 10-7 cm s-2. Many possible explanations of this have been discussed, of which several are instrument-related (see Bertolami & Paramos 2004, for a review). Among those which are astrophysics-related, a plausible one involves an acceleration of the Sun due to its own asymmetric activity, but this falls short of explaining the anomaly by 4 orders of magnitude (Bini et al. 2004). By coincidence, the force (6) fails to account for the motion of these spacecraft by approximately the same factor. (The escape velocity from the solar system at 20 AU is close to 10 km s-1, and with this value for v in (6) with $L \simeq 1\times 10^{28}$ cm, the result is as noted to within order of magnitude.) Nevertheless, we see here the opportunity for a future test of the 5D extra force (6). We need a high-velocity, radially-moving spacecraft. Better still would be two such craft, from which other influences could be cancelled as in the GRACE project (Tapley et al. 2004), leaving the cosmological effect we wish to verify.

3 Conclusions

There are many reasons for believing that general relativity - excellent though it is in comparison to observation - cannot be the last word in gravitational theory. A prime motivation for other theories is the wish to unify gravity with the interactions of particle physics. Most workers believe that the best route to this objective is by an extension of spacetime to 5D (Kaluza-Klein, induced-matter and membrane theory), 10D (supersymmetry), 11D (supergravity), 26D (string theory) or beyond. However, 5 dimensions is the simplest extension of Einstein theory, and is widely believed to be the low-energy limit of higher-dimensional theories which describe more forces than those associated with the gravitational, electromagnetic and scalar (mass) fields. But even in 5D, new effects necessarily appear. Conservation laws, for example, should be written in 5D format; and if we try to interpret these in 4D we necessarily find bits of them which by comparison with standard theory we regard as anomalous. The so-called fifth force (which is really an acceleration) falls into this category: it is the consequence of 5D as opposed to 4D laws of motion. It exists for both of the most-studied versions of 5D gravity (Mashhoon et al. 1998; Youm 2000). It is small in most situations, but can be significant in certain astrophysical ones.

In the present account, we have taken a broad approach, with the aim of outlining the consequences for astrophysics of extended gravity. Towards this end, we have noted that Einstein's 4D Eqs. (1) are contained in the 5D field Eqs. (2). A general class of 5D cosmological solutions which contains the standard 4D ones in conformally-flat form has line element (3). This has an effective 4D cosmological "constant'' (4) which depends on the extra coordinate. The latter's behaviour can be determined if we make the physically reasonable assumption that particles follow null paths in 5D like photons do in 4D (Seahra & Wesson 2001; Youm 2001). Then the cosmological "constant'' varies with time (5). There are six major implications of this approach: (a) inflation is inherent, with the cosmological constant decreasing with cosmic time; (b) there is an extra force (6) which assists gravity if the material is expanding, as with Hubble's law modified by the velocity (7), thus augmenting galaxy formation; (c) peculiar velocities are damped, so the standard comoving frame is a natural equilibrium state; (d) the kinetic energy lost via the damping mechanism can show up as an energy field whose density (8) is astrophysically significant; (e) the extra force modifies weak Newtonian gravity as in Eqs. (9)-(11), and affects the dynamics of galaxies outside and inside clusters; (f) the extra force does not significantly affect the motions of the planets and is too weak to explain the anomalous acceleration of the Pioneer probes; but this force and others like it could be tested using high-velocity spacecraft moving radially in the solar system.

The consequences of extending gravity from 4 to 5 dimensions are small for most situations but can clearly be major for the early universe. We are aware of observational data which bear on the issues we have raised (Henry 1997; Will 2001; Lineweaver 1998; Overduin 1999; Wesson 1999). We are dispassionate, and quite willing to believe that there are only four dimensions to the world. But if it has five or more dimensions, then further work on the astrophysical side is a good way to look for them.

Acknowledgements
This work grew out of earlier collaborations with H. Liu and B. Mashhoon, and the latter supplied useful comments on the Pioneer data. The referee made helpful comments. Support was provided in part by NSERC.

References

 
Copyright ESO 2005