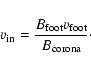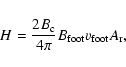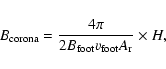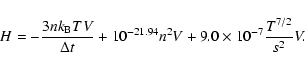A&A 441, 353-360 (2005)
DOI: 10.1051/0004-6361:20042255
Indirect calculation of the magnetic reconnection rate from flare loops
J. B. Noglik1 - R. W. Walsh1 - J. Ireland2
1 - Centre for Astrophysics, University of Central Lancashire, Preston, PR2 2HE, UK
2 -
L-3 Communications Government Services Inc, NASA GSFC, Greenbelt, Maryland 20771, USA
Received 26 October 2004 / Accepted 23 June 2005
Abstract
High time resolution Transition Region And Coronal Explorer (TRACE) 171 and 195 Å observations of the evolution of flare loops on 1999 March 18 have been investigated. Given the location of the magnetic loops on the northeast solar limb and the cadence of the TRACE observations (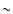 50 s), an estimation of the footpoint velocity due to ongoing reconnection was undertaken. This was achieved by calculating the velocity at which successive loops brighten in the emission lines during the postflare phase. A typical footpoint velocity of 1.5 km s
50 s), an estimation of the footpoint velocity due to ongoing reconnection was undertaken. This was achieved by calculating the velocity at which successive loops brighten in the emission lines during the postflare phase. A typical footpoint velocity of 1.5 km s
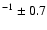 km s-1 is obtained and a reconnection rate of
km s-1 is obtained and a reconnection rate of 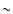 0.001-0.03 is determined using the method outlined in Isobe et al. (2002, ApJ, 566, 528). This value for the reconnection rate is consistent with the regime outlined by Petschek's model for magnetic reconnection.
0.001-0.03 is determined using the method outlined in Isobe et al. (2002, ApJ, 566, 528). This value for the reconnection rate is consistent with the regime outlined by Petschek's model for magnetic reconnection.
Key words: Sun: UV radiation - Sun: magnetic fields - Sun: corona
It is now accepted generally that magnetic reconnection is a commonly occuring phenomenon throughout the solar atmosphere. In particular, some of the clearest evidence for this process is in the occurence and subsequent dynamics of a solar flare (e.g. Yokoyama et al. 2001). The evolution/expansion of bright flare loops following an eruption are an indication of magnetic reconnection continuing in the corona (e.g. Kopp & Pneuman 1976).
Flare loop arcades have been studied extensively from either theoretical (Sturrock 1968; Kopp & Pneuman 1976; Yokoyama & Shibata 1998) or observational (McKenzie & Hudson 1999; Yokoyama et al. 2001; Isobe et al. 2002) perspectives or both (Forbes & Acton 1996). There are various models for the magnetic reconnection process itself which differ in their estimation of the reconnection rate in two spatial dimensions (e.g. 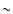 10-6 for the Sweet-Parker model and 0.1-0.01 for the Petschek model).
10-6 for the Sweet-Parker model and 0.1-0.01 for the Petschek model).
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{2255fig1.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg3.gif) |
Figure 1:
Schematic illustration of a reconnection model of a solar flare. The solid lines indicate the magnetic field lines, the thin arrows indicate the propogation of thermal conduction and the thick arrows show the plasma motion. |
| Open with DEXTER |
Shown in Fig. 1 is a schematic two dimensional diagram depicting the vital role magnetic reconnection plays in the formation of postflare loops (Hirayama 1974; Kopp & Pneuman 1976). As the reconnection process continues, new hotter loops form on top of the cooling loops below. This leads to what looks like a rising arcade of loop structures, with an increasing separation between their footpoints.
Estimating the magnetic reconnection rate indirectly has been undertaken by a number of authors and this work builds upon two recent papers.
Firstly, Isobe et al. (2002) uses Yohkoh Soft X-ray Telescope (SXT) data with the corresponding photospheric magnetogram taken with the Solar and Heliospheric Observatory using the Michelson Doppler Imager (SOHO/MDI) to analyse the decay phase of a long duration event (LDE) flare on the disc. They find the energy release rate in the decay phase to be ten times lower than in the rise phase and derive a magnetic reconnection rate of 0.001-0.01.
Secondly, Yokoyama et al. (2001) presents evidence for magnetic reconnection inflow in a flare on 1999 March 18. Using Yohkoh SXT and SOHO EIT images, they measure an apparent movement of material toward the magnetic X-point. This measured inflow velocity was 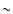 5 km s-1 and from this they derived a magnetic reconnection rate of 0.001-0.03.
5 km s-1 and from this they derived a magnetic reconnection rate of 0.001-0.03.
The observations examined in this paper are of the same flare event outlined by Yokoyama et al. (2001). However, the emphasis of this study is to consider the high resolution TRACE EUV data. These observations start at 06.07 UT (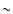 2 h after the actual flare event) and last for approximately 4 h. This paper attempts to calculate the reconnection rate from these observations and hence determine which theoretical model best fits the physical data. Two of the competing models are the Sweet-Parker model and the Petschek model. The Sweet (1958) and Parker (1963) model predicts the magnetic diffusion layer to be present along the whole boundary between the two opposing magnetic fields. Its length therefore is equal to the global external length scale and the reconnection rate is just the speed with which the field lines are entering the diffusion region. The Petschek (1964) model, however, limits the diffusion region to a small segment of the full length of the boundary between the opposing field lines. The diffusion region is smaller and thinner and so the diffusion and therefore the reconnection process can take place faster. Petschek also considered that slow-mode MHD shock waves propogate from the diffusion region, which acts as a type of obstacle in the flow.
2 h after the actual flare event) and last for approximately 4 h. This paper attempts to calculate the reconnection rate from these observations and hence determine which theoretical model best fits the physical data. Two of the competing models are the Sweet-Parker model and the Petschek model. The Sweet (1958) and Parker (1963) model predicts the magnetic diffusion layer to be present along the whole boundary between the two opposing magnetic fields. Its length therefore is equal to the global external length scale and the reconnection rate is just the speed with which the field lines are entering the diffusion region. The Petschek (1964) model, however, limits the diffusion region to a small segment of the full length of the boundary between the opposing field lines. The diffusion region is smaller and thinner and so the diffusion and therefore the reconnection process can take place faster. Petschek also considered that slow-mode MHD shock waves propogate from the diffusion region, which acts as a type of obstacle in the flow.
A detailed outline of the observations is given in Sect. 2 with an examination of how the emission from the flare loops decays during the observational period described in Sect. 2.1. Section 2.2 outlines the velocities derived for the expanding flare loops while our estimation of the indirectly calculated reconnection rate is given in Sect. 3. Section 4 discusses the implication of these results.
The onset of the flare occurred on 1999 March 18, at around 04:01:00 UT, on the northeast solar limb. Figure 2 is a SOHO/EIT 195 Å image which displays the location of the flare loop system on the northeast limb; the flare loops do not become apparent on the EIT images until 04:10:54 UT. SOHO/EIT 195 Å data is available of this region from before the flare occurred until the flare loops are no longer visible but only with a cadence of 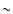 12 min. The 195 Å data is interspersed every few hours with a 171/284/195/304 Å cycle having a cadence of 6 min. The TRACE observations of 171 Å and 195 Å which are studied in this paper, were taken alternately at 25 s intervals giving them a cadence of 50 s. The data begins at 06:07:14 UT and continues until the flare loops are no longer visible; a 171 Å image showing a close up of the TRACE loop system is shown in Fig. 2.
12 min. The 195 Å data is interspersed every few hours with a 171/284/195/304 Å cycle having a cadence of 6 min. The TRACE observations of 171 Å and 195 Å which are studied in this paper, were taken alternately at 25 s intervals giving them a cadence of 50 s. The data begins at 06:07:14 UT and continues until the flare loops are no longer visible; a 171 Å image showing a close up of the TRACE loop system is shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{2255fig2.eps}\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg4.gif) |
Figure 2:
Location of the flare loop system on the northeast limb. The whole sun image is a SOHO/EIT 195 Å image while the inset is the loop system in TRACE 171 Å image. Both images were taken shortly after 06:00 on 1999 March 18. |
| Open with DEXTER |
Figure 3, shows both the Yohkoh and EIT data, displaying the flare loop system at about 07:00 UT on 1999 March 18. The crosses mark the footpoints of the EIT loops and it can be seen that the EIT EUV emission lies just beneath the hotter SXT loop system, as expected from Fig. 1.
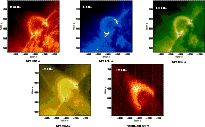 |
Figure 3:
Diagram showing Yohkoh SXT and SOHO EIT data displaying the loop system at 07:00 UT on 1999 March 18. The crosses mark the centre of the footpoints for the EIT images. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig4.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg6.gif) |
Figure 4:
Snapshots from TRACE 171 Å showing the time evolution of the flare loop system. |
| Open with DEXTER |
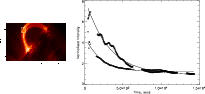 |
Figure 5:
Decay curves for 171 Å (asterix) and 195 Å (diamonds) for the observational box indicated in the left hand image. Time at 0 s is 06:00:00 UT. |
| Open with DEXTER |
Figure 4 shows the time evolution of the flare loop system between 06:07:14 UT and 09:59:50 UT, as observed in TRACE 171 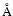 .
The increased spatial resolution in comparison to the SOHO/EIT data is evident. The images show a noteable difference from the start to the end of the observational run. At the start of the observations the loop system looks very bright and closely packed but as time progresses, the footpoint region begins to expand and separate. The apex of the loop system rises and expands and eventually begins to fade away, leaving only the now very broad footpoint area visible. Also shown in Fig. 4 (indicated by a white arrow) is the rebrightening of a thin strand, on the inner left hand side of the loop towards the end of the observations. To demonstrate the decay of these flare loops, Fig. 5 shows the fall in intensity in a small observational box over the 4 h period of the TRACE 171 Å and 195 Å observations. As Figs. 4 and 5 demonstrate, the loop intensity in both lines becomes very diffuse later on in the observations, so the calculation of the reconnection rate in this paper has been based on the first 2 h of the TRACE observations only.
.
The increased spatial resolution in comparison to the SOHO/EIT data is evident. The images show a noteable difference from the start to the end of the observational run. At the start of the observations the loop system looks very bright and closely packed but as time progresses, the footpoint region begins to expand and separate. The apex of the loop system rises and expands and eventually begins to fade away, leaving only the now very broad footpoint area visible. Also shown in Fig. 4 (indicated by a white arrow) is the rebrightening of a thin strand, on the inner left hand side of the loop towards the end of the observations. To demonstrate the decay of these flare loops, Fig. 5 shows the fall in intensity in a small observational box over the 4 h period of the TRACE 171 Å and 195 Å observations. As Figs. 4 and 5 demonstrate, the loop intensity in both lines becomes very diffuse later on in the observations, so the calculation of the reconnection rate in this paper has been based on the first 2 h of the TRACE observations only.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig6.eps}\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg9.gif) |
Figure 6:
Slice across the loop footpoints showing the rise and separation at 171 Å. The dashed line shows the slice taken through the footpoints and the solid lines show the velocity gradient for each footpoint. The dot-dash lines indicate the box used to calculate the error for the velocity (see Sect. 2.2). Time at 0 s is 06:00:00 UT. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig7.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg10.gif) |
Figure 7:
Slice through the left footpoint of the loop, showing the expansion velocity of the flare loops in 195 Å. The time-slice image was created by integrating the intensity between the dashed lines. |
| Open with DEXTER |
Given the advantageous location of the loop system on the solar limb, it is possible to determine the expansion and separation of both the loop system footpoint and apex regions during the postflare phase. Figure 6 displays a slice across both footpoints of the flare loops for the TRACE 171 Å data. The velocity gradients were measured as follows. Concentrating on the right hand footpoint shown in Fig. 6, the maximum intensity was calculated for the footpoint at each observed time and the white line shown is the line of best fit through these points. The box is due to the 1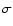 variation as it is assumed that the TRACE intensity has Poisson distributed noise (Handy et al. 1999). Given the non-uniform error obtained from the box the widest error margin was used. The left 171 Å footpoint gave an expansion velocity of
variation as it is assumed that the TRACE intensity has Poisson distributed noise (Handy et al. 1999). Given the non-uniform error obtained from the box the widest error margin was used. The left 171 Å footpoint gave an expansion velocity of 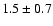 km s-1 whereas the right footpoint gave an expansion velocity of
km s-1 whereas the right footpoint gave an expansion velocity of 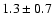 km s-1. Figure 7, shows the velocity from the left footpoint at 195 Å of
km s-1. Figure 7, shows the velocity from the left footpoint at 195 Å of
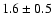 km s-1. Also in Fig. 8, velocities from the top of the loop arcade of
km s-1. Also in Fig. 8, velocities from the top of the loop arcade of
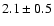 km s-1 and
km s-1 and 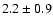 km s-1 were derived for 171 Å and 195 Å respectively. These results show that the apex of the loop structure is apparently expanding more rapidly than the system footpoint region (at around 0.7 km s-1). Possible reasons for this are outlined in Sect. 4.
km s-1 were derived for 171 Å and 195 Å respectively. These results show that the apex of the loop structure is apparently expanding more rapidly than the system footpoint region (at around 0.7 km s-1). Possible reasons for this are outlined in Sect. 4.
In our estimate of the reconnection rate, we have assumed that the reconnection is ongoing throughout the two hour window under investigation and that the X-point is a "fixed'' position. If the X-point was still in motion the magnetic field would stretch and our measured footpoint velocity would be a distorted value of the true footpoint motion, i.e. it would be the sum of both velocities.
The method for calculating the reconnection rate outlined by Isobe et al. (2002), derives the temperature T and the emission measure using the filter ratio method on SXT data. As this was not possible with this current data set, it is assumed that we have a temperature of 1.0 MK (peak formation temperature of 171 Å) and a density n of
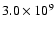 cm-3 (Isobe et al. 2002; Ramesh et al. 2005). The effect of varying these values is discussed later. The thermal energy
cm-3 (Isobe et al. 2002; Ramesh et al. 2005). The effect of varying these values is discussed later. The thermal energy
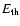 can be calculated using
can be calculated using
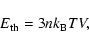 |
(1) |
where the volume of the arcade V is given by the area taken up by the flare loops on the image 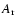 times the line-of-sight length l. We have assumed for this that
times the line-of-sight length l. We have assumed for this that 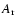 was equal to the number of pixels on the EUV image that had an intensity greater than 0.2 of the maximum intensity, as in Isobe et al. (2002). Also as a first approximation, it is taken that the line-of-sight l is equal to the distance between the footpoints of the arcade. A plasma filling factor of unity is assumed.
was equal to the number of pixels on the EUV image that had an intensity greater than 0.2 of the maximum intensity, as in Isobe et al. (2002). Also as a first approximation, it is taken that the line-of-sight l is equal to the distance between the footpoints of the arcade. A plasma filling factor of unity is assumed.
Next the energy release rate H (defined as the energy released per unit time) is calculated. H is a balance between the energy input and the energy lost through radiation and conduction, assuming all the energy released is converted into thermal energy. This is given by
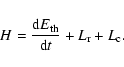 |
(2) |
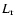 and
and 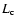 are the radiative and conductive loss rates, respectively,
are the radiative and conductive loss rates, respectively,
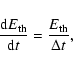 |
(3) |
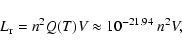 |
(4) |
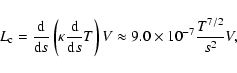 |
(5) |
in erg s-1 and where 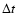 is the time period of the observations (7211 s), Q(T) is the radiative loss function for the temperature range 10
5.75 < T < 106.3 (Rosner et al. 1978),
is the time period of the observations (7211 s), Q(T) is the radiative loss function for the temperature range 10
5.75 < T < 106.3 (Rosner et al. 1978),
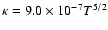 is the Spitzer thermal conductivity (Spitzer 1956), and s is the half length of the flare loop (estimated from Fig. 4 as
is the Spitzer thermal conductivity (Spitzer 1956), and s is the half length of the flare loop (estimated from Fig. 4 as
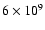 cm
cm 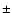
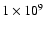 ). A value for d
). A value for d
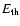 /dt of
/dt of
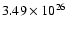 erg s-1 was calculated, and
erg s-1 was calculated, and 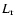 and
and 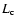 were found to be
were found to be
 erg s-1 and
erg s-1 and
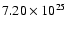 erg s-1 respectively.
erg s-1 respectively.
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig8.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg35.gif) |
Figure 8:
Slice through the peak of the loop, showing the expansion velocity of the flare loops in 171 Å and 195 Å. The time-slice image was created by integrating the intensity between the dashed lines. The white line indicates the gradient and hence calculated velocity taken from each image. |
| Open with DEXTER |
Isobe et al. (2002) make use of two relations:
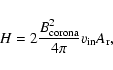 |
(6) |
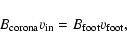 |
(7) |
where
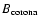 ,
,
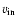 ,
,
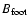 and
and
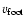 are the magnetic field strength of the corona, the inflow into the reconnection region, the magnetic field strength at the footpoints, and the separation velocity of the footpoints respectively.
are the magnetic field strength of the corona, the inflow into the reconnection region, the magnetic field strength at the footpoints, and the separation velocity of the footpoints respectively. 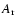 and
and
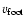 (which was taken to be
(which was taken to be 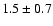 km s-1, the largest value of the footpoint velocity at 171 Å ) were obtained directly from the TRACE data. An initial estimation for
km s-1, the largest value of the footpoint velocity at 171 Å ) were obtained directly from the TRACE data. An initial estimation for
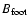 of 75 G was used. Looking at a SOHO/MDI magnetogram three days after the flare erupted once the active region has moved onto the disc of the Sun, shows the value of the photospheric magnetic field strength to be
of 75 G was used. Looking at a SOHO/MDI magnetogram three days after the flare erupted once the active region has moved onto the disc of the Sun, shows the value of the photospheric magnetic field strength to be  40 G. At this time the active region has become very diffuse and the magnetic structure has dissipated. The active region was quiet in between the time of our observations and the magnetic field strength reading, so this value must reflect a very lower limit estimate of the photosheric magnetic field strength during the period of our observations. By rearranging the above equations
40 G. At this time the active region has become very diffuse and the magnetic structure has dissipated. The active region was quiet in between the time of our observations and the magnetic field strength reading, so this value must reflect a very lower limit estimate of the photosheric magnetic field strength during the period of our observations. By rearranging the above equations
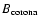 and then
and then
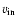 were determined;
were determined;
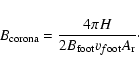 |
(8) |
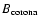 was found to be
was found to be 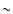 5.0-14 G and a
5.0-14 G and a
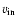 of
of  4.3-33 km s-1 was then calculated. These values are consistent with values found by Lin et al. (2005) who looked at an eruptive process on November 18, 2003 and found average reconnection inflow velocities near the current sheet over different time intervals of 10.5-106 km s-1. Also, Ko et al. (2003) looked at an eruption on 2002 January 8 and saw the northward motion of a current sheet moving at
4.3-33 km s-1 was then calculated. These values are consistent with values found by Lin et al. (2005) who looked at an eruptive process on November 18, 2003 and found average reconnection inflow velocities near the current sheet over different time intervals of 10.5-106 km s-1. Also, Ko et al. (2003) looked at an eruption on 2002 January 8 and saw the northward motion of a current sheet moving at  10 km s-1, the northward motion should be related to the relaxation of the large-scale magnetic field and therefore corresponds to the inflow rate into the current sheet. The Alfvén velocity is defined as:
10 km s-1, the northward motion should be related to the relaxation of the large-scale magnetic field and therefore corresponds to the inflow rate into the current sheet. The Alfvén velocity is defined as:
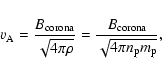 |
(9) |
where
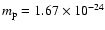 g is the proton mass and
g is the proton mass and 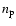 is the proton number density (
is the proton number density (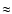 the electron number density
the electron number density
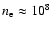 cm-3) outside the current sheet. Using our calculated value of
cm-3) outside the current sheet. Using our calculated value of
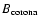 this gave
this gave
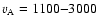 km s-1. The reconnection rate
km s-1. The reconnection rate 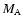 is defined as
is defined as
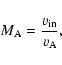 |
(10) |
using this relation the magnetic reconnection rate was found to be 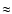 0.001-0.03. These values appear to overlap with those predicted by the Petschek model (Priest & Forbes 2000). If our original estimation for the density of
0.001-0.03. These values appear to overlap with those predicted by the Petschek model (Priest & Forbes 2000). If our original estimation for the density of
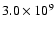 cm-3 is used in the equation for the Alfvén velocity, then the reconnection rate becomes 0.02-0.06, which is still in line with the values within the Petschek regime.
cm-3 is used in the equation for the Alfvén velocity, then the reconnection rate becomes 0.02-0.06, which is still in line with the values within the Petschek regime.
The aim of this paper was to calculate indirectly the magnetic reconnection rate from observations of flare loops using high resolution TRACE data. This was possible because the energy released during the decay phase of the flare was most likely due to ongoing magnetic reconnection. The cusp-shaped arcade seen in the soft X-ray (Fig. 3), which exists for the duration of our observations, or the separating footpoints (Figs. 4 and 6), cannot be explained by other mechanisms (e.g. current sheet dissipation contained within the loop itself).
However, there are a number of other possibilities that could be occurring. Firstly, the reconnection could be continuing and the magnetic structure is being dragged outwards by the expanding/escaping coronal mass ejection (CME). If this is true then our measurement of the velocity would be a combination of the brightening component and the X-point motion, however, the fact that the apex of the loop structure appears to be moving faster than the footpoints is more likely due to the magnetic field configuration and the fact that the footpoint magnetic field strength is greater than that at the apex.
Secondly, it could be that the reconnection has already ceased and we are only seeing fieldlines/fluxtubes that are cooling into passbands. However, the continuing presence of the cusp shaped loops seen by Yohkoh in the soft X-ray (Fig. 3) decreases the likelihood of this argument.
Thirdly, the brightening may be due to an observational view along a three dimensional structure. We may be observing a brightening arcade where the magnetic loops are substantially higher at one end of the arcade than the other, as shown in Fig. 9. However it is probably too late on after the onset of the flare for this to be a real possibility.
It must be noted that the motion of the footpoints appears to result in a "wider'' footpoint base on the left hand part of the possible arcade than the corresponding right hand side (see Fig. 4). Thus we could be observing an arcade at a slight angle from the central position - this would address the question as to why the velocity on the left footpoint is higher than the right one.
When following the method outlined in Isobe et al. (2002), we determine a value for the reconnection rate (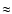 0.001-0.03) which is of the same order of magnitude but slightly higher than Isobe et al. (2002) (0.001-0.01). They explained their low value of the reconnection rate due to the fact that they were looking at the decay phase of the flare. The observations outlined here also look at the decay phase. However, due to the location of the loop system we can isolate a clearer picture of the dynamical structure and the results are consistent with Isobe et al. (2002). Yokoyama et al. (2001) calculated the reconnection rate for the same active region that is looked at here, using SOHO/EIT data and SXT data, during the impulsive phase of the flare. They also found a reconnection rate of 0.001-0.03. However it has been proposed that the supposed inflow velocity observed by Yokoyama et al. (2001) was mainly due to the rising motion of the reconnection X-point. This value would be several times slower than the in situ reconnection inflow (Chen et al. 2004) and so the derived value of the reconnection rate would also be several times slower. Therefore, the rise phase of this flare should have a much faster reconnection rate than the one calculated here in the decay phase. Previous studies have already demonstrated (Wang et al. 2003; and Asai et al. 2004) that the footpoint velocity and therefore the reconnection rate are usually larger in the rise phase of the flare.
0.001-0.03) which is of the same order of magnitude but slightly higher than Isobe et al. (2002) (0.001-0.01). They explained their low value of the reconnection rate due to the fact that they were looking at the decay phase of the flare. The observations outlined here also look at the decay phase. However, due to the location of the loop system we can isolate a clearer picture of the dynamical structure and the results are consistent with Isobe et al. (2002). Yokoyama et al. (2001) calculated the reconnection rate for the same active region that is looked at here, using SOHO/EIT data and SXT data, during the impulsive phase of the flare. They also found a reconnection rate of 0.001-0.03. However it has been proposed that the supposed inflow velocity observed by Yokoyama et al. (2001) was mainly due to the rising motion of the reconnection X-point. This value would be several times slower than the in situ reconnection inflow (Chen et al. 2004) and so the derived value of the reconnection rate would also be several times slower. Therefore, the rise phase of this flare should have a much faster reconnection rate than the one calculated here in the decay phase. Previous studies have already demonstrated (Wang et al. 2003; and Asai et al. 2004) that the footpoint velocity and therefore the reconnection rate are usually larger in the rise phase of the flare.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2255fig9.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg51.gif) |
Figure 9:
Diagram showing the line of sight which would depict a 3D arcade structure lighting up. |
| Open with DEXTER |
One needs to be aware that certain parameters have a greater impact upon the magnetic reconnection rate calculation than others. For example by simply increasing the density by 40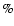 decreases the
decreases the 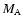 by 3.5, and similarly decreasing the density by 40
by 3.5, and similarly decreasing the density by 40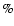 ,
increases the
,
increases the 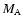 by 4. The density for this active region was calculated by Yokoyama et al. (2001) using the SXT filter ratio method obtaining values of
by 4. The density for this active region was calculated by Yokoyama et al. (2001) using the SXT filter ratio method obtaining values of
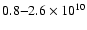 cm-3. However, we are concerned by these values because if you input their calculated T, L and n into the equation
cm-3. However, we are concerned by these values because if you input their calculated T, L and n into the equation
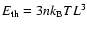 ,
the value obtained is an order of magnitude higher (i.e.
,
the value obtained is an order of magnitude higher (i.e.
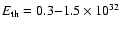 erg, and hence
erg, and hence
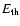 /
/
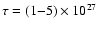 erg s-1) than the one stated in the paper. Using these values the newly calculated reconnection rate would be 0.002-0.02 and not 0.001-0.03 (Yokoyama, private communication). Values for the density calculated by Isobe et al. (2002) and Ramesh et al. (2005) looking at the plasma in the solar corona of certain active regions, have both yielded values of an order of magnitude lower than Yokoyama et al. (2001), therefore we estimated the density at
erg s-1) than the one stated in the paper. Using these values the newly calculated reconnection rate would be 0.002-0.02 and not 0.001-0.03 (Yokoyama, private communication). Values for the density calculated by Isobe et al. (2002) and Ramesh et al. (2005) looking at the plasma in the solar corona of certain active regions, have both yielded values of an order of magnitude lower than Yokoyama et al. (2001), therefore we estimated the density at
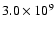 cm-3. A reconnection rate of
cm-3. A reconnection rate of 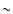 10-5 is estimated if the Yokoyama et al. (2001) density values are employed using the Isobe et al. method. Halving the reconnection area (
10-5 is estimated if the Yokoyama et al. (2001) density values are employed using the Isobe et al. method. Halving the reconnection area (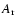 ),
), 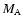 decreases by 4 and doubling the reconnection area (
decreases by 4 and doubling the reconnection area (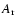 )
making it equivalent to the area on the SXT image (taken as our upper limit),
)
making it equivalent to the area on the SXT image (taken as our upper limit), 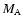 increases by 4. However the area parameter is well constrained as the images of the loop structure are bright. Changing the loop length and the time period of the observations by a factor of 2 has very little effect on the overall outcome of the reconnection rate. The temperature is constrained by the radiative loss function and so is consistent within this range. Naturally as you increase
increases by 4. However the area parameter is well constrained as the images of the loop structure are bright. Changing the loop length and the time period of the observations by a factor of 2 has very little effect on the overall outcome of the reconnection rate. The temperature is constrained by the radiative loss function and so is consistent within this range. Naturally as you increase 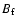 you increase the magnetic reconnection rate, from the increased build up of magnetic energy. Using this high resolution TRACE data at the same time as having good constraints on most of the parameters (i.e. being able to measure the
you increase the magnetic reconnection rate, from the increased build up of magnetic energy. Using this high resolution TRACE data at the same time as having good constraints on most of the parameters (i.e. being able to measure the 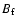 and temperature accurately) would be a helpful next step in finding a more accurate estimation of the reconnection rate and its comparison to a reconnection model. The magnetic reconnection rate found by these calculations coincides more with the Petscek model than with the Sweet-Parker model for reconnection even with the varying parameters.
and temperature accurately) would be a helpful next step in finding a more accurate estimation of the reconnection rate and its comparison to a reconnection model. The magnetic reconnection rate found by these calculations coincides more with the Petscek model than with the Sweet-Parker model for reconnection even with the varying parameters.
Acknowledgements
J.B.N. was supported in this research by a PPARC research studentship. R.W.W. was supported in this research by a Leverhulme Trust research fellowship. We would like to thank the anonymous referees for their useful comments that helped us to improve this paper.
By rearranging Eq. (7) we get this expression for the inflow velocity,
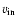 ,
,
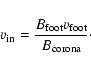 |
(A.1) |
If we then substitute this
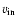 into Eq. (6), the energy release rate, H, becomes,
into Eq. (6), the energy release rate, H, becomes,
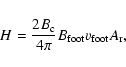 |
(A.2) |
and by rearranging the above equation we can get an equation in terms of
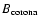 ,
,
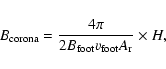 |
(A.3) |
one of the two unknown parameters. From Eqs. (2)-(5), we know that the energy release rate, H, is equal to,
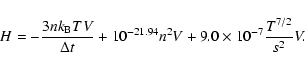 |
(A.4) |
Now we have an expression for the coronal magnetic field strength,
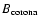 ,
in which all the parameters are known or can be estimated. Once the coronal magnetic field strength is determined, the inflow velocity,
,
in which all the parameters are known or can be estimated. Once the coronal magnetic field strength is determined, the inflow velocity,
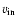 ,
can be calculated using Eq. (A.1) and the Alfvén velocity,
,
can be calculated using Eq. (A.1) and the Alfvén velocity, 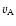 using Eq. (9). These values are then inserted into Eq. (10) to estimate the magnetic reconnection rates. From our calculated values for d
using Eq. (9). These values are then inserted into Eq. (10) to estimate the magnetic reconnection rates. From our calculated values for d
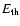 /dt of
/dt of
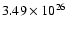 erg s-1,
erg s-1, 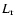 of
of
 erg s-1 and
erg s-1 and 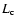 of
of
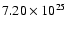 erg s-1 it is obvious that for this flare at 1 MK the radiative cooling is the dominant mechanism. Isobe et al. (2002) examined a much hotter X-ray flare loop (>3 MK) and at this temperature the conductive cooling was dominant. Using Eqs. (A.3) and (A.4) it can be shown that for a flare loop at 1-3 MK, if the density is higher than
erg s-1 it is obvious that for this flare at 1 MK the radiative cooling is the dominant mechanism. Isobe et al. (2002) examined a much hotter X-ray flare loop (>3 MK) and at this temperature the conductive cooling was dominant. Using Eqs. (A.3) and (A.4) it can be shown that for a flare loop at 1-3 MK, if the density is higher than
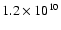 cm-3, then the coronal magnetic field strength is calculated to be higher than the photospheric magnetic field strength, which is in contradiction to what is believed to be the case. Thus the Isobe et al. (2002) method which relies on this heat balance Eq. (A.4) can no longer be applied.
cm-3, then the coronal magnetic field strength is calculated to be higher than the photospheric magnetic field strength, which is in contradiction to what is believed to be the case. Thus the Isobe et al. (2002) method which relies on this heat balance Eq. (A.4) can no longer be applied.
- Asai, A., Yokoyama,
T., Shimojo, M., et al. 2004, ApJ, 611, 557 [NASA ADS] [CrossRef] (In the text)
- Chen, P. F.,
Shibata, K., Brooks, D. H., & Isobe, H. 2004, ApJ, 602,
L61 [NASA ADS] [CrossRef] (In the text)
- Forbes, T. G.,
& Acton, L. W. 1996, ApJ, 459, 330 [NASA ADS] [CrossRef] (In the text)
- Hirayama,
T. 1974, Sol. Phys., 34, 323 [NASA ADS] [CrossRef] (In the text)
- Isobe, H.,
Yokoyama, T., Shimojo, M., et al. 2002, ApJ, 566, 528 [NASA ADS] [CrossRef] (In the text)
- Ko, Y.-K., Raymond, J.
C., Lin, J., et al. 2003, ApJ, 594, 1068 [NASA ADS] [CrossRef] (In the text)
- Kopp, R. A., &
Pneuman, G. W. 1976, Sol. Phys., 50, 85 [NASA ADS] (In the text)
- Lin, J., Ko, Y.-K.,
Sui, L., et al. 2005, ApJ, in press
(In the text)
- McKenzie,
D. E., & Hudson, H. S. 1999, ApJ, 519, L93 [NASA ADS] [CrossRef] (In the text)
- Parker, E. N.
1963, ApJS, 8, 177 [NASA ADS] [CrossRef] (In the text)
- Petschek,
H. E. 1964, in Proc. AAS-NASA Symp. Phys. Solar Flares, ed. W. N.
Hess, NASA SP-50 (Washington, DC: NASA), 425
(In the text)
- Priest, E.,
& Forbes, T. 2000, Magnetic reconnection: MHD theory and
applications (New York: Cambridge University Press)
(In the text)
- Ramesh, R.,
Narayanan, A. S., Kathiravan, Ch., Sastry, V., & Shankar, N. U.
2005, A&A, 431, 353 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Rosner, R.,
Tucker, W. H., & Vaiana, G. S. 1978, ApJ, 220, 643 [NASA ADS] [CrossRef] (In the text)
- Spitzer, L.
1956, Physics of Fully Ionized Gases (New York: Interscience)
(In the text)
- Sturrock,
P. A. 1968, in Structure and Development of Solar Active Regions,
ed. K. O. Kiepenheuer (Dordrecht: Reidel), IAU Symp., 35, 471
(In the text)
- Sweet, P. A.
1958, in Electromagnetic Phenomena in Cosmical Physics, ed. B.
Lehnert (Cambridge: Cambridge Univ. Press), IAU Symp., 6, 123
(In the text)
- Wang, H., Qiu, J.,
& Zhang, H. 2003, ApJ, 593, 564 [NASA ADS] [CrossRef] (In the text)
- Yokoyama,
T., & Shibata, K. 1998, ApJ, 494, L113 [NASA ADS] [CrossRef] (In the text)
- Yokoyama,
T., Akita, K., Morimoto, T., Inoue, K., & Newmark, J. 2001,
ApJ, 546, L69 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{2255fig1.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg3.gif)
![\begin{figure}
\par\includegraphics[width=11.3cm,clip]{2255fig2.eps}\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg4.gif)

![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig4.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg6.gif)

![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig6.eps}\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg9.gif)
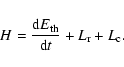
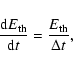
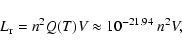
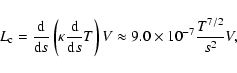
![\begin{figure}
\par\includegraphics[width=17.5cm,clip]{2255fig8.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg35.gif)
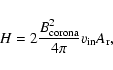
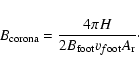
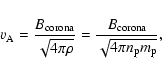
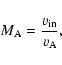
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2255fig9.eps}
\end{figure}](/articles/aa/full/2005/37/aa2255-04/Timg51.gif)