A&A 441, 117-129 (2005)
DOI: 10.1051/0004-6361:20042241

An analytical description of the disruption of star clusters in tidal fields with an application to Galactic open clusters

H. J. G. L. M. Lamers 1,2 - M. Gieles1 - N. Bastian 1 - H. Baumgardt3 - N. V. Kharchenko4,5,6 - S. Portegies Zwart7,8


1 - Astronomical Institute, Utrecht University, Princetonplein 5, 3584CC Utrecht, The Netherlands
2 - SRON Laboratory for Space Research, Sorbonnelaan 2, 3584CC Utrecht, The Netherlands
3 - Sternwarte, University of Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
4 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
5 - Astronomisches Rechen-Institut, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
6 - Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680 Kiev, Ukraine
7 - Astronomical Institute, University of Amsterdam, Kruislaan 403, 1098SJ Amsterdam, The Netherlands
8 - Informatics Institute, University of Amsterdam, Kruislaan 403, 1098SJ Amsterdam, The Netherlands

Received 23 October 2004 / Accepted 26 May 2005

Abstract
We present a simple analytical description of the disruption of star clusters in a tidal field. The cluster disruption time, defined as $\mbox{$t_{\rm dis}$ }= \{{\rm d}\!\ln ~M/{\rm d}t\}^{-1}$, depends on the mass M of the cluster as $\mbox{$t_{\rm dis}$ }=\mbox{$t_0$ }(M/\mbox{$M_{\odot}$ })^{\gamma}$ with $\gamma =0.62$ for clusters in a tidal field, as shown by empirical studies of cluster samples in different galaxies and by N-body simulations. Using this simple description we derive an analytic expression for the way in which the mass of a cluster decreases with time due to stellar evolution and disruption. The result agrees very well with those of detailed N-body simulations for clusters in the tidal field of our galaxy. The analytic expression can be used to predict the mass and age histograms of surviving clusters for any cluster initial mass function and any cluster formation history. The method is applied to explain the age distribution of the open clusters in the solar neighbourhood within 600 pc, based on a new cluster sample that appears to be unbiased within a distance of about 1 kpc. From a comparison between the observed and predicted age distributions in the age range between 10 Myr to 3 Gyr we find the following results: (1) The disruption time of a 104 $M_{\odot }$ cluster in the solar neighbourhood is about $1.3 \pm 0.5$ Gyr. This is a factor of 5 shorter than that derived from N-body simulations of clusters in the tidal field of the galaxy. Possible reasons for this discrepancy are discussed. (2) The present star formation rate in bound clusters within 600 pc of the Sun is  $5.9~ \pm~ 0.8~\times 10^2$ $M_{\odot }$ Myr-1, which corresponds to a surface star formation rate of bound clusters of  $5.2~ \pm~ 0.7 \times 10^{-10}$ $M_{\odot }$ yr-1 pc-2. (3) The age distribution of open clusters shows a bump between 0.26 and 0.6 Gyr when the cluster formation rate was 2.5 times higher than before and after. (4) The present star formation rate in bound clusters is about half that derived from the study of embedded clusters. The difference suggests that about half of the clusters in the solar neighbourhood become unbound within about 10 Myr. (5) The most massive clusters within 600 pc had an initial mass of about $3\times 10^4$ $M_{\odot }$. This is in agreement with the statistically expected value based on a cluster initial mass function with a slope of -2, even if the physical upper mass limit for cluster formation is as high as 106 $M_{\odot }$.

Key words: Galaxy: globular clusters: general - Galaxy: halo - Galaxy: kinematics and dynamics - Galaxy: open clusters and associations: general - Galaxy: solar neighbourhood - galaxies: star clusters

   
1 Introduction

Bound star clusters[*] in a tidal field lose mass due to internal effects, i.e. mass loss by stellar evolution, and by the external effect of tidal stripping. The combination of these effects results in a decreasing mass of the cluster until the cluster is destroyed completely. The time scale of this disruption depends on the initial conditions of the cluster, e.g. the stellar initial mass function and its concentration, and on the tidal forces experienced by the cluster during its galactic orbit.

The disruption of star clusters determines the mass and age distributions of the existing clusters. Therefore any study of the cluster formation history of a galaxy has to take into account the disruption of clusters.

The age and mass distribution of the initial cluster population is described by the cluster formation rate as a function of time, CFR(t), and the cluster initial mass function, CIMF. The distributions of the present observable star clusters is modified because: (a) the disruption time of the clusters depends on the initial mass, (b) the mass of each cluster decreases with time, (c) the clusters fade as they age due to stellar evolution. A (simple) description of these three effects would facilitate the studies of samples of star clusters. The purpose of this paper is to provide such a simple description and show how it can be used in the analysis of star cluster samples.

The structure of the paper is as follows:
In Sect. 2 we discuss the arguments that the cluster disruption time depends on its mass as a power law of the type $\mbox{$t_{\rm dis}$ }\propto M^{0.62}$. In Sect. 3 we calculate the evolution of a cluster in terms of its decreasing mass due to stellar evolution and disruption. In Sect. 4 we will show that the results agree very well with those of N-body simulations. In Sect. 5 we predict the mass and age distributions of cluster samples for various cluster formation histories. In Sect. 6 we apply the method to the age distribution of open clusters in the solar neighbourhood, using the new cluster sample from Kharchenko et al. (2005). We derive the disruption time of open clusters in the solar neighbourhood as well as the cluster formation rate and the star formation rate. The discussion and conclusions are given in Sect. 7.

2 A power law expression for the disruption time of star clusters

Boutloukos & Lamers (2003, hereafter BL03) have studied the mass and age distributions of magnitude-limited cluster samples in selected regions in four galaxies, and concluded that these distributions can be explained if the disruption time of clusters depends on the initial mass $M_{\rm i}$ of the clusters as $\mbox{$M_{\rm i}$ }^{\gamma}$, with $\gamma \simeq 0.6$ for clusters in very different local environments.

Baumgardt & Makino (2003, hereafter BM03) have calculated a grid of N-body simulations of clusters in the tidal field of our galaxy for different initial masses and initial concentration factors in circular and elliptical orbits at various galactocentric distances. They take into account mass loss by stellar evolution and by tidal relaxation. Their calculations show that the disruption time of a cluster, defined as the time when 5% of the initial number of stars remain in the cluster, scales with the half mass relaxation time  $t_{\rm rh}$ and the clusters crossing time  $t_{\rm cr}$ as  $\mbox{$t_{\rm dis}$ }\propto t_{\rm rh}^x t_{\rm cr}^{1-x}$with x=0.82 for clusters with an initial dimensionless depth W0=7 (which is a measure of the concentration index of the cluster, see King 1966) and x=0.75 for less concentrated clusters with W0=5. BM03 and Gieles et al. (2004) have shown that for all the models of BM03 the disruption time can be expressed as a function of the initial cluster mass as

 \begin{displaymath}\mbox{$t_{\rm dis}$ }= \mbox{$t_0$ }~ (\mbox{$M_{\rm i}$ }/\mbox{$M_{\odot}$ })^{0.62} \end{displaymath} (1)

where $\mbox{$t_0$ }$ is a constant that depends on the tidal field of the particular galaxy in which the cluster moves and on the ellipticity of its orbit. So the predicted dependence of the disruption time on the initial mass of a cluster agrees very well with the empirical relation derived by BL03. De la Fuente Marcos & de la Fuente Marcos (2004) also report a power law dependence of the characteristic life time $\tau$ of clusters on the number of stars. Based on a series of dynamical models they find that  $\tau \sim N^{0.68}$ where N is the initial number of stars of a cluster.) Lamers et al. (2005) showed that  $\mbox{$t_0$ }$ is expected to depend on the ambient density at the location of the clusters in that galaxy as $\mbox{$t_0$ }\propto \rho_{\rm amb}^{-1/2}$.

The discussion above has concentrated on the comparison between the disruption time of clusters of different initial masses, i.e. $\mbox{$t_{\rm dis}$ }\propto \mbox{$M_{\rm i}$ }^{0.62}$, within one galactic environment. We have not yet discussed how the mass of an individual cluster decreases with time. This is the topic of the next section.

3 The decrease of the cluster mass due to stellar evolution and tidal effects

The mass of a cluster decreases due to stellar evolution and tidal disruption. We will describe the evolution of the bound mass, using analytic expressions for the mass loss from the cluster by stellar evolution and by tidal effects.

3.1 Mass loss by stellar evolution

The mass loss from clusters due to stellar evolution has been calculated for cluster evolution models by several groups, e.g. Bruzual & Charlot (1993) and the Starburst99 models by Leitherer et al. (1999). We adopt the GALEV models for single stellar populations (Schulz et al. 2002; Anders & Fritze-v. Alvensleben 2003). These models contain stars in the mass range of 0.15 < M* < 85 $M_{\odot }$, distributed over this mass range with either the Salpeter or Scalo mass function. We adopt the models with the Salpeter mass function because deep photometry of clusters in the LMC shows that the cluster IMF is a powerlaw with a slope of about -2.35 down to at least 0.6 $M_{\odot }$ (de Marchi 2003). Lower mass stars hardly contribute to the luminosity at ages less than 10 Gyr, but may contribute significantly to the cluster mass. The GALEV models are based on stellar evolution tracks from the Padova group, which include mass loss and overshooting (Bertelli et al. 1994; Girardi et al. 2000). Lamers (2005) has shown that the fraction of the initial cluster mass, Mi, that is lost by stellar evolution in the GALEV models, i.e. $\mbox{$q_{\rm ev}$ }\equiv (\Delta M)_{\rm ev}/\mbox{$M_{\rm i}$ }$ where $(\Delta M)_{\rm ev}$is the mass lost by stellar evolution, can be approximated very accurately by a function of the form

 \begin{displaymath}\log \mbox{$q_{\rm ev}$ }(t)= (\log t-a_{\rm ev})^{b_{\rm ev}}+c_{\rm ev}~~{\rm for}~~ t>12.5~{\rm ~Myr}. \end{displaymath} (2)

The values of $a_{\rm ev}$, $b_{\rm ev}$ and $c_{\rm ev}$ are listed in Table 1 for different metallicities. This function describes the mass loss fraction of the models at t>12.5 Myr with an accuracy of a few percent. The mass loss at younger ages is negligible because the most massive stars with  $M_*>30~\mbox{$M_{\odot}$ }$ hardly contribute to the mass of the cluster. For cluster models with a lower limit of the stellar IMF different from 0.15 $M_{\odot }$, the value of  $q_{\rm ev}(t)$ can easily be adjusted, because stars with $M<0.6~\mbox{$M_{\odot}$ }$contribute to the cluster mass but not to its mass loss at ages less than 1010 yrs. (This mass loss rate is very different from that of the Starburst99 models, because the Starburst99 models have a lower limit for stellar mass of 1 $M_{\odot }$.)

In this paper we use the symbol $\mu(t) \equiv M(t)/\mbox{$M_{\rm i}$ }$ to describe the fraction of the mass of a cluster with initial mass $M_{\rm i}$ that is still bound at age t. We define

 \begin{displaymath}\mbox{$\mu_{\rm ev}(t)$ }=1-\mbox{$q_{\rm ev}(t)$ } \end{displaymath} (3)

as the fraction of the initial mass of the cluster that would have remained at age t, if stellar evolution would have been the only mass loss mechanism. The function  $\mbox{$\mu_{\rm ev}(t)$ }$ is independent of the initial mass of the cluster.

Table 1: Approximations to the mass lost by stellar evolution for ${\it GALEV}$ cluster models with a Salpeter IMF of $\alpha =-2.35$, $0.15 < M_* < 85~\mbox{$M_{\odot}$ }$ and 0.0004<Z<0.05.

3.2 Mass loss by stellar evolution and tidal effects

We describe the decreasing mass of a bound cluster that survived infant mortality ( $t \mathrel{\copy\gabox}10^7$ yrs) as a function of time. Let us define  $\mbox{$M(t;M_{\rm i})$ }$ as the mass of a cluster of initial mass  $\mbox{$M_{\rm i}$ }$ and age t, and $\mbox{$\mu(t;M_{\rm i})$ }=\mbox{$M(t;M_{\rm i})$ }/\mbox{$M_{\rm i}$ }$ as the fraction of the initial mass that is still in the cluster. The decrease of mass due to both stellar evolution and disruption can then be described as

 \begin{displaymath}\frac{{\rm d}\mbox{$M$ }}{{\rm d}t}= \left(\frac{{\rm d}\mbox... ... + \left(\frac{{\rm d}\mbox{$M$ }}{{\rm d}t}\right)_{\rm dis} \end{displaymath} (4)

where the first term describes the evolution by stellar mass loss and the second term by disruption. Following the arguments given in Sect. 2 we assume that we can describe the mass loss by disruption as

 \begin{displaymath}\left(\frac{{\rm d}\mbox{$M$ }}{{\rm d}t}\right)_{\rm dis} = ... ...eft( \frac{\mbox{$M$ }}{\mbox{$M_{\odot}$ }}\right)^{1-\gamma} \end{displaymath} (5)

with $\gamma =0.62$ and $\mbox{$t_0$ }$ is a constant that depends on the tidal field. (See Lamers et al. 2005, for the dependence of $\mbox{$t_0$ }$ on the conditions in different galaxies.) The first equality assumes that the mass lost by disruption can be approximated by an exponential decay with a time scale that decreases as the mass of the cluster decreases. This is equivalent to the statement that the disruption time in our description is defined as $\mbox{$t_{\rm dis}$ }^{-1}={\rm d}\!\ln \mbox{$M$ }/{\rm d}t$. The second equality assumes that this timescale depends on the mass as  $\mbox{$M$ }^{\gamma}$. (If $\gamma$ was equal to 1 and the evolutionary mass loss could be ignored, then the mass of the cluster would decrease linearly with time until  $t=\mbox{$t_0$ }\mbox{$M_{\rm i}$ }/\mbox{$M_{\odot}$ }$. For $\gamma=0$ the decrease would be exponential.)

Equation (4) can easily be solved numerically. It turns out that the mass decrease of a cluster can be approximated very accurately by the following formula

 \begin{displaymath}\mu(t;\mbox{$M_{\rm i}$ })\equiv \frac{M(t)}{M_i}\simeq \lef... ...}$ }}{\mbox{$M_{\rm i}$ }}\right)^{\gamma} \right\}^{1/\gamma} \end{displaymath} (6)

if the first term in brackets is larger than the second term. If the second term is larger than the first term, i.e. when the mass lost by disruption is larger than the mass that remained after mass loss by stellar evolution, then $\mbox{$\mu(t;M_{\rm i})$ }=0$and the cluster is completely disrupted. Approximation 6 is quite accurate because during the first 108 years mass loss is dominated by stellar evolution so the second term is negligible and $\mu_{\rm ev}(t)$ describes the fraction of the mass that survives mass loss by stellar evolution. During later years, when  $\mbox{$\mu_{\rm ev}(t)$ }$ decreases very slowly, the mass loss is dominated by disruption, which is described by the second term in brackets. Equation (6) can be inverted to express the initial cluster mass in terms of the present cluster mass:

 \begin{displaymath}M_i \simeq \left\{\left(\frac{\mbox{$M$ }}{\mbox{$M_{\odot}$... ...ox{$t_0$ }}\right\}^{1/\gamma} \mbox{$\mu_{\rm ev}(t)$ }^{-1}. \end{displaymath} (7)

Figure 1 compares the numerical solution with the analytic approximation for various initial masses, $10^3 \le \mbox{$M_{\rm i}$ }/\mbox{$M_{\odot}$ }\le 10^6$, for a short and a long disruption timescale, $\mbox{$t_0$ }=2$ Myr and 30 Myr, both for Z=0.02. In all cases the agreement between the analytic and the numerical solution is excellent, i.e. within about 0.015 dex, although the disruption times vary by more than 6 orders of magnitudes from model to model. Even for the low mass cluster model of  $\mbox{$M_{\rm i}$ }=10^3$ $M_{\odot }$ at  $\mbox{$t_0$ }=2$ Myr, for which the disruption is already effective during the first 10 Myr, the agreement between the numerical solution and the analytic expression is very good. (Tests show that Eq. (6) is also a very good approximation for all other values of $\gamma$ in the range of  $0<\gamma<1$.)


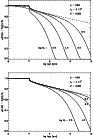  \begin{figure} {\psfig{figure=2241fig1a.ps,width=8cm} } \par\vspace*{2mm} {\psfig{figure=2241fig1b.ps,width=8cm} }\end{figure} Figure 1: The predicted decrease in cluster mass due to stellar evolution and disruption for Z=0.020 and four values of the initial cluster masses: 103, 104, 105 and  $10^6~\mbox{$M_{\odot}$ }$. Top panel: $\mbox{$t_0$ }=2$ Myr; lower panel: $\mbox{$t_0$ }=30$ Myr. The full lines give the exact decrease derived by numerical solution of the differential Eq. (4), and the dotted lines give the approximation (Eq. (6)). Notice the excellent agreement. The dashed lines gives the decrease in mass due to stellar evolution only.
Open with DEXTER

We define $\mbox{$t_{\rm dis}^{\rm total}$ }$ as the total disruption time and $t_{\rm dis}^{1-\Delta}$ as the time when only a fraction $\Delta$ of the initial mass remains. From Eq. (6) we find that $t_{\rm dis}^{\rm total}$ and $t_{\rm dis}^{1-\Delta}$ are described by the implicit relations

 \begin{displaymath}\mbox{$t_{\rm dis}^{\rm total}$ }=\frac{\mbox{$t_0$ }}{\gamma... ...left(\mbox{$t_{\rm dis}^{\rm total}$ }\right)\right\}^{\gamma} \end{displaymath} (8)

and

 \begin{displaymath}\mbox{$t_{\rm dis}^{1-\Delta}$ }=\frac{\mbox{$t_0$ }}{\gamma}... ...m dis}^{1-\Delta}$ })\right\}^{\gamma}-\Delta^{\gamma}\right). \end{displaymath} (9)

We will use this last expression for a comparison of our analytic solution with those of N-body-simulations. In the range of  $10^4<\mbox{$t_0$ }<10^7$ years and $10^3 <\mbox{$M_{\rm i}$ }< 10^6$ $M_{\odot }$ the values of  $t_{\rm dis}^{\rm total}$ can be approximated by


 
$\displaystyle \log(\mbox{$t_{\rm dis}^{\rm total}$ }) \simeq \log \left(\frac{\... ...ot}$ }}\right) \times \log\left(\frac{\mbox{$t_0$ }}{10^4~{\rm yr}}\right)\cdot$     (10)

This approximation is valid within 0.03 dex for all metallicities. For all models we find that $\mbox{$t^{\rm 95\%}_{\rm dis}$ }\simeq 0.89~\mbox{$t_{\rm dis}^{\rm total}$ }$.

These equations imply that the total disruption time of a cluster with an initial mass of 104 $M_{\odot }$, which was referred to as t4 in BL03 and in Lamers et al. (2005), is related to t0 by

 \begin{displaymath}t_4^{\rm total} = \frac{1.355\times 10^{4 \gamma}}{\gamma} \mbox{$t_0$ }^{0.967} = 6.60\times 10^2 ~\mbox{$t_0$ }^{0.967} \end{displaymath} (11)

where the last equation is only valid if $\gamma =0.62$ and t0 is in yrs.

Equation (8) shows that $\mbox{$t_{\rm dis}^{\rm total}$ }(\mbox{$M_{\rm i}$ })$ is approximately proportional to  $\mbox{$M_{\rm i}$ }^{\gamma}$, which was the relation adopted in the study of the disruption times of clusters in different galaxies by BL03 and Lamers et al. (2005).

4 Comparison of the analytic solution with results of N-body simulations


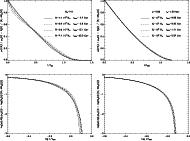  \begin{figure} {\psfig{figure=2241fig2a.ps,width=8.2cm}\hspace*{2mm} \psfig{fig... ...dth=8.2cm}\hspace*{2mm} \psfig{figure=2241fig2d.ps,width=8.2cm} }\end{figure} Figure 2: Comparison of the decrease of the cluster mass with time between the results of the N-body simulations by BM03 ( left) and our description ( right) for clusters of different initial numbers of stars, $N_{\rm i}$ or mass $M_{\rm i}$. The mass has been corrected to first order for the mass lost by stellar evolution. In all figures the time t is scaled to  $\mbox{$t^{\rm 95\%}_{\rm dis}$ }$, i.e. the time when 95% of the cluster mass is lost due to stellar evolution and disruption. The upper figures are for mass versus time and the lower figures are for log (Mass) versus log (time). Notice the strong similarity between the results of the N-body simulations and our simple description (Eq. (6)).
Open with DEXTER

We can compare our analytic expression for the decreasing mass of a cluster with the results of N-body simulations. We adopt the simulations by BM03 who calculated the fate of clusters under various conditions. Before making this comparison, we would like to point out that:

(a)
BM03 adopted the stellar IMF of Kroupa (2001), which have an initial mean mass of 0.547 $M_{\odot }$, whereas our calculations are based on the GALEV cluster evolution models (see Sect. 3.1) which have a Salpeter (1955) IMF with a lower mass cut-off of 0.15 $M_{\odot }$ and a maximum mass of 85 $M_{\odot }$, resulting in an initial mean mass of 0.516 $M_{\odot }$.
(b)
BM03 adopted the evolutionary mass loss rates from Hurley et al. (2002), whereas those of the GALEV models are based on the calculations from the Padova-group (see Sect. 3.1).
(c)
BM03 define the disruption time of a clusters, $\mbox{$t_{\rm dis}^{\rm BM}$ }$, (called dissolution time in their paper) as the time at which only 5 percent of the initial mass is still in the cluster.
(d)
The simulations by BM03 show that the mean mass of the remaining stars in a dissolving cluster changes with time. In the early phase the mean mass decreases because stellar evolution removes the massive stars, but the mean mass increases in later phases when disruption becomes the dominant mass loss mechanism and low mass stars are lost preferentially. In the simulations by BM03 the mean mass near the end of the life of a cluster of initially  $3\times 10^5$ stars has increased from 0.516 to 1.2 $M_{\odot }$. In our analytic approximation this effect is not taken into account. Therefore we can expect a small offset in the timescale between the N-body and the analytic results due to mass segregation.
Because of differences in the adopted mass loss by stellar evolution between our and BM03 models, we compare the results for the decreasing mass of a cluster not directly, but corrected for the stellar evolution. This means that we compare the predictions for  $\mu(t;\mbox{$M_{\rm i}$ })/\mbox{$\mu_{\rm ev}$ }(t)$ rather than for  $\mu(t;\mbox{$M_{\rm i}$ })$. The function  $\mu(t;\mbox{$M_{\rm i}$ })/\mbox{$\mu_{\rm ev}$ }(t)$describes the fraction of the initial mass of the cluster that is lost by disruption only. This function, which is called  $M_{\rm rel}(t)$ by BM03, is expected to be approximately independent of the adopted evolutionary mass loss rates.

BM03 give the function $M_{\rm rel}(t)$ for their models of clusters of different initial numbers of stars, $8.2\times 10^3<N_{\rm i}<1.3\times 10^5$, and with an initial concentration described by W0=7, in circular orbits around the galactic center at a distance of 8.5 kpc. (See BM03 Fig. 6.) Their results show that  $M_{\rm rel}(t)$decreases almost linearly with time, and that the function plotted against  $t/\mbox{$t_{\rm dis}^{\rm BM}$ }$ is about the same for all clusters. We compare their results with our analytic expression Eq. (6).

The left hand panels of Fig. 2 show the normalized decrease in cluster mass, $M_{\rm rel}(t/\mbox{$t_{\rm dis}^{\rm BM}$ })$, of the models by BM03. The top figure gives the mass as a function of time, both on a linear scale. However, since the mass of clusters will decrease several orders of magnitudes before they are disrupted, we also plot the logarithm of  $M_{\rm rel}(t)$as a function of the logarithm of $t/\mbox{$t_{\rm dis}^{\rm BM}$ }$ in the lower figure. The right hand panels of Fig. 2 show the results of our models. For a fair comparison between our calculations and those of BM03, we plot $\mu(t;\mbox{$M_{\rm i}$ })/\mbox{$\mu_{\rm ev}$ }(t)$ as a function of $t/\mbox{$t^{\rm 95\%}_{\rm dis}$ }$. The agreement between the predictions of the N-body calculations and our description is very good, both on a linear and logarithmic scale. The very small difference of less than 5 percent during the early phase of the most massive models is probably due to the difference in the adopted mass loss by stellar evolution. (The plotted relations are to the first order corrected for the effects of stellar evolution. However because the cluster evolution is caused by the combination of stellar evolution and tidal effects, the corrected relations still bear the imprint of the adopted stellar evolution.) Figure 3 shows the direct comparison between the N-body prediction for a cluster of initial mass $M_i=8.9\times 10^3~\mbox{$M_{\odot}$ }$( Ni=16 384) with a concentration of W0=7 and our analytic solution. For the analytic solution we adopted the same mass and the parameter $\mbox{$t_0$ }=18$ Myr was chosen in such a way that the 95% disruption time is 5.7 Gyr, very close to that of the N-body simulation. The times are normalized to the time when $95\%$ of the cluster mass is gone. We see that the prediction by the N-body calculations (full line) and the analytic expression (dotted line) are very similar, apart from a small offset of the timescale. If we normalize the timescale of the analytic solution to the time when 96.5% of the initial mass is gone (dashed line), the agreement is almost perfect. The difference in timescale is due to the fact that in the N-body simulations there is a preference for the low mass stars to be ejected from the clusters, whereas in the analytical solution stars of all masses are lost. Apart from this small difference, the analytical solution with t0 as a free parameter describes the decrease of the mass of clusters surprisingly accurately.


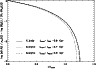  \begin{figure} {\psfig{figure=2241fig3.ps,width=8.4cm} }\end{figure} Figure 3: Comparison between the mass decrease of a cluster of $8.9\times 10^3~M_{\odot}$ predicted by N-body simulation of BM03 (full line) and our analytic approximation for $\mbox{$t_0$ }=18$ Myr (dashed and dotted line). The mass decrease has been corrected for the mass lost by stellar evolution. The timescale is normalized to the time when 95 or 96.5% of the initial mass is lost (see text).
Open with DEXTER

4.1 Explanation

We conclude that our analytic description of the decreasing mass of a cluster, with the adjustable free parameter t0, is very similar to the one derived by N-body simulations. This result is not trivial.

The values of $\mbox{$t_{\rm dis}^{\rm BM}$ }$that results from the N-body simulations by BM03 depend on the initial number of stars as $N_{\rm i}^{0.62}$, in excellent agreement with the dependence derived empirically by BL03 (see Sect. 2). However this does not automatically imply that the decrease of mass with time of each individual cluster can be described by a function that depends on the $\it present$ mass of that cluster to the same power $\gamma =0.62$ (Eq. (5)). However the good agreement between the simulations by BM03 and our result from the analytic description shows that it does depend on the mass in this way.

So, not only does the total lifetime of all clusters depend on their initial mass as $\mbox{$t_{\rm dis}^{\rm total}$ }\propto \mbox{$M_{\rm i}$ }^{0.62}$, but also at every moment during the lifetime of a cluster the exponential disruption time, $({\rm d}\!\ln \mbox{$M$ }/{\rm d}t)^{-1}$, scales with the mass to the same power, 0.62. This is a consequence of the fact that the timescale of the disruption process depends on both the half mass relaxation time, $t_{\rm rh}$ and the crossing time  $t_{\rm cr}$ as about $t_{\rm rh}^x t_{\rm cr}^{1-x}$, with $x \simeq 0.75$ for models with a concentration parameter W0=5.0 and x=0.82if W0=7.0 (BM03). For both sets of models the disruption time scales with mass as M0.62 (Gieles et al. 2004). It is the continuous adjustment of the half mass relaxation time and the crossing time to the changing conditions of the cluster that results in an exponential disruption time that varies during the life of a cluster as the present mass  $\mbox{$M$ }^{0.62}$.

   
5 The predicted mass and age distributions of cluster samples

Using the expression for the decreasing mass of clusters, Eq. (6), we can predict the mass and age distribution of cluster samples (for open clusters as well as globular clusters) for any adopted cluster formation rate, CFR(t), and cluster initial mass function, CIMF.

Suppose that the CIMF is a power law with a slope $-\alpha=-2$(Zhang & Fall 1999; Larsen 2002; Bik et al. 2003; de Grijs et al. 2003) in the range of $\mbox{$M_{\rm min}$ }< M_{\rm cl} < \mbox{$M_{\rm max}$ }$, $\mbox{$M_{\rm min}$ }\approx 10^2~\mbox{$M_{\odot}$ }$ and $\mbox{$M_{\rm max}$ }\approx 10^7~\mbox{$M_{\odot}$ }$, then the number of clusters with initial mass $M_{\rm i}$ formed at time t will be

 \begin{displaymath}\mbox{$N(M_i,t)$ }~=~S(t) \left( \frac{M_i}{\mbox{$M_{\odot}$... ...~{\rm for}~~\mbox{$M_{\rm min}$ }< M_i < \mbox{$M_{\rm max}$ } \end{displaymath} (12)

in Nr $\mbox{$M_{\odot}$ }^{-1}$ yr-1 if t is in years and Mi in $M_{\odot }$. The function S(t) is related to the cluster formation rate CFR(t)in Nr yr-1 as


 
                          $\displaystyle \mbox{$CFR(t)$ }$ = $\displaystyle \int^{\mbox{$M_{\rm max}$ }}_{\mbox{$M_{\rm min}$ }} \mbox{$N(M_i,t)$ }{\rm d}M_i$  
  = $\displaystyle \frac{S(t)}{1-\alpha} \left\{ \left( \frac{\mbox{$M_{\rm max}$ }}... ...rac{\mbox{$M_{\rm min}$ }}{\mbox{$M_{\odot}$ }}\right)^{1-\alpha} \right\}\cdot$ (13)

The total mass of the clusters formed per year is $S(t) \ln~(\mbox{$M_{\rm max}$ }/ \mbox{$M_{\rm min}$ })$ in $\mbox{$M_{\odot}$ }$ yr-1 for $\alpha=2$.

   
5.1 The distribution of the masses and ages

Given the initial mass distribution of the clusters, their formation rate, CFR(t), and an expression for the way in which the mass of each cluster changes with time (Eq. (6)), we can calculate the present distribution of existing clusters as a function of age or as a function of their mass.

If $N(\mbox{$M$ },t)$ is the number of clusters of mass M and age t in Nr $M_{\odot }$-1 yr-1, then $N(\mbox{$M$ },t)$ and $N(\mbox{$M_{\rm i}$ },t)$ are related by the conservation of the numbers of clusters

 \begin{displaymath}N(\mbox{$M$ },t)~{\rm d}\mbox{$M$ }= N(\mbox{$M_{\rm i}$ },t)~{\rm d}\mbox{$M_{\rm i}$ } \end{displaymath} (14)

with $\mbox{$M$ }(t)$ and $\mbox{$M_{\rm i}$ }(t)$ related via Eq. (6). Applying the derivative ${\rm d}(\mbox{$M$ },t)/{\rm d}(\mbox{$M_{\rm i}$ },t)$ that follows from Eq. (6), and combining this with Eq. (12) for the CIMF and Eq. (13) for the CFR we find the present distribution of clusters as functions of mass and age:
 
                  $\displaystyle N(\mbox{$M$ },t)$ = $\displaystyle S(t) \left(\frac{\mbox{$M$ }}{\mbox{$M_{\odot}$ }}\right)^{-\alpha} \mbox{$\mu_{\rm ev}(t)$ }^{\alpha-1}$  
    $\displaystyle \left\{ 1+\frac{\gamma t}{\mbox{$t_0$ }} \left(\frac{\mbox{$M$ }}{\mbox{$M_{\odot}$ }}\right)^{-\gamma} \right\}^{(1-\alpha-\gamma)/\gamma}\cdot$ (15)

This equation is valid for $\mbox{$M$ }$ smaller than some upper limit, $M_{\rm up}(t)$, which is the mass of a cluster of age t with the maximum initial mass $\mbox{$M_{\rm max}$ }$

 \begin{displaymath}\mbox{$M_{\rm up}(t)$ }= \mbox{$M_{\rm max}$ }\left\{(\mbox{$... ...mbox{$M_{\rm max}$ }}\right)^{\gamma} \right\}^{1/\gamma}\cdot \end{displaymath} (16)

Similarly, for a given value of $\mbox{$M$ }$, Eq. (15) is only valid for ages less than  $\mbox{$t_{\rm up}(M)$ }$ which is the age at which a cluster with an initial mass of  $M_{\rm max}$ has reached a mass M. So $\mbox{$t_{\rm up}(M)$ }$ is given by the condition

 \begin{displaymath}\left(\frac{\mbox{$M$ }}{\mbox{$M_{\rm max}$ }}\right)^{\gamm... ... -(\mbox{$\mu_{\rm ev}$ }(\mbox{$t_{\rm up}$ }))^{\gamma} = 0. \end{displaymath} (17)

Equation (15) allows us to calculate the predicted mass and age distribution of a cluster sample for any assumed cluster formation rate. The mass distribution is found by integrating  $N(\mbox{$M$ },t)$ over age for any mass, and the age distribution is found by integrating over mass between  $M_{\rm up}(t)$ and some lower mass limit  $M_{\rm low}(t)$, set by the detection limit, for any age.


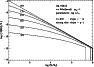  \begin{figure} {\psfig{figure=2241fig4.ps,width=8.2cm} }\end{figure} Figure 4: The changes in the mass distribution (Eq. (15)) of a sample of clusters as a function of their age, in the case where stellar evolution can be neglected. We adopted a cluster initial mass function in the range of $10^2<M<10^6~\mbox{$M_{\odot}$ }$ with  $\alpha =2.0$ and a disruption parameter  $\gamma =0.62$. The different curves refer to different ages, which are parametrized by log  $t/\mbox{$t_0$ }$. The maximum mass decreases with age due to disruption.
Open with DEXTER


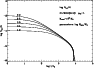  \begin{figure} {\psfig{figure=2241fig5.ps,width=8.2cm} }\end{figure} Figure 5: The age distribution of cluster samples formed at a constant formation rate, in cases where stellar evolution can be neglected. We adopted a cluster initial mass function in the range of $M_{\rm min}<M<M_{\rm max}$ with $M_{\rm max}=10^6~\mbox{$M_{\odot}$ }$ and different values of $M_{\rm min}$. We adopted $\alpha =2.0$ and a disruption parameter $\gamma =0.62$. The curves are labeled with log $(M_{\rm min}/\mbox{$M_{\odot}$ })$.
Open with DEXTER

The mass and age distribution of cluster samples N(M,t) depends on the stellar evolution and on disruption. To obtain insight into the effect of disruption on the evolution of a cluster sample we first consider a simplified case when mass loss by stellar evolution is neglected, i.e. $\mu_{\rm ev}(t)=1.0$. In that case the function  N(M,t)/S(t) depends only on the slope $\alpha$ of the cluster IMF, the mass-dependence $\gamma$ of the disruption and on the ratio  $t/\mbox{$t_0$ }$. Figure 4 shows the shape of N((M,t)/S(t). For very young ages or very long disruption time ( $t/\mbox{$t_0$ }\le 10 $) the distribution is the initial CIMF with slope $-\alpha$. For strong disruption, i.e. $t/\mbox{$t_0$ }\ge 10^2$, the distribution of the low mass clusters becomes flatter and approaches a power law of the type $N(M)\sim M^{\gamma-1}$. This distribution is similar to the one predicted by BL03 for instantaneous disruption, except that the transition between the two slopes is gradual, whereas it shows a sharp kink for models with instantaneous disruption.

Figure 5 shows the normalized age distribution $N_{\rm tot}(t)/S$, for cluster samples formed at a constant cluster formation rate in the mass range of $M_{\rm min}<M<M_{\rm max}$ for various values of  $M_{\rm min}$, when mass loss by stellar evolution can be ignored. The distribution is flat for young clusters at a value of $N/S \simeq M_{\rm min}^{-1}$and curves down to older clusters, approaching a slope $N \sim (t/\mbox{$t_0$ })^{-1/\gamma}$. This was predicted by BL03 for instantaneous disruption. The distribution drops to zero at the age at which the most massive clusters are disrupted, i.e. when $t/\mbox{$t_0$ }= M_{\rm max}^{\gamma}/\gamma$ (Eq. (16)), which is at $t/\mbox{$t_0$ }=8.46\times 10^3$ for $M_{\rm max}=10^6~\mbox{$M_{\odot}$ }$ and $\gamma =0.62$.

   
6 Application to Galactic open clusters

Ideally one would like to compare the predictions with complete (or at least unbiased) samples of clusters with known masses and ages. Unfortunately this is not possible at the moment, because samples of clusters in external galaxies are usually magnitude-limited. (The method for determining the disruption times from magnitude limited cluster samples with gradual disruption will be described by Lamers (2005) and applied to the cluster sample in M 51 by Gieles et al. (2005a).) Samples of open clusters in the solar neighbourhood are unbiased, but only the cluster ages have been determined systematically and not the cluster masses. We will compare our predictions for the age distribution to the sample of open clusters in the solar neighbourhood.

6.1 The sample of open clusters

Kharchenko et al. (2005) published a catalogue of astrophysical data of 520 galactic open clusters (COCD = Catalogue of Open Cluster Data) in the wider neighbourhood of the Sun with the values of angular sizes of cluster cores and coronae, heliocentric distances d, E(B-V), mean proper motions, radial velocities and ages. These parameters have been determined by homogeneous methods and algorithms including a careful procedure of cluster member selection. The basis of this study is the ASCC-2.5 - All-Sky Compiled Catalogue of about 2.5 million stars (Kharchenko 2001) down to $V \simeq 14$ (completeness limit at  $V \simeq 11.5$), with compiled proper motions and B,V magnitudes based on the Tycho-2 data and supplemented with ${\it Hipparcos}$ data sets, as well as with some ground-based catalogues[*]. Cluster membership is based on a combined probability which takes into account kinematic (proper motion), photometric and spatial selection criteria (see Kharchenko et al. 2004 for details). For stars within a circle with a cluster radius the membership probability is calculated as the measure of a deviation either from the cluster mean proper motion (kinematical probability), or from the Main Sequence edges (photometric probability). Stars deviating from the reference values by less than one $\sigma $ (rms) are classified as most probable cluster members (1$\sigma $-members, i.e., with a membership probability $P \ge 61$%). Those falling in semi-intervals [1$\sigma $,2$\sigma $) or [2$\sigma $,3$\sigma $) are considered as possible members (P=14-61%) or possible field stars (P=1-14%), respectively. Stars with deviations larger than 3$\sigma $ are regarded as definite field stars (P < 1%). As a rule, all cluster parameters were determined from the data of the most probable cluster members. Cluster ages were determined with an isochrone-based procedure which provides a uniform age scale (see Kharchenko et al. 2005 for details). Thus the COCD is the most homogeneous and most complete catalogue of open clusters in the solar neighbourhood available.


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{2241fig6.ps} \end{figure} Figure 6: Top: the surface density distribution projected onto the Galactic plane of open clusters in the solar neighbourhood from the homogeneous Kharchenko et al. (2005) catalogue. Error bars indicate 1$\sigma $ statistical uncertainties. The surface density is almost constant up to at least 600 pc and possibly 1 kpc. Bottom: the ratio between the numbers of old (> $2.5\times 10^8$ yr) and young (< $2.5\times 10^8$ yr) clusters as a function of distance. The ratio is almost constant up to 1 kpc.
Open with DEXTER

Figure 6 shows the distance distribution of the density of clusters projected onto the Galactic plane, in number per pc2. Within the statistical uncertainty the surface density is constant up to at least 600 pc, and possibly even up to 1 kpc. The lower part of the figure shows the ratio between old ( $ t> 2.5 \times 10^8$ yr) and young ( $ t< 2.5 \times 10^8$ yr) clusters as a function of distance. Up to a distance of about 1 kpc there is no significant change in this ratio within the statistical uncertainty. This is important for our study because it shows that the age distribution of open clusters within about 1 kpc is not affected by detection limits.

Figure 7 shows the age distribution in number per year of the 114 clusters within 600 pc in the Kharchenko et al. (2005) sample. The effect of binning is demonstrated by plotting two sets of data, where the bins have been shifted by 0.1 dex relative to one another. This distribution decreases with age, apart from a small local maximum around $\log~(t/{\rm yr}) \simeq 8.5$. The distribution at young ages is sensitive to the choice of the age-bins and shows a significant scatter. The steep slope at $\log~(t/{\rm yr}) > 8.8$demonstrates that cluster disruption is important.


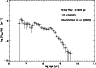  \begin{figure} {\psfig{figure=2241fig7.ps,width=8.4cm} }\end{figure} Figure 7: The age histogram in units of number per year, in logarithmic age-bins of 0.2 dex, of 114 open clusters within d<600 pc from Kharchenko et al. (2005). The distributions are plotted for two sets of bins, shifted by 0.1 dex, with and without squares respectively. The error bars indicate the 1$\sigma $ statistical uncertainty. The distribution decreases to older ages, with a small bump around $\log~ (t/{\rm yr}) \simeq 8.6$. For $\log~ (t/{\rm yr}) < 7.5$ the distribution is uncertain due to large error bars.
Open with DEXTER

6.2 The lower mass limit of the clusters

For the determination of the cluster formation rate and the disruption times we need an estimate of the minimum mass of the clusters in the Kharchenko et al. (2005) sample. This catalogue does not list the mass of the clusters, but it can be estimated roughly from the age, distance, extinction and the number of stars of each cluster. We have estimated the lower mass limit of the Kharchenko et al. cluster sample in the following way.

(a)
First we calculate the number of members brighter than the completeness limit, $V_{\rm lim} = 11.5$, within the cluster radius with the following constraints on cluster membership probabilities: $2\sigma$ photometric probability and $2\sigma$ kinematic probability. These probabilities were defined in Sect. 6.1. We did this separately for main sequence stars only, and for members of all spectral types.
(b)
Using the distance and E(B-V) of the clusters, we expressed $V_{\rm lim}$ in Mv. This limiting magnitude of the main sequence (MS) stars is expressed in  $M_{\rm bol}$ and mass, $M^*_{\rm lim}$, using the bolometric corrections and the mass luminosity relation of luminosity class V stars. With the cluster age known, the mass of the stars at the turn-off point of the MS, $M_{\rm TO}$, can be estimated from the relation between the MS lifetime and stellar mass, for which we adopted the relation by Schaller et al. (1992) for solar metallicity.
(c)
We then assumed a stellar IMF with a slope of -2.35, i.e. $N(M){\rm d}M=C M^{-2.35}{\rm d}M$, and calculated the value of C that gives the derived number of main sequence stars in the mass range of  $M^*_{\rm lim} <M < M_{\rm TO}$.
(d)
With this value of C we calculated the total mass of the cluster for all stars between the upper MS mass limit, $M_{\rm TO}$, and a lower limit for the stellar mass, $M^*_{\rm min}$, for which we adopted 0.15 $M_{\odot }$. (With this lower mass limit the mean stellar mass of a cluster with a Salpeter mass function is  $0.51~\mbox{$M_{\odot}$ }$, which is quite similar to the mean mass of  $0.55~\mbox{$M_{\odot}$ }$ for a Kroupa (2001) mass function.) We corrected this mass for the small number of stars with a MS age that is 15% shorter than the age of the cluster, in order to correct for the stars that have evolved off the MS but have not yet ended their lives. So the adopted mass range is  $M^{\rm max}_{\rm alive} < M < M^*_{\rm min}$, where  $M^{\rm max}_{\rm alive}$ is the mass of a star with a MS lifetime of 0.85 times the age of the cluster. (White dwarfs, neutron stars and black holes do not add significantly to the mass of clusters with ages less than about a few Gyr.) In this way we estimated the mass of all the clusters in the Kharchenko sample with d<600 pc.
(e)
We also applied this method directly to the observed number of the probable (2$\sigma $) member stars with V<11.50, of all luminosity class. These are the observed stars in the mass range of $M^{\rm max}_{\rm alive} < M < M^*_{\rm min}$. The resulting masses are very similar to those derived from the number of MS stars only, except for a few clusters of high extinction for which the $V_{\rm lim} = 11.5$ corresponds to stars near the top of the main sequence and the number of probable members brighter than V=11.5 is small.
(f)
To estimate the sensitivity of the resulting cluster mass to the adopted stellar lower mass limit, we repeated the analysis for an adopted lower mass of  $M^*_{\rm min}=0.25~\mbox{$M_{\odot}$ }$. In this case the estimated masses are about 80% of those estimated for $M^*_{\rm min}=0.15~\mbox{$M_{\odot}$ }$.
The resulting mass-age histogram of the clusters, for $M^*_{\rm min}=0.15~\mbox{$M_{\odot}$ }$, is shown in Fig. 8. Most of the clusters have a present mass in the range of about $5\times 10^1$ to $5\times 10^3$ $M_{\odot }$. The histogram of the resulting masses, Fig. 9, shows a peak in the range of about 100 to 300 $M_{\odot }$. The slow decline to the high mass end reflects the initial cluster mass function modified by mass loss and disruption. The steep decrease to low masses is due to the detection limit of the clusters and their members. The edge suggests that the mean lower mass limit of the Kharchenko et al. (2005) cluster sample is about $100~\mbox{$M_{\odot}$ }$. This mass corresponds to a minimum number of about 280 stars per cluster if  $M^*_{\rm min}=0.15~\mbox{$M_{\odot}$ }$. From Eq. (7) we find that a present mass of 100 $M_{\odot }$ corresponds to an initial mass of  $3.4\times 10^2$ $M_{\odot }$ if t=108 yr and  $5.8 \times 10^3$ $M_{\odot }$ if t=109 yr. These values are for a disruption parameter of t0 = 3.3 Myr (see below).

To estimate the sensitivity of the cluster masses to the adopted stellar lower mass limit we also determined the masses of the clusters in the Kharchenko et al. (2005) catalogue within 600 pc in the same way as described above but with an adopted minimum stellar mass of $M^*_{\rm min}=0.25~\mbox{$M_{\odot}$ }$instead of 0.15 $M_{\odot }$. The resulting cluster masses are about 80% of those for $M^*_{\rm min}=0.15~\mbox{$M_{\odot}$ }$, so in that case the minimum lower mass limit of the Kharchenko sample would be about 80 $M_{\odot }$. The limiting cluster mass of 80 $M_{\odot }$ corresponds to about 140 stars.


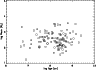  \begin{figure} {\psfig{figure=2241fig8.ps,width=8.4cm} }\end{figure} Figure 8: The mass-versus-age diagram of 114 clusters of the Kharchenko et al. (2005) catalogue within a distance of 600 pc. The mass is derived from the number of main sequence stars with V<11.50.
Open with DEXTER


  \begin{figure} {\psfig{figure=2241fig9.ps,width=8.4cm} }\end{figure} Figure 9: The mass histogram of 114 clusters of the Kharchenko et al. (2005) catalogue within a distance of 600 pc. The steep edge at the low mass side suggests that the sample is complete for clusters with a mass $M \mathrel{\copy\gabox}100~\mbox{$M_{\odot}$ }$.
Open with DEXTER

6.3 The disruption time of clusters in the solar neighbourhood

Figure 10 shows the fits to the data for $\gamma =0.62$ and various values of $\mbox{$t_0$ }$, based on the method described in Sect. 5.1. For the top figure we adopted a constant cluster formation rate and a CIMF with $\alpha=2$ and a mass upper limit of  $1\times 10^5$ $M_{\odot }$. This latter choice agrees with the steep decrease around $\log~ (t/{\rm yr}) \simeq 9.5$. We assumed a minimum detectable cluster mass of 100 $M_{\odot }$. The predicted distributions are normalized to the data point at $\log~ (t/{\rm yr})=8.1$, which is one of the most accurate data points. The best fit is reached for $\mbox{$t_0$ }\simeq 3.3$ Myr. (The low datapoint at  $\log~ (t/{\rm yr}) =7.3$ and the subsequent high point at 7.5 may be due to the adopted binning; see Fig. 7.)


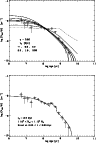  \begin{figure} {\psfig{figure=2241fig10a.ps,width=8.4cm} } \par\vspace*{2mm} {\psfig{figure=2241fig10b.ps,width=8.4cm} }\end{figure} Figure 10: Comparison between observed and predicted age histogram of clusters in the solar neighbourhood within d<600 pc. The data are fitted to predicted relations based on our analytical expression of the cluster disruption with various values of $\mbox{$t_0$ }$, normalized to the point at $\log~ (t/{\rm yr})=8.1$. The clusters are formed in the mass range of $10^2 < \mbox{$M_{\rm cl}$ }< 10^5$ $M_{\odot }$, with a CIMF of slope -2.0. Top figure: predictions for a constant CFR. The dotted line indicates the prediction if there was no cluster disruption, but only mass loss by stellar evolution. The shorter the disruption time, the steeper the decrease towards high ages. At young ages the shortest disruption time corresponds to the largest formation rate and vice versa. Lower figure: the best fit for an assumed burst between 250 and 600 Myr ago, with a CFR that was 2.5 times higher than before and after the burst.
Open with DEXTER

The distributions for $\mbox{$t_0$ }\gg 3.3$ Myr underpredict the observed numbers at $\log~ (t/{\rm yr}) < 7.2$ and overpredicts the numbers at old ages. The distribution for $\mbox{$t_0$ }\ll 1.6$ Myr overpredicts the distribution at young ages. We have applied a $\chi^2$ test to express the goodness of the fit. For this test we only considered the data at  $7.1 \le \log~ (t/{\rm yr}) \le 8.1$ and $\log~ (t/{\rm yr}) \ge 8.9$, i.e. we excluded the bump at $ 8.3 \le \log~ (t/{\rm yr}) \le 8.7$ which will be discussed below. We also excluded the data younger than 10 Myr, because they may be affected by infant mortality[*]. The criterion $\chi^2 \le \chi_{\rm min}^2 +1$ results in the best estimate of $\mbox{$t_0$ }=3.1^{+1.2}_{-0.8}$ Myr. The data of the fits are given in the top line of Table 2.

To investigate the effect of the adopted lower mass limit, we have also compared the observed age distribution with that predicted for $M_{\rm max}=1\times 10^5$ $M_{\odot }$ and $M_{\rm min}=80$ $M_{\odot }$. This last value is derived from the Kharchenko et al. cluster sample if the stellar lower mass limit of 0.25 $M_{\odot }$ is adopted instead of 0.15 $M_{\odot }$. This comparison is very similar to the one in the top panel of Fig. 10 and is not shown here. The resulting data are listed in the second line of Table 2. The best fit is at a slightly longer disruption time of $\mbox{$t_0$ }= 3.5^{+1.3}_{-0.8}$ Myr. Combining the two values of t0, derived for  $\mbox{$M_{\rm min}$ }=80$ and 100 $M_{\odot }$, we conclude that $\mbox{$t_0$ }=3.3^{+1.5}_{-1.0}$ Myr (see bottom line of Table 2).

The derived value of t0 implies a total disruption time of a 104 $M_{\odot }$ cluster of $1.3 \pm 0.5$ Gyr (Eq. (11)). This empirically-derived disruption time of open clusters is about a factor of 5 smaller than the value predicted by the N-body simulations of BM03, who predict a disruption time of 6.3 Gyr for a 104 $M_{\odot }$ cluster with an initial concentration factor of W0=5.0 and 5.9 Gyr if W0=7.0. The N-body simulations of clusters by Portegies Zwart et al. (1998) gave about twice as short disruption times as those of BM03 (see also Lamers et al. 2005). This is still longer than the empirically derived disruption time for open clusters in the solar neighbourhood.

We consider three possible reasons for this discrepancy: (a) the clusters do not start with the initial concentration factors adopted in the simulations by BM03 and (b) the presence of another mechanism (apart from the tidal field) that contributes to the destruction of clusters in the solar neighbourhood.

BM03 assumed in their N-body simulations that the clusters initially fill their tidal radius with a concentration factor of W0=5.0 or 7.0, defined by King (1966). These are the values suggested by the current density profiles of the globular clusters. However, open clusters are much less centrally condensed than globular clusters. Moreover they may not fill their tidal radius when they are formed. If the clusters are smaller than their tidal radius the internal relaxation will be faster than predicted and so the disruption might be faster. We suggest that open clusters are formed so far out of equilibrium that they lose a substantial fraction of their mass within a few crossing times. Most clusters will then disperse completely, in agreement with the high infant mortality rate. The surviving clusters might then dissolve along the lines predicted by the N-body simulations, but on a faster time scale. N-body simulations of clusters with various initial concentration factors and various initial radii are needed to test this suggestion.

The disruption times calculated by BM03 is an upper limit because the values are calculated for tidal disruption in a smooth tidal field without other destruction mechanisms. The destruction of open clusters by encounters with giant molecular clouds (GMCs) has been proposed by several authors, e.g. Oort (1958) and Terlevich (1987). The problem with this explanation is that disruption by a GMC is expected to result in a mass dependence disruption of $\mbox{$t_{\rm dis}$ }\sim M^{\gamma}$ with $\gamma=1.0$ (e.g. Spitzer 1987), whereas the observed age distribution agrees perfectly with $\gamma =0.62$ predicted for tidal effects. On the other hand, massive clusters are likely to have larger tidal radii and hence more interactions than low mass clusters and will therefore be more susceptible to the influence of GMCs. This might soften the mass dependence of the disruption time to $\gamma<1$.

Table 2: The disruption time and the formation rate of clusters within 600 pc from the Sun for two assumed values of the lower mass limit of clusters in the Kharchenko et al. (2005) sample.

6.4 The cluster formation rate, the star formation rate and the infant mortality rate

The vertical shift of the predicted relative to the observed age distribution in the top panel of Fig. 10 gives the CFR. We find a CFR of $0.93 \pm 0.04$ clusters per Myr. (This is about twice as high as the value derived by Battinelli & Capuzzo-Dolcetta (1991) based on the Lyngå (1987) catalogue of open clusters brighter than Mv=-4.5.) Our value of the CFR corresponds to a starformation rate in clusters of $5.9~ \pm~ 0.8 \times 10^2$ $M_{\odot }$/Myr within a region of 600 pc from the Sun for an CIMF with a slope of $\alpha=2$ and an adopted lower cluster mass limit of  $100~\mbox{$M_{\odot}$ }$. This corresponds to a surface formation rate of the galactic disk near the Sun of  $5.2 \pm 0.7\times 10^{-10}$ $M_{\odot }$ yr-1 pc-2.

This value can be compared with the present total star formation rate in the galactic disk near the Sun. Lada & Lada (2003) derived a SFR of 7 to  $10 \times 10^{-10}~\mbox{$M_{\odot}$ }$ yr-1 pc-2 from embedded clusters in the solar neighbourhood. This value is a factor of 1.3 to 1.9 higher than the value derived from the clusters in the Kharchenko sample. The difference is most likely due to the fact that many of the star clusters formed in embedded clouds will be dispersed within 10 Myr. At later ages they would not be recognized as clusters. Thus, if the sample of embedded stars studied by Lada & Lada (2003) is complete, the infant mortality rate of clusters in the solar neighbourhood is about 40 percent.

We can also estimate the infant mortality rate of the clusters from the data in the Kharchenko et al. (2005) catalogue. The mean cluster formation rate in the age bin of $6.6 < \log~(t) < 6.8$ is $1.3\times 10^{-6}$ clusters/yr, whereas it has dropped to $5.4\times 10^{-7}$ clusters/yr at  $6.8 < \log~(t) < 7.0$. This indicates a survival rate of about 40% and an infant mortality rate of about 60%. The same rates are found if we compare the mean value of the cluster formation rates in the age bin of $6.5 < \log~(t) < 6.9$ with that of $6.9 < \log~(t) < 7.3$. So, the comparison of the cluster formation rate with the star formation rate of Lada & Lada (2003) and the comparison between the formation rates of the youngest to the slightly older clusters both suggest an infant mortality rate of about 50%.

6.5 The burst between 250 and 600 Myr ago

The predictions shown in the top panel of Fig. 10 and discussed above do not explain the bump around $\log~(t/{\rm yr}) \simeq 8.5$ which is higher than any of the distributions for a constant cluster formation rate. Thus, the cluster sample of Kharchenko et al. (2005) suggests that there was an increased cluster formation rate around that time. We have modelled this with Eq. (15) for several non-constant CFRs. The best fit is shown in the lower part of Fig. 10, which was calculated for $\mbox{$t_0$ }= 3.3$ Myr and with a CFR that is increased by 0.40 dex between 250 and 600 Myr ago. The fit matches the data well. This suggests that the cluster formation rate was a factor of 2.5 higher during this age range. Taking into account this burst we find that the mean CFR within 600 pc from the Sun during the last Gyr in the solar neighbourhood was $9.1~ \pm~ 3.5\times 10^2$ $M_{\odot }$/Myr which corresponds to a surface formation rate of  $8.1 \pm 3.0\times 10^{-10}$ $M_{\odot }$ yr-1 pc-2.

Zaritzky & Harris (2005) found a peak near 400 Myr in the SFR of the SMC. During this peak the SFR was at least twice as high as the quiescent SFR of the SMC. They attribute this peak to the perigalactic passage of the SMC and the Galaxy. Possibly this passage also triggered the increased SFR in the galactic disk.

De la Fuente Marcos & de la Fuente Marcos (2004) have studied the star formation history in the solar neighbourhood, based on various open cluster catalogues. They identified five bursts at 0.35, 0.70, 1.13, 1.50 and 1.93 Gyrs respectively. The burst that we found between 0.25 and 0.6 Gyr may correspond to the one of 0.35 or, more likely, to a combination of those at 0.35 and 0.70 Gyr found by de la Fuente Marcos & de la Fuente Marcos (2004). Our analysis of the Kharchenko et al. (2005) cluster sample does not confirm the other bursts.

6.6 The upper mass limit of the clusters

The theoretical fits of the predicted age distribution to the observed one in Fig. 10 shows that the best fit is reached if the maximum mass of the clusters formed within 600 pc of the Sun during the last few Gyr was about 105 $M_{\odot }$. This upper limit explains the steep drop in the age distribution at $t \ge 1$ Gyr. To check the robustness of this conclusion we have also calculated models with higher mass upper limits for the clusters. For instance, if the upper mass limit was 106 $M_{\odot }$ then we would expect the following predicted and observed numbers of clusters in the oldest logarithmic agebins, indicated in a vector ( $\log t_{\rm min},\log t_{\rm up}$; nr predicted, nr observed): (8.9, 9.1; 5.1, 6), (9.1, 9.3; 4.1, 3), (9.2, 9.4; 3.3, 2), (9.3, 9.5; 2.9, 1). In these oldest agebins the number of observed clusters is within the statistical $1\sigma$ uncertainty of the number of predicted clusters. This means that we cannot exclude the possibility that the maximum cluster mass was higher than 105 $M_{\odot }$ and possibly as high as 106 $M_{\odot }$.

An alternative way to consider this point is to find the clusters in the Kharchenko sample with the highest initial mass. We use the estimate of the present cluster masses, derived from the number of member stars, as described in Sect. 6.1, and then applied Eq. (7) to convert the present mass into the initial mass with a disruption parameter  $\mbox{$t_0$ }= 3.3$ Myr. We find that the two initially most massive clusters within a distance of 600 pc, i.e. the ones with  $\{\log~(t),\log~(M)\}$ = {9.2, 3.5} and {9.4, 2.8} in Fig. 8, had an initial mass of  $2.5\times 10^4$ and  $3.2\times 10^4$ $M_{\odot }$ respectively. For a CIMF with $\alpha=2$ the number of clusters decreases with mass as $N\sim M^{-2}$, so the expected number of clusters initially more massive than e.g. 105 $M_{\odot }$ will be smaller than 1.

The observed mass upper limit is probably determined by statistical effects (Hunter et al. 2003; Gieles et al. 2005b). Its expected value can be estimated from the number of observed clusters within 600 pc. For a CIMF with a slope of -2 the maximum mass expected in the sample is roughly $M_{\rm max} \simeq N \times M_{\rm min}$, where N=114 is the number of observed clusters and $M_{\rm min}\simeq 10^2~\mbox{$M_{\odot}$ }$. So we expect a maximum initial mass, set by statistical effects, of about $1\times 10^4$ $M_{\odot }$. (In reality it should be slightly higher because the observed number of clusters is already affected by disruption.) This agrees quite well with the maximum initial mass of about  $3\times 10^4$ $M_{\odot }$ derived in the previous paragraph.

7 Discussion and summary

We have derived a simple analytical expression for the mass loss from star clusters due to stellar evolution and disruption as a function of time, Eq. (6). This expression agrees very well with results of N-body simulations of clusters in the tidal field of our galaxy. The expression is derived for mass loss by stellar evolution using the ${\it GALEV}$ cluster evolution models (Schulz et al. 2002; Anders & Fritze-v. Alvensleben 2003) but can easily be applied to other cluster evolution models, provided that the mass loss due to stellar evolution can be expressed by an analytic approximation (e.g. of the type proposed in Sect. 3.1). Our analytical expression for the mass loss from star clusters is different to the one by Vesperini & Heggie (1997) because they assumed that tidal effects decrease the mass of a cluster linearly with time.

Our method is based on the fact that the disruption time of clusters, defined as $\mbox{$t_{\rm dis}$ }\equiv ({\rm d}\!\ln \mbox{$M$ }/ {\rm d}t)^{-1}$, depends on the mass M as $\mbox{$t_{\rm dis}$ }=\mbox{$t_0$ }(M/\mbox{$M_{\odot}$ })^{\gamma}$ with $\gamma =0.62$ for disruption by two body relaxation in a tidal field. This dependence was found both empirically from a study of cluster samples in four galaxies by BL03 and by Lamers et al. (2005), and theoretically from N-body-simulations by Baumgardt (2001) and BM03. The description contains a normalization parameter, $\mbox{$t_0$ }$, that depends on the environment in the parent galaxy of the clusters. This parameter can vary by more than an order of magnitude between cluster samples of different galaxies, as shown by BL03. Simple theoretical predictions, numerical simulations and empirical determinations of cluster disruption in a few galaxies showed that $\mbox{$t_0$ }\simeq C_{\rm env} 10^{-4 \gamma} (\rho_{\rm amb}/\mbox{$M_{\odot}$ ~pc$^{-3}$ })^{-0.5}$, where $\rho_{\rm amb}$ is the ambient density in the galaxy at the location of the clusters, and $C_{\rm env} \simeq 300{-}800$ Myr (Lamers et al. 2005). The value of t0 may be shorter in interacting galaxies, as suggested by the study of the star cluster sample of M 51 by Gieles et al. (2005a).

Using our description of mass loss from clusters by stellar evolution and disruption, we can predict the resulting present day mass, M, and age distributions in terms of $N(\mbox{$M$ },t){\rm d}\mbox{$M$ }{\rm d}t$ of the surviving clusters for different cluster initial mass functions and different cluster formation histories. This is given by Eq. (15). An integration of  $N(\mbox{$M$ },t)$ over mass for different ages gives the expected age distribution of the surviving clusters. An integration of  $N(\mbox{$M$ },t)$ over age for different masses gives the expected mass distribution. This method can be applied to any cluster formation history.

A comparison between predicted and observed distributions of selected cluster samples can be used to derive the basic properties of that cluster population, such as the cluster formation rate, the cluster IMF, and the disruption parameter  $\mbox{$t_0$ }$. To demonstrate this method we have applied it to the age distribution of open clusters in the solar neighbourhood within 600 pc based on the new cluster catalogue by Kharchenko et al. (2005). Tests showed that the cluster sample in this catalogue is unbiased up to a distance of at least 600 pc and possibly 1 kpc. The predicted age distribution agrees very well with the empirical one (Fig. 10). The main uncertainty in the derived disruption time $\mbox{$t_0$ }$ is the unknown lower mass detection limit of this cluster sample. We estimated this mass limit from the given number of cluster members brighter than V=11.5 magn. and found it to be between 80 and 100 $M_{\odot }$. With these values, the fit of the predicted age distribution to the observed one shows that the disruption time  $\mbox{$t_0$ }$ is  3.3+1.4-1.0 Myr, which corresponds to a disruption time of a 104 $M_{\odot }$ cluster of $1.3 \pm 0.5$ Gyr. This is about a factor of 5 shorter than predicted by N-body simulations of clusters in the tidal field of the solar neighbourhood (BM03). The difference is possibly due to the fact that BM03 adopted a rather high initial central concentration of the clusters that is more applicable to globular clusters than to open clusters. Moreover encounters with giant molecular clouds may also shorten the lifetime of open clusters.

The present star formation rate in the solar neighbourhood within 600 pc, derived in this paper, is $5.9 \pm 0.8\times 10^2$ $M_{\odot }$/Myr for the last few Gyrs. This corresponds to a surface formation rate of  $5.2 \pm 0.7\times 10^{-10}$ $M_{\odot }$ yr-1 pc-2, which is about a factor of 0.5 to 0.7 smaller than derived from the formation rate of stars in embedded clusters (Lada & Lada 2003). This suggests that a considerable fraction of the embedded clusters will be dispersed before reaching an age of several Myr.

The observed age distribution clearly shows evidence for a bump in the cluster formation rate between 0.25 and 6 Gyr, when the formation rate was a factor 2.5 higher than before and after. This corresponds to two of the bumps in the star formation rate derived from cluster samples by de la Fuente Marcos & de la Fuente Marcos (2005). The observed bump might be due to an encounter between the SMC and the Galaxy (e.g. Zaritsky & Harris 2005).

Although the upper mass limit of the observed clusters in the solar neighbourhood is less than about 104 $M_{\odot }$, we show that this does not exclude the possible formation of higher mass clusters. Given a cluster IMF with a slope of -2, the absence of clusters more massive than 104 $M_{\odot }$ is in agreement with the statistical uncertainty, even if the real upper limit for the initial mass was as high as 106 $M_{\odot }$.

Acknowledgements

We thank R.-D. Scholz for his collaboration in the production of the new open cluster catalogue used in this study. Paul Hodge and Anil Seth are acknowledged for useful discussions and suggestions. We thank the kind referee, Douglas Heggie, for useful suggestions and critical comments that resulted in an improvement of this paper. This work is supported by a grant from the Netherlands Research School for Astronomy (NOVA) to HJGLML and by a grant from the University of Washington in Seattle where a major part of this research was carried out when the first author was on sabbatical. N.V. Kharchenko acknowledges financial support by the DFG grant 436 RUS 113/757/0-1, and the RFBR grant 03-02-04028.

References

 
Copyright ESO 2005