A&A 440, 1041-1049 (2005)
DOI: 10.1051/0004-6361:20053261

Stellar evolution with rotation and magnetic fields

III. The interplay of circulation and dynamo

A. Maeder - G. Meynet

Geneva Observatory, 1290 Sauverny, Switzerland

Received 19 April 2005 / Accepted 20 May 2005

Abstract
We examine the effects of the magnetic field created by the Tayler-Spruit dynamo in differentially rotating stars. Magnetic fields of the order of a few 10⁴ G are present through most of the stellar envelope, with the exception of the outer layers. The diffusion coefficient for the transport of angular momentum is very large and it imposes nearly solid body rotation during the MS phase. In turn, solid body rotation drives meridional circulation currents which are much faster than usual and leads to much larger diffusion coefficients than the magnetic diffusivity for the chemical species. The consequence is that the interplay of the thermal and magnetic instabilities favours the chemical transport of elements, while there would be no transport in models with magnetic field only. We also discuss the effects on the stellar interior, lifetimes and HR diagram.

Key words: stars: rotation - stars: magnetic fields - stars: evolution

1 Introduction

Stellar rotation influences all the outputs of stellar evolution and nucleosynthesis and several grids of models have been made for massive stars (Langer et al. 1999; Heger et al. 2000; Meynet & Maeder 2000). The effects of rotation are even more important at metallicities Z lower than solar (Maeder & Meynet 2001). However, we do not know the role of the magnetic field in stellar evolution and it is the purpose of this series of works to approach this matter, which is considered to be critical one (cf. Roxburgh 2003). Spruit (2002) proposed a dynamo mechanism operating in stellar radiative layers in differential rotation. This dynamo is based on the conjectured Tayler instability, which is apparently the first one to occur in a radiative zone (Tayler 1973; Pitts & Tayler 1986). For now, there is no empirical or observational proof of the existence of this instability. According to Pitts & Tayler (1986) and Spruit (2002), even a very weak horizontal magnetic field is subject to this instability, which then creates a vertical field component, which is wound up by differential rotation. As a result, the field lines become progressively closer and denser and thus a strong horizontal field is created at the energy expense of differential rotation.

In a first paper (Maeder & Meynet 2003, Paper I), we have shown that in a rotating star a magnetic field can be created during MS evolution by the Spruit dynamo. We have examined the timescale for the field creation, its amplitude and the related diffusion coefficients. The clear result is that magnetic field and its effects are quite important. In the second paper (Maeder & Meynet 2004, Paper II), a generalisation of the equations of the dynamo was developed. The solutions fully agree with Spruit's solution in the two limiting cases considered (Spruit 2002), i.e. "Case 0'' when the $\mu$-gradient dominates and "Case 1'' when the T-gradient dominates with large non-adiabatic effects. Our more general solution encompasses all cases of $\mu$- and T-gradients, as well as all cases from the fully adiabatic to non-adiabatic solutions.

Paper II suggested that there is a complex feedback between the magnetic instability, which generates the field, and the thermal instability which drives the meridional circulation (Maeder & Meynet 2004). However, it was beyond the scope of Paper II to make numerical models of the interaction between circulation currents and dynamo. In this paper we account for this feedback, the main steps of which are the following:

• differential rotation creates the magnetic field;
• magnetic field tends to suppress differential rotation;
• the absence of differential rotation strongly enhances meridional circulation;
• meridional circulation increases differential rotation;
• differential rotation creates the magnetic field (the loop is closed).

Thus, a delicate balance between the thermal and magnetic effects occurs during evolution. The balance of these effects influences the transport of chemical elements to the stellar surface and the internal transport of angular momentum, which determines the evolution of the surface rotation.

In Sect. 2, we collect in a consistent way the basic equations of the dynamo. In Sect. 3, we give the basic expressions for the transport coefficients. In Sect. 4, we calculate numerical models for the interaction of the dynamo and circulation on the internal stellar structure. In Sect. 5, the effects at the stellar surface and in particular the evolution of abundances are analysed. Section 6 gives the conclusions.

   
2 The general equations for the dynamo

The present set of equations for the dynamo based on Tayler-Spruit instability has three important advantages with respect to the system of equations by Spruit (2002).

1.

The equations by Spruit apply to the non-adiabatic case. As most of the stellar interior is adiabatic, this situation is not appropriate. The present equations fully treat the problem whether it is adiabatic or non-adiabatic.

2.

Either the $\mu$-gradient was considered to dominate or it was absent. Such a situation is not adequate when mild mixing effects, which produce small $\mu$-gradients, are studied. In addition, as always in all problems of mixing, the $\mu$-gradients need to be very carefully treated, otherwise the results are incorrect.

3.

There is no need to interpolate between the two asymptotic solutions called "Case 0'' or "Case 1''. The interpolation was made by Spruit (2002) as a function of the parameter q, which defines the amount of differential rotation (see definition given in Eq. (8)). This is hazardous, as it expresses the interpolation of effects concerning the $\mu$-gradient and the degree of non-adiabaticity as a function of differential rotation. This is not physically justified and it introduces an additional spurious dependence on the parameter q into the problem.

Let us briefly summarize the consistent system of equations. The energy density $u_{{\rm B}}$ of a magnetic field of intensity B per volume unity is

$$u_{{\rm B}} = \frac{B^2}{8 \; \pi} ~ = ~{1 \over 2} \; \rho \... ...ad \omega_{{\rm A}}= \frac{B}{(4\; \pi \rho)^{1\over 2} \;r} ,$$ (1)

where $\omega_{{\rm A}}$ is the Alfvén frequency in a spherical geometry, r is the radius and $\rho$ the density. In stable radiative layers, there is in principle no particular motion. However, if due to the magnetic field or rotation, some unstable displacements of vertical amplitude l/2 occur around an average stable position, the restoring buoyancy force produces vertical oscillations around the equilibrium position with a frequency equal to the Brunt-Väisälä frequency N. In a medium with both thermal and magnetic diffusivity K and $\eta$, the Brunt-Väisälä frequency becomes (Maeder & Meynet 2004)

$$N^2 = \frac{\eta / K} {\eta / K +2} \; N^2_{{\rm T}}+ N^2_{\mu} ,$$ (2)

with the radiative diffusivity $K= \frac{4ac T^3}{3 \kappa \rho^2 C_{{\rm p}}}$ and with the following partial frequencies

$$N_{\mu}^2 \; = \; \frac{g \varphi}{H_{{\rm P}}} \nabla_{\mu} ... ... = \; \frac{g \delta}{H_{{\rm P}}}(\nabla_{{\rm ad}}-\nabla) .$$ (3)

The thermodynamic coefficients $\delta$ and $\varphi$ are $\delta= - \left(\frac{\partial \ln \rho}{\partial \ln T}\right)_{{\rm P},\mu}$ and $\varphi= \left(\frac{\partial \ln \rho}{\partial \ln \mu}\right)_{{\rm T,P}}$. $H_{{\rm P}}$ is the pressure scale height. The restoring oscillations will have an average density of kinetic energy

$$u_{{\rm N}} \simeq \; f_{{\rm N}} \; \rho \; l^2 \; N^2 ,$$ (4)

where $f_{{\rm N}}$ is a geometrical factor of the order of unity. If the magnetic field produces some instability with a vertical component, one must have $u_{{\rm B}} > u_{{\rm N}}$. Otherwise, the restoring force of gravity which acts at the dynamical timescale would immediately counteract the magnetic instability. From this inequality, one obtains $l^2 < \frac{1}{2f_{{\rm N}}} \;r^2 \; \frac{\omega^2_{{\rm A}}}{N^2}$. If $f_{{\rm N}}= {1 \over 2}$, we have the condition for the vertical amplitude of the instability (Spruit 2002; Eq. (6)),

$$l < \; r \; \frac{\omega_{{\rm A}}}{N} ,$$ (5)

where r is the radius. This means that there is a maximum size of the vertical length l of a magnetic instability. In order not to be quickly damped by magnetic diffusivity, the vertical length scale of the instability must satisfy

$$l^2 > \frac{\eta}{\sigma_{{\rm B}}}= \frac{\eta \; \Omega} {\omega_{{\rm A}}^2} ,$$ (6)

where $\Omega$ is the angular velocity and $\sigma_{{\rm B}}$ is the characteristic frequency of the magnetic field. In a rotating star, this frequency is $\sigma_{{\rm B}} = (\omega_{{\rm A}}^2 / \Omega)$ due to the Coriolis force (Spruit 2002; see also Pitts & Tayler 1986). The combination of the limits given by Eqs. (5) and (6) gives for the case of marginal stability,

$$\left(\frac{\omega_{{\rm A}}}{\Omega}\right)^4 = \frac{N^2}{\Omega^2} \; \frac{\eta}{r^2 \; \Omega} \cdot$$ (7)

The equality of the amplification time of Tayler instability $\tau_{{\rm a}}= N /(\omega_{{\rm A}} \Omega q)$ with the inverse of the characteristic frequency $\sigma_{{\rm B}}$ of the magnetic field leads to the equation (Spruit 2002)

$$\frac{\omega_{{\rm A}}}{\Omega} = q \; \frac{\Omega}{N} \qua... ...th} \quad q= -\frac{\partial \ln \Omega}{\partial \ln r} \cdot$$ (8)

With account of the Brunt-Väisälä (Eq. (2)), one has

$$\left(\frac{\omega_{{\rm A}}}{\Omega}\right)^2 = \frac{\Omega... ...m T}} \; \frac{\eta / K} {\eta / K \;+ \; 2} + N^2_{\mu}}\cdot$$ (9)

By eliminating the expression of N² between Eqs. (7) and (9), we obtain an expression for the magnetic diffusivity,

$$\eta \;= \; \frac{r^2 \; \Omega}{q^2} \; \left( \frac{\omega_{{\rm A}}} {\Omega}\right)^6 \cdot$$ (10)

Equations (7) and (9) form a coupled system relating the two unknown quantities $\eta$ and $\omega_{{\rm A}}$. Instead, one may also consider for example the system formed by Eqs. (9) and (10). Formally, if one accounts for the complete expressions of the thermal gradient $\nabla$, the system of equations would be of degree 10 in the unknown quantity $x=\left(\frac{\omega_{{\rm A}}}{\Omega}\right)^2$ (Paper II). The fact that the ratio $\eta/K$ is very small allows us to bring these coupled equations to a system of degree 4,

$$\frac{r^2 \Omega}{q^2 K} \left(N_{{\rm T}}^2 + N_{\mu}^2 \rig... ...r^2 \Omega^3}{K} x^3 + 2 N_{\mu}^2 \; x - 2 \Omega^2 q^2 = 0 .$$ (11)

The solution of this equation, which is easily obtained numerically, provides the Alfvén frequency and by Eq. (10) the thermal diffusivity. As shown in Paper II, the various peculiar cases studied by Spruit (2002) are all contained in the more general solution given here.

3 Coefficients for the transport of angular momentum and chemical elements

The condition that the ratio $\omega_{{\rm A}}/\Omega$ given by Eq. (8) is equal to or larger than the minimum value defined by Eq. (7) leads to a condition on the minimum shear for the dynamo to work (cf. Spruit 2002)

$$q > \left({N \over \Omega}\right)^{7/4} \left({\eta \over r^2 N}\right)^{1/4}\cdot$$ (12)

There, N is given by Eq. (2) above and $\eta$ by Eq. (10). If this condition is not fulfilled, there is no stationary situation and we consider that there is no magnetic field present. In practice, we will see that this situation occurs in the outer stellar envelope. There is a second condition. We need to check that $\Omega > \omega_{{\rm A}}$. If this last condition is not realized, the present system of equations does not apply and we should consider the case of very slow rotation. This case is treated in the appendix. In the present models, the value of $\Omega$ considered is large enough so that we did not have to apply the solution for the case of very slow rotation.

The azimuthal component of the magnetic field is much stronger that the radial one in the Tayler-Spruit dynamo. We have for these components (Spruit 2002)

$$B_{\varphi}= (4 \pi \rho)^{\frac{1}{2}} \; r \; \omega_{{\rm ... ... and} \quad B_ {{\rm r}}= B_{\varphi} \; (l_{{\rm r}} / r) ,$$ (13)

where $\omega_{{\rm A}}$ is the solution of the general equation (11) and $l_{{\rm r}}$ is given by $l_{{\rm r}} = ~ r ~ \frac{\omega_{{\rm A}}}{N}$, which is obtained by assuming the marginal stability in Eq. (5).

Turning towards the transport of angular momentum by magnetic field, we first write the azimuthal stress by volume unity due to the magnetic field

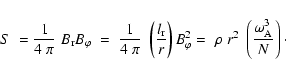$$S \; = \frac{1}{4 \; \pi} \; B_{{\rm r}} B_{\varphi} \; = \; ... ...rho \; r^2 \; \left(\frac{\omega_{{\rm A}}^3}{N}\right) \cdot$$ (14)

Then, the viscosity $\nu$ for the vertical transport of angular momentum can be expressed in terms of S (Spruit 2002),

$$\nu = \frac{S}{\rho \; q \; \Omega} = \; \frac{\Omega \; r^2... ...A}}}{\Omega}\right)^3 \; \left(\frac{\Omega}{N}\right) \cdot$$ (15)

This is the general expression of $\nu$ with $\omega_{{\rm A}}$ given by the solution of Eq. (11) and with N by Eq. (2). We have the full set of expressions necessary to obtain the Alfvén frequency $\omega_{{\rm A}}$ and the magnetic diffusivity $\eta$. The parameter $\eta$ also expresses the vertical transport of the chemical elements, while the viscosity $\nu$ determines the vertical transport of the angular momentum by the magnetic field.

In Paper II, we also checked that the rate of magnetic energy production $W_{{\rm B}}=\frac{B^2}{8 \pi} \frac{\omega_{{\rm A}}^2}{\Omega}= \frac{1}{2} \rho r^2 \frac{\omega_{{\rm A}}^4}{\Omega}$ per unit of time and volume is equal to the rate $W_{\nu}= {1\over 2}\rho\nu \Omega^2q^2$ of the dissipation of rotational energy by the magnetic viscosity $\nu$ as given above.

4 Numerical applications

4.1 The models

We consider here models of 15 $M_\odot$, with a standard composition of X=0.705 and Z=0.02. The physics of the models, opacities, nuclear reactions, mass loss rates, structural rotational effects, shear mixing, meridional circulation, etc. are the same as in recent models of the Geneva group (Meynet & Maeder 2005). We calculate 3 sets of models: the first is without rotation, the second with rotation and the third one with both rotation and magnetic field. The initial rotation velocity is 300 km s^-1, which leads to an average velocity on the MS phase of about 240 km s^-1 when no magnetic field is present (see Fig. 3). In Paper II, we did not include the effects of the meridional currents, in order to independently study the effects of the magnetic field. However, we showed that meridional circulation and the magnetic field may significantly interact, with possible consequences for the transport mechanisms. Thus, to examine this interplay, we also account here for meridional circulation currents. For the moment, we do not account for magnetic coupling by stellar winds, since there is no external convective zone in massive stars on the Main Sequence.

The choice of the time step is imposed by the most rapid process taking place. We checked that changing the time steps did not change the results. Here the fastest process is the transport of the angular momentum by the magnetic diffusivity. The diffusion coefficients $\nu$ for the angular momentum by the magnetic field reach in some cases values of 10¹³ cm² g^-1, while the average value is 1-2 orders of magnitude lower. The cases of strong coefficients lead to diffusion timescales $\tau \approx (\Delta R)^2/\nu \approx$ a few 10² yr, where D is the diffusion coefficient. For an appropriate treatment, we need to adopt very small time steps. In practice, we take time steps of the order of 20 years. This implies about $6 \times 10^5$ models to cover in a detailed way the exact interplay of the effects of the magnetic field and of the meridional circulation during the MS phase!

Clearly, the model properties do not change significantly over such a time scale as shown for example by Fig. 2. Thus, in future, faster processes of calculations may be devised. However, by imposing very short time steps on the two processes, we set the study in the linear regime for both instabilities and we may thus proceed to an addition of their own different effects.

4.2 Evolution of the internal and superficial rotation

In a rotating star, the internal profile of angular velocity $\Omega(M_{{\rm r}})$ changes with time during evolution, due to various effects (Meynet & Maeder 2000): central contraction and envelope expansion, transport of angular momentum by circulation and mass loss at the stellar surface. One assumes here that the mass lost by stellar winds just embarks its own angular momentum. The case of anisotropic stellar winds has been studied by Maeder (2002), who has shown that such effects are important only for very massive stars ($M \geq 60$ $M_\odot$) in fast rotation. Here, the loss of angular momentum at the stellar surface only has a limited importance for the evolution of rotation. Figure 1 shows the evolution of the internal profile of rotation. Differential rotation builds up during the MS phase, reaching about a factor of two between $\Omega$ at the surface and in the convective core, near the end of the MS when the central H-content is $X_{{\rm c}}=0.10$. Then, fast central contraction accelerates the core rotation.

	Figure 1: Internal distribution of the angular velocity $\Omega (r)$ as a function of the Lagrangian mass in solar units in a 15 $M_\odot$ model, without magnetic fields, at various stages of the model evolution indicated by the central H-content $X_{{\rm c}}$ during the MS-phase. The initial velocity $\upsilon _{\rm ini} = 300$ km s-1.
Open with DEXTER

	Figure 2: Same as in Fig. 1 but with magnetic fields. One notices the almost constant values of the angular velocity in the models.
Open with DEXTER

	Figure 3: Evolution of the rotation velocities at the surface of 15 $M_\odot$ models during the MS phase with and without magnetic fields H. The initial velocity $\upsilon _{\rm ini} = 300$ km s-1 in both cases. We see the much higher surface rotation when magnetic field is included.
Open with DEXTER

The situation is quite different when magnetic fields as described above are accounted for. As shown by Fig. 2, the angular velocity $\Omega$ is almost constant throughout the stellar interior. It is not exactly constant, otherwise q would be zero and the magnetic field would not be sustained anymore. Only at the very end of the MS phase does the fast central contraction bring about a small significant difference.

Figure 3 shows the evolution of the surface rotation velocities as a function of age in the models with and without magnetic field. We notice the higher velocity during the whole MS phase of the model with magnetic field, which has $v \approx 300$ km s^-1, compared to the model without a field, where $v \approx 250$ km s^-1. There are 3 effects intervening:

1.

The main part of the difference already occurs on the ZAMS. With rotation only, the model adjusts its rotation very quickly to an equilibrium profile determined by meridional circulation (Meynet & Maeder 2000) and this establishes an $\Omega$-gradient which reduces the surface velocity. On the contrary, with a magnetic field, the model can keep a constant $\Omega$ and there is no initial decrease.

2.

The other two smaller effects occur during MS evolution. The magnetic coupling forces the surface to co-rotate with the convective core, as contraction makes it spin-up. With rotation only, the coupling (due to meridional circulation) is much weaker.

3.

In the magnetic model, the surface enrichment in helium is slightly higher, this keeps the radius smaller. Thus, as the radius expansion is smaller, the decrease of surface rotation is also smaller.

The question of the differential rotation in the horizontal direction has also to be examined. In current rotating models without a magnetic field, it is assumed that the horizontal turbulence is strong enough to suppress the horizontal differential rotation, so that the hypothesis of shellular rotation with $\Omega= \Omega(r)$ applies (Zahn 1992). In the presence of a magnetic field, the horizontal turbulence is likely reduced. The numerical values for the field $B_{\varphi}$ found below is of the order of a few 10⁴ G (cf. Fig. 4). The horizontal coupling ensured by the magnetic field (cf. Fig. 4) is expressed by a coefficient $D_{{\rm B}_{{\rm h}}}$ (Maeder & Meynet 2003)

$$D_{{\rm B}_{{\rm h}}} = \;r^2 \; (\omega_{{\rm A}}^2/\Omega) ... ...a} \quad \quad {\rm for} \quad \Omega \gg \omega_{{\rm A}} .$$ (16)

The value of $D_{{\rm B}_{{\rm h}}}$ is of the order of 10¹¹ cm²/s in the present 15 $M_\odot$ model. Thus, the magnetic field is large enough to ensure the horizontal coupling, so that the assumption of shellular rotation is still valid.

4.3 Diffusion coefficients for the transports of the angular momentum and chemical elements

We need to determine in which regions of the star the magnetic field is present, its intensity and the run of the various diffusion coefficients. As an example, we examine the 15 $M_\odot$ model at the beginning of the evolution, when the central H-content is $X_{{\rm c}}=0.60$. In this model as in all MS models, $q ~ \geq ~ q_{{\rm min}}$ in a region which starts just above the core and extends over most of the envelope. In the model with $X_{{\rm c}}=0.60$, the magnetic field is present from $M_{{\rm r}} = 6.7$ $M_\odot$ to 13.4 $M_\odot$, as illustrated in Fig. 4. The average field is about $2 \times 10^4$ G and the corresponding value of $\omega_{{\rm A}}/\Omega$ is about $5 \times 10^{-4}$. Above 13.4 $M_\odot$, condition (12) is no longer satisfied. The region where magnetic field is present slightly increases during MS evolution as the convective core recedes. Near the end of the MS phase, when $X_{{\rm c}}=0.05$, the magnetic field is present from 4.2 $M_\odot$ up to 13.8 $M_\odot$.

	Figure 4: Distribution of the magnetic field in the model of initial 15 $M_\odot$ when the central hydrogen content is $X_{{\rm c}}=0.60$. The age of the model is $4.2798 \times 10^6$ yr and the actual mass is 14.97 $M_\odot$.
Open with DEXTER

	Figure 5: The diffusion coefficients in the model with central H-content $X_{{\rm c}}=0.60$. In the outer envelope, where the magnetic field is absent, the transports by shear and by combination of the meridional circulation and horizontal turbulence expressed by $D_{{\rm eff}}$ are present.
Open with DEXTER

The runs of the various diffusion coefficients are illustrated in Fig. 5. The largest diffusion coefficient is $\nu$ which acts for the vertical transport of angular momentum, the large value of $\nu$ imposes the nearly constant $\Omega$ in the interior. The value of $\nu$ is about 6 orders of magnitude larger than the diffusion coefficient $\eta$ for the transport of the chemical elements, so that the surface enrichments in products of the CNO cycle due to this magnetic diffusion coefficient only are rather limited. The coefficient $D_{{\rm eff}}$ which applies to the transport of chemical elements by meridional circulation is much larger than $D_{{\rm shear}}$, while in rotating stars without magnetic field, it is generally the opposite. This is due to the fact that the velocity of meridional circulation is much larger when $\Omega$ is almost constant throughout the stellar interior (about 10^-2 cm s^-1), while $D_{{\rm shear}}$ is much smaller. Indeed $D_{{\rm shear}}$ is about 4 orders of magnitude smaller than in rotating stars without a magnetic field, as a consequence of the near solid body rotation in magnetic models.

Figure 5 also shows that the value $\eta/K$ is always very small, which justifies the simplifications made in deriving Eq. (11). Apart from the slight extension of the zone covered by the magnetic field as mentioned above, the orders of magnitude and relative ratios of the diffusion coefficients remain about the same during the whole MS evolution.

An important result of Fig. 5 is that the transport by meridional circulation (expressed by $D_{{\rm eff}}$) is in general 2-3 orders of magnitude larger than the transport of the elements by the magnetic field (expressed by $\eta$). This clearly shows that the direct effect of the magnetic instability is of little importance with respect to thermal instability, which drives meridional circulation, for the transport of chemical elements. In addition, meridional circulation is important for the transport of the elements from the external edge of the magnetic zone to the stellar surface. However, for the coupling of $\Omega$, the magnetic field is much more efficient than meridional circulation. One can define a velocity $U_{{\rm B}}$ for the vertical transport of angular momentum by the magnetic field (cf. Paper I)

$$U_{{\rm B}}= 5 \; \frac{\nu}{r} \; \frac{\partial \ln \Omega}{\partial \ln r} \cdot$$ (17)

This quantity may be compared to the vertical component of the velocity U(r) of meridional circulation. In general $U_{{\rm B}}$ is much larger than U(r), which confirms the dominant role of the magnetic field for the transport of angular momentum.

4.4 Internal distribution of hydrogen

Figures 6 and 7 show the internal distribution of hydrogen in the cases without and with magnetic field. Firstly, rotation with a magnetic field leads to the formation of a larger core at the end of the MS phase compared to models with rotation only (models with rotation themselves have larger cores compared to models without rotation, cf. also Fig. 8).

	Figure 6: Internal distribution of the hydrogen mass fraction X as a function of the Lagrangian mass in a 15 $M_\odot$ model with rotation at various stages of the model evolution from top to bottom during the MS-phase. Some convective zones appear in the H-shell burning stage at the end of the MS phase.
Open with DEXTER

	Figure 7: Internal distribution of the hydrogen mass fraction X as a function of the Lagrangian mass in the model with magnetic field calculated according to expressions of the present paper at various stages of the model evolution from top to bottom during the MS-phase.
Open with DEXTER

Figure 8: Top lines near 15 $M_\odot$: evolution of the stellar mass. Lower lines: evolution of the mass of the convective core. The dotted line applies to the model without rotation, the short-broken line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) but without magnetic fields, the continuous line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) and magnetic fields.

Open with DEXTER

In models with rotation only, there is a significant erosion of the $\mu$-gradient at the immediate edge of the core, developing during the second half of the MS phase. This erosion directly at the edge of the core is absent in models with a magnetic field. The reason is Eq. (10), which gives, if the $\mu$-term dominates in the Brunt-Väisälä frequency,

$$\eta_0 = r^2 \Omega q^4 \; \left(\frac{\Omega}{N_{\mu}}\right)^6 \cdot$$ (18)

As noted in Paper II, the mixing of chemical elements decreases strongly if the $\mu$-gradient grows and this effect limits the chemical mixing of elements by the Tayler-Spruit dynamo in the regions just above the convective core.

	Figure 9: Evolutionary tracks in the HR diagram for 15 $M_\odot$ stellar models. The dotted line applies to the model without rotation, the short-broken line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) but without magnetic fields, the continuous line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) and magnetic fields.
Open with DEXTER

Finally, in models with a magnetic field the mixing in the envelope is much greater than in the case without a field. This effect appears during the entire MS phase and the final helium surface content reaches $Y_{{\rm s}} = 0.31$. This effect is not due to the shear, which is essentially absent in magnetic models. It is also not due to the magnetic diffusivity, because it is rather small and in the very external regions there is no magnetic field. However, the transport of chemical elements by the circulation (an effect described by $D_{{\rm eff}}$) is larger and is generally the main effect in the envelope. It produces a slight transport of the elements, which enriches the stellar surface in elements of the CNO cycle (cf. Fig. 10). The models of Paper II with a magnetic field, but without meridional circulation predict no N excesses and this was a difficulty. However, magnetic models, when the meridional circulation is included, lead to a significant N-enrichment, which compares with observations (cf. Sect. 5.2).

5 Evolution of observable parameters

The magnetic field created by the dynamo does not reach the stellar surface. However, there are consequences concerning the tracks in the HR diagram and especially the enrichment of surface abundances, which may lead to observable consequences.

Figure 10: Time evolution of the surface helium content $Y_{{\rm s}}$ in mass fraction, of the N/O, N/H and N/C in mass fraction for various models: the dotted line applies to the model without rotation, the short-broken line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) but without magnetic fields, the continuous line to the model with rotation ( $\upsilon _{\rm ini} = 300$ km s-1) and magnetic fields.

Open with DEXTER

5.1 Evolution of the core, lifetimes and tracks in the HR diagram

The evolution of the tracks in the HR diagram is determined by the evolution of the core mass fraction. Figure 8 shows the evolution of the total stellar mass in the magnetic case. When $X_{{\rm c}}=0.30$, the actual mass is 14.875 $M_\odot$. Mass loss increases near the end of the MS phase and the mass is 14.389 $M_\odot$ when $X_{{\rm c}}=0.000$. As is well known, rotational effects slightly increase the core mass fraction near the end of the MS phase and produces longer MS lifetimes. The account of the magnetic field further enlarges the core mass fraction as well as the MS lifetimes as illustrated in Fig. 8.

The effects on the tracks in the HR diagram are shown in Fig. 9. In addition to the structural changes, rotation also produces a distortion of the stellar surface and an increase of the average radius (estimated at $P_2 (\cos \vartheta)=0$, where $\vartheta$ is the colatitude). This makes a redwards shift of the tracks of rotating models in the HR diagram, especially visible near the ZAMS, since no other effects intervene there. For the model with rotation only, we see the upwards shift due to the slightly larger core and a slightly bluer track resulting from a tiny surface He-enrichment. The model with rotation and magnetic field reaches a higher luminosity at the end of the MS due to the larger core. It is also bluer due to the larger surface enrichment in helium, which lowers the opacity and decreases the stellar radius. It is doubtful that the above effects are sufficient to infer the presence or absence of magnetic fields.

   
5.2 Evolution of the abundances of helium and CNO elements at the stellar surface

The evolution of the surface abundances in helium and CNO elements results from the internal profiles shown in Figs. 6 and 7. Figure 10 shows for the 3 models considered the evolution of the helium abundance $Y_{{\rm s}}$ in mass fraction at the surface, the N/H, N/O and N/C ratios of numbers of atoms. We see the same trends in the four panels. There is no enrichment in absence of rotation. With rotation only, there are moderate enrichments, by a factor of 2 for N/H, 2.5 for N/C and 1.8 in N/O. With both rotation and magnetic field, the surface enrichments are much larger, particularly for the helium abundance which reaches $Y_{{\rm s}} = 0.31$ at the end of the MS phase. The increases in N/H reach a factor of 5, 11 for N/C and 6 for N/O.

Observationally, there are many estimates of N enrichments for OB stars. A recent review of the subject has been made by Herrero & Dufton (2004), who show clear evidence of rotationally-induced mixing in OB stars, also with the result that some fast rotating stars do not show N-enrichments. Four O9 stars were studied by Villamariz et al. (2002); three low rotators have an excess of $[{\rm N/O}] ~ < ~ 0.2$ dex, one fast rotating O9III star with $v \sin i =430$ km s^-1 has an excess of $[{\rm N/O}] ~ = ~ 0.7$ dex. The two most massive stars with fast rotation in the association Cep 2 have an excess of $[{\rm N/O}] ~ < ~ 0.3$ dex (Daflon et al. 2001). Two stars in Sher 25 have excesses in $[{\rm N/O}]$ by a factor of 3 to 4 (Smartt et al. 2002). Observations of the N/H ratios by Venn and Przybilla (2003) for galactic A-F supergiants show an average excess of a factor of 3, with extreme values up to a factor of 8. The orders of magnitude of the predicted and observed enrichments are similar. However, the situation is still uncertain due to the relative lack of accurate observational data for MS stars.

6 Conclusions

The main result is that a magnetic field imposes nearly solid body rotation and this favours higher rotational velocities during MS evolution compared to cases where the magnetic field is not accounted for. Due to the nearly constant $\Omega$ in the stellar interior, the transport of chemical elements by shear mixing is negligible. The transport of elements by Tayler-instability is also very limited. An interesting feature of the model is that meridional circulation is strongly enhanced by the flat $\Omega$-curve and this is the main effect influencing the transport of the chemical elements in the present models.

There remain however some doubts as to whether the Tayler-Spruit dynamo is really active in stellar interiors. Up to now, magnetohydrodynamic models expressing the growth and evolution of the magnetic field in rotating stars have not yet confirmed the existence and efficiency of this particular instability in stellar interiors (Mathis 2005). Even in the observationally and theoretically much better studied case of the Sun, the exact location, origin and evolution of the solar dynamo are still not fully understood.

The larger size of the predicted surface enrichments is well (or even better) supported by observations. However, this remains uncertain in view of the small number of accurate observations. In this respect, it might be crucial to also have such comparisons for stars in the Magellanic Clouds where the observed enrichments are much larger than in the Galaxy. The answer may come from asteroseismology. There are no p-modes expected, however g-modes may be present and yield some information on the internal $\Omega$-distribution. At present, this seems to be the most compelling possible test.

Appendix A: Equations for the case of low rotation

The dynamo properties were established (Spruit 2002 and Sect. 2) for the case of fast rotation, with the condition that the rotation rate $\Omega$ is larger than the Alfvén frequency $\omega_{{\rm A}}$, i.e. $\Omega \gg \omega_{{\rm A}}$. In the fast rotating case, the growth rate of the magnetic field is reduced by a factor $\omega_{{\rm A}}/\Omega$ as firstly suggested by Pitts & Tayler (1986). The above equations of the dynamo have been derived under this condition. However, if we want to study very slowly rotating stars, we need also to consider the case where

$$\Omega \ll \omega_{{\rm A}}.$$ (A.1)

This may be interesting also in central regions of radiative stars. There, as a result of the small value of r, the Alfvén frequency $\omega_{{\rm A}}$ becomes large so that the regime corresponding to Eq. (A.1) may apply instead of the usual one (cf. Sect. 2).

The energy of the Tayler instability (Tayler 1973) must be large enough to overcome the restoring force of buoyancy and this implies that the Alfvén frequency must be larger than some limit depending on N. The vertical extent $l_{{\rm r}}$ of the magnetic instability is also given by Eq. (5) above. In order that the perturbation is not too quickly damped by the diffusion of the magnetic field, one must have $l_{{\rm r}}^2 > \frac{\eta}{\sigma_{{\rm B}}}$. At low rotation, in the absence of significant Coriolis force, the frequency $\sigma_{{\rm B}}=\omega_{{\rm A}}$. The combination of these two limits in the low rotation case leads to the condition $\omega_{{\rm A}}^3 > N^2\; \frac{\eta}{r^2}$ and for the marginal situation corresponding to equality, we have

$$\left(\frac{\omega_{{\rm A}}}{\Omega}\right)^3 = \frac{N^2}{\Omega^2} \; \frac{\eta}{r^2 \; \Omega} \cdot$$ (A.2)

This equation relates the magnetic diffusivity $\eta$ and the Alfvén frequency $\omega_{{\rm A}}$ instead of Eq. (7).

The field amplitude may be fixed by the equality of the amplification time $\tau_{{\rm a}}$ of the Tayler instability and of the timescale  $\sigma_{{\rm B}}^{-1}$ of the field (Spruit 2002). One has

$$\tau_{{\rm a}}= N /(\omega_{{\rm A}} \Omega q).$$ (A.3)

Instead of the expression in (8), we get for the low rotation case with $\sigma_{{\rm B}}=\omega_{{\rm A}}$

$$\frac{N}{\Omega} \; = \; q .$$ (A.4)

$\omega_{{\rm A}}$ has disappeared from the equation. How should we interpret this? This can be done with the help of Eq. (2), which gives

$$\frac{ N^2_{{\rm T}}}{\Omega^2} \; \frac{\eta / K} {\eta / K \;+ \; 2} + \frac{N^2_{\mu}}{\Omega^2} =q^2.$$ (A.5)

The two Eqs. (A.2) and (A.5) form our basic system of equations with the two unknown quantities $\eta$ and $\omega_{{\rm A}}$. In order to have a diffusivity $\eta$ positively defined, Eq. (A.5) imposes that the differential rotation parameter q must be larger than some minimum value $q_{{\rm min}}$,

$$q^2_{{\rm min}}\; = \frac{N^2_{\mu}}{\Omega^2} \cdot$$ (A.6)

If this is the case, then according to Eq. (A.2) the same is true for $\omega_{{\rm A}}$ and thus a magnetic field is effectively created by the slow dynamo process.

Let us now estimate the transport coefficients. Equation (A.5) immediately leads to the following expression for the magnetic diffusivity $\eta$,

$$\eta = \frac{ 2 \; K \left( q^2 \; \Omega^2 - N^2_{\mu}\right)} {N^2_{{\rm T}}+N^2_{\mu} - q^2 \; \Omega^2} \cdot$$ (A.7)

In all cases, the ratio $\eta/K$ is very small, typically of the order of 10^-5 (cf. Fig. 5). Thus, we obtain the corresponding expression for the diffusivity,

$$\eta = \frac{2 \; K}{N^2_{{\rm T}}} \; \left( q^2 \; \Omega^2 - N^2_{\mu}\right) .$$ (A.8)

This equation provides the magnetic diffusivity $\eta$, if |q| is larger than $\vert q_{{\rm min}}\vert$. The coefficient $\eta$ determines the transport of the chemical elements by the magnetic instability.

Now, with Eq. (A.2), we obtain the Alfvén frequency $\omega_{{\rm A}}$at each location r in the star,

$$\left(\frac{\omega_{{\rm A}}}{\Omega}\right)^3= \frac{2 \; K}... ...t(q^2 \; \Omega^2 - N^2_{\mu}\right)} {r^2 \; \Omega} \; q^2 .$$ (A.9)

This confirms that for a star rotating with angular velocity $\Omega$ and having a certain $\mu$-gradient, a magnetic field is created only if the actual value of the differential rotation parameter |q| is larger than $\vert q_{{\rm min}}\vert$.

The azimuthal stress S due to the magnetic field generated by Tayler instability becomes

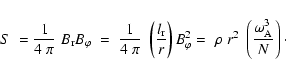$$S \; = \frac{1}{4 \; \pi} \; B_{{\rm r}} B_{\varphi} \; = \; ... ...rho \; r^2 \; \left(\frac{\omega_{{\rm A}}^3}{N}\right) \cdot$$ (A.10)

The viscosity $\nu$ is expressed in terms of S and we get

$$\nu = \frac{S}{\rho \; q \; \Omega}~ = ~\frac{\Omega \; r^2}{... ... A}}}{\Omega}\right)^3 \; \left(\frac{\Omega}{N}\right) \cdot$$ (A.11)

With Eq. (A.9) for the Alfvén frequency, we get finally

$$\nu = \frac{\Omega \; r^2}{q^2} \; \left( \frac{\omega_{{\rm... ...^2_{{\rm T}}} \; {\left(q^2 \; \Omega^2 - N^2_{\mu}\right)} ,$$ (A.12)

which determines the transport of angular momentum. The expression of $\nu$ is the same as the expression of $\eta$ (Eq. (A.8)). This means that in the case of low rotation, the Tayler magnetic instability transports in a similar way the chemical elements and the angular momentum, while at high rotation the magnetic coupling is stronger by a factor $\left(\frac{\Omega}{\omega_{{\rm A}}}\right)^2$than the transport of the elements, according to the general expressions by Maeder & Meynet (2004). This factor comes from the expression of $\sigma_{{\rm B}}$, and as in the present case the ratio $\left(\frac{\Omega}{\omega_{{\rm A}}}\right)$is absent in  $\sigma_{{\rm B}}$, we get equality of $\nu$ and $\eta$.

Condition (A.4) must also be satisfied in order to have angular momentum transport. The Eqs. (A.7) or (A.8) and (A.12) provide the transport coeffcients at each stellar layer as a function of the local quantities, such as $\Omega$, q, $N^2_{{\rm T}}$, $N^2_{\mu}$, etc. available in the stellar models. The Alfvén frequency and the magnetic field intensity are obtained by Eqs. (A.9) and (1).

The rate of magnetic energy production $W_{{\rm B}}$ per unit of time and volume must be equal to the rate $W_{\nu}$ of the dissipation of rotational energy by the magnetic viscosity $\nu$ as given above. This check of consistency was verified for the case of high rotation. One assumes here for simplification that all the energy dissipated is converted to magnetic energy. One has

$$W_\nu={1\over 2}\rho\nu \Omega^2q^2 ,$$ (A.13)

which with Eq. (A.12) gives the dissipation rate,

$$W_\nu= \rho \; \Omega^2 ~ q^2 \; \frac{ K}{N^2_{{\rm T}}} \; {\left(q^2 \; \Omega^2 - N^2_{\mu}\right)} .$$ (A.14)

The magnetic energy per unit volume is $\frac{B^2}{8 \pi}$, it is produced in a characteristic time given by $\sigma_{{\rm B}}^{-1} = \omega_{{\rm A}}^{-1}$. Thus, one has

$$W_{{\rm B}}= \frac{B^2}{8 \pi} \omega_{{\rm A}}= \frac{1}{2} ... ...^2_{{\rm T}}} \; {\left(q^2 \; \Omega^2 - N^2_{\mu}\right)} ,$$ (A.15)

where we have used the Eq. (A.9) for the Alfvén frequency. Thus, the expressions for $W_{\nu}$ and $W_{{\rm B}}$ are the same. We see that no magnetic energy is produced if condition (A.6) is not realized. This shows the consistency of the field expression for $B_{\varphi}$ and of the transport coefficient $\nu$.

References

• Daflon, S., Cunha, K., Butler, K., & Smith, V. V. 2001, ApJ, 563, 325 [NASA ADS] [CrossRef] (In the text)
• Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] (In the text)
• Herrero, A., & Lennon, D. J. 2004, in Stellar Rotation, ed. A. Maeder, & P. Eenens (ASP), IAU Symp., 215, 209 (In the text)
• Langer, N., Heger, A., Wellstein, S., & Herwig, F. 1999, A&A, 346, L37 [NASA ADS] (In the text)
• Maeder, A. 1995, A&A, 199, 84 [NASA ADS]
• Maeder, A. 2003, A&A, 399, 263 [EDP Sciences] [NASA ADS] [CrossRef]
• Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Maeder, A., & Meynet, G. 2003, A&A, 411, 543 [EDP Sciences] [NASA ADS] [CrossRef] (Paper I) (In the text)
• Maeder, A., & Meynet, G. 2004, A&A, 422, 225 [EDP Sciences] [CrossRef] (Paper II) (In the text)
• Mathis, S. 2005, Thesis, Paris Observatory (In the text)
• Maeder, A. 2002, A&A, 392, 575 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Meynet, G., & Maeder, A. 1997, A&A, 321, 465 [NASA ADS]
• Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] (In the text)
• Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [EDP Sciences] [NASA ADS] [CrossRef]
• Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Pitts, E., & Tayler, R. J. 1986, MNRAS, 216, 139 [NASA ADS] (In the text)
• Roxburgh, I. W. 2005, in Stellar Rotation, ed. A. Maeder, & P. Eenens (ASP Publ), IAU Symp., 215, 545 (In the text)
• Smartt, S. J., Lennon, D. J., Kudritzki, R. P., et al. 2002, A&A, 391, 979 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS]
• Spruit, H. C. 2002, A&A, 381, 923 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Talon, S., & Zahn, J. P. 1997, A&A, 317, 749 [NASA ADS]
• Tayler, R. J. 1973, MNRAS, 161, 365 [NASA ADS] (In the text)
• Venn, K., & Przybilla, N. 2003, in CNO in the Universe, ed. C. Charbonnel, D. Schaerer, & G. Meynet, ASP Conf. Ser., 304, 20 (In the text)
• Villamariz, M. R., Herrero, A., Becker, S. R., & Butler, K. 2002, A&A, 388, 940 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] (In the text)