A&A 440, 949-966 (2005)
DOI: 10.1051/0004-6361:20052889
P. Stäuber1 - S. D. Doty2 - E. F. van Dishoeck3 - A. O. Benz1
1 - Institute of Astronomy, ETH-Zentrum, 8092 Zurich, Switzerland
2 - Department of Physics and Astronomy, Denison University, Granville,
OH 43023, USA
3 - Sterrewacht Leiden, PO Box 9513, 2300 RA Leiden, The Netherlands
Received 16 February 2005 / Accepted 6 June 2005
Abstract
We present chemical models of the envelope of a young stellar
object (YSO) exposed to a central X-ray source. The models are applied to the
massive star-forming region AFGL 2591 for different X-ray fluxes. Model
results for this region show that the X-ray ionization rate with and without
the effects of Compton scattering differs by only a few percent and the influence
of Compton scattering on the chemistry is negligible. The total X-ray
ionization rate is dominated by the "secondary'' ionization rate of H2
resulting from fast electrons. The abundance profiles of several molecular and
atomic species are shown to depend on the X-ray luminosity and on the
distance from the source. The carbon, sulphur and nitrogen chemistries are
discussed. It is found that He+ and H3+ are enhanced and trigger a
peculiar chemistry. Several molecular X-ray tracers are found and compared to
tracers of the far ultraviolet (FUV) field. Like ultraviolet radiation fields,
X-rays enhance simple hydrides, ions and radicals. In contrast to ultraviolet
photons, X-rays can penetrate deep into the envelope and affect the chemistry
even at large distances from the source. Whereas the FUV enhanced species cover
a region of ![]() 200-300 AU, the region enhanced by X-rays is
200-300 AU, the region enhanced by X-rays is
![]() 1000 AU. We find that N2O, HNO, SO, SO+, HCO+, CO+,
OH+, N2H+, SH+ and HSO+ (among others) are more enhanced by
X-rays than by FUV photons even for X-ray luminosities as low as
1000 AU. We find that N2O, HNO, SO, SO+, HCO+, CO+,
OH+, N2H+, SH+ and HSO+ (among others) are more enhanced by
X-rays than by FUV photons even for X-ray luminosities as low as
![]() erg s-1. CO2 abundances are reduced in the
gas-phase through X-ray induced FUV photons. For temperatures
erg s-1. CO2 abundances are reduced in the
gas-phase through X-ray induced FUV photons. For temperatures
![]() K, H2O is destroyed by X-rays with luminosities
K, H2O is destroyed by X-rays with luminosities
![]() erg s-1. Best-fit models for AFGL 2591 predict an
X-ray luminosity
erg s-1. Best-fit models for AFGL 2591 predict an
X-ray luminosity
![]() erg s-1 with a hard
X-ray spectrum
erg s-1 with a hard
X-ray spectrum
![]() K. This is the first time
that the X-ray flux of a highly obscured source has been estimated by its
envelope chemistry. Furthermore, we find
K. This is the first time
that the X-ray flux of a highly obscured source has been estimated by its
envelope chemistry. Furthermore, we find
![]() .
The chemistry of the bulk of the envelope mass is dominated
by cosmic-ray induced reactions rather than by X-ray induced ionization for
X-ray luminosities
.
The chemistry of the bulk of the envelope mass is dominated
by cosmic-ray induced reactions rather than by X-ray induced ionization for
X-ray luminosities
![]() erg s-1. The
calculated line intensities of HCO+ and HCS+ show that high-J lines are
more affected than lower J lines by the presence of X-rays due to their
higher critical densities, and that such differences are detectable even with
large aperture single-dish telescopes. Future instruments such as Herschel-HIFI
or SOFIA will be able to observe X-ray enhanced hydrides whereas the
sensitivity and spatial resolution of ALMA is well-suited to measure the size
and geometry of the region affected by X-rays.
erg s-1. The
calculated line intensities of HCO+ and HCS+ show that high-J lines are
more affected than lower J lines by the presence of X-rays due to their
higher critical densities, and that such differences are detectable even with
large aperture single-dish telescopes. Future instruments such as Herschel-HIFI
or SOFIA will be able to observe X-ray enhanced hydrides whereas the
sensitivity and spatial resolution of ALMA is well-suited to measure the size
and geometry of the region affected by X-rays.
Key words: stars: formation - stars: individual: AFGL 2591 - ISM: molecules - X-rays: ISM
Observational studies of star-forming regions show that some young stellar
objects (YSOs) are very strong X-ray emitters. Typical X-ray luminosities range
from approximately
![]() erg s-1 to
erg s-1 to
![]() erg s-1 in the 0.5-10 keV band (e.g., Hofner & Churchwell
1997; Carkner et al. 1998; Feigelson & Montmerle 1999).
The heating of the X-ray emitting plasma is not well understood. In low-mass
YSOs the emission may originate from powerful magnetic activity near the
stellar surface or in the star-disk environment, whereas in high-mass YSOs wind
instabilities and shocks may cause the high X-ray flux. In the earliest stage
of evolution, the protostar is still deeply embedded in its natal molecular
cloud (
erg s-1 in the 0.5-10 keV band (e.g., Hofner & Churchwell
1997; Carkner et al. 1998; Feigelson & Montmerle 1999).
The heating of the X-ray emitting plasma is not well understood. In low-mass
YSOs the emission may originate from powerful magnetic activity near the
stellar surface or in the star-disk environment, whereas in high-mass YSOs wind
instabilities and shocks may cause the high X-ray flux. In the earliest stage
of evolution, the protostar is still deeply embedded in its natal molecular
cloud (
![]() mag). As a consequence, X-rays are not directly
observable toward very young objects, and the onset of the high energy
radiation remains a secret to this day. Indeed, X-ray observations
toward massive star-forming regions are still rare, which may be due to
absorption by the large hydrogen column densities toward these objects
(Grosso et al. 2005).
mag). As a consequence, X-rays are not directly
observable toward very young objects, and the onset of the high energy
radiation remains a secret to this day. Indeed, X-ray observations
toward massive star-forming regions are still rare, which may be due to
absorption by the large hydrogen column densities toward these objects
(Grosso et al. 2005).
Molecular gas exposed to X-rays forms an X-ray dissociation region (XDR) with a peculiar chemistry and physical structure. There has been a growing interest in XDRs in the past twenty years and several models have been developed in order to study these regions. Krolik & Kallman (1983) investigated the influence of X-ray ionization on the Orion molecular cloud assuming a fixed density and temperature. Lepp & McCray (1983) presented constant gas pressure models to calculate the temperature and infrared line emission from an interstellar gas cloud containing a compact X-ray source. Maloney et al. (1996) studied the influence of X-rays on the physical and chemical state of neutral gas over a wide range of densities and X-ray fluxes. In addition, they discussed diagnostic line ratios to distinguish XDRs from shocks and photodissociation regions (PDRs). However, their chemical network focused primarily on carbon and oxygen, whereas nitrogen-bearing species, for example, were neglected. Calculations of molecular abundances for varying X-ray ionization rates in interstellar clouds were presented by Lepp & Dalgarno (1996). They mainly concentrated on HCO+ and nitrogen-containing compounds. A thorough and more general treatment of the physics and chemistry in molecular clouds exposed to X-rays was done by Yan (1997). Tiné et al. (1997) calculated the infrared response of H2 in dense clouds. Other models concentrate on the X-ray ionization of protoplanetary disks (e.g., Glassgold et al. 1997; Aikawa & Herbst 1999; Markwick et al. 2002) or planetary nebulae (e.g., Natta & Hollenbach 1998). Most recently, Meijerink & Spaans (2005) presented a code for photodissociation and X-ray dissociation regions and discussed thermal and chemical differences between the two regions. They calculated four depth-dependent models for different densities and radiation fields that are typical in starburst galaxies and active galactic nuclei.
In this paper we study the influence of a central X-ray source on the chemistry
in the envelopes around massive YSOs, using updated atomic and molecular data.
The goal of this investigation is to find X-ray tracers that are observable with
current or future telescopes in the (sub)millimeter or near-infrared range. The
challenge is to distinguish between far ultraviolet (FUV) tracers (Stäuber et al.
2004) and X-ray tracers, since both kinds of high-energy radiation tend
to form ions and radicals. Further aims of this study are to estimate not only
the X-ray flux emitted by highly obscured objects but also the ionization rate
and ionization fraction in the envelopes around YSOs by carefully studying the
chemistry. The ionization fraction of a cloud is an important parameter in the
formation of a star as magnetic fields control the dynamics of ions. Ambipolar
diffusion may support the molecular cloud and regulate the process of mass
accretion. It may also influence disk viscosity and jet acceleration. Due to
the small atomic and molecular cross sections at high energy (the total cross
section summed over all species for a 1 keV photon is ![]()
![]() cm2 and decreases with energy as
cm2 and decreases with energy as ![]()
![]() ), X-rays can
penetrate deeper into the envelope than, for example, FUV photons and affect
the gas-phase chemistry even at large distances from the source. In addition,
the X-ray ionization rate may exceed the cosmic-ray ionization rate for a large
part of the envelope. X-rays are therefore a plausible candidate for the
ionization source in the inner, dense part of a YSO envelope.
), X-rays can
penetrate deeper into the envelope than, for example, FUV photons and affect
the gas-phase chemistry even at large distances from the source. In addition,
the X-ray ionization rate may exceed the cosmic-ray ionization rate for a large
part of the envelope. X-rays are therefore a plausible candidate for the
ionization source in the inner, dense part of a YSO envelope.
We have extended the time- and position-dependent chemical model of Doty et al. (2002) to allow the impact of X-rays on the envelope. The physical and chemical models are described in Sects. 2 and 3. Our results are presented and discussed in Sect. 4. A selection of possible X-ray tracers is discussed in Sect. 5. In Sect. 6 best-fit models for AFGL 2591 are evaluated. To compare the modeled abundance profiles to observations and to show that the influence of X-rays on the chemistry is observable with (large) existing single-dish telescopes, we have calculated emission lines for a selection of species using the Monte Carlo radiative transfer code of Hogerheijde & van der Tak (2000). These results are shown in Sect. 7. Although our calculations are focused on high-mass YSOs, the qualitative results should be equally applicable to the envelopes around low-mass YSOs. Doty et al. (2004) showed that the chemical models of the low-mass source IRAS 16293-2422 required only minor modifications to their high-mass model. We summarize and conclude this paper in Sect. 8.
The model is based on the detailed thermal and gas-phase chemistry models of Doty et al. (2002) and has been extended to allow the impact of X-rays on the envelope chemistry of young stellar sources.
The observed X-ray spectra from high-mass YSOs are usually fitted with the
emission spectrum of a thermal plasma (e.g., Hofner & Churchwell 1997;
Hofner et al. 2002). The thermal X-ray spectrum can be approximated with
The local (i.e., attenuated) X-ray flux per unit energy is finally given by
![]() ,
where
,
where ![]() is the total X-ray
attenuation and
is the total X-ray
attenuation and
![]() is the incident X-ray flux given by Eq. (1). At lower energies (
is the incident X-ray flux given by Eq. (1). At lower energies (
![]() keV), X-rays lose their
energy mainly through photoabsorption. Assuming that the photoabsorption cross
section of a molecule or atom is equal to its photoionization cross section,
the attenuation is given by
keV), X-rays lose their
energy mainly through photoabsorption. Assuming that the photoabsorption cross
section of a molecule or atom is equal to its photoionization cross section,
the attenuation is given by
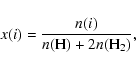 |
(4) |
For higher energies, X-rays also lose energy through inelastic Compton
scattering, and Compton ionization becomes the dominant ionization source. The
highly energetic X-ray photons interact mainly with free and bound electrons in
the gas. Since molecular hydrogen is the most abundant species in our models,
the total Compton cross section is dominated by hydrogen, rather than by heavy
elements. We have fitted the values provided by the XCOM-NIST database (Berger
et al. 1999) for hydrogen and assume that the Compton cross section of
molecular hydrogen is twice that of atomic hydrogen. The energy loss of a
Compton scattered photon is negligible compared to its initial energy, and
attenuation through Compton scattering becomes important only for hydrogen
column densities
![]() cm-2. However, since each
scattering process leads to an ionization, the total (effective) cross section
for ionizing H2,
cm-2. However, since each
scattering process leads to an ionization, the total (effective) cross section
for ionizing H2,
![]() (see Sect. 3.2), is the sum
of the total photoabsorption cross section
(see Sect. 3.2), is the sum
of the total photoabsorption cross section
![]() and the cross
section for Compton scattering
and the cross
section for Compton scattering
![]() .
The attenuation of the
X-rays is mainly through photoabsorption. Figure 1 shows the
photoabsorption cross sections for the element abundances given in
Table A.1, the Compton cross section of molecular hydrogen, and the
total (effective) ionization cross section
.
The attenuation of the
X-rays is mainly through photoabsorption. Figure 1 shows the
photoabsorption cross sections for the element abundances given in
Table A.1, the Compton cross section of molecular hydrogen, and the
total (effective) ionization cross section
![]() .
.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2889f01.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg51.gif) |
Figure 1: The photoionization cross sections for the elemental abundances given in Table A.1. The cross section for Compton scattering is calculated for hydrogen. |
| Open with DEXTER | |
Model results for AFGL 2591 show that the X-ray ionization rate with and without the effects of Compton scattering differs by at most 20% and that the influence of Compton scattering on the chemistry is negligible. Nevertheless, we include attenuation and ionization due to Compton scattering, using a simplified radiative transfer method to calculate the incident radiation field.
Although Eq. (1) approximates a thermal energy distribution, the X-ray spectrum of a thermal plasma has a more complex structure. In addition to the bremsstrahlung emission, line emission can become important. In order to evaluate the accuracy of the assumed X-ray spectrum, we have fitted the results of Raymond & Smith (1977) for an X-ray spectrum of a hot plasma. The results are very similar, leading to the same best-fit models (Sect. 6.1). The results in the following sections are therefore presented using the X-ray spectrum given by Eq. (1).
We have applied our model to the massive star-forming region AFGL 2591.
AFGL 2591 is taken as a prototypical example of a deeply embedded high-mass
YSO (a so-called high-mass protostellar object, HMPO) for which extensive
observational data exist and for which reference models without X-rays are
available (Doty et al. 2002; Stäuber et al. 2004). No X-ray
emission, however, has been observed to date toward this source. Assuming a
distance of 1 kpc, the bolometric luminosity is ![]()
![]() with a total mass of
with a total mass of ![]() 10
10
![]() (van der Tak et al.
1999).
(van der Tak et al.
1999).
We adopt the temperature and power-law density distribution proposed by van der
Tak et al. (1999) and Doty et al. (2002). The density
structure of the envelope has been constrained from continuum observations of
the dust and CS emission lines over a large range of critical densities. The
dust temperature profile was determined from the self-consistent solution of the
continuum radiative transfer problem. The gas temperature was calculated
explicitly by Doty et al. (2002) who found that
![]() .
The influence of the X-rays on the gas temperature can
be estimated by comparing the cooling rate due to gas-dust collisions
(Hollenbach & McKee 1989) and the X-ray heating rate provided by
Maloney et al. (1996)
.
The influence of the X-rays on the gas temperature can
be estimated by comparing the cooling rate due to gas-dust collisions
(Hollenbach & McKee 1989) and the X-ray heating rate provided by
Maloney et al. (1996)
![]() erg cm-3 s-1, where
erg cm-3 s-1, where
![]() is the energy
deposition rate per particle, defined by
is the energy
deposition rate per particle, defined by
![]() .
Our first point of interest is at
.
Our first point of interest is at
![]() AU from the central source where the density is already fairly high
(
AU from the central source where the density is already fairly high
(
![]() cm-3) but
cm-3) but
![]() is low due to absorption and
geometric dilution (
is low due to absorption and
geometric dilution (
![]() erg s-1,
for X-ray luminosities
erg s-1,
for X-ray luminosities
![]() erg s-1).
The cooling rate at this point is
erg s-1).
The cooling rate at this point is
![]() (
(
![]() ) erg cm-3 s-1. Thus,
in our modeled regions of AFGL 2591, a meaningful increase in the gas
temperature (
) erg cm-3 s-1. Thus,
in our modeled regions of AFGL 2591, a meaningful increase in the gas
temperature (
![]() K) can only be
expected for very high X-ray luminosities
K) can only be
expected for very high X-ray luminosities
![]() erg s-1. For our best-fit models (Sect. 6.1), a
difference of only 3 K at most is estimated between the gas and dust
temperature. We therefore neglect additional heating of the gas through X-rays
and assume
erg s-1. For our best-fit models (Sect. 6.1), a
difference of only 3 K at most is estimated between the gas and dust
temperature. We therefore neglect additional heating of the gas through X-rays
and assume
![]() throughout the envelope. This
is a reasonably good approximation as was shown by Doty & Neufeld
(1997) and Doty et al. (2002). Figure 2 shows the
adopted model for AFGL 2591. The model covers a region from
throughout the envelope. This
is a reasonably good approximation as was shown by Doty & Neufeld
(1997) and Doty et al. (2002). Figure 2 shows the
adopted model for AFGL 2591. The model covers a region from
![]() AU to
AU to
![]() AU.
AU.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2889f02.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg69.gif) |
Figure 2: Physical and thermal structure of AFGL 2591. The power-law density distribution is adopted from the model of van der Tak et al. (1999). The gas temperature profile was calculated by Doty et al. (2002). |
| Open with DEXTER | |
The chemical model is based upon the UMIST gas-phase chemical reaction network
(Millar et al. 1997) and calculates the time-dependent number density
n(i) of each species at a certain distance from the source by solving the
equations for molecular evolution given by
The assumed initial abundances given in Table A.1 are taken to be consistent with the models of Doty et al. (2002) and Stäuber et al. (2004). The initial gas-phase abundances allow us to reproduce many of the results of the hot core models of Charnley (1997). The effects of freeze-out onto dust grains are included by initially depleting certain species below 100 K. The temperature dependence of molecular depletion is discussed in detail by Boonman et al. (2003a) and Doty et al. (2004). The initial form of sulphur is not known. In our models we assume that sulphur is frozen out onto grains in the form of H2S and is evaporated into the gas-phase for T > 100 K. Solid H2S has not been detected, however (e.g., Boogert et al. 2000). On the other hand, Wakelam et al. (2004) have shown that it is likely that sulphur is in the icy mantles either as atomic S or in a form, perhaps polymerized S or S2, that is soon converted into S. The dependence of our model results on the initial form of sulphur is discussed in Sect. 4.3.
For the total elemental abundances given in Table A.1 we follow Yan (1997). These abundances are the sum of the gas-phase elemental abundances and the abundances on the dust grains that do not enter the chemistry. In addition to the total hydrogen abundance, the total elemental abundances are important for the attenuation of the X-rays (see Sect. 2.1).
X-rays ionize heavy elements preferentially by removing the K-shell electron. The vacancy is then filled by a cascade of radiative (fluorescent) and non-radiative Auger transitions. During this process other electrons and X-ray photons are emitted by the ion, leading finally to a multiply ionized species. The fluorescence probability is less than 10% for most species and approximately 30% for Fe (Dwek & Smith 1996). The contribution of the diffuse X-ray emission by fluorescence to the total X-ray flux can therefore be neglected.
We consider the ionization of atoms and atomic ions leading to a singly and
doubly ionized state by calculating explicitly the cross sections according to
Verner et al. (1996). The probability distribution for the number of
ejected electrons for inner shell ionizations are taken from Kaastra & Mewe
(1993). The (primary) X-ray ionization rate of species i at a point
r is then simply given by
![\begin{displaymath}\zeta_i = \int F(E,r) \sigma_i(E) {\rm d}E \qquad \bigl[\rm {s^{-1}}\bigr],
\end{displaymath}](/articles/aa/full/2005/36/aa2889-05/img72.gif) |
(6) |
Little is known about the impact of X-rays on molecules. Although there are a
few cross sections for photoabsorption in the literature, the destruction
channels and branching ratios of the dissociated and ionized species are widely
unknown. Following Maloney et al. (1996) we therefore consider only
diatomic molecules for direct X-ray impact and assume that the molecule
dissociates into singly charged ions after inner shell ionization. The cross
sections for this process are calculated by adding the atomic cross sections.
In general, primary X-ray ionization plays only a minor role in the chemistry
since the reactions are ![]() 1000 times slower compared to the relevant
chemical reactions and more than 10 times slower than electron impact
ionizations for the case of our AFGL 2591 model parameters.
1000 times slower compared to the relevant
chemical reactions and more than 10 times slower than electron impact
ionizations for the case of our AFGL 2591 model parameters.
The fast photoelectrons and Auger electrons carry the bulk of the initial X-ray photon energy and are therefore very efficient in ionizing other species. The "secondary'' ionization rate dominates the total ionization rate in XDRs (e.g., Maloney et al. 1996). The electrons can also excite hydrogen and helium. The electronically excited states of H, He and H2 decay back to the ground states by emitting UV photons. The internally generated ultraviolet photons can photoionize and photodissociate other species in the gas - similar to the case of cosmic-ray induced chemistry (e.g., Gredel et al. 1989). Nearly all these secondary processes induced by electron impact are more important for the chemical network than the primary interaction of the X-rays with the gas.
Energy deposition of fast electrons in a gas is characterized by a mean energy
per ion pair W(E) - the initial energy E of the electron divided by the
number of produced ionizations, N(E), in the gas (e.g., Voit 1991;
Dalgarno et al. 1999). To calculate W(E) and therefore the number of
secondary electrons, we follow Dalgarno et al. (1999) for a H, He and
H2 gas mixture. An electron with an initial energy of 1 keV will then
lead to ![]() 27 ionizations. The "secondary'' ionization rate per hydrogen
molecule at depth r can be calculated by
27 ionizations. The "secondary'' ionization rate per hydrogen
molecule at depth r can be calculated by
The electron impact ionization rates ![]() of other molecules or atoms can
be calculated as a first approximation by multiplying the H2 ionization rate
Eq. (7) with the ratio of the electron impact cross sections of species
i to H2 at a specific energy (Maloney et al. 1996). The average
electron energy is taken to be 100 eV. The cross sections for the species
were taken from Yan (1997), the NIST database (Kim et al. 2004)
or estimated. The ratios for most molecules are between
of other molecules or atoms can
be calculated as a first approximation by multiplying the H2 ionization rate
Eq. (7) with the ratio of the electron impact cross sections of species
i to H2 at a specific energy (Maloney et al. 1996). The average
electron energy is taken to be 100 eV. The cross sections for the species
were taken from Yan (1997), the NIST database (Kim et al. 2004)
or estimated. The ratios for most molecules are between ![]() 2-8. The
error due to the energy dependence of the cross sections or to our estimations
are therefore within a factor of a few but certainly
2-8. The
error due to the energy dependence of the cross sections or to our estimations
are therefore within a factor of a few but certainly ![]()
![]() .
.
The excited states in the Lyman-Werner bands of H2 determine the internally
generated FUV flux. The number of Ly![]() photons from H atoms are less
important due to the relatively small fractional abundance of atomic hydrogen
(
photons from H atoms are less
important due to the relatively small fractional abundance of atomic hydrogen
(
![]() ). Following Gredel et al. (1989) the
photodissociation and photoionization rate of species i is given by
). Following Gredel et al. (1989) the
photodissociation and photoionization rate of species i is given by
The He excited 21P state emits a 19.8 eV photon which ionizes mainly
H2, CO or H. The photoionization rate per He atom for these species is
(Yan 1997)
![\begin{displaymath}R_{i, {\rm He}} = \zeta_{{\rm He}} \frac{x({\rm He}) \sigma_i...
...+ x({\rm H}) \sigma({\rm H})} \qquad \bigl[\rm {s^{-1}}\bigr],
\end{displaymath}](/articles/aa/full/2005/36/aa2889-05/img95.gif) |
(10) |
The electron recombination and charge transfer reactions of the doubly-ionized species are presented in Table B.1 and Table B.2. We consider only C, O, N, S, Fe, Ne and Si in the doubly-ionized state. Other ions in this state are neglected due to their low fractional abundances.
For the recombination of ions on grains we have adopted the treatment of
Maloney et al. (1996) for all ions in the model. The grain surface
recombination of HCO+ is a critical reaction in dense regions
(Aikawa et al. 1999) and important for the abundances of CO-bearing
molecules. We follow the calculations of Aikawa et al. (1999) and
assume branching ratios of 0.7 for the dissociative recombination and 0.3
for the radiative recombination reaction. However, our models for AFGL 2591
are not very sensitive to these values as long as the ratio
dissociative/radiative recombination is >1. For example, no noticeable
differences were seen between models with ratios of 0.7/0.3 and 0.85/0.15,
respectively. In addition, results of models without any grain recombination
reactions of HCO+ have shown no difference for species with fractional
abundances
![]() and differences within only
and differences within only ![]() 30%
for less abundant species. The recombination of HCO+ in all our models
is therefore dominated by electron recombination. Aikawa et al.
(1999) further suggested that the dissociative recombination reaction
might be more likely for most molecules. We have therefore assumed a branching
ratio of 0.7/0.3 for all other molecules as well.
30%
for less abundant species. The recombination of HCO+ in all our models
is therefore dominated by electron recombination. Aikawa et al.
(1999) further suggested that the dissociative recombination reaction
might be more likely for most molecules. We have therefore assumed a branching
ratio of 0.7/0.3 for all other molecules as well.
Aside from the grain surface recombination reactions we have ignored
grain-surface chemistry, with the exception of the formation of H2. In our
model, the rate is
![]() cm-3 s-1, where
cm-3 s-1, where
![]() is the atomic hydrogen
density, and
is the atomic hydrogen
density, and
![]() is the density of hydrogen nuclei. Other reactions
that affect the H2 network are the formation of the H- ion by radiative
association H + e-
is the density of hydrogen nuclei. Other reactions
that affect the H2 network are the formation of the H- ion by radiative
association H + e-
![]() H- + h
H- + h![]() and the reaction H+
+ H
and the reaction H+
+ H
![]() H2+ + h
H2+ + h![]() .
For these rates we have adopted the fits
by Latter (1989). Since we are almost always in a pure molecular
environment, these reactions play only a minor role in our models though.
.
For these rates we have adopted the fits
by Latter (1989). Since we are almost always in a pure molecular
environment, these reactions play only a minor role in our models though.
The chemistry in the envelope around AFGL 2591 under the influence of X-rays
has been modeled assuming spherical symmetry. The parameters that were varied
are the X-ray luminosity, the plasma temperature and the inner hydrogen column
density. The inner hydrogen column density
![]() is the X-ray
absorbing column density between the central source and the first calculated
point at
is the X-ray
absorbing column density between the central source and the first calculated
point at
![]() AU (see also Eq. (3)). Since only the total
hydrogen column density is known,
AU (see also Eq. (3)). Since only the total
hydrogen column density is known,
![]() is treated as an unknown
parameter.
is treated as an unknown
parameter.
The equilibrium timescale for X-ray induced chemistry is
![]() yr. Thus, equilibrium
may not be reached for most parts of the envelope. The results in this section
are presented for
yr. Thus, equilibrium
may not be reached for most parts of the envelope. The results in this section
are presented for
![]() years according to our best-fit
models. This result is in good agreement with the chemical age of AFGL 2591
found by Doty et al. (2002). For simplicity, the luminosity was kept
constant with time. For all models an outer standard FUV field
years according to our best-fit
models. This result is in good agreement with the chemical age of AFGL 2591
found by Doty et al. (2002). For simplicity, the luminosity was kept
constant with time. For all models an outer standard FUV field
![]() has been assumed to be consistent with Doty et al. (2002) and
Stäuber et al. (2004). The effects of an enhanced outer FUV radiation
field will be discussed in Sect. 4.7.
has been assumed to be consistent with Doty et al. (2002) and
Stäuber et al. (2004). The effects of an enhanced outer FUV radiation
field will be discussed in Sect. 4.7.
Table 1 lists the models that are discussed in more detail in this
paper. In addition to the best-fit models (models 5,6,7), models with a plasma
temperature
![]() K and an inner column density of
K and an inner column density of
![]() cm-2 are presented. Model 0
corresponds to the standard model of Doty et al. (2002) without any
inner radiation field and model 1 assumes an inner FUV radiation field with
a field strength
cm-2 are presented. Model 0
corresponds to the standard model of Doty et al. (2002) without any
inner radiation field and model 1 assumes an inner FUV radiation field with
a field strength
![]() according to the models of Stäuber et al. (2004). The plasma temperature of models 2-4 has been chosen as
a mean value of the best-fit models (Sect. 6.1). The only parameter that
has been varied for the plots of the models 2-4 is the X-ray luminosity
according to the models of Stäuber et al. (2004). The plasma temperature of models 2-4 has been chosen as
a mean value of the best-fit models (Sect. 6.1). The only parameter that
has been varied for the plots of the models 2-4 is the X-ray luminosity
![]() .
This is useful since the energy deposition rate
.
This is useful since the energy deposition rate
![]() is
directly proportional to the X-ray luminosity and all the X-ray induced
reactions therefore scale with
is
directly proportional to the X-ray luminosity and all the X-ray induced
reactions therefore scale with
![]() .
Results for different X-ray
temperatures
.
Results for different X-ray
temperatures
![]() and inner hydrogen column densities
and inner hydrogen column densities
![]() are presented in Sect. 4.6.
are presented in Sect. 4.6.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2889f03.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg110.gif) |
Figure 3:
Ionization rates
|
| Open with DEXTER | |
Table 1: Model parameters for AFGL 2591.
![\begin{figure}
\par\resizebox{17.5cm}{!}{\includegraphics[clip]{2889f04.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg111.gif) |
Figure 4:
Depth dependent fractional abundances for the models described in
Table 1. The solid line corresponds to model 0, the dotted line is
model 2, the dashed line is model 3. The dashed-dotted line is model 4 and
the dashed-dotted-dotted line (model 6) corresponds to the best fitted X-ray
model with an inner UV field of
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17.45cm}{!}{\includegraphics[clip]{2889f05.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg112.gif) |
Figure 5:
Depth dependent fractional abundances for the models described in
Table 1. The solid line corresponds to model 0, the dotted line is
model 2, the dashed line is model 3. The dashed-dotted line is model 4 and
the dashed-dotted-dotted line (model 6) corresponds to the best fitted X-ray
model with an inner UV field of
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17.2cm}{!}{\includegraphics[clip]{2889f06.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg113.gif) |
Figure 6:
Depth dependent fractional abundances for the models described in
Table 1. The solid line corresponds to model 0, the dotted line is
model 2, the dashed line is model 3. The dashed-dotted line is model 4 and
the dashed-dotted-dotted line (model 6) corresponds to the best fitted X-ray
model with an inner UV field of
|
| Open with DEXTER | |
Figure 3 shows the H2 ionization rates
![]() for
the different X-ray models. In addition, the cosmic-ray ionization rate
for
the different X-ray models. In addition, the cosmic-ray ionization rate
![]() s-1 is shown which is taken
from van der Tak & van Dishoeck (2000). By taking the physical
parameters given in Fig. 2, it can be estimated that half of the
envelope mass is inside
s-1 is shown which is taken
from van der Tak & van Dishoeck (2000). By taking the physical
parameters given in Fig. 2, it can be estimated that half of the
envelope mass is inside
![]() cm. Comparison of
cm. Comparison of
![]() and
and
![]() in Fig. 3 therefore
shows that the bulk of the envelope mass is dominated by the cosmic-ray
ionization rate rather than by the X-ray ionization rate. X-ray luminosities
in Fig. 3 therefore
shows that the bulk of the envelope mass is dominated by the cosmic-ray
ionization rate rather than by the X-ray ionization rate. X-ray luminosities
![]() erg s-1 are required for the X-ray
ionization rate to dominate the cosmic-ray ionization rate. The influence of
different cosmic-ray ionization rates on the chemistry is shown in
Sect. 4.8.
erg s-1 are required for the X-ray
ionization rate to dominate the cosmic-ray ionization rate. The influence of
different cosmic-ray ionization rates on the chemistry is shown in
Sect. 4.8.
Abundances of various species are presented in Figs. 4-6
for models 0, 2-4 and model 6. Since it is more common to compare
number densities to the number density of molecular hydrogen rather than to the
total hydrogen density, the following results are presented with fractional
abundances
![]() .
.
The CO abundance profile in Fig. 4 shows that the total abundance of
this molecule is not significantly affected by X-rays. H2O and CO2 on the
other hand are destroyed in the gas-phase. CO2 is destroyed mainly by FUV
photons induced through electron impact on H2. The additional CO2 at
higher temperatures is primarily from the reaction of OH with CO. The bump at
![]() cm (
cm (
![]() K) is due to the reaction
of HCO2+ with CO which is slightly faster at this distance than the
destruction of CO2. HCO2+ is efficiently produced by the reaction of
HCO+ with OH. Detailed studies of Boonman et al. (2003b) showed
that the fractional CO2 abundance is
K) is due to the reaction
of HCO2+ with CO which is slightly faster at this distance than the
destruction of CO2. HCO2+ is efficiently produced by the reaction of
HCO+ with OH. Detailed studies of Boonman et al. (2003b) showed
that the fractional CO2 abundance is
![]()
![]() for
for
![]() K and
K and
![]() for
for
![]() K. This jump at
K. This jump at
![]() K is
well produced by our models for relatively high X-ray luminosities
K is
well produced by our models for relatively high X-ray luminosities
![]() erg s-1. The models of Doty et al. (2002) for
AFGL 2591 overpredicted the CO2 abundance in the gas phase and Stäuber
et al. (2004) showed that an inner FUV flux does not destroy CO2
significantly either. X-rays are therefore a possible explanation for the
observed gas-phase CO2 abundance profile.
erg s-1. The models of Doty et al. (2002) for
AFGL 2591 overpredicted the CO2 abundance in the gas phase and Stäuber
et al. (2004) showed that an inner FUV flux does not destroy CO2
significantly either. X-rays are therefore a possible explanation for the
observed gas-phase CO2 abundance profile.
H2O is most efficiently destroyed by reactions with HCO+ and H3+ for
![]() K. In the warm, inner region water is mainly produced by the reaction of
OH with H2. For temperatures
K. In the warm, inner region water is mainly produced by the reaction of
OH with H2. For temperatures
![]() K, however, most of the
gas-phase OH and O goes into O2, thus H2O is less abundant for these
temperatures. H2O has been observed and studied in detail towards AFGL 2591
by Boonman & van Dishoeck (2003). They derived a fractional
abundance of
K, however, most of the
gas-phase OH and O goes into O2, thus H2O is less abundant for these
temperatures. H2O has been observed and studied in detail towards AFGL 2591
by Boonman & van Dishoeck (2003). They derived a fractional
abundance of
![]() for
for
![]() K
(scenario 8 in Boonman & van Dishoeck 2003). Our models for high
X-ray fluxes (
K
(scenario 8 in Boonman & van Dishoeck 2003). Our models for high
X-ray fluxes (
![]() erg s-1) give such high
abundances only at
erg s-1) give such high
abundances only at
![]() K and are therefore inconsistent with the
observations of gas-phase water towards AFGL 2591. The low X-ray luminosity is
in contradiction with the overall best-fit results (Sect. 6.1) and with
the results for CO2. One possible solution to this problem could be the
evolution of water with time or related to this, the X-ray luminosity may not
be constant with time. However, the destruction of H2O starts already at
K and are therefore inconsistent with the
observations of gas-phase water towards AFGL 2591. The low X-ray luminosity is
in contradiction with the overall best-fit results (Sect. 6.1) and with
the results for CO2. One possible solution to this problem could be the
evolution of water with time or related to this, the X-ray luminosity may not
be constant with time. However, the destruction of H2O starts already at
![]() yr which would imply an implausibly young age. Another
possible origin of the discrepancy may be the chemical reaction coefficients
that cause the production of O2 rather than H2O for 100 K
yr which would imply an implausibly young age. Another
possible origin of the discrepancy may be the chemical reaction coefficients
that cause the production of O2 rather than H2O for 100 K
![]() 230 K. In particular, the coefficients may depend on the
populations of the fine-structure levels of atomic oxygen. A higher temperature
from
230 K. In particular, the coefficients may depend on the
populations of the fine-structure levels of atomic oxygen. A higher temperature
from
![]() cm would solve this problem as well.
cm would solve this problem as well.
In the models with X-rays, atomic carbon is particularly produced by the
photodissociation of CO by FUV photons from H2 excited by
electron impact. If a FUV field
![]() is turned on, however, carbon
is more efficiently created by the photons from the inner FUV field.
By comparing the two reaction rates, it can be shown that the production of
atomic carbon by dissociating CO is dominated by X-ray induced reactions if the
total ionization rate is
is turned on, however, carbon
is more efficiently created by the photons from the inner FUV field.
By comparing the two reaction rates, it can be shown that the production of
atomic carbon by dissociating CO is dominated by X-ray induced reactions if the
total ionization rate is
Neutral atomic carbon is mainly destroyed by ionization through FUV photons
from either X-ray induced processes or from the inner FUV field. Further in the
envelope (
![]() K), carbon is primarily destroyed in reactions with
O2 and HCO+. The most efficient way to produce C+ in the pure X-ray
models is the reaction He+ + CO
K), carbon is primarily destroyed in reactions with
O2 and HCO+. The most efficient way to produce C+ in the pure X-ray
models is the reaction He+ + CO
![]() C+ + O + He. For high
X-ray fluxes (
C+ + O + He. For high
X-ray fluxes (
![]() erg s-1), this
reaction even dominates the photoionization due to an inner FUV field once
erg s-1), this
reaction even dominates the photoionization due to an inner FUV field once
![]() .
The production of C+ through the X-ray induced FUV
photoionization of C or through the "primary'' X-ray ionization and dissociation
of CO (Sect. 3.1) is approximately 10 times less efficient. The
fastest destruction process for C+ is by reaction with H2O. This is also
the dominant production mechanism for HOC+. HCO+ on the other hand, is
more efficiently produced by the reaction of H3+ with CO. This is due to
the fact that the production of HCO+ through this reaction is
.
The production of C+ through the X-ray induced FUV
photoionization of C or through the "primary'' X-ray ionization and dissociation
of CO (Sect. 3.1) is approximately 10 times less efficient. The
fastest destruction process for C+ is by reaction with H2O. This is also
the dominant production mechanism for HOC+. HCO+ on the other hand, is
more efficiently produced by the reaction of H3+ with CO. This is due to
the fact that the production of HCO+ through this reaction is ![]() 60 times
faster compared to the production of HOC+. The destruction of HCO+
and HOC+ is mainly through reactions with water in the inner part of the
envelope and through electron recombination at larger distances from the source.
HOC+ is also destroyed in reactions with H2 which form HCO+.
60 times
faster compared to the production of HOC+. The destruction of HCO+
and HOC+ is mainly through reactions with water in the inner part of the
envelope and through electron recombination at larger distances from the source.
HOC+ is also destroyed in reactions with H2 which form HCO+.
CO+ is mainly produced by electron impact ionization of CO. Other important reactions are the charge exchange reaction of He+ with CO2 and the reactions of C+ with OH and O2, respectively. CO+ is quickly destroyed by H2 and forms HCO+.
Figures 4-6 show that sulphur and sulphur-bearing molecules are strongly enhanced by X-rays. The following (simple) network explains the relatively high fractional abundances of some of these species: the chemical sulphur network starts with the production of atomic sulphur through X-ray induced FUV photodissociation of H2S. Sulphur reacts then with OH to form either SO or SH. SO reacts with atomic carbon and can therefore form CS. Reactions of CS with H3O+ and HCO+ lead to HCS+. SH+ is efficiently produced by the reactions of atomic sulphur with H3+ or HCO+. The dominant destruction channel for S in the innermost part of the envelope is the photoionization due to an inner FUV field or due to FUV photons from X-ray induced reactions. These are also the most important reactions to produce S+. S+ reacts with OH and O2 and forms SO+. X-rays can ionize atomic sulphur even at large distances and the abundances of S+, SO+ and HCS+ are enhanced throughout the entire envelope.
In order to study the dependence of our model results on the form of the
initial sulphur, we have run models assuming the initial sulphur to be atomic
for
![]() K instead of being in the form of H2S with the following
result: for the best fitted X-ray models (Sect. 6.1) all species have
exactly the same abundances after a few 1000 yr as in the
models where the initial sulphur was assumed to be in H2S. In models without
X-rays, however, the results differ less than 20% once
K instead of being in the form of H2S with the following
result: for the best fitted X-ray models (Sect. 6.1) all species have
exactly the same abundances after a few 1000 yr as in the
models where the initial sulphur was assumed to be in H2S. In models without
X-rays, however, the results differ less than 20% once
![]() yr. For
yr. For
![]() yr, the chemical age of AFGL 2591
found by Doty et al. (2002), the column density of H2S is
yr, the chemical age of AFGL 2591
found by Doty et al. (2002), the column density of H2S is ![]() 25 times less in the model where the initial sulphur was in atomic form
compared to the model where sulphur was in the form of H2S. By comparing the
two models without X-rays but with different initial forms of sulphur to
observations of H2S (van der Tak et al. 2003) it is seen that the
model where sulphur is assumed to be initially in the form of H2S fits the
observations much better. Other species like S, SO2, CS and H2CS,
however, differ less than 30% for
25 times less in the model where the initial sulphur was in atomic form
compared to the model where sulphur was in the form of H2S. By comparing the
two models without X-rays but with different initial forms of sulphur to
observations of H2S (van der Tak et al. 2003) it is seen that the
model where sulphur is assumed to be initially in the form of H2S fits the
observations much better. Other species like S, SO2, CS and H2CS,
however, differ less than 30% for
![]() yr. Since we
will compare our results to the models of Doty et al. (2002) and
Stäuber et al. (2004) we assume sulphur initially to be in the form of
H2S.
yr. Since we
will compare our results to the models of Doty et al. (2002) and
Stäuber et al. (2004) we assume sulphur initially to be in the form of
H2S.
Since the initial nitrogen in our models is in molecular form, the
nitrogen chemistry starts with the photodissociation of N2 by either an
inner FUV field
![]() or by X-ray induced FUV photons from excited
H2. Atomic nitrogen is then transformed into NO in reactions with OH. NO
reacts with N and forms N2, or it reacts with C to make CN. HCN is then
efficiently produced by the reaction of CN with H2. The destruction of N2
by H3+ leads to N2H+ that is mainly destroyed by H2O or by
CO. The destruction of N2H+ by HCN leads to HNCH+ which can
recombine either back to HCN, HNC, or CN.
or by X-ray induced FUV photons from excited
H2. Atomic nitrogen is then transformed into NO in reactions with OH. NO
reacts with N and forms N2, or it reacts with C to make CN. HCN is then
efficiently produced by the reaction of CN with H2. The destruction of N2
by H3+ leads to N2H+ that is mainly destroyed by H2O or by
CO. The destruction of N2H+ by HCN leads to HNCH+ which can
recombine either back to HCN, HNC, or CN.
The bulk abundance of N+ in the gas stems from the ionization of N2 by He+. For N+, reactions with H2 lead to NH4+ which dissociates into NH2 and H2 via electron recombination. NH2 and O form HNO which on the other hand forms N2O by reaction with O. From Fig. 6 it can be seen that both HNO and N2O are greatly enhanced by X-rays.
Hydrides are strongly enhanced by X-rays as can be seen in
Figs. 4-6. The hydrides SH and SH+ have already been
discussed in Sect. 4.3. X-ray enhanced CH reaches a fractional abundance
of
![]() for high X-ray
fluxes (
for high X-ray
fluxes (
![]() erg s-1) and its abundance is
almost constant in the entire envelope. CH is mainly produced by the reaction
CH2 + H
erg s-1) and its abundance is
almost constant in the entire envelope. CH is mainly produced by the reaction
CH2 + H
![]() CH + H2. CH2 is efficiently produced in reactions
of C with H2 and by the X-ray induced photodissociation of CH4. At larger
distances of the source, electron recombination reactions of CH3+ become also
important for the production of both CH and CH2. CH is primarily destroyed
in reactions with H2. CH+ is mainly formed in reactions of H3+ or
HCO+ with atomic carbon. The fractional abundance of CH+ is also almost
constant throughout the envelope for the higher X-ray flux models, but with
CH + H2. CH2 is efficiently produced in reactions
of C with H2 and by the X-ray induced photodissociation of CH4. At larger
distances of the source, electron recombination reactions of CH3+ become also
important for the production of both CH and CH2. CH is primarily destroyed
in reactions with H2. CH+ is mainly formed in reactions of H3+ or
HCO+ with atomic carbon. The fractional abundance of CH+ is also almost
constant throughout the envelope for the higher X-ray flux models, but with
![]() ,
,
![]() .
However, CH+ is enhanced up to
.
However, CH+ is enhanced up to
![]() in the innermost part of the envelope
where it is
in the innermost part of the envelope
where it is ![]() 105 times more abundant in the best-fit models than in
the models without X-rays.
105 times more abundant in the best-fit models than in
the models without X-rays.
OH and OH+ are both enhanced by X-rays through the destruction of water in
the gas-phase. OH is the product of FUV photodissociation of H2O whereas
OH+ is mainly produced in reactions of He+ with H2O or in reactions of
H3+ with OH. Both, OH and OH+ are destroyed primarily by H2. For the
best-fit models, OH reaches fractional abundances
![]() in the outer part and
in the outer part and
![]() in the
innermost part of the envelope. OH+ has a fractional abundance of
in the
innermost part of the envelope. OH+ has a fractional abundance of
![]() in the outer part and
reaches
in the outer part and
reaches
![]() closer to the source.
closer to the source.
Hydrides like SH, SH+, CH, CH+, OH and OH+ are difficult to observe with ground based telescopes due to atmospheric absorption. These hydrides are therefore possible molecules to observe with the space-borne instrument Herschel-HIFI (de Graauw & Helmich 2001).
The influence of different X-ray temperatures
![]() and inner hydrogen
column densities
and inner hydrogen
column densities
![]() on the chemistry is shown in
Fig. C.1 for six species for
on the chemistry is shown in
Fig. C.1 for six species for
![]() erg s-1. It
can be seen that the results for
erg s-1. It
can be seen that the results for
![]() K and
K and
![]() K are very similar. A lower temperature of
K are very similar. A lower temperature of
![]() K, however, leads to lower abundances at larger
distances from the source since the softer X-rays are more absorbed on their
way through the envelope. The results for different inner column densities are
even less distinctive. In general, higher absorbing hydrogen column densities
lead to lower abundances. Comparison of the integrated column densities for all
species for the different models shows that the results differ only a factor of
2 at most for the different X-ray temperatures,
K, however, leads to lower abundances at larger
distances from the source since the softer X-rays are more absorbed on their
way through the envelope. The results for different inner column densities are
even less distinctive. In general, higher absorbing hydrogen column densities
lead to lower abundances. Comparison of the integrated column densities for all
species for the different models shows that the results differ only a factor of
2 at most for the different X-ray temperatures,
![]() ,
and absorbing
inner hydrogen column densities,
,
and absorbing
inner hydrogen column densities,
![]() .
The influence of the X-ray
temperature and the inner hydrogen column density on the chemistry is therefore
not as strong as it is for the X-ray luminosity where the abundances of species
like H3+ basically scale with the X-ray luminosity
(see also Table 2 in Sect. 5). Indeed, it will be shown in
Sect. 6.1 that the X-ray luminosity
.
The influence of the X-ray
temperature and the inner hydrogen column density on the chemistry is therefore
not as strong as it is for the X-ray luminosity where the abundances of species
like H3+ basically scale with the X-ray luminosity
(see also Table 2 in Sect. 5). Indeed, it will be shown in
Sect. 6.1 that the X-ray luminosity
![]() is the dominant
parameter in our models.
is the dominant
parameter in our models.
Regions of high-mass star formation often have FUV fields that are higher than the
average interstellar radiation field. Evolved massive stars emit a copious
amount of ultraviolet radiation. The immediate environment is ionized and a H II
region is formed. The FUV photons (
![]() eV), however, penetrate the
H II region and may influence the chemistry of a nearby cloud or the envelope
of a young stellar object, forming a photon-dominated region (e.g., Hollenbach & Tielens
1999). For AFGL 2591, a nearby H II region has been found (van der Tak
et al. 1999; Trinidad et al. 2003) whose exciting star may have an
influence on the outer part of the AFGL 2591 envelope.
eV), however, penetrate the
H II region and may influence the chemistry of a nearby cloud or the envelope
of a young stellar object, forming a photon-dominated region (e.g., Hollenbach & Tielens
1999). For AFGL 2591, a nearby H II region has been found (van der Tak
et al. 1999; Trinidad et al. 2003) whose exciting star may have an
influence on the outer part of the AFGL 2591 envelope.
Figure D.1 shows a selection of species for different outer FUV fields
![]() .
The influence of the outer FUV field is noticeable at
.
The influence of the outer FUV field is noticeable at
![]() cm from the source. The chemistry is that of a
photon-dominated region (e.g., Sternberg & Dalgarno 1995). The chemical
reaction network basically starts with the dissociation of CO and the
ionization of C leading to an enhancement of atomic and ionized carbon. Other
species that are enhanced by an outer FUV field are CH and CH+. In
our models, CH is mainly produced by the dissociation of CH4 and CH2.
Photoionization of CH leads to CH+. CO+ is enhanced through reactions of
C+ with OH and CH+ with O. HOC+ is only enhanced for a low outer FUV
field (
cm from the source. The chemistry is that of a
photon-dominated region (e.g., Sternberg & Dalgarno 1995). The chemical
reaction network basically starts with the dissociation of CO and the
ionization of C leading to an enhancement of atomic and ionized carbon. Other
species that are enhanced by an outer FUV field are CH and CH+. In
our models, CH is mainly produced by the dissociation of CH4 and CH2.
Photoionization of CH leads to CH+. CO+ is enhanced through reactions of
C+ with OH and CH+ with O. HOC+ is only enhanced for a low outer FUV
field (
![]() ). HOC+ is produced in reactions of water with
C+.
). HOC+ is produced in reactions of water with
C+.
Other molecules like HCO+, CN, HCN, HCS+ or SH+ that are enhanced by X-rays are destroyed by an outer FUV field. The increase of the electron abundance leads to relatively fast electron recombination reactions for HCO+, HCS+ and SH+. CN and HCN are efficiently photodissociated by the FUV field. Due to the lower density in the outer part of the envelope, however, these species differ less than 30% in the radial column density for the different outer FUV fields. C, C+, CH and CH+ on the other hand can be enhanced up to several orders of magnitude. Since the influence of the outer FUV field is limited to the outermost part of the envelope, spatially resolved data can distinguish between an abundance enhancement of these species due to an outer FUV field and due to X-rays or FUV photons from the inside. In addition, the excitation of these species is different in the inner part of the envelope where the density is higher than in the outer part of the envelope.
Like X-rays, cosmic rays are able to produce He+ and H3+ and
trigger a peculiar chemistry (e.g., Lepp et al. 1987; Herbst
2000). The cosmic-ray ionization rate
![]() s-1 in our models was derived from observations of
HCO+ by van der Tak & van Dishoeck (2000). In order to study the
influence of different cosmic-ray ionization rates on our X-ray models we have
run model 5 with a
s-1 in our models was derived from observations of
HCO+ by van der Tak & van Dishoeck (2000). In order to study the
influence of different cosmic-ray ionization rates on our X-ray models we have
run model 5 with a ![]() 5 times higher and lower cosmic-ray ionization
rate, respectively. Figure D.2 presents the result of this investigation
for a few species. Comparison of model 0 with
5 times higher and lower cosmic-ray ionization
rate, respectively. Figure D.2 presents the result of this investigation
for a few species. Comparison of model 0 with
![]() s-1 and model 5 with
s-1 and model 5 with
![]() s-1
and
s-1
and
![]() s-1 shows that the influence
of the cosmic-ray ionization rate dominates the chemistry for
s-1 shows that the influence
of the cosmic-ray ionization rate dominates the chemistry for
![]() cm from the source for
cm from the source for
![]() erg s-1 in agreement with Fig. 3. Cosmic-ray
ionization rates as high as
erg s-1 in agreement with Fig. 3. Cosmic-ray
ionization rates as high as
![]() s-1,
however, are able to dominate the gas-phase chemistry for
s-1,
however, are able to dominate the gas-phase chemistry for
![]() cm from the source, that is from where H2O freezes out on dust
grains. By comparing H13CO+ observations to a simple chemical model
with different cosmic-ray ionization rates van der Tak & van Dishoeck
(2000) showed for seven high-mass sources that the ionization rate
varies between
cm from the source, that is from where H2O freezes out on dust
grains. By comparing H13CO+ observations to a simple chemical model
with different cosmic-ray ionization rates van der Tak & van Dishoeck
(2000) showed for seven high-mass sources that the ionization rate
varies between
![]() s-1.
In addition, ionization rates as high as
s-1.
In addition, ionization rates as high as
![]() s-1 are not confirmed by our best-fit models
(Sect. 6.1). The influence of the cosmic-ray ionization rate on the
emission line profiles of H13CO+ will be discussed in
Sect. 7 (see also Doty et al. 2002).
s-1 are not confirmed by our best-fit models
(Sect. 6.1). The influence of the cosmic-ray ionization rate on the
emission line profiles of H13CO+ will be discussed in
Sect. 7 (see also Doty et al. 2002).
In order to find species that trace X-rays in highly obscured regions we have to
distinguish X-ray enhanced species from species that are enhanced by other mechanisms
such as inner FUV fields from the source, outer FUV fields from nearby stars or from
cosmic-ray induced chemistry. By focusing only on the innermost region of the envelope
(
![]() AU), the effects of the latter two mechanisms can be neglected. The
only challenge then is to separate species that are enhanced by X-rays from species
that trace more preferably the FUV field from the central source.
AU), the effects of the latter two mechanisms can be neglected. The
only challenge then is to separate species that are enhanced by X-rays from species
that trace more preferably the FUV field from the central source.
Table 2: AFGL 2591 predicted column densities (cm-2) for different X-ray models.
Figures 4-6 show that X-rays are capable of influencing
the atomic and molecular abundances throughout almost the entire envelope. This
is the main difference with the models of Stäuber et al. (2004) where
the influence of an inner FUV field has been examined. Due to their small cross
sections, X-rays penetrate deeper into the envelope and affect the chemistry on
large scales. The enhanced region due to a low inner FUV field
(
![]() )
is
)
is ![]() 300-500 AU (Stäuber et al.
2004) whereas the X-ray enhanced region is often
300-500 AU (Stäuber et al.
2004) whereas the X-ray enhanced region is often ![]() 1000 AU,
even for relatively low X-ray fluxes (
1000 AU,
even for relatively low X-ray fluxes (
![]() erg s-1). Current and future (sub)millimeter interferometers
like ALMA are able to resolve regions covering
erg s-1). Current and future (sub)millimeter interferometers
like ALMA are able to resolve regions covering ![]() 1-2
1-2
![]() .
At a
distance of 1 kpc, this corresponds to a region of
.
At a
distance of 1 kpc, this corresponds to a region of ![]() 1000-2000 AU.
However, it will be shown in Sect. 7 that the influence of X-rays and
therefore the enhanced emission of several species can also be seen in much
bigger single-dish beams.
1000-2000 AU.
However, it will be shown in Sect. 7 that the influence of X-rays and
therefore the enhanced emission of several species can also be seen in much
bigger single-dish beams.
X-rays and UV photons have similar effects on the chemistry. They both increase
the abundances of ions and radicals. However, X-rays can ionize atoms with an
ionization threshold
![]() eV like hydrogen, helium, oxygen
and nitrogen which is not possible for FUV photons (
eV like hydrogen, helium, oxygen
and nitrogen which is not possible for FUV photons (
![]() eV) and
can even doubly ionize many species. Reactions with ions like He+ or H3+
can therefore become important in X-ray induced chemistry. For example,
reactions of He+ or H3+ with CO efficiently produce C+ and HCO+,
respectively (Sect. 4.2). The main contribution to the He+ abundance,
however, is from electron impact ionization of He, rather than direct X-ray
ionization. H3+ is formed by the reaction of H2+ with H2 where
H2+ is also formed through electron impact ionization. Both He+ and
H2+ cannot be produced with FUV photons but with cosmic rays as discussed
in Sect. 4.8.
eV) and
can even doubly ionize many species. Reactions with ions like He+ or H3+
can therefore become important in X-ray induced chemistry. For example,
reactions of He+ or H3+ with CO efficiently produce C+ and HCO+,
respectively (Sect. 4.2). The main contribution to the He+ abundance,
however, is from electron impact ionization of He, rather than direct X-ray
ionization. H3+ is formed by the reaction of H2+ with H2 where
H2+ is also formed through electron impact ionization. Both He+ and
H2+ cannot be produced with FUV photons but with cosmic rays as discussed
in Sect. 4.8.
Table 2 presents beam averaged column densities of models 2, 3,
4 and model 6 for a selection of species for the inner ![]() 2000 AU,
that is the region that can be resolved by interferometers. The enhancement
factor
2000 AU,
that is the region that can be resolved by interferometers. The enhancement
factor
![]() in Table 2 is defined as the ratio
of the column density of a species predicted by the X-ray model x and the
column density of the model without any radiation field, that is model 0. The
enhancement factor
in Table 2 is defined as the ratio
of the column density of a species predicted by the X-ray model x and the
column density of the model without any radiation field, that is model 0. The
enhancement factor
![]() is defined as the ratio of the
calculated column density from X-ray model x and the column density of the model
without X-rays but with an inner FUV field with a field strength
is defined as the ratio of the
calculated column density from X-ray model x and the column density of the model
without X-rays but with an inner FUV field with a field strength
![]() (model 1). Since the results for the best-fit models
and model 4 are similar, the column densities of model 4 are representative
of all best fitted models.
(model 1). Since the results for the best-fit models
and model 4 are similar, the column densities of model 4 are representative
of all best fitted models.
Most species presented in Table 2 are enhanced due to X-rays
(
![]() )
and may therefore serve as possible tracers.
An enhancement factor
)
and may therefore serve as possible tracers.
An enhancement factor
![]() ,
however, distinguishes
X-ray tracers from species that are enhanced by an inner UV field. It can be
seen in Table 2 that species like N2O, HNO, SO, SO+, HCO+,
CO+, OH+, N2H+, SH+ and HSO+ are more enhanced by X-rays than by FUV photons even for X-ray
luminosities as low as
,
however, distinguishes
X-ray tracers from species that are enhanced by an inner UV field. It can be
seen in Table 2 that species like N2O, HNO, SO, SO+, HCO+,
CO+, OH+, N2H+, SH+ and HSO+ are more enhanced by X-rays than by FUV photons even for X-ray
luminosities as low as
![]() erg s-1. In addition,
the abundances for these species increase with increasing X-ray flux. Other species
like CS, SH, HCN, CH or HCS+ are enhanced either by X-rays or an inner FUV field,
depending on the incident X-ray or FUV flux, respectively. Species like C or HOC+
are more enhanced by an inner FUV field than by X-rays.
erg s-1. In addition,
the abundances for these species increase with increasing X-ray flux. Other species
like CS, SH, HCN, CH or HCS+ are enhanced either by X-rays or an inner FUV field,
depending on the incident X-ray or FUV flux, respectively. Species like C or HOC+
are more enhanced by an inner FUV field than by X-rays.
Table 2 and Fig. 6 show that HSO+ is a remarkable tracer
for X-rays. It is enhanced by more than a factor of 100 even for low X-ray fluxes
with fractional abundance
![]() in
the inner
in
the inner ![]() 1000 AU. In our models, HSO+ is primarily produced by the
reactions of H3+ and HCO+ with SO. Unfortunately though, little is known
about this molecule which has not been observed to date. In addition, spectral
information is missing and laboratory work is needed before HSO+ can be
searched in molecular clouds. SH+ is enhanced even more than 10 000 times
compared to model 0 and more than 1000 times compared to model 1 for the
best-fit models. Four hyperfine lines of SH+ have recently been measured by
Savage et al. (2004). It was found that the best candidates for
observations are the strongest lines near 526 GHz which requires instruments
such as Herschel-HIFI or SOFIA.
1000 AU. In our models, HSO+ is primarily produced by the
reactions of H3+ and HCO+ with SO. Unfortunately though, little is known
about this molecule which has not been observed to date. In addition, spectral
information is missing and laboratory work is needed before HSO+ can be
searched in molecular clouds. SH+ is enhanced even more than 10 000 times
compared to model 0 and more than 1000 times compared to model 1 for the
best-fit models. Four hyperfine lines of SH+ have recently been measured by
Savage et al. (2004). It was found that the best candidates for
observations are the strongest lines near 526 GHz which requires instruments
such as Herschel-HIFI or SOFIA.
Ratios like CN/HCN or HOC+/HCO+ are of specific interest since they
depend on the flux of FUV radiation (Fuente et al. 1995, 2003;
Stäuber et al. 2004). Since X-rays affect the abundances of ions and
radicals, these ratios may also depend on the incident X-ray flux. The ratios
CN/HCN, HNC/HCN, CO+/HCO+ and HOC+/HCO+ of the radial column
densities of the inner ![]() 2000 AU are presented in Fig. 7.
The ratios CO+/HCO+ and HOC+/HCO+ are effectively enhanced only by
models containing an inner FUV field. The ratio HNC/HCN is higher for the X-ray
models than for the FUV models but similar to the ratio of model 0. The
CN/HCN ratios depend strongly on the incident X-ray flux and vary within a
factor of 100. Models with high X-ray luminosities (
2000 AU are presented in Fig. 7.
The ratios CO+/HCO+ and HOC+/HCO+ are effectively enhanced only by
models containing an inner FUV field. The ratio HNC/HCN is higher for the X-ray
models than for the FUV models but similar to the ratio of model 0. The
CN/HCN ratios depend strongly on the incident X-ray flux and vary within a
factor of 100. Models with high X-ray luminosities (
![]() erg s-1) and models with X-rays and an inner FUV field, that is
model 6 and 7, are capable of increasing the CN/HCN ratio up to 0.01.
Although the CN/HCN ratio increases with increasing X-ray flux (models 2-4),
the ratio is also enhanced by an inner FUV field without X-rays. In general,
all these ratios give poor information about the X-ray flux, since they are
enhanced more likely by an inner FUV flux rather than by X-rays. The crucial
point for an enhanced CN/HCN ratio is the strength of the inner FUV field and
therefore the inner column density
erg s-1) and models with X-rays and an inner FUV field, that is
model 6 and 7, are capable of increasing the CN/HCN ratio up to 0.01.
Although the CN/HCN ratio increases with increasing X-ray flux (models 2-4),
the ratio is also enhanced by an inner FUV field without X-rays. In general,
all these ratios give poor information about the X-ray flux, since they are
enhanced more likely by an inner FUV flux rather than by X-rays. The crucial
point for an enhanced CN/HCN ratio is the strength of the inner FUV field and
therefore the inner column density
![]() .
For column densities
.
For column densities
![]() cm-2, the optical depth
cm-2, the optical depth
![]() is
is ![]() 20 and most FUV photons from the young star
will be absorbed. The enhancement of the CN/HCN ratio is then more likely
due to X-rays.
20 and most FUV photons from the young star
will be absorbed. The enhancement of the CN/HCN ratio is then more likely
due to X-rays.
Earlier models of molecules exposed to an X-ray source predicted similar
molecular X-ray tracers. Lepp & Dalgarno (1996) found that CN and NO
are particularly enhanced by X-rays. The enhancement of CN is confirmed with
our models. CN can be enhanced up to ![]() 50 times in the inner
2000 AU. The beam averaged column density of NO given in Table 2,
however, is smaller for the X-ray models than for the models without X-rays.
From Fig. 6 it can be seen that NO is enhanced in the outer parts of
the envelope and in the innermost part of the envelope (
50 times in the inner
2000 AU. The beam averaged column density of NO given in Table 2,
however, is smaller for the X-ray models than for the models without X-rays.
From Fig. 6 it can be seen that NO is enhanced in the outer parts of
the envelope and in the innermost part of the envelope (
![]() AU).
The `cut-off' of the bump in the middle part of the envelope causes the
decreasing NO column density with increasing X-ray flux. The bump of the NO
abundance profile is due to the evaporation of water at T = 100 K, a process
not included by Lepp & Dalgarno (1996). For
AU).
The `cut-off' of the bump in the middle part of the envelope causes the
decreasing NO column density with increasing X-ray flux. The bump of the NO
abundance profile is due to the evaporation of water at T = 100 K, a process
not included by Lepp & Dalgarno (1996). For
![]() K, NO is
efficiently produced by the reaction HNO+ + H2O
K, NO is
efficiently produced by the reaction HNO+ + H2O
![]() H3O+
+ NO. In our X-ray models NO is enhanced up to fractional abundances
H3O+
+ NO. In our X-ray models NO is enhanced up to fractional abundances
![]() in the innermost part of the
envelope. This is the same result found by Lepp & Dalgarno (1996). To
observe the enhanced region of NO towards the inner
in the innermost part of the
envelope. This is the same result found by Lepp & Dalgarno (1996). To
observe the enhanced region of NO towards the inner ![]() 500 AU of AFGL 2591 the sensitivity and spatial resolution of ALMA is needed. The model
results of Krolik & Kallman (1983) for the Orion molecular cloud are
generally in good agreement with our results. The enhancement factors they
derive are comparable to those of model 6. In particular, they also find that
NO is not changing in models with high ionization rates.
500 AU of AFGL 2591 the sensitivity and spatial resolution of ALMA is needed. The model
results of Krolik & Kallman (1983) for the Orion molecular cloud are
generally in good agreement with our results. The enhancement factors they
derive are comparable to those of model 6. In particular, they also find that
NO is not changing in models with high ionization rates.
To find the best fitting model for AFGL 2591 by varying the input parameters
![]() ,
,
![]() ,
,
![]() - the column density between
the X-ray source and the first radial model point - and the inner UV field
- the column density between
the X-ray source and the first radial model point - and the inner UV field
![]() ,
a
,
a ![]() statistic has been used defined by
statistic has been used defined by
As a first approach models with only X-rays are considered:
![]() was
varied from 1029 erg s-1 to
was
varied from 1029 erg s-1 to
![]() erg s-1,
erg s-1,
![]() from
from
![]() K to
K to
![]() K and
K and
![]() from 1022 cm-2 to 1024 cm-2. The
minimum and maximum values of the grid for the X-ray luminosity and plasma
temperature are based on results of X-ray observations toward YSOs. The
best fitted parameters out of
from 1022 cm-2 to 1024 cm-2. The
minimum and maximum values of the grid for the X-ray luminosity and plasma
temperature are based on results of X-ray observations toward YSOs. The
best fitted parameters out of ![]() 800 calculated models are
800 calculated models are
![]() erg s-1,
erg s-1,
![]() K,
K,
![]() cm-2 and
cm-2 and
![]() yr (model 5). The X-ray
luminosity and temperature are rather high and at the upper end of what has been
observed toward star forming regions (e.g., Feigelson & Montmerle 1999;
Hofner et al. 2002). If, however, the X-ray luminosity decreases as the
YSO evolves - like it does in low-mass YSOs (Feigelson & Montmerle
1999; Tsujimoto 2002) - such high luminosities and plasma
temperatures could be possible. The inner column density corresponds to
yr (model 5). The X-ray
luminosity and temperature are rather high and at the upper end of what has been
observed toward star forming regions (e.g., Feigelson & Montmerle 1999;
Hofner et al. 2002). If, however, the X-ray luminosity decreases as the
YSO evolves - like it does in low-mass YSOs (Feigelson & Montmerle
1999; Tsujimoto 2002) - such high luminosities and plasma
temperatures could be possible. The inner column density corresponds to
![]() which is in good agreement with the results of van der Tak et al. (1999) for r < 175 AU.
which is in good agreement with the results of van der Tak et al. (1999) for r < 175 AU.
As a second step in finding the best-fit X-ray model, an inner FUV field of
![]() has been assumed with an inner column density of
has been assumed with an inner column density of
![]() cm-2 in agreement with the
models of Stäuber et al. (2004). The parameters of the best fitted
model are then
cm-2 in agreement with the
models of Stäuber et al. (2004). The parameters of the best fitted
model are then
![]() erg s-1,
erg s-1,
![]() K and
K and
![]() yr (model 6). Models with higher
inner FUV fields in general lead to much higher
yr (model 6). Models with higher
inner FUV fields in general lead to much higher ![]() values. The assumption
of an inner FUV therefore yields a slightly lower X-ray luminosity.
values. The assumption
of an inner FUV therefore yields a slightly lower X-ray luminosity.
Using a reduced ![]() statistic where each addend in Eq. (12) is
divided by the number of observed lines of that species, the best fitted model
is
statistic where each addend in Eq. (12) is
divided by the number of observed lines of that species, the best fitted model
is
![]() erg s-1,
erg s-1,
![]() K with an inner column density of
K with an inner column density of
![]() cm-2 and an inner FUV field
cm-2 and an inner FUV field
![]() at
at
![]() yr (model 7).
yr (model 7).
Considering only species that are influenced most by X-rays in Eq. (12),
the best fitted parameters are
![]() erg s-1,
erg s-1,
![]() K and
K and
![]() yr which is
very similar to model 5. The species considered are HCN, HNC, H2S, CS,
CN, SO, HCO+, HCS+, H3+ and N2H+. The lower (dotted) curve
in Fig. 8 shows the results for this calculation whereas the upper
(solid) curve corresponds to the
yr which is
very similar to model 5. The species considered are HCN, HNC, H2S, CS,
CN, SO, HCO+, HCS+, H3+ and N2H+. The lower (dotted) curve
in Fig. 8 shows the results for this calculation whereas the upper
(solid) curve corresponds to the ![]() values for all species.
values for all species.
![\begin{figure}
\par\resizebox{8.8cm}{!}{\includegraphics[clip]{2889f08.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg182.gif) |
Figure 8:
|
| Open with DEXTER | |
In general all best-fit models have very similar ![]() values and the
differences may be too small to elect the winner. The goodness of fit of
the different parameters is further discussed in the next section.
Table E.1 lists the column densities of the observed species and the
modeled column densities for model 6. Further shown are the
parameters that fit each specific molecule best. It can be seen that the
parameters
values and the
differences may be too small to elect the winner. The goodness of fit of
the different parameters is further discussed in the next section.
Table E.1 lists the column densities of the observed species and the
modeled column densities for model 6. Further shown are the
parameters that fit each specific molecule best. It can be seen that the
parameters
![]() ,
,
![]() ,
,
![]() and time vary
from species to species. Only two species, H2CO and C2H2, are
modeled best with model 0, that is the model without any high energy radiation
from the source. All other species seem to require a more or less strong X-ray
flux from the source to match the observed column density.
and time vary
from species to species. Only two species, H2CO and C2H2, are
modeled best with model 0, that is the model without any high energy radiation
from the source. All other species seem to require a more or less strong X-ray
flux from the source to match the observed column density.
O- and B-type main sequence stars emit X-rays due to shocks from the radiation
driven stellar winds with
![]() (Berghöfer et al. 1997). A bolometric luminosity
(Berghöfer et al. 1997). A bolometric luminosity
![]() for AFGL 2591 implies an X-ray luminosity
for AFGL 2591 implies an X-ray luminosity
![]() erg s-1. If we assume that young
massive stars emit rather more X-rays, this value could be regarded as a lower
limit for the X-ray emission for AFGL 2591. The ratio of the luminosities for
our best-fit models is
erg s-1. If we assume that young
massive stars emit rather more X-rays, this value could be regarded as a lower
limit for the X-ray emission for AFGL 2591. The ratio of the luminosities for
our best-fit models is
![]() .
.
As can be seen in Fig. 3, the H2 ionization rates
![]() for the best-fit models (5,6,7) differ only little
throughout the envelope. The ionization rates of model 5 and model 6 are
somewhat flatter in radial dependence than that for model 7 due to the harder
spectrum. However, since similar ionization rates lead to similar abundance
profiles, the conclusion can be drawn that the X-ray induced chemistry depends mainly on the H2
ionization rate
for the best-fit models (5,6,7) differ only little
throughout the envelope. The ionization rates of model 5 and model 6 are
somewhat flatter in radial dependence than that for model 7 due to the harder
spectrum. However, since similar ionization rates lead to similar abundance
profiles, the conclusion can be drawn that the X-ray induced chemistry depends mainly on the H2
ionization rate
![]() .
.
To quantify the plausible ranges of the various parameters, contour plots
of the ![]() values for the species influenced most by X-rays are
shown in Fig. 9. It can be seen that the results are basically
independent of
values for the species influenced most by X-rays are
shown in Fig. 9. It can be seen that the results are basically
independent of
![]() and
and
![]() for different
for different
![]() .
The plot of
.
The plot of
![]() vs. t shows that the results become independent
of t for high X-ray luminosities once
vs. t shows that the results become independent
of t for high X-ray luminosities once
![]() yr.
yr. ![]() does
not change with time anymore, thus equilibrium is reached for the species
in our statistical sample.
does
not change with time anymore, thus equilibrium is reached for the species
in our statistical sample.
![\begin{figure}
\par\resizebox{8cm}{!}{\includegraphics[clip]{2889f09.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg187.gif) |
Figure 9:
|
| Open with DEXTER | |
| |
Figure 10:
|
| Open with DEXTER | |
A region of confidence can be defined by the contours that are twice the
minimum ![]() value, which is
value, which is ![]() 0.6. The constraint on the X-ray
luminosity is then
0.6. The constraint on the X-ray
luminosity is then
![]() erg s-1 with
erg s-1 with
![]() yr. The plot of
yr. The plot of
![]() vs.
vs.
![]() in
Fig. 9 shows that for low temperatures (
in
Fig. 9 shows that for low temperatures (
![]() K), the column density is
K), the column density is
![]() cm-2. Higher temperatures allow higher column densities.
However, the extra photons at higher energies are not efficiently absorbed
by the inner column and the results become independent of the inner column density
cm-2. Higher temperatures allow higher column densities.
However, the extra photons at higher energies are not efficiently absorbed
by the inner column and the results become independent of the inner column density
![]() .
.
Figure 10 shows contour plots for
![]() vs.
vs.
![]() and
and
![]() vs.
vs.
![]() .
The plot for the
different outer FUV fields shows that the results depend mainly on the
X-ray luminosity
.
The plot for the
different outer FUV fields shows that the results depend mainly on the
X-ray luminosity
![]() rather than on the outer FUV field
rather than on the outer FUV field
![]() .
Models with higher FUV fields than the standard radiation
field (
.
Models with higher FUV fields than the standard radiation
field (
![]() )
generally lead to higher
)
generally lead to higher ![]() values.
values.
The values in the plot for the cosmic-ray ionization rate have been scaled
by a factor of 100 in Eq. (12) since only HCO+ was considered.
The cosmic-ray ionization rate is well constrained between
![]() s-1 and
s-1 and
![]() s-1 in good agreement with the results of van der Tak
& van Dishoeck (2000) and Doty et al. (2002). The X-ray luminosity is well constrained
between
s-1 in good agreement with the results of van der Tak
& van Dishoeck (2000) and Doty et al. (2002). The X-ray luminosity is well constrained
between
![]() erg s-1 and
erg s-1 and
![]() erg s-1.
erg s-1.
![\begin{figure}
\par\resizebox{17.5cm}{!}{\includegraphics[clip]{2889f11.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg194.gif) |
Figure 11:
Calculated H13CO+ line profiles for model 0 (solid line),
model 1 (dotted line), model 3 (short dashed line), model 4
(dashed-dotted line) and model 5 (long dashed line). The H13CO+
3-2 line (260 GHz) was convolved with a 18
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17.5cm}{!}{\includegraphics[clip]{2889f12.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg195.gif) |
Figure 12:
Calculated HCS+ line profiles for model 0 (solid line),
model 1 (dotted line), model 3 (short dashed line), model 4
(dashed-dotted line) and model 5 (long dashed line). The HCS+ 6-5
line (256 GHz) was convolved with a 18
|
| Open with DEXTER | |
![\begin{figure}
\par\resizebox{17.5cm}{!}{\includegraphics[clip]{2889f13.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg196.gif) |
Figure 13:
Calculated H13CO+ line profiles for model 0 (solid line) and
model 5 (dashed line) with a cosmic-ray ionization rate
|
| Open with DEXTER | |
Molecules with high critical densities
![]() are likely to probe the
inner dense part of the envelope (see, e.g., van Dishoeck & Hogerheijde
1999, for a review). Since the critical density of a molecule is
proportional to the Einstein A coefficient for spontaneous transitions and
therefore
are likely to probe the
inner dense part of the envelope (see, e.g., van Dishoeck & Hogerheijde
1999, for a review). Since the critical density of a molecule is
proportional to the Einstein A coefficient for spontaneous transitions and
therefore
![]() ,
higher frequency transitions have
also higher critical densities. Stäuber et al. (2004) show that
enhancements of molecules due to an inner FUV field should already be detectable with
single-dish telescopes having beam widths
,
higher frequency transitions have
also higher critical densities. Stäuber et al. (2004) show that
enhancements of molecules due to an inner FUV field should already be detectable with
single-dish telescopes having beam widths ![]() 11
11
![]() .
To show this for
the case of X-ray enhanced molecules, the density profiles of HCO+ and
HCS+ presented in Sect. 4 are used to compute the line
intensities with the Monte Carlo radiative transfer code Hogerheijde &
van der Tak (2000). The intrinsic (turbulent) line profile is taken to be a
Gaussian with a Doppler parameter of 1.6 km s-1, independent of
radius. Molecular data are taken from the Leiden atomic and molecular database
(Flower 1999; Schöier et al. 2005).
The line profiles are convolved to an appropriate telescope beam size. In order
to avoid optical depth effects we have modeled the isotope H13CO+. The
assumed isotope ratio is HCO+/H13CO+ = 60 (Wilson & Rood 1994).
.
To show this for
the case of X-ray enhanced molecules, the density profiles of HCO+ and
HCS+ presented in Sect. 4 are used to compute the line
intensities with the Monte Carlo radiative transfer code Hogerheijde &
van der Tak (2000). The intrinsic (turbulent) line profile is taken to be a
Gaussian with a Doppler parameter of 1.6 km s-1, independent of
radius. Molecular data are taken from the Leiden atomic and molecular database
(Flower 1999; Schöier et al. 2005).
The line profiles are convolved to an appropriate telescope beam size. In order
to avoid optical depth effects we have modeled the isotope H13CO+. The
assumed isotope ratio is HCO+/H13CO+ = 60 (Wilson & Rood 1994).
Figures 11 and 12 show that high-J transitions are indeed sensitive to the different models and may therefore be used as tracers for high energy radiation. The enhancement factors for the higher transitions presented in Table 3 confirm the results of Sect. 4. H13CO+ and HCS+ are clearly enhanced by X-rays. The enhancement factors for the H13CO+ J = 8-7 transition are between 2-43 compared to model 0 and between 1-11 compared to the FUV model 1. The J = 10-9 line of HCS+ is enhanced between 2 and 169 times compared to the models without X-rays or FUV field and between 0.2 and 21 times compared to the FUV model. No influence is seen, however, from an enhanced outer FUV field in the emission lines of H13CO+ and HCS+.
Figure 13 shows calculated H13CO+ lines for model 0 and
model 5 with cosmic-ray ionization rates
![]() s-1 and
s-1 and
![]() s-1. As
expected, the strongest line is that of model 5 with
s-1. As
expected, the strongest line is that of model 5 with
![]() s-1. For the J = 3-2 and the J = 4-3
transitions model 5 and model 0 with
s-1. For the J = 3-2 and the J = 4-3
transitions model 5 and model 0 with
![]() s-1 differ less than 30-50% and are therefore hardly
distinguishable. At higher frequencies, however, the two lines of model 5
clearly dominate the two lines of model 0. The J = 8-7 transitions
of model 5 are enhanced by a factor of
s-1 differ less than 30-50% and are therefore hardly
distinguishable. At higher frequencies, however, the two lines of model 5
clearly dominate the two lines of model 0. The J = 8-7 transitions
of model 5 are enhanced by a factor of ![]() 5 compared to that of model 0 with the higher cosmic-ray ionization rate. Higher J transitions of
H13CO+ can therefore be used to distinguish between the effects of a
central X-ray source and the effects of an enhanced cosmic-ray ionization. The
X-ray luminosity, however, should be of the order of
5 compared to that of model 0 with the higher cosmic-ray ionization rate. Higher J transitions of
H13CO+ can therefore be used to distinguish between the effects of a
central X-ray source and the effects of an enhanced cosmic-ray ionization. The
X-ray luminosity, however, should be of the order of ![]() 1031 erg s-1 as can be seen in Fig. 11 to distinguish
cosmic-ray ionization rates as high as
1031 erg s-1 as can be seen in Fig. 11 to distinguish
cosmic-ray ionization rates as high as
![]() s-1 from the effects of X-rays.
s-1 from the effects of X-rays.
Table 3:
Enhancement factors
![]() for different line transitions.
for different line transitions.
We have extended the chemical models of Doty et al. (2002) to study the impact of X-rays from a central source on the chemistry of YSO envelopes. The models are applied to the massive star-forming region AFGL 2591 using the physical structure proposed by van der Tak et al. (1999) and Doty et al. (2002). Our major results are summarized below:
1. X-rays can penetrate deep into the envelope due to their small cross
sections and affect the chemistry even at large distances from the source.
The abundances of many species are enhanced by 2-3 orders of magnitude.
Like FUV radiation, X-rays preferably enhance simple hydrides, ions and
radicals. The region which is influenced most by X-rays is ![]() 1000 AU.
Some species are enhanced throughout the entire envelope. The greater penetration
of X-rays is the main difference to the models of Stäuber et al.
(2004) where the influence of an inner FUV field on YSO envelopes was
studied (Sect. 4).
1000 AU.
Some species are enhanced throughout the entire envelope. The greater penetration
of X-rays is the main difference to the models of Stäuber et al.
(2004) where the influence of an inner FUV field on YSO envelopes was
studied (Sect. 4).
2. He+ and H3+ have enhanced abundances up to a factor of 1000 in the innermost region compared to models without X-rays. These two ions trigger an X-ray characteristic chemistry which is similar to that induced by cosmic rays. Although the X-ray ionization rate exceeds the cosmic-ray ionization rate for a large part of the envelope, it is found that in the case of AFGL 2591 the chemistry of the bulk of the envelope mass is dominated by the cosmic-ray induced reactions rather than X-ray induced ionization (Sect. 4).
3. The X-ray ionization rate is dominated by the "secondary'' H2
ionization rate resulting from fast electrons. The X-ray induced chemistry
therefore depends mainly on the H2 ionization rate
![]() which
is directly proportional to the X-ray luminosity (Sects. 4 and 6.1).
which
is directly proportional to the X-ray luminosity (Sects. 4 and 6.1).
4. Several molecules - among them N2O, HNO, SO, SO+, HCO+, CO+, OH+, N2H+, SH+ and HSO+ - are pure X-ray tracers, that is they are more likely to be enhanced by X-rays than by FUV radiation (Sect. 5.1). The ratio CN/HCN increases with increasing X-ray flux whereas the ratios HNC/HCN, HOC+/HCO+ and CO+/HCO+ are not sensitive to the X-ray flux and trace the FUV field as confirmed by observations and models of PDRs by several authors. Whether the CN/HCN ratio is enhanced by an inner FUV field or by X-rays depends mainly on the FUV absorbing inner column density (Sect. 5.2).
5. SH+ and HSO+ are found to be excellent X-ray tracers. They are 100-10 000 times more abundant in models with X-rays. Both are more likely to be enhanced by X-rays than by an inner FUV source. In addition, the abundance of SH+ correlates with the X-ray flux. Only four hyperfine lines of SH+ have so far been measured in the laboratory whereas no information is available for HSO+. We would therefore like to encourage laboratories to further investigate these molecules (Sect. 5).
6. CO2 abundances are reduced in the gas-phase through X-ray induced
FUV photons. For temperatures
![]() K, H2O is destroyed by
X-rays with luminosities
K, H2O is destroyed by
X-rays with luminosities
![]() erg s-1
(Sect. 4.1).
erg s-1
(Sect. 4.1).
7. An enhanced outer FUV field increases the column densities of C, C+ and simple carbon-hydrides like CH and CH+. The influence on the total column density of other species is minor, however (Sect. 4.7).
8. Comparison between observations and models is in general improved with
models containing an inner X-ray source. Best-fit models for AFGL 2591
predict an X-ray luminosity
![]() erg s-1 with
a hard X-ray spectrum
erg s-1 with
a hard X-ray spectrum
![]() K. The ratio of
the X-ray luminosity to the total luminosity is found to be
K. The ratio of
the X-ray luminosity to the total luminosity is found to be
![]() .
Best-fit models also confirm the
chemical age
.
Best-fit models also confirm the
chemical age
![]() yr of AFGL 2591 suggested by Doty et al.
(2002). The results become independent of time at high X-ray
luminosities once
yr of AFGL 2591 suggested by Doty et al.
(2002). The results become independent of time at high X-ray
luminosities once
![]() yr (Sect. 6.1).
yr (Sect. 6.1).
9. Previously proposed X-ray tracers like CN or NO are confirmed by our
models. The enhancement of NO, however, is not obvious since it is only
prominent in the inner ![]() 500 AU of the envelope. Small
(0.5
500 AU of the envelope. Small
(0.5
![]() -1
-1
![]() )
beams are therefore required to observe the
enhanced region of NO (Sect. 5.3).
)
beams are therefore required to observe the
enhanced region of NO (Sect. 5.3).
10. Calculated line intensities of H13CO+ and HCS+ show that the
enhancement due to X-rays is detectable for these species with
single-dish telescopes. Due to the frequency dependence of the critical
density, the influence of X-rays is more prominent in higher frequency
transitions. High-J lines of H13CO+ can be used to separate the
effects of X-ray and cosmic-ray ionization for
![]() erg s-1 and
erg s-1 and
![]() s-1 (Sect. 7).
s-1 (Sect. 7).
11. The effects of Compton ionization on the chemistry are studied and
compared to results of models without Compton scattering. It is found that the
differences are minor and that the effects of Compton ionization can be
neglected for column densities
![]() cm-2
(Sect. 2.1).
cm-2
(Sect. 2.1).
12. Future instruments like Herschel-HIFI, SOFIA and ALMA are needed to verify our models. In particular, Herschel-HIFI will be able to observe many hydrides whereas the sensitivity and spatial resolution of ALMA is well-suited to measure the size and geometry of the emitting region.
Acknowledgements
The authors are grateful to Michiel Hogerheijde and Floris van der Tak for the use of their Monte Carlo code. We thank the referee for the valuable comments. The authors would further like to thank Manuel Güdel, Paolo Grigis and Kevin Briggs for useful discussions. This work was partially supported under grants from The Research Corporation (SDD). Astrochemistry in Leiden is supported by the Netherlands Research School for Astronomy (NOVA) and by a Spinoza grant from the Netherlands Organization for Scientific Research (NWO).
![\begin{figure}
\par\resizebox{7.8cm}{!}{\includegraphics[clip]{2889f07.eps}}\end{figure}](/articles/aa/full/2005/36/aa2889-05/Timg204.gif) |
Figure 7:
Column density ratios for the inner |
| Open with DEXTER | |
Table A.1: Initial gas-phase and total abundances.
Table B.1: Electronic recombination reactions.
Table B.2: Charge transfer reactions.
Emission lines on the other hand arise from throughout the envelope. The column densities for the emission lines in Table E.1 are calculated from the fractional abundances that were determined through detailed, non local thermodynamic equilibrium (NLTE) radiative transfer modeling (e.g., van der Tak et al. 1999). For a density distribution like that of AFGL 2591 (Sect. 2.2), the mass is dominated by the outer part of the envelope and emission measurements often probe the exterior (see also Doty et al. 2002 for a detailed discussion).
Table E.1: Comparison of best-fitting models with observed radial column densities for AFGL 2591.