A&A 440, 845-853 (2005)
DOI: 10.1051/0004-6361:20040196
E. J. Lindfors 1,2 - E. Valtaoja1,3 - M. Türler4,5
1 - Tuorla Observatory, Väisälä Institute of Space Physics and Astronomy, University of Turku, 21500 Piikkiö, Finland
2 -
Metsähovi Radio Observatory, Helsinki University of Technology, 02540 Kylmälä, Finland
3 -
Department of Physics, University of Turku, 20100 Turku, Finland
4 -
Geneva Observatory, ch. des Maillettes 51, 1290 Sauverny, Switzerland
5 -
INTEGRAL Science Data Centre, ch. d'Ecogia 16, 1290 Versoix, Switzerland
Received 4 February 2004 / Accepted 13 May 2005
Abstract
The high-energy spectral energy distributions of blazars have been
modelled many times, but none of the previous studies have started from
synchrotron components derived from observations. The common approach has
instead been to start with a one-component theoretical synchrotron
spectrum, although it is well established both from observations and from
theory that the synchrotron emission originates from several components:
from a constant jet component and from shocks propagating downstream in
the jet. Furthermore, the observed synchrotron flux variability appears
to be entirely due to evolving shocks.
In this paper we present the first attempt to model the synchrotron, and consequently also the inverse Compton, spectral energy distributions in a more realistic manner. Instead of assuming a single theoretical spectrum as the basis of modelling, we use a code based on the standard shocked jet framework to identify the spectra and the time evolution of both the jet and of the many shock components in 3C 279, one of the best-observed blazars. These semiempirical components, derived from extensive multifrequency monitoring, are then used to estimate the inverse Compton component produced by each component.
Previous studies have shown that gamma-ray flaring occurs preferentially after a new mm-radio flare begins, or, equivalently, after a new VLBI shock component has separated from the core. Observed time delays indicate that the shock component is already well outside the broad line region when gamma-ray flaring occurs, casting doubt on the efficiency of external Compton mechanisms. We therefore apply our modelling to the synchrotron self-Compton scenario in order to estimate how large a fraction of the high energy flux during two EGRET observing periods could be explained by SSC radiation. We find that the X-ray flux during both a quiescent and a flaring stage of 3C 279 can be explained by SSC from the jet and from several shocks, but that the gamma-ray fluxes cannot.
Key words: galaxies: active - galaxies: jets - galaxies: quasars: individual: 3C 279
The EGRET instrument on-board the Compton Gamma-Ray Observatory (CGRO) detected about 60 quasars during its 10 years of observations (Mukherjee et al. 1997; Hartman et al. 1999). All the detected quasars belong to the blazar class and no radio-quiet AGNs have been detected.
Correlations between radio and gamma-ray emission in samples of compact, flat-spectrum, highly variable radio sources have been studied by Reich et al. (1993), Valtaoja & Teräsranta (1995, 1996), Mücke et al. (1996), Lähteenmäki et al. (1997, 2000), Tornikoski & Lähteenmäki (2000) and Lähteenmäki & Valtaoja (2001), all concluding that correlations exist. The total flux density variations at radio frequencies are also closely related to ejections of superluminal jet components seen with Very Long Baseline Interferometry (VLBI) (e.g. Savolainen et al. 2002). This indicates that the total flux density variations at radio frequencies are due to shocks propagating downstream in the jet and would lead to the natural assumption that also the variable gamma-ray emission originates in the shocks. The connection between gamma-ray flares and superluminal ejections at 22 GHz and 43 GHz has been studied recently by Jorstad et al. (2001), who found that 50% of the gamma-ray flares in their data set were associated with ejections of superluminal jet components.
According to most models, the gamma-ray emission is produced via the inverse Compton mechanism in the relativistic jet. There have been several suggestions for the origin of the low frequency seed photons which are up-scattered into gamma-rays. The seed photons could be produced within the jet via synchrotron radiation. This mechanism is called synchrotron self-Compton (SSC) (Maraschi et al. 1992; Bloom & Marscher 1996). The seed photons could also be external to the jet and originate in the accretion disk (Dermer & Schlickeiser 1993). These seed photons could also be reprocessed by broad line region clouds (Ghisellini & Madau 1996) or originate in the dust torus surrounding the BLR (Sikora et al. 1994). These mechanisms are referred to as external Compton (EC).
3C 279 (z= 0.538) was the first blazar discovered as a ![]() -ray source with
the CGRO (Hartman et al. 1992), and was thereafter regularly observed by
CGRO. It is the object for which there are most Compton data available and was
thus chosen to be used in this study. 3C 279 has also been frequently observed
in the radio regime. It has also been the target of many multi-wavelength
campaigns and therefore the spectral energy distributions (SEDs) are well sampled.
-ray source with
the CGRO (Hartman et al. 1992), and was thereafter regularly observed by
CGRO. It is the object for which there are most Compton data available and was
thus chosen to be used in this study. 3C 279 has also been frequently observed
in the radio regime. It has also been the target of many multi-wavelength
campaigns and therefore the spectral energy distributions (SEDs) are well sampled.
The SED of 3C 279 has been modeled many times before, most recently by Hartman et al. (2001) and Ballo et al. (2002). In these papers most of the gamma-ray emission is generated via the EC mechanism while the SSC mechanism contributes mainly to the X-ray emission. In common with other previous model fits, the synchrotron emitting region is assumed to be either an inhomogeneous jet (Hartman et al. 2001) or a single homogeneous component (Ballo et al. 2002). In both cases only the innermost portion of the emitting region is modeled and the radio emission is neglected, because it comes from much further out along the jet. The changes in gamma-ray flux are ascribed mainly to variations of the bulk Lorentz factor of the plasma.
It is well known that the synchrotron radiation at any given time originates in many components: in the underlying jet and in the shock components propagating downstream of the jet with relativistic velocities. This shock-in-jet scenario (e.g. Marscher & Gear 1985) has been commonly accepted for the last 20 years, as it is able to explain radio to sub-millimeter continuum spectra, variability and VLBI data. Whatever the assumed inverse Compton mechanism, a more realistic starting point in modelling the high-energy emission is therefore to consider a multi-component model, where the synchrotron radiation originates from the jet and from the shocks propagating downstream in the jet. This is the new approach used here.
Another new aspect is that we identify the synchrotron components from multi-frequency flux variations, and derive the spectra of these components based on observations from radio to optical range instead of theoretical models, using a minimum of assumptions consistent with the shock-in-jet framework. Such an approach makes the calculation of the inverse Compton components from the semiempirical component spectra more difficult, but in compensation it gives a much more realistic picture of what synchrotron components actually are available for IC modelling. For reasons given in Sect. 2 we apply our modelling to the synchrotron self-Compton case; however, the properties of the identified synchrotron components also constrain external Compton models.
In this paper we fit the SEDs of two EGRET epochs (P1, 1991.47 and P2, 1993.0) assuming that as large a fraction as possible of both the X-ray and the gamma-ray emission is the sum of SSC emission from the jet component and the strongest shock components. In the standard shocked jet scenario the synchrotron flux variations are mainly due to the formation and evolution of shocks, not to changes in the jet flow parameters. Independent of the IC mechanism assumed, this means that the changes in the gamma-ray flux are also due to shocks in the jet: we expect that at high gamma states there is a strong, variable shock component present, while at low states a contribution from the underlying constant jet component is also apparent. Our modelling in this paper and in Lindfors et al. (2005) shows that this is indeed the case for at least 3C 279.
The observed SEDs of 3C 279 (and ![]() -ray loud blazars generally)
show two peaks (see e.g. Fig. 5), which are interpreted as due to the
maximum output of the synchrotron and of the inverse Compton mechanisms.
The frequency and the luminosity of the inverse Compton maximum
depends on the Doppler factor, the magnetic field strength and, in the case of
an external Compton mechanism, on the luminosity of the external photon
field. All these quantities are difficult or impossible to determine
exclusively from observations.
-ray loud blazars generally)
show two peaks (see e.g. Fig. 5), which are interpreted as due to the
maximum output of the synchrotron and of the inverse Compton mechanisms.
The frequency and the luminosity of the inverse Compton maximum
depends on the Doppler factor, the magnetic field strength and, in the case of
an external Compton mechanism, on the luminosity of the external photon
field. All these quantities are difficult or impossible to determine
exclusively from observations.
For the inverse Compton maximum to be in the gamma-ray energy range the Doppler boosting factor has to be high. Additionally, if we assume the SSC mechanism to be working, the magnetic field strength is required to be low. The EC mechanism requires stronger magnetic fields, and also the luminosity of the external photon field has to be high. Therefore it is obvious that the EC mechanism can produce gamma-rays only very close to the apex of the jet, not at large distances beyond the BLR clouds. Reverberation mapping has shown that the broad line region sizes are smaller than 1 parsec even for luminous quasars. If 3C 279 follows the size-luminosity relation of Kaspi et al. (2000) the radius of its BLR is about 0.1 parsec.
The spectra of a large number of Compton-detected sources have been modeled using a variety of approaches and emission mechanisms. Although the first model fits to the gamma-ray spectra used the SSC mechanism (e.g. Maraschi et al. 1992), more recent modeling efforts have in general favored the EC mechanism as the main contributor to the gamma-ray flux in blazars. The most extreme TeV blazars are an exception, since for them SSC models seem to provide very good fits to the data (e.g. Konopelko et al. 2003).
In the particular case of 3C 279, the extensive modeling effort of Hartman et al. (2001), which included both SSC and EC with cloud and disk seed photons, resulted in good fits to most of the high frequency data for 11 epochs. During high gamma ray states, the disk and BLR cloud EC dominate the gamma-ray flux above 1020 Hz, while the 1017 to 1019 Hz X-ray flux is exclusively SSC from the jet. The SSC component is very broad, and cannot reproduce the apparent sharp bumps and other details in the gamma-ray spectrum.
However, there are several reasons to question the validity of EC mechanisms
for both 3C 279 and for blazars in general. First of all, it is well known
that variability of the Compton peak tends to be stronger than that of the
synchrotron peak. In the simplest EC models, the dependence should be linear,
which is not what is usually detected. In general, the quadratic dependence of
the SSC model fits the data much better. This is also the case for 3C 279. We
have estimated the synchrotron flux, S(s), at 1014 Hz and the IC flux,
![]() ,
at 1023 Hz during the 11 observing periods using the data
presented in Hartman et al. (2001). As Fig. 1 shows, the dependence is
quadratic rather than linear. In particular, during the two adjacent viewing
periods 5a (start date Jan. 16, 1996) and 5b (start date Jan. 30, 1996),
,
at 1023 Hz during the 11 observing periods using the data
presented in Hartman et al. (2001). As Fig. 1 shows, the dependence is
quadratic rather than linear. In particular, during the two adjacent viewing
periods 5a (start date Jan. 16, 1996) and 5b (start date Jan. 30, 1996),
![]() with a>2. Similar strong changes
are also seen during the two other closely spaced viewing periods 3a/3b
(separated by one month) and 6a/6b (five months).
with a>2. Similar strong changes
are also seen during the two other closely spaced viewing periods 3a/3b
(separated by one month) and 6a/6b (five months).
![\begin{figure}
\par\includegraphics[angle=-90,width=8.3cm,clip]{0196fig1.ps}\end{figure}](/articles/aa/full/2005/36/aa0196-04/Timg5.gif) |
Figure 1:
The synchrotron flux at 1.36 |
| Open with DEXTER | |
A stronger than linear dependence can be achieved in the EC scenario by
letting the bulk Lorentz factor of the emission region change. This was the
method used by Hartman et al. (2001), who let the jet Lorentz factor vary
between 4 and 14 during the epochs in 1991-2000. The change between adjacent
periods 5a and 5b was estimated to be from ![]() to
to
![]() .
However, its seems very doubtful whether such a rapid change in
the global properties of the flow is physically feasible. As far as we know,
there is no observational evidence, such as VLBI data, for such rapid changes
in the Lorentz factor. It is also easy to calculate that about one month later
the more rapid flow should have collided with the preceding slower one,
possibly causing observable internal shocks such as those modelled by Spada et al. (2001). However, the synchrotron flux of 3C 279 continued to decay
smoothly in February-March 1996.
.
However, its seems very doubtful whether such a rapid change in
the global properties of the flow is physically feasible. As far as we know,
there is no observational evidence, such as VLBI data, for such rapid changes
in the Lorentz factor. It is also easy to calculate that about one month later
the more rapid flow should have collided with the preceding slower one,
possibly causing observable internal shocks such as those modelled by Spada et al. (2001). However, the synchrotron flux of 3C 279 continued to decay
smoothly in February-March 1996.
One would also expect that such large changes in the Lorentz factor of the
flow should be seen in the observed expansion speeds of the components ejected
during the same period. For example, assuming that the viewing angle ![]() is two degrees (Lähteenmäki & Valtaoja 1999; Wehrle et al. 2001),
is two degrees (Lähteenmäki & Valtaoja 1999; Wehrle et al. 2001),
![]() corresponds to
corresponds to ![]() (app) = 1.1 and
(app) = 1.1 and ![]() to
to ![]() (app) =
11. However, the observed range of
(app) =
11. However, the observed range of ![]() (app) is much smaller, from 4.8 to 7.5 (Wehrle et al. 2001). Turning the argument around, a simple calculation shows that the ranges
(app) is much smaller, from 4.8 to 7.5 (Wehrle et al. 2001). Turning the argument around, a simple calculation shows that the ranges ![]() (app)
= 4.8-7.5 and
(app)
= 4.8-7.5 and
![]() are compatible only if
are compatible only if ![]() is around 14 degrees, or changes from less than one degree to 14 degrees during the Compton epochs. Both alternatives
conflict with VLBI and other data. While this in itself does not make the
modelling of Hartman et al. invalid, it demonstrates that the wide range of
Lorentz factors necessary in the EC scenario is rather problematic.
is around 14 degrees, or changes from less than one degree to 14 degrees during the Compton epochs. Both alternatives
conflict with VLBI and other data. While this in itself does not make the
modelling of Hartman et al. invalid, it demonstrates that the wide range of
Lorentz factors necessary in the EC scenario is rather problematic.
Since the synchrotron flux variations are mainly, if not exclusively, due to the new shocks forming in the jet, a change in the jet flow parameters is not the proper way to model either the synchrotron or the IC variability, whatever the emission mechanism.
A third, arguably the strongest, reason to consider SSC models for 3C 279, and for blazars in general, comes from the radio/gamma correlation studies of samples of EGRET sources. The millimeter radio emission starts to rise when a new shock forms in the jet; this also corresponds to the extrapolated zero separation epoch of a new VLBI component (Savolainen et al. 2002). Valtaoja & Teräsranta (1995, 1996) found that the gamma-ray flare occurs preferably after the mm-flux and cm-flux (Mücke et al. 1996) starts to rise. In a recent analysis of EGRET data, Lähteenmäki & Valtaoja (2003) confirmed that there were more gamma-ray detections during the rising than during the falling radio state, a result significant at the 99.9% level. The average delay from the onset of the mm-flare to a strong gamma-ray flare was between 30 to 70 days. A similar result was found by Jorstad et al. (2001), who found that the gamma-ray flares occur on average 52 days after the estimated VLBI zero separation epoch. A Monte Carlo analysis showed that the radio and the gamma-ray events were associated with each other with greater than 99.999% confidence.
The available evidence thus indicates that strong gamma-ray flares are connected with new shocks developing in the jet. In general, one then expects the observed sequence of events. First the shock forms, separates from the VLBI core, and the high radio frequency flux starts to rise as the shock grows and its spectrum propagates to lower frequencies. As the seed electron population evolves, the IC flux also starts to rise, and the gamma-ray flux peaks usually before the shock spectrum turnover reaches the millimeter range and the radio flux starts to decay again.
In itself, the above sequence can be similar both for the SSC and for the EC cases. However, the observed average time delay from the onset of the radio
flare (or, equivalently, from the zero separation epoch) translates into a
distance of several parsecs from the apex of the jet at the time the gamma-ray
flaring occurs; Lähteenmäki & Valtaoja (2003) found an average distance
of 4.9 parsec for the events in their sample. Virtually all EC models assume
that the gamma-ray emission comes from the apex of the jet, much closer to the
accretion disk and well within the BLR. This is necessary to obtain sufficient
external photon densities. In this case the ![]() -ray flare should be seen
at the very beginning, or even slightly before, the mm-flare, contrary to
observations. For example, in Hartman et al. (2001) the "injection radius'' is
assumed to be 0.025 pc, with the BLR stretching from 0.1 to 0.4 pc. In such a
scenario one expects first to see a
-ray flare should be seen
at the very beginning, or even slightly before, the mm-flare, contrary to
observations. For example, in Hartman et al. (2001) the "injection radius'' is
assumed to be 0.025 pc, with the BLR stretching from 0.1 to 0.4 pc. In such a
scenario one expects first to see a ![]() -ray flare, and only later a radio
flare as the perturbation travels down the jet and results in a
new shock. This is contrary to observations.
-ray flare, and only later a radio
flare as the perturbation travels down the jet and results in a
new shock. This is contrary to observations.
On the other hand, if gamma rays are emitted much further out, as the evidence seems to indicate, the external photon fields are far too weak to provide a significant EC contribution to the gamma-ray flux. Some variant of the SSC mechanism then appears to be the only viable alternative, despite the problems associated with it.
For the radio to optical light-curve decomposition we used radio data at 12 radio-to-submillimetre frequencies, four infrared and two optical wavebands from 1989 to the end of 1993. The 4.8 GHz, 8.0 GHz and 14.5 GHz data are from the University of Michigan Radio Astronomy Observatory (UMRAO). The other radio data as well as the infrared data are from Stevens et al. (1994), who collected them from six observatories: James Clerk Maxwell Telescope (JCMT), Institut de Radio Astronomie Millimetrique (IRAM), Swedish-ESO Submillimeter Telescope (SEST) and Metsähovi Radio Observatory, United Kingdom Infrared Telescope and the ESO 2.2 m telescope. The optical data from R- and V-bands has been published in Hartman et al. (1996) and Maraschi et al. (1994).
The gamma-ray data are from the CGRO-satellite as reanalyzed by Hartman et al. (2001). For epoch P1 we also used X-ray data from Ginga, which were published in Hartman et al. (1996). For P2 we used ultraviolet data from IUE and X-ray data from ROSAT, published in Maraschi et al. (1994).
There have been many efforts to identify the individual components from radio to sub-millimeter light-curves using the shocked jet framework. Litchfield et al. (1995) and Stevens et al. (1995, 1996, 1998) managed to follow the early evolution of individual outbursts by subtracting a quiescent spectrum (assumed to be constant) from the total spectrum. Valtaoja et al. (1999) identified outbursts by decomposing the variations in millimeter light-curves into exponential flares. Türler et al. (1999) used a decomposition of multi-wavelength light-curves into a series of self-similar flaring events to derive the observed properties of synchrotron outbursts. The method was further developed in Türler et al. (2000), where the shock model of Marscher & Gear (1985) was used to describe physically both the average evolution of the outbursts and their individual characteristics. The Marscher & Gear model was found to provide a good description of the radio to sub-millimeter light-curves of 3C 273.
![\begin{figure}
\par\includegraphics[width=10.8cm,clip]{0196fig2.ps}\end{figure}](/articles/aa/full/2005/36/aa0196-04/Timg13.gif) |
Figure 2: The multi-frequency light-curves and model fits for 3C 279. The best-fit total flux density light-curve (solid line) is the sum of a constant jet component (long-dashed line), the global decay of all outbursts peaking before 1989.0 (thick dotted line) and 6 outbursts (dotted lines). The outburst fluxes are shown in a cumulative manner. The starting times of the outbursts are shown above the light-curves. |
| Open with DEXTER | |
To determine the spectra and the evolution of individual shock components from
the radio light-curves of 3C 279 we used the method introduced in Türler et al. (2000). The code uses a generalization of the original shock model of
Marscher & Gear, describing an accelerating or decelerating shock wave in a
non-adiabatic jet. The shock is described by parameters r, k, b and d,
which determine the radius of the shock (
![]() ), the energy density
of the electrons (
), the energy density
of the electrons (
![]() ), the magnetic field strength (
), the magnetic field strength (
![]() )
and the Doppler factor (
)
and the Doppler factor (
![]() )
at a distance L along
the jet. The shape of the emission spectrum behind the shock front is assumed
to be that of a simple synchrotron spectrum (with electron energy distribution
)
at a distance L along
the jet. The shape of the emission spectrum behind the shock front is assumed
to be that of a simple synchrotron spectrum (with electron energy distribution
![]() )
with two spectral breaks, which is fitted to all the
light-curves simultaneously. The breaks in the spectrum are a low frequency
break, which is needed to bring the optically thick spectral index to +2.5,
and a high frequency break steepening the optically thin spectral index
by 0.5 for higher frequencies and corresponding to a break in electron energy
distribution. These breaks are smoothened to achieve a more realistic model
(Türler et al. 2004). The shock model and the parameterizations of the code
are presented in detail in Türler et al. (2000).
)
with two spectral breaks, which is fitted to all the
light-curves simultaneously. The breaks in the spectrum are a low frequency
break, which is needed to bring the optically thick spectral index to +2.5,
and a high frequency break steepening the optically thin spectral index
by 0.5 for higher frequencies and corresponding to a break in electron energy
distribution. These breaks are smoothened to achieve a more realistic model
(Türler et al. 2004). The shock model and the parameterizations of the code
are presented in detail in Türler et al. (2000).
In this work we wanted to decompose lightcurves from radio to infrared and optical frequencies (in total 19 frequencies). In order to do this we added a smooth turnover to the spectrum at the highest frequencies. The turnover corresponds to a exponential cut-off in the electron energy distribution at high energies. Otherwise only minor changes to the code were made. As we wanted to take into account the flux of the underlying jet, we added to the code a constant synchrotron component which also has a high frequency break. The turnover flux and frequency are left as free parameters of the fit. In 3C 279 the contribution of the outer jet to the observed flux is negligible, so this additional component used for 3C 273 in Türler et al. (2000) could be ignored. The specifity of the individual outbursts is modelled by varying the flux, the frequency and the time of outbursts as done in Türler et al. (1999).
All the 19 frequencies were used in the model fit. The light-curves and the
resulting model fits using six outbursts are shown for 10 of the frequencies
in Fig. 2. The best-fit decomposition has a reduced ![]() value of 10.0. In the highest frequencies (infrared and optical), fitting the details
of the lightcurves was impossible due to a lack of monitoring data. Still, the
general flux level of our fit agrees well with the observed levels. However,
a much better fit is achieved for later epochs, for which more
optical data are available and, consequently, the code gives more weight to
the goodness of the optical fit (Lindfors et al. 2005).
value of 10.0. In the highest frequencies (infrared and optical), fitting the details
of the lightcurves was impossible due to a lack of monitoring data. Still, the
general flux level of our fit agrees well with the observed levels. However,
a much better fit is achieved for later epochs, for which more
optical data are available and, consequently, the code gives more weight to
the goodness of the optical fit (Lindfors et al. 2005).
The model used here assumes fixed values for parameters d and b. Fixing d=0.0 means that we keep the Doppler factor constant during the shock evolution. b is fixed to 1.0 as for 3C 279 the magnetic field is known to be perpendicular to the jet (Marscher, private communication). For s, rand k the light-curve decomposition gives values of 2.25, 0.78 and 4.0 respectively and these are same for all shocks. A more detailed analysis of 3C 279 during 1989-1999, with a discussion of the physical significance of the shock parameters, will be presented in Lindfors et al. (2005).
As the purpose of the fit was to identify the radiating synchrotron
components, we extracted the spectra of the components from the model fits for
two epochs when EGRET was observing 3C 279, namely the high state on June 1991
(epoch P1) and the low state in December 1992-January 1993 (epoch P2). During P1 (Fig. 3a) there are two shock components that are brighter than the underlying jet component: the shock number 1 (starting at 1989.7) and the shock number 3. The shock number 1 decays very slowly and is the dominant component at millimeter frequencies at both epochs. The shock number 3 on the
other hand is short-lived and only important at highest frequencies, where it
dominates the IR-to-optical flux. According to our fits, this outburst started
at 1991.25 so that at the epoch of EGRET observations (1991.47) it has
propagated about 16 parsec (![]() = 0.22 years, assuming our IC model fit
value D=19 and a viewing angle of 2 degrees) from the apex of the jet and is
therefore also well outside the BLR.
= 0.22 years, assuming our IC model fit
value D=19 and a viewing angle of 2 degrees) from the apex of the jet and is
therefore also well outside the BLR.
![\begin{figure}
\par\includegraphics[angle=-90,width=13.8cm,clip]{0196fig3.ps}\end{figure}](/articles/aa/full/2005/36/aa0196-04/Timg21.gif) |
Figure 3: The synchrotron components at epochs P1 a) and P2 b). The squares indicate the measured fluxes with error bars and the solid line corresponds to the total model spectrum, which is the sum of a constant jet component (long-dashed line) and the individual synchrotron outbursts (dotted lines). The dotted line at the lowest frequencies is the contribution from all outbursts peaking before 1989. Outbursts 1-4 (of Fig. 2) are identified. |
| Open with DEXTER | |
In the low gamma level state P2 the dominant component is the shock number 1. The shock number 3 and the shock number 4 (started at 1992.51, D=10, distance 10 parsec) is also stronger than the underlying jet component. The spectra of the components are shown in Fig. 3b.
It is possible to use a numerical code to model the inverse Compton emission from the jet. This was the approach used by Hartman et al. (2001) and Ballo et al. (2002). However, such calculations require many parameters describing the electron population (the low and the high energy cut-off of the population, the spectral index and the electron density), the assumed geometry, and the external photon field (accretion disk luminosity, Thomson depth of the BLR, the inner and outer boundary of the BLR). Most of these parameters cannot be estimated from the data, but they significantly affect the calculated IC spectrum (see Bloom & Marscher 1996 for some examples). Numerical codes may appear more accurate, but they are not necessarily more realistic.
A fully self-consistent treatment would require a code fitting simultaneously not only the synchrotron components but also the gamma-ray flux (i.e., the sum of the IC fluxes from the corresponding synchrotron components). However, at present we do not have any data on the temporal behavior of the gamma-ray component, and therefore the inverse Compton losses and their effect on the synchrotron components can be treated only in an approximate way. In effect, we can ensure self-consistency only at the epoch of the gamma-ray observation.
We use a simple analytical method, similar to that presented in Ghisellini et al. (1996), to estimate the flux of each IC component in terms of B, D and the variability timescale (
![]() ). The frequency of the SSC photons depends on the frequency of the synchrotron photons (e.g. Ghisellini et al. 1996):
). The frequency of the SSC photons depends on the frequency of the synchrotron photons (e.g. Ghisellini et al. 1996):
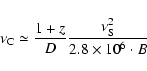 |
(1) |
The SSC flux can be calculated from (Ghisellini et al. 1996):
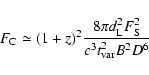 |
(2) |
The frequency and the flux of the SSC spectrum depends on D, B and
![]() (fixing the radius of the emitting region with
(fixing the radius of the emitting region with
![]() ), which cannot be determined conclusively from the observations. We vary these parameters to see what fraction of the
high-energy component can be due to SSC, given the jet and the shock
components we have derived from the model fitting.
), which cannot be determined conclusively from the observations. We vary these parameters to see what fraction of the
high-energy component can be due to SSC, given the jet and the shock
components we have derived from the model fitting.
We can set limitations for values of D from VLBI (Wehrle et al. 2001; Jorstad et al. 2004) and variability temperature observations (Lähteenmäki & Valtaoja 1999), giving a range of values from 7 to 39.
The magnetic field strength typically used in theoretical modelling is 1 G
close to the central engine, but in fact there is no accurate way to
derive its value from the observations. We therefore
cannot set straight limitations on magnetic field strength values, but note
that the shocks are far away from the apex of the jet and the magnetic field
there is weaker than at the apex as we assume
![]() .
.
We get a lower limit to the magnetic field strength when we consider the
cooling time scale of the electrons. In 3C 279 at epoch P1 the inverse Compton
luminosity is about 10 times higher than the synchrotron luminosity. Therefore
the dominating cooling mechanism of the electrons is inverse Compton
cooling, if we assume that the gamma-ray flare lasts long enough to
contribute significantly to the overall cooling. This is of course not true
for all shock components at all epochs, but as we are most interested in fresh
components which contribute most to the high energy spectrum, this
approximation is justified. The inverse Compton cooling time in the observer
frame in seconds is then ten times shorter than the synchrotron
cooling time, giving:
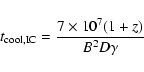 |
(3) |
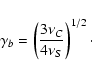 |
(4) |
We have very little information on typical gamma-ray variability timescales. It is often stated that gamma-rays show significant variability in daily timescales, and consequently the size of the emitting region is assumed to be quite small. However, if we look at the best data sets on day-to-day variations, presented in Wehrle et al. (1998) and Hartman et al. (2001), we can see that these extreme variations are based on just one or two data points. In addition, due to the relatively poor sensitivity of EGRET they refer to the strongest ever observed flares. Even if real, such gamma-ray flickering is not necessary an indication of the source size, for example if the flickering is due to perturbations along the jet (Ghisellini & Madau 1996). In fact, the three 3C 279 flares with daily sampling can be well fitted with an exponential rise or decay with timescales of 19 days (the Jan./Feb. 1999 flare), 8 days (Feb./Mar. 2000 flare) and 4 days (Jan./Feb. 1996); the X-ray data give similar timescales.
On the other hand, the upper limit for variability timescales in 3C 279 is
provided by the well-sampled radio fluxcurves from the Metsähovi monitoring
program. The modelled radio flares in Lähteenmäki & Valtaoja (1999) have
timescales ranging from 100 to 600 days, and the most rapid radio flare ever
detected in 3C 279 (occurring outside EGRET observing epochs) had
![]() = 25 days. We therefore adopt
= 25 days. We therefore adopt
![]() = 25 days
as the upper limit for the variability time scale. This is then also the upper
limit for the cooling time of the electrons.
= 25 days
as the upper limit for the variability time scale. This is then also the upper
limit for the cooling time of the electrons.
These constraints do not fix uniquely the SSC component corresponding to a given synchrotron spectrum. Varying the values of B and D, we have therefore searched for a solution that maximizes the total SSC flux during epochs P1 and P2, while still conforming with the assumptions listed above.
In order to estimate the constant underlying jet component, the low state of P2 was fitted first. We cannot reproduce the observed EGRET fluxes with the synchrotron self-Compton emission from the shock components because this would require unrealistically long cooling times for the electrons (several
years). With the underlying jet component the cooling time scale is not an
issue, as we do not have any information on the variability
timescale. But fitting the observed EGRET points with the underlying jet
component would require unrealistically low magnetic field strengths (50 ![]() G, assuming a variability timescale of 100 days), and moreover we would be
above the upper limits from OSSE and COMPTEL observations. Therefore we assume
that since the synchrotron radiation from the fresh shock component (outburst 4) is stronger than the synchrotron emission from the underlying jet, the same
is also the case for SSC. With the assumed timescale of 25 days, the
best we can achieve is to reproduce the X-ray flux, where we have only one data point. Our fit for this epoch is shown in Fig. 4, which presents the
best fit possible with our constrains. As can be seen, a simple multicomponent
SSC model is not able to explain the gamma-ray emission at this epoch, but the
whole X-ray flux can be due to SSC, with roughly equal contributions from the
jet and from the shock.
G, assuming a variability timescale of 100 days), and moreover we would be
above the upper limits from OSSE and COMPTEL observations. Therefore we assume
that since the synchrotron radiation from the fresh shock component (outburst 4) is stronger than the synchrotron emission from the underlying jet, the same
is also the case for SSC. With the assumed timescale of 25 days, the
best we can achieve is to reproduce the X-ray flux, where we have only one data point. Our fit for this epoch is shown in Fig. 4, which presents the
best fit possible with our constrains. As can be seen, a simple multicomponent
SSC model is not able to explain the gamma-ray emission at this epoch, but the
whole X-ray flux can be due to SSC, with roughly equal contributions from the
jet and from the shock.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0196fig4.ps}\end{figure}](/articles/aa/full/2005/36/aa0196-04/Timg37.gif) |
Figure 4: The spectral energy distribution of 3C 279 during epoch P2 (1993.0). The total inverse Compton energy spectrum (solid line) is the sum of the SSC spectrum of the underlying jet component (dashed line) and of the SSC spectrum of the 1st and 4th shock component (dotted lines). Arrows indicate upper limits. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{0196fig5.ps}\end{figure}](/articles/aa/full/2005/36/aa0196-04/Timg38.gif) |
Figure 5: The spectral energy distributions of 3C 279 during epoch P1 (1991.47). The total inverse Compton energy spectrum (solid line) is composed of the SSC spectrum of the underlying jet component (dashed line) and the SSC spectrum of the shock components 1, 2 and 3 (dotted lines). |
| Open with DEXTER | |
In the SED of the high state P1 of 1991.47, shown in Fig. 5, the SSC jet
component was fixed to the same frequency and flux as at P2, as it is assumed
to stay constant. At this epoch there are two synchrotron shock components
that are stronger than the underlying jet component. In our best model fit the
X-ray emission originates from shock number 1 and shock number 3, shock
number 3 contributing slightly more to higher frequencies. The flux from shock
number 3 is not sufficient to explain the gamma-ray data points; given the our
constraints, the maximum flux is only about 10% of the observed one. (If we
force the IC flux from component number 3 to pass through the X- and the
gamma-ray data points, we get B = 2 mG, D = 11 and
![]() d
according to Eq. (3), obviously a too large value for
d
according to Eq. (3), obviously a too large value for
![]() .) The
contribution from the jet is negligible at all frequencies.
.) The
contribution from the jet is negligible at all frequencies.
At both epochs the fit to IR-optical data is not very convincing due to the lack of monitoring data (as noted in previous chapter) and we therefore tested if fitting the newest shock components according to IR-optical SED points (with a considerably worse lower frequency fits) would improve the high energy fit. We found that only the Doppler factors of the components would change slightly and that the resulting high-energy fit would look very much like the fits presented in Figs. 4 and 5.
Inclusion of second order SSC does not change our conclusions since the peak flux of the second order SSC component is at best comparable to that of the first order component, whatever parameters we choose (Bloom & Marscher 1996).
Table 1 shows the Doppler factors, magnetic field strengths and
![]() for the underlying jet and for shock components corresponding to our SSC fits
presented in Figs. 4 and 5. For all relevant shock components we assume the
variability timescale to be 25 days as this gives the maximal IC output from
these components. For the underlying jet we have no information on the
variability timescale, but we assume 100 days for the calculations. We
note that slightly different combinations of B and D for the contributing
shock components would result in very similar total flux density fits, since
our SSC component is mainly constrained just by the X-ray flux.
for the underlying jet and for shock components corresponding to our SSC fits
presented in Figs. 4 and 5. For all relevant shock components we assume the
variability timescale to be 25 days as this gives the maximal IC output from
these components. For the underlying jet we have no information on the
variability timescale, but we assume 100 days for the calculations. We
note that slightly different combinations of B and D for the contributing
shock components would result in very similar total flux density fits, since
our SSC component is mainly constrained just by the X-ray flux.
The D range from 10 to 19, given the ![]() (app) constraints, would
require a change in the jet direction from 2 to 5 degrees and a change in the
Lorentz factor from 11 to 7 from one shock to another, both compatible with,
e.g., VLBI data of Wehrle et al. (2001). With the modelfit values given in the
table, shock 3 should have collided with shock 2 during 1991. During that
period both shocks were already decaying, and a possible internal shock
signature should have been weaker than in the epoch 5a/5b case discussed in
Sect. 2. However, a very similar model fit to that shown in Fig. 5 can also be
found assuming similar Doppler factors for the three shocks, and thus avoiding
internal collisions, or the need to assume significant changes in either
(app) constraints, would
require a change in the jet direction from 2 to 5 degrees and a change in the
Lorentz factor from 11 to 7 from one shock to another, both compatible with,
e.g., VLBI data of Wehrle et al. (2001). With the modelfit values given in the
table, shock 3 should have collided with shock 2 during 1991. During that
period both shocks were already decaying, and a possible internal shock
signature should have been weaker than in the epoch 5a/5b case discussed in
Sect. 2. However, a very similar model fit to that shown in Fig. 5 can also be
found assuming similar Doppler factors for the three shocks, and thus avoiding
internal collisions, or the need to assume significant changes in either
![]() or
or ![]() .
.
As we have noted earlier, lacking temporal data on the IC fluxes our modelling cannot be fully self-consistent, in that the effect of the IC losses is not incorporated in the evolution of the synchrotron components. In particular, the temporal evolution of the synchrotron break frequencies depends on the IC losses, while in our model it evolves according to adiabatic losses resulting from the expansion of the underlying jet. However, as Figs. 4 and 5 show, the IC spectral fits are mainly determined by the X-ray data and the high frequency synchrotron break frequencies, determining the turnovers of the gamma-ray spectra, are not important in the present case.
Finally, given our conclusion that SSC can explain only about one tenth of the
total IC flux during epoch P1, it is also clear that the cooling
corresponding to a 25 day radio variability timescale cannot be provided by
the synchrotron and the SSC losses of shock number 3 according to Eq. (3),
given the B and D values in Table 1. Knowing neither the origin nor the
timescale of the major part of the gamma-ray flux of Fig. 5, very little can
be said of the actual cooling mechanisms. We can
consider the possibility that the strong gamma-ray flare is a very
short-lived phenomenon and its contribution to the longer term cooling of
the synchrotron component is not significant. In that case, shock number 3 can provide the required 25 day cooling timescale (with approximately
equal synchrotron and SSC cooling) if we increase its magnetic field to 17 mG and decrease the Doppler factor to 14, with
![]()
![]() 104. Such a change does not appreciably worsen the fit to the X-ray data.
104. Such a change does not appreciably worsen the fit to the X-ray data.
Table 1: Underlying jet and shock parameters.
Previous gamma-ray modelling efforts have usually started from a single theoretical, model-dependent synchrotron spectrum, which has then been fitted to observed optical flux levels. In this paper we have used a more realistic multicomponent approach, where the synchrotron emission originates both from the jet and from the shocks propagating downstream in the jet. A code was used to identify these components from multifrequency monitoring data and to derive their spectra at the time of the Compton observations. Our code provides a consistent description of the flux variations from optical to cm-radio frequencies in terms of shocks growing and decaying in an underlying jet. These variations cannot be modelled using the theoretical synchrotron components assumed in virtually all published IC model fits. We note that at any given time there are generally several components which can contribute to the high energy flux, and that their spectra are quite different from those assumed in the models. (One may, for example, compare our data-derived multicomponent spectra during epoch P1 with the single model spectra assumed by Hartman et al. 2001, as the basis for their IC flux calculations.)
Using the semiempirical synchrotron spectra, we have further estimated the SSC fluxes from these components using a simple analytical approximation. We have studied the SSC model because available evidence indicates that strong gamma-ray flares are connected with new shocks developing in the jet. From observed time delays from the onset of the radio flare to the gamma-ray flare one can estimate that these shocks are already at distances of several parsecs from the jet apex, well beyond the broad line region, where there may not be enough external photons for significant EC radiation. (We note that this conclusion holds even for D = 5, the lowest value compatible with other data on 3C 279).
If the gamma-ray flux originates at distances of parsecs from the core, the SSC mechanism is the most obvious candidate. However, our approach can be equally well applied to the EC case. With sufficient flux variability data, preferably supplemented by VLBI observations, it is possible to identify the synchrotron jet and shock components and to derive their spectra. These can then be used as inputs in calculating the IC component spectra. As it is generally accepted that the synchrotron flux variations are due to shock growth and decay, all gamma-ray variability modelling should also be based on the observed spectral evolution of the synchrotron components, not to changes in the jet flow parameters.
We find that given the size, the Doppler boosting and the variability timescale constraints, the SSC model cannot reproduce all of the high energy flux during either a relatively quiescent or a high state, although our fits show that the X-ray emission can plausibly be produced by the shocks. There have been some apparently successful SSC model fits for 3C 279 (Maraschi et al. 1993; Marscher & Travis 1996; Hartman et al. 1996). However, these fits require that all the observed synchrotron flux comes from the inhomogeneous jet with its SED peaking in the optical to UV range. As our Fig. 3 shows, this cannot be the case. Although the physical situation is completely different from theoretical work by Sikora et al. (2001) the conclusion that the X-ray emission is produced via SSC is similar. Other recent modelling, such as by Hartman et al. (2001), has also reached the conclusion that the X-ray flux in 3C 279 can have an SSC origin, while the gamma-ray flux cannot, but again the physical assumptions are quite different, and, as we have argued in this paper, are probably not valid.
If the shocks are already well outside the broad line region during the strongest gamma-ray flaring, as has been argued previously on the basis of radio, VLBI and gamma-ray comparisons, and the SSC mechanism appears insufficient, the origin of the major part of highest energy gamma radiation remains a puzzle. Scenario, where a significant external seed photon field is provided by dust, extending further than the BLR, should be investigated further (Sikora et al. 1994; Blazejowski et al. 2000), as should the mirror Compton scenario proposed by Ghisellini & Madau (1996) and hadronic models (Mannheim 1993). In a jet where the shocks have variable Lorentz factors, a slower shock could possibly provide an enhanced synchrotron seed photon field for a faster, approaching shock (Georganopoulos & Kazanas 2003).
Acknowledgements
This research has made use of data from the University of Michigan Radio Astronomy Observatory which is supported by funds from the University of Michigan. E.V. gratefully acknowledges the hospitality and the Distinguished Visitor grant of the Australian Telescope National Facility. This research has been supported by the Academy of Finland grants 74886 and 80450 and Jenny and Antti Wihuri Foundation. We also thank the anonymous referee for constructive criticism of the earlier versions of this paper.