1 - Institut f
2 - On leave from Department of Physics and Asher Space Research Institute, Technion, 32000 Haifa, Israel
A&A 440, L13-L16 (2005)
DOI: 10.1051/0004-6361:200500157
G. Shaviv1,2 - R. Wehrse1
1 - Institut f
![]() r Theoretische Astrophysik Tiergartenstrasse 15, 69121 Heidelberg, Germany
r Theoretische Astrophysik Tiergartenstrasse 15, 69121 Heidelberg, Germany
2 -
On leave from Department of Physics and Asher Space Research Institute, Technion, 32000 Haifa, Israel
Recieved 10 June 2005 / Accepted 19 July 2005
Abstract
We estimate the effect of the shear flow in accretion disks on the radiation field. We apply the recent results of Wehrse et al. (2003, A&A, 401, 43) for the expansion line opacity in shear flows. We use an approximation and derive an approximate equation for the radiation field in an accretion disk in the diffusion approximation. We find that in the appropriate limit for the flow in disks:
- The effect depends on a product of three factors: the first depends solely atomic physics and hence on the composition of the accreted matter, the second depends on the density while the third depends solely on the shear flow.
- The radiation field in accretion disks around neutron stars, black holes and white dwarfs is strongly affected by the expansion line opacity.
- The radiation field is very non isotropic leading to significantly higher specific intensities in the vertical direction, a higher temperature gradient and increased susceptibility to convection and other instabilities.
Key words: disks, shear flow, expansion opacity
Radiative transfer in moving media is affected by velocity gradients. The effect, dubbed "expansion opacity'', was first evaluated by Karp et al. (1977). In the simplest model of an accretion disks the flow is Keplerian and hence possess a shear in the radial direction. Hence, a photon propagating inside the disk sees an anisotrpic shear flow. The enhanced effective line opacity, called expansion opacity, is very non isotropic. The main purpose of this letter is to expose the importance of this effect to the structure of accretion disks (here after AD).
Let ![]() be a unit vector in the direction of the ray and
be a unit vector in the direction of the ray and
![]() a velocity field. Define the scalar "velocity gradient'' as:
a velocity field. Define the scalar "velocity gradient'' as:
![\begin{displaymath}%
{\vec F}_w(s_0,\xi )={{4\pi } \over 3}{{\partial B(T,\xi )}...
...artial T}}\left[ {{\vec X}_\beta (\xi )} \right]^{-1}\nabla T,
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img8.gif) |
(2) |
![\begin{displaymath}%
\left[ {\vec X}_{\beta} (\xi ) \right]^{-1}=
{3 \over {2\pi...
...[ \chi _{n}(\xi, w({\vec n})) \right]^{-1}n_in_j{\rm d}\omega
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img10.gif) |
(3) |
![\begin{displaymath}%
F(s_0,\xi )={{4\pi } \over 3}{{\partial B(T,\xi )} \over {\partial T}}\left[ {\chi _0(\xi )} \right]^{-1}\nabla T.
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img13.gif) |
(4) |
Clearly,
![]() is a scalar function, the value of which depends on direction. Consequently, the effective opacity is a function of direction. On the other hand, the extinction
is a scalar function, the value of which depends on direction. Consequently, the effective opacity is a function of direction. On the other hand, the extinction
![]() becomes a tensor. The deviation of the radiation vector, which is proportional to
becomes a tensor. The deviation of the radiation vector, which is proportional to
![]() ,
from
,
from ![]() is important for induced circulation in the ADs and will be treated elsewhere.
The total flux in direction
is important for induced circulation in the ADs and will be treated elsewhere.
The total flux in direction ![]() is obtained by integration over the solid angle and is:
is obtained by integration over the solid angle and is:
![\begin{displaymath}%
F_{\rm tot}(s_0,w )={{4\pi } \over 3}{{\partial B(T)} \over...
...ine{ \left[ {\chi _n(w)} \right]^{-1} } {\vec n}\cdot \nabla T
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img18.gif) |
(5) |
![\begin{displaymath}%
\overline{ \left[ {\chi _n(w)} \right]^{-1} } =\int\limits_...
... \exp ( \xi ) \left[ {\chi _n(\xi, w)} \right]^{-1}{\rm d}\xi
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img19.gif) |
(6) |
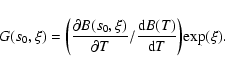 |
(7) |
We consider here a general case of a series of infinitely sharp lines with a distribution in amplitude. Let the line density be:
| (8) |
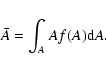 |
(9) |
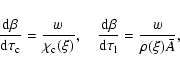 |
(11) |
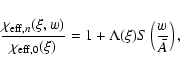 |
(12) |
The function
![]() was calculated by Wehrse et al. (2003, Paper III) for several assumptions about the distribution of lines. For example, in the case of Poisson distributed infinitely sharp lines it has the form:
was calculated by Wehrse et al. (2003, Paper III) for several assumptions about the distribution of lines. For example, in the case of Poisson distributed infinitely sharp lines it has the form:
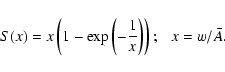 |
(13) |
For ![]() we find (Wehrse et al., Paper III) that
we find (Wehrse et al., Paper III) that
![\begin{displaymath}%
F(s_0,\xi, w)=\left[ {{{\chi _n(\xi, w)} \over {\chi _0(\xi )}}} \right]^{-1}F(s_0,\xi )
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img49.gif) |
(16) |
![\begin{displaymath}%
F_w(s_0,\xi )={{4\pi } \over 3}{{\partial B(T,\xi )} \over {\partial T}}\left[ {\chi _\beta (\xi )} \right]^{-1}\nabla T,
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img50.gif) |
(17) |
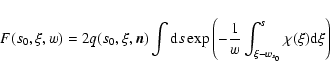 |
(18) |
Define now an effective opacity as:
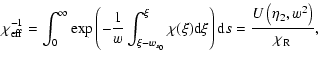 |
(19) |
The function
![]() is given in Fig. 6 of Wehrse et al. (2003) in the case of Poisson distributed spectral lines and for a range of parameters for the spectral lines. The sensitivity to the parameters of the spectral lines (as is clear from the figure) is small and will be neglected here. The general behavior of
is given in Fig. 6 of Wehrse et al. (2003) in the case of Poisson distributed spectral lines and for a range of parameters for the spectral lines. The sensitivity to the parameters of the spectral lines (as is clear from the figure) is small and will be neglected here. The general behavior of
![]() is as follows: for
is as follows: for
![]() there is no significant effect, while for
there is no significant effect, while for
![]() the function reaches saturation at about
102-104 times the value at
the function reaches saturation at about
102-104 times the value at
![]() (cf. Table 2 ibid.). In the limit of very large velocity gradients we get:
(cf. Table 2 ibid.). In the limit of very large velocity gradients we get:
In the limit of small velocity gradients we can write
![]() .
.
Clearly, the diffusion flux is very non-isotropic. Expanding the flux in the direction ![]() in terms of w yields:
in terms of w yields:
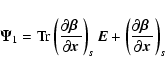 |
(24) |
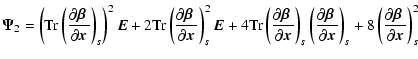 |
(25) |
![\begin{displaymath}%
\left( {{{\partial {\mbox{\boldmath {$\beta$ }}} } \over {\...
... {$\beta$ }}} } \over {\partial {\vec x}}}} \right)^T} \right]
\end{displaymath}](/articles/aa/full/2005/34/aahf101/img69.gif) |
(26) |
The zeroth order disk structure is a Keplerian shear flow, namely
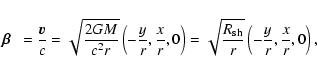 |
(27) |
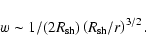 |
(28) |
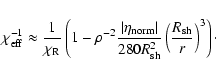 |
(29) |
The effect contains three factors, the density, the composition and the geometry. For given density and composition the effect is largest near the surface of the accreting star or the Schwarzchild radius in the case of a black hole. The effect is important for
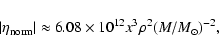 |
(30) |
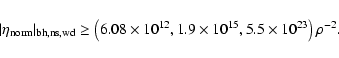 |
(31) |
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{one.eps}\end{figure}](/articles/aa/full/2005/34/aahf101/Timg84.gif) |
Figure 1:
The dependence of
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=5.85cm,clip]{two.eps}\end{figure}](/articles/aa/full/2005/34/aahf101/Timg85.gif) |
Figure 2:
The critical density for saturation of the expansion opacity as a function of the location in the disk for an accreting object of
|
| Open with DEXTER | |
| |
Figure 3: The dependence of the shear as a function of direction. |
| Open with DEXTER | |
The enhancement of the opacity is very anisotropic. In Fig. 3 we show the geometrical factor
![]() as a function of
as a function of
![]() at the location (1,0,0). In reality, this term is multiplied by
at the location (1,0,0). In reality, this term is multiplied by
![]() which accentuates the unisotropy.
which accentuates the unisotropy.
Because of the extremely large
![]() ,
saturation is reached very quickly and radiation escapes in the directions of smallest opacity. Namely,
,
saturation is reached very quickly and radiation escapes in the directions of smallest opacity. Namely,
![]() where
where
![]() is the solid angle in the direction of unchanged opacity, F0 is the would be radiative flux if no expansion opacity effects existed and
is the solid angle in the direction of unchanged opacity, F0 is the would be radiative flux if no expansion opacity effects existed and
![]() is the specific intensity.
is the specific intensity.
The extremely large
![]() plus the very anisotropic
plus the very anisotropic
![]() leads to a situation where the effect enters already at very small shear. In other words, already in a very small deviation from the primary directions where the shear vanishes, the effect is at its maximum value so that
leads to a situation where the effect enters already at very small shear. In other words, already in a very small deviation from the primary directions where the shear vanishes, the effect is at its maximum value so that
![]() is extremely small.
is extremely small.
As a consequence, the temperature gradient increases and leads right away to convective instability. This instability can be the source of macroscopic viscosity in the above ADs. The temperature gradient is given by
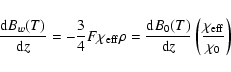 |
(32) |
Clearly, the problem of an ideal ADs with only continuum opacity remains. The shear in the velocity has no effect when spectral lines are absent.
In the particular case of ADs we have to substitute the divergence of the total flux vector into the energy equation. Under the present approximation we return to Eq. (23) which transforms to
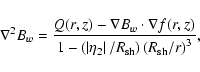 |
(33) |
where Q(r,z) is the energy source and f(r,z) a known function of position.
Since the total energy radiated away is essentially
fixed (for fixed ![]() )
the increase in
)
the increase in
![]() increases
increases
![]() but does not increase the location of the surface and the overall averaged
but does not increase the location of the surface and the overall averaged
![]() .
(Saturation prevents the singularity.)
.
(Saturation prevents the singularity.)
While the velocity gradients keep the effect in the limit of low w, the large ![]() drives the effect into saturation.
drives the effect into saturation.
We assumed that averaging over angle is plausible (as first order). The strong anisotropy calls for an improved treatment of the radiation field. This extension is underway and will be reported in due course along with the stability analysis.
The limb darkening effect of the disk must be very peculiar with significant consequences to the estimated total luminosity of disks observed at various angles. The expected structure of the atmosphere with non isotropic effective opacity differs significantly from hitherto assumed structure (work in progress).
Magnetic fields, which were ignored here, add to the velocity fields and hence broaden the lines sooner without affecting the global Keplerian flow and general effect.
Acknowledgements
G.S. acknowledges partial support by the Israel Science Foundation and by the DFG (Sonderforschungsberiech 359/C2)