A&A 440, 385-390 (2005)
DOI: 10.1051/0004-6361:20053121
M. Selwa1 - K. Murawski1 - S. K. Solanki2 - T. J. Wang2 - G. Tóth3
1 - Institute of Physics, UMCS, ul. Radziszewskiego 10, 20-031 Lublin, Poland
2 -
Max-Planck-Institut für Sonnensystemforschung, Max-Planck-Str. 2, 37191 Katlenburg-Lindau, Germany
3 -
Department of Atomic Physics, Loránd Eötvös University, Pázmány Péter sétány 1/A, Budapest 1117, Hungary
Received 23 March 2005 / Accepted 23 May 2005
Abstract
We consider the impulsive excitation of fast vertical
kink standing waves in a solar coronal loop that is embedded in a potential arcade.
The two-dimensional numerical model we implement includes the effects of field
line curvature and nonlinearity on the excitation and damping of standing fast magnetosonic waves.
The results of the numerical simulations reveal wave signatures which are characteristic
of vertical loop oscillations seen
in recent TRACE observational data.
Key words: Sun: oscillations - Sun: corona - magnetohydrodynamics (MHD)
Solar magnetohydrodynamic (MHD) waves are an important diagnostic tool of the medium through which they propagate (Roberts at al. 1984; Roberts 2000, 2002; Nakariakov 2003; Klimchuk et al. 2004). They are also natural carriers of energy and probably transport some of the energy needed to heat the solar corona.
The last decade has seen the discovery of a variety of coronal loop oscillations and waves.
Both propagating waves and various standing modes
have been detected. These include transverse oscillations (i.e. oscillations of the loop
perpendicular to the plane containing the unperturbed loop; Aschwanden et al. 1999),
standing longitudinal slow modes (Wang et al. 2002),
and most recently vertical oscillations (i.e. transverse oscillations within the plane containing
the unperturbed loop; Wang & Solanki 2004).
Here we are interested in the vertical oscillations of a solar coronal loop.
The observed loop (recorded by TRACE in active region 9893 at the northwest limb)
expanded and contracted with an oscillation period of about 230 s
after being triggered by a flare. The initial velocity of the loop was estimated as
![]() 130 km s-1 and the displacement amplitude of the loop apex as 7900 km.
The loop length was estimated as 300-400 Mm. An interesting feature of these oscillations is the evidence that they are compressible.
130 km s-1 and the displacement amplitude of the loop apex as 7900 km.
The loop length was estimated as 300-400 Mm. An interesting feature of these oscillations is the evidence that they are compressible.
Oscillations that are presumably triggered by sudden energy release processes such as solar flares were discussed recently by Nakariakov & Ofman (2001), Cooper et al. (2003), and Nakariakov et al. (2004). Terradas & Ofman (2004) discussed the possibility that transverse waves in coronal loops can produce density enhancements at the apex. The mechanism involved was the ponderomotive force of standing MHD waves. Terradas et al. (2005) studied the excitation and damping of transversal coronal loop oscillations, using a simple line-tied one-dimensional model. Shergelashvili et al. (2005) demonstrated swing interaction between fast magnetosonic and Alfvén waves in an inhomogeneous medium. They showed that the fast magnetosonic waves propagating across an applied non-uniform magnetic field can parametrically amplify Alfvén waves propagating along the field, through the periodical variation of the Alfvén speed. Slow standing waves were discussed by Selwa et al. (2005) using parametric studies in the one-dimensional approximation. Fast standing waves were numerically simulated by Murawski et al. (2005a) who found high-order standing fast kink mode oscillations in a loop that is embedded in a weak magnetic environment. Murawski et al. (2005b) extended this work to the case of a general magnetic field neglecting gas pressure. They showed that impulsively triggered fast magnetosonic waves in a cold loop have periods which are compatible with both the period of the fast kink mode in the arcade and the observational data provided by TRACE. Transverse oscillations in solar coronal loops induced by propagating Alfvénic pulses were discussed by del Zanna et al. (2005).
In this paper we extend the models of Murawski et al. (2005a,b) by taking into account small but finite gas pressure effects. We aim to explain the recent observational findings by Wang & Solanki (2004). We consider a two-dimensional curved magnetic field topology in a strongly magnetized coronal plasma.
The paper is organized as follows: the physical model and numerics are described in Sect. 2. The numerical results are presented in Sect. 3. This paper is concluded by a short summary of the main results in Sect. 4.
Our model system is taken to be composed of a magnetized plasma with infinite electrical conductivity that behaves like an ideal gas with polytropic index
![]() .
As we are interested in characteristic spatial scales lower than the pressure scale height in the solar corona, we neglect the effect of gravitational stratification.
This assumption is not fully justified as the density scale height
H=46 Mm for an isothermal loop with electron temperature
.
As we are interested in characteristic spatial scales lower than the pressure scale height in the solar corona, we neglect the effect of gravitational stratification.
This assumption is not fully justified as the density scale height
H=46 Mm for an isothermal loop with electron temperature
![]() MK (Aschwanden 2002),
while the loop height considered here is h=70 Mm. Indeed, the effect of gravity is
important in giving the plasma
MK (Aschwanden 2002),
while the loop height considered here is h=70 Mm. Indeed, the effect of gravity is
important in giving the plasma ![]() a realistic distribution with height.
a realistic distribution with height.
With the above assumptions, the evolution of the system is modeled by the ideal MHD equations, which describe the conservative transport of mass, momentum, energy, and magnetic flux, viz.
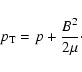 |
(6) |
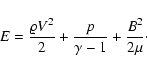 |
(7) |
We use the coronal arcade model that has been described by Oliver et al. (1998).
In this model the coronal arcade is settled in a motionless environment (
![]() ).
The assumption of a low plasma
).
The assumption of a low plasma ![]() implies that the pressure gradient
implies that the pressure gradient ![]() can be neglected in comparison to the Lorentz force, so that
can be neglected in comparison to the Lorentz force, so that
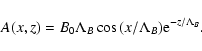 |
(11) |
| (12) | |||
| (13) |
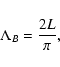 |
(14) |
For the potential magnetic arcade the equilibrium pressure ![]() has to be constant.
This pressure can be evaluated from the reference sound speed
has to be constant.
This pressure can be evaluated from the reference sound speed ![]() as
as
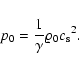 |
(15) |
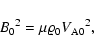 |
(16) |
Table 1: Scale and equilibrium parameters.
We consider a "loop'' that is embedded in the arcade such that its edges
follow magnetic field lines![]() .
We chose the mass density contrast
.
We chose the mass density contrast
![]() given by a step-function profile with
given by a step-function profile with
![]() corresponding to the internal
mass density. This loop does not have a perfect circular shape, but its average radius and length
can be estimated as 70 Mm and 190 Mm, respectively. These values are similar to those of the loop observed by Wang & Solanki (2004). The loop half-width at the foot-points is chosen as 2.5 Mm. Due to the absence of gravity the plasma
corresponding to the internal
mass density. This loop does not have a perfect circular shape, but its average radius and length
can be estimated as 70 Mm and 190 Mm, respectively. These values are similar to those of the loop observed by Wang & Solanki (2004). The loop half-width at the foot-points is chosen as 2.5 Mm. Due to the absence of gravity the plasma
![]() grows from 0.012 at the loop foot-points to 0.054 at the loop apex
in the ambient medium. This growth is not quite realistic, but cannot be avoided in the absence of gravity. Importantly, the value of
grows from 0.012 at the loop foot-points to 0.054 at the loop apex
in the ambient medium. This growth is not quite realistic, but cannot be avoided in the absence of gravity. Importantly, the value of ![]() is low everywhere in the loop.
is low everywhere in the loop.
As we are interested in impulsively excited waves, we launch a hot pulse in
temperature or, equivalently, in the mass density and pressure at time t=0 from the location x=z=0, i.e. below the loop apex. This pulse has the spatial form:
It is noteworthy here that the observed relative dimension of the flaring site w with respect to the loop size is rather large (e.g., Nakariakov et al. 2004). The initial location of the pulse corresponds to the flaring site. Unfortunately, the observations do not indicate directly the location of the flaring site (Wang & Solanki 2004). However, we expect that in order to produce a vertical oscillation of a loop the flare site must be located close to the plane containing the loop. Thus it is well suited to be modelled in 2-D. The adopted pulse parameters were chosen such that they lead to numerical results which show encouraging agreement with observations.
We use the Versatile Advection Code (VAC) developed by Tóth (1996). This code provides a choice of different numerical schemes to advance a system of hyperbolic equations in 1, 2 or 3D. Here we use the Flux Corrected Transport scheme (Boris & Book 1973) to solve the MHD equations in 2-D. Numerical tests obtained with VAC can be found in Tóth & Odstrcil (1996).
In multi-dimensional MHD simulations the numerical value of the divergence of the magnetic field can become different from zero. There are several options in VAC to fix this problem. Here we use the projection scheme, which eliminates the divergence of the magnetic field after each time step by solving a Poisson equation iteratively.
Equations (1)-(5) are solved numerically in an Eulerian box
with the x- and z-dimensions (-L,L) ![]() (0,2 L).
This box is covered by a grid of 600
(0,2 L).
This box is covered by a grid of 600 ![]() 600 numerical cells. Grid convergence
studies based on grid refinement (300
600 numerical cells. Grid convergence
studies based on grid refinement (300 ![]() 300, 400
300, 400 ![]() 500, 600
500, 600 ![]() 600 and 900
600 and 900 ![]() 900) were performed to show that the numerical results
are not affected by poor spatial resolution. We apply line-tying boundary conditions, with
900) were performed to show that the numerical results
are not affected by poor spatial resolution. We apply line-tying boundary conditions, with
![]() ,
at the bottom and at the left and right hand sides of the simulation region.
Open boundary conditions, with zero-gradient extrapolation of all plasma variables, are adopted
for the top boundary.
,
at the bottom and at the left and right hand sides of the simulation region.
Open boundary conditions, with zero-gradient extrapolation of all plasma variables, are adopted
for the top boundary.
Figure 1 displays time-signatures of the mass density
of the loop apex (shown is a cut along the line x=0).
The presence of two temporal scales of oscillation can be distinguished:
(a) long period oscillations associated with global loop movement which is triggered by
the initial pulse and (b) short period oscillations seen in mass density, although with a relatively low amplitude. The long period fluctuations are strongly damped fast kink oscillations.
The short period oscillations represent magnetosonic waves which are trapped by the loop cavity.
The general resemblance of Fig. 1
to the observational data of Wang & Solanki (2004) is striking, although there are differences in detail. Similarities include the strong damping, and the depletion of mass density
at times of maximum expansion. The loop system moved outward by a maximum distance of about 4000 m with an initial velocity of Vz=22 km s-1, which are smaller than the observational values of 7900 m and 130 km s-1 (Wang & Solanki 2004). The initial pulse in the simulations is obviously weaker than the one giving rise to the observed
oscillations. We found, however, that if we increase the strength of the initial pulse by a factor of two, the loop becomes unstable. The relatively low stability of the loop in our simulations may have to do with the neglect of gravity (plasma ![]() increasing with height)
or with the simple magnetic field topology applied.
The seeming filamentation of the loop seen in Fig. 1 may be a numerical artifact which is an inherent feature of the Flux Corrected Transport (FCT) method (Boris & Book 1973) that was used in the VAC code. This feature was not observed with the second-order TVD Lax-Friedrich method implemented in the code.
increasing with height)
or with the simple magnetic field topology applied.
The seeming filamentation of the loop seen in Fig. 1 may be a numerical artifact which is an inherent feature of the Flux Corrected Transport (FCT) method (Boris & Book 1973) that was used in the VAC code. This feature was not observed with the second-order TVD Lax-Friedrich method implemented in the code.
Figure 2 shows difference images of mass density evaluated at two times corresponding to consecutive peaks in the displacements (see Fig. 1). White (black) shading denotes an excess (depletion) of mass density in comparison to the earlier moment of time. Note that the loop is uniformly displaced and the maximum density displacement occurs near the loop apex. These profiles reveal that the first kink mode is excited, in agreement with the observations (Wang & Solanki 2004, their Figs. 3c,d).
The global oscillations of the loop can be traced by following the position of the loop apex in time (Fig. 3). The apex position is estimated as the maximum of
the Gaussian function
![\begin{displaymath}%
G(z)=G_{\rm0} \cdot \exp\left[-\frac{(z-G_1)^2} {2{G_{\rm 2}}^2}\right]+G_{\rm 3}
\end{displaymath}](/articles/aa/full/2005/34/aa3121-05/img59.gif) |
(18) |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{3121fig1.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg62.gif) |
Figure 1: Time-signature of the mass density (colour) at the apex of the loop. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3121fg2a.eps}\vspace*{3mm}
\includegraphics[width=7.7cm,clip]{3121fg2b.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg65.gif) |
Figure 2:
Difference images of mass density spatial profiles
evaluated over two different intervals of time:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3121fg3a.eps}\vspace*{5mm}
\includegraphics[width=6.5cm,clip]{3121fg3b.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg66.gif) |
Figure 3: Solid lines denote the position of the loop apex a) and mass density at the loop apex b) vs. time. Dotted lines correspond to damped sine functions fitted to the solid lines. |
| Open with DEXTER | |
We get a wave period and damping time of the oscillation by fitting the apex position vs. time
(Fig. 3) to the damped sine function
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{3121fig4.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg73.gif) |
Figure 4: Time-signature of the vertical component of the flow for the same cut as shown in Fig. 1. |
| Open with DEXTER | |
A comparison between Figs. 3a and 3b reveals that whereas the loop apex shows a smooth oscillation that is well fit by a damped sine function, the mass density, in addition to showing an oscillation with the same period and damping time, also exhibits high frequency oscillations. After removing the longer term variations we determine a period of 150 s for the higher frequency component. The fact that these short periods are not visible in Fig. 3a suggests that the short period pulsations do not correspond to higher harmonic kink modes.
It is noteworthy that, unlike in the analyzed observational data of Wang & Solanki (2004), the simulated loop does not return to its original position at large times, but retains an offset to higher z. As this feature is present for all numerical methods and resolutions that we have tried, we conclude that the offset reflects a new equilibrium the loop attains after being perturbed by the initial pulse. This offset can also be a result of the added energy/mass under the loop by the pulse (17) which prevents it from settling the same equilibrium height.
In Fig. 3b it is discernible that the loop is rarified when it is largest,
while it is denser in its most compact state. Using
![]() ,
where I denotes intensity, this
implies that the loop is darker and brighter when it has expanded and compressed, again in good agreement with the observations (Wang & Solanki 2004). Note that the phase shift
between position and density is not exactly 180
,
where I denotes intensity, this
implies that the loop is darker and brighter when it has expanded and compressed, again in good agreement with the observations (Wang & Solanki 2004). Note that the phase shift
between position and density is not exactly 180![]() (as determined from the dotted curves
in Fig. 3). At the end of the simulation the loop is clearly less dense
than at the beginning. This loop evacuation is due to the energy leakage. During this process plasma flows into the ambient medium, smoothing initially sharp loop edges and evacuating its interior.
As we have verified that numerical diffusion is negligibly small, this process is not an inherent
numerical artifact.
(as determined from the dotted curves
in Fig. 3). At the end of the simulation the loop is clearly less dense
than at the beginning. This loop evacuation is due to the energy leakage. During this process plasma flows into the ambient medium, smoothing initially sharp loop edges and evacuating its interior.
As we have verified that numerical diffusion is negligibly small, this process is not an inherent
numerical artifact.
![\begin{figure}
\par\includegraphics[width=7.25cm,clip]{3121fig5.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg76.gif) |
Figure 5: Half-width of the loop at the apex vs. time. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3121fig6.eps}\end{figure}](/articles/aa/full/2005/34/aa3121-05/Timg77.gif) |
Figure 6: Short period oscillations of mass density at the loop apex (solid line) and half-width of the loop (dashed line) at the apex vs. time. These oscillations are obtained from Figs. 3b and 5 by filtering out long period oscillations. |
| Open with DEXTER | |
The oscillation is thus not a pure kink mode, but shows some compressibility. The initial pulse excites a packet of waves in which kink waves have the highest contribution but compressible waves like fast magnetosonic sausage or slow waves are present too. This conclusion is supported by Fig. 5, which displays the half-width of the loop at the apex vs. time. The dominant feature of the figure is the broadening of the loop when the pulse hits it, followed by a slow relaxation to roughly its original width. In addition, a shorter period oscillation of the half-width is also visible. This oscillation, with a period of 130-140 s, is more clearly seen in Fig. 6, where the half-width has been plotted after removing the longer term changes. The similarly filtered density at the loop apex is also plotted. For the density profile the dotted curve in Fig. 3b, described by Eq. (19), was first removed.
Figure 6 clearly shows the anti-correlation between half-width and density.
This antiphase behavior is consistent with the expectations for a fast sausage mode.
It is noteworthy here that a sausage mode can propagate freely only for wave periods ![]() shorter than the cut-off period
shorter than the cut-off period
![]() that is given by (Edwin & Roberts 1982, 1983)
that is given by (Edwin & Roberts 1982, 1983)
In this paper we have studied numerically the impulsive excitation of oscillations of a highly magnetised solar coronal loop that is embedded in a two-dimensional magnetic arcade. In the applied model we have neglected several important factors such as: the three-dimensional geometry of loops and the flare site, radiative losses, and gravitational stratification. A 2-D model may be more apropriate for the excitation of vertical oscillations than of other transverse oscillation modes, since the source of the initial pulse must be located in or near the loop plane. Of particular interest is the influence of gravity, which will be studied in a future investigation. Among loop oscillations two scales were distinguished: (a) long period (496 s) oscillations were interpreted as standing fast kink modes and (b) short period (140 s) oscillations we associate with leaky sausage waves. The observational signature of the kink wave is similar to the actual TRACE observations reported by Wang & Solanki (2004), showing rapid damping and an anti-correlation between displacement and density. Differences in amplitude and period are probably due to differences in the strength of the initial pulse, the Alfvén speed, and loop length between modeled and the observed loop. The short period sausage mode, although so far not observed, may play a role in explaining the damping of the kink mode. It would be of great interest to look for such waves in conjunction with transverse loop oscillations.
The conjecture made here regarding the damping of the excited waves is that it is due to leakage. However, it cannot be explained fully on the basis of our present arguments. The issue of damping of loop oscillations is a rather intricate one and requires farther studies.
Acknowledgements
K.M. expresses his sincere thanks to Dr. Luigi Nocera for stimulating discussions. M.S. thanks Dr. Gherardo Valori for his helpful comments on running the VAC code which is provided at http://www.phys.uu.nl/~toth/. G.T. acknowlegdes support from the Hungarian Science Fundation (OTKA, grant No. T047042). The authors thank the referee for his/her stimulating comments. M.S.'s & K.M.'s work was financially supported by a grant from the State Committee for Scientific Research Republic of Poland, with KBN grant No. 2 PO3D 016 25.