A&A 440, 53-58 (2005)
DOI: 10.1051/0004-6361:20052852
E. R. Gaynullina1 - R. W. Schmidt2 - T. Akhunov1,3 - O. Burkhonov3 - S. Gottlöber4 - K. Mirtadjieva1,3 - S. N. Nuritdinov1,3 - I. Tadjibaev1,3 - J. Wambsganss2 - L. Wisotzki4
1 - National University of Uzbekistan,
Physics Faculty,
Tashkent 700174, Uzbekistan
2 -
Astronomisches Rechen-Institut,
Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg,
Germany
3 - Ulugh Beg Astronomical Institute of the Uzbek Academy of Sciences and Isaac Newton Institute of Chile, Uzbek Branch, Astronomicheskaya 33, Tashkent 700052, Uzbekistan
4 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
Received 9 February 2005 / Accepted 13 May 2005
Abstract
We present the results of a monitoring campaign of the
double quasar SBS 1520+530 at Maidanak observatory from April 2003 to
August 2004. We obtained light curves in V and R filters that show
small-amplitude
![]() mag intrinsic variations of the
quasar on time scales of about 100 days. The data set is consistent
with the previously determined time delay of
mag intrinsic variations of the
quasar on time scales of about 100 days. The data set is consistent
with the previously determined time delay of
![]() days
by Burud et al. (2002, A&A, 391, 481). We find that the time delay corrected magnitude
difference between the quasar images is now larger by
days
by Burud et al. (2002, A&A, 391, 481). We find that the time delay corrected magnitude
difference between the quasar images is now larger by
![]() mag than during the observations by Burud et al. (2002). This confirms the
presence of gravitational microlensing variations in this system.
mag than during the observations by Burud et al. (2002). This confirms the
presence of gravitational microlensing variations in this system.
Key words: gravitational lensing - dark matter - quasars: individual: SBS 1520+530 - cosmology: observations
The broad absorption line (BAL) quasar SBS 1520+530 (
![]() )
was
discovered by Chavushyan et al. (1997) as a gravitationally lensed double
quasar with an angular separation of 1
)
was
discovered by Chavushyan et al. (1997) as a gravitationally lensed double
quasar with an angular separation of 1
![]() 56. The lensing galaxy was
detected by Crampton et al. (1998) using infrared adaptive optics imaging
at the Canada-France-Hawaii Telescope. Faure et al. (2002) observed the
lensing galaxy with the Hubble Space Telescope (Burud et al. 2002, in
the following B02) finally succeeded in obtaining both the redshift
56. The lensing galaxy was
detected by Crampton et al. (1998) using infrared adaptive optics imaging
at the Canada-France-Hawaii Telescope. Faure et al. (2002) observed the
lensing galaxy with the Hubble Space Telescope (Burud et al. 2002, in
the following B02) finally succeeded in obtaining both the redshift
![]() (consistent with absorption lines first found by
Chavushyan et al. 1997) of the lensing galaxy with a Keck obervatory
spectrum and the time delay of
(consistent with absorption lines first found by
Chavushyan et al. 1997) of the lensing galaxy with a Keck obervatory
spectrum and the time delay of
![]() days between the
two quasar images using monitoring data from the Nordic Optical
Telescope (NOT). For this, B02 obtained an almost gapless lightcurve
of the object of about 800 days between February 1999 and May 2001. An
almost continuous coverage of the light curve of SBS 1520+530 is made
possible by its high declination. Further photometry obtained at
Maidanak observatory on the system was published by
Zheleznyak et al. (2003).
days between the
two quasar images using monitoring data from the Nordic Optical
Telescope (NOT). For this, B02 obtained an almost gapless lightcurve
of the object of about 800 days between February 1999 and May 2001. An
almost continuous coverage of the light curve of SBS 1520+530 is made
possible by its high declination. Further photometry obtained at
Maidanak observatory on the system was published by
Zheleznyak et al. (2003).
Interestingly, B02 found that by simply shifting the light curve of
image B backward by 130 days and correcting for the magnitude
difference
![]() mag of the images made the quasar light
curves align only approximately. They obtained a better match by
allowing for an additional linear trend, and by correcting for faster
variations using an iterative scheme (Burud et al. 2001). B02 interpret
these additional variations to be probably due to microlensing
variability.
mag of the images made the quasar light
curves align only approximately. They obtained a better match by
allowing for an additional linear trend, and by correcting for faster
variations using an iterative scheme (Burud et al. 2001). B02 interpret
these additional variations to be probably due to microlensing
variability.
SBS 1520+530 thus is one of the prime targets for microlensing studies since it provides at once the prospects for long, uninterrupted light curves with a known, relatively short time delay and known microlensing variations. For this reason we decided to continue the optical monitoring of this system.
We report here on our observations of SBS 1520+530 (Fig. 1) with the 1.5 m AZT-22 telescope in Maidanak, Uzbekistan (Ehgamberdiev et al. 2000), between April 25 and October 12 in 2003, and again between January 16 and August 22 in 2004. In these intervals we observed the object almost daily whenever the weather permitted it. The V and R-filters provide photometry in the Johnson-Cousins system. We observed on average four frames per night with an exposure of 3.5 min in V and 3 min in R with a median seeing of 1.07 arcsec.
In total we obtained 116 nights in the V band and 191 nights in the Rband. After selecting for good seeing (better than 1.4 arcsec full-width at half maximum) and low sky-background we finally used 80 nights in the V-band and 123 nights in the R-band. The observations were made with the BROCAM CCD detector with a pixel scale of 0.26 arcsec. Bias correction and flat fielding of the images were done using standard IRAF software.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2852_fig1.ps}
\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg13.gif) |
Figure 1:
R-band image of SBS 1520+530 obtained on May 7, 2003. The quasar
images, the reference stars S3 and S4, and the star we use for the
PSF are labelled. The field size is
|
| Open with DEXTER | |
A special property of the SBS 1520+530 system is its location within 14 arcsec of a bright 12th mag star (Fig. 2). This is great for adaptive optics studies of the system because a bright reference star is at hand (Crampton et al. 1998). For photometry, however, the bright halo and the diffraction pattern caused by the star on the CCD needs to be subtracted carefully.
In order to do this, we followed the method described by Zheleznyak et al. (2003); we extracted the western half of the star and subtracted it from the eastern part where SBS 1520 is situated. This procedure also efficiently subtracts the light due to the horizontal diffraction spike that extends towards the double quasar.
Photometry on the quasar components A and B was performed using the
DAOPHOT package (Stetson 1987). We chose this method because
it is well-suited to the mildly asymmetric and time-variable AZT-22
point spread function (PSF). Because of the variable PSF it was not
possible to use the image subtraction technique
(Alard & Lupton 1998; Alard 2000). The quoted error bars are the standard ![]() errors determined by DAOPHOT. Since there are four point sources (the
quasar components A and B, and the stars S1 and S2) crowded in a
rather small region, we had to fit the positions and magnitudes of all
four components at the same time.
Absolute quasar magnitudes were calibrated using the
brightness of the reference star S3 (see Fig. 1) in the
V-band (
errors determined by DAOPHOT. Since there are four point sources (the
quasar components A and B, and the stars S1 and S2) crowded in a
rather small region, we had to fit the positions and magnitudes of all
four components at the same time.
Absolute quasar magnitudes were calibrated using the
brightness of the reference star S3 (see Fig. 1) in the
V-band (
![]() mag) and R-band (
mag) and R-band (
![]() mag) determined by Zheleznyak et al. (2003). The star
we used as a template to model the point spread function in DAOPHOT is
marked with "PSF'' in Fig. 1.
mag) determined by Zheleznyak et al. (2003). The star
we used as a template to model the point spread function in DAOPHOT is
marked with "PSF'' in Fig. 1.
In our analysis we ignore the presence of the lensing galaxy near
image B because it is too faint to be detected in our images
(
![]() mag, Crampton et al. 1998). If all of the
galaxy light contributes to our magnitude estimate of quasar image B,
the measured brightness would increase by a constant offset of 0.08
mag (assuming
mag, Crampton et al. 1998). If all of the
galaxy light contributes to our magnitude estimate of quasar image B,
the measured brightness would increase by a constant offset of 0.08
mag (assuming
![]() mag).
mag).
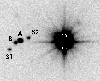 |
Figure 2:
R-band zoom of the central part of SBS 1520+530. The field
size is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2852_fig3.ps}
\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg21.gif) |
Figure 3:
R-band light curves of the two quasar images A and B in
SBS 1520+530 and the reference star S4. For clarity the magnitude for
image B was shifted by -0.4 mag, S4 was shifted by +2.4 mag. The
dotted vertical line indicates the day with the Julian
Date-2 452 000=880 when the mirror was cleaned. The dashed horizontal
line shows the magnitude of the reference star S4
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2852_fig4.ps}
\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg22.gif) |
Figure 4: V-R colour curve for the quasar images A ( top) and B ( bottom). The best-fitting value for each quasar image is plotted with a dashed line. |
| Open with DEXTER | |
We present the results of the R-band photometry of SBS 1520+530 in
Fig. 3 and Table 1![]() . The light curves of
the two quasar components A and B are plotted together with the light
curve of an additional reference star S4 (see Fig. 1,
mR=15.76 mag). This shows that both S3 (which is used for the
absolute magnitude calibration) and S4 do not vary.
. The light curves of
the two quasar components A and B are plotted together with the light
curve of an additional reference star S4 (see Fig. 1,
mR=15.76 mag). This shows that both S3 (which is used for the
absolute magnitude calibration) and S4 do not vary.
Both quasar components show low-amplitude
![]() mag
variations on time scales of about 100 days. As we will show in the
next section, the overall similarity of the two quasar image light
curves is due to a gradual brightness decrease of the lensed quasar.
On the day with Julian Date-2 452 000=880 the telescope mirror was
cleaned. This led to a large sensitivity improvement that visibly
improved the accuracy of the quasar brightness measurements,
especially for the fainter image B.
mag
variations on time scales of about 100 days. As we will show in the
next section, the overall similarity of the two quasar image light
curves is due to a gradual brightness decrease of the lensed quasar.
On the day with Julian Date-2 452 000=880 the telescope mirror was
cleaned. This led to a large sensitivity improvement that visibly
improved the accuracy of the quasar brightness measurements,
especially for the fainter image B.
In Fig. 4 and Table 2![]() we
show the difference between our V-band and R-band light curves of
SBS 1520+530. We find an average V-R colour
mV-mR=0.15 mag
for image A and
mV-m R=0.18 mag for image B. We do not find
any evidence for significant colour variations during our observing
interval. The small difference
we
show the difference between our V-band and R-band light curves of
SBS 1520+530. We find an average V-R colour
mV-mR=0.15 mag
for image A and
mV-m R=0.18 mag for image B. We do not find
any evidence for significant colour variations during our observing
interval. The small difference
![]() mag of the
V-R colour between the quasar images indicates the presence of a
small level of differential reddening along the light paths.
mag of the
V-R colour between the quasar images indicates the presence of a
small level of differential reddening along the light paths.
A wide variety of algorithms have been developed for the determination of time delays in gravitational lens systems (e.g., Kundic et al. 1997; Burud et al. 2001; Gil-Merino et al. 2002). We choose here a strightfoward linear interpolation scheme because our light curve mainly consists of two frequently sampled observing intervals. The unfrequently sampled gap in the middle cannot be confidently interpolated with any method. In detail we use the following recipe:
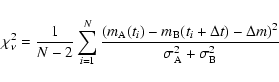 |
(1) |
The best-fitting time delay can be determined by calculating
![]() values for a range of time delays, and by choosing the
time delay with the lowest
values for a range of time delays, and by choosing the
time delay with the lowest
![]() value. In order to determine
the associated measurement uncertainties we used 10 000 bootstrap
resamplings of the observed light curve, smoothed by a triangular
filter with a full width of 20 days (e.g., Kundic et al. 1997). For
each smoothed resampling the best-fitting time delay was determined
for time delays between 0 and 220 days (image A leading). This
procedure is robust with respect to the size of the filter. We always
interpolated image A because in this case the sparse sampling of our
light curve between Julian Date-2 452 000=900 and 1100 has a smaller
impact on the determined limits. We have verified that interpolating
image B does not change the answers. It would only weaken the
determined constraints.
value. In order to determine
the associated measurement uncertainties we used 10 000 bootstrap
resamplings of the observed light curve, smoothed by a triangular
filter with a full width of 20 days (e.g., Kundic et al. 1997). For
each smoothed resampling the best-fitting time delay was determined
for time delays between 0 and 220 days (image A leading). This
procedure is robust with respect to the size of the filter. We always
interpolated image A because in this case the sparse sampling of our
light curve between Julian Date-2 452 000=900 and 1100 has a smaller
impact on the determined limits. We have verified that interpolating
image B does not change the answers. It would only weaken the
determined constraints.
The result of the Monte-Carlo resampling is shown in
Fig. 5. For two-day bins of the time delay ![]() the
number of Monte-Carlo light curves with a best-fitting time delay in
the given range has been calculated. The probability p of each bin
was calculated by dividing by the total number of resamplings. We find
that there are several time delays that are consistent with our data;
the 95 percent confidence region consists of four separate
regions. For these sub-regions we can calculate the average time delay
and the standard deviation, yielding
the
number of Monte-Carlo light curves with a best-fitting time delay in
the given range has been calculated. The probability p of each bin
was calculated by dividing by the total number of resamplings. We find
that there are several time delays that are consistent with our data;
the 95 percent confidence region consists of four separate
regions. For these sub-regions we can calculate the average time delay
and the standard deviation, yielding
![]() days,
days,
![]() days,
days,
![]() days and
days and
![]() days. The regions carry 33 percent, 54 percent, 2 percent and
6 per cent, respectively, of the statistical weight.
days. The regions carry 33 percent, 54 percent, 2 percent and
6 per cent, respectively, of the statistical weight.
The sub-region with the largest statistical weight is consistent with
the time delay
![]() days found by B02. For this
time delay our data require an offset of
days found by B02. For this
time delay our data require an offset of
![]() mag. In the
remainder of this paper we will use this time delay for our
data.
mag. In the
remainder of this paper we will use this time delay for our
data.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2852_fig5.eps} %\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg34.gif) |
Figure 5: Probability p for time delays based on our SBS 1520+530 light curve. The probability was calculated from 10 000 Monte-Carlo realizations of the light curve, and by interpolating quasar A each time. 95 per cent of the probability is contained in the four separate regions above the dashed line. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2852_fig6.ps}
\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg35.gif) |
Figure 6: Top panel: R-band light curves of the two quasar images A (filled circles) and B (open circles). The B light curve has been shifted by -130 days, as indicated by the arrow, and by -0.83 mag. Bottom panels: difference light curve between the shifted and interpolated quasar images. This was calculated in both ways: by interpolating image A or by interpolating image B (see text). |
| Open with DEXTER | |
In the top panel of Fig. 6 we show the quasar A and B
light curves in one plot, where image B was shifted to the left by the
time delay of 130 days and up by the magnitude offset of -0.83 mag
(see Sect. 4.2). The composite light curve has no large
gaps. It shows that the quasar has been going through a series of
three small
![]() mag brightness variations that each
lasted about 100 days.
mag brightness variations that each
lasted about 100 days.
Microlensing in the lens galaxy would only affect one of the light
paths to the quasar and could thus be detected as a residual light
curve difference (e.g., Schmidt & Wambsganss 1998; Wambsganss et al. 2000). In order to
study whether microlensing variations are present in our data, we
calculated the difference between the two observed light curves for
the time delay
![]() days found by B02 and the magnitude
offset of
days found by B02 and the magnitude
offset of
![]() mag.
mag.
To calculate the difference light curve, quasar B was shifted in time and magnitude. The rest of the procedure is identical to the one described in Sect. 4.2; we calculated the difference by linearly interpolating the light curves of quasar A or B. The light curves were interpolated whenever the gap was less than 40 days. No difference was calculated for larger gaps. The error bars were added in quadrature. The resulting two difference light curves are plotted in the bottom two panels of Fig. 6.
It can be taken from these plots that we do not detect a significant
difference between the two quasar light curves. We can calculate the
goodness-of-fit estimator for the null hypothesis that there is no
difference between the light curves on the N days for which the
difference was calculated (yielding ![]() degrees of freedom):
degrees of freedom):
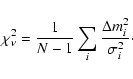 |
(2) |
Assuming that the data have a Gaussian scatter around zero we can
determine the standard deviation
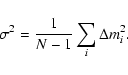 |
(3) |
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{2852_fig7.ps}
\end{figure}](/articles/aa/full/2005/34/aa2852-05/Timg44.gif) |
Figure 7: Composite of the difference light curves based on our Maydanak data (filled circles, see Fig. 6) and the data published by Burud et al. (2002) (open circles, the linear trend determined by them is shown with a dashed line). In both cases image A was linearly interpolated. |
| Open with DEXTER | |
In their earlier data taken between February 1999 and May 2001, B02 did find a difference between the light curves of the two quasar images in this system. Applying our procedure to the light curves in their Table 2, we can also calculate the difference light curve of their data. The result is shown with in Fig. 7 (open circles) together with our difference light curve (filled circles) from the first of the two bottom panels in Fig. 6 (image A was linearly interpolated). The difference curve in this figure is plotted without offset.
Figure 7 shows that B02 observed a coherent and highly
significant difference light curve with a maximum amplitude of
![]() mag. Since the time of the observations by B02 the
magnitude difference between the quasar images has increased by
mag. Since the time of the observations by B02 the
magnitude difference between the quasar images has increased by
![]() mag (see the discussion in Sect. 5). B02
already identified a linear trend (dashed line) in their data. Our
data are consistent with this linear trend having continued until the
epoch of our observations.
mag (see the discussion in Sect. 5). B02
already identified a linear trend (dashed line) in their data. Our
data are consistent with this linear trend having continued until the
epoch of our observations.
Although the exposure times for the Maidanak and the B02 data are similar, the error bars of the Maidanak data are larger than the error bars obtained by B02. The main reason for this are the different telescope apertures (1.5 m at the AZT-22 vs. 2.5 m at the NOT). In addition, however, the AZT-22 transmission was reduced by about one magnitude before the mirror was cleaned on Julian Date-2 452 000=880(see Fig. 3).
We note that the long-term variation of the difference light curve may even be slightly larger than shown in this plot because some light from the lensing galaxy could be included in our magnitude estimate of image B (see Sect. 3). If all of the lensing galaxy light were included, the Maidanak difference light curve would have to be shifted upward by a constant offset of -0.08 mag to correct for the galaxy contribution.
We have presented V-band and R-band photometry of the gravitational
lens system SBS 1520+530 taken at Maidanak Observatory in the years
2003 (April to October) and 2004 (January to August). During the
![]() 500 day observation period with 80 data points in V and
123 data points in R we find small amplitude intrinsic variations
(
500 day observation period with 80 data points in V and
123 data points in R we find small amplitude intrinsic variations
(
![]() mag) on time scales of about 100 days in both
quasar images. The V-R colour of the quasar is consistent with being
constant during the observed period.
mag) on time scales of about 100 days in both
quasar images. The V-R colour of the quasar is consistent with being
constant during the observed period.
Using linear interpolation of the quasar light curves, we have
determined the 95 percent confidence region of time delays for our
data set. Due to gaps in the light curve, our data allow four separate
values of the time delay, the best one of which agrees with the time
delay of ![]() days found by B02. Image A is leading, which is
also consistent with lens models of the system
(Asano 2000; Faure et al. 2002; B02; Zheleznyak et al. 2003).
days found by B02. Image A is leading, which is
also consistent with lens models of the system
(Asano 2000; Faure et al. 2002; B02; Zheleznyak et al. 2003).
Using the B02 time delay, we calculated the difference light curve
between the two quasar images. This shows that within the statistical
uncertainty the two quasar light curves are identical during our
observing interval (Fig. 6). In the observations taken by
B02 between 1999 and 2001, a highly significant and variable
difference with an amplitude of
![]() mag was present
for a fraction of the observing interval. Since then, the overall
R-band magnitude difference between the A and B light curves has
changed by
mag was present
for a fraction of the observing interval. Since then, the overall
R-band magnitude difference between the A and B light curves has
changed by
![]() mag, the difference being larger in our data
(Fig. 7).
mag, the difference being larger in our data
(Fig. 7).
Any variable difference between the light curves of SBS 1520+530 can be
interpreted as gravitational microlensing because other changes of the
source would be visible in both quasar images, delayed by the time
delay. In addition to the microlensing variability on short
time-scales (![]() 100 days and less) found by B02, our data show
that there are also variations on longer time-scales of
100 days and less) found by B02, our data show
that there are also variations on longer time-scales of
![]() 100-1000) days. This overall level of microlensing
variations in SBS 1520+530 appears comparable to variations seen in
other lens systems (e.g., Wyithe & Loeb 2002; Hjorth et al. 2002; Schechter et al. 2003).
100-1000) days. This overall level of microlensing
variations in SBS 1520+530 appears comparable to variations seen in
other lens systems (e.g., Wyithe & Loeb 2002; Hjorth et al. 2002; Schechter et al. 2003).
An exciting prediction for the microlensing effect of quasars is the colour-dependence of the microlensing light curve in the vicinity of caustics (Wambsganss & Paczynski 1991). In such a situation the difference between the V and the R light curve could provide valuable clues to the source structure of the quasar. We will continue to observe SBS 1520+530 from Maidanak observatory because frequent sampling of the source remains crucial to derive limits on microlensing variability. If colour variations associated with microlensing could be proven in this system, there would be a strong case for parallel spectral observations of the quasar (see also B02).
Since microlensing currently remains the only technique with the promise to scan the continuum emission regions of quasars on microarcsecond scales, SBS 1520+530 should be viewed as a prime target because of the combination of known quasar variability and the at least occasional occurence of microlensing diagnostics at the same time.
Acknowledgements
We thank B. P. Artamonov and V. N. Dudinov for useful advice on the realization of our observations. We thank the former German Ambassador to Uzbekistan, Dr. Martin Hecker, for his support of our collaboration. The Uzbek team thanks the AIP and the University of Potsdam for hospitality during visits. S.G. and R.W.S. thank the Ulugh Begh Astronomical Institute for hospitality. This project was supported by the German Research Foundation (DFG), grant 436 USB 113/5/0-1. We also acknowledge support by the European Community's Sixth Framework Marie Curie Research Training Network Programme, Contract No. MRTN-CT-2004-505183 "ANGLES''.