A&A 440, 185-198 (2005)
DOI: 10.1051/0004-6361:20052706
J. B. G. Canalle1,2 - C. J. Saxton1,3 - K. Wu1 - M. Cropper1 - G. Ramsay1
1 - Mullard Space Science Laboratory,
University College London,
Holmbury St. Mary, Dorking, Surrey
RH5 6NT, UK
2 -
State University of Rio de Janeiro,
Rua São Francisco Xavier, 524/3023-D,
CEP 20559-900, Rio de Janeiro, RJ, Brazil
3 -
Max-Planck-Institut für Radioastronomie,
Auf dem Hügel 69, 53121 Bonn, Germany
Received 16 January 2005 / Accepted 12 March 2005
Abstract
Field-channelled accretion flows occur in a variety of
astrophysical objects, including T Tauri stars,
magnetic cataclysmic variables and X-ray pulsars.
We consider a curvilinear coordinate system
and derive a general hydrodynamic formulation
for accretion onto stellar objects
confined by a stellar dipole magnetic field.
The hydrodynamic equations are solved to determine
the velocity, density and temperature profiles of the flow.
We use accreting magnetic white-dwarf stars
as an illustrative example of astrophysical applications.
Our calculations show that
the compressional heating due to the field geometry
is as important as radiative cooling and gravity
in determining the structure of the post-shock flow
in accreting white-dwarf stars.
The generalisation of the formulation
to accretion flows channelled by higher-order fields
and the applications to other astrophysical systems are discussed.
Key words: accretion, accretion disks - hydrodynamics - shock waves - stars: magnetic fields - stars: novae, cataclysmic variables - stars: pre-main-sequence
Accretion is a common phenomenon in astrophysical systems ranging from young stellar objects, interacting binaries, galaxies to galaxy clusters. When the magnetic-field stress is larger than the ram pressure of the accreting material, the flow is confined to follow the magnetic-field lines. The accretion hydrodynamics in these systems are therefore dependent on the magnetic-field geometry.
Field-channelled accretion flow can occur in young stellar objects (e.g. Gullbring et al. 2000; Lamzin et al. 2001; Königl 1991; Hartman et al. 1994; Li 1996; Calvet & Gullbring 1998; Koldoba et al. 2002; Stelzer & Schmitt 2004; Lamzin 1998; Romanova et al. 2003), neutron star accretion from inter-stellar medium (e.g. Toropina et al. 2003), and interacting binaries containing a white dwarf or a neutron star (e.g. Koldoba et al. 2002; Li et al. 1996; Arons 1993; Kryukov et al. 2000; Lovelace et al. 1995; Elsner & Lamb 1977; Ghosh & Lamb 1978). In white-dwarf and neutron-star binaries the magnetic field of the compact star can also be strong enough to affect the cooling processes. Despite the fact that these stars may have complex magnetic-field structures, the dipole field component is important, as it has a longer range than the higher-order field components and dominates in the regions sufficiently far from the star.
Here we investigate the accretion flow onto stellar objects
in the regime
![]() (where B is the magnetic field,
and
(where B is the magnetic field,
and ![]() and v are the density
and velocity of the accreting material respectively),
so that the flow is strictly confined by the magnetic field.
We apply a curvilinear coordinate system
that is natural to the dipole-field geometry
for the hydrodynamic formation.
We solve the hydrodynamic equations
for an accretion flow
in which the cooling function
has a power-law dependence on the temperature and density
and thereby obtain the flow-velocity, density and temperature profiles.
and v are the density
and velocity of the accreting material respectively),
so that the flow is strictly confined by the magnetic field.
We apply a curvilinear coordinate system
that is natural to the dipole-field geometry
for the hydrodynamic formation.
We solve the hydrodynamic equations
for an accretion flow
in which the cooling function
has a power-law dependence on the temperature and density
and thereby obtain the flow-velocity, density and temperature profiles.
We apply the model to the post-shock flow in magnetic cataclysmic variables (mCVs), which are close binary systems containing a magnetic white dwarf accreting from a red-dwarf companion star (see Warner 1995). We calculate the temperature, velocity and density structure of the post-shock emission region and model the X-ray line and continuum emission. We compare our results to those obtained by the plane-parallel model (Chevalier & Imamura 1982; Cropper et al. 1999; Wu 1994; Wu et al. 1994) which is generally used in spectral analysis of X-rays emitted from mCVs.
The paper is organised as follows: in Sect. 2 we derive the hydrodynamic equations in curvilinear coordinates; in Sect. 3 we present the treatment of the boundary conditions and discuss briefly the numerical scheme that we use; and in Sects. 4 to 6 we show an illustrative example - accretion onto a magnetic white dwarf stars - and present hydrodynamic structure and spectral calculations. In Sect. 7 we consider the use of this formulation in some other astrophysical applications. Our summary and conclusions comprise Sect. 8.
For the analytic study of field-channelled accretion flow,
we choose a coordinate system
with one component along the magnetic-field lines.
In this representation,
the flow is at most 2-dimensional (2D);
and it can often be reduced to 1-dimensional (1D) form
when the system has a special geometric symmetry.
In the present study we consider accretion channelled by a dipole field,
which is axi-symmetric and, it can be shown, essentially 1D.
We define a curvilinear coordinate system (u, w, ![]() )
for the dipolar field as follows.
The first coordinate u is defined by the magnetic-field lines
generated by a point magnetic dipole.
The dipole is oriented in the z direction
and located at the center of the accreting star
(the origin of the coordinate systems),
where (x,y,x) are the usual Cartesian coordinates.
As a static magnetic field is the gradient of a potential,
we use the equipotential curves of the dipole field
as second coordinate w.
The third coordinate is the azimuthal coordinate,
)
for the dipolar field as follows.
The first coordinate u is defined by the magnetic-field lines
generated by a point magnetic dipole.
The dipole is oriented in the z direction
and located at the center of the accreting star
(the origin of the coordinate systems),
where (x,y,x) are the usual Cartesian coordinates.
As a static magnetic field is the gradient of a potential,
we use the equipotential curves of the dipole field
as second coordinate w.
The third coordinate is the azimuthal coordinate, ![]() ,
the same as that in the conventional spherical coordinate system
(r,
,
the same as that in the conventional spherical coordinate system
(r, ![]() ,
, ![]() ).
The unit vectors
).
The unit vectors
![]() ,
,
![]() and
and
![]() are orthogonal to each other, as shown in Fig. 1.
are orthogonal to each other, as shown in Fig. 1.
In spherical coordinates,
the field lines and equipotential surfaces of a dipole field
satisfy
![]() and
and
![]() respectively,
where a1 is the radius
at which the field line intercepts the mid-plane of the dipole
and a2 is the radius
at which the equipotential surface meets the polar axis.
Thus, we have
respectively,
where a1 is the radius
at which the field line intercepts the mid-plane of the dipole
and a2 is the radius
at which the equipotential surface meets the polar axis.
Thus, we have
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{2706f01.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg44.gif) |
Figure 1:
The projection of the ( u, w, |
| Open with DEXTER | |
For stationary flows, the time derivatives are zero.
For one temperature flows,
the electron and the ion energy equations can be combined
by eliminating
![]() ,
yielding
,
yielding
![\begin{displaymath}(\vec{ v}.\nabla)P - \frac{\gamma P}{\rho}(\vec{ v}.\nabla)\r...
...nabla\cdot(\vec{ q}+\vec{ F}_{\rm rad})
- \Lambda_{\rm h}] ,
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img59.gif) |
(9) |
As we have assummed by default that the flow follows the field lines,
the velocity has only the component along the ![]() direction, i.e.
direction, i.e.
The hydrodynamic equations decomposed into the orthogonal components
in the (u, w, ![]() )-coordinate system are
)-coordinate system are
Direct integration of the mass-continuity Eq. (17) yields
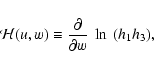 |
(24) |
In this study, we simply consider an ideal-gas law
For non-relativistic, spherical (Bondi-Hoyle type) accretion onto stellar objects, there are two classes of physical solutions (see e.g. Frank et al. 1992). In the first class, the flow is subsonic from infinity to the surface of the accreting star. In the second class, the flow is initially subsonic and becomes supersonic at certain radius from the star. As it requires the flow velocity to be zero at the stellar surface, the flow will become subsonic again via a shock, which converts the kinetic energy of the flow to the thermal energy of accreting material.
The situation is the same for flows channelled by a dipole magnetic field, although the dipole field lines, except the two originating from the poles, are all closed at finite distances. (See e.g. Koldoba et al. 2002, for more details.) In this study we consider the second class and focus on determining the density and temperature structures of the region between the shock and the star. We will show how to construct the shock boundary conditions within the hydrodynamic framework that we use and solve the hydrodynamic equations with these boundary conditions.
We apply the Rankine-Hugoniot condition
to derive the shock boundary condition,
assuming that the pre-shock flow is supersonic and cold,
such that the Mach number
![]() ,
we have
,
we have
If the collisional energy exchange between electrons and ions
is efficient compared to radiative cooling
then the electrons and ions have approximately equal temperatures.
The shock temperature is given by
| (36) |
The stellar surface corresponds to r=1 in the spherical coordinates,
but the functional form of the stellar surface
in the
![]() coordinates is not trivial.
At the surface the independent variable w
has different values for different magnetic field lines.
The boundary value of w for a field line
is determined (using Eq. (2))
only after we specify the colatitude on the stellar surface
at which the field line is anchored
(which we shall denote as
coordinates is not trivial.
At the surface the independent variable w
has different values for different magnetic field lines.
The boundary value of w for a field line
is determined (using Eq. (2))
only after we specify the colatitude on the stellar surface
at which the field line is anchored
(which we shall denote as ![]() ).
).
As the boundary values of w both at the shock and at the stellar surface are not easily specified in terms of simple functions of w and u, we search for an alternative independent variable. The criterion for the variable is that it increases or decreases montonically in the region of interest. As shown above (Sect. 3.1) the velocity v is better defined at the shock boundary and the stellar-surface boundary. It should be smooth in the post-shock region and is monotonic in at least in the region just beneath the shock and in the region just above the stellar surface.
Without losing qualitative generality,
hereafter we will use
![]() and
and
![]() (Eq. (29), describing Bremsstrahlung cooling)
in our calculations.
Then the energy-conservation Eq. (30)
can be expressed with v the independent variable
and w the dependent variable,
(Eq. (29), describing Bremsstrahlung cooling)
in our calculations.
Then the energy-conservation Eq. (30)
can be expressed with v the independent variable
and w the dependent variable,
The corresponding hydrodynamic equations,
for
![]() and
and
![]() ,
can be obtained
using the chain rule of differentiation with
,
can be obtained
using the chain rule of differentiation with
![\begin{displaymath}\frac{{\rm d}\tau}{{\rm d}v} = \tau \biggl[
{\frac{\sqrt{r(...
...u,w)}{r(u,w)}\biggr)
{\frac{{\rm d}w} {{\rm d}v}} \biggr] ,
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img128.gif) |
(40) |
The use of ![]() as an independent variable
provides a convenient way to treat the boundary conditions
at both the shock and the stellar surface.
However
as an independent variable
provides a convenient way to treat the boundary conditions
at both the shock and the stellar surface.
However ![]() (like v) is not guaranteed to be monotonic in w for all systems and all choices of u.
Thus we cannot use it as the independent variable
throughout the entire post-shock region.
In contrast, the coordinate w is always monotonic along a field line,
but it is not practically usable at the stellar surface,
where the velocity gradient
(like v) is not guaranteed to be monotonic in w for all systems and all choices of u.
Thus we cannot use it as the independent variable
throughout the entire post-shock region.
In contrast, the coordinate w is always monotonic along a field line,
but it is not practically usable at the stellar surface,
where the velocity gradient
![]() approaches infinity.
approaches infinity.
Given that it is straightforward to use w as the independent variable
in the numerical integration in the entire flow
except at the stellar surface,
we consider a hybrid numerical scheme in our calculations.
Therefore we use ![]() or v as the variable of integration
in the vinicity of the stellar surface,
or v as the variable of integration
in the vinicity of the stellar surface,
![]() with
with
![]() ,
but we switch to integration in terms of w in the upper parts of the post-shock structure.
This algorithm allows us to solve the flow profile
along each field line.
,
but we switch to integration in terms of w in the upper parts of the post-shock structure.
This algorithm allows us to solve the flow profile
along each field line.
We calculate the pressure and velocity profiles of the post-shock structure
by numerically integrating a set of differential equations
between the upper and lower boundaries.
In regions where we treat w as the independent variable,
we use Eqs. (25) and (26).
Where v or ![]() serves as the independent variable then
we use equations such as Eqs. (37) and (38)
or the equivalent with derivatives in
serves as the independent variable then
we use equations such as Eqs. (37) and (38)
or the equivalent with derivatives in ![]() .
.
Neither boundary condition is completely specified from first principles:
the position of the shock (expressed in terms of ![]() or
or ![]() )
is not initially known.
Nor do we have foreknowledge of
the momentum flux at the stellar surface (
)
is not initially known.
Nor do we have foreknowledge of
the momentum flux at the stellar surface (![]() ).
In practice we choose trial values of
).
In practice we choose trial values of
![]() and test how the resulting profile conforms to the conditions required
at the opposite boundary.
In one method, we choose trial values of
and test how the resulting profile conforms to the conditions required
at the opposite boundary.
In one method, we choose trial values of ![]() ,
and integrate upwards from the stellar surface until a shock is found.
We adjust
,
and integrate upwards from the stellar surface until a shock is found.
We adjust ![]() until we match the conditions
until we match the conditions
![]() and
and
![]() simultaneously.
Alternatively, we may try values of
simultaneously.
Alternatively, we may try values of ![]() and integrate downwards from the shock to the point where v=0.
If
and integrate downwards from the shock to the point where v=0.
If ![]() when v=0 then we adjust the trial value of
when v=0 then we adjust the trial value of ![]() and retry.
These tests are applied iteratively in a root-finding routine.
and retry.
These tests are applied iteratively in a root-finding routine.
We now apply our formulation to an astrophysical system as an illustration. We consider a simple case: accretion onto a magnetised white dwarf, in which free-free emission is the dominant cooling mechanism. This kind of system can be found in intermediate polars and polars, which are cataclysmic variables containing a magnetic white dwarf accreting material from a low-mass companion star (for reviews of magnetic cataclysmic variables, see e.g. Cropper 1990; and Warner 1995). The post-shock accretion flow in magnetic cataclysmic variables have been investigated by many workers and analytic and semi-analytic results were obtained (e.g. Chevalier & Imamura 1982; Aizu 1973; Imamura et al. 1996; Wu 1994; Saxton & Wu 2001,1999; Wu et al. 1994; Cropper et al. 1999). Their studies address various issues such as the cooling processes and the effect due to gravity, and the calculations either planar or spherical geometries were considered. (For reviews of the hydrodynamics of post-shock accretion in magnetic cataclysmic variables, see Wu 2000; Beuermann 2004.) Because of the assumed geometry, these studies have not quantified the effects of the curvature of field lines in determining the hydrodynamic structure of shock-heated region.
For the application of our formulation in the accretion onto white dwarfs,
we simply set
![]() and
and
![]() ,
where
,
where
![]() and
and
![]() and white-dwarf mass and radius,
in the hydrodynamic equations
and scale the variables accordingly.
The white-dwarf mass and radius are not independent
- when the mass is specified
one can calculate the radius by means of a mass-radius relation.
In our calculations,
we adopt the Nauenberg (1972) mass-radius relation
and white-dwarf mass and radius,
in the hydrodynamic equations
and scale the variables accordingly.
The white-dwarf mass and radius are not independent
- when the mass is specified
one can calculate the radius by means of a mass-radius relation.
In our calculations,
we adopt the Nauenberg (1972) mass-radius relation
We consider a strong shock for the upper boundary condition
and a cool stationary wall for the lower boundary condition.
The accreting material is an ideal gas with
![]() and approximately solar abundances (Anders & Ebihara 1982).
The mean ionic mass and charge are
and approximately solar abundances (Anders & Ebihara 1982).
The mean ionic mass and charge are
![]() and
and
![]() respectively,
and
respectively,
and
![]() ,
,
![]() ,
,
![]() .
We omit other radiative transport and microscopic effects
at the shock and the stellar-surface boundary
(see e.g. Wu & Cropper 2001; Saxton & Wu 2001; Imamura et al. 1996).
.
We omit other radiative transport and microscopic effects
at the shock and the stellar-surface boundary
(see e.g. Wu & Cropper 2001; Saxton & Wu 2001; Imamura et al. 1996).
If the white dwarf has a weak magnetic field
or sufficiently high accretion rate
then the cooling of the post-shock flow is dominated by free-free emission,
and Cyclotron cooling is unimportant.
The cooling function is then
A natural extension of the case for accretion onto weakly magnetic white dwarfs
is the accretion onto strong-field systems
(i.e. polars, see Cropper 1990)
the flow is cooled
by emitting both optical Cyclotron radiation and free-free X-rays.
We can use a composite cooling function to describe the cooling process, i.e.
![\begin{displaymath}\Lambda = A \rho^2 \sqrt{\frac{P}{\rho}}\
\left[{\ 1+\epsilon_{\rm s} f(P,\rho,u,w) \ }\right]
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img155.gif) |
(43) |
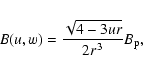 |
(45) |
Then, we replace ![]() by
C/h1 h3 v and
by
C/h1 h3 v and ![]() by
by ![]() throughout the f cooling function,
and substitute
throughout the f cooling function,
and substitute ![]() into Eq. (26).
The resulting hydrodynamic equations can be solved
using the numerical scheme described in Sect. 3.
into Eq. (26).
The resulting hydrodynamic equations can be solved
using the numerical scheme described in Sect. 3.
We note that the formulation we derive
can reduce to the formulations obtained in the previous studies
under certain approximations and restricted conditions.
Take, for instance, Eqs. (37) and (38).
If we set
h1 = h2 = h3 =1,
![]() and gw =0,
and fix
and gw =0,
and fix ![]() to be a constant
equal to the free-fall velocity at the white-dwarf surface,
then Eq. (38) vanishes
and Eq. (37) becomes the same as
that in Chevalier & Imamura (1982) and Wu (1994) for the planar flows.
If we set u=0,
w=1/r2,
to be a constant
equal to the free-fall velocity at the white-dwarf surface,
then Eq. (38) vanishes
and Eq. (37) becomes the same as
that in Chevalier & Imamura (1982) and Wu (1994) for the planar flows.
If we set u=0,
w=1/r2,
![]() ,
,
![]() ,
and
,
and
![]() then we obtain the same set of two equations of Cropper et al. (1999).
then we obtain the same set of two equations of Cropper et al. (1999).
Comparing the formulation of Cropper et al. (1999)
with Chevalier & Imamura (1982)
and Wu (1994)
reveals that the former needs two equations to describe the flow
while the later requires only one.
It is because in the presence of gravity
the quantity ![]() ,
which describes the specific momentum flux,
is no longer conserved along the field lines.
In our formulation, despite the presence of a dipole field,
two differential equations are sufficient
to determine the hydrodynamics,
as in the case of Cropper et al. (1999).
We still have two differential equations
when we set gw=0
in both Eqs. (37) and (38).
,
which describes the specific momentum flux,
is no longer conserved along the field lines.
In our formulation, despite the presence of a dipole field,
two differential equations are sufficient
to determine the hydrodynamics,
as in the case of Cropper et al. (1999).
We still have two differential equations
when we set gw=0
in both Eqs. (37) and (38).
To further illustrate the importance of the effects due to the field geometry, in the next section we present the numerical results of calculations, in which typical parameters of magnetic cataclysmic variables are used. We will show that the results can differ substantially from those obtained by formulations (e.g. Cropper et al. 1999) without taking account of the geometric effects.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f02.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg169.gif) |
Figure 2:
Variation of the local mass accretion rate |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f03.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg171.gif) |
Figure 3:
Variation of the component of the gravitational acceleration
tangential to the magnetic field line.
The five curves correspond to cases of
hot-spot colatitude
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f04.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg173.gif) |
Figure 4:
Post-shock pressure profiles
with the parameters (
|
| Open with DEXTER | |
The gravitational acceleration component
in the direction tangential to the magnetic field lines,
which we call gw in
Eq. (16),
is a fraction of the total gravitational acceleration g.
Figure 3
shows the relation gw/g.
Except for the special case of accretion onto the pole,
![]() ,
the magnetic field lines are nowhere vertical to the stellar surface.
Thus the component gw is not equal to the total acceleration on the surface of the white dwarf.
,
the magnetic field lines are nowhere vertical to the stellar surface.
Thus the component gw is not equal to the total acceleration on the surface of the white dwarf.
Scaled relative to the shock height and parameters of the accretion, there are several qualitative differences between the post-shock flows in the present dipolar model and the cylindrical accretion model of Cropper et al. (1999).
The distribution of pressure is shown in Fig. 4. The dipolar accretion model results in proportionally higher pressures throughout the post-shock region.
Corresponding profiles of the density structures are shown in Fig. 5. The dipolar funnel results in greater densities throughout most of the post-shock region (relative to the gas density at the shock), than in the cylindrical accretion case. As in previous models with a power-law expression for Bremsstrahlung cooling (e.g. Chevalier & Imamura 1982; Cropper et al. 1999; Wu 1994), the density necessarily increases asymptotically near the stellar surface.
Figure 6 shows the gas velocity between the white dwarf surface (r=1) and the shock. The velocity profiles show the most significant qualitative difference between dipolar and cylindrical accretion models: in the Bremsstrahlung-dominated case that we have illustrated, the cylindrical model results in a much more constant velocity gradient throughout most of the post-shock region.
Figure 6 also displays a significant quantitative difference
between the predicted shock positions in the cylindrical and dipolar models.
For the cases shown,
with accretion colatitudes
![]() ,
the shock occurs at a radius around
,
the shock occurs at a radius around
![]() .
In the equivalent cylindrical accretion model,
the shock height is much lower,
.
In the equivalent cylindrical accretion model,
the shock height is much lower,
![]() ,
i.e. just over half the height
that we would obtain by using the dipole field geometry.
,
i.e. just over half the height
that we would obtain by using the dipole field geometry.
As the magnetic field strength is increased
to some tens of ![]() ,
the radiative cooling due to Cyclotron emission
becomes large compared to the Bremsstrahlung cooling.
As
,
the radiative cooling due to Cyclotron emission
becomes large compared to the Bremsstrahlung cooling.
As
![]() increases,
the shock height decreases in both
the cylindrical accretion model (Cropper et al. 1999)
and our dipole model.
For any set of system parameters,
increases,
the shock height decreases in both
the cylindrical accretion model (Cropper et al. 1999)
and our dipole model.
For any set of system parameters,
![]() ,
the dipolar model predicts the shock to occur higher
than in the cylindrical model.
However the difference is insignificant
in high-
,
the dipolar model predicts the shock to occur higher
than in the cylindrical model.
However the difference is insignificant
in high-
![]() cases
where the shock height
is sufficiently low and curvature effects are negligible.
For instances in cases with
cases
where the shock height
is sufficiently low and curvature effects are negligible.
For instances in cases with
![]() we calculate
we calculate
![]() according to the cylindrical model,
but the dipolar model yields
according to the cylindrical model,
but the dipolar model yields
![]() when
when
![]() .
.
Figure 7 shows the dependence of shock height
upon the colatitude of the accretion spot (![]() )
for several cases of B* appropriate for polars.
The maximum shock height generally occurs
for accretion along the field line with
)
for several cases of B* appropriate for polars.
The maximum shock height generally occurs
for accretion along the field line with
![]() .
In cases with low B* the variation of
.
In cases with low B* the variation of ![]() with
with ![]() is less than in the stronger field cases.
When the magnetic field is stronger
the shock height is smaller compared to the white dwarf radius,
and the dipolar funnel effects less significant.
is less than in the stronger field cases.
When the magnetic field is stronger
the shock height is smaller compared to the white dwarf radius,
and the dipolar funnel effects less significant.
Figure 8 shows equivalent relations between
shock height and ![]() ,
but for a greater accretion rate,
,
but for a greater accretion rate,
![]() .
Bremsstrahlung cooling is more efficient in this denser flow,
and the shock heights are lower than in Fig. 7,
as expected from previous studies
(e.g. Imamura et al. 1996; Aizu 1973; Wu 1994).
Again, as in Fig. 7,
.
Bremsstrahlung cooling is more efficient in this denser flow,
and the shock heights are lower than in Fig. 7,
as expected from previous studies
(e.g. Imamura et al. 1996; Aizu 1973; Wu 1994).
Again, as in Fig. 7,
![]() is more variable in
is more variable in ![]() in the cases with weaker magnetic field and greater shock height.
in the cases with weaker magnetic field and greater shock height.
Figure 9
shows the temperature as a function of height within the column
in our standard illustrative case.
For comparison we calculate the temperature profile
with the same parameters for the white dwarf and accretion rate,
but applied in the cylindrical accretion model.
In this specific case
the shock temperature in the cylindrical accretion model
is
![]() greater than it is in the dipolar accretion model.
The dipolar accretion model generally yields a lower shock temperature
than cylindrical accretion,
because of the greater shock height
and thus lower free-fall velocity at the shock.
The temperature predictions of cylindrical and dipolar accretion models
are much more alike for cases where
the shock is closer to the white dwarf surface
(and dipolar funnel effects are less significant).
greater than it is in the dipolar accretion model.
The dipolar accretion model generally yields a lower shock temperature
than cylindrical accretion,
because of the greater shock height
and thus lower free-fall velocity at the shock.
The temperature predictions of cylindrical and dipolar accretion models
are much more alike for cases where
the shock is closer to the white dwarf surface
(and dipolar funnel effects are less significant).
Figure 10 compares the cylindrical and dipolar models' results for the temperature structure of the accretion column, for four different values of the white dwarf mass, in the Bremsstrahlung-dominated limit. The dipolar model generally has a lower shock temperature than the equivalent cylindrical model. The difference between models is greatest for the most massive white dwarfs, as their accretion shocks are higher (and thus more affected by funnel geometry).
In the next section we present calculations of the X-ray spectrum emitted from the post-shock flow, for two represenative cases of M*. We compare the predictions of the dipolar accretion model with those of the planar models, thereby showing the precise effects of curvature.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f05.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg190.gif) |
Figure 5:
Density profiles of the accretion columns shown in
Fig. 4,
scaled to the gas density immediately downstream of the shock
(
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f06.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg191.gif) |
Figure 6:
Velocity profile of the post-shock structure,
normalised to the escape velocity and the stellar surface, V*.
The upper curve represents the model of Cropper et al. (1999).
The lower curve shows the effects
of accretion in a dipole-field accretion funnel,
with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2706f07.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg193.gif) |
Figure 7:
Effect of the accretion colatitude, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2706f08.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg194.gif) |
Figure 8:
Radial location of the shock as a function of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f09.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg195.gif) |
Figure 9:
Variation of the gas temperature in the accretion column
as a function of altitude scaled to the shock location.
System parameters
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f10.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg196.gif) |
Figure 10:
Comparison between cylindrical and dipolar geometry
for four different values of white dwarf mass.
From bottom to top each pair of curves represents:
M* = 0.7, 0.8, 0.9 and
|
| Open with DEXTER | |
In Sect. 5
we use an accreting magnetic white-dwarf star as an illustration
and demonstrate
that the role of the field geometry can be as important as
(or even more than) the role of gravity
in determining the velocity, density and temperature profiles of the flow.
We can elaborate this more clearly
by inspecting the meanings of the terms in the hydrdodynamic equations.
Each of the terms in the square brackets
in the right side of Eq. (26)
corresponds to an energy-transport process.
The first represents the radiative loss,
the second is determined by the geometry of flow,
and the third is due to an external force field,
which is only gravity here.
A characteristic of the second term is the
![]() function.
In the curvilinear coordinates that we use,
h1 and h3 are the metric elements
corresponding to the coordinates perpendicular to w.
Thus
function.
In the curvilinear coordinates that we use,
h1 and h3 are the metric elements
corresponding to the coordinates perpendicular to w.
Thus
![]() is the measure of the changes in cross-section area
of the magnetic-flux tube along the flow,
and it plays an important role
in determining the efficiency of compressional heating.
is the measure of the changes in cross-section area
of the magnetic-flux tube along the flow,
and it plays an important role
in determining the efficiency of compressional heating.
It is worth noting that
the
![]() function also equals to
function also equals to
![]() ,
where
,
where ![]() is the unit vector tangential to the magnetic field,
and h2 is the metric for the coordinate component along the field line.
We may also use this relation to determine the
is the unit vector tangential to the magnetic field,
and h2 is the metric for the coordinate component along the field line.
We may also use this relation to determine the
![]() function.
function.
For accretion onto stellar objects,
![]() and
and
![]() ,
where
,
where
![]() is the mean free-fall velocity.
The metric element
is the mean free-fall velocity.
The metric element
![]() ,
and hence, the geometry function
,
and hence, the geometry function
![]() .
From Eq. (38),
we can deduce that the effects due to field curvature (geometry)
and gravity are often comparable.
Generally, the geometry effect is more important
for regions close to the stellar surface
than for regions further away,
because the convergence of the dipole field lines.
.
From Eq. (38),
we can deduce that the effects due to field curvature (geometry)
and gravity are often comparable.
Generally, the geometry effect is more important
for regions close to the stellar surface
than for regions further away,
because the convergence of the dipole field lines.
We note that Eqs. (25) and (26)
are general equations,
in principle, applicable for accretion flows
channelled by any field geometries.
For example, if the magnetic field has planar parallel structure,
then we have
h1 = h2 = h3 =1.
It follows that
![]() .
In this flow, the accreting material will not be compressed by the magnetic field.
If the flow is spherical,
then h1=1, h2 = r,
.
In this flow, the accreting material will not be compressed by the magnetic field.
If the flow is spherical,
then h1=1, h2 = r,
![]() (see e.g. Arfken & Weger 2001),
and
(see e.g. Arfken & Weger 2001),
and
![]() .
The flows channelled by dipole field have been shown in the sections above.
The generalisation to channelled flows in higher-order fields
is possible.
What one needs are first
to find the functional expressions of the field lines and the equipotential surfaces,
and use them to define the coordinates.
After the coordinate system is specified,
we can derive the metric elements h1, h2 and h3 and determine the
.
The flows channelled by dipole field have been shown in the sections above.
The generalisation to channelled flows in higher-order fields
is possible.
What one needs are first
to find the functional expressions of the field lines and the equipotential surfaces,
and use them to define the coordinates.
After the coordinate system is specified,
we can derive the metric elements h1, h2 and h3 and determine the
![]() function.
The effects of more complex field geometries depend on
the alignment and distribution of the higher-order field components.
If the field lines near the accretion spot diverge more rapidly
than in the dipolar model (i.e. a more flared accretion funnel)
then we expect an accentuation of the
effects found in the present work:
a higher shock position and lower shock temperature.
If the field lines near the accretion spot diverge less rapidly
then the accretion flow will be a closer approximation to
the older, planar accretion models.
function.
The effects of more complex field geometries depend on
the alignment and distribution of the higher-order field components.
If the field lines near the accretion spot diverge more rapidly
than in the dipolar model (i.e. a more flared accretion funnel)
then we expect an accentuation of the
effects found in the present work:
a higher shock position and lower shock temperature.
If the field lines near the accretion spot diverge less rapidly
then the accretion flow will be a closer approximation to
the older, planar accretion models.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f11.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg208.gif) |
Figure 11:
Comparison of X-ray spectra calculated using
(I) the dipole accretion model with gravity;
(II) CWRK accretion model with gravity but without curvature effects;
(III) planar accretion model of Wu (1994) without gravity or curvature;
(IV) isothermal model using the post-shock temperature and density
derived from model (I).
The upper panel shows the X-ray spectrum of model (I) directly.
The remaining panels present ratios between
the dipole model spectrum and the other models.
In all cases we set
|
| Open with DEXTER | |
We use the analytic model
to provide electron density and temperature values
throughout the post-shock flow.
The structure is divided into between
![]() and
and
![]() strata,
depending on the adaptive integration steps
chosen by the routine that solves the set of differential equations.
Using these
strata,
depending on the adaptive integration steps
chosen by the routine that solves the set of differential equations.
Using these
![]() values,
an XSPEC subroutine
for a MEKAL model of an optically thin plasma
(Phillips et al. 1999; Mewe et al. 1995)
calculates the X-ray emission spectrum of each layer.
The total X-ray spectrum of the accretion column
is a sum over all the layers' spectra,
weighted by cell volume.
We omit the few cells for which
values,
an XSPEC subroutine
for a MEKAL model of an optically thin plasma
(Phillips et al. 1999; Mewe et al. 1995)
calculates the X-ray emission spectrum of each layer.
The total X-ray spectrum of the accretion column
is a sum over all the layers' spectra,
weighted by cell volume.
We omit the few cells for which
![]() ,
for which the MEKAL model is inapplicable and fails.
In reality the gas at these densities is optically thick
and merges into the stellar atmosphere.
,
for which the MEKAL model is inapplicable and fails.
In reality the gas at these densities is optically thick
and merges into the stellar atmosphere.
Figure 11
presents the X-ray spectrum
calculated for a high-mass white dwarf (
![]() )
with a magnetic field strength of
)
with a magnetic field strength of
![]() at the accretion hot-spot.
The uppermost panel represents
the dipolar accretion model (I).
The lower panels are ratio plots,
comparing the dipolar model with:
(II) the model of Cropper et al. (1999)
(planar geometry, including gravity);
(III) the model of Wu (1994)
(planar, but without gravity);
and (IV) an isothermal, homogeneous post-shock model.
For photon energies ranging from 0.2 to
at the accretion hot-spot.
The uppermost panel represents
the dipolar accretion model (I).
The lower panels are ratio plots,
comparing the dipolar model with:
(II) the model of Cropper et al. (1999)
(planar geometry, including gravity);
(III) the model of Wu (1994)
(planar, but without gravity);
and (IV) an isothermal, homogeneous post-shock model.
For photon energies ranging from 0.2 to
![]() ,
the spectrum of model (II) is harder than that of the dipolar model (I),
and has less line emission.
It may be unsurprising that the CWRK model has a harder spectrum,
since the shock temperature is higher than in the dipolar accretion model.
The planar accretion model without gravity (III)
produces a softer spectrum than the dipolar accretion model,
and more line emission.
The homogeneous shock model (IV) yields a spectrum that is
qualitatively very different from any of the inhomogeneous shock models.
It shows a much harder spectal slope.
,
the spectrum of model (II) is harder than that of the dipolar model (I),
and has less line emission.
It may be unsurprising that the CWRK model has a harder spectrum,
since the shock temperature is higher than in the dipolar accretion model.
The planar accretion model without gravity (III)
produces a softer spectrum than the dipolar accretion model,
and more line emission.
The homogeneous shock model (IV) yields a spectrum that is
qualitatively very different from any of the inhomogeneous shock models.
It shows a much harder spectal slope.
Curvature effects are strongest for those cases
where the shock height is significant compared to the stellar radius,
and thus the differences between spectra in comparable
CWRK and dipolar accretion models
is most noticeable for the cases of the most massive white dwarfs.
For lower mass white dwarfs the shock height is small
compared to the stellar radius,
curvature effects are minor,
and the dipolar and CWRK models predict similar X-ray spectra.
For the case of
![]() (Fig. 12)
the spectra predicted from these models are almost indistinguishable.
(Fig. 12)
the spectra predicted from these models are almost indistinguishable.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f12.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg217.gif) |
Figure 12:
Comparison of X-ray spectra calculated according to the four models,
labelled as in Fig. 11
but with stellar mass
|
| Open with DEXTER | |
For white dwarfs of low or medium mass
(e.g.
![]() )
the shock temperatures, post-shock structures and X-ray spectra
are nearly the same in the dipolar accretion model
as in the earlier planar accretion model of Cropper et al. (1999).
For white dwarfs of higher mass
(e.g.
)
the shock temperatures, post-shock structures and X-ray spectra
are nearly the same in the dipolar accretion model
as in the earlier planar accretion model of Cropper et al. (1999).
For white dwarfs of higher mass
(e.g.
![]() ),
the dipolar accretion model predicts
greater shock heights,
lower shock temperatures
and softer X-ray spectra
in the band from
),
the dipolar accretion model predicts
greater shock heights,
lower shock temperatures
and softer X-ray spectra
in the band from
![]() .
This implies that for a given observed spectrum,
the mass estimate M* is necessarily greater
when dipole field curvature is taken into account.
.
This implies that for a given observed spectrum,
the mass estimate M* is necessarily greater
when dipole field curvature is taken into account.
The lower shock temperature does not at first sight provide a route to resolving the high white dwarf masses derived using spectral fits to X-ray data, and which are the subject of some controversy (e.g. Schwope et al. 2002), since even higher mass white dwarfs are required to provide sufficient hard X-ray flux to fit the observed spectrum.
The formulation that we derived is not restricted to accretion in magnetic white dwarfs. It is applicable to a variety of astrophysical systems, provided that the flow is strictly confined by the magnetic field lines, and the radiative heating and cooling processes can be parametrised in terms of the hydrodynamic variables.
An example is accretion in young stellar objects. There are strong observational evidence that accretion flow in T Tauri stars are channelled by the stellar magnetic fields (e.g. Basri et al. 1992). The main differences between the mCV case and the accretion in T Tau stars are: that the cooling process is dominated by line cooling instead of free-free and cyclotron cooling. Moreover, irradiative heating of both pre- and post-shock flow is important in determining the flow hydrodynamics (see e.g. Martin 1996). Under these conditions, we need to relax the assumption of a completely dissociated gas and generalise the hydrodynamical equations to multi-ion and electron flow. In a fully self-consistent treatment the equations of hydrodynamics need to be solved simultaneously with the ionization structure equations (e.g. Lamzin 1998).
Another example of application is
the accretion onto a slowly rotating neutron star in a binary system
(i.e. X-ray pulsars).
The accretion flow is magnetically funnelled,
from either the wind of the companion star
or an accretion disk
(e.g. Koldoba et al. 2002; Lovelace et al. 1995; Elsner & Lamb 1977; Ghosh & Lamb 1978).
In cases of disk accretion,
the gas is funnelled from the inner edge of the disk,
and the radius of this location effectively determines
the colatitude of the accretion hot-spot on the stellar surface
(![]() in our formulation).
For details of interaction of the channelled flow
and the accretion disk in X-ray pulsars, see e.g.
Anzer & Boerner (1983); Li et al. (1996); Spruit & Taam (1990).
in our formulation).
For details of interaction of the channelled flow
and the accretion disk in X-ray pulsars, see e.g.
Anzer & Boerner (1983); Li et al. (1996); Spruit & Taam (1990).
We have investigated accretion onto stellar systems
in which the flow is strictly channelled by a dipole magnetic field.
Such flow occurs in regions close to the stellar surface,
where
![]() .
We derive a set of hydrodynamic equations
using the curvilinear coordinates natural to the field geometry.
The equations are solved
to determine the flow velocity, density and temperature profiles.
We show that the dipole-field geometry
can cause significant compressional heating,
and this effect can be comparable to radiative cooling and gravity
in determining the structures of the flow
near the surface of the accreting star.
.
We derive a set of hydrodynamic equations
using the curvilinear coordinates natural to the field geometry.
The equations are solved
to determine the flow velocity, density and temperature profiles.
We show that the dipole-field geometry
can cause significant compressional heating,
and this effect can be comparable to radiative cooling and gravity
in determining the structures of the flow
near the surface of the accreting star.
The formulation that we have derived is applicable to a variety of astrophysical systems, from white-dwarf stars in magnetic cataclysmic variables to young stellar objects. It would be possible to generalise the formulation for dipole-field channelled flow to the flow channelled by a higher-order field using curvilinear coordinates.
We demonstrate that our analytic model can be efficiently interfaced with spectral software to reproduce fits in analysis of high quality X-ray spectra, obtained by satellites such as Chandra and XMM-Newton. This is a next-generation model for fitting accretion parameters, including white dwarf mass, magnetic field strength, accretion colatitude and mass flux, to specific observed systems.
Acknowledgements
J.B.G.C. is very grateful for the great hospitality of all people of the Mullard Space Science Laboratory (MSSL) and particularly to Gavin Ramsay and Mark Cropper for the invitation to visit MSSL for one year. J.B.G.C. also thanks Roberto Soria, Mat Page and Christian Bridge for discussions. J.B.G.C. acknowledges the support from the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) of Brazil and from the State University of Rio de Janeiro (UERJ) for the one-year leave inside the PROCAD program.
Let
![]() ,
,
![]() and
and
![]() be the standard orthogonal unit vectors in the Cartesian coordinates.
The unit vectors of our dipolar curvilinear coordinate system
(
be the standard orthogonal unit vectors in the Cartesian coordinates.
The unit vectors of our dipolar curvilinear coordinate system
(
![]() )
and (
)
and (
![]() ,
,
![]() ,
,
![]() )
are related to the Cartesian unit vectors via
)
are related to the Cartesian unit vectors via
![\begin{displaymath}\left[\begin{array}{c}
\hat{\vec u}\\
\hat{\vec w}\\
\ha...
...\\
\hat{\vec{\jmath}}\\
\hat{\vec{k}}
\end{array}\right],
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img225.gif) |
(A.1) |
![\begin{displaymath}\left[\begin{array}{c}
\hat{\vec{r}}\\
\hat{\vec{\theta}}\...
...
\hat{\vec{w}}\\
\hat{\vec{\varphi}}
\end{array} \right] ,
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img229.gif) |
(A.4) |
With u and w defined according to Eqs. (1) and (2)
we have
![]() and
and
![]() ,
and as
,
and as
![]() ,
we therefore have
,
we therefore have
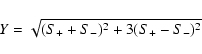 |
(A.8) |
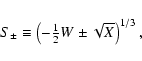 |
(A.9) |
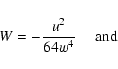 |
(A.10) |
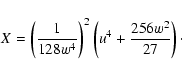 |
(A.11) |
The function
![]() is a purely geometrical function,
dependent on the curvature of the coordinate system.
In the (u, w,
is a purely geometrical function,
dependent on the curvature of the coordinate system.
In the (u, w, ![]() )
coordinate systems that we use,
it is
)
coordinate systems that we use,
it is
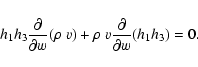 |
(B.5) |
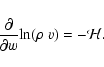 |
(B.6) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2706f13.ps}
\end{figure}](/articles/aa/full/2005/34/aa2706-05/Timg268.gif) |
Figure B.1:
From top to bottom, the
|
In our illustrative system
the Cyclotron emission from the post-shock region
is optically thick at frequencies up to some cut-off,
![]() (e.g. Langer et al. 1982; Chanmugam & Wagner 1979; Wada et al. 1980).
As derived in Saxton (1999)
and the appendices of Cropper et al. (1999),
the effective volumetric cooling function is
(e.g. Langer et al. 1982; Chanmugam & Wagner 1979; Wada et al. 1980).
As derived in Saxton (1999)
and the appendices of Cropper et al. (1999),
the effective volumetric cooling function is
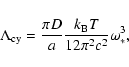 |
(C.1) |
However there is a practical problem to performing calculations
starting from a chosen value of
![]() ,
since Eq. (44)
depends on functions of the shock position,
which is initially unknown.
In the earliest cylindrical accretion models
(Chevalier & Imamura 1982; Aizu 1973; Wu 1994)
it was possible to eliminate the shock height by normalisation,
but this is impossible for formulations that include
explicitly position-dependent effects such as gravity
(Cropper et al. 1999).
For computational convenience, we modify the definition by
replacing the
,
since Eq. (44)
depends on functions of the shock position,
which is initially unknown.
In the earliest cylindrical accretion models
(Chevalier & Imamura 1982; Aizu 1973; Wu 1994)
it was possible to eliminate the shock height by normalisation,
but this is impossible for formulations that include
explicitly position-dependent effects such as gravity
(Cropper et al. 1999).
For computational convenience, we modify the definition by
replacing the ![]() -subscripted quantities in Eq. (44) with
reference values at the stellar surface (B*, h1*, h3*),
and ideal post-shock pressure and densities
-subscripted quantities in Eq. (44) with
reference values at the stellar surface (B*, h1*, h3*),
and ideal post-shock pressure and densities
![]() of the zero-gravity, cylindrical model of Wu (1994).
In that model the shock was assumed to occur close to the stellar surface.
The corresponding efficiency parameter is denoted
of the zero-gravity, cylindrical model of Wu (1994).
In that model the shock was assumed to occur close to the stellar surface.
The corresponding efficiency parameter is denoted
![]() ,
and it yields, after solving for the actual shock location,
the value of
,
and it yields, after solving for the actual shock location,
the value of
![\begin{displaymath}\epsilon_{\rm s}
=
\epsilon_{{\rm s}*}
\left({
{P_{\rm s}}\ov...
...rm s}}\over{(4-3u)r_{\rm s}^6}}
}\right]^{\frac{57}{40}}\cdot
\end{displaymath}](/articles/aa/full/2005/34/aa2706-05/img281.gif) |
(C.2) |