A&A 439, 835-843 (2005)
DOI: 10.1051/0004-6361:20053221
A. Brandenburg1 - K. Subramanian2
1 -
NORDITA, Blegdamsvej 17, 2100 Copenhagen Ø, Denmark
2 -
IUCAA, Post Bag 4, Pune University Campus, Ganeshkhind, Pune 411 007, India
Received 10 April 2005 / Accepted 30 May 2005
Abstract
The validity of a closure called
the minimal tau approximation (MTA),
is tested in the context of dynamo theory,
wherein triple correlations are assumed to
provide relaxation of the turbulent electromotive force.
Under MTA, the alpha effect in mean field dynamo theory becomes
proportional to a relaxation time scale multiplied by
the difference between kinetic and current helicities.
It is shown that the value of the relaxation time is positive and,
in units of the turnover time at the forcing wavenumber,
it is of the order of unity.
It is quenched by the magnetic field - roughly independently of the
magnetic Reynolds number.
However, this independence becomes uncertain
at large magnetic Reynolds number.
Kinetic and current helicities are shown to be dominated by
large scale properties of the flow.
Key words: magnetohydrodynamics (MHD) - turbulence
In many branches of astrophysics it is necessary to use turbulent transport
coefficients.
This allows one to describe the collective effects of turbulence
(e.g. diffusive and non-diffusive effects) without the need to resolve
the small scale turbulence.
Non-diffusive effects include the ![]() effect in mean-field dynamo
theory (Krause & Rädler 1989) and the
effect in mean-field dynamo
theory (Krause & Rädler 1989) and the ![]() effect in the theory
of stellar differential rotation (Rüdiger 1989).
In order to calculate turbulent transport coefficients
one usually makes the assumption that the
equations for the fluctuating quantities can be linearized
(Moffatt 1978; Krause & Rädler 1980).
This implies that one is forced to restrict oneself to the case where
the fluctuations are weak compared with the mean field.
This is clearly not very useful for astrophysical applications.
Nevertheless, mean-field theory is usually applied in the astrophysically
interesting parameter regime (e.g., Rüdiger & Kitchatinov 1993;
Kitchatinov et al. 1994), which should in principle be well beyond the
regime of validity of such a linear approximation.
How is it then possible that the results are actually quite reasonable?
effect in the theory
of stellar differential rotation (Rüdiger 1989).
In order to calculate turbulent transport coefficients
one usually makes the assumption that the
equations for the fluctuating quantities can be linearized
(Moffatt 1978; Krause & Rädler 1980).
This implies that one is forced to restrict oneself to the case where
the fluctuations are weak compared with the mean field.
This is clearly not very useful for astrophysical applications.
Nevertheless, mean-field theory is usually applied in the astrophysically
interesting parameter regime (e.g., Rüdiger & Kitchatinov 1993;
Kitchatinov et al. 1994), which should in principle be well beyond the
regime of validity of such a linear approximation.
How is it then possible that the results are actually quite reasonable?
The approximation under which higher order terms are neglected is known as the quasilinear, the first order smoothing, or the second order correlation approximation. With the exception on an important additional term, the results derived under this approximation turn out to be similar to those derived under a more general approximation, which is sometimes referred to as the minimal tau approximation (MTA). This approximation has its roots in early papers by Vainshtein & Kitchatinov (1983), Kleeorin et al. (1990, 1996), and its general usefulness has recently been stressed further with the papers by Blackman & Field (2002) and Rädler et al. (2003). A recent review of nonlinear dynamo theory and MTA has been given by Brandenburg & Subramanian (2005a). MTA has also been applied to the case of passive scalar diffusion (Blackman & Field 2003), where its validity has been tested numerically (Brandenburg et al. 2004).
In the hydromagnetic case, the single most important addition to the
theory is the attenuation of the ![]() effect by a term proportional
to the current helicity of the small scale field.
The beauty of MTA is that this term emerges in a completely natural fashion.
In the first order smoothing approach this term is absent, although even
there it can be incorporated in a more phenomenological and hence less
convincing fashion (Brandenburg & Subramanian 2005a).
The role of the current helicity term was first identified by
Pouquet et al. (1976) and later associated with catastrophic
quenching by Gruzinov & Diamond (1994) and many others after them.
The purpose of the present paper is to test MTA in the context of
dynamo theory.
effect by a term proportional
to the current helicity of the small scale field.
The beauty of MTA is that this term emerges in a completely natural fashion.
In the first order smoothing approach this term is absent, although even
there it can be incorporated in a more phenomenological and hence less
convincing fashion (Brandenburg & Subramanian 2005a).
The role of the current helicity term was first identified by
Pouquet et al. (1976) and later associated with catastrophic
quenching by Gruzinov & Diamond (1994) and many others after them.
The purpose of the present paper is to test MTA in the context of
dynamo theory.
In mean field dynamo theory one splits the magnetic
field ![]() into a mean
magnetic field
into a mean
magnetic field
![]() and a small scale
field
and a small scale
field
![]() ,
and
derives the mean-field dynamo equation
,
and
derives the mean-field dynamo equation
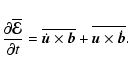 |
(2) |
As was first shown by Blackman & Field (2002), the use of MTA leads to
an explicitly time-dependent equation for the electromotive force which,
in the isotropic approximation, is
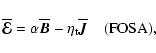 |
(5) |
In the passive scalar case a relatively robust method
for estimating ![]() from turbulence simulations
is to impose a mean concentration gradient across
the box, and to treat the deviations from this mean gradient as periodic
in all three directions (Brandenburg et al. 2004).
In the present case this corresponds to imposing a mean magnetic field,
from turbulence simulations
is to impose a mean concentration gradient across
the box, and to treat the deviations from this mean gradient as periodic
in all three directions (Brandenburg et al. 2004).
In the present case this corresponds to imposing a mean magnetic field,
![]() .
The magnetic field is then given by
.
The magnetic field is then given by
![]() ,
where
,
where ![]() is the departure from the mean field,
is the departure from the mean field, ![]() .
Since
.
Since
![]() ,
the evolution of
,
the evolution of ![]() is given by
is given by
In the main part of this paper we adopt combined volume and
time averages, so,
![]() .
This means that in Eq. (4) both
.
This means that in Eq. (4) both
![]() and
and
![]() vanish.
Therefore we simply have
vanish.
Therefore we simply have
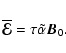 |
(9) |
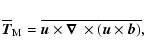 |
(12) |
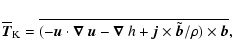 |
(13) |
So far, and throughout most of this paper,
we consider the case of an imposed constant mean field,
![]() ,
with zero mean current,
,
with zero mean current,
![]() .
While this is reasonable for measuring the value of
.
While this is reasonable for measuring the value of ![]() ,
it is of course unrealistic for dynamo calculations, where there
must be a mean current proportional to the curl of the mean field.
Furthermore, if a mean field is imposed, this mean field
can obviously not change by the dynamo action.
Nevertheless, it provides a useful method for calculating
,
it is of course unrealistic for dynamo calculations, where there
must be a mean current proportional to the curl of the mean field.
Furthermore, if a mean field is imposed, this mean field
can obviously not change by the dynamo action.
Nevertheless, it provides a useful method for calculating ![]() .
This method gives similar results than the more complicated and less accurate
methods that can be invoked in dynamo simulations (Brandenburg 2001,
see his Figs. 14 and 15).
However, in order to show that Eq. (3) has any justification,
we insert a discussion (Sect. 3) where we consider the local
correlation in a simulation without an imposed field.
.
This method gives similar results than the more complicated and less accurate
methods that can be invoked in dynamo simulations (Brandenburg 2001,
see his Figs. 14 and 15).
However, in order to show that Eq. (3) has any justification,
we insert a discussion (Sect. 3) where we consider the local
correlation in a simulation without an imposed field.
Before we present in detail results for the case of an imposed field, we consider first the case of a dynamo-generated magnetic field. In that case the magnetic field shows a marked sinusoidal variation in one of three possible directions. Which of the three directions is chosen depends on chance. In the following we compare with a simulation of homogeneous helically forced turbulence of Brandenburg (2001); in his Run 3 the magnetic field shows a slow variation in the y direction, so we define mean fields by averaging over the x and z directions.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{fig1}
\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg88.gif) |
Figure 1:
Comparison of the spatial dependence of two components of the mean
magnetic field and the triple correlation in Run 3 of B01.
The magnetic field is normalized by the equipartition field strength,
|
| Open with DEXTER | |
Figure 1 shows that the x and z components of
![]() have a positive correlation with the mean magnetic field.
Note that
have a positive correlation with the mean magnetic field.
Note that
![]() itself has a negative correlation with
itself has a negative correlation with
![]() ,
for a negative
,
for a negative ![]() .
And since this simulation has positive
kinetic helicity, the
.
And since this simulation has positive
kinetic helicity, the ![]() obtained is indeed negative.
Therefore the positive correlation
of
obtained is indeed negative.
Therefore the positive correlation
of
![]() with
with
![]() is consistent with Eq. (3) with a positive
is consistent with Eq. (3) with a positive ![]() .
(The term
.
(The term
![]() does not change the sign of
does not change the sign of
![]() ,
but only reduces its magnitude. This follows
from the fact that in a dynamo simulation
,
but only reduces its magnitude. This follows
from the fact that in a dynamo simulation
![]() has to
overcome the magnetic diffusion term.)
We have used
has to
overcome the magnetic diffusion term.)
We have used
![]() as a proxy for
as a proxy for
![]() in order to study the
correlation of
in order to study the
correlation of
![]() with
with
![]() ,
because
,
because
![]() itself is even more noisy than
itself is even more noisy than
![]() .
This is because
.
This is because
![]() almost cancels
almost cancels
![]() and the fact that
and the fact that
![]() consists of
derivatives of
consists of
derivatives of
![]() which contributes further to the noise.
which contributes further to the noise.
In conclusion, our first assessment of
![]() is very encouraging
in that its phase relation with the magnetic field is such that
it would indeed contribute as a damping term, i.e. that it has
the expected sign.
is very encouraging
in that its phase relation with the magnetic field is such that
it would indeed contribute as a damping term, i.e. that it has
the expected sign.
Having shown that
![]() varies locally in the expected
sense, we now concentrate on the case of a uniform imposed field where
it is possible to use averages over the full box.
(In the dynamo case considered in the previous section such averages
would have given zero.)
We solve Eqs. (6)-(8) numerically.
The forcing amplitude is such that
we are in the low Mach number regime, i.e.
varies locally in the expected
sense, we now concentrate on the case of a uniform imposed field where
it is possible to use averages over the full box.
(In the dynamo case considered in the previous section such averages
would have given zero.)
We solve Eqs. (6)-(8) numerically.
The forcing amplitude is such that
we are in the low Mach number regime, i.e.
![]() ,
so for all practical purposes the flows can be
considered nearly incompressible.
We consider runs with different hydrodynamic and hydromagnetic Reynolds
numbers,
,
so for all practical purposes the flows can be
considered nearly incompressible.
We consider runs with different hydrodynamic and hydromagnetic Reynolds
numbers,
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig2}
\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg97.gif) |
Figure 2:
|
| Open with DEXTER | |
We measure velocity in units of the sound speed ![]() ,
density in units of the average density
,
density in units of the average density ![]() ,
magnetic field in units of
,
magnetic field in units of
![]() ,
and length in units of k1-1, where k1 is the smallest
possible wavenumber in the box.
Whenever possible we present the result in normalized
(explicitly nondimensional) form.
,
and length in units of k1-1, where k1 is the smallest
possible wavenumber in the box.
Whenever possible we present the result in normalized
(explicitly nondimensional) form.
We begin by considering the dependence of
![]() on
on ![]() ;
see Fig. 2.
We focus on the results for two different field strengths,
B0=0.03, corresponding to
;
see Fig. 2.
We focus on the results for two different field strengths,
B0=0.03, corresponding to
![]() ,
and
B0=0.1, corresponding to
,
and
B0=0.1, corresponding to
![]() .
Throughout this paper, error bars are obtained by taking the extrema
from 5 separate averages, each over 1/5 of the full time series.
.
Throughout this paper, error bars are obtained by taking the extrema
from 5 separate averages, each over 1/5 of the full time series.
In both kinetically and magnetically driven cases ![]() is
negative when the helicity of the forcing is positive.
It turns out that, when the turbulence is kinetically forced,
is
negative when the helicity of the forcing is positive.
It turns out that, when the turbulence is kinetically forced, ![]() decreases with increasing
decreases with increasing ![]() like
like
![]() where n is between 1/2 and 1.
For large field strengths and large values of
where n is between 1/2 and 1.
For large field strengths and large values of ![]() we expect
an asymptotic dependence with n=1 (Cattaneo & Hughes 1996),
but when these values are not yet
large enough the data are best fitted with values of n less than 1.
we expect
an asymptotic dependence with n=1 (Cattaneo & Hughes 1996),
but when these values are not yet
large enough the data are best fitted with values of n less than 1.
In the magnetically driven case ![]() is generally, at comparable
values of
is generally, at comparable
values of
![]() ,
larger than in the kinetically driven case.
Furthermore, in the magnetically driven case
,
larger than in the kinetically driven case.
Furthermore, in the magnetically driven case ![]() does not show the
systematic decrease of
does not show the
systematic decrease of ![]() seen in the kinetically driven case.
This can be understood as a result of a modified Keinigs (1983) relation;
see Appendix B.
seen in the kinetically driven case.
This can be understood as a result of a modified Keinigs (1983) relation;
see Appendix B.
Next, we consider the values of
![]() and
and
![]() in both kinetically and magnetically
driven cases; see Figs. 3 and 4.
The results depend on the values of
in both kinetically and magnetically
driven cases; see Figs. 3 and 4.
The results depend on the values of ![]() and
and ![]() .
In the kinetically driven case there is a clear tendency for
.
In the kinetically driven case there is a clear tendency for
![]() to increase with
to increase with ![]() until it
approaches and slightly exceeds the value of
until it
approaches and slightly exceeds the value of
![]() .
For larger values of
.
For larger values of ![]() ,
,
![]() and
and
![]() are constant and close to each other.
are constant and close to each other.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig3}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg111.gif) |
Figure 3:
Dependence of
|
| Open with DEXTER | |
In the magnetically driven case,
![]() and
and
![]() depend only weakly on
depend only weakly on ![]() .
Furthermore,
.
Furthermore,
![]() can exceed
can exceed
![]() by even an order of magnitude; see the first panel of Fig. 4.
by even an order of magnitude; see the first panel of Fig. 4.
![\begin{figure}
\includegraphics[width=6cm,clip]{fig4}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg114.gif) |
Figure 4:
Dependence of
|
| Open with DEXTER | |
It is not easy to present the data of all runs in a meaningful way in a single graph. This is why we have summarized the results of all runs in tabular form; see Table 1, allowing alternative representations and interpretations to be made.
After these preparations we can now return to the main question addressed
in this paper: what is the relevant relaxation time in MTA and how does
it depend on ![]() .
Assuming a steady state, we can use Eq. (4) and calculate
.
Assuming a steady state, we can use Eq. (4) and calculate
| (15) |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig5}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg116.gif) |
Figure 5:
Strouhal numbers as a function of |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig6}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg117.gif) |
Figure 6:
Magnetic and kinetic Strouhal numbers as a function of |
| Open with DEXTER | |
As we have discussed above, at large ![]() ,
,
![]() can even slightly exceeds the value of
can even slightly exceeds the value of
![]() .
Since
.
Since ![]() itself does not change sign, this would imply that
itself does not change sign, this would imply that ![]() would become negative for large
would become negative for large ![]() .
An obvious solution to this problem is that
.
An obvious solution to this problem is that
![]() and
and
![]() should be preceded by some additional
quenching functions,
should be preceded by some additional
quenching functions, ![]() and
and ![]() ,
respectively.
Both functions are expected to be of the order of unity, but they may
not be exactly equal; see Kleeorin et al. (2002).
In the following we combine the information from the kinetically and
magnetically driven runs to compute separately
,
respectively.
Both functions are expected to be of the order of unity, but they may
not be exactly equal; see Kleeorin et al. (2002).
In the following we combine the information from the kinetically and
magnetically driven runs to compute separately
![]() and
and
![]() ,
and assume
,
and assume
![]() and
and
![]() .
We thus have an equation with two unknowns,
.
We thus have an equation with two unknowns,
Table 1:
Summary of the measured rms velocity and normalized ![]() s
for kinetically and magnetically forced runs, together with
the resulting Strouhal numbers and their corresponding errors
obtained by taking the extrema from 5 separate averages over
1/5 of the full time series.
Values in parenthesis show departures from the trend
and should be regarded as uncertain.
For
s
for kinetically and magnetically forced runs, together with
the resulting Strouhal numbers and their corresponding errors
obtained by taking the extrema from 5 separate averages over
1/5 of the full time series.
Values in parenthesis show departures from the trend
and should be regarded as uncertain.
For
![]() the resolution varies between 643 and 5123meshpoints for
the resolution varies between 643 and 5123meshpoints for
![]() and
and
![]() ,
respectively,
while for
,
respectively,
while for
![]() the resolution varies between 323 and 2563meshpoints for
the resolution varies between 323 and 2563meshpoints for
![]() and
and
![]() ,
respectively.
,
respectively.
In order to obtain a second equation, we can consider the simulations for
kinetically and magnetically driven turbulence as two independent measurement.
This leads to two separate measurements of ![]() ,
,
![]() ,
and
,
and
![]() ,
distinguished by superscripts (k) and (m), respectively.
In this way, Eq. (16) becomes a matrix equation
,
distinguished by superscripts (k) and (m), respectively.
In this way, Eq. (16) becomes a matrix equation
| (17) |
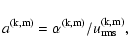 |
(18) |
![\begin{displaymath}\tilde{a}^{\rm (k,m)}_{\rm K,M}=
\tilde\alpha^{\rm (k,m)}_{\rm K,M}/
\left[k_{\rm f}u_{\rm rms}u_{\rm rms}^{\rm (k,m)}\right],
\end{displaymath}](/articles/aa/full/2005/33/aa3221-05/img143.gif) |
(19) |
| (20) |
| |
Figure 7:
Magnetic and kinetic Strouhal numbers as a function of
|
| Open with DEXTER | |
When the field strength is increased, both
![]() and
and
![]() are quenched uniformly, i.e. approximately
independently of
are quenched uniformly, i.e. approximately
independently of ![]() .
This becomes clear when comparing the first two panels of Fig. 6,
or by inspecting the data of Table 1.
For a fixed value of
.
This becomes clear when comparing the first two panels of Fig. 6,
or by inspecting the data of Table 1.
For a fixed value of ![]() (around 50) the quenching with
increasing field strength is shown in Fig. 7.
This quenching, which sets in once
(around 50) the quenching with
increasing field strength is shown in Fig. 7.
This quenching, which sets in once
![]() is of the order of unity,
is rather strong (proportional to B0-3).
Similarly strong quenching has previously been found for
is of the order of unity,
is rather strong (proportional to B0-3).
Similarly strong quenching has previously been found for ![]() if the contribution from
if the contribution from
![]() is ignored (Moffatt 1972; Rüdiger 1974; Rüdiger & Kitchatinov 1993).
is ignored (Moffatt 1972; Rüdiger 1974; Rüdiger & Kitchatinov 1993).
In Figs. 8 and 9 we present,
both for the kinetically and magnetically driven cases, shell-integrated
spectra of magnetic and kinetic energies, M(k) and E(k), respectively,
as well as current and kinetic helicities, C(k) and F(k), respectively.
They are normalized such that
![]() ,
,
![]() ,
,
![]() ,
and
,
and
![]() .
The two helicity spectra are subject to a realizability condition,
.
The two helicity spectra are subject to a realizability condition,
![]() and
and
![]() (Moffatt 1978).
If the bound is nearly saturated, we say that the field is fully helical.
It turns out that for
(Moffatt 1978).
If the bound is nearly saturated, we say that the field is fully helical.
It turns out that for
![]() we have
we have
![]() and
and
![]() ,
so magnetic and velocity fields are
in fact not fully helical at small scales.
,
so magnetic and velocity fields are
in fact not fully helical at small scales.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig8}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg161.gif) |
Figure 8:
Compensated shell-integrated power spectra of magnetic energy M(k)and kinetic energy E(k) (the upper solid and dotted lines in the
upper panel), and current helicity C(k) and kinetic helicity F(k)(the lower solid and dotted red or gray lines in the upper panel).
The energy spectra spectra a made dimensionless by scaling with
|
| Open with DEXTER | |
Since both C(k) and F(k) seem to scale like k-5/3 in the inertial
range, both helicities are governed by contributions from large scales.
This implies in particular that the small scale current helicity,
![]() ,
and hence also
,
and hence also
![]() ,
should not
depend on the length of the inertial range and hence should be
independent of
,
should not
depend on the length of the inertial range and hence should be
independent of ![]() .
If this were not the case, i.e. if the magnetic field were fully helical
with a k-2/3 current helicity spectrum,
.
If this were not the case, i.e. if the magnetic field were fully helical
with a k-2/3 current helicity spectrum,
![]() would be
asymptotically proportional to
would be
asymptotically proportional to
![]() (Blackman & Brandenburg 2002).
Our results suggest that this is not the case here.
This seems to be in conflict with earlier results for helical dynamos
(Brandenburg 2001), but those results were at 4 times smaller resolution
(1203 instead of 5123 meshpoints)
and the forcing was at 3 times smaller scale, so
the effective length of the inertial range was 12 times smaller and
hence completely absent.
What remains true, however, is that the field is nearly fully helical
at the energy carrying scale, i.e. at wavenumber
(Blackman & Brandenburg 2002).
Our results suggest that this is not the case here.
This seems to be in conflict with earlier results for helical dynamos
(Brandenburg 2001), but those results were at 4 times smaller resolution
(1203 instead of 5123 meshpoints)
and the forcing was at 3 times smaller scale, so
the effective length of the inertial range was 12 times smaller and
hence completely absent.
What remains true, however, is that the field is nearly fully helical
at the energy carrying scale, i.e. at wavenumber ![]() .
.
In order to gain more insight into the nature of the turbulence
in kinetically and magnetically forced cases we show visualizations
of the field-aligned components of velocity and magnetic field,
uz and Bz, respectively.
In the kinetically driven case we see a large scale pattern in velocity,
consistent with power at the expected energy-carrying scale corresponding
to the forcing wavenumber
![]() ;
see Fig. 10.
The magnetic field, on the other hand, is dominated by smaller scale
structures.
The strength of the imposed field is still less than the equipartition value
(
;
see Fig. 10.
The magnetic field, on the other hand, is dominated by smaller scale
structures.
The strength of the imposed field is still less than the equipartition value
(
![]() )
and there is no obvious anisotropy.
Although the velocity field is helical, there is no obvious large-scale
pattern in the magnetic field.
There are two possible reasons for this: lack of scale separation
(see Sect. V of Haugen et al. 2004) and suppression of large scale
dynamo action by the large scale field (Montgomery et al. 2002;
Brandenburg & Matthaeus 2004).
)
and there is no obvious anisotropy.
Although the velocity field is helical, there is no obvious large-scale
pattern in the magnetic field.
There are two possible reasons for this: lack of scale separation
(see Sect. V of Haugen et al. 2004) and suppression of large scale
dynamo action by the large scale field (Montgomery et al. 2002;
Brandenburg & Matthaeus 2004).
The magnetically driven case is quite different.
There seems to be a large scale pattern in the magnetic field (Fig. 11).
Although there is no scale separation, it is possible to drive a larger
scale field in this case.
The main difference is that in the kinetically driven case,
dynamo-generated large scale and small scale fields have opposite sign
of current helicity (Brandenburg 2001).
In the absence of sufficient scale separation this leads to cancelation.
In the magnetically driven case the current helicity has the same sign
at all scales, so there is no cancellation and therefore the build-up
of a large scale field is possible.
However, when the field is too strong (B0=0.1, corresponding to
![]() )
no large scale pattern in the magnetic field
develops; see Fig. 12.
)
no large scale pattern in the magnetic field
develops; see Fig. 12.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{fig9}
\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg165.gif) |
Figure 9: Same as Fig. 8, but for the magnetically forced case with B0=0.1, 5123 meshpoints. |
| Open with DEXTER | |
Although a closure hypothesis of the form
![]() has a plausible physical interpretation as a relaxation term,
(Blackman & Field 2002), it is nevertheless
quite crude and lacks a rigorous physical basis.
However, on empirical grounds this closure assumption is quite
appealing.
First of all, unlike the first order smoothing approximation, MTA provides
a natural and convincing explanation for the
has a plausible physical interpretation as a relaxation term,
(Blackman & Field 2002), it is nevertheless
quite crude and lacks a rigorous physical basis.
However, on empirical grounds this closure assumption is quite
appealing.
First of all, unlike the first order smoothing approximation, MTA provides
a natural and convincing explanation for the
![]() correction term to the
correction term to the ![]() effect in Eq. (10).
This is indeed a key ingredient to the dynamical quenching model
(Kleeorin & Ruzmaikin 1982), where the evolution of
effect in Eq. (10).
This is indeed a key ingredient to the dynamical quenching model
(Kleeorin & Ruzmaikin 1982), where the evolution of
![]() is obtained by solving the magnetic helicity
equation for the small scale field.
The dynamical evolution of the
is obtained by solving the magnetic helicity
equation for the small scale field.
The dynamical evolution of the
![]() term
provides a good model for the resistively limited saturation
(Field & Blackman 2002; Blackman & Brandenburg 2002;
Subramanian 2002),
which is seen in helically forced simulations in periodic boxes
(Brandenburg 2001; Mininni et al. 2005).
Another appealing property of MTA is that the additional time derivative,
term
provides a good model for the resistively limited saturation
(Field & Blackman 2002; Blackman & Brandenburg 2002;
Subramanian 2002),
which is seen in helically forced simulations in periodic boxes
(Brandenburg 2001; Mininni et al. 2005).
Another appealing property of MTA is that the additional time derivative,
![]() in Eq. (4), restores causality
and prevents infinitely fast signal propagation.
In the case of turbulent passive scalar diffusion, one can easily see
that this term turns the heat equation into a damped wave equation,
where the maximum signal speed is the rms velocity of the turbulence
(Brandenburg et al. 2004).
in Eq. (4), restores causality
and prevents infinitely fast signal propagation.
In the case of turbulent passive scalar diffusion, one can easily see
that this term turns the heat equation into a damped wave equation,
where the maximum signal speed is the rms velocity of the turbulence
(Brandenburg et al. 2004).
One of the striking features of the dynamical quenching model is that
the resistively limited saturation and the resistive quenching of the
effective ![]() can already be explained without invoking any explicit
can already be explained without invoking any explicit
![]() dependence of
dependence of ![]() .
Instead, the
.
Instead, the ![]() dependence of the steady state values of
dependence of the steady state values of ![]() emerges solely as a
result of magnetic helicity conservation and might hence be alleviated
if there is a helicity flux that offsets magnetic helicity conservation
(Blackman & Field 2000; Kleeorin et al. 2000, 2002; Vishniac & Cho 2001;
Subramanian & Brandenburg 2004; Brandenburg & Sandin 2004; Brandenburg 2005;
Brandenburg & Subramanian 2005b).
However, there is no compulsory reason that there might not be
an explicit
emerges solely as a
result of magnetic helicity conservation and might hence be alleviated
if there is a helicity flux that offsets magnetic helicity conservation
(Blackman & Field 2000; Kleeorin et al. 2000, 2002; Vishniac & Cho 2001;
Subramanian & Brandenburg 2004; Brandenburg & Sandin 2004; Brandenburg 2005;
Brandenburg & Subramanian 2005b).
However, there is no compulsory reason that there might not be
an explicit ![]() dependence of
dependence of ![]() after all.
Our present simulations begin to shed some light on this question.
However, the results are still not as clear cut as one would like
them to be.
Looking at Fig. 6, it is evident that for
after all.
Our present simulations begin to shed some light on this question.
However, the results are still not as clear cut as one would like
them to be.
Looking at Fig. 6, it is evident that for
![]() ,
St
is independent of
,
St
is independent of ![]() and depends only on
and depends only on
![]() ;
cf. the
uniform decrease of St between the first and second panels of Fig. 6.
However, for
;
cf. the
uniform decrease of St between the first and second panels of Fig. 6.
However, for
![]() ,
St may actually decrease with
,
St may actually decrease with ![]() ,
although the error bars also increase.
If this decrease is indeed real, it might indicate that the closure
hypothesis adopted here is too simplistic.
,
although the error bars also increase.
If this decrease is indeed real, it might indicate that the closure
hypothesis adopted here is too simplistic.
We should emphasize that, although we have in this work focused on
the ![]() effect, this is not the only effect that produces large
scale dynamo action.
An example is the shear-current effect of
Rogachevskii & Kleeorin (2003, 2004).
Here the electromotive force has a component in the direction
of
effect, this is not the only effect that produces large
scale dynamo action.
An example is the shear-current effect of
Rogachevskii & Kleeorin (2003, 2004).
Here the electromotive force has a component in the direction
of
![]() ,
where
,
where
![]() is the
vorticity of the mean flow.
(In the present work this effect is of course absent because there
is no mean flow and our mean fields are defined as volume averages,
so
is the
vorticity of the mean flow.
(In the present work this effect is of course absent because there
is no mean flow and our mean fields are defined as volume averages,
so
![]() .)
Our work is relevant even in this nonhelical case because, like the
.)
Our work is relevant even in this nonhelical case because, like the
![]() effect, the
effect, the
![]() effect produces mean fields
that are helical.
Depending on the amount of magnetic helicity losses from open
boundaries, there will be a tendency to limit the production of net
magnetic helicity within the domain, so small scale current helicity
of opposite sign must be produced at the same time as large scale
field is generated.
The presence of small scale current helicity implies that there must
be a finite
effect produces mean fields
that are helical.
Depending on the amount of magnetic helicity losses from open
boundaries, there will be a tendency to limit the production of net
magnetic helicity within the domain, so small scale current helicity
of opposite sign must be produced at the same time as large scale
field is generated.
The presence of small scale current helicity implies that there must
be a finite
![]() .
This is an example where there can be an
.
This is an example where there can be an
![]() term
even though
term
even though
![]() .
Related examples where
.
Related examples where
![]() ,
but
,
but
![]() ,
are the reversed field pinch (e.g. Ho et al. 1989),
and the so-called selective decay (e.g. Montgomery et al. 1978),
as described in Blackman & Brandenburg (2002) and Yousef et al. (2003).
Another example where
,
are the reversed field pinch (e.g. Ho et al. 1989),
and the so-called selective decay (e.g. Montgomery et al. 1978),
as described in Blackman & Brandenburg (2002) and Yousef et al. (2003).
Another example where
![]() ,
but
,
but
![]() ,
is the Vishniac & Cho (2001) mechanism whereby dynamo action is
accomplished through the current helicity flux that drives
,
is the Vishniac & Cho (2001) mechanism whereby dynamo action is
accomplished through the current helicity flux that drives
![]() ;
see Brandenburg & Subramanian (2005b) for model calculations showing that
this effect produces saturation field strengths independent of the
magnetic Reynolds number when the flux exceeds a certain threshold.
;
see Brandenburg & Subramanian (2005b) for model calculations showing that
this effect produces saturation field strengths independent of the
magnetic Reynolds number when the flux exceeds a certain threshold.
In the present paper we have only discussed the case where the
helicity of the turbulence is driven explicitly.
Although this is a common assumption that allows progress to be made in
that the flow can be taken to be statistically
isotropic, it should be noted that in
astrophysical applications helicity is usually introduced by the
interaction between stratification and rotation (Krause & Rädler 1980).
To calculate this effect, MTA has to be used once more
(e.g. Rädler et al. 2003), which then renders the ![]() effect
proportional to
effect
proportional to ![]() .
Nevertheless, as is emphasized in Brandenburg & Subramanian (2005a),
also in this case the
.
Nevertheless, as is emphasized in Brandenburg & Subramanian (2005a),
also in this case the ![]() effect is attenuated by the current
helicity contribution from the small scale field.
effect is attenuated by the current
helicity contribution from the small scale field.
Earlier simulations of helical dynamos (no imposed field) suggested that
the field is bihelical, i.e. with one sign of helicity at large
scales, corresponding to wavenumber k1, and the opposite sign at
small scales, corresponding to wavenumber ![]() (Brandenburg 2001).
If the field were to continue to be nearly fully helical even at smaller
scales, this would have implied that
(Brandenburg 2001).
If the field were to continue to be nearly fully helical even at smaller
scales, this would have implied that
![]() would be
attenuated by a
would be
attenuated by a
![]() factor (Blackman & Brandenburg 2002).
Our present results suggest that this is not the case.
In agreement with both closure calculations (André & Lesieur 1977)
and direct numerical simulations (Borue & Orszag 1997) we find
approximate k-5/3 scaling for the kinetic helicity
(see also Ditlevsen & Giuliani 2001).
Again, this implies that the velocity field is not fully helical beyond
wavenumber
factor (Blackman & Brandenburg 2002).
Our present results suggest that this is not the case.
In agreement with both closure calculations (André & Lesieur 1977)
and direct numerical simulations (Borue & Orszag 1997) we find
approximate k-5/3 scaling for the kinetic helicity
(see also Ditlevsen & Giuliani 2001).
Again, this implies that the velocity field is not fully helical beyond
wavenumber ![]() ,
so
,
so
![]() should also be
independent of
should also be
independent of ![]() .
This is indeed the case, except for very small values of
.
This is indeed the case, except for very small values of ![]() .
.
There are various ways of extending the present studies of turbulent
transport to other fields.
An obvious possibility is turbulent viscosity and the ![]() effect
for modeling the Reynolds stress tensor (Käpylä et al. 2005).
For example, one would expect the relaxation time to depend on the
angular velocity (Kitchatinov & Rüdiger 1993).
This dependence could be measured in a similar way as the dependence
on the magnetic field studied in the present paper.
Another related application is the study of passive scalar transport
in the present of rotation.
Both aspects are quite essential for many astrophysical applications.
effect
for modeling the Reynolds stress tensor (Käpylä et al. 2005).
For example, one would expect the relaxation time to depend on the
angular velocity (Kitchatinov & Rüdiger 1993).
This dependence could be measured in a similar way as the dependence
on the magnetic field studied in the present paper.
Another related application is the study of passive scalar transport
in the present of rotation.
Both aspects are quite essential for many astrophysical applications.
Acknowledgements
We thank Eric G. Blackman for the many discussions we had on the subject, and Günther Rüdiger for comments on the manuscript. We also thank the organizers of the programs on "Astrophysical Discs'' in Aspen (USA), "Magnetohydrodynamics of Stellar Interiors'' at the Isaac Newton Institute in Cambridge (UK), and "Grand Challenge Problems in Computational Astrophysics'' at the Institute for Pure and Applied Mathematics at the University of California in Los Angeles, for providing a stimulating environment. The Danish Center for Scientific Computing is acknowledged for providing time on the Linux cluster in Odense.
For completeness we specify here the forcing function used in the
present paper![]() .
It is defined as
.
It is defined as
![\begin{displaymath}\mbox{\boldmath$f$ } {}(\mbox{\boldmath$x$ } {},t)={\rm Re}\{...
...math$k$ } {}(t)\cdot\mbox{\boldmath$x$ } {}+{\rm i}\phi(t)]\},
\end{displaymath}](/articles/aa/full/2005/33/aa3221-05/img177.gif) |
(A.1) |
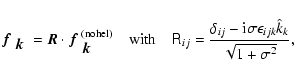 |
(A.2) |
The ![]() dependence of
dependence of ![]() can generally be understood
as a direct consequence of magnetic helicity conservation
(Gruzinov & Diamond 1994).
Dotting Eq. (6) with the vector potential
can generally be understood
as a direct consequence of magnetic helicity conservation
(Gruzinov & Diamond 1994).
Dotting Eq. (6) with the vector potential ![]() ,
where
,
where
![]() ,
and adding the corresponding evolution of
,
and adding the corresponding evolution of
![]() ,
averaging over a periodic volume, and using
,
averaging over a periodic volume, and using
![]() we obtain
we obtain
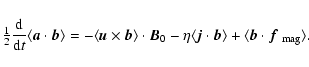 |
(B.1) |
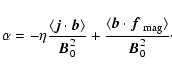 |
(B.2) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig10a}\hspace*{2mm}
\includegraphics[width=8cm,clip]{fig10b}
\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg199.gif) |
Figure 10:
Visualizations of uz ( left) and bz ( right) in the
kinetically forced case.
B0=0.03,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig11a}\hspace*{2mm}
\includegraphics[width=8cm,clip]{fig11b}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg200.gif) |
Figure 11:
Visualizations of uz ( left) and bz ( right) in the
magnetically forced case.
B0=0.03,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{fig12a}\hspace*{2mm}
\includegraphics[width=8cm,clip]{fig12b}\end{figure}](/articles/aa/full/2005/33/aa3221-05/Timg201.gif) |
Figure 12: Same as Fig. 11, but for B0=0.1. There is no clear evidence for a large scale field. |
| Open with DEXTER | |