A&A 439, 1191-1203 (2005)
DOI: 10.1051/0004-6361:20052663
E. Pariat1 - P. Démoulin1 - M. A. Berger2
1 - Observatoire de Paris, LESIA, UMR 8109 (CNRS), 92195 Meudon, France
2 -
Department of Mathematics, University College London, UK
Received 10 January 2005 / Accepted 12 May 2005
Abstract
Several recent studies have developed the measurement
of magnetic helicity flux from the time evolution of photospheric
magnetograms. The total flux is computed by summing the flux
density over the analyzed region. All previous analyses used the
density GA (=
![]() )
which involves the vector
potential
)
which involves the vector
potential ![]() of the magnetic field. In all the studied active
regions, the density GA has strong polarities of both signs
with comparable magnitude. Unfortunately, the density GA can
exhibit spurious signals which do not provide a true
helicity flux density. The main objective of this study is to
resolve the above problem by defining
the flux of magnetic helicity per unit surface. In a first step,
we define a new density,
of the magnetic field. In all the studied active
regions, the density GA has strong polarities of both signs
with comparable magnitude. Unfortunately, the density GA can
exhibit spurious signals which do not provide a true
helicity flux density. The main objective of this study is to
resolve the above problem by defining
the flux of magnetic helicity per unit surface. In a first step,
we define a new density,
![]() ,
which reduces the fake
polarities by more than an order of magnitude in most cases (using
the same photospheric data as GA). In a second step, we show
that the coronal linkage needs to be provided in order to define
the true helicity flux density. It represents how all the
elementary flux tubes move relatively to a given elementary flux
tube, and the helicity flux density is defined per elementary flux
tube. From this we define a helicity flux per unit surface,
,
which reduces the fake
polarities by more than an order of magnitude in most cases (using
the same photospheric data as GA). In a second step, we show
that the coronal linkage needs to be provided in order to define
the true helicity flux density. It represents how all the
elementary flux tubes move relatively to a given elementary flux
tube, and the helicity flux density is defined per elementary flux
tube. From this we define a helicity flux per unit surface,
![]() .
We show that it is a field-weighted average of
.
We show that it is a field-weighted average of
![]() at both photospheric feet of coronal connections. We compare these three densities (GA,
at both photospheric feet of coronal connections. We compare these three densities (GA,
![]() ,
,
![]() )
using theoretical examples representing the main cases found in magnetograms (moving magnetic
polarities, separating polarities, one polarity rotating around another one and emergence of a twisted flux tube). We conclude that
)
using theoretical examples representing the main cases found in magnetograms (moving magnetic
polarities, separating polarities, one polarity rotating around another one and emergence of a twisted flux tube). We conclude that
![]() is a much better proxy of the magnetic helicity
flux density than GA because most fake polarities are removed. Indeed
is a much better proxy of the magnetic helicity
flux density than GA because most fake polarities are removed. Indeed
![]() gives results close to
gives results close to ![]() and should be used to monitor the photospheric injection of helicity (when
coronal linkages are not well known). These results are applicable to the results of any method
determining the photospheric velocities. They can provide separately the flux density coming from shearing and advection motions if plasma motions are known.
and should be used to monitor the photospheric injection of helicity (when
coronal linkages are not well known). These results are applicable to the results of any method
determining the photospheric velocities. They can provide separately the flux density coming from shearing and advection motions if plasma motions are known.
Key words: Sun: magnetic fields - Sun: photosphere - Sun: corona
The theoretical importance of magnetic helicity in understanding the magnetohydrodynamic (MHD) evolution of magnetic fields was recognized a long time ago (e.g. Berger & Field 1984). However it is only during the last years that attempts were made to measure magnetic helicity from solar and interplanetary observations. Magnetic helicity (unlike current helicity) is one of the few global quantities that is conserved even in resistive MHD on a time-scale less than the global diffusion time-scale. Thus magnetic helicity studies make it possible to trace helicity as it emerges from the sub-photospheric layers to the corona and then is ejected via coronal mass ejections (CMEs) into interplanetary space, reaching the Earth as magnetic clouds (MCs).
Presently most developments have been done at the photospheric level because the magnetic field is mainly measured there in the solar atmosphere. The flux of magnetic helicity from differential motion is usually found to be too small (typically a factor 10) to explain the helicity ejected in CMEs (Nindos et al. 2003; Démoulin et al. 2002; Green et al. 2002). Most of the helicity flux comes from local motions within ARs (e.g. Nindos et al. 2003; Chae et al. 2004; Kusano et al. 2005), with a negligible contribution from the quiet Sun (Welsch & Longcope 2003).
The horizontal photospheric velocities, needed to compute the helicity flux, are determined by tracking the evolution of the magnetic field. The most widely used are local correlation tracking (LCT) methods. Two important parameters in LCT have to be properly chosen: the FWHM (full width at half maximum) of the apodizing function and the time interval between the two images to be compared. Chae et al. (2004) made a quantitative estimate of the effects of both parameters. They found that, when averaged over a time period of, or larger than, one hour the average flux of helicity is the same within 10%. The LCT method still has limitations (Démoulin & Berger 2003; Kusano et al. 2005), e.g. it gives only the mean velocity of several flux tubes (the average is done by the apodizing function which needs to be several pixels width). Then Kusano et al. (2002) proposed a method which uses the vertical component of the induction equation. In fact the velocity of flux tubes cannot fully be deduced from the induction equation and part of the velocity is still computed from the LCT method (Welsch et al. 2004). When the transverse magnetic field is available, Kusano et al. (2005) developed a method which minimize the input from the LCT, while Longcope (2004) proposed a method which uses only the induction equation and minimizes the photospheric "kinetic energy''.
Whatever is the method used to derive the photospheric velocities, the injection of magnetic helicity has complicated patterns both in space and time. In particular, Nindos et al. (2003); Moon et al. (2002b); Kusano et al. (2002); Chae et al. (2004,2001); Kusano et al. (2005) found that the total flux of magnetic helicity over an AR is usually the summation of opposite sign contributions which usually have similar magnitude (then the net flux is much lower than the unsigned flux).
Why does the derived helicity flux have so much mixed-sign polarity? It could come from the effect of turbulence on the magnetic flux tubes in the convection zone. But before looking for any physical implications, either in the convective zone, or in the corona, the notion of helicity flux (per unit surface) should be re-visited. Magnetic helicity is a global quantity, and it is not obvious if a helicity density and a helicity flux per unit surface have any physical meaning.
The definition of the relative magnetic helicity and its injection via boundary motions are briefly
summarized in Sect. 2. Then we explore three different possibilities to define a helicity flux per unit surface: the first one, GA, was used to analyze all previous observations
(Sect. 3.1), a second one,
![]() ,
which gives better results (Sect. 3.2) and a third one,
,
which gives better results (Sect. 3.2) and a third one, ![]() ,
which has the required property of a density
(Sect. 3.3). The two first densities, GA and
,
which has the required property of a density
(Sect. 3.3). The two first densities, GA and
![]() ,
can be computed with only photospheric observations while
,
can be computed with only photospheric observations while ![]() needs the coronal connectivities which are, in
practice, difficult to observe. We then explore, with basic configurations, the advantages of using
needs the coronal connectivities which are, in
practice, difficult to observe. We then explore, with basic configurations, the advantages of using
![]() rather than GA, and compare with
rather than GA, and compare with ![]() ,
in Sect. 4. Then we
conclude on the best way to derive the photospheric flux of magnetic helicity with present observations (Sect. 5).
,
in Sect. 4. Then we
conclude on the best way to derive the photospheric flux of magnetic helicity with present observations (Sect. 5).
The magnetic helicity of a divergence-free field ![]() within a volume
within a volume
![]() ,
bounded by a surface
,
bounded by a surface
![]() ,
was first defined by:
,
was first defined by:
In the case where
![]() is part of the corona, we clearly have magnetic fluxes crossing
is part of the corona, we clearly have magnetic fluxes crossing
![]() (in particular for the part of
(in particular for the part of
![]() located at the photospheric level).
Berger & Field (1984) have shown that for cases where
located at the photospheric level).
Berger & Field (1984) have shown that for cases where
![]() on
on
![]() one can define a relative magnetic helicity, H,
by subtracting the helicity of the potential field
one can define a relative magnetic helicity, H,
by subtracting the helicity of the potential field
![]() (
(
![]() has the same normal component Bn on
has the same normal component Bn on
![]() ). An expression for H, valid for any gauge is (Finn & Antonsen 1985):
). An expression for H, valid for any gauge is (Finn & Antonsen 1985):
The time variation of H can be written in general as (Berger & Field 1984):
With
![]() in resistive MHD,
in resistive MHD, ![]() being the non-ideal resistive term, Eq. (3) becomes:
being the non-ideal resistive term, Eq. (3) becomes:
Present magnetograms provide ![]() on
on
![]() located in the photosphere. From Bn distribution on
located in the photosphere. From Bn distribution on
![]() and Eq. (4) one can derive the vector potential
and Eq. (4) one can derive the vector potential
![]() (an explicit formula is given below in Eq. (14)). The
observed evolution of the magnetic field can provide an estimation
of the velocities. It is then possible to estimate the
photospheric flux of helicity from present observations.
(an explicit formula is given below in Eq. (14)). The
observed evolution of the magnetic field can provide an estimation
of the velocities. It is then possible to estimate the
photospheric flux of helicity from present observations.
Initially, since only horizontal velocities were deduced from the temporal
evolution of Bn, it was supposed that only the shear term could be
derived (e.g. Moon et al. 2002b; Chae et al. 2001; Nindos & Zhang 2002). However, the
magnetograms of Bn permit us to follow the photospheric
intersection of the magnetic flux-tubes but not the evolution of the plasma (even
if the plasma is frozen in the field, the two velocities are
usually different). From the observed magnetic evolution one
can estimate the flux-tube motion, not the plasma motion, parallel
to
![]() .
Let
.
Let
![]() be the plasma velocity tangent to
the photosphere and vn be the velocity perpendicular to the
photosphere. With the velocity of the footpoints of flux tubes,
be the plasma velocity tangent to
the photosphere and vn be the velocity perpendicular to the
photosphere. With the velocity of the footpoints of flux tubes, ![]() ,
defined as
,
defined as
Several methods have been developed to derive the velocities from
observed Bn evolution (see Sect. 1).
The LCT method follow explicitly the magnetic flux, so derive an
estimation of ![]() .
But even the methods using the normal component
of the ideal induction equation (combined in different ways with the
LCT method) can only give an estimation of
.
But even the methods using the normal component
of the ideal induction equation (combined in different ways with the
LCT method) can only give an estimation of ![]() ,
since the induction equation
can be rewritten as (Démoulin & Berger 2003):
,
since the induction equation
can be rewritten as (Démoulin & Berger 2003):
The above arguments imply that we cannot fully separate the shear and
advection terms in Eq. (6) if we are using the LCT or/and
the induction equation to derive the velocities. The only part which
can be separated un-ambiguously
is the part of the shearing term associated to the velocity component
orthogonal both to
![]() and
and
![]() (this part cannot come
from emergence as shown by Eq. (7)). The other part of the
shearing term can always be re-interpreted as an advection term and vice versa.
(this part cannot come
from emergence as shown by Eq. (7)). The other part of the
shearing term can always be re-interpreted as an advection term and vice versa.
In order to separate the shearing and advection terms, we need to
derive the full plasma velocity vector ![]() .
Measuring the
Doppler velocity gives only one component of the plasma velocity
but it can be combined with the determination of
.
Measuring the
Doppler velocity gives only one component of the plasma velocity
but it can be combined with the determination of ![]() to get an
estimate of
to get an
estimate of ![]() .
The method of Longcope (2004) provides this
possibility within the framework of minimizing a functional. Then,
if we know both
.
The method of Longcope (2004) provides this
possibility within the framework of minimizing a functional. Then,
if we know both ![]() and
and ![]() ,
we can separate the shearing and
advection terms in Eq. (6). However we can always
rewrite them as in Eq. (8) with
,
we can separate the shearing and
advection terms in Eq. (6). However we can always
rewrite them as in Eq. (8) with ![]() replaced
by
replaced
by
![]() for the shearing term, and
for the shearing term, and
![]() for the advection term.
So we have:
for the advection term.
So we have:
Equations (8), (11), (12) seem to suggest that the quantity
However GA is non null even with simple flows which do not input
any magnetic helicity to the coronal field! For example, consider
a simple circular magnetic region (with Bn>0) moving in a
straight line. In the classical Coulomb gauge, the vector field
![]() is toroidal, while
is toroidal, while ![]() is constant (say,
is constant (say,
![]() ). Then GA will be positive in the top half
(y>0) of the region, and negative in the bottom half (see Fig. 1). Indeed GA introduces artificial polarities of both signs with most of the flow patterns. These amplitudes are
analyzed for some basic flows in Sect. 4.
). Then GA will be positive in the top half
(y>0) of the region, and negative in the bottom half (see Fig. 1). Indeed GA introduces artificial polarities of both signs with most of the flow patterns. These amplitudes are
analyzed for some basic flows in Sect. 4.
In order to solve the above problem,
![]() should be explicitly written in terms of the magnetic field (using the gauge of Eq. (4)). For simplicity we assume that the solar
photosphere
should be explicitly written in terms of the magnetic field (using the gauge of Eq. (4)). For simplicity we assume that the solar
photosphere
![]() is planar. In this geometry the field
is planar. In this geometry the field
![]() is especially simple (Berger 1984):
is especially simple (Berger 1984):
Using Eq. (14), we obtain an expression for
![]() (Eq. (8), but also Eqs. (11), (12))
that depends only on observable photospheric quantities (Bn,
(Eq. (8), but also Eqs. (11), (12))
that depends only on observable photospheric quantities (Bn, ![]() and
and ![]() ):
):
| |
Figure 1: Map of GA (Eq. (13)) for a single magnetic region executing a simple translational motion towards the right (arrow). The normal magnetic field component Bn is uniform. The grey levels shows the strength of GA with middle grey being 0, lighter grey positive, and darker grey negative (a color version is available in the electronic version at http://www.edpsciences.org with red/blue coding the positive/negative values). The computation has been done with U0 R B02=2 (Eq. (30)). |
Equation (16) is transformed to
For the non-rotating motion of a single footpoint illustrated in
Fig. 1, we have
![]() everywhere. Thus
everywhere. Thus
![]() does not suffer the same problem as GA, which displays two artificial polarities.
does not suffer the same problem as GA, which displays two artificial polarities.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2663F-2.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg97.gif) |
Figure 2:
Maps of GA and
|
However, we can still find configurations where
![]() does not give physically sensible results. For example, consider the case when two magnetic regions simply separate without any rotation. The total helicity flux is zero. However, as seen from a position
does not give physically sensible results. For example, consider the case when two magnetic regions simply separate without any rotation. The total helicity flux is zero. However, as seen from a position ![]() within region 1, some points in region 2 will change their relative angle; i.e.
within region 1, some points in region 2 will change their relative angle; i.e.
![]() .
For positions off axis, there will be a net
contribution to
.
For positions off axis, there will be a net
contribution to
![]() (Fig. 2).
(Fig. 2).
The definition of
![]() (Eq. (19)) has not fully reached our goal of defining a flux density of magnetic helicity. For that purpose we need to consider the
magnetic connectivity in the volume
(Eq. (19)) has not fully reached our goal of defining a flux density of magnetic helicity. For that purpose we need to consider the
magnetic connectivity in the volume
![]() as shown below.
as shown below.
The magnetic helicity injected (Eq. (18)) can be separated into two terms:
Let us define the elementary fluxes: in the positive polarity
![]() and a similar one for the negative polarity:
and a similar one for the negative polarity:
![]() .
Then we get:
.
Then we get:
Now let us organize the integrals of Eq. (22) according
to the field line connectivity. Let a be the label of a generic
field line going from
![]() to
to
![]() Similarly, the field line labeled c travels from
Similarly, the field line labeled c travels from
![]() to
to
![]() (Fig. 3). Then we can
reorganize Eq. (22) as:
(Fig. 3). Then we can
reorganize Eq. (22) as:
While the helicity flux density has a meaning only for each
individual flux tube, it is convenient to define a flux per unit
surface area. This will enable us to compare helicity injection
with other sets of observations (e.g. the location of emergence or
of flaring). A helicity flux density per unit of surface,
![]() ,
can be assigned to either the positive or the
negative polarity. Equivalently the helicity input in an
elementary flux tube can be shared at both footpoints, e.g.
setting a fraction f+ =f in the positive polarity and f-
=1-f in the negative polarity.
Then we define the helicity flux density through
,
can be assigned to either the positive or the
negative polarity. Equivalently the helicity input in an
elementary flux tube can be shared at both footpoints, e.g.
setting a fraction f+ =f in the positive polarity and f-
=1-f in the negative polarity.
Then we define the helicity flux density through
![]() as:
as:
One can relate ![]() to
to
![]() at both feet of flux
tube a using Eqs. (27) and (28):
at both feet of flux
tube a using Eqs. (27) and (28):
The expression ![]() (Eq. (28)) defines the correct
helicity flux density. However accurately measuring
(Eq. (28)) defines the correct
helicity flux density. However accurately measuring ![]() will certainly be difficult because coronal connectivities are
only marked by a few loops. Moreover the ends of such loops are
below coronal temperatures and so usually not observed. In
addition, active region connectivity is usually complex, involving
quasi-separatrix layers (QSLs): on both sides of a QSL field lines
link very distant photospheric regions (Démoulin et al. 1997).
Usually, only some flux tubes on one side of a QSL are dense
enough to be observed. All these considerations imply that the
use of
will certainly be difficult because coronal connectivities are
only marked by a few loops. Moreover the ends of such loops are
below coronal temperatures and so usually not observed. In
addition, active region connectivity is usually complex, involving
quasi-separatrix layers (QSLs): on both sides of a QSL field lines
link very distant photospheric regions (Démoulin et al. 1997).
Usually, only some flux tubes on one side of a QSL are dense
enough to be observed. All these considerations imply that the
use of ![]() is practically limited by the available number
of connectivities that observations can provide. Thus it is worth
considering the densities GA (Eq. (13)) and
is practically limited by the available number
of connectivities that observations can provide. Thus it is worth
considering the densities GA (Eq. (13)) and ![]() (Eq. (19)) (which do not involve connectivity). Do these simpler densities provide measurements
representative of the
(Eq. (19)) (which do not involve connectivity). Do these simpler densities provide measurements
representative of the ![]() distribution?
distribution?
In observed magnetograms, magnetic flux tubes are frequently observed to
move bodily, so we consider a simple circular magnetic region
(with Bn uniform, = B0, in the disk of radius R) moving
with a constant velocity
![]() .
.
In this basic example, GA is positive in the top half of the region, and negative in the bottom half (Fig. 1):
The total amount of helicity in each polarity of GA is large. For both polarities the total absolute flux is:
The above spurious contribution of GA can easily mask the true helicity flux density, especially because the values of UR are expected to be substantially lower than those of U0. For example, with a twist of one turn in 10 days, UR will be in the interval [0.005,0.05] km s-1 with R belonging to [103,104] km; meanwhile U0 is frequently observed to be of the order of several 0.1 km s-1 (e.g. maximum values 0.3 to 0.7 km s-1 for the ARs analyzed by Nindos et al. 2003). The maximum rotation velocities deduced from the best examples of rotating asymmetric sunspots are in the interval [0.03,0.1] km s-1 (Brown et al. 2003), a range which is just around the maximal magnitude estimated above for UR. Thus U0 is expected to dominate UR in most ARs. Moreover, tracking methods detect translational motions much more easily than rotating ones (Gibson et al. 2004; Démoulin & Berger 2003), so it is vital to not include the strong translational signal in the helicity flux density.
In the above case of the translation motion of a single magnetic polarity, both
![]() and
and ![]() solve the problem perfectly: since the rotation rate
solve the problem perfectly: since the rotation rate
![]() is null for every pairs of elementary fluxes, we have
is null for every pairs of elementary fluxes, we have
At the photospheric level, magnetic flux tubes move relative to each other. A basic motion is the separation of two opposite polarities (e.g. after emergence of a bipole). For concreteness,
we consider two circular opposite polarities (P+ and P-) which separate without any rotation (so there is no helicity injection). Their velocities are:
The values of GA and
![]() at the point M(
at the point M(![]() )
are:
)
are:
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2663F-4.ps} \end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg148.gif) |
Figure 4:
Total positive fluxes for GA and
|
The total positive helicity fluxes of each magnetic polarity are:
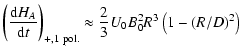 |
|||
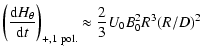 |
The helicity flux density defined by the linkage, ![]() ,
averages
the values of
,
averages
the values of
![]() at both footpoints of each flux tube
(Eq. (29)). For a potential field connection
between the two moving magnetic regions we have:
at both footpoints of each flux tube
(Eq. (29)). For a potential field connection
between the two moving magnetic regions we have:
![]() and
and
![]() ,
which implies
,
which implies
![]() (Eq. (27)) and
(Eq. (27)) and
![]() (Eq. (29)). There is no helicity flux density as expected.
(Eq. (29)). There is no helicity flux density as expected.
However when the magnetic polarities are linked by a twisted flux tube, there is in general a non null flux density as follows. For simplicity, suppose that the flux tube, which links the
magnetic regions, has a uniform twist T in its cross-section. Let ![]() be fixed as the magnetic polarities separate (so there is no twisting motions and no net injection of
magnetic helicity) and analyze the effect of T on the distribution of
be fixed as the magnetic polarities separate (so there is no twisting motions and no net injection of
magnetic helicity) and analyze the effect of T on the distribution of ![]() .
For T>0,
.
For T>0,
![]() and the difference increases from
T=0 to T=1/2 (for a half turn
and the difference increases from
T=0 to T=1/2 (for a half turn
![]() ). Thus
). Thus ![]() depends on the amount of twist in the volume. More precisely, taking
f+ = f- = 0.5 (so sharing the flux equally in each magnetic polarity)
depends on the amount of twist in the volume. More precisely, taking
f+ = f- = 0.5 (so sharing the flux equally in each magnetic polarity) ![]() is in the interval
is in the interval
![]() when T is in [0,1/2]!
when T is in [0,1/2]!
The twist T indeed creates an asymmetry between the elementary fluxes
linking the polarities. Let us call ![]() the field line linking the centre of the polarities (axis of the torus). When T is in [0,1/2], part of the flux linkage lies below
the field line linking the centre of the polarities (axis of the torus). When T is in [0,1/2], part of the flux linkage lies below ![]() while the other part lies above
while the other part lies above ![]() and at T=1/2, this effect is maximum. As the magnetic polarities separate, the elementary flux tubes going above (resp. below)
and at T=1/2, this effect is maximum. As the magnetic polarities separate, the elementary flux tubes going above (resp. below) ![]() get a
magnetic helicity flux which increases (resp. decreases) their positive helicity. Although there is no net global flux of helicity, the footpoint separation creates a reorganization in
the helicity distribution and thus the appearance of positive/negative helicity flux densities.
For T> 1/2,
get a
magnetic helicity flux which increases (resp. decreases) their positive helicity. Although there is no net global flux of helicity, the footpoint separation creates a reorganization in
the helicity distribution and thus the appearance of positive/negative helicity flux densities.
For T> 1/2, ![]() decreases and goes to zero for T=1 since all the flux is now passing below
decreases and goes to zero for T=1 since all the flux is now passing below ![]() .
Finally, the distribution of
.
Finally, the distribution of ![]() is modified periodically with T with
a period of 1. This example illustrates that the remnant polarities in
is modified periodically with T with
a period of 1. This example illustrates that the remnant polarities in
![]() can be artificial or real depending on the coronal linkage.
can be artificial or real depending on the coronal linkage.
We have assumed above a uniform field component Bn in the
magnetic regions. We investigate below how profile dependent
the above result is. The selected profiles are ordered from
a profile where the flux is mostly at the border of the magnetic region
to a profile where the flux is concentrated around the centre
of the region (keeping the same total magnetic flux):
![\begin{figure}
\par\hspace*{4.5mm}\includegraphics[width=7.05cm,clip]{2663F-5a.ps}\vspace*{5mm}
\includegraphics[width=7.4cm,clip]{2663F-5b.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg174.gif) |
Figure 5:
Top panel: different profiles of
|
Finally, consider the same configuration as above except that the two magnetic regions have the same Bn sign. The main difference is that the - sign in Eq. (36) is replaced by a + sign (also
![]() changes sign in Eq. (37)). It implies that
Eq. (38) is replaced with a summation of two terms of like sign, so the ratio
changes sign in Eq. (37)). It implies that
Eq. (38) is replaced with a summation of two terms of like sign, so the ratio
![]() is always greater. Thus in the case of two magnetic regions of same sign the use of
is always greater. Thus in the case of two magnetic regions of same sign the use of
![]() ,
rather than GA, is even more recommended.
,
rather than GA, is even more recommended.
Another basic motion is the rotation of one magnetic region around
another one. For concreteness we consider that the magnetic region P- is rotating around the magnetic region P+, but for the following helicity flux results the field sign can be reversed.
Each magnetic region is circular with a radius R and
|Bn|= B0 uniform. The centres of the polarities, O+ and O-, are separated by
D=|O+O-|. We suppose that only P- has a solid rotation around P+ with the angular velocity
![]() ;
the velocity field at the point
;
the velocity field at the point
![]() is given by:
is given by:
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{2663F-6.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg189.gif) |
Figure 6:
Maps of GA (Eq. (13), top panel) and
|
Like when two polarities separate (Sect. 4.2),
GA has both positive and negative values on the rotating
region, a result which could lead to misinterpretation
(Fig. 6). At the opposite of the separating case,
![]() is positive in all of the motionless region (P+).
The possible misinterpretation in that case is that the helicity
flux is concentrated in P+. Using
is positive in all of the motionless region (P+).
The possible misinterpretation in that case is that the helicity
flux is concentrated in P+. Using ![]() (Eq. (28)) solves this problem.
(Eq. (28)) solves this problem.
When ![]() ,
,
![]() is almost
uniform in P+ which is just what is expected for a solid
rotation. However GA is growing with the separation, D, of
the magnetic polarities. For
is almost
uniform in P+ which is just what is expected for a solid
rotation. However GA is growing with the separation, D, of
the magnetic polarities. For ![]() ,
the ratio between GA in P- and
,
the ratio between GA in P- and
![]() in P+ is approximately:
in P+ is approximately:
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{2663F-7.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg195.gif) |
Figure 7:
Total positive and negative helicity flux for GA and total positive flux for
|
Furthermore, the sum
![]() gives only approximately the correct injected helicity; the error
grows with D/R. It shows that, not only the local density
values, but also the total helicity flux can be affected by using GA. Large positive and negative fluxes are cancelled in the total flux; moreover the computation of
gives only approximately the correct injected helicity; the error
grows with D/R. It shows that, not only the local density
values, but also the total helicity flux can be affected by using GA. Large positive and negative fluxes are cancelled in the total flux; moreover the computation of ![]() is affected by
the periodicity of the fast Fourier transform (used to compute it). In the present case the periodic boundary effect is dominant and we describe it below.
is affected by
the periodicity of the fast Fourier transform (used to compute it). In the present case the periodic boundary effect is dominant and we describe it below.
In order to accurately compute ![]() using the fast Fourier transform method, one must place the magnetogram in a larger field of view that contains no magnetic field. In this
paper, the data box was a 512
using the fast Fourier transform method, one must place the magnetogram in a larger field of view that contains no magnetic field. In this
paper, the data box was a 512 ![]() 512 mesh representing a region of 40
512 mesh representing a region of 40 ![]() 40. To compute
40. To compute ![]() we put this data box in the centre of a 4
we put this data box in the centre of a 4 ![]() 4 times larger box. Thus the fast fourier transform is here done with 2048
4 times larger box. Thus the fast fourier transform is here done with 2048 ![]() 2048 modes, a much larger number of modes than what is usually used with observations. This large number reduces the effect of the periodic
boundary here (so that it is small in Fig. 7). This effect would become even more important with real observations and when the polarities are well separated. This is another important point in favor of
2048 modes, a much larger number of modes than what is usually used with observations. This large number reduces the effect of the periodic
boundary here (so that it is small in Fig. 7). This effect would become even more important with real observations and when the polarities are well separated. This is another important point in favor of ![]() since only GA is affected by this numerical problem.
since only GA is affected by this numerical problem.
Frequently new bipoles appear in magnetograms. The associated magnetic flux tube is expected to be twisted in the convective zone in order to be able to reach the photosphere without being destroyed (Emonet & Moreno-Insertis 1998). There is also evidence for the emergence of twisted flux tubes (Leka et al. 1996).
We consider a simple model to simulate the main helicity properties
of this emergence. The magnetic field is confined in a torus with
a main axial radius ![]() and a small radius R. The
longitudinal field strength inside the torus is uniform for
simplicity (similar results are obtained with a different profile,
as in Fig. 5). The field is uniformly twisted,
both across and along the flux tube, with a number N>0 of turns
for half the torus.
and a small radius R. The
longitudinal field strength inside the torus is uniform for
simplicity (similar results are obtained with a different profile,
as in Fig. 5). The field is uniformly twisted,
both across and along the flux tube, with a number N>0 of turns
for half the torus.
We simulate the emergence of half the torus with a constant vertical
velocity. The horizontal velocity of the footpoints of field
lines is given by Eq. (7), with no horizontal plasma
velocity. The helicity flux is thus given by Eq. (12).
The height of the axis apex above the "photosphere''
(boundary) is used to monitor the emergence. Its value is -Rwhen the first amount of field is about to cross the
"photosphere'', 0, when the torus axis is just tangent to the
"photosphere'', R when the top of the torus (its central cross
section) has completely emerged and ![]() when the torus is half
emerged. Normalizing the height with
when the torus is half
emerged. Normalizing the height with ![]() ,
the relative height
Z runs from
,
the relative height
Z runs from
![]() to 1.
to 1.
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2663F-8.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg199.gif) |
Figure 8:
Rows from top to bottom: maps of GA,
|
As in the other examples, GA and
![]() have some negative helicity flux densities while the rising of this twisted flux tube should only inject positive helicity (Fig. 8).
Since the magnetic field is known in the volume, we know the connectivities and we can
compute
have some negative helicity flux densities while the rising of this twisted flux tube should only inject positive helicity (Fig. 8).
Since the magnetic field is known in the volume, we know the connectivities and we can
compute ![]() (Fig. 8).
(Fig. 8). ![]() has no negative polarities and it is almost homogeneous over the flux tube section. The evolution of the helicity flux during the emergence is summarized by the total fluxes (Fig. 9). All total helicity injections are maximum just before
has no negative polarities and it is almost homogeneous over the flux tube section. The evolution of the helicity flux during the emergence is summarized by the total fluxes (Fig. 9). All total helicity injections are maximum just before
![]() ,
i.e. just before the top of the flux tube has completely emerged.
The helicity injections are related to the modification of the flux-tube cross section with Z, called the Cassini surface, but cannot be expressed only as a function of this surface (even with
a uniform longitudinal field and twist as considered here).
,
i.e. just before the top of the flux tube has completely emerged.
The helicity injections are related to the modification of the flux-tube cross section with Z, called the Cassini surface, but cannot be expressed only as a function of this surface (even with
a uniform longitudinal field and twist as considered here).
For cases with low N even ![]() maps have fake polarities but
they are at least a factor 10 lower than the fake polarities of GA. For example, with a flux tube twisted by only one tenth of turn (N=0.1) the fake polarities of
maps have fake polarities but
they are at least a factor 10 lower than the fake polarities of GA. For example, with a flux tube twisted by only one tenth of turn (N=0.1) the fake polarities of ![]() are of the
same magnitude than the real flux values given by the
are of the
same magnitude than the real flux values given by the ![]() maps (see the scales in the bottom of the maps of Fig. 8), while the fake polarities of GA are completely masking the real helicity injection during almost all the emergence (except when the torus is nearly half emerged: Fig. 9).
maps (see the scales in the bottom of the maps of Fig. 8), while the fake polarities of GA are completely masking the real helicity injection during almost all the emergence (except when the torus is nearly half emerged: Fig. 9).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2663F-9.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg201.gif) |
Figure 9:
Total positive and negative helicity flux for GA,
|
As in the case of a single polarity translating and rotating (see Sect. 4.1 and Eq. (33)), the relative importance of the fake polarities depends of the amount
on helicity injected (so on the number of turns N) and on the aspect ratio
![]() .
We define a proxy, called the Fake Relative Flux (
.
We define a proxy, called the Fake Relative Flux (
![]() ), to quantify the relative importance of the fake polarities due to the use of GX (where X= A or
), to quantify the relative importance of the fake polarities due to the use of GX (where X= A or ![]() ):
):
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{2663F-10.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg208.gif) |
Figure 10:
Dependence on R of the Fake Relative Fluxes,
|
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2663F-11.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg209.gif) |
Figure 11:
Dependence on the number of turns N of the Fake Relative Fluxes (
|
Both
![]() and
and
![]() are decreasing functions of R(Fig. 10), but the variation is relatively small,
in particular with
are decreasing functions of R(Fig. 10), but the variation is relatively small,
in particular with
![]() which is only lightly
influenced by R (less than a factor 3 of variation for one order
of magnitude in R).
which is only lightly
influenced by R (less than a factor 3 of variation for one order
of magnitude in R).
![]() is slightly more dependent on R and its variation goes approximately as R-1. However, R (or the aspect ratio
is slightly more dependent on R and its variation goes approximately as R-1. However, R (or the aspect ratio
![]() )
is not a parameter as important as N (see next paragraphs), and thus, for helicity injection maps
coming from observations, the flux measurements in the large flux
tubes will only be slightly less affected by the fake polarities
than smaller flux tubes.
)
is not a parameter as important as N (see next paragraphs), and thus, for helicity injection maps
coming from observations, the flux measurements in the large flux
tubes will only be slightly less affected by the fake polarities
than smaller flux tubes.
The main effects of N are the following ones. For small N, both
![]() and
and
![]() are rapidly decreasing functions of N (more rapidly than N-2), but for large N they are increasing functions of N (Fig. 11). The minimum point is located at a lower N for
are rapidly decreasing functions of N (more rapidly than N-2), but for large N they are increasing functions of N (Fig. 11). The minimum point is located at a lower N for
![]() than for
than for
![]() (as well as for larger R).
(as well as for larger R).
The decrease for small N can be easily understood.
The total amount of helicity injected increases with N while the
separation velocity of the magnetic polarities, at the origin of
the fake polarities, does not change. It implies that the fake polarities
are more dominated by the real injected helicity at larger N values.
For example with
![]() (Fig. 11), as soon as Nbecomes bigger than 0.15,
(Fig. 11), as soon as Nbecomes bigger than 0.15,
![]() is lower than 1. With
lower radius, this transition happens for larger N. In the case
of
is lower than 1. With
lower radius, this transition happens for larger N. In the case
of
![]() ,
whatever the radius is (in the range:
,
whatever the radius is (in the range:
![]() ), when N > 0.04 (a low amount of
twist), the fake polarities of
), when N > 0.04 (a low amount of
twist), the fake polarities of ![]() do not mask the true helicity flux density.
do not mask the true helicity flux density.
The above dependence on N is modified when N is high enough
so that it drastically changes the distribution of Bn(Fig. 12). This occurs only at the top of the
flux tube when Bn is dominated by the azimuthal field. There,
the two magnetic polarities are separating in a direction almost
orthogonal to the torus axis (while they are separating nearly
along the torus axis for smaller N values,
Fig. 12). The separation of the polarities leads
to fake polarities of both GA and ![]() as in previous
examples. Since in the case of separating polarities the strength
of GA and
as in previous
examples. Since in the case of separating polarities the strength
of GA and ![]() depends on the magnetic vertical field
and since in the top of the flux tube
depends on the magnetic vertical field
and since in the top of the flux tube
![]() ,
the importance of these fake polarities will increase with N.
However, even in the case of these
large values of N, the values of both
,
the importance of these fake polarities will increase with N.
However, even in the case of these
large values of N, the values of both
![]() and
and
![]() are
still far below 1, implying a small influence of the fake polarities.
are
still far below 1, implying a small influence of the fake polarities.
![\begin{figure}
\par\includegraphics[angle=-90,width=6.8cm,clip]{2663F-12.ps}\end{figure}](/articles/aa/full/2005/33/aa2663-05/Timg213.gif) |
Figure 12:
Maps of
|
We conclude this emergence study with the hope of applying it
to observations in a further study. The most important result is
that, for the same evolving magnetic configuration,
![]() is always lower by a factor 10 than
is always lower by a factor 10 than
![]() ,
and this can be by more than a factor 103 (for example with
,
and this can be by more than a factor 103 (for example with
![]() and N=1). This strongly indicates
that it is always better to use
and N=1). This strongly indicates
that it is always better to use ![]() than GA in order to map the helicity flux density. Another important point is that with
than GA in order to map the helicity flux density. Another important point is that with ![]() the fake polarities become negligible for lower
values of N than with GA (typically a factor 10 lower).
the fake polarities become negligible for lower
values of N than with GA (typically a factor 10 lower).
Magnetic helicity is a basic MHD quantity. Important developments have been achieved in recent years in observing the photospheric flux of magnetic helicity. It is also worthwhile to derive maps of the magnetic flux density in order to follow where the helicity is coming from (e.g. is it coming into the corona mainly in emerging magnetic fields or is a significant flux also present well after emergence?).
All previous analyses used the density GA (
![]() )
which involves the vector potential
)
which involves the vector potential ![]() of the magnetic field
(Moon et al. 2002a; Kusano et al. 2002; Chae et al. 2004,2001; Chae 2001; Nindos et al. 2003; Moon et al. 2002b; Nindos & Zhang 2002; Kusano et al. 2005). In all the studied active regions, the density GA has strong polarities of both sign with comparable magnitude. In fact, we show above that a large part of these
polarities are likely to be fake polarities: they are due to the
intrinsic property of GA which is not a true helicity flux
density. The simplest case is when a magnetic region is moving
bodily (so no helicity is injected): GA has two strong
polarities which can easily mask a real input of helicity, for
example, by twisting motions (Sect. 4.1). Examples
of these fake polarities associated with the global motion of a
magnetic region can be found in all the above published maps of GA; the clearest examples are in Nindos et al. (2003). The fake polarities induced by GA could represent significant,
if not dominant, contributions to the observed positive and negative flux
of magnetic helicity, maybe even masking the real helicity flux injection.
The precision of the much lower net flux of helicity can be
affected by this subtraction of close numbers (which, moreover,
are affected by the periodicity used to compute
of the magnetic field
(Moon et al. 2002a; Kusano et al. 2002; Chae et al. 2004,2001; Chae 2001; Nindos et al. 2003; Moon et al. 2002b; Nindos & Zhang 2002; Kusano et al. 2005). In all the studied active regions, the density GA has strong polarities of both sign with comparable magnitude. In fact, we show above that a large part of these
polarities are likely to be fake polarities: they are due to the
intrinsic property of GA which is not a true helicity flux
density. The simplest case is when a magnetic region is moving
bodily (so no helicity is injected): GA has two strong
polarities which can easily mask a real input of helicity, for
example, by twisting motions (Sect. 4.1). Examples
of these fake polarities associated with the global motion of a
magnetic region can be found in all the above published maps of GA; the clearest examples are in Nindos et al. (2003). The fake polarities induced by GA could represent significant,
if not dominant, contributions to the observed positive and negative flux
of magnetic helicity, maybe even masking the real helicity flux injection.
The precision of the much lower net flux of helicity can be
affected by this subtraction of close numbers (which, moreover,
are affected by the periodicity used to compute ![]() ).
).
In this study, the main objective was to solve the above problem by defining
the flux of magnetic helicity per unit surface. In a first step,
we define a new density,
![]() (Eq. (19)), by
writing explicitly the vector potential
(Eq. (19)), by
writing explicitly the vector potential ![]() and rearranging
the double summations over the magnetogram
(Sect. 3.2). For an elementary magnetic region,
and rearranging
the double summations over the magnetogram
(Sect. 3.2). For an elementary magnetic region,
![]() sums up the rotation of all the other magnetic
regions taking into account their magnetic flux.
sums up the rotation of all the other magnetic
regions taking into account their magnetic flux.
![]() vanishes for one magnetic region moving uniformly, so, in this
case, it solves the problem of GA. However
vanishes for one magnetic region moving uniformly, so, in this
case, it solves the problem of GA. However
![]() can
still have weaker fake polarities when several magnetic regions
are moving. For example when two magnetic regions are separating
or approaching each other, two polarities of
can
still have weaker fake polarities when several magnetic regions
are moving. For example when two magnetic regions are separating
or approaching each other, two polarities of
![]() are
present on each magnetic region (Sect. 4.2). They
are usually weaker by more than one order of magnitude than those
obtained with GA (Sects. 4.2
and 4.4) or even absent in some cases (e.g.
Sect. 4.3). These results make
are
present on each magnetic region (Sect. 4.2). They
are usually weaker by more than one order of magnitude than those
obtained with GA (Sects. 4.2
and 4.4) or even absent in some cases (e.g.
Sect. 4.3). These results make
![]() much
better suited to follow the injection of helicity in ARs, i.e. to
detect the real flux density of magnetic helicity.
much
better suited to follow the injection of helicity in ARs, i.e. to
detect the real flux density of magnetic helicity.
While
![]() will be of great practical use, it is still not
the flux density of magnetic helicity. Indeed to define it one
needs more information than the normal field component evolution
(which is sufficient to compute
will be of great practical use, it is still not
the flux density of magnetic helicity. Indeed to define it one
needs more information than the normal field component evolution
(which is sufficient to compute
![]() ): we need the
coronal connectivities for all the elementary flux tubes. This
information enables us to define the helicity flux per elementary
flux tube (Eq. (25)), a quantity which can be rewritten
as a flux of magnetic helicity per unit surface (
): we need the
coronal connectivities for all the elementary flux tubes. This
information enables us to define the helicity flux per elementary
flux tube (Eq. (25)), a quantity which can be rewritten
as a flux of magnetic helicity per unit surface (![]() ,
Eq. (28)).
,
Eq. (28)). ![]() is a field-weighted average of
is a field-weighted average of
![]() at both feet of the coronal connections, and it removes the remnant fake polarities associated to
at both feet of the coronal connections, and it removes the remnant fake polarities associated to
![]() (Sects. 4.2 and 4.4). However some
mixed polarities of
(Sects. 4.2 and 4.4). However some
mixed polarities of ![]() can be still present, e.g. when a
coronal twisted field is moved by horizontal photospheric flows
(Sect. 4.2.2). It is a clear warning that, even when using
can be still present, e.g. when a
coronal twisted field is moved by horizontal photospheric flows
(Sect. 4.2.2). It is a clear warning that, even when using ![]() ,
the
presence of both signs in the helicity flux density should be
analyzed with care (e.g. it does not necessarily mean cancellation
of magnetic helicity due to magnetic reconnection).
,
the
presence of both signs in the helicity flux density should be
analyzed with care (e.g. it does not necessarily mean cancellation
of magnetic helicity due to magnetic reconnection).
The present results are directly applicable to observations.
They are independent of the method used to get the photospheric
velocities. When local correlation tracking and/or the induction
equation are used, one can deduced only the total flux density, but
if plasma motions are available the flux density can be derived
separately
for the shear (horizontal motions) and advection (emergence) terms.
While ![]() provides the true helicity flux density, its
practical use is presently limited by our ability to define the
coronal linkage for all the magnetic polarities. This situation
will be well improved in a near future with the high resolution
and multi-wavelength observations of Solar-B (Shimizu 2002), as
well as the development of numerical techniques to compute the
coronal field from photospheric data. So presently
provides the true helicity flux density, its
practical use is presently limited by our ability to define the
coronal linkage for all the magnetic polarities. This situation
will be well improved in a near future with the high resolution
and multi-wavelength observations of Solar-B (Shimizu 2002), as
well as the development of numerical techniques to compute the
coronal field from photospheric data. So presently
![]() is of most use, but it will be replaced by
is of most use, but it will be replaced by ![]() later on.
This will bring another step in detecting weaker input of helicity
flux density (which when summed over an AR and time can bring a
significant amount of magnetic helicity). It will also permit us
to track the emergence of truly opposite magnetic polarity to the
dominant one in an AR, a case which could be important for flaring
(Kusano et al. 2004).
later on.
This will bring another step in detecting weaker input of helicity
flux density (which when summed over an AR and time can bring a
significant amount of magnetic helicity). It will also permit us
to track the emergence of truly opposite magnetic polarity to the
dominant one in an AR, a case which could be important for flaring
(Kusano et al. 2004).
Acknowledgements
We thank the referee for her/his helpful comments.
We complement in this appendix Sect. 4.3. The velocity field at a point M (![]() )
given by Eq. (42) can be decomposed in two different movements:
)
given by Eq. (42) can be decomposed in two different movements:
The rotation rate between M and another point M' also belonging to P- is then simply deduced from Eq. (17):
The writhe is given when M' belongs to P+; the rotation rate is then a bit more complex:
and so,
In the case where M is in the polarity P+, which is not
moving, the rotation rate is only non-null for the points M'located in the opposite polarity P-, and can be expressed as:
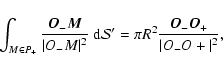 |
(A.10) |
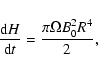 |
(A.11) |