A&A 439, 1057-1060 (2005)
DOI: 10.1051/0004-6361:20042587
Envelope models for the supersoft X-ray emission of V1974 Cyg
G. Sala - M. Hernanz
Institut d'Estudis Espacials de Catalunya and Institut de Ciències de l'Espai (CSIC), Campus UAB, Facultat de Ciències, Torre C5-parell, 2a planta, 08193 Bellaterra (Barcelona), Spain
Received 29 December 2004 / Accepted 7 February 2005
Abstract
The evolution of the soft X-ray emission of V1974 Cyg
has been simulated by a white dwarf envelope model with steady hydrogen
burning. The comparison of the results obtained from ROSAT observations with
the results of our envelope models indicates that the post-outburst
evolution of the nova can be explained by steady H-burning
on either a 0.9
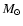 white dwarf with 50% degree
of mixing between solar-like accreted material and the
ONe degenerate core, or on a 1.0
white dwarf with 50% degree
of mixing between solar-like accreted material and the
ONe degenerate core, or on a 1.0 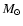 ONe white dwarf with 25% mixing.
ONe white dwarf with 25% mixing.
Key words: stars: individual: V1974 Cygni
- stars: novae, cataclysmic variables
- stars: white dwarfs
- X-rays: binaries
V1974 Cyg (Nova Cygni 1992), discovered on 1992 February 19, was the first classical
nova to be observed in all wavelengths, from radio to 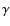 -rays.
The P Cyg profiles found in all the UV resonance lines of the
emission line spectra observed by IUE (Shore et al. 1993,1994) and
the strong [Ne III]
-rays.
The P Cyg profiles found in all the UV resonance lines of the
emission line spectra observed by IUE (Shore et al. 1993,1994) and
the strong [Ne III]
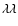 3869, 3968 and [NeIV]
3869, 3968 and [NeIV]
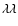 3346, 3426 emission lines that dominated the nebular spectrum (Barger et al. 1993)
established V1974 Cyg as a neon nova. V1974 Cyg was observed
by ROSAT between 1992 April 22 and 1993 December 3 (Krautter et al. 1996).
The X-ray light-curve showed three phases: a first rise phase up
to day 255 after outburst, a plateau phase without great variation
in flux from day 255 to 511, and a final and fast decline from
day 511 to day 653 after outburst.
During the plateau and decline phases, the X-ray spectrum was dominated
by the soft photospheric emission, which was well fitted by
MacDonald & Vennes (1991) ONe enhanced
white dwarf atmosphere models (Balman et al. 1998).
3346, 3426 emission lines that dominated the nebular spectrum (Barger et al. 1993)
established V1974 Cyg as a neon nova. V1974 Cyg was observed
by ROSAT between 1992 April 22 and 1993 December 3 (Krautter et al. 1996).
The X-ray light-curve showed three phases: a first rise phase up
to day 255 after outburst, a plateau phase without great variation
in flux from day 255 to 511, and a final and fast decline from
day 511 to day 653 after outburst.
During the plateau and decline phases, the X-ray spectrum was dominated
by the soft photospheric emission, which was well fitted by
MacDonald & Vennes (1991) ONe enhanced
white dwarf atmosphere models (Balman et al. 1998).
Classical nova outbursts are caused by the explosive burning of hydrogen
on the surface of a white dwarf in a cataclysmic variable.
When a critical amount of H-rich material has been accumulated on the white dwarf surface,
ignition in degenerate conditions takes place and thermonuclear runaway is initiated in
the accreted layer. The envelope expands and a fraction of it is ejected at large velocities,
while the rest returns to hydrostatic equilibrium and remains in steady
nuclear burning with constant bolometric luminosity (Starrfield 1989).
As the envelope expands, the photosphere recedes
and the effective temperature increases, shifting the spectrum from
optical through UV to soft X (MacDonald 1996; Krautter 2002).
The soft X-ray emission, arising as the ejecta becomes optically thin
to X-rays, is thus a direct indicator of the thermonuclear burning in the
post-outburst white dwarf envelope.
All novae are expected to undergo this phase, showing the
spectrum of a hot white dwarf atmosphere (MacDonald & Vennes 1991),
with effective temperatures in the range
105-106 K and
luminosities close to the Eddington limit.
The duration of the soft X-ray emitting phase is expected to depend
on the white dwarf mass and the envelope mass left after the outburst.
Without any model of the post-outburst nova, it has been usually estimated
as the nuclear time-scale of the envelope left, assumed to have a mass similar
to the accreted layer needed to trigger the outburst, 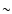
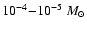 ,
indicating
nuclear time-scales of tens or hundreds of years
(Starrfield 1989; MacDonald 1985).
,
indicating
nuclear time-scales of tens or hundreds of years
(Starrfield 1989; MacDonald 1985).
Nevertheless, X-ray observations indicate much shorter turn-off times for
classical novae. During the last decade, ROSAT observed a total of 39 novae
less than 10 years after outburst, but only three were found to emit
soft X-rays (Orio et al. 2001):
V1974 Cyg 1992 (with turn-off 18 months after outburst;
Krautter et al. 1996),
GQ Mus 1983 (with turn-off 9 years after outburst;
Ögelman et al. 1993; Shanley et al. 1995)
and Nova LMC 1995 (still bright in the year 2000,
when observed with XMM-Newton; Orio & Greiner 1999;
Orio et al. 2003). Out of these three novae detected, the
best observed one was V1974 Cyg, for which the whole evolution of the soft X-ray
emission was followed.
Here we present a model for a post-outburst white dwarf envelope
that can explain the evolution of the soft X-ray emission and turn-off of V1974 Cyg.
Furthermore, from the comparison of the model with ROSAT observations,
the white dwarf mass, envelope composition and envelope mass of V1974 Cyg are constrained.
A numerical model has been developed to simulate the physical conditions
in the steady hydrogen burning envelope of post-outburst novae.
A grid of white dwarf envelope models
has been computed for white dwarf masses from 0.9 to 1.3
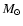 .
Three compositions from José & Hernanz (1998) hydrodynamic nova models
have been considered, corresponding
to ONe novae with different degrees of mixing
between the solar accreted matter and the degenerate core:
ONe25 models, with 25% mixing (in mass fractions
X=0.53, Y=0.21,
.
Three compositions from José & Hernanz (1998) hydrodynamic nova models
have been considered, corresponding
to ONe novae with different degrees of mixing
between the solar accreted matter and the degenerate core:
ONe25 models, with 25% mixing (in mass fractions
X=0.53, Y=0.21,
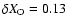 - extra O mass fraction
beyond that in Z -,
- extra O mass fraction
beyond that in Z -,
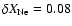 - extra Ne mass fraction -;
Z contains metals in solar fractions);
ONe50, with 50% mixing (X=0.35, Y=0.14,
- extra Ne mass fraction -;
Z contains metals in solar fractions);
ONe50, with 50% mixing (X=0.35, Y=0.14,
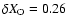 ,
,
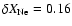 ); and ONe75, with 75% mixing
(X=0.18, Y=0.08,
); and ONe75, with 75% mixing
(X=0.18, Y=0.08,
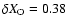 ,
,
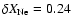 ).
Evolution is approximated as a sequence of steady state models
(for a description of the envelope models see Sala & Hernanz 2005).
).
Evolution is approximated as a sequence of steady state models
(for a description of the envelope models see Sala & Hernanz 2005).
The results show that an envelope with steady H-burning
proceeds along a plateau of quasi-constant
luminosity, shrinking its photospheric radius as the envelope mass
is reduced, and increasing its effective temperature
as the photosphere sinks into deeper and hotter layers of the envelope.
The average plateau luminosity increases for increasing
white dwarf masses and for decreasing hydrogen abundances, according to the expression
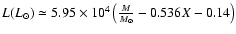 .
Thermonuclear reactions continue until the envelope mass is reduced
to the minimum critical mass for stable hydrogen burning,
which occurs shortly after the maximum
effective temperature is reached. Since no equilibrium configuration
for a smaller envelope mass exists, the shell sources turn-off
and the white dwarf starts to cool down.
The upper panel in Fig. 1 shows the
photospheric radius versus the effective temperature for some
of our models. The lower panels show the
envelope mass for the same models, with the time intervals, in days,
spent by the envelopes in evolving between adjacent points.
.
Thermonuclear reactions continue until the envelope mass is reduced
to the minimum critical mass for stable hydrogen burning,
which occurs shortly after the maximum
effective temperature is reached. Since no equilibrium configuration
for a smaller envelope mass exists, the shell sources turn-off
and the white dwarf starts to cool down.
The upper panel in Fig. 1 shows the
photospheric radius versus the effective temperature for some
of our models. The lower panels show the
envelope mass for the same models, with the time intervals, in days,
spent by the envelopes in evolving between adjacent points.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2587fig1.eps}
\end{figure}](/articles/aa/full/2005/33/aa2587-04/Timg15.gif) |
Figure 1:
Observational results for V1974 Cyg compared to our envelope models.
Upper panel: spectral parameters (photospheric radius,
 ,
and effective temperature, ,
and effective temperature,
 )
for ROSAT observations
on days 255(A), 261(B), 291(C), 434(D) and 511(E) after outburst
(from Balman et al. 1998). Solid line contours for a distance of 2.5 kpc;
dotted line contours for all the distance range of 1.7-3.3 kpc).
Observational results are overplotted on ONe25 (dashed) and ONe50 (solid) envelope models, for
white dwarf masses 0.9, 1.0 and 1.1 )
for ROSAT observations
on days 255(A), 261(B), 291(C), 434(D) and 511(E) after outburst
(from Balman et al. 1998). Solid line contours for a distance of 2.5 kpc;
dotted line contours for all the distance range of 1.7-3.3 kpc).
Observational results are overplotted on ONe25 (dashed) and ONe50 (solid) envelope models, for
white dwarf masses 0.9, 1.0 and 1.1  .
Numbers indicate days between observations.
Vertical lines are orientative for comparison with the lower panels.
Middle panel: envelope masses for ONe25 models.
Numbers indicate days spent by the envelope model between two adjacent points.
Lower panel: same as in middle panel for ONe50 models. .
Numbers indicate days between observations.
Vertical lines are orientative for comparison with the lower panels.
Middle panel: envelope masses for ONe25 models.
Numbers indicate days spent by the envelope model between two adjacent points.
Lower panel: same as in middle panel for ONe50 models. |
| Open with DEXTER |
For the comparison of our models with V1974 Cyg,
results from Table 1 in Balman et al. (1998) have been used (see Table 1).
For each observation, they obtained a 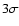 confidence range for all model parameters,
including the effective temperature and the atmosphere normalization constant,
defined as (R/D)2, where R is the photospheric radius and D is the distance to the
source. Several determinations of the distance to V1974 Cyg can be found in the
literature
(Quirrenbach et al. 1993; Shore et al. 1994;
Paresce et al. 1995; Chochol et al. 1997; Balman et al. 1998;
Cassatella et al. 2004).
In this work, we adopt the mean value and the whole uncertainty
derived from these distance determinations,
confidence range for all model parameters,
including the effective temperature and the atmosphere normalization constant,
defined as (R/D)2, where R is the photospheric radius and D is the distance to the
source. Several determinations of the distance to V1974 Cyg can be found in the
literature
(Quirrenbach et al. 1993; Shore et al. 1994;
Paresce et al. 1995; Chochol et al. 1997; Balman et al. 1998;
Cassatella et al. 2004).
In this work, we adopt the mean value and the whole uncertainty
derived from these distance determinations, 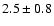 kpc,
to obtain the photospheric radius from the normalization constants listed
in Table 1 of Balman et al. (1998).
The contours resulting from this derived radius and the effective temperature range from
Balman et al. (1998) are overplotted on our models in Fig. 1 (upper panel).
The large uncertainty in the distance
makes an analysis based on the photospheric radius rather unreliable.
Nevertheless, the evolution of the effective temperature alone restricts the
possible models for V1974 Cyg to very few,
and makes our main results independent of the distance determination.
kpc,
to obtain the photospheric radius from the normalization constants listed
in Table 1 of Balman et al. (1998).
The contours resulting from this derived radius and the effective temperature range from
Balman et al. (1998) are overplotted on our models in Fig. 1 (upper panel).
The large uncertainty in the distance
makes an analysis based on the photospheric radius rather unreliable.
Nevertheless, the evolution of the effective temperature alone restricts the
possible models for V1974 Cyg to very few,
and makes our main results independent of the distance determination.
Table 1:
ROSAT observational results for V1974 Cyg.
A first distance-independent parameter to compare observations and
models is the maximum effective temperature. According to
Balman et al. (1998), the maximum effective temperature observed by ROSAT
was 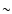 50 eV, on day 511 after outburst.
Nevertheless, the actual maximum temperature
could have been missed by ROSAT, since no observations were
performed between days 511 and 612.
The V1974 Cyg X-ray light curve (Krautter et al. 1996)
indicates that the end of the
plateau phase, and therefore the maximum effective temperature, occurred
between these two ROSAT observations. Furthermore,
UV observations indicated that the hot central source had
ceased to photoionize the ejecta at about day
50 eV, on day 511 after outburst.
Nevertheless, the actual maximum temperature
could have been missed by ROSAT, since no observations were
performed between days 511 and 612.
The V1974 Cyg X-ray light curve (Krautter et al. 1996)
indicates that the end of the
plateau phase, and therefore the maximum effective temperature, occurred
between these two ROSAT observations. Furthermore,
UV observations indicated that the hot central source had
ceased to photoionize the ejecta at about day 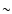 530 after outburst
(Shore et al. 1996). In this case, the actual maximum effective
temperature should have been reached before day 530 and thus
should be not much higher than the value obtained for day 511,
530 after outburst
(Shore et al. 1996). In this case, the actual maximum effective
temperature should have been reached before day 530 and thus
should be not much higher than the value obtained for day 511, 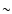 50 eV.
50 eV.
Taking into account this limit, we find that some envelope models
are unlikely to represent the observed evolution: for the ONe75 models,
any white dwarf more massive than 0.9 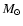 has
an effective temperature higher than observed.
For the ONe50 models, we find that only the 0.9
has
an effective temperature higher than observed.
For the ONe50 models, we find that only the 0.9 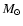 white dwarf envelopes have a good maximum effective temperature (53 eV, see Fig. 1). Finally, in the case of the ONe25 composition, this requirement
could be fullfilled by a white dwarf of mass between 0.9
white dwarf envelopes have a good maximum effective temperature (53 eV, see Fig. 1). Finally, in the case of the ONe25 composition, this requirement
could be fullfilled by a white dwarf of mass between 0.9 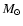 (
(
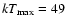 eV) and 1.0
eV) and 1.0 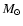 (
(
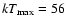 eV).
Nevertheless, since evolution at high effective temperatures could proceed faster
than the time interval between observations, this criterion alone is not enough to
reject models with maximum effective temperatures larger than observed.
The evolution of the effective temperature adds more constrains.
eV).
Nevertheless, since evolution at high effective temperatures could proceed faster
than the time interval between observations, this criterion alone is not enough to
reject models with maximum effective temperatures larger than observed.
The evolution of the effective temperature adds more constrains.
The evolution of the effective temperature provides a second and
more powerful distance-independent diagnostic tool.
Only some combinations of core mas and envelope composition can
reproduce the observed evolution.
Interestingly enough, these cases are among the ones with good
maximum effective temperature: 0.9 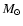 for ONe50 and 1.0
for ONe50 and 1.0 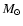 for ONe25.
The days elapsed between ROSAT observations during the
plateau phase are indicated in the upper panel in Fig. 1,
and the corresponding time intervals for the models, in the lower panels.
Table 2 lists the interval times for the models of each composition
that could better fit the observed evolution.
The time elapsed until day 511 should be taken
with care: if the maximum effective temperature and the subsequent
turn-off occurred close to that day, several factors can affect the
evolution. It is possible that the X-ray observation took place shortly
after reaching the maximum effective temperature, and not before.
In this case, if the envelope was already starting to cool down, with
still a high effective temperature, the luminosity and effective radius
would have been slightly smaller than the corresponding values for
the source still on, which could explain the fact that the
photospheric radius on day 511 is smaller than predicted by models.
The time estimated from the envelope models for evolution along
the high luminosity branch would then be smaller than observed, and
this is indeed the case for the envelope models with time-scales more
similar to observations.
for ONe25.
The days elapsed between ROSAT observations during the
plateau phase are indicated in the upper panel in Fig. 1,
and the corresponding time intervals for the models, in the lower panels.
Table 2 lists the interval times for the models of each composition
that could better fit the observed evolution.
The time elapsed until day 511 should be taken
with care: if the maximum effective temperature and the subsequent
turn-off occurred close to that day, several factors can affect the
evolution. It is possible that the X-ray observation took place shortly
after reaching the maximum effective temperature, and not before.
In this case, if the envelope was already starting to cool down, with
still a high effective temperature, the luminosity and effective radius
would have been slightly smaller than the corresponding values for
the source still on, which could explain the fact that the
photospheric radius on day 511 is smaller than predicted by models.
The time estimated from the envelope models for evolution along
the high luminosity branch would then be smaller than observed, and
this is indeed the case for the envelope models with time-scales more
similar to observations.
The ONe75 envelope models (with
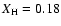 )
cannot, in any
case, simulate the observed evolution. Even for the smallest white
dwarf in our grid (
)
cannot, in any
case, simulate the observed evolution. Even for the smallest white
dwarf in our grid (
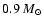 ,
which is too small for an ONe white dwarf,
according to stellar evolution models),
the total time elapsed between effective temperatures corresponding
to days 255 and 511 is
,
which is too small for an ONe white dwarf,
according to stellar evolution models),
the total time elapsed between effective temperatures corresponding
to days 255 and 511 is 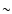 40 days, smaller than the 256 days elapsed
between observations. For the ONe50 0.9
40 days, smaller than the 256 days elapsed
between observations. For the ONe50 0.9 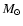 white dwarf
envelope models, the time-scale for the same interval of effective
temperatures (141-181 days) is closer to the observed one. Finally, time-scales for
ONe25 1.0
white dwarf
envelope models, the time-scale for the same interval of effective
temperatures (141-181 days) is closer to the observed one. Finally, time-scales for
ONe25 1.0 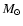 models are also similar to the observed ones.
In summary, the best candidates for V1974 Cyg are either
a 0.9
models are also similar to the observed ones.
In summary, the best candidates for V1974 Cyg are either
a 0.9 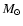 white dwarf with 50% mixing (with X=0.35)
or a 1.0
white dwarf with 50% mixing (with X=0.35)
or a 1.0 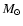 white dwarf with a 25% mixing (with X=0.53).
white dwarf with a 25% mixing (with X=0.53).
In both cases, the envelope mass is in the range 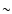
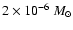 (see low panels in Fig. 1) and the luminosity of the model is
(see low panels in Fig. 1) and the luminosity of the model is 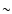
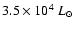 .
Since the
comparison with models is based on the effective temperature, this
luminosity determination is independent of distance.
.
Since the
comparison with models is based on the effective temperature, this
luminosity determination is independent of distance.
Table 2:
Time intervals observed and simulated by envelope models.
Among our two candidate envelope models, the 50% mixing case
is favoured by independent determinations
of the hydrogen mass fraction in the V1974 Cyg ejecta.
Austin et al. (1996) found X=0.17 from optical and ultraviolet observations,
which is similar to the hydrogen abundance in our ONe75 models (X=0.18).
Nevertheless, as mentioned above, this model would imply a too fast
evolution compared to ROSAT data. Using mid-infrared spectroscopy,
Hayward et al. (1996) determined X=0.30,
very close to the value in our ONe50 models.
Later works (Moro-Martín et al. 2001;
Vanlandigham et al. 2002) determined smaller metal enhancements than
Austin et al. (1996), which also agrees with a hydrogen abundance higher
than X=0.18.
In any of our candidate models, the white dwarf mass
lies at the lower end of previous determinations.
From their X-ray observations,
Balman et al. (1998) used the mass-luminosity
relation from Iben & Tutukov (1996) to find a
white dwarf mass in the range 0.9-1.4 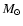 .
Krautter et al. (1996) estimated
the star mass to be 1.25
.
Krautter et al. (1996) estimated
the star mass to be 1.25 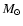 using the mass-luminosity relation of
Iben (1982), which is reproduced by our core-mass luminosity relation above
for the hydrogen mass fraction of his models, X=0.64.
They took the nova luminosity early in the outburst,
using the mass-luminosity relation of
Iben (1982), which is reproduced by our core-mass luminosity relation above
for the hydrogen mass fraction of his models, X=0.64.
They took the nova luminosity early in the outburst,
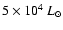 ,
determined by Shore et al. (1993,1994),
who assumed a distance of 3 kpc. Nevertheless,
later distance determinations situated the nova closer than 3 kpc and thus the luminosity would be smaller, indicating a less massive
white dwarf. Moreover, envelope models of Iben (1982) and
Iben & Tutukov (1996)
used in both previous mass determinations were hydrogen richer (X=0.64)
than our models, requiring a more massive white dwarf for the same luminosity.
Our mass determination is in agreement with Retter et al. (1997),
who estimated the mass of the white dwarf to be in the range
0.75-1.07
,
determined by Shore et al. (1993,1994),
who assumed a distance of 3 kpc. Nevertheless,
later distance determinations situated the nova closer than 3 kpc and thus the luminosity would be smaller, indicating a less massive
white dwarf. Moreover, envelope models of Iben (1982) and
Iben & Tutukov (1996)
used in both previous mass determinations were hydrogen richer (X=0.64)
than our models, requiring a more massive white dwarf for the same luminosity.
Our mass determination is in agreement with Retter et al. (1997),
who estimated the mass of the white dwarf to be in the range
0.75-1.07 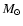 from the periodicities oberved in the light-curve
and the precessing disc model for the superhump phenomenon.
A factor cited in previous works
(Austin et al. 1996) in favour of a massive white dwarf
was the minimum mass for ONe degenerate cores,
from the periodicities oberved in the light-curve
and the precessing disc model for the superhump phenomenon.
A factor cited in previous works
(Austin et al. 1996) in favour of a massive white dwarf
was the minimum mass for ONe degenerate cores, 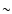
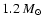 .
Recent evolutionary calculations
in Gil-Pons et al. (2003) have fixed a smaller lower limit,
showing that final ONe white dwarfs in cataclysmic variables
have typical masses between 1.0 and 1.1
.
Recent evolutionary calculations
in Gil-Pons et al. (2003) have fixed a smaller lower limit,
showing that final ONe white dwarfs in cataclysmic variables
have typical masses between 1.0 and 1.1 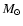 ,
thus including
our 1.0
,
thus including
our 1.0 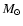 ONe25 model as a possible one according to
stellar evolution.
ONe25 model as a possible one according to
stellar evolution.
The accreted mass to trigger the outburst of a 1 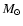 white dwarf with 50% mixing predicted by theoretical models is
white dwarf with 50% mixing predicted by theoretical models is 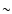
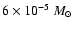 ,
whereas the
ejected mass is
,
whereas the
ejected mass is 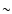
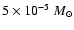 (José & Hernanz
1998). Therefore,
models do not predict remnant envelope masses as low as those with steady
hydrogen burning that can explain the soft X-ray emission observed for V1974 Cyg
(
(José & Hernanz
1998). Therefore,
models do not predict remnant envelope masses as low as those with steady
hydrogen burning that can explain the soft X-ray emission observed for V1974 Cyg
(
 ). Since the evolution of V1974 Cyg from day
255 after outburst to the end of the constant bolometric luminosity phase can
be explained solely as a result of pure hydrogen burning, there should be a mass-loss
mechanism able to get rid of most of
the envelope mass in around 8 months (Tuchman & Truran 1998),
but acting at a much lower
level later on. A mechanism such as a radiation driven wind (Kato
& Hachisu 1994)
approaches this, evolving from large to small rates as envelope mass
is depleted; however, a fine tuning of various model parameters would be
required to
obtain the particular amount of mass-loss needed. Thus, it is not well
known what mechanisms are responsible for the depletion of the envelope
mass down to the levels required for the correct interpretation of the X-ray
emission observed in V1974 Cyg.
). Since the evolution of V1974 Cyg from day
255 after outburst to the end of the constant bolometric luminosity phase can
be explained solely as a result of pure hydrogen burning, there should be a mass-loss
mechanism able to get rid of most of
the envelope mass in around 8 months (Tuchman & Truran 1998),
but acting at a much lower
level later on. A mechanism such as a radiation driven wind (Kato
& Hachisu 1994)
approaches this, evolving from large to small rates as envelope mass
is depleted; however, a fine tuning of various model parameters would be
required to
obtain the particular amount of mass-loss needed. Thus, it is not well
known what mechanisms are responsible for the depletion of the envelope
mass down to the levels required for the correct interpretation of the X-ray
emission observed in V1974 Cyg.
Acknowledgements
This research has been partially funded by the MCYT project
AYA2004-06290-C02-01
and by the EU FEDER funds. G.S. acknowledges a FPI grant from the MEC.
- Austin, S. J., Wagner, R.
M., Starrfield, S., et al. 1996, AJ, 111, 2 (In the text)
- Balman, S., Krautter, J.,
& Ögelman, H. 1998, ApJ, 499, 395 [CrossRef] (In the text)
- Barger, A. J., Gallagher,
J. S., Bjorkman, K. S., Johansen, K. A., & Nordsieck, K. H.
1993, ApJ, 419, L85 [CrossRef] (In the text)
- Cassatella, A., Lamers, H.
J. G. L. M., Rossi, C., Altamore, A., & Gonzalez-Riestra, R.
2004, A&A, 420, 571 [EDP Sciences] [CrossRef] (In the text)
- Chochol, D., Grygar, J.,
Pribulla, T., et al. 1997, A&A, 318, 908 (In the text)
- Gil-Pons, P.,
García-Berro, E., José, J., Hernanz, M., & Truran, J.
W. 2003, A&A, 407, 1021 [EDP Sciences] [CrossRef] (In the text)
- Hayward, T. L., Saizar,
P., Gehrz, R. D., et al. 1996, ApJ, 469, 854 [CrossRef] (In the text)
- Iben, I., Jr. 1982, ApJ,
259, 244 [CrossRef] (In the text)
- Iben, I., Jr., &
Tutukov, A. V. 1996, ApJS, 105, 145 [CrossRef] (In the text)
- José, J., &
Hernanz, M. 1998, ApJ, 494, 680 [CrossRef] (In the text)
- Kato, M., & Hachisu,
I. 1994, ApJ, 437, 802 [CrossRef] (In the text)
- Krautter, J. 2002, in
Classical Nova Explosions, ed. M. Hernanz, & J. José, AIP
Conf. Proc., 637, 345
(In the text)
- Krautter, J.,
Ögelman, H., Starrfield, S., Wichmann, R., & Pfeffermann,
E. 1996, ApJ, 456, 788 [CrossRef] (In the text)
- MacDonald, J. 1996, in
Cataclysmic Variables and Related Objects (Dordrecht: Kluwer),
281
(In the text)
- MacDonald, J., &
Vennes, S. 1991, ApJ, 373, L51 [CrossRef] (In the text)
- MacDonald, J., Fujimoto,
M. Y., & Truran, J. 1985, ApJ, 294, 263 [CrossRef] (In the text)
- Moro-Martín, A.,
Garnavich, P. M., & Noriega-Crespo, A. 2001, ApJ, 121,
1636 (In the text)
- Ögelman, H., Orio,
M., Krautter, J., & Starrfield, S. 1993, Nature, 361, 331 [CrossRef] (In the text)
- Orio, M., & Greiner,
J. 1999, A&A, 344, L13 (In the text)
- Orio, M., Covington, J.,
& Ögelman, H. 2001, A&A, 373, 542 [EDP Sciences] [CrossRef] (In the text)
- Orio, M., Hartmann, W.,
Still, M., & Greiner, J. 2003, ApJ, 594, 435 [CrossRef] (In the text)
- Paresce, F., Livio, M.,
Hack, W., & Korista, K. 1995, A&A, 299, 823 (In the text)
- Quirrenbach, A., Elias II,
N. M., Mozurkewich, D., et al. 1993, AJ, 106, 1118 [CrossRef] (In the text)
- Retter, A., Leibowitz, E.
M., & Ofek, E. O. 1997, MNRAS, 286, 745 (In the text)
- Sala, G., & Hernanz,
M. 2005, submitted
(In the text)
- Shanley, L., Ögelman,
H., Gallagher, J. S., Orio, M., & Krautter, J. 1995, ApJ, 438,
L95 [CrossRef] (In the text)
- Shore, S. N., Starrfield,
S., & Sonneborn, G. 1996, ApJ, 463, L21 [CrossRef] (In the text)
- Shore, S. N., Sonneborn,
G., Starrfield, S., Gonzalez-Riestra, R., & Ake, T. B. 1993,
AJ, 106, 2408 [CrossRef] (In the text)
- Shore, S. N., Sonneborn,
G., Starrfield, S., Gonzalez-Riestra, R., & Polidan, R. S.
1994, ApJ, 421, 344 [CrossRef]
- Starrfield, S. 1989, in
Classical Novae (New York: Wiley), 39
(In the text)
- Tuchman, Y., & Truran,
J. W. 1998, ApJ, 503, 381 [CrossRef] (In the text)
- Vanlandingham, K. M.,
Starrfield, S., Shore, S. N., & Wagner, R. M. 2002, in
Classical Nova Explosions, ed. M. Hernanz, & J. José, AIP
Conf. Proc., 637, 224
(In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2587fig1.eps}
\end{figure}](/articles/aa/full/2005/33/aa2587-04/Timg15.gif)