A&A 439, 1075-1091 (2005)
DOI: 10.1051/0004-6361:20042396
Full computation of massive AGB evolution
II.
The role of mass loss and cross-sections
P. Ventura
-
F. D'Antona
Osservatorio Astronomico di Roma,
via Frascati 33, 00040 Monte Porzio Catone, Italy
Received 19 November 2004 / Accepted 26 April 2005
Abstract
In the course of a systematic exploration of the uncertainties
associated with the input micro- and macro-physics in the modeling of
the evolution
of intermediate mass stars during their Asymptotic Giant Branch (AGB) phase,
we focus on the role of the nuclear reactions rates and mass loss. We
consider masses 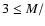

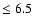 for a metallicity
typical for globular clusters, Z=0.001, and compare the results
obtained by computing the full
nucleosynthesis with hot bottom burning (HBB), for a network of
30 elements, using either the NACRE or the Cameron & Fowler (CF88)
cross-sections.
The results differ in particular with respect to the 23Na nucleosynthesis (which is more efficient in the NACRE case) and the
magnesium isotopes ratios. For both choices, however, the CNO nucleosynthesis shows that the C+N+O is constant within a factor
of two, in our models
employing a very efficient convection treatment. Different mass loss rates
alter the physical conditions for HBB and the length of the AGB phase,
indirectly changing the chemical yields. These computations show that the
predictive power of our AGB models is undermined by these uncertainties. In
particular, it appears at the moment very difficult to strongly accept
or dismiss that these sources play a key-role in
the pollution of Globular Clusters (GCs), and
that they have been the main stellar site
responsible for the chemical anomalies that
are observed at the surface of giant and turn-off stars of GCs, in the
self-enrichment scenarios.
for a metallicity
typical for globular clusters, Z=0.001, and compare the results
obtained by computing the full
nucleosynthesis with hot bottom burning (HBB), for a network of
30 elements, using either the NACRE or the Cameron & Fowler (CF88)
cross-sections.
The results differ in particular with respect to the 23Na nucleosynthesis (which is more efficient in the NACRE case) and the
magnesium isotopes ratios. For both choices, however, the CNO nucleosynthesis shows that the C+N+O is constant within a factor
of two, in our models
employing a very efficient convection treatment. Different mass loss rates
alter the physical conditions for HBB and the length of the AGB phase,
indirectly changing the chemical yields. These computations show that the
predictive power of our AGB models is undermined by these uncertainties. In
particular, it appears at the moment very difficult to strongly accept
or dismiss that these sources play a key-role in
the pollution of Globular Clusters (GCs), and
that they have been the main stellar site
responsible for the chemical anomalies that
are observed at the surface of giant and turn-off stars of GCs, in the
self-enrichment scenarios.
Key words: stars: evolution -
stars: interiors -
stars: AGB and post-AGB -
stars: abundances
Since the pioneering works by Schwarzschild & Harm (1965, 1967), and Iben
(1975, 1976), it is now well known that intermediate mass stars (i.e. stars
with initial masses 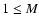 /
/
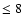 ,
hereinafter IMS) soon after the
exhaustion of central helium experience a phase of thermal pulses (TPs), during
which a CNO burning shell supplies for most of the time the global nuclear
energy release; periodically, a He-burning shell is activated in thermally
unstable conditions, triggering an expansion of all the outer layers, with the
consequent extinction of CNO burning (Lattanzio & Karakas 2001). During the
AGB evolution these stars suffer a strong mass loss, which ultimately
peels off all the envelope mass, leaving a carbon-oxygen compact remnant
which evolves as a white dwarf.
The base of the external convective zone of the most massive IMS may become so
hot (
,
hereinafter IMS) soon after the
exhaustion of central helium experience a phase of thermal pulses (TPs), during
which a CNO burning shell supplies for most of the time the global nuclear
energy release; periodically, a He-burning shell is activated in thermally
unstable conditions, triggering an expansion of all the outer layers, with the
consequent extinction of CNO burning (Lattanzio & Karakas 2001). During the
AGB evolution these stars suffer a strong mass loss, which ultimately
peels off all the envelope mass, leaving a carbon-oxygen compact remnant
which evolves as a white dwarf.
The base of the external convective zone of the most massive IMS may become so
hot (
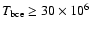 K) so as to favor an intense nucleosynthesis
(hot bottom burning, HBB), whose results can be directly seen at the surface of
the star due to the rapidity of convective motion (e.g. Ventura et al. 2002).
K) so as to favor an intense nucleosynthesis
(hot bottom burning, HBB), whose results can be directly seen at the surface of
the star due to the rapidity of convective motion (e.g. Ventura et al. 2002).
The ejecta of these stars might thus pollute the surrounding medium with
material which was at least partially nuclearly processed: this is the reason
why this class of objects has been invoked as a possible explanation for the
chemical anomalies observed at the surface of giants and turn-off
globular clusters stars (see e.g. Gratton et al. 2004), in what is commonly
known as the self-enrichment scenario. An early generation of IMS evolved within the first  100-200 Myr of the cluster life,
contaminated the interstellar-medium with gas which would be already
nuclearly processed; this gas might have favored the formation of a later
generation of stars, which would then show the observed chemical anomalies
(Cottrell & Da Costa 1981; D'Antona et al. 1983; Ventura et al. 2001, 2002).
100-200 Myr of the cluster life,
contaminated the interstellar-medium with gas which would be already
nuclearly processed; this gas might have favored the formation of a later
generation of stars, which would then show the observed chemical anomalies
(Cottrell & Da Costa 1981; D'Antona et al. 1983; Ventura et al. 2001, 2002).
While there is a general agreement that the solution of
this problem may be looked for in early AGB pollution,
(Gratton et al. 2004), the quantitative agreement between
the models and the abundance patterns shown by GC stars
is not good (Denissenkov & Herwig 2003;
Denissenkov & Weiss 2004).
On the other hand, the AGB evolution of these stars is
found to be strongly dependent on the convective model
which is used to find out the temperature gradient within
the external convective zone (Renzini & Voli 1981;
Blöcker & Schonberner 1991; Sackmann & Boothroyd 1991;
D'Antona & Mazzitelli 1996; Ventura & D'Antona 2005,
hereinafter Paper I).
The chemical content of their ejecta, in particular
for some key-elements that are anticorrelated
like oxygen and sodium and magnesium and aluminum,
is strongly dependent
not only on convection, but also on the assumed mass
loss rate and on the nuclear reaction rates.
At the moment these uncertainties seriously undermine
the predictive power of AGB models, and thus limit the
predictions that can be made concerning their role
within the framework of the self-enrichment scenario.
We investigate the AGB evolution of initial
masses 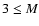 /
/
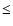 6.5, and
focus our attention on their main physical
properties, and on the chemical content of
their ejecta. In Paper I we explored the
dependence of the results
on the convective model. In this work we complete
the exploration by investigating the sensitivity of
the results on: 1) the
nuclear cross sections: we compare two sets
of models calculated by assuming the Angulo et al.
(1999) NACRE cross sections and those by Caughlan
& Fowler (1988, hereinafter CF88); 2) the mass loss
rate.
6.5, and
focus our attention on their main physical
properties, and on the chemical content of
their ejecta. In Paper I we explored the
dependence of the results
on the convective model. In this work we complete
the exploration by investigating the sensitivity of
the results on: 1) the
nuclear cross sections: we compare two sets
of models calculated by assuming the Angulo et al.
(1999) NACRE cross sections and those by Caughlan
& Fowler (1988, hereinafter CF88); 2) the mass loss
rate.
The stellar evolutions discussed
in this paper were calculated by
the code ATON2.1, a full description of which can be found in
Ventura et al. (1998) (ATON2.0 version).
The latest updates of the code, concerning the nuclear network,
are given in Paper I.
The interested reader may find in these
papers a detailed description
of the numerical structure of the code, and
of the macro and micro-physics
used to simulate the stellar evolutions.
The code allows us to calculate the temperature gradient
within instability regions either by adopting the
traditional MLT (Vitense 1953; Böhm-Vitense 1958),
or the FST model (Canuto & Mazzitelli 1991;
Canuto et al. 1996) for turbulent convection.
The interested reader may find in
Canuto & Mazzitelli (1991) a detailed
description of the physical differences between
the two models.
As we shall see, during the AGB evolution a non negligible
fraction of the global nuclear release is generated within
the convective envelope, therefore it is mandatory
to adopt a diffusive approach, treating simultaneously
mixing and nuclear burning.
We therefore solve for each element the diffusion equation
(Cloutman & Eoll 1976):
![\begin{displaymath}\left( {{\rm d}X_i\over {\rm d}t} \right)=\left( {\partial X_...
... r^2 \rho)^2 D {\partial X_i
\over \partial m_{\rm r}}\right]
\end{displaymath}](/articles/aa/full/2005/33/aa2396-04/img22.gif) |
(1) |
stating mass conservation of element i. The diffusion
coefficient D is taken as
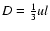 ,
where u is the convective velocity and l is
the convective scale length.
We allow velocity to decay exponentially starting from the
formal convective boundaries as:
,
where u is the convective velocity and l is
the convective scale length.
We allow velocity to decay exponentially starting from the
formal convective boundaries as:
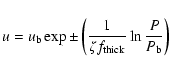 |
(2) |
where 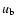 and
and 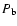 are, respectively, turbulent
velocity and pressure at the convective boundary, P is the local pressure,
are, respectively, turbulent
velocity and pressure at the convective boundary, P is the local pressure, 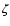 a free parameter
connected with the e-folding distance of the decay,
and
a free parameter
connected with the e-folding distance of the decay,
and
 is the thickness of the convective
regions in fractions of
is the thickness of the convective
regions in fractions of 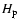 .
.
A detailed description of the treatment of convective velocities in the
proximity of the formal borders of the convective zones (fixed by the
Schwarzschild criteria) can be found in Sect. 2.2 of Ventura et al. (1998).
In the same paper (Sect. 4.2) there is also an
extensive discussion on the extra mixing determined by the use of a
non-zero 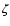 .
.
The models presented in this paper adopt the FST convection,
and the parameter 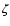 is fixed at
is fixed at
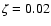 .
No extra-mixing has been assumed from the
base of the convective envelope: therefore
the extension of the various dredge-up episodes,
and the consequent changes of the surface
chemical composition, must be considered
as lower limits.
.
No extra-mixing has been assumed from the
base of the convective envelope: therefore
the extension of the various dredge-up episodes,
and the consequent changes of the surface
chemical composition, must be considered
as lower limits.
The nuclear network includes 30 chemical
species up to 31P and 64 nuclear reactions.
The list of all the reactions included in the
nuclear network can be found in Paper I.
The relevant cross-sections are taken either from
Caughlan & Fowler (1988, CF88) or from Angulo et al.
(1999, NACRE). In the range of
temperatures of interest here (
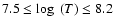 ,
which are
the typical values at the base of
the external convective zone of massive AGBs)
the largest differences between the two sets of
cross-sections are the following:
,
which are
the typical values at the base of
the external convective zone of massive AGBs)
the largest differences between the two sets of
cross-sections are the following:
The mass loss rate is calculated according to Blöcker (1995),
who modifies the Reimer's formula in order to simulate the
strong mass loss suffered by these stars as they climb
along the AGB. The complete expression is:
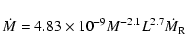 |
(3) |
where
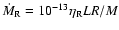 is the canonical Reimer's
rate, and
is the canonical Reimer's
rate, and
 is a free parameter directly connected to
the mass loss rate.
is a free parameter directly connected to
the mass loss rate.
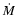 was described according to Eq. (3),
with the parameter
was described according to Eq. (3),
with the parameter
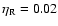 for the "standard''
case; we then consider evolutions with
for the "standard''
case; we then consider evolutions with
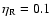 and
and
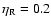 .
In all cases mass loss was applied
for all the evolutionary phases.
.
In all cases mass loss was applied
for all the evolutionary phases.
We evolved models with initial masses
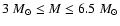 starting from the pre-main
sequence along the whole TP phase. Above the upper
mass limit, models ignite carbon
in the center, skipping the AGB phase. Below the
lower limit models do not achieve HBB conditions.
starting from the pre-main
sequence along the whole TP phase. Above the upper
mass limit, models ignite carbon
in the center, skipping the AGB phase. Below the
lower limit models do not achieve HBB conditions.
When the envelope mass becomes "small''
(
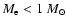 )
a much higher temporal resolution
is required, which renders the computations extremely
time-consuming; since the chemical yields are almost
unaffected by the following phases, we decided to stop
the evolution when the mass of the envelope falls below
)
a much higher temporal resolution
is required, which renders the computations extremely
time-consuming; since the chemical yields are almost
unaffected by the following phases, we decided to stop
the evolution when the mass of the envelope falls below 
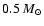 .
.
We adopted an initial metallicity, Z,
typical of those globular clusters (GCs) like NGC 6752,
M 3, M 13, whose stars show the largest chemical
anomalies, i.e. Z=0.001 and Y=0.24. For all
the elements included in our network, we adopted
solar-scaled initial abundances. This is to be taken into
account if we want to compare the results with observations,
as the starting initial mass fractions
of abundant elements play a role
in the determination of the final yield.
e.g., as [O/Fe
![$]\sim +0.3$](/articles/aa/full/2005/33/aa2396-04/img42.gif) in population II stars, this
initial abundance will be reflected in the evolution
with oxygen depletion. Numerical tests show
that the results for oxygen may be roughly scaled up by
the initial enhancement with respect to the solar scaled
value. For instance, if the solar scaled model produces a
yield with [O/Fe]=-0.5, the yield starting from initial
[O/Fe]=+0.3 would have been [O/Fe]=-0.2.
in population II stars, this
initial abundance will be reflected in the evolution
with oxygen depletion. Numerical tests show
that the results for oxygen may be roughly scaled up by
the initial enhancement with respect to the solar scaled
value. For instance, if the solar scaled model produces a
yield with [O/Fe]=-0.5, the yield starting from initial
[O/Fe]=+0.3 would have been [O/Fe]=-0.2.
Table 1 summarizes the main physical
properties of our models, related to the evolutionary
phases preliminary to the AGB evolution.
During the main sequence phase the models develop a central
convective region which progressively shrinks in mass,
with a maximum extension ranging from  0.72
0.72  for the 3
for the 3  model up to
model up to  2
2  for the 6.5
for the 6.5  model.
model.
The total duration of the H-burning phase (t(H)) is a decreasing
function of mass: the less massive model, with initial
mass M=3  ,
consumes central hydrogen in
,
consumes central hydrogen in  275 Myr, while the 6.5
275 Myr, while the 6.5  model keeps burning hydrogen
for 54 Myr (Fig. 1, top panel).
model keeps burning hydrogen
for 54 Myr (Fig. 1, top panel).
Table 1:
Physical properties of the NACRE models.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2396fg01.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg48.gif) |
Figure 1:
The duration of the phases of hydrogen and
helium burning as a function of the initial
mass for the NACRE intermediate mass models.
Top: H-burning time; middle:
He-burning time; bottom: ratio between
the He-burning and the H-burning times. |
| Open with DEXTER |
During the first dredge-up, following H-exhaustion, the
convective envelope reaches stellar layers which were
previously touched by CNO burning via the CN cycle, with
the conversion of some 12C to 14N:
consequently, the surface 14N is increased by
a factor of  2, while 12C decreases from
the initial value of X(12C
2, while 12C decreases from
the initial value of X(12C
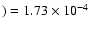 to X(12C
to X(12C
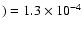 .
The lithium
surface abundance drops by a factor of
.
The lithium
surface abundance drops by a factor of  50,
because surface lithium is mixed within an
extended region where lithium was previously destroyed
via proton fusion; this drop is dependent
on the stellar mass, and a spread of a factor
of
50,
because surface lithium is mixed within an
extended region where lithium was previously destroyed
via proton fusion; this drop is dependent
on the stellar mass, and a spread of a factor
of  2 is found among the models.
2 is found among the models.
During the following phase of core helium burning
a convective core is formed, again with a dimension
increasing with mass: it is 
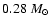 for
the
for
the
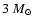 model, while it is
model, while it is 
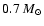 for the
for the
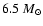 model (see the 5th column of
Table 1).
We see from Fig. 1 (bottom panel)
that the ratio between the He-burning (t(He))
and the MS times is decreasing with mass, ranging from
model (see the 5th column of
Table 1).
We see from Fig. 1 (bottom panel)
that the ratio between the He-burning (t(He))
and the MS times is decreasing with mass, ranging from 
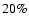 to slightly higher than
to slightly higher than 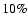 for the 6.5
for the 6.5  model. Once helium is burnt-out in
the stellar core,
model. Once helium is burnt-out in
the stellar core, 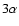 reactions carry on in an intermediate layer, triggering
a general expansion of the structure, which eventually
extinguishes the CNO burning shell. The general cooling
of the star favors the formation of a very deep and
extended external convective zone, in what is commonly
known as the second dredge-up episode.
reactions carry on in an intermediate layer, triggering
a general expansion of the structure, which eventually
extinguishes the CNO burning shell. The general cooling
of the star favors the formation of a very deep and
extended external convective zone, in what is commonly
known as the second dredge-up episode.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2396fg02.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg58.gif) |
Figure 2:
Top: the mass coordinate of the
innermost point reached by the base of the envelope
during the second dredge-up for the same models
discussed in Fig. 1. Bottom:
the penetration (in solar masses) of the base
of the external convective zone beyond the location
of the CNO burning shell during the second
dredge-up. |
| Open with DEXTER |
From the top panel of Fig. 2 we see that the mass coordinate
corresponding to the maximum penetration of the outer
envelope is slightly increasing with mass, with a
difference of  0.2
0.2  between the 3
and 6.5
between the 3
and 6.5  models. The most interesting quantity
is however shown in the bottom panel of the same
figure, where we report the variation as a function of
the initial mass of
models. The most interesting quantity
is however shown in the bottom panel of the same
figure, where we report the variation as a function of
the initial mass of
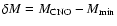 ,
where
,
where
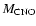 and
and
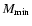 are, respectively, the location of
the CNO burning shell immediately before the second
dredge-up, and the minimum point (in mass) reached by the
base of the outer convective zone.
are, respectively, the location of
the CNO burning shell immediately before the second
dredge-up, and the minimum point (in mass) reached by the
base of the outer convective zone. 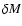 is therefore
a measure of the amount of processed material which is
carried to the surface during the second dredge-up.
We see that a poor mixing is expected in the 3
is therefore
a measure of the amount of processed material which is
carried to the surface during the second dredge-up.
We see that a poor mixing is expected in the 3  model, while in the 6.5
model, while in the 6.5  case
case 
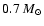 of CNO processed material is mixed with the surface layers.
During the second dredge-up the surface 14N is
increased by another factor of
of CNO processed material is mixed with the surface layers.
During the second dredge-up the surface 14N is
increased by another factor of  2, the carbon abundance
decreases to X(12C
2, the carbon abundance
decreases to X(12C
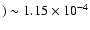 ,
while
lithium is not dramatically affected, because the surface
lithium abundance was already heavily lowered during the
first dredge-up. At the second dredge-up, the
helium, sodium and oxygen
abundances are changed (depending on the stellar mass),
as can be seen in the three panels of Fig. 3.
This can be understood on the basis of the following considerations:
,
while
lithium is not dramatically affected, because the surface
lithium abundance was already heavily lowered during the
first dredge-up. At the second dredge-up, the
helium, sodium and oxygen
abundances are changed (depending on the stellar mass),
as can be seen in the three panels of Fig. 3.
This can be understood on the basis of the following considerations:
- The amount of mixed material during the second
dredge-up sensibly increases with the stellar mass
(see Fig. 2).
- During the second dredge-up the base of the
outer envelope reaches layers which were previously
touched by full CNO burning, thus explaining the
oxygen reduction.
- The amount of material previously touched
by CNO burning and mixed to the surface is
larger than in the first dredge-up case, thus
the increase of the surface helium abundance
is very large, especially in the most massive
models.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2396fg03.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg64.gif) |
Figure 3:
The variation of the surface chemical abundances
of some elements following the 2nd dredge-up.
Top: helium mass fraction; middle:
variation of the 16O abundance, expressed
as the logarithm of ratio between the final
abundance and the initial mass fraction;
bottom: the same as the middle panel, but for 23Na. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg04.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg65.gif) |
Figure 4:
The maximum luminosity ( top) and temperature
at the base of the convective envelope ( bottom)
achieved by the standard NACRE models
during their AGB evolution. |
| Open with DEXTER |
Table 2:
Chemical content of the ejecta of the NACRE models.
For most of the AGB evolution the global nuclear energy
release is generated within a CNO burning shell, which
may also overlap, in some cases, with the external
convective zone. As hydrogen is consumed, the core mass
increases, and the CNO burning takes place at higher
temperatures, thus favoring an increase of the
stellar luminosity. This is halted by mass loss,
which progressively reduces the mass of the envelope,
and eventually leads to a general cooling of the
outer stellar layers. The base of the convective zone
becomes cooler and cooler in the latest evolutionary
stages; when the mass of the envelope drops below  1
1  the temperatures within the whole
external zone become so small to prevent any further
nucleosynthesis. For each model, we may therefore
find out maximum values of both luminosity and
the temperatures within the whole
external zone become so small to prevent any further
nucleosynthesis. For each model, we may therefore
find out maximum values of both luminosity and
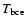 ,
which we report as a function of the initial
mass of the star in the two panels of Fig. 4.
We see that even the least massive of our models, i.e.
the 3
,
which we report as a function of the initial
mass of the star in the two panels of Fig. 4.
We see that even the least massive of our models, i.e.
the 3  model, achieves at the base of the
external convective zone temperatures so large
(
model, achieves at the base of the
external convective zone temperatures so large
(
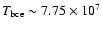 K) to trigger HBB.
K) to trigger HBB.
In all the models, shortly after the
beginning of the TPs phase, the TDU operates
following each TP, changing the
surface chemistry. The efficiency 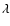 of
the TDU increases with the evolution, and is
higher in the less massive models. We find that
for
of
the TDU increases with the evolution, and is
higher in the less massive models. We find that
for
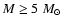 a maximum value of
a maximum value of
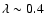 is attained in the latest
evolutionary stages, while a significantly
larger value of
is attained in the latest
evolutionary stages, while a significantly
larger value of
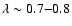 is
reached along the evolutions of the models
with masses
is
reached along the evolutions of the models
with masses
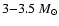 .
.
The chemical composition of the ejecta of our NACRE models, calculated over the lifetime of the star,
is summarized in Table 2. With
the only exception of lithium, for the other
elements we indicate the logarithm of the ratio
between the average chemical
abundance of the ejecta and the initial value.
Therefore, a value of 0 indicates that the chemical
content of the ejecta is the same as the initial
chemistry.
![\begin{figure}
{
\includegraphics[width=7.5cm,clip]{2396fg5a.eps}\hspace*{4mm}
\includegraphics[width=7.5cm,clip]{2396fg5b.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg77.gif) |
Figure 5:
Variation of the surface chemical abundances
of the CNO elements during the evolution of the
same models as in Fig. 1. For clarity reason,
for 12C we decided to show only the variation
at the surface of the models with initial masses 3, 4, 5 and 6  . . |
| Open with DEXTER |
In the three panels of Fig. 5 we show the variation
during the AGB evolution (including also the changes
due to the second dredge-up) of the surface abundances
of the CNO elements; we chose the stellar mass as abscissa
in order to have an idea of the average chemical content
of the ejecta of these stars.
We see (left-lower panel) that oxygen is depleted in
all cases apart from the 3  model,
the heaviest depletion being for the largest masses,
in agreement with the physical situation present at the
base of the external convective zone.
We note the apparently anomalous behavior
of the 6 and 6.5
model,
the heaviest depletion being for the largest masses,
in agreement with the physical situation present at the
base of the external convective zone.
We note the apparently anomalous behavior
of the 6 and 6.5  models, which have a flatter
declining profile of the surface oxygen with mass: this
can be understood on the basis of the fact that these
latter models are already extremely luminous during the
pre-AGB phase, so that a large fraction of the mass is lost
when the oxygen abundance is still close to the value
left behind by the second dredge-up.
models, which have a flatter
declining profile of the surface oxygen with mass: this
can be understood on the basis of the fact that these
latter models are already extremely luminous during the
pre-AGB phase, so that a large fraction of the mass is lost
when the oxygen abundance is still close to the value
left behind by the second dredge-up.
In the right panel we may follow the evolution of the
surface abundance of carbon: we note an early phase of
destruction in all models, which corresponds to the stage when
only the CN cycle is active, followed by a later increase,
when the full CNO cycle is activated; in the less massive
models we recognize the signature of an efficient third
dredge-up.
Even in this case we note the peculiar behavior
of the 3  model, in which the 3rd dredge-up
is highly efficient since the first TPs, so that the
surface 12C abundance increases up to
model, in which the 3rd dredge-up
is highly efficient since the first TPs, so that the
surface 12C abundance increases up to
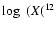 C)
C)
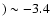 ;
only in a later time,
;
only in a later time,  200 000 yr after the beginning of the AGB phase, when
200 000 yr after the beginning of the AGB phase, when 
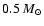 have been lost,
HBB occurs, and the 12C abundance starts to
decrease. The 3rd dredge-up after 10 TPs is so
efficient that also some 16O is carried outwards;
16O reaches a maximum abundance after 15 TPs
and then decreases approximately to the initial
value: this is the only model for which we find an
oxygen content of the ejected material that is
larger than the original composition (see the 6th column of Table 2 and the top panel of
Fig. 9).
The combination of the effects of HBB and of
the almost constant surface abundance of 16O prevents the formation of a carbon star.
From this discussion we argue that 3
have been lost,
HBB occurs, and the 12C abundance starts to
decrease. The 3rd dredge-up after 10 TPs is so
efficient that also some 16O is carried outwards;
16O reaches a maximum abundance after 15 TPs
and then decreases approximately to the initial
value: this is the only model for which we find an
oxygen content of the ejected material that is
larger than the original composition (see the 6th column of Table 2 and the top panel of
Fig. 9).
The combination of the effects of HBB and of
the almost constant surface abundance of 16O prevents the formation of a carbon star.
From this discussion we argue that 3  is
approximately the lower limit for models achieving HBB with the full CNO cycle operating during the AGB evolution. No 16O depletion can be achieved
in less massive models.
is
approximately the lower limit for models achieving HBB with the full CNO cycle operating during the AGB evolution. No 16O depletion can be achieved
in less massive models.
The carbon, nitrogen and oxygen abundance of the ejecta
are reported in Cols. 4-6 of Table 2.
We see that the carbon content of the expelled material
is always smaller than the initial value, due to the drop
of the surface carbon which follows the first and
especially the second dredge-up. The depletion factor
is lower the lower is the mass, because in the less
massive models more carbon is produced later in the
AGB evolution by the 3rd dredge-up. We note that even for
the 3  model, despite the early phase of
12C production at the beginning of the TPs phase
(see the right panel of Fig. 5), we find
a negative [12C], due to a later phase of
12C depletion at the base of the convective envelope
via proton fusion.
model, despite the early phase of
12C production at the beginning of the TPs phase
(see the right panel of Fig. 5), we find
a negative [12C], due to a later phase of
12C depletion at the base of the convective envelope
via proton fusion.
From Col. 5 of Table 2 we see that the
nitrogen abundance of the ejecta is always at least
a factor of  10 larger than the initial value.
Nitrogen is mixed to the surface through
the first and second dredge-up, then its
surface abundance increases due to HBB, via CN and ON cycling, and may further increase following each third
dredge-up episode, via the conversion of additional primary
12C mixed into the envelope.
Also in this case, the reason for the larger 14N abundances found in the ejecta of the less
massive models is the higher number of TPs
and the larger efficiency of 3rd dredge-up
episodes.
10 larger than the initial value.
Nitrogen is mixed to the surface through
the first and second dredge-up, then its
surface abundance increases due to HBB, via CN and ON cycling, and may further increase following each third
dredge-up episode, via the conversion of additional primary
12C mixed into the envelope.
Also in this case, the reason for the larger 14N abundances found in the ejecta of the less
massive models is the higher number of TPs
and the larger efficiency of 3rd dredge-up
episodes.
As for oxygen, with the only exception of the
3  model we find, in agreement with what
is shown in the left-lower panel of Fig. 5,
[16O]<0 in all cases (see also the top
panel of Fig. 9). We note that the minimum
value of [16O], i.e. [16O]=-0.61, is reached
for
model we find, in agreement with what
is shown in the left-lower panel of Fig. 5,
[16O]<0 in all cases (see also the top
panel of Fig. 9). We note that the minimum
value of [16O], i.e. [16O]=-0.61, is reached
for
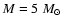 ,
because the yield of more massive
models is influenced by the very strong mass loss
already efficient at the 2nd dredge-up, when no HBB had started yet.
,
because the yield of more massive
models is influenced by the very strong mass loss
already efficient at the 2nd dredge-up, when no HBB had started yet.
The oxygen isotopes show a similar behavior in all
our models. The surface abundance of 17O is increased
during the second dredge-up by  0.2 dex; at the
very beginning of the AGB evolution 17O is produced
at the base of the external zone due to partial 16O burning, so that, particularly in the most
massive models, its abundance is increased by a factor
of
0.2 dex; at the
very beginning of the AGB evolution 17O is produced
at the base of the external zone due to partial 16O burning, so that, particularly in the most
massive models, its abundance is increased by a factor
of  10. Later on, when 16O burning is more
efficient, the surface 17O abundance reaches an
equilibrium value, and then decreases as the 16O.
The maximum surface 17O abundance is log [X(17O)
10. Later on, when 16O burning is more
efficient, the surface 17O abundance reaches an
equilibrium value, and then decreases as the 16O.
The maximum surface 17O abundance is log [X(17O)
![$]
\sim -5.5$](/articles/aa/full/2005/33/aa2396-04/img81.gif) for the model with initial mass 6.5
for the model with initial mass 6.5  ,
while it is log [X(17O)
,
while it is log [X(17O)
![$] \sim -5.8$](/articles/aa/full/2005/33/aa2396-04/img82.gif) for the
3
for the
3  model.
The 18O abundance is dramatically decreased during the
second dredge-up, passing from log [X(18O)
model.
The 18O abundance is dramatically decreased during the
second dredge-up, passing from log [X(18O)![$] \sim -6$](/articles/aa/full/2005/33/aa2396-04/img83.gif) to log [X(18O)
to log [X(18O)
![$] \sim -10$](/articles/aa/full/2005/33/aa2396-04/img84.gif) .
At the beginning of the
TPs phase some 18O is produced
via proton capture by 17O,
so that its abundance rises up by 2 orders of magnitude
for the 6.5
.
At the beginning of the
TPs phase some 18O is produced
via proton capture by 17O,
so that its abundance rises up by 2 orders of magnitude
for the 6.5  model (and by one order of magnitude
in the 3.5
model (and by one order of magnitude
in the 3.5  model). Like 17O, a maximum
value is reached, after which the surface 18O abundance decreases as 16O is consumed within the
envelope.
model). Like 17O, a maximum
value is reached, after which the surface 18O abundance decreases as 16O is consumed within the
envelope.
An important outcome of most of our models is that
the global C+N+O abundance of the ejecta is constant
within a factor of  2. This can be seen in the
7th column of Table 2, where we report the
ratio between the global CNO abundance of the ejecta
and the initial value. With the only
exception of the 3
2. This can be seen in the
7th column of Table 2, where we report the
ratio between the global CNO abundance of the ejecta
and the initial value. With the only
exception of the 3  model, for which the
effects of the 3rd dredge-up overwhelm those of HBB,
the values of the ratio between the average (C+N+O)
abundance of the ejecta and the initial value
are always
model, for which the
effects of the 3rd dredge-up overwhelm those of HBB,
the values of the ratio between the average (C+N+O)
abundance of the ejecta and the initial value
are always 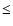 2, being close to 1 for
the most massive models.
2, being close to 1 for
the most massive models.
These results are at odds with recent computations
of AGB models of the same metallicity by Fenner et al.
(2004), where it was shown that:
- Only models more massive than 6
 achieve
surface oxygen depletion.
achieve
surface oxygen depletion.
- The material expelled by AGBs is for all the
computed masses both carbon and nitrogen rich.
- The C+N+O strongly increases with respect to
the initial value.
These findings led the authors to conclude that massive AGBs
hardly played a relevant role in the pollution of
the interstellar medium of GCs, since spectroscopic analysis
of NGC 6752 stars found an anti correlation between [C/Fe] and
[N/Fe] independent of the luminosity (Grundahl et al. 2002);
besides, the C+N+O sum is approximately constant in many CGs
(Ivans et al. 1999).
The different convective model adopted is the reason for the
difference between our results and those obtained by Fenner
et al. (2004) (see the
detailed discussion in Paper I), the FST model
leading much more easily to efficient HBB which, in turn,
triggers larger luminosities, shorter AGB life-times, and a
smaller number of 3rd dredge-up episodes.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2396fg06.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg85.gif) |
Figure 6:
The variation of the surface sodium abundance
for the standard NACRE models. |
| Open with DEXTER |
Figure 6 shows the behavior of surface
sodium. In all cases we see an increase due to the
second dredge-up, followed by an early phase of sodium
production due to 22Ne burning during the first
TPs. Later on, when the whole Ne-Na cycle is active,
the sodium abundance declines. For
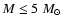 the third dredge-up favors a
later phase of sodium production, via proton capture
by 22Ne mixed into the envelope.
The 22Ne itself is a result of two
the third dredge-up favors a
later phase of sodium production, via proton capture
by 22Ne mixed into the envelope.
The 22Ne itself is a result of two 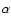 captures on the 14N mixed into the
helium intershell at each third dredge up episode.
captures on the 14N mixed into the
helium intershell at each third dredge up episode.
Particularly in the models with masses 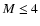
 a considerable amount of sodium is produced.
In the 3
a considerable amount of sodium is produced.
In the 3  model, following each TP,
sodium is produced by 22Ne burning; during the
quiescent CNO burning phases the bottom of the envelope
is hot enough to activate the Ne-Na chain, but not
to allow the Ne-Na reactions to act as a cycle (Arnould
et al. 1999), which favors large production of sodium.
model, following each TP,
sodium is produced by 22Ne burning; during the
quiescent CNO burning phases the bottom of the envelope
is hot enough to activate the Ne-Na chain, but not
to allow the Ne-Na reactions to act as a cycle (Arnould
et al. 1999), which favors large production of sodium.
The bottom panel of Fig. 9 shows
the average sodium abundance of the ejected material,
as a function of the stellar initial mass. Sodium
is produced within the less massive models due to the
third dredge-up and to the modest sodium burning, but
is destroyed within the massive models, so that
the sodium content of the ejecta of these latter
is under abundant with respect to the initial value.
We see that only the models with initial
masses clustering around 4  are able to
expell material that is both sodium rich and
oxygen poor, and so only the abundances in
these ejecta would be in agreement with the
oxygen-sodium anti correlation observed within GCs stars
(Gratton et al. 2001; Sneden et al. 2004).
are able to
expell material that is both sodium rich and
oxygen poor, and so only the abundances in
these ejecta would be in agreement with the
oxygen-sodium anti correlation observed within GCs stars
(Gratton et al. 2001; Sneden et al. 2004).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2396fg07.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg88.gif) |
Figure 7:
Observed data which define the anticorrelation sodium vs. oxygen in the stars of several GCs. Stars: M 13, open squares: M 3 (both from Sneden et al. 2004);
full squares: NGC 6752 from Grundahl et al. (2002); full triangles: M 4 and open
triangles: M 5 (both from Ivans et al. 1999); full dots: NGC 2808 from
Carretta et al. (2003). Models by Fenner et al. (2004) of 3.5, 5 and 6.5  ,
and models of this paper are also shown. The standard models
with ,
and models of this paper are also shown. The standard models
with 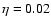 (left line, points labelled by the mass
value) and the models with
(left line, points labelled by the mass
value) and the models with 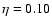 have been shifted by 0.3 dex in [O/Fe] to be compared with the observations.
Equal masses are joined.
have been shifted by 0.3 dex in [O/Fe] to be compared with the observations.
Equal masses are joined. |
| Open with DEXTER |
Also in regard to sodium, we note the different
predictions of our models compared to those by
Fenner et al. (2004), who expect extremely high
sodium production for all the masses considered here.
(see their Figs. 1 and 7). Within their models the
sodium produced is primary, and is produced via
22Ne burning, this latter being dredged-up
from the inner helium layers.
In principle, this mechanism could work also in our
models (see Fig. 6), but sodium
production is made much less efficient due to:
i) the smaller number of 3rd dredge-up episodes;
ii) the larger temperatures, which favor sodium
destruction.
We therefore see that again the treatment of
convection is the main reason for the differences
found in terms of the sodium content of the ejecta
of AGBs. It is interesting to note that, in terms
of the self-enrichment scenario, we have the opposite
problem compared to the Fenner et al. (2004) models:
they produce too much sodium, in great excess with
the increase observed in some GCs stars (that is
at most of  0.5 dex), while in our case, for
the most massive models, we destroy it, as also
predicted by Denissenkov & Weiss (2004).
0.5 dex), while in our case, for
the most massive models, we destroy it, as also
predicted by Denissenkov & Weiss (2004).
Figure 7 compares our results with
those by Fenner et al. (2004) in the plane of oxygen
versus sodium abundances, in which we have
reported several sets of observational data.
Our results should be shifted by +0.3 dex in oxygen to
be properly compared with the observations. We see
that both sets are unable to reproduce the data.
![\begin{figure}
\par {\includegraphics[width=4.7cm,clip]{2396fg8a.eps}\hspace*{4m...
...}\hspace*{4mm}
\includegraphics[width=4.7cm,clip]{2396fg8c.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg89.gif) |
Figure 8:
The variation of the magnesium and aluminum isotopes
for the standard NACRE models of 3.5, 4 and 5  . . |
| Open with DEXTER |
Figure 8 shows the variation of the magnesium and aluminum
isotopes along the standard evolutions of 3.5, 4 and 5  .
As the rate of
proton capture on this isotope increases with temperature at the bottom of
the convective envelope, 24Mg is more depleted for larger masses.
Masses M>5
.
As the rate of
proton capture on this isotope increases with temperature at the bottom of
the convective envelope, 24Mg is more depleted for larger masses.
Masses M>5  have qualitatively the same behavior, with more efficient 24Mg destruction. The heaviest destruction is found within the 6.5
have qualitatively the same behavior, with more efficient 24Mg destruction. The heaviest destruction is found within the 6.5  model, in which the surface final abundance is lower with respect to the
initial value by a factor of
model, in which the surface final abundance is lower with respect to the
initial value by a factor of  500. We see from Table 2 that the
24Mg abundance of the ejecta is lower the larger the initial mass,
reaching a minimum value of [24Mg
500. We see from Table 2 that the
24Mg abundance of the ejecta is lower the larger the initial mass,
reaching a minimum value of [24Mg
![$] \sim -1.3$](/articles/aa/full/2005/33/aa2396-04/img90.gif) for the 6.5
for the 6.5  model. The abundance of 25Mg, on the contrary, in a first stage
increases due to the 24Mg proton capture during the first TPs, and later
on its abundance decreases (e.g. in the 5
model. The abundance of 25Mg, on the contrary, in a first stage
increases due to the 24Mg proton capture during the first TPs, and later
on its abundance decreases (e.g. in the 5  )
due to burning to 26Al.
The 26Al however decays into 26Mg only on a timescale of
)
due to burning to 26Al.
The 26Al however decays into 26Mg only on a timescale of
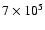 yr, and so this element is a bottleneck for further proton capture on 26Mg, which leads to 27Al. A direct path to 25Mg and 26Mg
is through the third dredge up, as these isotopes are synthesized in the helium
shell via capture of
yr, and so this element is a bottleneck for further proton capture on 26Mg, which leads to 27Al. A direct path to 25Mg and 26Mg
is through the third dredge up, as these isotopes are synthesized in the helium
shell via capture of 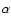 on 22Ne, and release respectively a neutron
or a gamma ray. This production mechanism is evident in Fig. 8 for 26Mg, while it is also clear (especially in the left figure, relative to
the 3.5
on 22Ne, and release respectively a neutron
or a gamma ray. This production mechanism is evident in Fig. 8 for 26Mg, while it is also clear (especially in the left figure, relative to
the 3.5  evolution) that the production of 25Mg is due to two
mechanisms, dredge up and proton capture on 24Mg. As we do not have a
large number of thermal pulses, the 27Al abundance can not rise by the
huge factor (close to 10) shown by Globular Cluster stars (see Grundhal et al.
2002, for the giants of the cluster NGC 6752). Further, the ratios between the
magnesium isotopes are not consistent with the results by Yong et al. (2003),
which indicate that 25Mg remains at 10% of the 24Mg abundance, and
26Mg reaches at most
evolution) that the production of 25Mg is due to two
mechanisms, dredge up and proton capture on 24Mg. As we do not have a
large number of thermal pulses, the 27Al abundance can not rise by the
huge factor (close to 10) shown by Globular Cluster stars (see Grundhal et al.
2002, for the giants of the cluster NGC 6752). Further, the ratios between the
magnesium isotopes are not consistent with the results by Yong et al. (2003),
which indicate that 25Mg remains at 10% of the 24Mg abundance, and
26Mg reaches at most  50%. The observational result both implies a
not dramatic burning of 24Mg, and a mild, if any, increase in 25Mg and 26Mg. Notice that, in addition, we have to count into the 26Mg abundance also the abundance of the unstable isotope 26Al, and the result
is at variance with observations.
50%. The observational result both implies a
not dramatic burning of 24Mg, and a mild, if any, increase in 25Mg and 26Mg. Notice that, in addition, we have to count into the 26Mg abundance also the abundance of the unstable isotope 26Al, and the result
is at variance with observations.
In spite of the not good agreement of these abundances with the observation, at
least the trend of our models is in the right direction, as the ratios 25Mg/24Mg and 26Mg/24Mg do not exceed  3 for masses
up to 5
3 for masses
up to 5  .
The corresponding models by Fenner et al. (2004), in which the
smaller efficiency of convection allows a longer evolutionary phase and many
episodes of third dredge up provide ratios larger than 100. Notice also that
for elements whose abundances are very small, also the initial abundances and
the exact modeling of the thermal pulses may influence strongly the results.
The central part of Fig. 8 in fact shows that the evolution of
the 4
.
The corresponding models by Fenner et al. (2004), in which the
smaller efficiency of convection allows a longer evolutionary phase and many
episodes of third dredge up provide ratios larger than 100. Notice also that
for elements whose abundances are very small, also the initial abundances and
the exact modeling of the thermal pulses may influence strongly the results.
The central part of Fig. 8 in fact shows that the evolution of
the 4  suffers an anomalous episode of third dredge up, which we are
uncertain whether to attribute to numerics or to a real effect. This lonely
episode changes the surface abundances of sodium and magnesium in such a way
that the resulting yields of the elements having low abundances are affected,
although the most abundant yields (e.g. CNO) are not. This requires an
additional detailed study before we can reject or accept these results as
conclusive for the problem of abundance variations in GCs.
suffers an anomalous episode of third dredge up, which we are
uncertain whether to attribute to numerics or to a real effect. This lonely
episode changes the surface abundances of sodium and magnesium in such a way
that the resulting yields of the elements having low abundances are affected,
although the most abundant yields (e.g. CNO) are not. This requires an
additional detailed study before we can reject or accept these results as
conclusive for the problem of abundance variations in GCs.
We conclude this general description with lithium, which
is created during the first TPs via the Cameron & Fowler
(1971) mechanism, and then destroyed as soon as 3He is extinguished in the envelope.
We see from the 3rd column of Table 2 that
the lithium content of the ejecta first decreases
with increasing mass. In fact, the larger
the mass, the hotter the base of the convective envelope, the more
rapidly 3He is destroyed, the shorter the
phase during which the star shows up as lithium-rich;
for models more massive than 5  ,
as
already discussed for the oxygen content of the ejecta,
we have that the mass loss is so strong during the
first TPs that a considerable fraction of the mass
is lost when lithium has been produced and not yet
destroyed. The differences among the lithium
abundances of the various models is however within
a factor of
,
as
already discussed for the oxygen content of the ejecta,
we have that the mass loss is so strong during the
first TPs that a considerable fraction of the mass
is lost when lithium has been produced and not yet
destroyed. The differences among the lithium
abundances of the various models is however within
a factor of  2, and is about a factor 2
smaller than the average
abundance which is observed in population II stars.
2, and is about a factor 2
smaller than the average
abundance which is observed in population II stars.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg09.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg92.gif) |
Figure 9:
The average chemical content of the ejecta
of the standard NACRE models as a function
of the initial mass. Top: oxygen
abundance; bottom: sodium abundance. |
| Open with DEXTER |
In examining the overall chemical content of the ejecta
of our models, there are four common features, which
hold independently of mass:
- 1.
-
The lithium content is within a factor 2
of the value observed in population II stars.
- 2.
- The ejecta are helium rich: particularly
models with initial mass
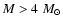 during the second dredge-up reach surface
helium mass fractions of
during the second dredge-up reach surface
helium mass fractions of
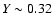 .
Helium
is also produced during the AGB phase during any
interpulse phase, but the consequent overall
increase of Y is limited in all cases to
.
Helium
is also produced during the AGB phase during any
interpulse phase, but the consequent overall
increase of Y is limited in all cases to
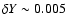 .
.
- 3.
- When compared with the initial abundances, we see that the material lost
during the evolutions is enhanced in 14N by at least a factor of
 10
and depleted in 12C by a factor of
10
and depleted in 12C by a factor of  4. This trend is consistent
with the observations, indicating CN cycled composition and no carbon
enhancement (Cohen et al. 2002; Cohen & Melendez 2004). However, the
anticorrelation between carbon and nitrogen is not found in the yields
as a function of the initial mass (see Table 2).
4. This trend is consistent
with the observations, indicating CN cycled composition and no carbon
enhancement (Cohen et al. 2002; Cohen & Melendez 2004). However, the
anticorrelation between carbon and nitrogen is not found in the yields
as a function of the initial mass (see Table 2).
- 4.
- The (C+N+O) abundance is constant within a
factor of
 2, due to the small number of
3rd dredge-up episodes.
2, due to the small number of
3rd dredge-up episodes.
For the other elements, the stellar yields depend
sensibly on the stellar mass, both quantitatively and
qualitatively.
The more massive models pollute the interstellar
medium with material that is oxygen and (partially)
sodium depleted. 24Mg is heavily depleted
(a factor of  10 with respect to the initial
value), so that high magnesium isotopic ratios
(larger than solar) are expected.
10 with respect to the initial
value), so that high magnesium isotopic ratios
(larger than solar) are expected.
Conversely, within models less massive than 
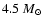 ,
the temperature at the base of the
external zone is such that the Ne-Na cycle is only
partially activated, and only in the last AGB phases; consequently, the ejecta of these stars
are sodium rich and oxygen poor. The 24Mg depletion is negligible due to the low temperatures,
therefore the magnesium isotopic ratios are reduced,
although not at the level that would provide
agreement with the relevant observations by
Yong et al. (2003). Further, the magnesium - aluminum
anti correlation
(see e.g. Grundahl et al. 2002) is not
fully reproduced, as the 27Al production is not
very efficient.
,
the temperature at the base of the
external zone is such that the Ne-Na cycle is only
partially activated, and only in the last AGB phases; consequently, the ejecta of these stars
are sodium rich and oxygen poor. The 24Mg depletion is negligible due to the low temperatures,
therefore the magnesium isotopic ratios are reduced,
although not at the level that would provide
agreement with the relevant observations by
Yong et al. (2003). Further, the magnesium - aluminum
anti correlation
(see e.g. Grundahl et al. 2002) is not
fully reproduced, as the 27Al production is not
very efficient.
The nuclear cross-sections play a delicate role in
determining the main physical and chemical properties
of the AGB evolutions.
From a physical point of view, a variation of the
cross-sections of the nuclear reactions mostly
contributing to the global energy
release might influence the thermal stratification
of the star; from a chemical
point of view, a change in the cross-sections of
those reactions involving key elements like sodium or
magnesium, though energetically not relevant,
might alter the equilibrium abundances, hence
the average chemical content of the ejecta.
We explore the uncertainty of
the results connected with the cross-sections of the
various reactions included within our network by
performing a detailed comparison
between the results presented in the previous section
and those obtained with the CF88 release, which are
still widely used in modern AGB computations.
This was made also to have an idea of
the degree of uncertainty of the results
connected with the cross-sections of the
various reactions included within our network.
We calculated a new set of models with the same
physical and chemical inputs of the NACRE models,
but adopting the CF88 rates for the nuclear
cross-sections.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg10.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg97.gif) |
Figure 10:
The comparison between the time-scale
for helium burning ( top) and the
ratio between the time-scales for helium
and for hydrogen burning ( bottom)
for the NACRE (solid) and CF88 (dotted)
models of intermediate mass. |
| Open with DEXTER |
We did not find any appreciable difference during the
MS evolution for the whole range of masses involved,
as the cross-sections of the relevant reactions
are the same for both sets of models. For each value
of the initial mass, we could verify that the duration
of the H-burning phase, the innermost
point reached during the first dredge-up and
the consequent changes in the surface chemistry
are unchanged.
The first differences between the models
appear in the duration of the helium burning phase,
as can be seen in Fig. 10.
Also the ratio between the times of helium
and hydrogen burning are consequently affected.
The reason for this difference is the rate of the reaction
12C +
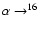 O, which
is larger by a factor of
O, which
is larger by a factor of  1.7in the NACRE case. This leads to slightly
longer time-scales for helium burning (see
the discussion in Imbriani et al. 2001; and Ventura & Castellani 2005).
1.7in the NACRE case. This leads to slightly
longer time-scales for helium burning (see
the discussion in Imbriani et al. 2001; and Ventura & Castellani 2005).
The AGB evolution of the models is physically
very similar, because the global nuclear energy
release during the quiescent phase of CNO burning
(which, we recall, is for most of the time the
only nuclear source active within the star) is
dominated by the proton captures by 12C,
13C and 14N nuclei, whose corresponding
cross-sections are similar in the two cases.
We could verify that the duration of the whole
AGB phase for the two sets of models, as well as
the temporal evolution of the most relevant
physical quantities, are essentially the same.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg11.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg99.gif) |
Figure 11:
The average chemical content of the
ejecta of the NACRE (solid) and CF88
(dotted) models of intermediate mass in
terms of lithium, carbon, nitrogen and
oxygen abundances. |
| Open with DEXTER |
In the four panels of Fig. 11
we show the average chemical content of the
ejecta, in terms of lithium and CNO abundances.
We see that the lithium content is extremely
similar for the two sets of models,
while the 12C, 14N and 16O abundances are lower in the CF88 models,
when compared to NACRE.
This difference is due to the cross-sections
of the reactions of proton capture by 17O atoms, which, as already discussed in Sect. 2,
are much lower in the CF88 case.
The three left-panels of Fig. 12 show,
respectively, the variation with temperature of
the ratio (CF88/NACRE) between the rates of the
reactions 17O(p,
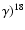 F (top panel),
17O(p,
F (top panel),
17O(p,
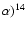 N (middle panel),
and of the ratio
N (middle panel),
and of the ratio
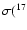 O(p,
O(p,
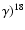 F)/
F)/
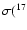 O(p,
O(p,
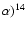 N)
in the two cases. We can see that in the range of temperatures
of interest here (
N)
in the two cases. We can see that in the range of temperatures
of interest here (
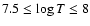 )
the reaction
17O(p,
)
the reaction
17O(p,
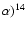 N is more efficient in the NACRE case
by a factor of a few hundred, while the difference for
the reaction 17O(p,
N is more efficient in the NACRE case
by a factor of a few hundred, while the difference for
the reaction 17O(p,
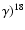 F is a factor
of
F is a factor
of  5. In the third panel, more importantly, we can see
that the favorite channel of 17O destruction switches
from 17O(p,
5. In the third panel, more importantly, we can see
that the favorite channel of 17O destruction switches
from 17O(p,
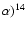 N to 17O(p,
N to 17O(p,
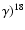 F passing from the NACRE to the CF88 cross-sections.
F passing from the NACRE to the CF88 cross-sections.
![\begin{figure}
{
\includegraphics[width=7cm,clip]{2396f12a.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{2396f12b.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg101.gif) |
Figure 12:
Left: variation with temperature of the
logarithm of the ratio between the CF88 and the NACRE
cross section of the reaction 17O(p,
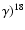 F
( top), 17O(p, F
( top), 17O(p,
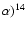 N
( middle) and of the
ratio N
( middle) and of the
ratio
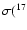 O(p, O(p,
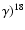 F)/ F)/
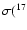 O(p, O(p,
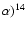 N) ( bottom).
Right: the same as the left panel, but for
reactions 23Na(p, N) ( bottom).
Right: the same as the left panel, but for
reactions 23Na(p,
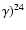 Mg and 23Na(p, Mg and 23Na(p,
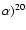 Ne. Ne. |
| Open with DEXTER |
This, in turn, has two important consequences:
- In the CF88 models we have a much larger
production of the heaviest oxygen isotopes.
- In the NACRE case, the equilibrium abundance
of 17O is much lower, and the nucleosynthesis
favors a return to 14N rather than a production
of 18F: this explains the differences between
the CNO abundances of the ejecta of the two sets of models
which can be seen in Fig. 11.
Turning to heavier elements, we show in the
four panels of Fig. 13
the abundances of 23Na
and 24Mg of the ejecta of the different models,
and the ratio of the magnesium isotopes,
25Mg/24Mg and 26Mg/24Mg. We note
from the left-upper panel of Fig. 13 that sodium
production can be achieved efficiently in the NACRE
case, while it is not present in the CF88 models.
This can be explained very simply on the basis
of the cross-section of the reaction 22Ne(p,
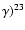 Na, which, in the range
of temperatures relevant in this case, is lower
in the CF88 case by at least a factor of
Na, which, in the range
of temperatures relevant in this case, is lower
in the CF88 case by at least a factor of  100,
reaching a maximum difference of a factor
of
100,
reaching a maximum difference of a factor
of  2000 for
2000 for
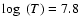 .
.
In the two panels of Fig. 14 we compare the variation
with mass of the 22Ne and 23Na surface
abundances within two models of initial mass 5  calculated with the NACRE and CF88 nuclear cross sections.
We see an early phase of sodium production and neon
destruction during the first thermal pulses in the
NACRE model, and a later increase of the sodium
abundance due the dredging-up of 22Ne, which
is later converted to 23Na. In the CF88 case the surface 22Ne never decreases,
and sodium is destroyed when the temperatures at the
base of the external zone become large enough to
efficiently activate the Ne-Na cycle.
calculated with the NACRE and CF88 nuclear cross sections.
We see an early phase of sodium production and neon
destruction during the first thermal pulses in the
NACRE model, and a later increase of the sodium
abundance due the dredging-up of 22Ne, which
is later converted to 23Na. In the CF88 case the surface 22Ne never decreases,
and sodium is destroyed when the temperatures at the
base of the external zone become large enough to
efficiently activate the Ne-Na cycle.
The top and middle right panels of Fig. 12
show the ratio of the cross-sections corresponding
to the two channels of sodium destruction
(23Na(p,
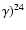 Mg and 23Na(p,
Mg and 23Na(p,
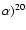 Ne) (always in terms of CF88/NACRE value) and the ratio
Ne) (always in terms of CF88/NACRE value) and the ratio
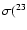 Na(p,
Na(p,
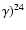 Mg)/
Mg)/
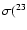 Na(p,
Na(p,
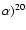 Ne)
in the two cases. In the NACRE case
sodium is destroyed more easily, and the favorite
channel is magnesium production in the relevant
range of temperatures; this determines a larger 24Mg equilibrium abundance, and explains the
difference between the models which can be seen
in the right-upper panel of Fig. 13.
Ne)
in the two cases. In the NACRE case
sodium is destroyed more easily, and the favorite
channel is magnesium production in the relevant
range of temperatures; this determines a larger 24Mg equilibrium abundance, and explains the
difference between the models which can be seen
in the right-upper panel of Fig. 13.
Turning to the magnesium isotopic ratios,
25Mg/24Mg is similar in the
two cases (see the left-lower
panel of Fig. 13), while 26Mg/24Mg
is lower in the CF88 models; the reason is that
the rate of the reaction 26Mg(p,
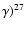 Al
is a factor of
Al
is a factor of  10 larger in the CF88 case, thus
favouring 26Mg destruction in favor of 27Al production.
10 larger in the CF88 case, thus
favouring 26Mg destruction in favor of 27Al production.
By comparing the AGB models calculated with
the two sets of cross-sections we conclude that the physical
behavior is essentially the same, because the rates
of the reactions mostly contributing to the global energy
release are barely changed. In terms of nucleosynthesis
(and therefore of the average chemical content of the
ejecta) we find important variations only for sodium and
the heavier isotopes of oxygen. The former is not produced
at all in the CF88 models (contrary to the NACRE case)
due to the extremely low cross-section of the 22Ne proton capture reaction; the equilibrium abundances of 17O and 18O are much lower in the NACRE case,
because of the larger values of both the 17O proton
capture reactions.
The effects of mass loss on the evolution of AGB stars
is well documented in the literature (Schönberner 1979):
mass loss halts the increase of luminosity,
and progressively peels off all the envelope,
eventually leaving a central remnant
which evolves as a white dwarf. It determines a
general cooling of the structure, therefore reducing
the intensity of HBB at the base of the external convective
zone. Since the effects of mass loss
become evident only when the mass of the envelope
is considerably reduced, models
with different mass loss rates will differ only in the
terminal part of their evolution, while the general
physical behavior during the first TPs is unchanged.
The NACRE and CF88 models presented in the previous sections
were calculated with the parameter
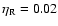 ,
in Blöcker's formula.
This choice is due to a previous calibration, made on
the basis of a detailed comparison
between the observed and the theoretical luminosity
function of lithium rich AGB stars in the Magellanic
Clouds (Ventura et al. 2000). For our models, a value of
,
in Blöcker's formula.
This choice is due to a previous calibration, made on
the basis of a detailed comparison
between the observed and the theoretical luminosity
function of lithium rich AGB stars in the Magellanic
Clouds (Ventura et al. 2000). For our models, a value of
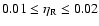 for stars with initial
mass in the range
for stars with initial
mass in the range 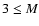 /
/
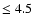 is able to
reproduce the observed trend of surface lithium vs.
luminosity which is observed in the Clouds.
is able to
reproduce the observed trend of surface lithium vs.
luminosity which is observed in the Clouds.
We cannot completely rule out the possibility that
the parameter
 to be used during the AGB evolution might show a dependency on the metallicity
(we recall that the models discussed
in this paper have a metallicity which is a factor of 10 lower than the LMC stars) and on the stellar mass,
or that the mass loss is heavily influenced by the
environment.
In order to test the level of uncertainty
connected to the mass loss, we decided to explore
the sensitivity of our results on changes in the
value of
to be used during the AGB evolution might show a dependency on the metallicity
(we recall that the models discussed
in this paper have a metallicity which is a factor of 10 lower than the LMC stars) and on the stellar mass,
or that the mass loss is heavily influenced by the
environment.
In order to test the level of uncertainty
connected to the mass loss, we decided to explore
the sensitivity of our results on changes in the
value of
 ,
and we discuss it for
for two representative examples of our stars.
,
and we discuss it for
for two representative examples of our stars.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg13.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg108.gif) |
Figure 13:
Average chemical content of the ejecta
of IMS models calculated with NACRE (solid)
and CF88 (dotted) sets of nuclear
cross-sections in terms of 23Na and 24Mg. The bottom panels show the
isotopic ratios of magnesium. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg14.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg109.gif) |
Figure 14:
The AGB evolution of the surface abundances
of 23Na ( top) and 22Ne ( bottom) of two models with initial
mass 5  calculated with the NACRE (solid) and CF88(dotted) nuclear cross-sections.
calculated with the NACRE (solid) and CF88(dotted) nuclear cross-sections. |
| Open with DEXTER |
We compare the standard model
of initial mass 5  already presented in
Sect. 3 (eta002 model) with two models of the
same initial mass, computed by assuming,
respectively,
already presented in
Sect. 3 (eta002 model) with two models of the
same initial mass, computed by assuming,
respectively,
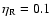 (eta010 model) and
(eta010 model) and
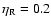 (eta020 model). Figure 15
shows the variation with time of the mass.
Times have been set to 0 at the beginning of the
AGB evolution. We see that the total duration of
the AGB phase is strongly dependent on
(eta020 model). Figure 15
shows the variation with time of the mass.
Times have been set to 0 at the beginning of the
AGB evolution. We see that the total duration of
the AGB phase is strongly dependent on
 ,
ranging from
,
ranging from
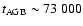 yr for the eta002 model down to
yr for the eta002 model down to  27 000 yr in the eta020 case.
The eta002 model reaches a maximum luminosity of
27 000 yr in the eta020 case.
The eta002 model reaches a maximum luminosity of
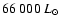 during the 20th interpulse period,
while the eta010 and eta020 models achieve a
maximum luminosity of, respectively,
during the 20th interpulse period,
while the eta010 and eta020 models achieve a
maximum luminosity of, respectively,
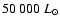 (13th interpulse period), and
(13th interpulse period), and
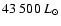 (10th interpulse period).
In conjunction with the maximum luminosity, all the models
also attain the largest temperature at the base of the
external envelope. The maximum
(10th interpulse period).
In conjunction with the maximum luminosity, all the models
also attain the largest temperature at the base of the
external envelope. The maximum
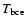 are:
are:
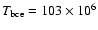 K (eta002),
K (eta002),
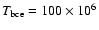 K (eta010) and
K (eta010) and
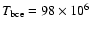 K (eta020). These values are
quite similar, especially when compared to the differences in the
maximum values of luminosity reached by the three models.
This is not surprising, as a main
feature of the FST convective model is that, within
the most massive AGBs, it leads to a very efficient
HBB already during the first TPs: even a strong
increase of mass loss cannot prevent the base
of the external zone from becoming extremely hot. On the
basis of these results, we may expect deep nucleosynthesis
to take place at the base of the external convective zone
even in the eta020 model.
K (eta020). These values are
quite similar, especially when compared to the differences in the
maximum values of luminosity reached by the three models.
This is not surprising, as a main
feature of the FST convective model is that, within
the most massive AGBs, it leads to a very efficient
HBB already during the first TPs: even a strong
increase of mass loss cannot prevent the base
of the external zone from becoming extremely hot. On the
basis of these results, we may expect deep nucleosynthesis
to take place at the base of the external convective zone
even in the eta020 model.
In the four panels of Fig. 16
we show the evolution of the
surface CNO abundances for the three models, plus the
variation of the total C+N+O abundance. For each of these
elements we show both the variation with time and with mass.
In the left-upper panel we show the variation of surface 12C. In the top of this panel we see that
the temporal evolution is very similar, with an early
phase of destruction at the beginning of the AGB evolution
followed by a later phase of production, when the temperatures
at the base of the external zone are sufficient to allow
the full CNO cycle to be activated, and the effects
of the 3rd dredge-up become more evident.
The only difference among the three models
is that the AGB evolution is halted earlier for larger
values of
 .
Since for
all the models the evolution stops when the carbon
abundance was increasing, this acts in favor of
a larger 12C content of the ejecta for lower
mass loss rates. In the lower part of this panel we see
the evolution of 12C with
the stellar mass. The
above effect is partly compensated by the fact that,
for larger
.
Since for
all the models the evolution stops when the carbon
abundance was increasing, this acts in favor of
a larger 12C content of the ejecta for lower
mass loss rates. In the lower part of this panel we see
the evolution of 12C with
the stellar mass. The
above effect is partly compensated by the fact that,
for larger
 ,
the star loses a not negligible
fraction of its mass when the carbon abundance was
still unchanged, even before the early phase of
destruction at the beginning of AGB. This is the reason
why the average 12C abundance of the ejecta of our
models show a maximum difference of
,
the star loses a not negligible
fraction of its mass when the carbon abundance was
still unchanged, even before the early phase of
destruction at the beginning of AGB. This is the reason
why the average 12C abundance of the ejecta of our
models show a maximum difference of  0.1 dex,
and is therefore consistent with the value
[12C]=-0.7 given in Sect. 3.
0.1 dex,
and is therefore consistent with the value
[12C]=-0.7 given in Sect. 3.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg15.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg118.gif) |
Figure 15:
Variation with time of the total mass
of three models of initial mass
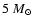 calculated with three different value of the
parameter for mass loss,
calculated with three different value of the
parameter for mass loss,
 .
Time
has been set to 0 at the beginning of the AGB evolution. .
Time
has been set to 0 at the beginning of the AGB evolution. |
| Open with DEXTER |
An analogous discussion can be made for nitrogen, as can
be seen in the right-upper panel of Fig. 16.
The surface 14N increases in all cases, because
nitrogen is created at the base of the external envelope
due to HBB and, in the final part of the evolution, also
due to the effects of the 3rd dredge-up. Again we note a strong
similarity in the temporal evolution, the only difference
being that in the large
 models the 14N content of the ejecta is expected to be lower because
the AGB evolution is halted earlier. In reality, at odds
with the 12C case, we expect a larger nitrogen
content of the ejecta of the eta002 model because
this latter case loses less mass at the very beginning of
the AGB evolution, when the 14N abundance was still
unchanged since the second dredge-up (see
the lower part of the right-upper panel
of Fig. 16).
The 14N average content of the ejecta is
therefore more dependent on mass loss, ranging
from [14N]=1.15 in the eta002 model, down to
[14N]=0.83 in the eta020 model; the eta010 model,
with [14N]=0.92, shows an intermediate behavior.
The global spread of the [14N] value varies
at most by a factor of
models the 14N content of the ejecta is expected to be lower because
the AGB evolution is halted earlier. In reality, at odds
with the 12C case, we expect a larger nitrogen
content of the ejecta of the eta002 model because
this latter case loses less mass at the very beginning of
the AGB evolution, when the 14N abundance was still
unchanged since the second dredge-up (see
the lower part of the right-upper panel
of Fig. 16).
The 14N average content of the ejecta is
therefore more dependent on mass loss, ranging
from [14N]=1.15 in the eta002 model, down to
[14N]=0.83 in the eta020 model; the eta010 model,
with [14N]=0.92, shows an intermediate behavior.
The global spread of the [14N] value varies
at most by a factor of  2 if
2 if
 varies
by one order of magnitude.
varies
by one order of magnitude.
![\begin{figure}
{
\includegraphics[width=5.5cm]{2396f16a.eps}\hspace*{4mm}
\inclu...
...c.eps}\hspace*{4mm}
\includegraphics[width=5.5cm]{2396f16d.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg119.gif) |
Figure 16:
Variation with time and total mass of the
CNO surface abundances of the same models
presented in Fig. 15. The
right-lower panel shows the total C+N+O
abundance. The abundances are given
in mass fraction. |
| Open with DEXTER |
As already pointed out, the temperatures at the base
of the convective zone are sufficiently high to
activate the full CNO cycle in all the models, so that
in all cases we have a certain amount of 16O depletion,
as can be seen in the left-lower panel of Fig. 16.
The trend of the 16O average content of the ejected
material for various
 is straightforward:
is straightforward:
- For larger values of
 a consistent part
of the envelope mass (
a consistent part
of the envelope mass (
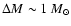 )
is
lost when the oxygen abundance is still unchanged.
)
is
lost when the oxygen abundance is still unchanged.
- Since the temperature at the base of the envelope
reached by the large
 models is lower,
in these cases 16O is destroyed less heavily,
and this leads to higher oxygen equilibrium abundances.
models is lower,
in these cases 16O is destroyed less heavily,
and this leads to higher oxygen equilibrium abundances.
We thus find that a strong oxygen destruction is
hardly found within the models with the largest
mass loss rates. The [16O] of the ejecta
is more dependent than [14N] on the
assumed
 :
we have [16O]=-0.6
for the eta002 model, [16O]=-0.3 in the
:
we have [16O]=-0.6
for the eta002 model, [16O]=-0.3 in the
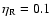 case, and [16O]=-0.15 for
case, and [16O]=-0.15 for
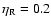 .
.
In the right-bottom panel of Fig. 16
we show the
total C+N+O abundance. In the eta010 and eta020 models the sum of the CNO abundances is constant,
because mass is lost so rapidly that the effects of the
3rd dredge-up are negligible. In the eta002 model,
during the last TPs, carbon is efficiently dredged-up,
and is later converted to 14N by HBB; however, the
total increase of the C+N+O is within  0.2 dex.
We may therefore conclude that within the FST framework
the most massive AGB models show surface C+N+O abundances
that are constant within a factor of
0.2 dex.
We may therefore conclude that within the FST framework
the most massive AGB models show surface C+N+O abundances
that are constant within a factor of  2,
independently of mass loss.
2,
independently of mass loss.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg17.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg121.gif) |
Figure 17:
AGB evolution of the surface abundances of 23Na ( top) and 22Ne ( bottom) of the
same models presented in Fig. 15. |
| Open with DEXTER |
Turning to heavier nuclei, we focus our attention
on sodium. Figure 17 shows the
variation of the surface sodium
abundance as a function of time (top panel) and
mass (bottom). An early phase of production, due to proton
capture by 22Ne nuclei, is followed by a phase
of sodium destruction when the temperatures at the
base of the outer convective zone become large
enough that sodium is destroyed by proton capture.
A larger mass loss rate acts in favor of larger
sodium yield because a large fraction of the stellar
mass is lost
when sodium is produced, and also because the evolution
is halted when the surface sodium has not yet
been completely destroyed (bottom panel).
Actually, sodium turns out to be the element
most sensitive to variations of the mass loss
rate. A larger
 changes completely
the situation, in the sense that now we expect
the mass expelled by massive AGBs to be sodium
rich (with respect to the initial mass fraction)
rather than sodium poor. [23Na] linearly increases with
changes completely
the situation, in the sense that now we expect
the mass expelled by massive AGBs to be sodium
rich (with respect to the initial mass fraction)
rather than sodium poor. [23Na] linearly increases with
 ,
while a
positive sodium yield is not possible at
,
while a
positive sodium yield is not possible at
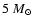 with the standard
with the standard
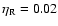 value. The oxygen
yield shows a similar
behavior, though in this case the convection is so
efficient that [16O] is negative in all
cases. A simultaneous sodium production and oxygen
depletion in the chemistry of the ejecta, in agreement
with the observed anti correlation, is possible
only for
value. The oxygen
yield shows a similar
behavior, though in this case the convection is so
efficient that [16O] is negative in all
cases. A simultaneous sodium production and oxygen
depletion in the chemistry of the ejecta, in agreement
with the observed anti correlation, is possible
only for
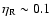 .
.
We find that 24Mg is depleted
in all cases, but the final abundance is a factor of  500 lower in the eta002 case, while it is just a
factor of 2 lower in the eta020 model. The 24Mg abundance of the ejecta is a factor of
500 lower in the eta002 case, while it is just a
factor of 2 lower in the eta020 model. The 24Mg abundance of the ejecta is a factor of  10lower than the initial value for the eta002 model,
while it is lower by only
10lower than the initial value for the eta002 model,
while it is lower by only  0.1 dex for
0.1 dex for
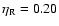 .
.
The average content of 25Mg is not strongly dependent
on the mass loss rate, because it reaches a maximum value
and then declines as 24Mg is destroyed; in reality,
in the eta010 and eta020 models the evolution is completed
when the 25Mg is almost at its maximum value. The net
result is that within  0.1 dex we find
[25Mg]=0.5 for all the models.
The situation is different for the heaviest isotope,
because the surface 26Mg increases for the whole
evolution. In this case a larger mass loss rate leads
to a lower final abundance, so that the yield is lower.
For the eta002 model we find [26Mg]=0.35, while
[26Mg]=0.15 in the
0.1 dex we find
[25Mg]=0.5 for all the models.
The situation is different for the heaviest isotope,
because the surface 26Mg increases for the whole
evolution. In this case a larger mass loss rate leads
to a lower final abundance, so that the yield is lower.
For the eta002 model we find [26Mg]=0.35, while
[26Mg]=0.15 in the
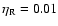 case. The average
26Mg content of the eta020 model is practically
unchanged with respect to the initial value.
case. The average
26Mg content of the eta020 model is practically
unchanged with respect to the initial value.
In terms of isotopic ratios, lower values of both
25Mg/24Mg and 26Mg/24Mg are expected
for larger mass loss rates, because in that case we
have a lower depletion of 24Mg. In agreement
with that, we find isotopic ratios  3 for
3 for
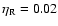 ,
,
 1 for
1 for
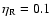 and
and  .4 for
.4 for
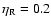 ,
the 25Mg/24Mg
ratio being always slightly larger than the
26Mg/24Mg.
,
the 25Mg/24Mg
ratio being always slightly larger than the
26Mg/24Mg.
The situation is a bit more complex for
lower masses, because in that
case the temperature reached by the base of
the outer convective zone never exceeds  108 K, therefore they achieve only
in a later phase of their AGB evolution the
conditions necessary to trigger a
deep nucleosynthesis within the convective
envelope. In these cases, at odds with the
most massive models, we expect that a stronger
mass loss, triggering an earlier cooling of
the structure, may prevent some reactions
from occurring at all.
108 K, therefore they achieve only
in a later phase of their AGB evolution the
conditions necessary to trigger a
deep nucleosynthesis within the convective
envelope. In these cases, at odds with the
most massive models, we expect that a stronger
mass loss, triggering an earlier cooling of
the structure, may prevent some reactions
from occurring at all.
We therefore calculated a model with initial
mass
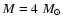 with a parameter for mass
loss
with a parameter for mass
loss
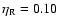 (eta010 model), and we
compare it with the model with the same initial
mass calculated with
(eta010 model), and we
compare it with the model with the same initial
mass calculated with
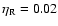 ,
presented
in Sect. 3.
The total duration of the AGB phase for the eta010 model
is shorter, as expected: the total mass of the star
reduces to
,
presented
in Sect. 3.
The total duration of the AGB phase for the eta010 model
is shorter, as expected: the total mass of the star
reduces to 
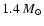 within
within
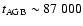 yr, to be compared to
yr, to be compared to
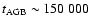 yr of the eta002 model.
yr of the eta002 model.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg18.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg130.gif) |
Figure 18:
The evolution of luminosity ( top) and temperature
at the base of the envelope (bottom) of two models
with initial mass 4  calculated with two
values of the parameter entering Blöcker (1995)
prescription for mass loss:
calculated with two
values of the parameter entering Blöcker (1995)
prescription for mass loss:
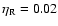 (solid track)
and
(solid track)
and
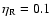 (dotted).
(dotted). |
| Open with DEXTER |
In Fig. 18 we compare
the variation with time of the
luminosity and of the temperature at the base of the
envelope of the two models, as a function of the
AGB time. We see from the top panel that there is
a difference of  0.2 dex between the maximum
value of the luminosity reached by the two models, while,
in terms of temperature, the base of the convective zone
of the eta002 model achieves a maximum value of
0.2 dex between the maximum
value of the luminosity reached by the two models, while,
in terms of temperature, the base of the convective zone
of the eta002 model achieves a maximum value of
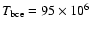 K, to be compared
to the maximum temperature
K, to be compared
to the maximum temperature
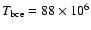 K
reached in the
K
reached in the
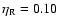 case.
In terms of the chemical content of the ejecta,
we may repeat for 12C and 14N the same
discussion as for the 5
case.
In terms of the chemical content of the ejecta,
we may repeat for 12C and 14N the same
discussion as for the 5  model,
because the temperatures in this case, though
lower, are still sufficient to favor an early
phase of 12C destruction followed by a later
phase of production, and a progressive increase
of the surface 14N abundance due both to HBB and to the effects of the 3rd dredge-up.
Thus, the 12C abundance
of the ejecta is almost the same for both
models, while the 14N abundance is lower
in the eta010 model by a factor of
model,
because the temperatures in this case, though
lower, are still sufficient to favor an early
phase of 12C destruction followed by a later
phase of production, and a progressive increase
of the surface 14N abundance due both to HBB and to the effects of the 3rd dredge-up.
Thus, the 12C abundance
of the ejecta is almost the same for both
models, while the 14N abundance is lower
in the eta010 model by a factor of  2.
2.
The different values of the temperatures reached
at the base of the outer convective zone in the
two models lead to a different degree of
oxygen depletion at the base of the envelope, as
can be seen in the two panels of Fig. 19,
where we show the variation of the surface 16O
with time (top panel) and mass (bottom).
We see that both models start to deplete oxygen
after  40 000 yr, but the depletion is made
difficult in the eta010 model by the lower
temperatures, so that the final abundance is only
40 000 yr, but the depletion is made
difficult in the eta010 model by the lower
temperatures, so that the final abundance is only
 0.15 dex lower than the 16O present in
the envelope at the beginning of the TPs phase.
In the eta002 model a stronger depletion is achieved.
The average oxygen content of the ejecta is
[16O]=-0.4 in the eta002 model, while it
is [16O]=-0.1 for
0.15 dex lower than the 16O present in
the envelope at the beginning of the TPs phase.
In the eta002 model a stronger depletion is achieved.
The average oxygen content of the ejecta is
[16O]=-0.4 in the eta002 model, while it
is [16O]=-0.1 for
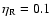 .
Even for the
.
Even for the
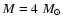 model we find that
the C+N+O abundance is constant within a factor
of
model we find that
the C+N+O abundance is constant within a factor
of  2 for the whole evolution, the eta002 model showing the largest increase due to
the higher number of 3rd dredge-up episodes.
2 for the whole evolution, the eta002 model showing the largest increase due to
the higher number of 3rd dredge-up episodes.
The situation concerning sodium is more complex.
The eta002 model, after the initial phase of
production, destroys sodium more efficiently
due to the larger temperatures reached; yet, the
evolution is so long that some sodium is dredged-up
later on; as a consequence, the sodium content
of the ejecta is almost the same in the two cases,
i.e. [23Na]=0.5. The less massive models are
therefore efficient sodium producers, independently
of the mass loss rate adopted.
In terms of the oxygen-sodium anti-correlation, the
eta002 model in this case is consistent with
simultaneous oxygen depletion and sodium production,
while only a poor oxygen depletion is expected
for higher mass loss rates.
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg19.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg133.gif) |
Figure 19:
Comparison between the depletion of
surface oxygen within two models with initial mass
4  calculated with two different values
of
calculated with two different values
of
 . . |
| Open with DEXTER |
For magnesium, the situation is very different
to the 5  case. The temperatures
here are not sufficiently high to favor an efficient
magnesium destruction, so that even in the eta002 model 24Mg is reduced by only a factor of
case. The temperatures
here are not sufficiently high to favor an efficient
magnesium destruction, so that even in the eta002 model 24Mg is reduced by only a factor of  2.
For
2.
For
 the surface 24Mg is almost
unchanged.
Even for the heavier isotopes the production is
much lower than in the 5
the surface 24Mg is almost
unchanged.
Even for the heavier isotopes the production is
much lower than in the 5  model.
In terms of the isotopic ratios, we find
25Mg/24Mg
model.
In terms of the isotopic ratios, we find
25Mg/24Mg  0.9 and 0.2, respectively,
for
0.9 and 0.2, respectively,
for
 and
and
 ,
while
26Mg/24Mg is 0.7 for
,
while
26Mg/24Mg is 0.7 for
 and 0.2 for
and 0.2 for
 .
.
We may therefore summarize the influence of mass
loss on the AGB models as follows:
- 1.
- The carbon content of the ejecta is almost
independent of mass loss, while the nitrogen abundance
may vary by a factor of
 2, lower
2, lower
 models showing greater enhancement. This holds
for all the masses calculated, because at least the
CN cycle is always operating.
models showing greater enhancement. This holds
for all the masses calculated, because at least the
CN cycle is always operating.
- 2.
- The oxygen abundance of the ejecta proves to be
more sensitive to mass loss; a lower
 favors
larger oxygen depletion. For all the masses considered
we achieve oxygen depletion for
favors
larger oxygen depletion. For all the masses considered
we achieve oxygen depletion for
 ,
while
a poor depletion is expected for larger values of
,
while
a poor depletion is expected for larger values of
 ,
particularly for the lowest masses.
,
particularly for the lowest masses.
- 3.
- The C+N+O sum is in all cases constant within
a factor of
 2, independently of mass and mass
loss.
2, independently of mass and mass
loss.
- 4.
- Larger
 favor sodium production in the more
massive models, because in that case the AGB evolution is
halted when the surface sodium has not yet been destroyed.
The less massive models are efficient sodium producers,
independently of the mass loss rate.
favor sodium production in the more
massive models, because in that case the AGB evolution is
halted when the surface sodium has not yet been destroyed.
The less massive models are efficient sodium producers,
independently of the mass loss rate.
- 5.
- The isotopic magnesium isotopes stay below unity
independently of mass loss for the less massive models.
For higher masses we have a steeper dependence on
 :
we find 25Mg/24Mg
:
we find 25Mg/24Mg  26Mg/24Mg
26Mg/24Mg  3for
3for
 ,
down to
25Mg/24Mg
,
down to
25Mg/24Mg  26Mg/24Mg
26Mg/24Mg  0.4 for
0.4 for
 .
.
There is still a strong debate concerning the role
that AGBs may have played in the pollution of the
interstellar medium of GCs: Fig. 7
shows that we are far from being able to falsify the hypothesis
that the chemical content of their ejecta
may account for the chemical anomalies observed
in GC stars (Denissenkov & Herwig 2003;
Fenner et al. 2004; Ventura et al. 2002; Paper I).
Within the MLT framework for the treatment of
convection the most recent work by Fenner et al.
(2004) shows that it is hardly possible to reconcile
the theoretical findings with the observational
scenario, because the expected chemical content
of the ejecta show a largely increased value
of the global C+N+O abundance, a very poor oxygen
depletion, and an extremely large sodium production.
These results are all in contrast with the
observational evidence.
Their findings were confirmed by our AGB models
calculated with the MLT convection, presented
and extensively discussed in Paper I.
If the FST model is used, due to the higher
temperatures reached at the bottom of the external
envelope, we find on the contrary that the C+N+O
is always constant within a factor of  2,
in agreement with the results of Ivans et al. (1999).
Also, oxygen depletion is easily achieved in all
models more massive than
2,
in agreement with the results of Ivans et al. (1999).
Also, oxygen depletion is easily achieved in all
models more massive than
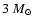 .
.
The FST models in the range
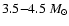 with a mass loss rate in agreement with the
calibration given in Ventura et al. (2000)
pollute the interstellar medium with material
having a chemistry qualitatively in agreement with the
chemical anomalies observed, that is:
with a mass loss rate in agreement with the
calibration given in Ventura et al. (2000)
pollute the interstellar medium with material
having a chemistry qualitatively in agreement with the
chemical anomalies observed, that is:
- The C+N+O sum is almost constant.
- Oxygen and sodium are anticorrelated,
in qualitative agreement with the observed trend.
From a quantitative point of view a larger sodium
content, coupled to an even stronger oxygen depletion
would be necessary to match the observational
evidence.
- The magnesium isotopic ratios are well below
unity, but the 26Mg/24Mg
ratio is larger than the 25Mg/24Mg,
contrary to observations (Yong et al. 2003). In addition,
the magnesium vs. aluminum anti-correlation is not reproduced.
In the most massive models, on the contrary, the
temperatures are so high that sodium, after an
early phase of production at the beginning of the
AGB phase, is destroyed; with the standard
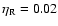 value for the mass loss rate
parameter we expect to have a negative [Na/Fe]
and a correlation between sodium and oxygen.
One further problem in this case would be the
extremely high values of the magnesium isotopic
ratios, which cluster around
value for the mass loss rate
parameter we expect to have a negative [Na/Fe]
and a correlation between sodium and oxygen.
One further problem in this case would be the
extremely high values of the magnesium isotopic
ratios, which cluster around  3, due to
strong 24Mg burning. If a larger
mass loss rate is adopted, we expect poor oxygen
depletion and sodium destruction, which would be
more consistent with the observations. The
magnesium isotopic ratios would be in this case
below unity, which is also in better agreement
with the observed abundances (Yong et al. 2003).
3, due to
strong 24Mg burning. If a larger
mass loss rate is adopted, we expect poor oxygen
depletion and sodium destruction, which would be
more consistent with the observations. The
magnesium isotopic ratios would be in this case
below unity, which is also in better agreement
with the observed abundances (Yong et al. 2003).
The CF88 models share almost the same properties
of the NACRE models, with the only difference of
sodium, which cannot be produced in this
latter case, because of the extremely low values
of the 22Ne proton capture reaction
cross-sections.
We present AGB models of intermediate mass in the
range
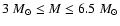 with
metallicity Z=0.001.
with
metallicity Z=0.001.
This work, together with the results of Paper I,
explores the role of some parameters of AGB evolution and shows
that it is affected by so many uncertainties
that it is still implausible to use the results of a unique set of
AGB computations to falsify the self-enrichment scenario for
globular cluster stars. Nevertheless, these results show trends
in the yields that are different from those of other researchers,
and may be relevant for a solution of the self-enrichment
problem. In particular, contrary to several recent
AGB computations, and by the use of the FST model, we find
that convection at the base of the external
zone during the quiescent phase of CNO burning is
so efficient as to lead to extremely high temperatures
(
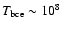 K), sufficient to trigger strong
HBB. We find that oxygen is depleted in all cases,
with the only exception of the 3
K), sufficient to trigger strong
HBB. We find that oxygen is depleted in all cases,
with the only exception of the 3  model.
model.
Our main findings are the following:
- 1.
-
The physical behavior of the models turns out to be
independent of the nuclear cross-sections used, the
results obtained with the NACRE rates being very similar
to CF88: this is due to the fact that the reactions
most contributing to the global energy release, i.e.
proton capture by carbon and nitrogen nuclei, are
the same in the two cases.
- 2.
-
One strong prediction, which holds independently of
mass, is that the total C+N+O abundance of the
ejecta is almost constant, at odds with previous
investigations.
- 3.
-
Sodium is produced within the NACRE models with
M < 4.5
 ,
while it is destroyed in
the more massive stars, due to an efficient
action of the Ne-Na cycle. In the CF88 models
sodium is systematically destroyed, because
of the extremely low values of the 22Ne proton
capture reaction.
,
while it is destroyed in
the more massive stars, due to an efficient
action of the Ne-Na cycle. In the CF88 models
sodium is systematically destroyed, because
of the extremely low values of the 22Ne proton
capture reaction.
- 4.
-
In terms of magnesium isotopes, the
25Mg/24Mg and 26Mg/24Mg ratios
are well below unity in the models with
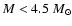 ,
while they reach values
approaching
,
while they reach values
approaching  10 for
10 for
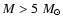 ,
due to strong 24Mg burning.
,
due to strong 24Mg burning.
- 5.
-
Mass loss influences the global duration of the AGB life; it also determines a general cooling of the
structure before some nuclear reactions
can be efficiently activated, therefore changing the
average chemical content of the ejecta. With
very strong mass loss, the HBB nucleosynthesis
has no time to be completely established. This
affects
mainly the oxygen and sodium yields, while it
leaves almost unaltered the lithium yield.
In the most massive models a stronger
mass loss rate (with respect to the standard value
adopted, calibrated on slightly less massive
models to reproduce the lithium-rich stars
luminosity function in the LMC)
might lead to ejecta that are sodium rich,
and that show low magnesium isotopic ratios;
there are two factors behind such findings:
- i) Massive AGBs achieve large luminosities
already during the first TPs; if mass loss is
increased during these phases, we have a larger
ejection of material that is still sodium
rich and not extremely 24Mg depleted.
- ii) As a consequence of the
reduction of the mass of the envelope, the
evolution is halted earlier, before strong sodium and
24Mg depletion can take place.
For models with masses
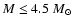 the ejecta are sodium rich and with
low magnesium isotopic ratios, with
the only difference that, for larger values
of
the ejecta are sodium rich and with
low magnesium isotopic ratios, with
the only difference that, for larger values
of
 ,
oxygen is scarcely depleted, as
the increase of the temperature at the base of
the external envelope is halted before it
reaches values sufficiently high to activate
efficiently the full CNO cycle.
,
oxygen is scarcely depleted, as
the increase of the temperature at the base of
the external envelope is halted before it
reaches values sufficiently high to activate
efficiently the full CNO cycle.
These models show that
the predictive power of AGB models is still
undermined by many uncertainties. The parameter
space, however, has not yet been fully explored
(e.g. the role of extra-mixing at the bottom of
the envelope) and for this reason we should not
discard the hypothesis that massive AGB stars are
responsible for the chemical anomalies observed
in GC stars.
- Angulo, C.,
Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [CrossRef] (In the text)
- Arnould, M.,
Goriely, S., & Jorissen, A. 1999, A&A, 347, 572 (In the text)
- Blöcker, T.
1995, A&A, 297, 727 (In the text)
- Blöcker, T.,
& Schönberner, D. 1991, A&A, 244, L43 (In the text)
-
Böhm-Vitense, E. 1958, Z. Astroph., 46, 108 (In the text)
-
Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390,
91 [EDP Sciences]
- Canuto, V. M.,
& Mazzitelli, I. 1991, ApJ, 370, 295 [CrossRef] (In the text)
- Canuto, V. M.,
Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 570 (In the text)
- Carretta,
E. 2003, Mem. S.A.It. Suppl., 3, 90
- Carretta,
E., Bragaglia, A., Cacciari, C., & Rossetti, E. 2003, A&A,
410, 143 [EDP Sciences] [CrossRef] (In the text)
- Caughlan,
G. R., & Fowler, W. A. 1988, At. Data Nucl. Tab., 40, 283 (In the text)
- Cloutman,
L., & Eoll, J. G. 1976, ApJ, 206, 548 [CrossRef] (In the text)
- Cloutman,
L., & Whitaker, R. W. 1980, ApJ, 237, 900 [CrossRef]
- Cohen, J. G.,
& Meléndez, J. 2005, AJ, 129, 303 [CrossRef]
- Cohen, J. G.,
Briley, M. M., & Stetson, P. B. 2002, AJ, 123, 2525 [CrossRef] (In the text)
- D'Antona, F.,
& Mazzitelli, I. 1996, ApJ, 470, 1093 [CrossRef] (In the text)
- D'Antona, F.,
Gratton, R., & Chieffi, A. 1983, Mem. S.A.It., 54, 173 (In the text)
- D'Antona, F.,
Caloi, V., Montalban, J., Ventura, P., & Gratton, R. 2002,
A&A, 395, 69 [EDP Sciences] [CrossRef]
-
Denissenkov, P., & Herwig, F. 2003, ApJ, 590, L99 [CrossRef] (In the text)
-
Denissenkov, P., & Weiss, A. 2004, ApJ, 603, 119 [CrossRef] (In the text)
- Fenner, Y.,
Campbell, S., Karakas, A. I., Lattanzio, J. C., & Gibson, B. K.
2004, MNRAS, 353, 789 [CrossRef] (In the text)
- Gratton, R.,
Bonifacio, P., Bragaglia, A., et al. 2001, A&A, 369, 87 [EDP Sciences] (In the text)
- Gratton, R.,
Sneden, C., & Carretta, E. 2004, ARA&A, 42, 385 (In the text)
- Grundahl,
F., Briley, M., Nissen, P. E., & Feltzing, S. 2002, A&A,
385, L14 [EDP Sciences] [CrossRef] (In the text)
- Herwig, F.
2000, A&A, 360, 952
- Herwig, F.
2004, A&A, 605, 425
- Herwig, F.,
Blöcker, T., & Schönberner, D. 1997, A&A, 324,
L81
- Iben, I. J. 1975,
ApJ, 196, 525 [CrossRef] (In the text)
- Iben, I. J. 1976,
ApJ, 208, 165 [CrossRef] (In the text)
- Ivans, I. I.,
Sneden, C., Kraft, R. P., et al. 1999, AJ, 118, 1273 [CrossRef] (In the text)
-
Lattanzio, C. L., & Karakas, A. I. 2001, M.S.A.It., 72,
255 (In the text)
-
Mazzitelli, I., D'Antona, F., & Ventura, P. 1999, A&A, 348,
846
-
Pilachowski, C. A. 1988, ApJ, 326, L57 [CrossRef]
- Ramirez, S.,
& Cohen, J. G. 2002, AJ, 123, 3277 [CrossRef]
- Ramirez, S.,
& Cohen, J. G. 2003, AJ, 125, 224 [CrossRef]
- Renzini, A.,
& Voli, M. 1981, A&A, 94, 175 (In the text)
- Sackmann,
J., & Boothroyd, A. I. 1991, ApJ, 366, 529 [CrossRef] (In the text)
-
Schönberner, D. 1979, A&A, 79, 108 (In the text)
-
Schwarzschild, M., & Harm, R. 1965, ApJ, 142, 855 [CrossRef] (In the text)
-
Schwarzschild, M., & Harm, R. 1967, A&A, 145, 486 (In the text)
- Smith, G. H.,
Shetrone, M. D., Bell, R. A., Churchill, C. W., & Briley, M. M.
1996, AJ, 112, 1511 [CrossRef]
- Sneden, C.,
Kraft, R. P., Guhathakurta, P., Peterson, R. C., & Fulbright,
J. P. 2004, AJ, 127, 2162 [CrossRef] (In the text)
- Ventura,
P., & Castellani, M. 2005, A&A, 430, 1035 [EDP Sciences] [CrossRef] (In the text)
- Ventura,
P., & D'Antona, F. 2005, A&A, 431, 279 [EDP Sciences] [CrossRef] (In the text)
- Ventura, P.,
Zeppieri, A., D'Antona, F., & Mazzitelli, I. 1998, A&A,
334, 953 (In the text)
- Ventura, P.,
D'Antona, F., & Mazzitelli, I. 2000, A&A, 363, 605 (In the text)
- Ventura, P.,
D'Antona, F., Mazzitelli, I., & Gratton, R. 2001, ApJ, 550,
L65 [CrossRef] (In the text)
- Ventura, P.,
D'Antona, F., & Mazzitelli, I. 2002, A&A, 393, 215 [EDP Sciences] [CrossRef] (In the text)
- Vitense, E.
1953, Zs.Ap., 32, 135 (In the text)
- Yong, D., Grundahl,
F., Nissen, P. E., & Shetrone, M. D. 2003, A&A, 402,
985 [EDP Sciences] [CrossRef] (In the text)
Copyright ESO 2005
![\begin{displaymath}\left( {{\rm d}X_i\over {\rm d}t} \right)=\left( {\partial X_...
... r^2 \rho)^2 D {\partial X_i
\over \partial m_{\rm r}}\right]
\end{displaymath}](/articles/aa/full/2005/33/aa2396-04/img22.gif)
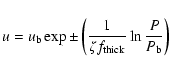
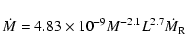
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2396fg01.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2396fg02.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2396fg03.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg64.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg04.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg65.gif)
![\begin{figure}
{
\includegraphics[width=7.5cm,clip]{2396fg5a.eps}\hspace*{4mm}
\includegraphics[width=7.5cm,clip]{2396fg5b.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2396fg06.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{2396fg07.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg88.gif)
![\begin{figure}
\par {\includegraphics[width=4.7cm,clip]{2396fg8a.eps}\hspace*{4m...
...}\hspace*{4mm}
\includegraphics[width=4.7cm,clip]{2396fg8c.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg89.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg09.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg92.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg10.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg11.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg99.gif)
![\begin{figure}
{
\includegraphics[width=7cm,clip]{2396f12a.eps}\hspace*{4mm}
\includegraphics[width=7cm,clip]{2396f12b.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2396fg13.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg14.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg109.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg15.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg118.gif)
![\begin{figure}
{
\includegraphics[width=5.5cm]{2396f16a.eps}\hspace*{4mm}
\inclu...
...c.eps}\hspace*{4mm}
\includegraphics[width=5.5cm]{2396f16d.eps} }\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg119.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg17.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg18.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg130.gif)
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2396fg19.eps}
\end{figure}](/articles/aa/full/2005/33/aa2396-04/Timg133.gif)