O. Le Fèvre1 - L. Guzzo2 - B. Meneux1 - A. Pollo2 - A. Cappi3 - S. Colombi9 - A. Iovino2 - C. Marinoni1,2 - H. J. McCracken9,12 - R. Scaramella7 - D. Bottini4 - B. Garilli4 - V. Le Brun1 - D. Maccagni4 - J. P. Picat5 - M. Scodeggio4 - L. Tresse1 - G. Vettolani6 - A. Zanichelli6 - C. Adami1 - M. Arnaboldi11 - S. Arnouts1 - S. Bardelli3 - J. Blaizot1 - M. Bolzonella8 - S. Charlot9,10 - P. Ciliegi6 - T. Contini5 - S. Foucaud4 - P. Franzetti4 - I. Gavignaud5,13 - O. Ilbert1,3 - B. Marano8 - G. Mathez5 - A. Mazure1 - R. Merighi3 - S. Paltani1 - R. Pellò5 - L. Pozzetti3 - M. Radovich11 - G. Zamorani3 - E. Zucca3 - M. Bondi6 - A. Bongiorno8 - G. Busarello11 - F. Lamareille5 - Y. Mellier9,12 - P. Merluzzi11 - V. Ripepi11 - D. Rizzo5,2
1 - Laboratoire d'Astrophysique de Marseille, UMR 6110 CNRS-Université
de Provence, Traverse
du Siphon, BP 8, 13012 Marseille, France
2 -
INAF - Osservatorio Astronomico di Brera, via Brera 28, 20121 Milan, Italy
3 -
INAF - Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
4 -
INAF - IASF, via Bassini, 15, 20133 Milano, Italy
5 -
Laboratoire d'Astrophysique de l'Observatoire Midi-Pyrénées, UMR 5572,
14 Av. Ed. Belin, 31400 Toulouse, France
6 -
INAF - Istituto di Radio-Astronomia, via Gobetti 101, 40129 Bologna, Italy
7 -
INAF - Osservatorio Astronomico di Roma, Italy
8 -
Dipartimento di Astronomia, Università di Bologna, via Ranzani 1, 40127 Bologna, Italy
9 -
Institut d'Astrophysique de Paris, UMR 7095, 98bis Bd. Arago, 75014 Paris, France
10 -
Max-Planck-Institut für Astrophysik, 85741 Garching, Germany
11 -
INAF - Osservatorio Astronomico di Capodimonte, via Moiariello 16, 80131 Napoli, Italy
12 -
Observatoire de Paris, LERMA, UMR 8112, 61 Av. de l'Observatoire, 75014 Paris, France
13 -
European Southern Observatory, Karl Schwarzschild Str. 2, 85748 Garching
bei München, Germany
Received 6 September 2004 / Accepted 11 April 2005
Abstract
This paper presents the evolution of the
clustering of the main population of
galaxies from ![]() to z=0.2, from the first epoch
VIMOS VLT Deep Survey (VVDS), a magnitude limited sample with
to z=0.2, from the first epoch
VIMOS VLT Deep Survey (VVDS), a magnitude limited sample with
![]() .
The sample allows a direct estimate of evolution from within the same survey over the time base sampled.
We have computed the correlation functions
.
The sample allows a direct estimate of evolution from within the same survey over the time base sampled.
We have computed the correlation functions
![]() and
and
![]() ,
and the correlation length r0(z),
for the VVDS-02h and VVDS-CDFS fields,
for a total of 7155 galaxies in a
0.61 deg2 area. We find that the correlation length
in this sample slightly increases from z=0.5 to z=1.1,
with
r0(z)=2.2-2.9 h-1 Mpc (comoving), for galaxies
comparable in luminosity to the local 2dFGRS
and SDSS samples,
indicating that the amplitude of the correlation function
was
,
and the correlation length r0(z),
for the VVDS-02h and VVDS-CDFS fields,
for a total of 7155 galaxies in a
0.61 deg2 area. We find that the correlation length
in this sample slightly increases from z=0.5 to z=1.1,
with
r0(z)=2.2-2.9 h-1 Mpc (comoving), for galaxies
comparable in luminosity to the local 2dFGRS
and SDSS samples,
indicating that the amplitude of the correlation function
was ![]() 2.5 times lower at
2.5 times lower at ![]() than observed
locally. The correlation length in our lowest redshift bin
z=[0.2, 0.5]is r0=2.2 h-1 Mpc, lower than for any other population at
the same redshift, indicating the low clustering of
very low luminosity galaxies, 1.5 mag fainter than in the
2dFGRS or SDSS. The correlation length
increases to
than observed
locally. The correlation length in our lowest redshift bin
z=[0.2, 0.5]is r0=2.2 h-1 Mpc, lower than for any other population at
the same redshift, indicating the low clustering of
very low luminosity galaxies, 1.5 mag fainter than in the
2dFGRS or SDSS. The correlation length
increases to
![]() h-1 Mpc at higher redshifts
z=[1.3, 2.1],
as we are observing increasingly brighter galaxies, comparable
to galaxies with
MBAB=-20.5 locally.
We compare our measurement to the DEEP2 measurements in
the range
z=[0.7, 1.35] (Coil et al. 2004, ApJ, in press) and find comparable results
when applying the same magnitude and color selection
criteria as in their survey.
The slowly varying clustering of VVDS galaxies as redshift increases
is markedly different from the predicted evolution
of the clustering of dark matter,
indicating that bright galaxies traced higher density
peaks when the large scale structures were emerging from the
dark matter distribution 9-10 billion years ago,
being supporting evidence for a strong evolution of the
galaxy vs. dark matter bias.
h-1 Mpc at higher redshifts
z=[1.3, 2.1],
as we are observing increasingly brighter galaxies, comparable
to galaxies with
MBAB=-20.5 locally.
We compare our measurement to the DEEP2 measurements in
the range
z=[0.7, 1.35] (Coil et al. 2004, ApJ, in press) and find comparable results
when applying the same magnitude and color selection
criteria as in their survey.
The slowly varying clustering of VVDS galaxies as redshift increases
is markedly different from the predicted evolution
of the clustering of dark matter,
indicating that bright galaxies traced higher density
peaks when the large scale structures were emerging from the
dark matter distribution 9-10 billion years ago,
being supporting evidence for a strong evolution of the
galaxy vs. dark matter bias.
Key words: surveys - galaxies: evolution - cosmology: large scale structure of Universe
The evolution of the clustering of galaxies is a key diagnostic
element to test the evolution of the universe, allowing direct
comparison between observations and theory.
In the current paradigm of galaxy formation and evolution,
dark matter halos that contain galaxies are expected to merge and grow
under the action of gravity. This translates into a
continuous evolution of the correlation function ![]() of
dark matter halos, now quite well understood from extensive
high resolution numerical simulations
(see Benson et al. 2001; Kauffmann et al. 1999; Weinberg et al. 2004; Somerville et al. 2001). As a direct
measurement of the space distribution
of dark matter halos
is not yet feasible, we are compelled to use
galaxies as indirect tracers of the dark matter. Unfortunately,
as galaxies are complex physical systems, their relationship
to
the underlying mass,
the "bias'', is difficult to estimate.
As galaxies and dark matter evolve, the bias may evolve and relating the
measurements of galaxy clustering to the evolution of the total mass
is not easy, with the bias
shown to depend upon galaxy type, luminosity
and local environment (Norberg et al. 2002).
of
dark matter halos, now quite well understood from extensive
high resolution numerical simulations
(see Benson et al. 2001; Kauffmann et al. 1999; Weinberg et al. 2004; Somerville et al. 2001). As a direct
measurement of the space distribution
of dark matter halos
is not yet feasible, we are compelled to use
galaxies as indirect tracers of the dark matter. Unfortunately,
as galaxies are complex physical systems, their relationship
to
the underlying mass,
the "bias'', is difficult to estimate.
As galaxies and dark matter evolve, the bias may evolve and relating the
measurements of galaxy clustering to the evolution of the total mass
is not easy, with the bias
shown to depend upon galaxy type, luminosity
and local environment (Norberg et al. 2002).
The most straigthforward indicator of galaxy clustering is
the correlation function ![]() ,
representing the excess
probability over random
of finding a galaxy in a given volume,
at a fixed distance from another galaxy.
The shape and amplitude of the galaxy correlation function at the
current epoch is now established to high accuracy.
,
representing the excess
probability over random
of finding a galaxy in a given volume,
at a fixed distance from another galaxy.
The shape and amplitude of the galaxy correlation function at the
current epoch is now established to high accuracy. ![]() is well
described by a power law
is well
described by a power law
![]() over scales
0.1-10 h-1 Mpc (Zehavi et al. 2004; Davis & Peebles 1983; Hawkins et al. 2003),
with a more refined
modelling requiring some extra power over this shape for separations
larger than 2-3 h-1 Mpc (Zehavi et al. 2004; Guzzo et al. 1991),
a feature possibly encoding information on the
relation between galaxies and their host dark-matter halos.
The local clustering measurements have shown that the
correlation length r0 increases from late types to early type
galaxies, from low luminosity to high luminosity and from low to high
galaxy density environments (see Norberg et al. 2001; Guzzo et al. 1997; Giovanelli et al. 1986; Benoist et al. 1996), with luminosity being the
dominant effect (Norberg et al. 2002).
The most recent estimates of the
correlation length from the 2dFGRS and SDSS vary from r0=3 for late type
star-forming galaxies in low density environments to r0=5-6 for
galaxies with M*=-19.5, with the clustering amplitude
reaching r0=7.5 h-1 Mpc for galaxies four times L*.
over scales
0.1-10 h-1 Mpc (Zehavi et al. 2004; Davis & Peebles 1983; Hawkins et al. 2003),
with a more refined
modelling requiring some extra power over this shape for separations
larger than 2-3 h-1 Mpc (Zehavi et al. 2004; Guzzo et al. 1991),
a feature possibly encoding information on the
relation between galaxies and their host dark-matter halos.
The local clustering measurements have shown that the
correlation length r0 increases from late types to early type
galaxies, from low luminosity to high luminosity and from low to high
galaxy density environments (see Norberg et al. 2001; Guzzo et al. 1997; Giovanelli et al. 1986; Benoist et al. 1996), with luminosity being the
dominant effect (Norberg et al. 2002).
The most recent estimates of the
correlation length from the 2dFGRS and SDSS vary from r0=3 for late type
star-forming galaxies in low density environments to r0=5-6 for
galaxies with M*=-19.5, with the clustering amplitude
reaching r0=7.5 h-1 Mpc for galaxies four times L*.
At higher redshifts
the situation is less clear.
Analysis of the projected angular correlation function favors
a stable clustering (Roche et al. 1999; Cabanac et al. 2000; McCracken et al. 2001; Postman et al. 1998)
but it requires a priori knowledge of the redshift distribution
of the galaxy population sampled.
A variety of results have been obtained from smaller
spectroscopic samples, with comoving
correlation lengths r0 in the range 2-5 h-1 Mpc at ![]() (Small et al. 1999; Carlberg et al. 1999; Le Fèvre et al. 1996; Shepherd et al. 2001)
and r0=3-5 h-1 Mpc at
(Small et al. 1999; Carlberg et al. 1999; Le Fèvre et al. 1996; Shepherd et al. 2001)
and r0=3-5 h-1 Mpc at ![]() (Foucaud et al. 2003; Giavalisco et al. 1998).
Recently, first results from the DEEP2 survey have been presented,
indicating a correlation length
(Foucaud et al. 2003; Giavalisco et al. 1998).
Recently, first results from the DEEP2 survey have been presented,
indicating a correlation length
![]() h-1 Mpc in
z=[0.7, 0.9], and
h-1 Mpc in
z=[0.7, 0.9], and
![]() h-1 Mpc in
z=[0.9, 1.35](Coil et al. 2004).
The main difficulty in interpreting these results in terms of
evolution of the clustering is to relate the
population of galaxies observed at a given redshift to a lower
redshift population of "descendants'', identified from
a well-defined selection function enabling comparisons.
Some of these surveys are targeted to specific classes of
galaxies, pre-selected via photometric methods, whose relation to the
global population is not obvious. The most notable example is
represented by galaxies selected via the Lyman-break technique around
h-1 Mpc in
z=[0.9, 1.35](Coil et al. 2004).
The main difficulty in interpreting these results in terms of
evolution of the clustering is to relate the
population of galaxies observed at a given redshift to a lower
redshift population of "descendants'', identified from
a well-defined selection function enabling comparisons.
Some of these surveys are targeted to specific classes of
galaxies, pre-selected via photometric methods, whose relation to the
global population is not obvious. The most notable example is
represented by galaxies selected via the Lyman-break technique around
![]() and
and ![]() (Steidel et al. 1998), which
display a clustering strength similar to present-day normal galaxies
and therefore represent a very biased population, possibly the
precursors of giant cluster ellipticals (Governato et al. 1998).
(Steidel et al. 1998), which
display a clustering strength similar to present-day normal galaxies
and therefore represent a very biased population, possibly the
precursors of giant cluster ellipticals (Governato et al. 1998).
On the other hand, even when selecting purely magnitude-limited samples, one cannot avoid being affected by the complex dependence of clustering on morphology and luminosity evidenced by the wide range of correlation lengths measured in the local Universe, and its evolution as a function of redshift. One needs to observe samples at increasingly high redshifts with the same luminosities, colors (type) and local environments in order to derive the evolution of the clustering of galaxies and hence attempt to derive how the correlation properties of the mass evolve. At high redshifts, the natural observational bias is to sample increasingly brighter and more actively star forming galaxies, which may have a direct impact on our current vision of the evolution.
Finally, high-redshift samples of spectroscopically measured galaxies have been inevitably limited so far to relatively bright objects in small areas on the sky, which contributes to increase the scatter between independent measurements, further complicating their interpretation.
In this paper we present the first attempt to measure
the evolution of the clustering
in a consistant way accross the redshift range
![]() ,
using 7155 galaxies from the VIMOS VLT Deep Survey (VVDS)
over more than 0.61 deg2.
The VVDS is designed to sample the
high redshift population of galaxies in the most unbiased
way possible, using a simple
magnitude selection in the range
,
using 7155 galaxies from the VIMOS VLT Deep Survey (VVDS)
over more than 0.61 deg2.
The VVDS is designed to sample the
high redshift population of galaxies in the most unbiased
way possible, using a simple
magnitude selection in the range
![]() ,
using several independant fields up to 4 deg2 each (Le Fèvre et al. 2005).
This analysis uses the high-quality First Epoch VVDS sample,
which includes 6117 galaxy redshifts in the VVDS-02h
(Le Fèvre et al. 2005) and another 1368 galaxies in the VVDS-CDFS
(Le Fèvre et al. 2004b) field. We have measured the redshift-space
correlation function
,
using several independant fields up to 4 deg2 each (Le Fèvre et al. 2005).
This analysis uses the high-quality First Epoch VVDS sample,
which includes 6117 galaxy redshifts in the VVDS-02h
(Le Fèvre et al. 2005) and another 1368 galaxies in the VVDS-CDFS
(Le Fèvre et al. 2004b) field. We have measured the redshift-space
correlation function
![]() ,
and computed the projected
function
,
and computed the projected
function
![]() ,
to recover the value of the
galaxy correlation length r0(z) up to
,
to recover the value of the
galaxy correlation length r0(z) up to ![]() ,
therefore tracing the evolution of the clustering over
more than 10 Gy, or 70% of the current age of the universe.
,
therefore tracing the evolution of the clustering over
more than 10 Gy, or 70% of the current age of the universe.
In Sect. 2 we recall the properties of the VVDS First Epoch sample.
In Sect. 3, we describe how the correlation function has been
computed, referring in large part to the accompanying paper by Pollo et al. (2005)
which describes all the methods set up to validate the measurements
and compute the errors. In Sect. 4, we present the results
in terms of the evolution of r0(z), and
we compare our results to previous measurements where possible.
In Sect. 5, we discuss the evolution of the clustering of
the global population of galaxies from ![]() ,
before concluding
in Sect. 6.
,
before concluding
in Sect. 6.
This paper is the first in a series of papers to study the
clustering of galaxies at high redshift from the VVDS
first epoch data. Guzzo et al. (2005, in prep.)
will present the clustering evolution from volume limited
samples and infer the dependence of clustering
upon luminosity; Meneux et al. (2005, in prep.) will present the differences
in clustering observed as a function of galaxy type and its
evolution and Pollo et al. (2005, in prep.)
will investigate the dependence and evolution of clustering as a function
of the local environment. Marinoni et al. (2005) and Le Fèvre et al.
(2005, in prep.) will look
at the evolution of the galaxy - dark matter
bias, and subsequent papers will study the
clustering from the redshift population
![]() .
.
We have used a Concordance Cosmology with
![]() ,
and
,
and
![]() throughout this paper. The Hubble constant is
normally parameterized via h=H0/100, to ease comparison to
previous works, while a value H0=70 km s-1 Mpc-1 has
been used when computing absolute magnitudes. All correlation
length values are quoted in comoving coordinates.
throughout this paper. The Hubble constant is
normally parameterized via h=H0/100, to ease comparison to
previous works, while a value H0=70 km s-1 Mpc-1 has
been used when computing absolute magnitudes. All correlation
length values are quoted in comoving coordinates.
The VVDS-Deep sample is stricly selected in magnitude in the
range
![]() ,
from a complete deep
photometric survey (Le Fèvre et al. 2004a; McCracken et al. 2003)
without any color or
shape selection (Le Fèvre et al. 2004b).
We have analysed two fields, the VVDS-02h and the VVDS-CDFS.
Over the
,
from a complete deep
photometric survey (Le Fèvre et al. 2004a; McCracken et al. 2003)
without any color or
shape selection (Le Fèvre et al. 2004b).
We have analysed two fields, the VVDS-02h and the VVDS-CDFS.
Over the ![]() 9600 redshifts measured in these two fields,
we have used in the following analysis
only objects with a redshift confidence level
higher than or equal to
9600 redshifts measured in these two fields,
we have used in the following analysis
only objects with a redshift confidence level
higher than or equal to ![]() 80% (quality flags 2 to 9
as defined in Le Fèvre et al. 2004b),
excluding QSOs. We will only mention briefly below
the effect on measured
correlations of relaxing the quality threshold, including the
poorest redshift measurements (flag 1).
The complete sample analysed concerns a total of 7155 galaxies
in 2203 arcmin2, with 6137 galaxies in
the 1750 arcmin2VVDS-02h field with
80% (quality flags 2 to 9
as defined in Le Fèvre et al. 2004b),
excluding QSOs. We will only mention briefly below
the effect on measured
correlations of relaxing the quality threshold, including the
poorest redshift measurements (flag 1).
The complete sample analysed concerns a total of 7155 galaxies
in 2203 arcmin2, with 6137 galaxies in
the 1750 arcmin2VVDS-02h field with
![]() ,
and 1038 galaxies
in the 453 arcmin2 VVDS-CDFS
(Chandra Deep Field South, Giacconi et al. 2002) area with
,
and 1038 galaxies
in the 453 arcmin2 VVDS-CDFS
(Chandra Deep Field South, Giacconi et al. 2002) area with
![]() .
The accuracy of the redshift measurements
is
.
The accuracy of the redshift measurements
is ![]() 275 km s-1 (Le Fèvre et al. 2004a). The distribution of
redshifts for the VVDS-02h field is presented in Fig. 1.
The redshift distribution peaks at
275 km s-1 (Le Fèvre et al. 2004a). The distribution of
redshifts for the VVDS-02h field is presented in Fig. 1.
The redshift distribution peaks at
![]() ,
and there
are 300 galaxies with
,
and there
are 300 galaxies with
![]() ,
and 132 galaxies
with
,
and 132 galaxies
with
![]() .
.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{1962fig1.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg43.gif) |
Figure 1:
The redshift distribution in the VVDS-02h field. The
filled histogram contains 6137 galaxies with quality flag |
| Open with DEXTER | |
We have split the sample into 6 redshift bins, as described in Table 1. The rest frame B-IAB(0) color and absolute magnitude MBAB distribution within each bin is shown in Fig. 2, from z=0.2 to z=2.1, and the mean values are reported in Table 1. B-IAB(0) and MBAB have been computed using template fitting of the photometric spectral energy distribution in B, V, R, and I bands, to derive the k(z) corrections (see Ilbert et al. 2005, for details).
Table 1:
Measurements of the correlation length r0(z)and the correlation function slope ![]() .
The associated
.
The associated
![]() errors are reported. r0 values are computed
both with letting
errors are reported. r0 values are computed
both with letting ![]() free, and setting
free, and setting ![]() to
the mean 1.78 in the range
z=[0.2, 1.3] in the VVDS-F02 and VVDS-CDFS.
To compare to the DEEP2 measurements of Coil et al. (2004),
we have set
to
the mean 1.78 in the range
z=[0.2, 1.3] in the VVDS-F02 and VVDS-CDFS.
To compare to the DEEP2 measurements of Coil et al. (2004),
we have set
![]() for the VVDS-F02-DEEP2 in
z=[0.7, 0.9] and
z=[0.9, 1.35], and
for the VVDS-F02-DEEP2 in
z=[0.7, 0.9] and
z=[0.9, 1.35], and
![]() for the VVDS-F02-DEEP2 in
z=[0.7, 1.35].
The redshift range,
number of galaxies used, mean absolute magnitude
MBAB and
rest frame color
B-IAB(z=0), are indicated for each subsample.
for the VVDS-F02-DEEP2 in
z=[0.7, 1.35].
The redshift range,
number of galaxies used, mean absolute magnitude
MBAB and
rest frame color
B-IAB(z=0), are indicated for each subsample.
Up to redshift
z=1.3, the
B-IAB(0) color distribution stays
quite similar with increasing redshift,
from blue star forming
B-IAB(0)=0to red
![]() ,
while for
,
while for
![]() ,
the
reddest
,
the
reddest
![]() galaxies, if
present, are not observed.
The magnitude selection of the VVDS-Deep,
therefore, allows us to sample the global population of galaxies,
for all galaxy types from late to early types, up to
galaxies, if
present, are not observed.
The magnitude selection of the VVDS-Deep,
therefore, allows us to sample the global population of galaxies,
for all galaxy types from late to early types, up to ![]() ,
while for z>1.3, as we are selecting galaxies from their UV
rest frame continuum at these redshifts, the VVDS is increasingly
biased towards late-type, higher star-forming galaxies.
We therefore expect that in the farthest redshift bin,
the clustering measurement in the VVDS is the result
of the effects of looking at intrinsicaly more luminous
and more actively star forming galaxies.
,
while for z>1.3, as we are selecting galaxies from their UV
rest frame continuum at these redshifts, the VVDS is increasingly
biased towards late-type, higher star-forming galaxies.
We therefore expect that in the farthest redshift bin,
the clustering measurement in the VVDS is the result
of the effects of looking at intrinsicaly more luminous
and more actively star forming galaxies.
The range of absolute
MBAB magnitudes sampled
is quite large, and changes strongly with redshift
as shown in Fig. 2. While at redshift ![]() ,
the absolute magnitude range sampled is
,
the absolute magnitude range sampled is
![]() ,
only bright galaxies with
,
only bright galaxies with
![]() are sampled
at z>1.3. The absolute luminosity of galaxies
in the VVDS is shown to increase as redshift increases,
as computed from the Luminosity Function (Ilbert et al. 2005).
If one assumes a pure luminosity evolution,
galaxies observed at high redshift
are expected to have faded to fainter absolute magnitudes
at the present time, by as much as MB=1.5 to 2 mag. This should be
taken into account when comparing the clustering of the
high redshift population to local populations.
are sampled
at z>1.3. The absolute luminosity of galaxies
in the VVDS is shown to increase as redshift increases,
as computed from the Luminosity Function (Ilbert et al. 2005).
If one assumes a pure luminosity evolution,
galaxies observed at high redshift
are expected to have faded to fainter absolute magnitudes
at the present time, by as much as MB=1.5 to 2 mag. This should be
taken into account when comparing the clustering of the
high redshift population to local populations.
The consequences on the correlation function measurements of the change in the population sampled as a function of redshift are discussed in Sect. 5.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1962fig2.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg51.gif) |
Figure 2:
The rest frame B-IAB color ( left) and
absolute magnitude
MBAB ( right) from the VVDS-02h data up
to |
| Open with DEXTER | |
The methods applied on the VVDS first epoch data to derive the real space correlation parameters are described extensively in the accompanying paper by Pollo et al. (2005). We summarize below the main elements of this method.
To measure the galaxy real-space correlation length r0 and
slope ![]() from our survey, we have used the projection of the
bi-dimensional correlation function
from our survey, we have used the projection of the
bi-dimensional correlation function
![]() .
This function was estimated
using the well-known Landy & Szalay (1993) estimator
.
This function was estimated
using the well-known Landy & Szalay (1993) estimator
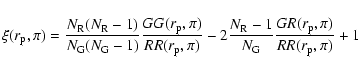 |
(1) |
Since we are not computing the correlation function from the full magnitude-limited survey altogether, there is no point here in using the so-called J3 minimum-variance weighting. This usually has been adopted in the analysis of large flux-limited local surveys (Guzzo et al. 2000; Fisher et al. 1994), in which the sampling of the clustering process varies dramatically between the nearby and distant parts of the sample. Its main scope is to avoid excessive weighting of the most distant parts of the sample, where only sparse bright galaxies trace structures. Within each of our redshift bins, the density of objects varies only slightly and equal weighting of the pairs is the most appropriate choice (Fisher et al. 1994).
We have computed the two point correlation function
![]() in increasing redshift bins, selecting the bin boundaries to
maximize the number of objects, hence the signal to noise of the
correlation function, in each of the bins.
in increasing redshift bins, selecting the bin boundaries to
maximize the number of objects, hence the signal to noise of the
correlation function, in each of the bins.
The formalism developed by Davis & Peebles (1983) has been used to derive
the real space correlation function in the presence of
redshift-space distortions along the line of sight.
We integrate
![]() along the line of sight,
computing
along the line of sight,
computing
If we assume a power-law form for ![]() ,
i.e.
,
i.e.
Fitting the
![]() measurements in each redshift bin
then provides a measurement of r0(z) and
measurements in each redshift bin
then provides a measurement of r0(z) and ![]() .
.
The uncertainty associated with the computation of r0(z) and
![]() is largely dominated by cosmic variance. Although
our spectroscopic sample is the largest available to date at the
redshifts probed, both in the number of galaxies
and area surveyed, only two fields have been sampled,
with the VVDS-02h largely dominating over the VVDS-CDFS in
terms of the number of galaxies observed and area covered,
and it is therefore
inappropriate
to estimate errors
on
is largely dominated by cosmic variance. Although
our spectroscopic sample is the largest available to date at the
redshifts probed, both in the number of galaxies
and area surveyed, only two fields have been sampled,
with the VVDS-02h largely dominating over the VVDS-CDFS in
terms of the number of galaxies observed and area covered,
and it is therefore
inappropriate
to estimate errors
on
![]() ,
r0(z), and
,
r0(z), and ![]() directly from
field-to-field variations within our data set.
Instead, we have been using
ensemble errors derived from the
scatter in the correlation function computed from 50
mock VVDS surveys constructed using the GalICS simulations
(Blaizot et al. 2005), as thoroughly described in the parallel
paper by (Pollo et al. 2005).
These realistic mock samples specifically include the same
selection function and observational biases present in the
VVDS First Epoch data set, and allow us to compute
ensemble statistical averages and scatters of the quantities
we measure on the real data. In particular, the standard
deviation of the measured
directly from
field-to-field variations within our data set.
Instead, we have been using
ensemble errors derived from the
scatter in the correlation function computed from 50
mock VVDS surveys constructed using the GalICS simulations
(Blaizot et al. 2005), as thoroughly described in the parallel
paper by (Pollo et al. 2005).
These realistic mock samples specifically include the same
selection function and observational biases present in the
VVDS First Epoch data set, and allow us to compute
ensemble statistical averages and scatters of the quantities
we measure on the real data. In particular, the standard
deviation of the measured
![]() from the mock VVDS samples
provides us with a realistic set of error bars
that include also the effect of
field-to-field variations due to fluctuations on scales larger than the
observed field, i.e. cosmic variance (obviously assuming that the
from the mock VVDS samples
provides us with a realistic set of error bars
that include also the effect of
field-to-field variations due to fluctuations on scales larger than the
observed field, i.e. cosmic variance (obviously assuming that the
![]() -CDM power spectrum and normalization are a good match to the
observed one, which is indeed the case).
-CDM power spectrum and normalization are a good match to the
observed one, which is indeed the case).
The comparison of the VVDS-02h and VVDS-CDFS
correlation functions gives us an
external check to this procedure, with a
relatively noisy indication of the amplitude of cosmic variance,
as described below.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{1962fig3.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg62.gif) |
Figure 3:
The correlation function from the VVDS-02h data up
to |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{1962fig4.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg63.gif) |
Figure 4:
The correlation function
|
| Open with DEXTER | |
We have computed the correlation function
![]() and its projection
and its projection
![]() on both the VVDS-02h and
VVDS-CDFS fields.
on both the VVDS-02h and
VVDS-CDFS fields.
The correlation function
![]() is presented in the
left panel of Fig. 3 for the VVDS-02h field, and in Fig. 4
for the VVDS-CDFS field. The number of galaxies observed
in each field is indicated for each redshift bin
in Fig. 3, so far the largest sample of galaxies
used to compute the correlation function at these redshifts.
The large sample allows to compute
is presented in the
left panel of Fig. 3 for the VVDS-02h field, and in Fig. 4
for the VVDS-CDFS field. The number of galaxies observed
in each field is indicated for each redshift bin
in Fig. 3, so far the largest sample of galaxies
used to compute the correlation function at these redshifts.
The large sample allows to compute
![]() in 6 redshift bins up to z=2.1 for the VVDS-02h field,
and in 3 bins up to z=1.5 for the VVDS-CDFS field.
Error bars are ensemble errors computed
as described in Sect. 3.3.
A positive correlation signal is measured
out to at least 30 h-1 Mpc in all bins, and
in 6 redshift bins up to z=2.1 for the VVDS-02h field,
and in 3 bins up to z=1.5 for the VVDS-CDFS field.
Error bars are ensemble errors computed
as described in Sect. 3.3.
A positive correlation signal is measured
out to at least 30 h-1 Mpc in all bins, and
![]() is well described
by a power law in the range
is well described
by a power law in the range
![]() h-1 Mpc (note
however that any redshift space feature
in
h-1 Mpc (note
however that any redshift space feature
in ![]() is smoothed out in
is smoothed out in
![]() ,
which is its integral).
The measured correlation function
amplitude is relatively low at low redshifts
,
which is its integral).
The measured correlation function
amplitude is relatively low at low redshifts
![]() ,
and
stays essentially constant as a function of redshift, with just a
mild increase in the farthest bins.
A possible interpretation of these results is discussed in the next sections.
,
and
stays essentially constant as a function of redshift, with just a
mild increase in the farthest bins.
A possible interpretation of these results is discussed in the next sections.
The measured values of the correlation length
r0(z) and the correlation function slope
![]() computed from the fitting of
computed from the fitting of
![]() are reported in Table 1. For the
VVDS-02h field, we have used all
are reported in Table 1. For the
VVDS-02h field, we have used all ![]() points for
points for
![]() h-1 Mpc.
For the VVDS-CDFS field, we have used points in the range
h-1 Mpc.
For the VVDS-CDFS field, we have used points in the range
![]() h-1 Mpc only, because of the smaller
field size. We also report in Table 1 the values of
r0(z) obtained after fitting
h-1 Mpc only, because of the smaller
field size. We also report in Table 1 the values of
r0(z) obtained after fitting ![]() with the slope
with the slope ![]() fixed to the average slope measured in the range
z=[0.2, 1.3].
In the VVDS-CDFS, a strong wall-like
large scale structure has been identified
at
fixed to the average slope measured in the range
z=[0.2, 1.3].
In the VVDS-CDFS, a strong wall-like
large scale structure has been identified
at
![]() ,
with more than 130 galaxies
in a velocity range
,
with more than 130 galaxies
in a velocity range ![]() 2000 km s-1 (Le Fèvre et al. 2004b), and is
expected to strongly affect the correlation function
computation. The correlation
function in this field has been computed
in the redshift interval
z=[0.6, 0.8] which
includes this strong structure, as well as in
z=[0.4, 0.7]and
z=[0.8, 1.5] to specifically exclude it,
as reported in Table 1.
While we find a slightly higher correlation length in the
VVDS-CDFS, the measurements are compatible, within
the errors, with the values reported for the VVDS-02h.
2000 km s-1 (Le Fèvre et al. 2004b), and is
expected to strongly affect the correlation function
computation. The correlation
function in this field has been computed
in the redshift interval
z=[0.6, 0.8] which
includes this strong structure, as well as in
z=[0.4, 0.7]and
z=[0.8, 1.5] to specifically exclude it,
as reported in Table 1.
While we find a slightly higher correlation length in the
VVDS-CDFS, the measurements are compatible, within
the errors, with the values reported for the VVDS-02h.
We have investigated how our results change when
using the full set of available redshifts, i.e. including also the
1300 less accurate measurements (flag 1),
which are shown to be ![]() 55% correct (Le Fèvre et al. 2005).
The result is that the measured
correlation lengths are lowered by
55% correct (Le Fèvre et al. 2005).
The result is that the measured
correlation lengths are lowered by ![]()
![]() ,
which we interpret as
a consequence of the significant fraction of poorly measured redshifts
which dilute the actual correlation function.
,
which we interpret as
a consequence of the significant fraction of poorly measured redshifts
which dilute the actual correlation function.
The results strikingly show a slowly increasing correlation length
over the complete redshift range
z=[0.2, 2.1]. The lowest value
measured is in the lowest redshift bin probed, then r0is constant
![]() h-1 Mpc over the range
z=[0.5, 1.1] and increases slightly to
h-1 Mpc over the range
z=[0.5, 1.1] and increases slightly to
![]() h-1 Mpc
over
z=[1.1, 2.1]. When we fit the slope
h-1 Mpc
over
z=[1.1, 2.1]. When we fit the slope ![]() of the correlation function
at the same time as r0, it varies between 1.67 and 1.96, slightly
increasing with redshift, as reported
in Table 1. The average slope in the range
z=[0.2, 1.3] is
of the correlation function
at the same time as r0, it varies between 1.67 and 1.96, slightly
increasing with redshift, as reported
in Table 1. The average slope in the range
z=[0.2, 1.3] is
![]() .
.
In redshift surveys of the local Universe (z<0.2), the lowest values for the correlation length have been measured for late-type star forming galaxies as e.g. H-II galaxies (r0=2.7 h-1 Mpc, Iovino et al. 1988) and infrared-selected IRAS galaxies (r0=3.76 h-1 Mpc, Fisher et al. 1994). Here we measure an even lower correlation length for galaxies with z=[0.2, 0.5] in the VVDS, coherent with their very low intrinsic luminosity as discussed in Sect. 5.
In order to compare our measurements at higher redshifts
to the measurements
of the DEEP2 survey (Coil et al. 2004), we have restricted our data
by applying a-posteriori
the same color and magnitude selection function as the DEEP2 survey
applied a-priori to pre-select its spectroscopic targets
in the redshift range
0.7-1.35. With this "DEEP2'' selection function
(
![]() ,
,
![]() ,
,
![]() or
or
![]() )
only 59% of the VVDS I-band magnitude-limited sample galaxies are
selected (in the desired redshift range).
The correlation function
)
only 59% of the VVDS I-band magnitude-limited sample galaxies are
selected (in the desired redshift range).
The correlation function
![]() ,
and the
corresponding r0(z) and
,
and the
corresponding r0(z) and ![]() of this sample are shown in Fig. 5. We find that
of this sample are shown in Fig. 5. We find that
![]() h-1 Mpc for the full
z=[0.7, 1.35] sample,
compared to
h-1 Mpc for the full
z=[0.7, 1.35] sample,
compared to
![]() by Coil et al. (2004). Separating in
the same redshift bins, and setting the slope to
by Coil et al. (2004). Separating in
the same redshift bins, and setting the slope to
![]() as measured in DEEP2, we find that
as measured in DEEP2, we find that
![]() h-1 Mpc
in
z=[0.7, 0.9],
h-1 Mpc
in
z=[0.7, 0.9],
![]() h-1 Mpc in
z=[0.9, 1.35],
while Coil et al. (2004) find
h-1 Mpc in
z=[0.9, 1.35],
while Coil et al. (2004) find
![]() h-1 Mpc and
h-1 Mpc and
![]() h-1 Mpc, respectively, as shown
in Fig. 6. Given
the relative uncertainties of both surveys, these results
are therefore in excellent agreement.
The correlation function for the DEEP2 survey therefore
differs from the correlation function of the complete VVDS sample
because of the different selection function applied that
selects galaxies brighter than in the
VVDS and excludes galaxies relatively blue in R-I
(R-I<0.7) but still red
in B-R (B-R>0.6), resulting in a larger
correlation length.
h-1 Mpc, respectively, as shown
in Fig. 6. Given
the relative uncertainties of both surveys, these results
are therefore in excellent agreement.
The correlation function for the DEEP2 survey therefore
differs from the correlation function of the complete VVDS sample
because of the different selection function applied that
selects galaxies brighter than in the
VVDS and excludes galaxies relatively blue in R-I
(R-I<0.7) but still red
in B-R (B-R>0.6), resulting in a larger
correlation length.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{1962fig5.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg80.gif) |
Figure 5: Correlation function computed from the VVDS sample, applying the same color-magnitude selection function as for the DEEP2 survey (Coil et al. 2004): ( bottom) the full sample in the redshift range [0.7, 1.35], ( top two panels) the lower [0.7, 0.9] and higher [0.9, 1.35] redshift samples. The slope has been fixed to the same slope as measured in the DEEP2 to ease r0 comparison. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{1962fig6.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg81.gif) |
Figure 6:
Comparison of the correlation length r0(z) (comoving)
measured in the VVDS-Deep survey
applying a color-color and magnitude
selection as in the DEEP2 survey, and the DEEP2 survey
measurements (Coil et al. 2004): VVDS-02h, with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{1962fig7.ps}
\end{figure}](/articles/aa/full/2005/33/aa1962-04/Timg82.gif) |
Figure 7:
Evolution of the correlation length r0(z) (comoving) from the VVDS.
Black circles are for the VVDS-02h data, open squares are for the VVDS-CDFS
data. The doted points indicate the measurements
when setting the slope to the mean
|
| Open with DEXTER | |
The evolution of the clustering length r0(z) from the VVDS first
epoch "Deep'' sample of galaxies with
![]() is presented in Fig. 7. The redshift of each bin is computed
as the mean of the redshifts of galaxies in each bin.
We find that r0 is roughly constant or possibly
slightly increasing, within our measurement
errors, as redshift increases,
with a low value of
r0=2.35-0.37+0.36 h-1 Mpc for
z=[0.2,0.5],
to
r0=3.03-0.56+0.51 h-1 Mpc for
z=[1.3,2.1].
is presented in Fig. 7. The redshift of each bin is computed
as the mean of the redshifts of galaxies in each bin.
We find that r0 is roughly constant or possibly
slightly increasing, within our measurement
errors, as redshift increases,
with a low value of
r0=2.35-0.37+0.36 h-1 Mpc for
z=[0.2,0.5],
to
r0=3.03-0.56+0.51 h-1 Mpc for
z=[1.3,2.1].
Ideally, one would like to follow the evolution of the
clustering of the mass in the universe, translated into
the gravitational growth of structures. To access to this
measurement from the correlation
length of galaxies requires understanding of the evolution
of galaxies as complex physical systems,
and to be able to relate the populations of galaxies observed at different
redshifts as descendents of a well-identified original population
of matter halos at early epochs. Although the VVDS
I-band magnitude selection is the minimum selection bias one can
impose selecting a distant sample, this faint magnitude limit
leads to a broad redshift coverage, and to a population mix in the
VVDS sample that changes with redshift as described in Sect. 2.2.
Over the redshift range considered here, the
luminosity function of galaxies in the VVDS is strongly
evolving up to ![]() 1.5-2 mag (Ilbert et al. 2005).
The interpretation of the evolution of r0(z)is therefore not direct.
1.5-2 mag (Ilbert et al. 2005).
The interpretation of the evolution of r0(z)is therefore not direct.
In the lower redshift bin ![]() ,
we find a correlation
length smaller than any other population of galaxies observed today.
The mean absolute luminosity of the
low redshift sample is
MBAB=-17.5 with a significant
number of objects fainter than
MBAB=-16 (Fig. 2),
while bright galaxies are under-represented
due to the small volume available at these low redshifts.
Not surprisingly given the faint IAB=24 cutoff in the VVDS,
this makes it the faintest galaxy population
for which 3D clustering has ever been probed at low
redshifts, about 1.5 mag fainter than the 2dFGRS sample
with a mean
MbJ=-17.98 equivalent to
MBAB=-18.9 (Norberg et al. 2001).
This low clustering of the low luminosity population of galaxies
measured in the VVDS is roughly consistent with
an extrapolation to fainter luminosities of the trend
for a lower correlation length as galaxies become fainter,
as observed locally in the 2dFGRS and SDSS surveys
(Norberg et al. 2001; Zehavi et al. 2002), and at intermediate
redshifts in the CNOC2 survey (Shepherd et al. 2001).
,
we find a correlation
length smaller than any other population of galaxies observed today.
The mean absolute luminosity of the
low redshift sample is
MBAB=-17.5 with a significant
number of objects fainter than
MBAB=-16 (Fig. 2),
while bright galaxies are under-represented
due to the small volume available at these low redshifts.
Not surprisingly given the faint IAB=24 cutoff in the VVDS,
this makes it the faintest galaxy population
for which 3D clustering has ever been probed at low
redshifts, about 1.5 mag fainter than the 2dFGRS sample
with a mean
MbJ=-17.98 equivalent to
MBAB=-18.9 (Norberg et al. 2001).
This low clustering of the low luminosity population of galaxies
measured in the VVDS is roughly consistent with
an extrapolation to fainter luminosities of the trend
for a lower correlation length as galaxies become fainter,
as observed locally in the 2dFGRS and SDSS surveys
(Norberg et al. 2001; Zehavi et al. 2002), and at intermediate
redshifts in the CNOC2 survey (Shepherd et al. 2001).
As redshift increases, the VVDS probes
more of the bulk of the general population of galaxies.
Galaxies sampled at redshifts
0.5-1.1 become increasingly similar in luminosity and
color to the population sampled by the low
redshift 2dFGRS and SDSS surveys. As
can be seen from Fig. 2, at ![]() we
measure the clustering of galaxies with a mean absolute magnitude
MBAB=-18.5, after taking into
account
we
measure the clustering of galaxies with a mean absolute magnitude
MBAB=-18.5, after taking into
account ![]() 1 mag of luminosity brightening
at
1 mag of luminosity brightening
at ![]() (Ilbert et al. 2005), thus comparable
to the bulk of the galaxies probed by 2dF and SDSS at
(Ilbert et al. 2005), thus comparable
to the bulk of the galaxies probed by 2dF and SDSS at
![]() .
.
Over the redshift range
z=[0.5, 1.1],
we find a slightly increasing correlation length
![]() h-1 Mpc. For a similar, blue-selected, population of
galaxies at
h-1 Mpc. For a similar, blue-selected, population of
galaxies at
![]() ,
the 2dFGRS finds
,
the 2dFGRS finds
![]() h-1 Mpc
(Norberg et al. 2001), using the same technique we use here. Note that at a
redshift similar to the 2dFGRS, the SDSS tends to sample a different mix of
morphological types, due to its red-based selection, and for this
reason measures a larger correlation length,
h-1 Mpc
(Norberg et al. 2001), using the same technique we use here. Note that at a
redshift similar to the 2dFGRS, the SDSS tends to sample a different mix of
morphological types, due to its red-based selection, and for this
reason measures a larger correlation length,
![]() h-1 Mpc (Zehavi et al. 2002; see Hawkins et al. 2003, for discussion).
Our results
therefore seem to indicate that the amplitude of the correlation
function of galaxies which would have luminosities
MBAB=-19.5
after correction for luminosity evolution is
about 2.5 times lower at z=1 than observed locally by the
2dFGRS.
h-1 Mpc (Zehavi et al. 2002; see Hawkins et al. 2003, for discussion).
Our results
therefore seem to indicate that the amplitude of the correlation
function of galaxies which would have luminosities
MBAB=-19.5
after correction for luminosity evolution is
about 2.5 times lower at z=1 than observed locally by the
2dFGRS.
While we know that galaxies with similar luminosities at different redshifts may not be tracing the underlying dark matter in a similar way (see Marinoni et al. 2005), this result is in qualitative agreement with the expectations of the simple gravitational growth of primordial fluctuations (see e.g. Fig. 5 of Weinberg et al. 2004).
In the highest redshift bins
z=[1.1, 1.3] and
z=[1.3, 2.1],
we are measuring the correlation function
of the brightest
![]() galaxies,
with a mean of
galaxies,
with a mean of
![]() and
and
![]() -21.0 respectively. We observe that
the correlation length increases compared
to the measurements in the range
z=[0.5, 1.1], up to
-21.0 respectively. We observe that
the correlation length increases compared
to the measurements in the range
z=[0.5, 1.1], up to
![]() h-1 Mpc
at z=1.2 and
h-1 Mpc
at z=1.2 and
![]() h-1 Mpc in the highest redshift bin
to
h-1 Mpc in the highest redshift bin
to ![]() .
The luminosity function of galaxies at these redshifts
shows a marked evolution, equivalent to an increase in
luminosity of
.
The luminosity function of galaxies at these redshifts
shows a marked evolution, equivalent to an increase in
luminosity of ![]() 1.5 and
1.5 and ![]() 2 mag
in
z=[1.1, 1.3] and
z=[1.3, 2.1], respectively (Ilbert et al. 2005).
These galaxies will therefore be expected to have a mean
2 mag
in
z=[1.1, 1.3] and
z=[1.3, 2.1], respectively (Ilbert et al. 2005).
These galaxies will therefore be expected to have a mean
![]() at low redshifts after evolution. Again, comparing
the clustering observed in the VVDS to the clustering length
of
at low redshifts after evolution. Again, comparing
the clustering observed in the VVDS to the clustering length
of
![]() h-1 Mpc measured for
MBAB=-19.5 in the 2dFGRS
(Norberg et al. 2001), we find that the clustering amplitude
has increased by a factor
h-1 Mpc measured for
MBAB=-19.5 in the 2dFGRS
(Norberg et al. 2001), we find that the clustering amplitude
has increased by a factor ![]() 2.4 from
2.4 from
![]() to z=0.
to z=0.
The evolution of the correlation length observed in our data is
in broad agreement with the results of computer simulations
of galaxy formation and evolution. In their SPH simulation,
Weinberg et al. (2004) find that the clustering length of galaxies decreases
from
![]() h-1 Mpc at z=3 to a minimum
h-1 Mpc at z=3 to a minimum
![]() h-1 Mpc at z=1.5, then increases again to
h-1 Mpc at z=1.5, then increases again to
![]() h-1 Mpc at z=1. Note, however, that these
predictions refer to the correlation length of the same class of
galaxies, corresponding to
h-1 Mpc at z=1. Note, however, that these
predictions refer to the correlation length of the same class of
galaxies, corresponding to
![]() ,
ideally
followed at different redshifts. In a real, magnitude-limited
observation, as we have discussed, this effect is related to the
different range of luminosities sampled at each redshift, and the
changing clustering strength at different luminosities.
Besides the simulated clustering of galaxies,
the dark matter correlation
length is expected from theory and N-body simulations
to drop steeply with increasing redshift, from
,
ideally
followed at different redshifts. In a real, magnitude-limited
observation, as we have discussed, this effect is related to the
different range of luminosities sampled at each redshift, and the
changing clustering strength at different luminosities.
Besides the simulated clustering of galaxies,
the dark matter correlation
length is expected from theory and N-body simulations
to drop steeply with increasing redshift, from
![]() h-1 Mpc at z=0 to
h-1 Mpc at z=0 to
![]() h-1 Mpc at z=1.5(see e.g. Weinberg et al. 2004). In comparison to these predictions, our
data clearly show that the clustering evolution of galaxies
does not follow the predicted trend for dark matter.
h-1 Mpc at z=1.5(see e.g. Weinberg et al. 2004). In comparison to these predictions, our
data clearly show that the clustering evolution of galaxies
does not follow the predicted trend for dark matter.
We have computed the
evolution of the correlation function
![]() and its
integral along the line of sight
and its
integral along the line of sight
![]() ,
from the VVDS
first epoch "deep'' survey. The VVDS contains a large
spectroscopically-selected sample of 7155 galaxies representative
of the global galaxy population in the redshift range
z=[0, 2.1], in
a large 0.61deg2 total area.
The correlation length r0 is observed to be low,
,
from the VVDS
first epoch "deep'' survey. The VVDS contains a large
spectroscopically-selected sample of 7155 galaxies representative
of the global galaxy population in the redshift range
z=[0, 2.1], in
a large 0.61deg2 total area.
The correlation length r0 is observed to be low,
![]() h-1 Mpc, for the low
redshift
h-1 Mpc, for the low
redshift
![]() population, indicating the low
clustering of the very low
luminosity population sampled in this redshift range. Over the
redshift range
z=[0.5, 1.1], the correlation length of the population
of galaxies, with a luminosity range comparable to the lower redshift
2dFGRS and SDSS, stays roughly constant with
population, indicating the low
clustering of the very low
luminosity population sampled in this redshift range. Over the
redshift range
z=[0.5, 1.1], the correlation length of the population
of galaxies, with a luminosity range comparable to the lower redshift
2dFGRS and SDSS, stays roughly constant with
![]() h-1 Mpc.
At the highest redshifts probed in this paper,
z=[1.1, 2.1], we find
that the correlation length increases slightly to
h-1 Mpc.
At the highest redshifts probed in this paper,
z=[1.1, 2.1], we find
that the correlation length increases slightly to
![]() h-1 Mpc.
h-1 Mpc.
After applying the same selection function as
in the DEEP2 survey, our results are found to be in excellent
agreement with the results of Coil et al. (2004).
However, the significantly different DEEP2 selection function
excludes up to 41% of the galaxy population observed by the VVDS,
making the correlation length of the DEEP2 sample larger than
in the purely magnitude-selected VVDS. The VVDS results demonstrate
that the clustering of the whole
galaxy population at the same redshift is indeed significantly lower,
with
![]() in the VVDS vs.
in the VVDS vs.
![]() h-1 Mpc
in the DEEP2,
further emphasizing the importance of our simple, purely
magnitude-limited selection function.
h-1 Mpc
in the DEEP2,
further emphasizing the importance of our simple, purely
magnitude-limited selection function.
Our measurements clearly show that the correlation length
evolves only slowly with redshift
in the range
![]() ,
in
a magnitude limited sample with
,
in
a magnitude limited sample with
![]() .
Taking into account the different
VVDS galaxy populations probed as a function of redshift, with
intrinsically brighter galaxies probed
as redshift increases, we find that
the clustering of galaxies at
.
Taking into account the different
VVDS galaxy populations probed as a function of redshift, with
intrinsically brighter galaxies probed
as redshift increases, we find that
the clustering of galaxies at
![]() in the VVDS
is about 2.5 times lower in amplitude than for the
galaxies probed by the 2dFGRS at
in the VVDS
is about 2.5 times lower in amplitude than for the
galaxies probed by the 2dFGRS at ![]() ,
for populations with similar absolute MB magnitudes.
This result provides unambiguous evidence for clustering
evolution.
,
for populations with similar absolute MB magnitudes.
This result provides unambiguous evidence for clustering
evolution.
Our results are in broad agreement with simulations accounting for both gravitational growth and baryonic physics (Benson et al. 2001; Weinberg et al. 2004). These simulations show that the underlying dark matter correlation evolves strongly with redshift, as expected in a hierarchical growth of structures. Our observation that the clustering of galaxies does not follow such a strong evolution therefore fully supports the model in which luminous galaxies at z=1-2 (or 9-10 billion years ago) trace the emerging peaks of the large-scale dark-matter distribution and implies a strongly evolving galaxy bias.
We will investigate the evolution of the galaxy - dark matter bias elsewhere (Marinoni et al. 2005). A more detailed study of the dependance of clustering on luminosity and galaxy type will be presented in forthcoming papers.
Acknowledgements
This research has been developed within the framework of the VVDS consortium (formerlly VIRMOS consortium).
This work has been partially supported by the CNRS-INSU and its Programme National de Cosmologie (France), and by Italian Research Ministry (MIUR) grants COFIN2000 (MM02037133) and COFIN2003 (No. 2003020150).
The VLT-VIMOS observations have been carried out on guaranteed time (GTO) allocated by the European Southern Observatory (ESO) to the VIRMOS consortium, under a contractual agreement between the Centre National de la Recherche Scientifique of France, heading a consortium of French and Italian institutes, and ESO, to design, manufacture and test the VIMOS instrument.