A&A 439, L27-L30 (2005)
DOI: 10.1051/0004-6361:200500151

An explanation for the kHz-QPO twin peaks separation in slow and fast rotators

J. Pétri

Max-Planck-Institut für Kernphysik, Saupfercheckweg 1, 69117 Heidelberg, Germany

Received 10 June 2005 / Accepted 6 July 2005

Abstract
In this Letter we further explore the idea, suggested previously by Kluzniak and collaborators, that the high frequency QPOs may be explained as a resonant coupling between the neutron star spin and two epicyclic modes of accretion disk oscillations. We confirm result of Lee et al. (2004, ApJ, 603, L93) that the strongest response occurs when the frequency difference of the two modes equals either the spin frequency (for "slow rotators'') or half of it (for "fast rotators''). New points discussed in this Letter are: (1) we suggest that the coupling is gravitational, and due to a non-axially symmetric structure of the rotating neutron star; (2) we found that two excited modes may be both connected to vertical oscillations of the disk, and that strong gravity is not needed to excite the modes.

Key words: accretion, accretion disks - hydrodynamics - methods: analytical - relativity - stars: neutron - X-rays: binaries

1 Introduction

To date, quasi-periodic oscillations (QPOs) have been observed in about twenty Low Mass X-ray Binaries (LMXBs) sources containing an accreting neutron star. Among these systems, the high-frequency QPOs (kHz-QPOs) which mainly show up by pairs, denoted by frequencies $\nu_1$ and $\nu_2>\nu_1$, possess strong similarities in their frequencies, ranging from 300 Hz to about 1300 Hz, as well as in their shape (see van der Klis 2000 for a review). For slow rotators (i.e. with rotation rate $\nu_* \approx 300$ Hz), the frequency difference between the two peaks is around $\Delta \nu \approx \nu_*$ and  $\nu_2 \approx 3~\nu_1/2$ whereas for fast rotators (i.e. $\nu_*\approx 600$ Hz), this difference is around $\Delta \nu \approx \nu_*/2$, (van der Klis 2004). For black hole candidates the 3:2 ratio was first noticed by Abramowicz & Kluzniak (2001) who also recognized and stressed its importance. Now the 3:2 ratio of black hole QPOs frequencies is well established (McClintock & Remillard 2003).

Many attempts have been made to explain this phenomenology. The relativistic precession model introduced by Stella & Vietri (1998, 1999) makes use of the motion of a single particle in the Kerr-spacetime. However, the peak separation is not naturally deduced from their model. More promisingly, Abramowicz & Kluzniak (2001) introduced a resonance between orbital and epicyclic motion that can account for the 3:2 ratio around Kerr black holes leading to an estimate of their mass and spin. Kluzniak et al. (2004a) showed that the twin kHz-QPOs is explained by a non linear resonance in the epicyclic motion of the accretion disk. Rebusco (2004) developed the analytical treatment of these oscillations. Bursa et al. (2004) suggested a gravitational lens effect exerting a modulation of the flux intensity induced by the vertical oscillations of the disk while simultaneously oscillating radially. More recently, Török et al. (2005) applied this resonance to determine the spin of some microquasars.

It was recognized (Kluzniak et al. 2004a,b) that because in the accreting millisecond pulsar SAX J1808.4-3658 the difference in frequencies of the double peaked QPOs is clearly equal to half of the pulsar spin (Wijnands et al. 2003), the epicyclic resonance must be excited by a coupling of the accretion disk oscillation modes to the neutron star spin. Numerical simulations by Lee et al. (2004) modelled the coupling by an unspecified external forcing of the disk (with periodicity equal to that of the spin) and found that resonant response occurs when the difference between frequencies of the two modes equals to one-half of the spin frequency (as observed in SAX J1808.4-3658 and other "fast rotators''), and when it equals to the spin frequency (as observed in "slow rotators'' like XTE J1807-294).

In this Letter we further explore these ideas by showing that the desired coupling may be provided by gravity of a sufficiently non-axially symmetric neutron star. (Discussion of a physical plausibility of non-axially symmetric neutron stars is beyond the scope of this Letter.) In such a case, the accretion disk will experience a gravitational field with dipolar, quadrupolar and octupolar moments (m=1, 2, 3) that vary periodically in time.

   
2 The model

In this section, we describe the main features of the model, starting with a simple treatment of the accretion disk, assumed to be made of non interacting single particles orbiting in the equatorial plane of the star. We thus neglect the hydrodynamical aspect of the disk like pressure. Particles evolve in a perfectly spherically symmetric gravitational potential until, at the origin of time t=0, a rotating asymmetric part is added to the stellar gravitational field. This perturbation is issued from an inhomogeneity in the neutron star interior, for instance, as explained in the following subsection.

2.1 Distorted stellar gravitational field

We assume that the stellar interior is inhomogeneous and anisotropic. In some regions inside the star, clumps of matter generate locally a stronger or weaker gravitational potential than the average, depending on their density. In order to compute analytically such kind of gravitational field, we idealize this situation by assuming that the star is made of an homogeneous and isotropic matter everywhere (with total mass M* and angular speed $\Omega_*$). To this perfect spherically symmetric geometry, we add a small mass point, the perturber having a mass  $M_{\rm p}\ll M_*$ located inside the star at a position  $\vec{R}_{\rm p} = (r_{\rm p}, \varphi_{\rm p} = \Omega_*~t, z_{\rm p})$ with $r_{\rm p}^2 + z_{\rm p}^2 \le R_*^2$. We use cylindrical coordinates denoted by  $\vec{R}=(r, \varphi, z)$. The origin of the coordinate system coincides with the location of the neutron star. A finite size inhomogeneity can then be thought as a linear superposition of such point masses. The total gravitational potential induced by this idealized rotating inhomogeneous star is:

 \begin{displaymath} \Phi(r,\varphi,z,t) = - G~M_* / \vert\vert \vec{R} \vert\ve... ... G~M_{\rm p} / \vert\vert \vec{R} - \vec{R}_{\rm p} \vert\vert \end{displaymath} (1)

where the first term in the right hand side corresponds to the unperturbed spherically symmetric gravitational potential whereas the second term is induced by the small point like inhomogeneity. Using the cylindrical frame of reference, the gravitational potential reads:

 \begin{displaymath} \Phi(r,\varphi,z,t) = - G~M_* / \sqrt{r^2+z^2} - G~M_{\... ...{\rm p}^2+z_{\rm p}^2} / \sqrt{r^2+z^2} \right) \cos(m~\psi) \end{displaymath} (2)

where the azimuth in the corotating frame is  $\psi = \varphi - \Omega_* ~ t$ and the Laplace coefficients  bmn(x) of celestial mechanics are:

 \begin{displaymath} b_m^{n}(x) = \frac{2-\delta_m^0}{2~\pi} ~ \int_0^{2~\pi} \frac{ \cos(m~\psi)}{(1 + x^2 - 2~x~\cos\psi)^n } ~ {\rm d}\psi \end{displaymath} (3)

where $\delta_m^0$ is the Kronecker symbol. The total linear response of the disk is then the sum of each perturbation corresponding to one particular mode m. Because the perturber is inside the star and the disk never reaches the stellar surface, x<1 and thus the Laplace coefficients  bm1/2(x) never diverge. Moreover, because of the term  $\cos(m~\psi)$ in the integrand Eq. (3), the value of the Laplace coefficients decreases rapidly with the azimuthal number m. As a result, only the low azimuthal modes will influence significantly the evolution of the disk. Keeping only the few first terms in the expansion is sufficient to achieve reasonable accuracy.

2.2 Equation of motion for a test particle

All particles evolve in the gravitational field imposed by the neutron star. Their equation of motion reads

   
$\displaystyle \ddot{r} - r ~ \dot{\varphi}^2$ = $\displaystyle g_{\rm r} + \delta g_{\rm r}$ (4)
$\displaystyle 2 ~ \dot{r} ~ \dot{\varphi} + r ~ \ddot{\varphi}$ = $\displaystyle \delta g_\varphi$ (5)
$\displaystyle \ddot{z}$ = $\displaystyle g_{z} + \delta g_{z}.$ (6)

The gravitation field of the star $M_{\rm *}$ is denoted by $\vec{g}$ whereas that of the perturber $M_{\rm p}$ is denoted by  $\delta\vec{g}$ and the dot means time derivative ${\rm d}/{\rm d}t$. We are only interested in the vertical motion experienced by the test particles in response to the vertical perturbed gravitational field. We therefore neglect the radial and azimuthal perturbations, $\delta g_{\rm r} = \delta g_\varphi = 0$. We keep only the vertical component, $\delta g_{z}\ne0$. According to this simplification, the second equation then integrates immediately. It states the conservation of the angular momentum of the particle $L = m~r^2~\dot{\varphi} = {\rm const}$. This is the obvious integral of motion for this problem.

Perturbing Eq. (6) and developing to first order in the perturbation around the equilibrium Keplerian orbit defined by $(r = r_0, \varphi = \Omega_{\rm k}~t, z_0=0)$, the vertical motion reads:

 \begin{displaymath} \ddot{z} + \left ( \Omega_{\rm k}^2 + \Omega_{\rm p}^2 ~ ... ... b_m^{3/2~(0)} ~ \cos ~ ( m ~ (\Omega_{\rm k}-\Omega_*) ~ t) \end{displaymath} (7)

where the Laplace coefficient are evaluated at the point (r0,z0), $b_m^{3/2~(0)} = b_m^{3/2} \left( \sqrt{r_{\rm p}^2 + z_{\rm p}^2}/\sqrt{r_0^2+z_0^2} \right)$, $\Omega_{\rm k} = (G~M_*/r_0^3)^{1/2}$ is the Keplerian orbital frequency and $\Omega_{\rm p} = (G~M_{\rm p}/r_0^3)^{1/2}$. We recognize a Hill equation (periodic variation of the eigenfrequency of the system on the left hand side) with a periodic driving force (on the right hand side).

2.3 Resonance conditions

Equation (7) describes an harmonic oscillator with periodically varying eigenfrequency which is also excited by a driven force. It is well known that some resonances will therefore occurs in this system. Namely, we expect three kind of resonances corresponding to:

where $n\ge 1$ is a natural integer. Note that the driven resonance is a special case of the the parametric resonance for n=2. However, their growth rate differ by the timescale of the amplitude magnification. Driving causes a linear growth in time while parametric resonance causes an exponential growth. We also rewrite the vertical epicyclic frequency as  $\kappa_{z}$ instead of  $\Omega_{\rm k}$ in order to apply the results to a more general case which could include magnetic field or general relativistic effects. Indeed, in Sect. 3 we will apply the aforementioned resonance criteria also to the Kerr spacetime for which the degeneracy between orbital and vertical epicyclic frequency is lifted ( $\kappa_{z} \ne \Omega_{\rm k}$).

   
3 Results

3.1 Newtonian disk

From Eq. (8), we can find the radius where each of this resonance will occur. Beginning with the Newtonian potential, it is well known that the angular velocity and the vertical epicyclic frequencies for a single particle are equal so that  $\Omega_{\rm k} = \kappa_{z}$. This conclusion remains true for a thin accretion disk having  $c_{\rm s} / r ~ \Omega_{\rm k} \ll 1$where $c_{\rm s}$ is the sound speed. Distinguishing between the two signs of the absolute value, we get for the parametric resonance condition Eq. (8) the following orbital rotation rate:

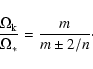\begin{displaymath}\frac{\Omega_{\rm k}}{\Omega_*} = \frac{m}{m \pm 2/n}\cdot \end{displaymath} (9)

As a consequence, the resonances are all located in the frequency range  $\Omega_{\rm k}\in[\Omega_*/3, 3~\Omega_*]$. In Table 1, we indicate the results for a slow as well as for a fast rotator (respectively $\nu_*=300$ Hz and $\nu_*=600$ Hz). Numerical applications are given for a spinning neutron star, showing the first three modes m and the first two integers n=1,2. The pair of highest orbital frequencies for the $\nu_*=300$ Hz spinning neutron star are $\nu_1 = 600$ Hz and $\nu_2 = 900$ Hz. The twin peak separation frequency is then  $\Delta\nu = 300~{\rm Hz} = \nu_*$. The vertical motion induced by the parametric resonance at that location will appear as a modulation in the luminosity of the accretion disk. For the $\nu_*=600$ Hz spinning neutron star, the highest orbital frequencies are 1800 Hz and 1200 Hz. However, due to the ISCO, the former one is not observed because it is located inside the ISCO and therefore does not correspond to a stable orbit. Indeed, remind that for a $1.4~M_\odot$ neutron star, the maximal orbital frequency in the Schwarzschild spacetime at the ISCO is $\nu_{\rm isco} = 1571$ Hz. Therefore, the first two highest observable frequencies are $\nu_1=900$ Hz and $\nu_2=1200$ Hz. This is confirmed in the next subsection where the Newtonian field is replaced by the Kerr geometry. The peak separation frequency becomes then  $\Delta\nu = 300$ Hz $= \nu_*/2$. Thus the peak separation for slow spinning neutron stars is $\Delta\nu = \nu_*$ whereas for fast spinning neutron star it becomes $\Delta\nu = \nu_*/2$. This segregation between slow and fast rotating neutron stars is well observed in several accreting systems (van der Klis 2004). A similar reason for the dichotomy between fast and slow rotators (location of the resonance radius), was previously suggested by Lee et al. (2004).

Table 1: Value of the orbital frequencies at the parametric resonance for the first three modes m and with n=1,2, in the case of a Newtonian gravitational potential. The results are given for a  $1.4~M_\odot$ neutron star rotating respectively at 300 and 600 Hz. The value on the left of the symbol/corresponds to the absolute value sign taken to be - and on the right to be +.

3.2 General relativistic disk

When the inner edge of the accretion disk reaches values of a few gravitational radii, the general relativistic effects become important. The degeneracy between the frequencies  $\Omega_{\rm k}$and  $\kappa_{z}$ is lifted and will depend on the angular momentum of the star. The characteristic orbital and vertical epicyclic frequencies in the accretion disk around a Kerr black hole (or a rotating neutron star) are the orbital angular velocity, $\Omega(r,a_*) = G~M_*/(r^{3/2} + R_{\rm g}^{3/2} ~ a_*)$ where $R_{\rm g} = G~M_*/c^2$ is the gravitational radius and the vertical epicyclic frequency,  $\kappa_{z}(r,a_*) = \Omega(r,a_*)~\sqrt{1 -4~(R_{\rm g}/r)^{3/2} ~ a_* + 3 ~ (R_{\rm g} / r )^2 ~ a_*^2 }$. The parameter a* corresponds to the angular momentum of the star, in geometrized units. For a neutron star of mass M*, moment of inertia I* and rotating at the angular velocity $\Omega_*$, it is given by $a_* = c~ I_* ~ \Omega_*/ G~ M_*^2$. The parametric resonance conditions Eq. (8) splits into two cases, depending on the sign of the absolute sign:

 \begin{displaymath} \Omega(r,a_*) \pm \frac{2~\kappa_{z}(r,a_*)}{m~n} = \Omega_* . \end{displaymath} (10)

For a given angular momentum a*, Eq. (10) have to solved for the radius r. For a neutron star, we adopt the typical parameters: The angular momentum is then given by  $a_* = 5.79 \times10^{-5} ~ \Omega_*$. Solving Eq. (10) for the radius and then deducing the orbital frequency at this radius we get the results shown in Table 2. For the above chosen stellar spin rate we find  a*=0.1/0.2 for the slow and fast rotator respectively. Therefore the vertical epicyclic frequency remains close to the orbital one  $\kappa_{z} \approx \Omega_{\rm k}$. As a consequence, for the vertical resonance, the Newtonian approximation mentioned in the previous subsection remains valid. Indeed, for a slow rotator, the two highest frequencies are  $\nu_1 = 599$ Hz and  $\nu_2 = 898$ Hz, therefore $\Delta\nu = 299$ Hz which is still very close to $\nu_*$ whereas for a fast rotator, $\nu_1 = 899$ Hz and  $\nu_2 = 1198$ Hz, therefore $\Delta\nu = 299$ Hz which is close to $\nu_*/2$(the orbit located within the ISCO has been discarded). Numerical simulations in which the disk was disturbed by an external periodic field confirmed this point of view (Lee et al. 2004). We emphasize the fact that these results apply to a rotating asymmetric magnetic field with exactly the same resonance conditions Eq. (8) provided that the flow is not to far from its Keplerian motion, i.e. a weakly magnetized accretion disk with high $\beta$-plasma parameter. Note also that these results are quiet general and independent of the spacetime geometry. General relativity is not required to account for the 3:2 ratio. This model therefore also encompasses the accreting white dwarfs for which QPOs have been observed in the same 3:2 ratio and show strong similarities with X-ray binaries (Warner & Woudt 2005).

Table 2: Same as Table 1 but in the general relativistic Kerr spacetime.

   
4 Conclusion

In this Letter, the consequences of a weak rotating asymmetric gravitational potential perturbation on the evolution of a thin accretion disk initially in a stationary axisymmetric state have been explored. For gravitational perturbation with multipolar components, the response of the disk is the sum of individual modes as long as it remains in the linear regime. The physical processes at hand does not require any general relativistic effect. Indeed, the resonances behave identically in the Newtonian as well as in the Kerr field. As a consequence, the QPO phenomenology is unified in a same picture, whatever the nature of the compact object. Indeed, observations in accretion disks orbiting around white dwarfs, neutron stars or black holes have shown a strong correlation between their low and high frequencies QPOs (Mauche 2002; Psaltis et al. 1999). The relation is found to be same irrespective of the nature of the compact object. This strongly supports the idea of one and same general mechanism at hand in this accretion disks. The twin peaks ratio around 3:2 for the kHz-QPOs is naturally explained not only for black hole candidates or neutron stars but also for white dwarfs as reported by Warner et al. (2003). Indeed, the presence or the absence of a solid surface, a magnetic field or an event horizon play no relevant role in the production of the X-ray variability (Wijnands 2001). The twin peak separation being either $\Delta\nu = \nu_*$ for slow rotator ( $\nu_* \approx 300$ Hz) or $\Delta\nu = \nu_*/2$ for fast rotator ( $\nu_*\approx 600$ Hz) is also explained. Indeed, it was previously argued by Kluzniak et al. (2005) that the 3:2 QPOs recently observed in white dwarf sources by Warner & Woudt (2005) have the same nature as the strong gravity 3:2 QPOs observed in neutron star and black hole sources. All of them areresonant accretion disk oscillations. Differences are attributed to different modes that are involved, to different mechanisms of resonance excitation, and to different modulations of the X-ray flux.

To conclude, to date we know about 20 LMXBs containing a neutron star and all of them show kHz-QPOs. These QPOs can be explained by a mechanism similar to those exposed here. We need only to replace the gravitational perturbation by a magnetic one as described in Pétri (2005). However, in an accreting system in which the neutron star is an oblique rotator, we expect a perturbation in the magnetic field to the same order of magnitude than the unperturbed one. Therefore, the linear analysis developed in this paper has to be extended to oscillations having non negligible amplitude compared to the stationary state. Nonlinear oscillations therefore arise naturally in the magnetized accretion disk, leading to a shift in the resonance criteria and accounting for a change in the peak separation in relation with the accretion rate.

Acknowledgements
I am grateful to the referee Marek A. Abramowicz for his valuable comments and remarks. This work was supported by a grant from the G.I.F., the German-Israeli Foundation for Scientific Research and Development.

References

 
Copyright ESO 2005