A&A 439, 551-558 (2005)
DOI: 10.1051/0004-6361:20052911

Structure in the motions of the fastest halo stars

P. Re Fiorentin 1,2 - A. Helmi 3 - M. G. Lattanzi 2 - A. Spagna 2


1 - Dipartimento di Fisica Generale, via Pietro Giuria 1, 10125 Torino, Italy
2 - INAF - Osservatorio Astronomico di Torino, Strada dell'Osservatorio 20, 10025 Pino Torinese, Italy
3 - Kapteyn Astronomical Institute, PO Box 800, 9700 AV Groningen, The Netherlands

Received 21 February 2005 / Accepted 2 April 2005

Abstract
We analyzed the catalog published by Beers et al. (2000, ApJ, 119, 2866) of 2106 non-kinematically selected metal poor stars in the solar neighborhood, with the goal of quantifying the amount of substructure in the motions of the fastest halo stars. We computed the two-point velocity correlation function for a subsample of halo stars within 1-2 kpc of the Sun, and found statistical evidence of substructure with a similar amplitude to that predicted by high resolution CDM simulations. The signal is due to a small kinematic group whose dynamical properties are compared to the stellar "stream'' previously discovered by Helmi et al. (1999). If real, this high velocity moving group would provide further support for the idea that substructures remain as fossils from the formation of the Galaxy as expected in the CDM scenario.

Key words: Galaxy: formation - Galaxy: halo - Galaxy: kinematics and dynamics

1 Introduction

Observations of metal-poor stars have been used many times to discriminate between alternative galaxy formation scenarios (e.g.,  Searle & Zinn 1978; Eggen et al. 1962), although not yet conclusively. In recent years, considerable effort has been made toward understanding the properties of galaxies within the hierarchical paradigm of structure formation in the Universe which, so far, looks like the most successful theory. In a CDM Universe, the first objects to form are small galaxies which then merge and give rise to the larger scale structures we observe today. Thus, structure formation occurs in a "bottom up'' fashion. This theory predicts the presence of substructures (tidal tails, streams) due to the mergers and accretion that galaxies have experienced over their lifetimes.

Direct comparisons to observations have shown that this model can reproduce the properties of both the local and the distant Universe. Several examples of mergers and galaxy interactions have been observed in the Milky Way, such as the disrupted Sagittarius and Canis Major dwarf galaxies (e.g., Martin et al. 2004; Ibata et al. 1995), the phase-space stream of halo stars in the solar neighborhood (Helmi et al. 1999) and the ring in the outer Galaxy (Newberg et al. 2002). Similar substructures have also been found in the halos of other nearby galaxies, such as M 31 (Ferguson et al. 2002) and NGC 5907 (Zheng et al. 1999), showing that accretion may be a common phenomenon in the evolution of galaxies.

Although the stellar halo accounts for only about $1\%$ of the luminous mass, it plays a crucial role in studies of the formation and evolution of the Galaxy. Signatures of the hierarchical nature of galaxy assembly are expected to be most obvious in this component. Moreover, stars in the halo are generally very old and metal poor; i.e. they can be considered more pristine. These are, in fact, the stars thought to have been formed in satellite galaxies that merged to form our Galactic halo (Robertson et al. 2005).

At present, the best measurements of the halo kinematics are obtained from analysis of samples of stars located in the solar neighborhood. Studies of the kinematics of various stellar populations in the Galaxy have long been limited - especially for the inner Halo - by the lack of large samples of stars with accurate distances, metallicity, and kinematics.

Beers et al. (2000) compiled an extensive catalog of metal-poor stars selected without kinematic bias and with available proper motions, radial velocities, and distance estimates for stars with a wide range of metal abundances. In this paper we analyze this data-set, which has already provided support for constraining plausible scenarios for the formation and evolution of the Milky Way (e.g., Chiba & Beers 2000,2001).

In Sect. 2, we assemble a sample of metal-deficient ( ${\rm [Fe/H]\le -1.5~dex}$) halo stars up to 2 kpc of the Sun selected from the Beers et al. (2000) catalog. In Sect. 3, we explore their phase-space distribution and quantify clustering by means of the two-point correlation analysis. In Sect. 4, we compare our results to theoretical predictions from CDM simulations. In Sect. 5, we further examine evidence for kinematic substructure in the space of adiabatic invariants, and our conclusions are given in Sect. 6.

2 Halo samples from the Beers et al. (2000) catalog

Beers et al. (2000) presented a revised large catalog of 2106 metal-poor stars in the solar neighborhood selected without kinematic bias. Within this sample, 1258 stars have distance estimates and radial velocities, as well as proper motions, so that the three components of the space velocities can be derived.

Throughout this work we adopted Galactic velocity components relative to the Galactic center, where as usual U, V, and W are positive toward the center in the direction of the rotation and toward the north Galactic pole, respectively. We assumed that the local standard of rest (LSR) rotates with a velocity of $220~{\rm km~s^{-1}}$ about the Galactic center and that the peculiar velocity of the Sun relative to the LSR is given by $(10.00,~5.25,~7.17)~{\rm km~s^{-1}}$(Dehnen & Binney 1998).

2.1 Selection criteria and selected sets

Since we were interested in constructing a sample of halo stars, we only considered those stars in the Beers et al. (2000) catalog with metallicities ${\rm [Fe/H]\le -1.5}$ dex.

To minimize any possible contamination from the thick disk, we further excluded low metallicity stars near the plane and with coplanar and circular orbits, i.e. with disk-like kinematics. Assuming an exponential thick disk with scale height $0.8~{\rm kpc}<h_Z<1.5~{\rm kpc}$ (Robin et al. 1996; Reid & Majewski 1993) and with a velocity ellipsoid $(\sigma_R,~\sigma_{\phi},~\sigma_Z;~\langle V_{\phi}\rangle) = (61,~58,~39;~-36)~{\rm km~s^{-1}}$ (Binney & Merrifield 1998), we excluded those stars for which the following conditions are simultaneously satisfied: $\vert Z \vert \le 1.5$ kpc, $126~{\rm km~s^{-1}}\le V_{\phi}\le 242~{\rm km~s^{-1}}$, $\vert V_R\vert \le 61~{\rm km~s^{-1}}$, low angular momentum ${L_{xy}=\sqrt{L_x^2+L_y^2}}$ with respect to Lz, namely ${\vert{\vec L}\vert \le 1.1~L_z}$.

Table 1: Selected sets of metal deficient ( ${\rm [Fe/H]\le -1.5~dex}$) halo stars. See text for explanation.

The remaining stars define our selected sample, which contains 192 stars within 1 kpc and 410 within 2 kpc of the Sun. These sets include subdwarfs, giants, and variables, as described in Table 1, with the following properties:

3 Kinematic analysis


  \begin{figure} \par\includegraphics[angle=0,width=13.5cm]{2911fig1.ps} \end{figure} Figure 1: Distribution of nearby halo stars in velocity space for our selected sample with ${\rm [Fe/H]\le -1.5}$ dex within 1 kpc of the Sun. ( a)-c)) Velocity projections in the (U, V, W) space; d) Velocity direction: the position of each particle is given by the spherical angular coordinates ${\mbox{\boldmath $\alpha$ }}=(\phi, \theta)$ of the velocity vector. Of the 192 stars present in this volume, the 5% fastest are highlighted as light color dots. Among them, the asterisks identify those objects/groups with velocity difference less than ${\rm 42~km~s^{-1}}$.
Open with DEXTER

Analytic arguments and high-resolution cosmological simulations of the formation of dark matter halos (Helmi & White 1999; Helmi et al. 2002; Moore et al. 2001) suggest that the halo should be spatially smooth in the Solar neighborhood, although see some recent discussion in Diemand et al. (2005) and Zhao et al. (2005). This is also supported by measurements of the degree of lumpiness in the angular distribution of halo stars (e.g. Lemon et al. 2004). However, the same simulations predict that while the kinematics of halo objects near the Sun can be represented by a smooth multivariate Gaussian distribution, the motions of the most energetic particles should be strongly clumped and anisotropic. This result has motivated us to analyze the kinematics of the halo samples we identified above in more detail.

3.1 Velocity distribution

The motion of each star in the sample can be specified by the velocity vector ${\vec v}=(U,~V,~W)$ in 3D linear space, as well as in 2D angular space, by spherical angular coordinates ${\rm\mbox{\boldmath$\alpha$ }}=(\phi,~\theta)$, where $\sin{\theta} = V_z/\vert{\vec v}\vert$ and $\tan\phi = V_y/V_x$. Figure 1 shows the kinematic distribution of the selected sample within 1 kpc. In Figs. 1a-c we plot the U, V, Wvelocities, while Fig. 1d shows the distribution of velocity directions $\mbox{\boldmath$\alpha$ }=(\phi,~\theta)$.

The velocity distribution is relatively smooth and appears to be consistent with a Gaussian Schwarzschild distribution. The mean velocities are $(\langle U\rangle,~\langle V+220\rangle,~\langle W\rangle)= (-26\pm 11,~21\pm 8,~-1\pm 7)~{\rm km~s^{-1}}$, and the velocity ellipsoid is radially elongated, namely $(\sigma_U,~\sigma_V,~\sigma_W)=(150\pm 8,~106\pm 5,~96~\pm~5)~\rm {km~s^{-1}}$. However, a smooth description does not seem to reproduce the kinematics of the fastest objects, as shown by the highlighted points. The 5% fastest moving stars (light color dots) seem to be more clumped. The characteristics of the observed velocity distribution appear to agree roughly with the results of CDM simulations, as we shall show in Sect. 4.

We performed two different statistical tests on the data with the aim of quantifying the presence of large and small scale anisotropies in the motions of our stars. To establish the significance of our results we then compared our results to suitable Monte Carlo simulations.

Our synthetic data sets have the same number of stars and the same spatial distribution as the observed sample. The characteristic parameters of the multivariate Gaussian used to describe the kinematics were obtained by fitting to the observed mean values and variances after appropriate convolution with observational errors. We generated 100 "observed'' samples as follows. A velocity was drawn from the underlying multivariate Gaussian, which was transformed to a proper motion and radial velocity (assuming the observed parallax and position on the sky). Observational "errors'' of the magnitude described in Sect. 2 were added to the parallax, the radial velocity, and the proper motion, and these "observed'' quantities then transformed back to an "observed'' velocity.

The first test we performed on the data consists in quantifying the presence of large-scale anisotropies. We implemented this test by partitioning the 2D angular space $(\phi,~\theta)$ - see Fig. 1d - into cells with roughly similar area. We then counted how many stars fall in each cell and compared it to the expected number in our Monte Carlo simulations. Figure 2 shows the results for the partition with 24 cells (with an area of 1800-1500 deg2) along 4 strips: $0^\circ<\vert\theta\vert<45^\circ$ (with $\Delta\phi=45^\circ$) and $45^\circ<\vert\theta\vert<90^\circ$ (with $\Delta\phi=90^\circ$). Plotted are the counts in each cell for the selected halo sample within 1 kpc of the Sun (solid line) and for the average of 100 Monte Carlo realizations (dashed line). The east-west large-scale anisotropy seen in this figure is due to the radially elongated velocity ellipsoid in combination with a small amount of prograde rotation.

At the $1\sigma$ level we found an excess of stars due to residual contamination from the thick-disk ( $\phi\sim 90^\circ$) and a lack of stars moving toward the SGP ( $\theta\sim -90^\circ$). In this regard, it is interesting to note that this deficiency is at odds with some models of the Sagittarius dwarf evolution which predict the presence of a stellar stream that should cross the Solar neighborhood. The stream would be visible as an excess of stars moving toward the SGP (e.g. Helmi 2004a; Law et al. 2005). Even though it could be argued that this sample may be too bright and possibly too metal-poor, this result could rule out an oblate or spherical shape for the Galactic dark-matter halo and favor a prolate mass distribution as suggested by Helmi (2004b).

In summary, the observed and simulated counts are statistically indistinguishable for all partition choices. There is no evidence (at >2$\sigma$-level) for large scale flows crossing the Solar neighborhood.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[angle=90,width=8.8cm]{2911fig2.ps}} \end{figure} Figure 2: $(\phi,~\theta)$-space number counts for a partition with 24 cells with $\Delta \theta =45^\circ $ (mean value $\theta _{\rm c}$) and $\Delta \phi =45^\circ /90^\circ $ for the stripes along the equator and close to the poles, respectively. The solid line corresponds to the selected sample within 1 kpc of the Sun and the dashed histogram to the average number of counts in our Monte Carlo simulations. Error bars are based on Poisson statistics.
Open with DEXTER

3.2 Correlation function

We quantified the deviations from a smooth Gaussian distribution due to kinematic substructures by means of the two-point correlation function, defined as

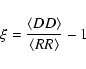\begin{displaymath}% \xi =\frac{\langle DD\rangle}{\langle RR\rangle} -1 \end{displaymath} (1)

where $\langle DD\rangle$ is the number of pairs of stars in our data with velocity difference less than a given value, namely

\begin{displaymath}% \langle DD\rangle =\sum {{\rm pairs~of~stars}~i,j~{\rm with}~\vert {\vec v}_i-{\vec v}_j \vert \le \Delta} \end{displaymath} (2)

and $\langle RR\rangle$ is defined analogously for the same number of random points drawn from a multivariate Gaussian distribution derived from the data set, convolved with expected observational errors and averaged over a hundred realizations. Note that the points are not statistically independent and that our definition of $\xi $ actually corresponds to the cumulative correlation function often used in cosmology in studies of the large-scale structure of the Universe (e.g., Mullis et al. 2004; Coil et al. 2004).

Based on Poisson counts, we estimated the error of the two-point correlation function as

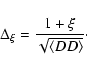\begin{displaymath}% \Delta_{\xi}=\frac{1+\xi}{\sqrt{\langle DD\rangle}}\cdot \end{displaymath} (3)

Thus, in the 3D linear space (U,V,W) - say $v=\vert {\vec v}_i-{\vec v}_j\vert$ - $\xi (v)$ measures the excess of pairs of stars moving with velocity difference equal to or smaller than a given value, above that expected from a random sample. Clumping due to kinematic substructures (i.e. groups of stars moving with similar velocities) is manifested by an excess at small velocity separations.

In Fig. 3 we show the two-point correlation function $\xi (v)$ for our selected sample within 1 kpc of the Sun (asterisks) and a subset comprising the 5% fastest-moving stars (diamonds). We use bins of width $21~\rm {km~s^{-1}}$ up to separations of  $840~\rm {km~s^{-1}}$. The figure shows that at a $1\sigma$ level there is a small but statistically significant excess of stars with similar velocities with respect to what would be expected for a smooth Gaussian distribution. The signal in the first bin is weak but significant. No correlation is observed at larger separations.


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[angle=90,width=8.8cm]{2911fig3.ps}} \end{figure} Figure 3: Two-point velocity correlation function for our selected sample within 1 kpc (asterisks) and for the 5% fastest moving stars (diamonds). In both cases, there is a signal at small velocity differences indicative of the presence of streams. The error bars are based on Poisson counts.
Open with DEXTER

This signal is, however, clearly much stronger for the subset of $5\%$fastest moving stars; in this case, the excess of pairs of stars with similar velocities is very noticeable and directly indicates the presence of clumps/streams. This signal is indeed due to a moving group that is formed by three stars (described in Table 2) and indicated by the asterisks in Fig. 1. Note also the presence of a certain degree of anti-correlation for the interval 200-400 km s-1. This may be due to a type of "clear out effect'' as the result of the clumping of few objects within the first bins. This effect would have a considerably smaller amplitude for a larger sample, as is the case when our selected sample is considered in its entirety.

Table 2: Members of the identified moving group.

So far we have focused on the $5\%$ fastest moving particles within 1 kpc of the Sun. Analysis performed with the $10\%$ fastest subsample still shows a significant deviation from a multivariate Gaussian, albeit of smaller amplitude.

Turning to an eight times larger volume (we considered those stars within 2 kpc of the Sun) allows us to increase the number of stars, but only by a factor of $\sim$2. This increase in the number of stars does not necessarily translate into an enlargement of the number of streams but could also lead to a better representation of each stream.

However this effect is not obvious in our sample; for the larger volume the kinematic group previously singled out loses one star, BPS CS 30339-0037, which is no longer selected in the $5\%$ high velocity tail, simply as a consequence of small number statistics. Up to a velocity difference smaller than 42 km s-1, a weak signal (at the 1$\sigma$ level) is noticeable; it is due to the two remaining stars of our moving group and a second structure with two other stars. Given the low amplitude of this signal in comparison to the 1 kpc sample, we are led to believe that this second structure is probably a statistical fluke rather than a true physical system.

In summary, we detected a moving group (with three members) among the 5% most energetic stars within 1 kpc of the Sun, and no other members could be found by increasing the volume or relaxing the velocity threshold (from 5 to 10%).

4 Comparison to the theory: simulations


  \begin{figure} \par\includegraphics[angle=0,width=13cm]{2911fig4.ps}\end{figure} Figure 4: Distribution of 2348 dark matter particles from a CDM simulation located in a sphere of 2 kpc radius centered at 8 kpc from the Galaxy center. ( a)-c)) Velocity projections in the (v1, v2, v3) space; d) Velocity directions. The solid gray circles denote the 5% most energetic particles, while the asterisks identify those subsets whose velocity difference is less than 42  km s-1. The kinematics characteristics observed in this set of plots are representative of what is seen in other similar volumes.
Open with DEXTER

In order to compare our results from the previous section to theoretical models, we used a high-resolution simulation of the formation of a dark matter halo in a ${\rm\Lambda CDM}$cosmology (Springel et al. 2001). From this simulation, we derived the kinematics of dark matter particles inside spheres of 2 kpc radius, located at 8 kpc from the Galactic center. In doing so, we are assuming that these volumes are representative of the solar neighborhood.

In Fig. 4 we plot the kinematics of 2348 particles selected within one of the 2 kpc spheres. Their velocity distribution is relatively smooth and appears to be quite consistent with a multivariate Gaussian (see Fig. 5) with principal axes $(\sigma_1,~\sigma_2,~\sigma_3)=(143,~118,~110)~{\rm km~s^{-1}}$. However, if we focus on the motions of the most energetic particles (indicated with gray symbols in Fig. 4), this is no longer the case. The 5% fastest moving particles are strongly clumped, and their distribution is highly anisotropic.

To quantify the substructures present in this volume we computed the velocity correlation function $\xi $ described in Sect. 3. The random comparison sample in this case is the result of averaging 100 realizations of a trivariate Gaussian with similar moments as found in the dark matter velocity distribution. In Fig. 5 we observe a weak signal in the first bins produced by a small excess of particles with similar velocities (asterisks). However, if we focus on the 5% fastest moving particles (diamonds), the excess has a much larger amplitude particularly at small velocity differences (i.e. $\Delta v < 42~{\rm km~s^{-1}}$), and simply reflects the presence of kinematic groups clearly visible in Fig. 4.

Although the number and the properties of stellar streams are likely to be rather different from pure dark-matter streams, it is worth noting that these results are qualitatively similar to those found for our stellar samples. To try to quantify the degree of similarity, it is simplest to assume that 10% of the particles in these volumes represent stars (i.e. reflecting a "universal'' baryon fraction). In this way we can randomly define "stellar samples'', which we subjected to statistical analysis, such as the velocity correlation function. Such analysis shows a weak signal at the $1\sigma$ level, which has a smaller amplitude than found for the selected stellar sample discussed in Sect. 3. This result could suggest that stars are not just a random subset of dark-matter particles. This would not be very surprising since stars are expected to be much more clustered in the centers of dark-matter halos.

It should theoretically be possible to identify which particles might represent stars using better motivated physical arguments, e.g., by selecting those that have the largest binding energies at redshift $\sim$10 (Moore 2001). However, this is not straightforward, as it involves, for example, determining the efficiency of star formation in each progenitor halo (Robertson et al. 2005).


  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics[angle=90,width=8.8cm]{2911fig5.ps}}\end{figure} Figure 5: Velocity correlation function $\xi (v)$ for the volume shown in Fig. 4. Asterisks and diamonds correspond to $\xi $ for the full sample and for the subset of 5% fastest moving particles, respectively.
Open with DEXTER

In any case, our main limitation in quantifying the degree of similarity between the stellar sample and the dark-matter simulation lies in the number of particles available in this simulation. We expect that, typically, only 1 in 250 particles will be a star (Helmi et al. 2003)[*]. If this is the case, to reproduce our selected sample with $\sim$400 stars, our simulations should have 105 particles in each volume.

5 Adiabatic invariants


  \begin{figure} \par\includegraphics[angle=0,width=13cm]{2911fig6.ps} \end{figure} Figure 6: Distribution of the selected sample of 410 stars with D<2 kpc in the space of adiabatic invariants. The asterisks denote our kinematic group (RHLS), and the grey diamonds the clump identified by Helmi et al. (1999) (HWdZZ). These stars are used to define a region (limited by the dashed lines in the left panel), which also encompasses other stars with similar angular momenta and which are indicated as diamonds in both panels. CD - 80 328, the candidate from the Nordström et al. (2004) catalog, has been added and is shown as a triangle.
Open with DEXTER

We were also interested in understanding the properties of our selected sample in the space of adiabatic invariants, since this is generally the preferred space when looking for evidence of substructures related to past mergers. Here clumping should be strong, since all stars originating from the same progenitor have very similar integrals of motion, resulting in the superposition of the corresponding streams. In particular, Helmi et al. (1999) and Chiba & Beers (2000) have examined the kinematics of metal-poor stars in the solar neighborhood and identified a statistically significant clumping of stars in the angular momentum diagram Lz versus ${L_{xy}=\sqrt{L_x^2+L_y^2}}$.

The substructure identified by Helmi et al. (1999) consists of 7 (12) stars with ${\rm [Fe/H] \le -1.6~(-1.0)}$ dex and D<1 (2.5) kpc and was discovered in a sample that was primarily the result of the combination of HIPPARCOS data with the Beers & Sommer-Larsen catalog (1995). Chiba & Beers, using the Beers et al. (2000) catalog (i.e. a revised edition of the previous compilation), confirmed 9 of their stars in the clump region that also includes one of the stars in our kinematic group, HD 214161. However, they later discarded this star for having quite different orbital properties than other clump members.

Here we focus on the space of adiabatic invariants E, Lz, and Lxy, although the last is not fully conserved in an axisymmetric potential, and its use may not be all that appropriate for the study of a substructure in the halo. Nevertheless, we hope to obtain further insight into our previous analysis based only on kinematics. We assume that the Galactic potential is represented by three components (Johnston et al. 1996): a dark halo with logarithmic potential, a Miyamoto-Nagai disk, and a spherical Hernquist bulge:

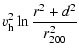                              $\displaystyle % \Phi _{\rm halo}$ = $\displaystyle v^2_{\rm h}\ln{\frac{r^2+d^2}{r^2_{200}}}$  
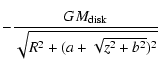$\displaystyle \Phi_{\rm disk}$ = $\displaystyle -\frac{GM_{\rm disk}}{\sqrt{R^2+(a+\sqrt{z^2+b^2})^2}}$ (4)
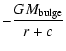$\displaystyle \Phi_{\rm bulge}$ = $\displaystyle -\frac{GM_{\rm bulge}}{r+c}$  

where $M_{\rm disk}=1.0\times 10^{11}~M_{\odot}$, $M_{\rm bulge}= 3.4\times 10^{10}~M_{\odot}$; $v_{\rm h}= 131.5~{\rm km~s^{-1}}$ and $r_{200}=300~{\rm kpc}$; a=6.5 kpc, b=0.26 kpc, c=0.7 kpc, and d=12 kpc. This choice of parameters gives a circular velocity at the solar radius of $210~{\rm km~s^{-1}}$.

Figure 6 shows the distribution of the selected sample within 2 kpc of the Sun in the space of adiabatic invariants. Note that the sample includes 8 stars (hereafter HWdZZ stars) from the stream identified by Helmi et al. (1999). These stars are shown by solid gray diamonds, while our own kinematic clump (hereafter RHLS) is plotted as asterisks. It is clear that these groups have similar momenta (see left panel). If $L_{xy}^{\rm min}$ ( $L_z^{\rm min}$) and $L_{xy}^{\rm max}$ ( $L_z^{\rm max}$) denote the minimum and maximum Lxy(Lz) values for the HWdZZ and RHLS stars, the region $L_{xy}^{\rm min}<L_{xy}<L_{xy}^{\rm max}$ and $L_z^{\rm min}<L_z<L_z^{\rm max}$(dotted box) encompasses stars with similar momenta. There are 16 stars located in this region, among which are five new objects shown as black diamonds in Fig. 6. Some of these stars are also members of the "clump-trail'' structure identified by Chiba & Beers (2000) (hereafter CB). The orbital properties of these 16 stars, based on the Galactic potential defined above, are listed in Table 3. The last column serves to indicate membership in the various groups.

Table 3: Characteristics of the stars located in the region $L_{xy}^{\rm min}<L_{xy}<L_{xy}^{\rm max}$ and $L_z^{\rm min}<L_z<L_z^{\rm max}$ defined by the Helmi et al. (1999) structure (within the box shown in the left panel of Fig. 6.)

We looked for additional members of our kinematic group in the Nordström et al. (2004) catalog of nearby stars. Selecting stars with ${\rm [Fe/H]\le -1.5~dex}$ and similar kinematic characteristics as those we identified, we found only one possible candidate: ${\rm CD-80~328}$ is a metal poor star ( ${\rm [Fe/H]=-1.98~dex}$) with $(U,~V+220,~W)=(-193,~125,~303)~\rm {km~s^{-1}}$ and a highly eccentric orbit e=0.83. It is shown as a triangle in Fig. 6. ${\rm CD-80~328}$, having $L_z=1009~\rm {kpc~km~s^{-1}}$ and $L_{xy}=2422~\rm {kpc~km~s^{-1}}$, is located well within the box-region defined by the HWdZZ stars. However, given its much lower binding energy ( $E=-0.84\times 10^5~\rm {km^2~s^{-2}}$), it is more likely that ${\rm CD-80~328}$ is a member of our moving group.

According to numerical simulations carried out by Brook et al. (2003), stars from an accreted satellite typically show highly eccentric orbits (e>0.8) and strongly correlated velocities. In view of this, the stars of our kinematic group (with 0.81<e<0.85) could well share a common origin and be stellar debris from an accreted satellite.

It is worth noting that, while having similar momenta, our kinematic structure and the HWdZZ clump have somewhat different energies, which could imply that these groups have different origins. However, it also seems plausible that these groups have been stripped off from the same progenitor at different times. In this scenario, HWdZZ stars should have been released in a later galactic passage than those in our kinematic clump. The difference in orbital energy between the groups could be the result of different binding energies of the progenitor galaxy (higher and lower, respectively) due to the effects of dynamical friction upon this system while orbiting the Milky Way.

6 Conclusions

We have extracted samples of metal-poor ( ${\rm [Fe/H]\le -1.5}$ dex) halo stars in the Solar neighborhood from the Beers et al. (2000) catalog and carried out a statistical analysis of their kinematics.

Based on clustering in the velocity space, we found evidence of substructures in the motions of the fastest moving stars at a level which seems to be consistent with that predicted by high resolution simulations of dark matter halos in a hierarchical universe. The moving group responsible for this signal is comprised of three stars whose kinematic and metallicity characteristics are similar to the streams found by Helmi et al. (1999), albeit on somewhat more loosely bound orbits.

Our sample of halo and high velocity stars is too small to make definite statements about the importance of accretion in the formation of the Galactic halo. This would require a sample with a few thousand nearby halo stars (i.e., $\sim$10 times larger than our selected sample) with accurate space velocities. Such sample sizes will become available in the near future thanks to spectroscopic surveys like RAVE (Steinmetz 2003) and SDSS-II/SEGUE (Beers et al. 2004), which could be combined with proper motion catalogs such as UCAC2 (Zacharias et al. 2004), SPM (Platais et al. 1998), GSC-II (McLean et al. 2000), and USNO-B (Monet et al. 2003) to obtain full phase-space information.

The existence of structures in the halo, if confirmed by further studies, is very important for constraining models of the formation and evolution of the Galaxy. The space astrometric mission Gaia (Perryman et al. 2001) will collect samples of millions of stars in our Galaxy, as well as in our nearest neighbours with very accurate positions, proper motions, and trigonometric parallaxes, which will dramatically improve the situation and revolutionize our knowledge of the Galaxy.

Acknowledgements
We wish to thank: Volker Springel and Simon White, who allowed us to use data from their simulations; Antonaldo Diaferio and Ronald Drimmel for suggestions and many useful comments; and Attilio Ferrari for his constant support of this project. This work was initiated at the Astronomical Institute in Utrecht, which is gratefully acknowledged. P.R.F. wishes to thank the Astronomical Institute in Utrecht for hospitality during her visit. Partial financial support for this research comes from the Italian Ministry of Research (MIUR) through the COFIN-2001 program and from the Netherlands Organization for Scientific Research (NWO) and the Netherlands Research School for Astronomy (NOVA). Finally, we thank the referee, Timothy Beers, for a careful reading of this manuscript and for his useful remarks.

References

 
Copyright ESO 2005