A&A 439, 751-760 (2005)
DOI: 10.1051/0004-6361:20041544

A new method to predict meteor showers

I. Description of the model

J. Vaubaillon1 - F. Colas1 - L. Jorda2


1 - Institut de mécanique céleste et de calcul des éphémérides - Observatoire de Paris, 77 avenue Denfert-Rochereau, 75014 Paris, France
2 - Laboratoire d'Astrophysique de Marseille, Site Pereisc, BP 8, 13376 Marseille Cedex 12, France

Received 28 June 2004 / Accepted 17 March 2005

Abstract
Observations of meteor showers allow us to constrain several cometary parameter and to retrieve useful parameters on cometary dust grains, for instance the dust size distribution index s. In this first paper, we describe a new model to compute the time and level of a meteor shower whose parent body is a known periodic comet.

The aim of our work was to use all the available knowledge on cometary dust to avoid most of the "a priori'' hypotheses of previous meteoroid stream models. The ejection velocity is based on a hydrodynamic model. Because of the large amount of particles released by the comet, it is impossible to compute the orbits of all of them. Instead, we link each computed particle with the real number of meteoroids ejected in the same conditions, through a "dirty snowball'' cometary model calibrated with the $[A f \rho]$ parameter. We used a massive numerical integration for all the particles without hypotheses about size distribution. The time of maximum is evaluated from the position of the nodes of impacting meteoroids. The model allows us to compute ephemerides of meteors showers and the spatial density of meteors streams, from which a ZHR can be estimated. At the end a fit of our predictions with observations allows us to compute the dust size distribution index. We used 2002 and 2003 leonid meteor showers to illustrate our method. The application of our model to the Leonid meteor shower from 1833 to 2100 is given in Paper II.

Key words: meteors, meteoroids - comets: general - ephemerides

   
Introduction

The prediction of meteor showers is particularly important for the operation of satellites in Earth orbit. It can also play a significant role in better understanding the physical properties of cometary dust and the replenishment of the interplanetary dust cloud.

From 1998 to 2002, there has been an increase in the activity of the Leonid meteor shower, and several papers dealing with the forecasting of this phenomenon have been published. Realistic methods involve modeling of the dynamics of meteoroids ejected from the parent body (McNaught & Asher 1999; Lyytinen & Van Flandern 2000; Brown & Jones 1998). The predicted level and shape of a shower depends on the model used to describe it. Therefore, the models can be refined by new observations (McNaught & Asher 2002; Jenniskens et al. 2000; Jenniskens 1994; Lyytinen et al. 2001) and become more realistic. Several impressive results have been obtained since 1999. McNaught & Asher (1999) were the first to perform correct predictions of the instant of the Leonid meteor storm with an accuracy of a few tens of minutes. Lyytinen & Van Flandern (2000) computed a Zenith Hourly Rate (hereafter ZHR, see also Koschack & Rendtel 1990a) value with an error of less than 50% compared to the observations. Jenniskens et al. (2000) derived a Lorentzian profile of the number of meteors visible during a shower observed as a function of time, instead of the previous Gaussian profile. Jenninskens (2001) and later Jenniskens (2002) derived a model of the meteor stream. His predictions for the $\it ZHR$are based on accurate observations (the Multi-instrument Aircraft Campaign) and the results of the dynamical study led by McNaught & Asher (1999). These methods use numerical simulations of the evolution of meteoroid streams in the solar system and a model of $\it ZHR$, based on an empirical formula taking into account different factors. These factors are for example $\Delta a$ and fM, measuring respectively the orbital distance between the meteoroids and the parent body and the dispersion of the stream.

Continuum photometric measurements of cometary dust coma can allow us to evaluate the amount of dust produced by a comet nucleus at a given time. We introduce for the first time this information in a model to accurately simulate the number of particles observed during meteor showers. Our model has been briefly presented in several colloquia and WGN[*] articles (Vaubaillon 2002; Vaubaillon & Colas 2002; Vaubaillon 2004a; Vaubaillon et al. 2003; Vaubaillon & Colas 2005), but we present here the complete method with detailed calculations. In this paper, we present a full description of the model. In Paper II, we will provide an application of the model to the Leonid meteoroid stream.

A general overview of the model and of its assumptions is given in Sect. 1. We then describe how the ejection process (Sect. 2) and the cometary dust production (Sect. 3) are treated. A detailed description of the dynamical model and the simulation are given in Sect. 4. We discuss the validity of the model and its limits in Sect. 5.

  
1 General description of the method and hypotheses

The method described here is based on a new approach that combines a physical model of a comet nucleus (based on the "dirty snowball'' comet model of Whipple 1950) and a dynamical model of individual meteoroid particles. The aim of our approach is to avoid any assumption concerning the level of the shower, and to perform quantitative predictions. In particular we do not consider here the fM parameter (mean anomaly factor) introduced by McNaught & Asher (1999) because a particular stream can have a very complex density distribution with gaps in it (McNaught & Asher 2002; Vaubaillon et al. 2003; Vaubaillon 2002). We also do not consider any a priori model of $\it ZHR$or of the profile encountered by the Earth during a meteor shower.

To do this, we introduce several new improvements in our model in comparison with previous ones. First, the total quantity of dust produced by the comet nucleus at a given time is scaled to be consistent with photometric observations of the dust coma at visible wavelengths. Second, the initial dust velocity is in agreement with hydrodynamical simulations of the inner coma of comets. Third, heavy numerical integrations of the trajectory of thousands of individual particle were applied. These improvements in the description of both the physical and dynamical aspects of meteor showers yield potentially more accurate predictions of their dates of apparition and intensities (Vaubaillon 2002; Vaubaillon & Colas 2002). It represents the first step of a long-term effort towards a full physical description of all the phenomena driving dust particles from the close neighborhood of a cometary nucleus to the Earth's atmosphere.

This task is possible only if we know all cometary and meteoroidal parameters involved in the model, such as their composition, shape and density distributions, etc. As we are far from knowing all of them, a certain number of assumptions about the parent body and the particles need to be made. Therefore, we assume that:

1.
the nucleus is a mixture of water ice and dust;  
2.
the nucleus is spherical and homogeneous;  
3.
its water production rate is proportional to $(\frac{q}{r_{\rm h}})^\gamma$(q: perihelion, $r_{\rm h}$: heliocentric distance, $r_{\rm h} \le 3~{\rm au}$); 
4.
the water is produced in the sunlit hemisphere of the nucleus; 
5.
the dust particles are spherical, homogeneous, of density  $\rho_{\rm g}$;  
6.
their size distribution follows a power law, of index s (see also Appendix C);  
7.
the particles giving meteors have radii greater than 0.1 mm (Hughes 1995);  
8.
the particles are ejected within 3.0 au, from the Sun, in the sunlit hemisphere;  
9.
the local dust number production rate is proportional to the local gas sublimation rate, and the coefficient of proportionality K does not depend on the heliocentric distance;  
10.
the local gas sublimation rate is proportional of the cosine of the zenith angle of the Sun;  
11.
the $[A f \rho]$ parameter is proportional to the dust number production rate (A'Hearn et al. 1984);
12.
the particles are submitted to the gravitational force of the Sun, the nine planets and the Moon, as well as to non-gravitational forces (see also Sect. 4.2 for further details).  
To understand the formation of a meteoroid stream, one has to know the orbit and physical properties of the parent body. The initial conditions of particles depends on the orbit of the parent body (position and velocity), but also on the ejection velocity.

   
2 Terminal velocity of dust particles ejected by the comet

The classical model of a cometary nucleus is that of the "dirty snowball'' (Whipple 1950). When the gas sublimates, meteoroids leave the surface and are accelerated by the gas drag and decelerated by the faint comet nucleus gravity. After a few kilometers (about 10 times the radius of the cometary nucleus), they reach their terminal velocity and travel into space without further interacting with the gas or with the nucleus. The terminal velocity depends on the size, density and composition of the particles. The problem of calculating this velocity was tackled by several authors (Ferrin 1999; Olsson-Steel 1987; Jones 1995; Whipple 1951; Wu & Williams 1996). The ejection velocities deduced are within the range 10 to 103 m $~{\rm s}^{-1}$, depending on the particle size, density, etc. In all these works, a hydrodynamical model with gas and dust components allows them to describe the dust-gas interaction in the inner coma and compute the terminal dust velocity. A review of several models is given by Brown & Jones (1998). Göckel & Jehn (2000) found that Crifo (1995)'s model best fit Leonid meteor storm observations.

Here we applied a realistic model, based on hydrodynamical calculations by Crifo & Rodionov (1997). Note that this model is not "Crifo (1995)'s model'' quoted by Brown & Jones (1998) or Göckel & Jehn (2000). However, this model is closer to the classical "dirty snowball'' (Whipple 1950) view of a cometary nucleus. Under the assumptions (2) and (5) (see Sect. 1), the modulus of the terminal velocity $V_\infty$ is given by Eqs. (18)-(21) in the Appendix D of Crifo & Rodionov (1997). A way to determine f is given in Appendix A of the same paper, Eq. (9), where Z can be derived from $f~ Z~ \pi R_n^2 = Q_{{\rm H_2O}}$, with  $Q_{{\rm H_2O}}$ the molecular flux. $Q_{{\rm H_2O}}$ is computed from the visual magnitude using the correlation law of Jorda et al. (1992). All the parameters used in these relationships are summarized in Table 1.

Table 1: Values of different parameters used in Crifo & Rodionov (1997) equations. $T_{\rm g}$ is taken from Rodionov et al. (2002); $\rho _{\rm d}$ from Olsson-Steel (1987).

To model a meteoroid stream, particles are ejected at heliocentric distances of less than 3 AU on the cometary path under the assumptions (3) and (8). The radii of the particles considered here are those leading to visual meteors (assumption 7). For 105 particles of radius between 0.1 to 1 mm, ejected in a random direction (assumptions 4 and 8), Fig. 1 gives the histogram of the modulus of the terminal velocity. The median value is $11~{\rm m~s}^{-1}$. This result is in agreement with previous works (Brown & Jones 1998; Jenninskens 2001).

  
3 Cometary dust production

3.1 Gas production rate

We present in this section a way to derive the amount of dust produced by the nucleus from the $[A ~ f ~ \rho]$ parameter introduced by A'Hearn et al. (1984). We assume that this parameter is proportional to the dust number production rate (assumption 9). Note that we will only consider here the sublimation of water ice (assumption 1). The gas production rate  $Q_{{\rm H_2O}}$ is assumed to vary according to the following relationship (assumption 3):

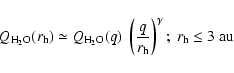\begin{displaymath}% Q_{{\rm H_2O}}(r_{\rm h}) \simeq Q_{{\rm H_2O}}(q) \; \left... ...ac{q}{r_{\rm h}}\right)^\gamma ; \; r_{\rm h} \leq 3 ~{\rm au} \end{displaymath} (1)

with: The number of gas molecules produced by unit of time on the sunlit hemisphere is (in  ${\rm s}^{-1}$):
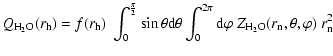$\displaystyle % Q_{{\rm H_2O}}(r_{\rm h}) = f(r_{\rm h}) ~ \int_{0}^{\frac{\pi}... ...\pi} {\rm d}\varphi \; Z_{{\rm H_2O}}(r_{\rm n}, \theta, \varphi) ~ r_{\rm n}^2$     (2)

with: We also assume that:

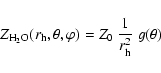\begin{displaymath}% Z_{{\rm H_2O}}(r_{\rm h} , \theta , \varphi) = Z_0 ~ \frac{1}{r_{\rm h}^2} \; g(\theta) \end{displaymath} (3)

and $g(\theta) = \cos(\theta)$ (hypothesis 10). After integration we find:

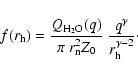\begin{displaymath}% f(r_{\rm h}) = \frac{Q_{{\rm H_2O}}(q)}{\pi ~ r_{\rm n}^2 Z_0} ~ \frac{q^\gamma}{r_{\rm h}^{\gamma-2}}\cdot \end{displaymath} (4)

The "effective'' local sublimation rate of cometary material therefore becomes:
              $\displaystyle % Z_{{\rm H_2O}}^{{\rm eff}}(r_{\rm h} , \theta)$ = $\displaystyle f(r_{\rm h}) Z_{{\rm H_2O}}(r_{\rm h} , \theta)$  
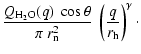  = $\displaystyle \frac{Q_{{\rm H_2O}}(q)~ \cos \theta}{\pi ~ r_{\rm n}^2} ~ \left(\frac{q}{r_{\rm h}}\right)^\gamma \cdot$ (5)


  \begin{figure} \par\includegraphics[width=6.4cm,clip]{1544Fig1.eps} \end{figure} Figure 1: Histogram of ejection velocity for 105 particles of radius in the range 0.1 to 1 mm, ejected during the whole ejection process ( $r_{\rm h} \le 3~{\rm au}$) of the 1767 return of comet Tempel-Tuttle.
Open with DEXTER

3.2 Dust production rate

The next step leads us to compute the absolute number of dust particles produced in a bin of radii  [a'1,a'2]. This interval is obviously included in the bin [a1,a2], where a1 is the radius of the smallest particle produced by the nucleus and a2 is the radius of the largest particle which can be lifted off by the gas. The local dust sublimation rate (in  ${\rm m}^{-2}~{\rm s}^{-1}$) is (assumption 9):

 \begin{displaymath}% Z_{\rm g}(r_{\rm h} , \theta) = K ~ Z_{{\rm H_2O}}^{{\rm eff}}(r_{\rm h} , \theta) \end{displaymath} (6)

and the size distribution law is (assumption 6):

 \begin{displaymath}% h(a) = \frac{N}{a^s} \; \left({\rm unit:\; m}^{-1}\right) \end{displaymath} (7)

with: The differential local sublimation rate per unit of dust radius (in ${\rm m}^{-3}~{\rm s}^{-1}$) is (assumption 10):
 
              $\displaystyle % z_{\rm g}(r_{\rm h}, \theta, a)$ = $\displaystyle Z_{\rm g}(r_{\rm h}, \theta) \; h(a)$  
  = $\displaystyle K \frac{Q_{{\rm H_2O}}(q) ~ \cos \theta}{\pi ~ r_{\rm n}^2}~ \left(\frac{q}{r_{\rm h}}\right)^\gamma ~ \frac{N}{a^s}\cdot$ (8)

We used the $[A f \rho]$ parameter to derive K (assumption 11). $[A f \rho]$ (m) is defined as (A'Hearn et al. 1984):

 \begin{displaymath}% [A f \rho] = A(\phi) \: \left( \frac{\Sigma}{\pi \rho^2} \right) \: \rho \end{displaymath} (9)

with: The parameter $\Sigma$ depends on the dust density $n_{\rm g}$ (in  ${\rm m}^{-3}$) of grains. Of course, the density $n_{\rm g}$ depends on the dust terminal velocity. We recall that the terminal velocity $v_{\rm g}$ of the dust is given by Crifo & Rodionov (1997):

 \begin{displaymath}% v_{\rm g}(a,\theta,r_{\rm h}) = W \Phi = W \frac{1}{1.2 + 0.72 \sqrt{\frac{a}{a_{\star}}}} \end{displaymath} (10)

and

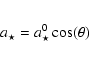
\begin{eqnarray*}a_{\star} = a_{\star}^0 \cos(\theta) \end{eqnarray*}


with $a_{\star}^0$ considered as constant here. It follows that:

 \begin{displaymath}% \phi(\theta,a) = \frac{1}{\alpha~ +~ \beta ~\sqrt{\frac{a}{\cos \theta}}} \end{displaymath} (11)

with: From Eqs. (8)-(11), we can compute the value of K as a function of the $[A f \rho]$ parameter (see Appendix A for details of the calculations):
 
                                          K = $\displaystyle K([A f \rho]_{r_{\rm h}=q})$  
  = $\displaystyle \frac{W ~ [A f \rho]_0}{2 ~ N.Q_{{\rm H_2O}}(q) ~ A(\phi)} \left[... ...left(a_1;a_2\right) \!+\! \beta ~ I ~ A_{3.5}\left(a_1;a_2\right) \right]^{-1}.$ (12)

Taking Eq. (8), the differential local dust sublimation rate $z_{\rm g}$ at a heliocentric distance $r_{\rm h}$, at phase angle $\theta$ and for a particle of radius a is (see Appendix B for further details):

 \begin{displaymath}% z_{\rm g}(r_{\rm h}, \theta, a) = \frac{1}{\pi r_{\rm n}^2}... ...frac{q}{r_{\rm h}}\right)^\gamma ~\frac{\cos \theta}{a^s}\cdot \end{displaymath} (13)

The number of particles emitted by unit of time, in all directions in the bin of radii  [a'1;a'2] (hypothesis 7), at a heliocentric distance $r_{\rm h}$ is then given by (see Appendix B.2):
 
$\displaystyle % N_{\rm g}\left(r_{\rm h},a'_1,a'_2\right) = r_{\rm n}^2 ~ \int_... ...i}{\rm d}\varphi ~ \int_{a'_1}^{a'_2} z_{\rm g}(r_{\rm h}, \theta, a) {\rm d}a.$     (14)

From Eqs. (13) and (14), the total number of meteoroids in the interval of radii  [a'1,a'2]ejected by the comet in the interval of heliocentric distances  $[r_{\rm h}-\Delta r_{\rm h},r_{\rm h}+\Delta r_{\rm h}]$ in the solid angle defined by the angles  $[\theta-\Delta \theta,\theta+\Delta \theta]$and  $[\varphi-\Delta \varphi,\varphi+\Delta \varphi]$, during the time $\Delta t$ is given by:
 
$\displaystyle % N_{\rm g}\left(r_{\rm h},\theta,\varphi,a'_1,a'_2\right)$ = $\displaystyle r_{\rm n}^2 ~ \Delta t ~ \int_{\theta-\frac{\Delta \theta}{2}}^{\... ...i-\frac{\Delta \varphi}{2}}^{\varphi+\frac{\Delta \varphi}{2}} {\rm d}\varphi ~$  
    $\displaystyle \times \int_{r_{\rm h}-\frac{\Delta r_{\rm h}}{2}}^{r_{\rm h}+\fr... ...{\rm d} r_{\rm h} ~ \int_{a'_1}^{a'_2} z_{\rm g}(r_{\rm h}, \theta, a) {\rm d}a$  
  = $\displaystyle \Delta t \: \Delta \varphi \: \frac{J [A f \rho]}{4 \pi A(\phi)}$  
    $\displaystyle \times \frac{\sin^2\left(\theta+\frac{\Delta \theta}{2}\right)-\sin^2\left(\theta-\frac{\Delta \theta}{2}\right)}{2}$  
    $\displaystyle \times \left(\frac{q}{1-\gamma}\right)^\gamma \left[\left(r_{\rm h}+\frac{\Delta r_{\rm h}}{2}\right)^{1-\gamma} \right.$  
    $\displaystyle \left. - \left(r_{\rm h}-\frac{\Delta r_{\rm h}}{2}\right)^{1-\gamma}\right] \: A_1\left(a'_1,a'_2\right).$ (15)

  
4 From cometary dust production to ZHR determination

  
4.1 Statistical weights

Now that we have calculated the number of grains ejected by the nucleus, we need to know how many of them will fall into the Earth's atmosphere at a given time. The instant of a shower can only be provided by a numerical integration of the orbit of test particles (Asher 1999; McNaught & Asher 1999; Vaubaillon et al. 2003; Vaubaillon 2002; Lyytinen & Van Flandern 2000). The idea here is to perform a simulation of a meteoroid stream following the orbit of a certain number of individual particles with radii in the interval [a1,a2], covering the full range of possible dust sizes. We then assign a statistical weight to each of simulated particle in order to mimic the dust size distribution of index s (see Appendix C) and to be consistent with the measured $[A f \rho]$ parameter (Vaubaillon 2004a). This weight represents the total number of real particles ejected in the same conditions as the simulated one. When a simulated particle is selected as hitting the Earth's atmosphere, we can compute in this way the real number of particles that fall onto the planet.

The main advantage of this method is that the heavy dynamical simulations (see Sect. 4.3) remain independent of a certain number of unknown cometary constants, in particular of the size distribution index s (Eq. (7)). Therefore, there is no need to run several dynamical simulations with different values of the parameters involved (for instance, s). Furthermore, one can fit these poorly-known cometary parameters from observations of meteor showers. This reveals the power of this new method. The better we know the comet, the better is the ejection velocity model and the resulting fit.

The weight set to each simulated particle is computed with Eq. (15). The values of each $\Delta i$ parameter depends on how the simulations is performed (see Sect. 4.3).

  
4.2 The dynamical model

According to hypothesis 12, the orbit of a given meteoroid depends on the gravity of solar system bodies, as well as on the non-gravitational forces acting on the particle. These forces are summarized in Fig. 2.

It has been shown that the diurnal Yarkovky-Radzievskii's effect cannot work on such tiny particles, whereas the seasonal one can. The net effect is to spread the meteoroids in the solar system. As many parameters are unknown, it is usual to build a model that averages all the different effects that take place. This was done by Lyytinen & Van Flandern (2000), and they expressed the seasonal Yarkovky's effect as a change of the velocity of meteoroids at each perihelion return. We did not want to build such an averageing model here, since the perturbation is not uniform with time, unlike in reality. To build a complete model would require many assumptions about the physical properties and spin axis direction changes. The net effect of the Yarkovky's force is an additional spread of meteoroids in all directions. In our approach based on a dirty snowball model of the comet, this spreading process is carried out by the ejection velocity that occurs in the whole sunlitt hemisphere.

Initial positions of meteoroids are given by the cometary path. We consider here both the planetary perturbations and the nongravitational forces acting on the comet (Marsden 1969) to compute its position and velocity at a given time. The initial velocity of a particle is the sum of the comet velocity and the dust terminal velocity (see Sect. 2). The ejection of dust particles occurs in the sunlit hemisphere (assumption 4).

Once a meteoroid is ejected, we consider that there is no interaction with the parent body. This is true if the particle is located at $\simeq$10 nucleus radii, a quantity negligible compared to typical distances considered in the numerical integrations. Therefore, we assume that the particle is emitted at the nucleus. Finally, we also assume that meteoroids do not interact one with another.

Following Olsson-Steel (1987), the influence of the solar wind will be "absorbed'' in the expression of the radiation pressure. We will neglect here any sublimation process that could occur on a meteoroid, leading to ejection velocities higher than those considered here (Hughes 2000). Any influence of asphericity, porosity, electric charging or collisional processes of dust particles are also neglected (Gustafson 1994; Mukai et al. 1992).


  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1544Fig2.eps}\end{figure} Figure 2: Non-gravitational forces acting on a meteoroid. The solar direction is bottom left. The solar radiation is responsible for the solar radiation pressure directed in the opposite direction. The Poynting-Robertson force drags the particle in the direction opposite to its velocity vector. The (diurnal) Yarkovsky-Radzievskii force is produced by the anisotropy of the thermal radiation from the particle and is roughly oriented towards the "morning side'' of the particle (upper left in the figure). The seasonal effect (winter "summer warmer than winter'') has been taken into account by Lyytinen & Van Flandern (2000). (see also Radzievskii 1952; Olsson-Steel 1987; Lyytinen & Van Flandern 2000; Burns et al. 1979).
Open with DEXTER

  
4.3 Technical details of the simulation

As it is impossible to solve analytically the equations of motion of meteoroids in the solar system (taking into account all the phenomenons described above), we have performed numerical integrations of the trajectories. For this purpose, we used a 15th order Radau integrator (Everhart 1985).

The ephemeris of the planets have been taken from JPL's DE406 theory, as it provides the planetary ephemeris on a long time scale. The cometary orbit has been computed using the ephemeris provided by P. Rocher (IMCCE), which take into account the non-gravitational forces. Its position and velocity vectors have been stored at each entire Julian day. This fixes in Eq. (15) the following parameters: $\Delta t=86400~{\rm s}$ and $\Delta r_{\rm h} \simeq 0.01~{\rm AU}$. The total number of days the parent body is outgassing during one perihelion return is $N_j \simeq 417$ days in the case of comet 55P/Tempel-Tuttle (see Paper II).

Five bins of radii have been defined: [0.1;0.5], [0.5;1], [1;5], [5;10]and [10;100] mm. For the Leonid meteor shower, $N_{\rm p} = 5$ $\times$ 104 particles have been simulated in each bin. This number is necessary to produce a significant number of impacting particles, and to allow us to perform a statistic study of the characteristics of these particles. The total integration time is about 30 cometary perihelion returns, making in total $\simeq$7 $\times$ 106 simulated particles. This is comparable to the Perseid study done by Brown & Jones (1995), and represents much more particles than in the simulations of McNaught & Asher (1999); Göckel & Jehn (2000); Lyytinen & Van Flandern (2000) and Messenger (2002). The two other parameters of Eq. (15) are now fixed to $\Delta \theta = \frac{\pi}{2} ~ \frac{N_j}{N_{\rm p}} ~ (^{\circ})$ and $\Delta \varphi = 2 \pi ~ \frac{N_j}{N_{\rm p}} ~ (^{\circ})$.

The execution time of a simulation for a single bin of size would amounts to several days on a powerful workstation. A complete simulation during more than 20 perihelion returns would require about one year. Therefore, we decided to parallelize our program and to run it using 10 to 50 processors of an IBM SP located at CINES (Centre Informatique de l'Enseignement Supérieur, Montpellier, France). On this machine, the computational time is reduced to a few hours for a typical run (5 $\times$ 104 particles, i.e. one bin of size, integrated during 500 years), and of one week at most for millions of particles. The gain over a single work station is appreciably higher than the number of processors used, since each one is dedicated to a unique job (Vaubaillon 2004a).

  
4.4 Time of maximum

The particles emitted by the comet may hit the Earth's atmosphere when they cross the ecliptical plane. We store each node "close enough'' to the Earth[*] during the numerical integration.

Göckel & Jehn (2000) defined two criteria to select the particles encountered by the Earth: a space and a time criterion. The time criterion was used to decrease the statistical weight of particles selected by the space criterion and crossing the ecliptic at a time slightly different from the time of maximum of Leonid shower. Brown (cited by Göckel & Jehn 2000) defined this time criterion as $\Delta T \simeq 0.002~{\rm yr}$. This value is taken from the total duration of the Leonid meteor showers ($\simeq$2 weeks at most), and is valid as long as the orbit of the meteoroids do not drastically change during this period. Göckel & Jehn (2000) decreased it to $\Delta T \simeq 0.001~{\rm yr}$ to fit the tested models of ejection velocity[*]. This was possible because they already knew the time of maximum they were looking for. In our case, this time of maximum is unknown, as our aim is to find it without any a priori knowledge. We then have defined what we will call hereafter a first space criterion $\Delta X$, which is consistent with Brown & Jones (1998) and Göckel & Jehn (2000)'s approaches, such as:

\begin{displaymath}% \Delta X = V_{\rm r} \times \Delta T \end{displaymath} (16)

with: The aim of this first space criterion is to keep only the nodes of the particles that reach the vicinity of the Earth. This does not mean that all these particles will actually hit the Earth (see Fig. 3).


  \begin{figure} \par\includegraphics[width=6.8cm,clip]{1544Fig3.eps}\end{figure} Figure 3: Nodes of Leonid meteoroids ejected during the 1767 return of comet 55P/Tempel-Tuttle, selected by the first space criterion $\Delta X$ in 2002 (out of 104 particles in the size range 0.1 to 10 mm). The line represents the trajectory of the Earth in the ecliptic J2000 plane. Scale is in AU. The circle symbolizes the zone where the density of particles is computed (see Sect. 4.5).
Open with DEXTER

From these nodes, we can compute what we will call hereafter the "center'' of the stream. The position of this center is computed as the median position of all node coordinates ( $X_{{\rm center}} = median(X_{{\rm nodes}})$ and $Y_{{\rm center}} = median(Y_{{\rm nodes}})$). We choose the median rather than the average because it is a more robust estimator ith respect to extreme values. As seen in Fig. 3, the stream is far from symmetric, so this center does not automatically fall into the densest part of the stream. It only allows us to define the closest point of the Earth orbit to the stream. This point will allow us to compute the time of the maximum of the shower. In Fig. 3, this method predicts a maximum on the 19th November at 4:02 UT (Vaubaillon 2002).

  
4.5 ZHR computation

The Zenith Hourly Rate, or $\it ZHR$, is the number of meteors visible in one hour by a human eye under perfect weather conditions (Koschack & Rendtel 1990b,a). Only a very small fraction of the stream will penetrate into the Earth's atmosphere, and even in a realistic simulation with millions of particles, only very few of them will actually encounter the planet. On the other hand, the computation of the exact density distribution of particles in the vicinity of the Earth is required if one wants to achieve realistic calculations of $\it ZHR$ values. As a compromise, we have decided to reject the particles located "too far'' from the Earth, but we still consider particles with nodes at more than one Earth diameter.

Therefore, we need to define a second criterion to select particles that contribute to the $\it ZHR$. The density is computed in a circle centered on the maximum of the shower projected on the orbital plane of the Earth (see Fig. 3). The radius of the circle $\delta x$ corresponds to the distance that Earth travels in the time $\delta t = 1~{\rm h}$, as meteor showers last a few hours; $\delta x = V_{\rm t} \times \delta t$, with $V_{\rm t}$ the Earth's velocity. The parameter $\delta x$ is called the second space criterion.

The flux density $D_{\rm f}$ is linked to spatial density by (Brown et al. 2000; Arlt et al. 1999):

 \begin{displaymath}% D_{\rm f} = D ~ V_{\rm r} \end{displaymath} (17)

where: The link with $\it ZHR$ is given by Koschack & Rendtel (1990b):

 \begin{displaymath}% ZHR = \frac{A \: D_{\rm f}}{c(r)} \end{displaymath} (18)

with: The density of simulated particles is then related to the density of real particles using the statistical weights of the Eq. (15), and the $\it ZHR$ value is provided by the Eqs. (17) and (18).

  
5 Discussion

5.1 Advantages and limitations of the method

The method described in Sect. 4 allows us to compute the ephemeris of meteor showers with high accuracy (Vaubaillon 2002), and to establish a link for the first time meteors observations with photometric observations of the dust coma of comets. The model implies no a priori knowledge of meteor showers based on past measurements of $\it ZHR$ profiles.

The dynamical simulation of the formation and evolution of a meteoroids stream is made efficient by the use of a parallel computer which allows us to simulate the orbits of millions of particles. The initial velocity vector is based on a simplified but self-consistent physical model (Crifo & Rodionov 1997), which allows us to avoid the use of ad-hoc parameters such as fM, $\Delta a$ or $\Delta r$(McNaught & Asher 1999; Lyytinen & Van Flandern 2000; Jenninskens 2001) when computing $\it ZHR$ values.

As all cometary parameters used in this model are not always available, a fit of the size distribution index is required. The $\it ZHR$ predictions based on our model are very sensitive to this variable, which in turn should allow us to constrain the value of this parameter from $\it ZHR$ measurements. The range of possible s value varies from a shower to another, but generally $2.0 \leq s \leq 4.5$. Note that the cumulative mass distribution index is sometimes measured from the analysis of cometary dust comae (Fulle et al. 2000) (see Appendix C for further details).

Numerical values provided in Table C.1 assume that the index is constant for particles with radii between a few microns and several millimeters. We know that this is not the case (Jenninskens 2001). The $[A f \rho]$ value may vary slowly from one perihelion to another. However, no such strong temporal variations have been observed in a survey of more than 80 comets by A'Hearn et al. (1995).

The density of simulated particles makes sense only if there is a sufficient number of nodes in the vicinity of the Earth. Our model becomes less efficient for weak meteor showers with ${\it ZHR} < 10{-}20$.

If the nodes are widely spread, with several dense parts far away one from another, the computation of the time of maximum has to be done only with particles whose orbit is nearby that of the Earth (see Fig. 4). Further details on this problem are given in Vaubaillon et al. (2003).


  \begin{figure} \par\includegraphics[width=7.2cm,clip]{1544Fig4.eps}\end{figure} Figure 4: Nodes of Leonid meteoroids ejected during the 1499 return of comet 55P/Tempel-Tuttle, selected by the (wide) first space criterion $\Delta X$ in 2003. The very perturbed stream is divided into 3 different parts. The computation of $\it ZHR$ value is done only where particles encounter the Earth (coordinates: [0.63; 0.77]). See also Vaubaillon et al. (2003).
Open with DEXTER

In the case of a low level shower, the $\it ZHR$ uncertainty grows, and at least a hundred simulated particles are required to provide a confident prediction. The computed density is globaly valid, and no profile of the shower has been determined by this method. This is not impossible to do, but implies modeling the orbit of a sufficiently high number of particles in order to compute the density at several points on the orbit of the Earth.

5.2 Future applications and developments

The application of this model to the Leonid meteor showers will be described in Paper II, but preliminary results are already available (Vaubaillon et al. 2003; Vaubaillon 2002; Vaubaillon & Colas 2002; Vaubaillon 2004a,b). A comparison between theoretical results and meteor shower observations is required (see Paper II). The dynamical model can also be compared to infrared observation of dust filaments (Jenniskens 1996; Reach et al. 2000; Sykes & Walker 1992) if images can be coupled to a thermal model of the dust particles.

This general method can be applied to all meteoroid streams of known comets, such as the Perseids or the Orionids.

The Rosetta spacecraft will offer a unique opportunity to perform detailed in-situ measurements of the activity and dust properties of comet 67P/Churyumov-Gerasimenko. Our model could be refined to compare these observations with observations of its dust trails, which could provide a framework for the modeling of other meteoroid streams.

The model can also be used to estimate the amount of cometary dust injected by comets in our solar system and compare it to large-scale infrared observations (such as that performed by the IRAS satellite). However, for a long term study on timescales long enough for chaos to play a role in the dynamic (e.g. 106 years), our integrator (see Sect. 4.2) should be replaced by symplectic-like ones.

The model itself can be improved. Indeed, the computation of the density is global, and no information about fine structure in the density distribution of the stream has been considered here. This would require simulating more particules than we do at the moment[*]. The model may also help us understand the origin of the observed Lorentzian profile (Jenniskens et al. 2000).

Conclusion

We have developed a new physical model of meteor shower forecasting, without any assumption on the profile of the meteor shower or on the shape of the meteoroid stream. It is based on a simple but realistic "dirty snowball'' cometary model, and a complete hydrodynamical model of ejection velocity provided by Crifo & Rodionov (1997). The modulus of ejection velocity is found to be a few tens of  $\rm m~s^{-1}$. The cometary model uses observations of cometary dust via the $[A f \rho]$ parameter (A'Hearn et al. 1984). In particular, we have shown how to derive the amount of dust emitted by the nucleus, according to a simple cometary model (symmetric, homogeneous etc.) This allows us to constrain the size distribution index s from meteor observation. On the other hand, it allows us to perform meteor shower forecasting, once this parameter is constrained. This provides a direct link between meteor and comet observations.

The method is also based on a numerical simulation of the formation and evolution of the meteoroid stream. Two criteria (large and small) have been defined to select Earth's impacting meteoroids. Each simulated particle is associated to a "weight'' that represents the real number of particles ejected in the same conditions. This allows us to compute the density of particles when a planet encounters the stream. The ephemeris (time and level) of meteor shower can then be provided.

Details about the Leonid meteoroid stream are given in Paper II. This method has allowed us to perform the 2002 and 2003 Leonid meteor shower forecasting (Vaubaillon et al. 2003; Vaubaillon 2002,2004a).

Acknowledgements
We are grateful to J.F. Crifo for his advice on the model of ejection velocity. We also thank the CINES team for their help in parallelizing our code and for the authorization to use their computer. This work is supported by CNES (Centre National d'Études Spatiales).

  
Appendix A: How to compute the K parameter

This section explains in detail how to derive the K parameter from observations. The parameter measuring the amount of dust emitted by the nucleus is $[A f \rho]$ (A'Hearn et al. 1984).

We will start from Eq. (8). The local production rate $z_{\rm g}$, in  ${\rm m}^{-3}~{\rm s}^{-1}$ is related to the density  $n_{\rm g}~({\rm m}^{-4}) $ of dust of radius  $[a, a+{\rm d}a]$ (m) in the vicinity of the nucleus by:

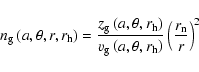\begin{displaymath}% n_{\rm g}\left(a, \theta,r,r_{\rm h}\right) = \frac{z_{\rm ... ...(a,\theta,r_{\rm h}\right)} \left(\frac{r_{\rm n}}{r}\right)^2 \end{displaymath} (A.1)

with: For a given angle $\theta$ (see Fig. A.1), we have:

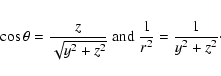
\begin{eqnarray*}\cos \theta = \frac{z}{\sqrt{y^2+z^2}}\; {\rm and} \; \frac{1}{r^2}=\frac{1}{y^2+z^2}\cdot \end{eqnarray*}



  \begin{figure} \par\includegraphics[width=7.5cm,clip]{1544Fig5.eps} \end{figure} Figure A.1: Configuration of the view of the nucleus.

Using Eq. (8), $n_{\rm g}$ becomes:

 
$\displaystyle % n_{\rm g}(a, z,y,r_{\rm h}) = K ~ \frac{Q_{{\rm H_2O}}(q) N}{\p... ..._{\rm g}(a,\theta,r_{\rm n})} \frac{z}{\left(y^2+z^2\right)^{\frac{3}{2}}}\cdot$     (A.2)

The $[A f \rho]$ parameter (Eq. (9), A'Hearn et al. (1984)) is measured from observations of the coma at continuum wavelengths in a diaphragm of projected radius $\rho$ (in m). The sum of the geometric cross sections of dust particles in this diaphragm, $\Sigma$ (m2), is given by:

 \begin{displaymath}% \Sigma = \int_{0}^{\rho} 2 \pi y {\rm d}y \: \int_{0}^{+\in... ...\int_{a_1}^{a_2} \pi a^2 n_{\rm g}(a, z,y,r_{\rm h}) {\rm d}a. \end{displaymath} (A.3)

Using Eqs. (10), (11) and (A.2) one gets:
 
$\displaystyle % n_{\rm g}\left(a,z,y,r_{\rm h}\right) = \frac{K^{\prime}}{a^s}~... ...^{3/2}} + \beta~ \sqrt{a}~ \frac{\sqrt{z}}{\left(y^2~+~z^2\right)^{5/4}}\right]$     (A.4)

with:

 \begin{displaymath}% K^{\prime} = \frac{N.K.Q_{{\rm H_2O}}(q)}{\pi} ~ \left(\fra... ...\gamma ~ \frac{1}{W} \; \left({\rm unit\!: \; m}^{s-2}\right). \end{displaymath} (A.5)

The $\Sigma$ parameter (Eq. (A.3)) then becomes:
 
$\displaystyle % \Sigma = 2 \pi^2 ~ K^{\prime} \: \int_{a_1}^{a_2} \int_{0}^{\rh... ...y ~ \sqrt{z}}{\left(y^2~+~z^2\right)^{5/4}}\right] ~{\rm d}z {\rm d}y {\rm d}a.$     (A.6)

The first term is equal to $\int_{a_1}^{a_2} a^{2.s} {\rm d}a$. The second one, according to Gradshteyn & Ryzhik (1965) (Eq. (3.194-2)), is equal to $\int_{a_1}^{a_2} \beta ~ \sqrt{a} ~ \rho ~ I ~ {\rm d}a$, with

 \begin{displaymath}% I = \frac{1}{2} ~ B \left(\frac{3}{4} ; \frac{1}{2}\right) \end{displaymath} (A.7)

and B the beta function (Abramowitz & Stegun 1972).

Equation (A.6) now becomes:

 \begin{displaymath}% \Sigma = 2 \pi^2 \rho ~ K^{\prime} ~ \left[\alpha~ A_3\left... ..._2\right) ~ + ~ \beta ~ I ~ A_{3.5}\left(a_1;a_2\right)\right] \end{displaymath} (A.8)

where:

 \begin{displaymath}% A_x = \int_{a_1}^{a_2} ~ \frac{{\rm d}a}{a^{s-x+1}} = \left... ...] \ln{\frac{a_2}{a_1}} & \mbox{ if } x = s. \end{array}\right. \end{displaymath} (A.9)

The dimension of Ax is mx-s. We can now completely rewrite the $[A f \rho]$ parameter as a function of K using Eqs. (9) and (A.8):
 
$\displaystyle % [A f \rho] = 2 ~ \frac{N.K.Q_{{\rm H_2O}}(q)}{W} ~ \left(\frac{... ...lpha ~ A_3\left(a_1;a_2\right) + \beta ~ I ~A_{3.5}\left(a_1;a_2\right)\right].$     (A.10)

This naturally leads to Eq. (12) (hypothesis 9).

  
Appendix B: Total dust production rates

We will start from Eq. (12). and define:

 \begin{displaymath}% J = \frac{W}{\left[\alpha ~ A_3\left(a_1;a_2\right) ~ + ~ \... ...)\right]} \; \left({\rm unit: \; m}^{s-2}~{\rm s}^{-1}\right). \end{displaymath} (B.1)

One can see that:

 \begin{displaymath}% N.K.Q_{{\rm H_2O}}(q) = \frac{J ~\left[A f \rho\right]_0 }{2~ A(\phi)} \; \left({\rm unit: \; m}^{s-1}~{\rm s}^{-1}\right). \end{displaymath} (B.2)

  
B.1 Local dust production rate

Taking Eq. (8), the local dust production rate (in  ${\rm m}^{-3}~{\rm s}^{-1}$, at a heliocentric distance $r_{\rm h}$ at a phase angle $\theta$ for a particle of radius a is then:

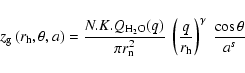\begin{displaymath}% z_{\rm g}\left(r_{\rm h}, \theta, a\right) = \frac{N.K.Q_{{... ...eft(\frac{q}{r_{\rm h}}\right)^\gamma ~\frac{\cos \theta}{a^s} \end{displaymath} (B.3)

which can be rewritten in the same format as Eq. (13).

  
B.2 Total dust production rate

From Eqs. (13) and (14), the number of particles emitted by the whole active surface in all directions, in the bin of radii  [a'1;a'2] (hypothesis 7), at a heliocentric distance $r_{\rm h}$ is given by (in  ${\rm s}^{-1}$):

 \begin{displaymath}% Q_{\rm g}\left(r_{\rm h},a'_1,a'_2\right) = \frac{J ~\left[... ...t(\frac{q}{r_{\rm h}}\right)^\gamma~ A_1\left(a'_1,a'_2\right) \end{displaymath} (B.4)

with A1 defined in Eq. (A.9).

  
B.3 Total dust production during a perihelion return

From Eq. (B.4), the total number of particles in the size range  [a'1;a'2]emitted by the nucleus during the whole ejection process is then:

 \begin{displaymath}% N_{\rm g}^{{\rm tot}}\left(a'_1,a'_2\right) = f^{\rm t} ~ f^{r_{\rm h}} ~ Q_g\left(q,a'_1,a'_2\right) \end{displaymath} (B.5)

with:

  
B.4 Equivalent mass production

In the same way, we can compute the local mass production rate (hypothesis 5, in ${\rm kg}~{\rm m}^{-3}~{\rm s}^{-1})$):

 
                       $\displaystyle % z_{\rm m}\left(r_{\rm h}, \theta, a\right)$ = $\displaystyle \frac{4}{3} \pi \rho_{\rm g} a^3 ~ z\left(r_{\rm h}, \theta, a\right)$  
  = $\displaystyle \frac{4}{3} \pi \rho_{\rm g} \frac{1}{\pi r_{\rm n}^2}~ \frac{J ~... ...hi)}~ \left(\frac{q}{r_{\rm h}}\right)^\gamma ~\frac{\cos \theta}{a^{s-3}}\cdot$ (B.7)

The total mass production rate of particles of radii in the range [a'1,a'2]ejected by the whole active surface, by unit of time in all directions, at a heliocentric distance $r_{\rm h}$ is (in  ${\rm kg}~{\rm s}^{-1}$):
 
                 $\displaystyle % Q_{\rm m}\left(r_{\rm h},a'_1,a'_2\right)$ = $\displaystyle r_{\rm n}^2 ~ \int_{0}^{\frac{\pi}{2}} \sin \theta {\rm d}\theta ~ \int_0^{2\pi}{\rm d}\varphi$  
    $\displaystyle \times \int_{a'_1}^{a'_2} \frac{4}{3} \pi \rho_{\rm g} a^3 ~ z\left(r_{\rm h}, \theta, a\right) {\rm d}a$  
  = $\displaystyle \frac{4}{3}\pi \rho_{\rm g} ~ \frac{J ~[A f \rho]_0 }{A(\phi)}~\left(\frac{q}{r_{\rm h}}\right)^\gamma~ A_4\left(a'_1,a'_2\right).$ (B.8)

The total mass of particles of size in the bin of radii [a'1,a'2]ejected in all directions, during one comet return is (in kg):

 \begin{displaymath}% M_{\rm g}^{{\rm tot}}\left(a'_1,a'_2\right) = f^{\rm t} ~ f^{r_{\rm h}} ~ Q_{\rm m}\left(a'_1,a'_2,q\right). \end{displaymath} (B.9)

We can also define the R factor as the gas to dust mass ratio:

 \begin{displaymath}% R = \frac{M_{\rm g}^{{\rm tot}}\left(a'_1,a'_2\right)}{M_{{\rm H_2O}}^{{\rm tot}}} \end{displaymath} (B.10)

with:

 \begin{displaymath}% M_{{\rm H_2O}}^{{\rm tot}} = f^{\rm t}~f^{r_{\rm h}} ~ Q_{{\rm H_2O}} ~ m_{{\rm H_2O}}. \end{displaymath} (B.11)

  
Appendix C: Different index

The specialized literature reports many different distribution indices. We provide here the relationships that link them together and a table (Table C.1) with numerical examples.

Table C.1: Different values of population indices for meteoroids and meteors. r: meteors population index; $s_{\rm m}$: meteoroids mass distribution index; $s_{\rm mc}$ meteoroid cumulative mass distribution index; s: meteoroids size distribution index.


    
                           $\displaystyle s_{\rm m} = 1+2.3 \log r$ (C.1)
    $\displaystyle s_{{\rm mc}} = s_{\rm m} - 1$ (C.2)
    $\displaystyle s = 3 s_{{\rm mc}} + 1$ (C.3)
    $\displaystyle s = 3 s_{\rm m} - 2$ (C.4)
    $\displaystyle s = 6.9 \log r +1.$ (C.5)

Note that extreme values of r have been reached respectively in 1998 (Brown & Arlt 1998) and 2002 (Arlt et al. 2002).

References

 
Copyright ESO 2005