A&A 439, 159-169 (2005)
DOI: 10.1051/0004-6361:20052952
How to identify the youngest protostars
D. Stamatellos - A. P. Whitworth - D. F. A. Boyd - S. P. Goodwin
School of Physics & Astronomy, Cardiff University,
5 The Parade, Cardiff CF24 3YB, Wales, UK
Received 28 February 2005 / Accepted 25 April 2005
Abstract
We study the transition from a prestellar core to a Class 0 protostar,
using SPH to simulate the dynamical evolution, and a Monte Carlo radiative
transfer code to generate the SED and isophotal maps. For a prestellar core
illuminated by the standard interstellar radiation field, the luminosity
is low and the SED peaks at 
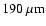 .
Once a protostar has
formed, the luminosity rises (due to a growing contribution from accretion
onto the protostar) and the peak of the SED shifts to shorter wavelengths
(
.
Once a protostar has
formed, the luminosity rises (due to a growing contribution from accretion
onto the protostar) and the peak of the SED shifts to shorter wavelengths
(
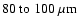 ). However, by the end of the Class 0 phase,
the accretion rate is falling, the luminosity has decreased, and the peak of
the SED shifts back towards longer wavelengths (
). However, by the end of the Class 0 phase,
the accretion rate is falling, the luminosity has decreased, and the peak of
the SED shifts back towards longer wavelengths (
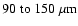 ).
In our simulations, the density of material around the protostar remains
sufficiently high well into the Class 0 phase that the protostar only
becomes visible in the NIR if it is displaced from the centre dynamically.
Raw submm/mm maps of Class 0 protostars tend to be much more centrally
condensed than those of prestellar cores. However, when convolved with a
typical telescope beam, the difference in central concentration is less
marked, although the Class 0 protostars appear more circular. Our results
suggest that, if a core is deemed to be prestellar on the basis of having
no associated IRAS source, no cm radio emission, and no
outflow, but it has a circular appearance and an SED which peaks at
wavelengths below
).
In our simulations, the density of material around the protostar remains
sufficiently high well into the Class 0 phase that the protostar only
becomes visible in the NIR if it is displaced from the centre dynamically.
Raw submm/mm maps of Class 0 protostars tend to be much more centrally
condensed than those of prestellar cores. However, when convolved with a
typical telescope beam, the difference in central concentration is less
marked, although the Class 0 protostars appear more circular. Our results
suggest that, if a core is deemed to be prestellar on the basis of having
no associated IRAS source, no cm radio emission, and no
outflow, but it has a circular appearance and an SED which peaks at
wavelengths below 
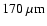 ,
it may well contain a very
young Class 0 protostar.
,
it may well contain a very
young Class 0 protostar.
Key words: stars: formation - ISM: clouds - dust, extinction - methods:
numerical - radiative transfer - hydrodynamics
The details of how molecular clouds form, why they collapse, and how
the collapse proceeds to form stars are not very well understood. Over
the last two decades, observations of the different stages of this
process have lead to an evolutionary scenario of star formation:
starless core
 prestellar core
prestellar core
 Class 0
object
Class 0
object
 Class I object
Class I object
 Class II object
Class II object
 Class III object (see André et al. 2000).
Class III object (see André et al. 2000).
Starless cores (e.g. Myers et al. 1983; Myers & Benson 1983) are
dense cores in molecular clouds in which there is no evidence that
star formation has occurred (i.e. no IRAS detection, Beichman et al.
1986). Some of these starless cores are thought to be close to
collapse or already collapsing, and they are labelled prestellar
cores (Ward-Thompson et al. 1994, 1999); for the rest, it is not
always clear whether they are in hydrostatic equilibrium (e.g.
Alves et al. 2001) or transient structures
within a turbulent cloud (e.g. Ballesteros-Paredes et al. 2003).
Prestellar cores have been observed both in
relative isolation (e.g. L1544, L63; Ward-Thompson et al. 1999) and
in protoclusters (e.g. 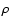 Oph, Motte et al. 1998; NGC 2068/2071,
Motte et al. 2001). They have typical sizes
Oph, Motte et al. 1998; NGC 2068/2071,
Motte et al. 2001). They have typical sizes
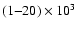 AU
and masses from 0.05 to
AU
and masses from 0.05 to
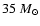 .
From statistical arguments
(e.g. André et al. 2000) it is inferred that prestellar cores live
only a few million years.
.
From statistical arguments
(e.g. André et al. 2000) it is inferred that prestellar cores live
only a few million years.
Class 0 objects represent the stage when a protostar has just been
formed in the centre of the core, but the protostar is still less
massive than its surrounding envelope (André et al. 1993). The
protostar is deeply embedded in the core and cannot be observed
directly, but its presence can often be inferred from bipolar
molecular outflows or compact centimetre radio emission. The Class 0 phase last
for a few
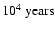 and is characterised by a
large accretion rate (
and is characterised by a
large accretion rate (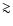
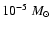 yr-1). Most of
the mass of the protostar is delivered during this phase (e.g.
Whitworth & Ward-Thompson 2001).
yr-1). Most of
the mass of the protostar is delivered during this phase (e.g.
Whitworth & Ward-Thompson 2001).
Once the protostar becomes more massive than its surrounding envelope,
the core enters the Class I phase. Accretion onto the central protostar,
or onto the disc around the protostar, continues, but at a lower rate
(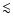
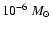 yr-1). This phase lasts for a few
yr-1). This phase lasts for a few
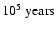 ,
and delivers most of the rest of the mass of the protostar.
,
and delivers most of the rest of the mass of the protostar.
Finally, Class II and Class III objects correspond to even later stages
of star formation, when most of the envelope has disappeared, and the
star is visible in the optical. Class I objects are Classical T Tauri
stars (CTTSs), with ongoing accretion (but at much lower levels than
before, 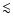
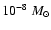 yr-1) and well defined discs. Class III objects are weak-line T Tauri stars (WTTs) with little sign of
accretion and no inner disc.
yr-1) and well defined discs. Class III objects are weak-line T Tauri stars (WTTs) with little sign of
accretion and no inner disc.
In their quest to identify the youngest protostars, André et al.
(1993, 2000) set 3 criteria for Classifying an object as Class 0: (i) the presence of a central luminosity source, as indicated by the
detection of a compact centimetre radio source, or a bipolar molecular
outflow, or internal heating; (ii) centrally peaked but extended
submillimetre continuum emission, indicating the presence of an
envelope around the central source; and (iii) a high ratio (>0.005)
of submillimetre to bolometric luminosity, where the submillimetre is
defined as
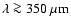 .
Criteria (ii) and (iii) are
used to distinguish between Class 0 and Class I objects, whereas
criterion (i) is used to distinguish between Class 0 objects and
prestellar cores. However, criterion (i) may be inadequate to
distinguish between the youngest Class 0 objects and the oldest
prestellar cores: (a) the cm emission may be be too weak to be
observed, especially in the earliest stages of protostar formation;
(b) the region may be too complex for the molecular outflows to be
detectable; and (c) internal heating may be difficult to establish,
if the protostar is deeply embedded in the core.
.
Criteria (ii) and (iii) are
used to distinguish between Class 0 and Class I objects, whereas
criterion (i) is used to distinguish between Class 0 objects and
prestellar cores. However, criterion (i) may be inadequate to
distinguish between the youngest Class 0 objects and the oldest
prestellar cores: (a) the cm emission may be be too weak to be
observed, especially in the earliest stages of protostar formation;
(b) the region may be too complex for the molecular outflows to be
detectable; and (c) internal heating may be difficult to establish,
if the protostar is deeply embedded in the core.
The origin of radio emission from Class 0 objects is uncertain (cf. Gibb
1999). Theoretical models show that once a protostar forms at the centre
of a collapsing core, the infalling gas accelerates to supersonic velocities
and an accretion shock develops on the surface of the protostar and/or on
the surface of the disc that surrounds the protostar (Winkler & Newman
1980; Cassen & Moosman 1981). The heating provided by the shock ionises
the surrounding gas, which then emits free-free radio radiation (e.g.
Bertout 1983; Neufeld & Hollenbach 1994, 1996). The radio luminosity
depends on the mass of the protostar, the accretion rate and the observer's
viewing angle. For a low-mass protostar, 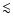
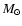 ,
the
predicted flux is below detection limits (Neufeld & Hollenbach 1996),
unless the accretion rate is high,
,
the
predicted flux is below detection limits (Neufeld & Hollenbach 1996),
unless the accretion rate is high, 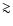
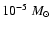 yr-1. Another
possibility is that the radio emission is produced by an ionised disc wind
(e.g. Martin 1996), or from a partially ionised jet that emanates from the
protostar and propagates into the collapsing envelope producing shocks
(Curiel et al. 1987). The detection of radio emission from many Class 0
protostars, using the VLA (e.g. Bontemps et al. 1995), points toward the
latter two explanations.
yr-1. Another
possibility is that the radio emission is produced by an ionised disc wind
(e.g. Martin 1996), or from a partially ionised jet that emanates from the
protostar and propagates into the collapsing envelope producing shocks
(Curiel et al. 1987). The detection of radio emission from many Class 0
protostars, using the VLA (e.g. Bontemps et al. 1995), points toward the
latter two explanations.
Recently Young et al. (2004), using the Spitzer space telescope, detected NIR radiation from L1014, a dense core that was previously classified as
prestellar. The detection of NIR radiation strongly suggests that this is
a young Class 0 object, and supports the view that even younger Class 0
objects may not be detectable in the NIR, with IRAS, or even with Spitzer.
The goal of this paper is to study the transition from prestellar cores to
Class 0 objects, and to seek new criteria for distinguishing between these
two stages, in particular criteria which can be used before the standard
signatures of protostar birth, such as compact radio emission and/or bipolar
molecular outflows, become detectable. We use SPH to simulate to the dynamics
of a collapsing molecular core, and a Monte Carlo code to treat the transfer
of radiation within the core. The radiative transfer is treated fully in 3D,
which is important for the correct interpretation of the observations (cf.
Boss & Yorke 1990; Whitney et al. 2003a,b; Steinacker et al. 2004). We
use a newly developed method for performing Monte Carlo radiative transfer
simulations on SPH density fields, which constructs radiative transfer cells
using the SPH tree structure (Stamatellos 2003; Stamatellos & Whitworth 2005,
hereafter Paper I).
In Sect. 2 we describe the SPH simulation of the collapse of a turbulent
molecular core. In Sect. 3 we describe the radiative transfer method,
focusing on how we construct radiative transfer cells. We also discuss the
radiation sources and the properties of the dust used in our model. In
Sect. 4 we present our results for the dust temperature fields, SEDs and
isophotal maps of prestellar cores and young Class 0 protostars. In Sect. 5 we discuss how SEDs and isophotal maps at submm and mm wavelengths might
be used to distinguish between late-phase prestellar cores and early-phase
Class 0 objects. In Sect. 6 we summarise our results.
2 The SPH simulation
We use the Smoothed Particle Hydrodynamics code DRAGON (Goodwin et al. 2004a) to simulate the collapse of a turbulent molecular core and the
resulting star formation. Here, we briefly describe the main elements
of the model. For a more detailed discussion we refer to Goodwin et al.
(2004b).
The initial conditions in the core, before the start of collapse, are
dictated by observations of prestellar cores (e.g. Ward-Thompson et al.
1999; Alves et al. 2001). Prestellar cores appear to have approximately
uniform density in their central regions, and the density then falls off
in the envelope. If the density in the envelope is fitted with a power
law,
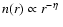 ,
then
,
then
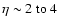 .
Here
.
Here
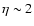 is characteristic of more extended prestellar cores in
dispersed star formation regions (e.g. L1544, L63 and L43), whereas
is characteristic of more extended prestellar cores in
dispersed star formation regions (e.g. L1544, L63 and L43), whereas
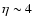 is characteristic of more compact cores in protoclusters (e.g.
is characteristic of more compact cores in protoclusters (e.g.
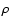 Oph and NGC 2068/2071). These features can be represented by a
Plummer-like density profile (Plummer 1915),
Oph and NGC 2068/2071). These features can be represented by a
Plummer-like density profile (Plummer 1915),
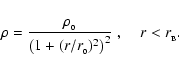 |
(1) |
The density profile is almost flat for
r < r0, and falls off as
r-4 in the outer envelope (
r > r0). We set
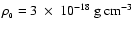 ,
,
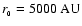 ,
and
,
and
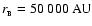 .
The core mass is then 5.4
.
The core mass is then 5.4 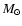 .
The core is initially isothermal at 10 K, hence the thermal virial ratio
is
.
The core is initially isothermal at 10 K, hence the thermal virial ratio
is
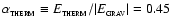 .
Observations of star forming cores (e.g. Jijina et al. 1999) show
that their line widths have a non-thermal contribution, which may be due
to turbulence. We impose a low level of turbulence (
.
Observations of star forming cores (e.g. Jijina et al. 1999) show
that their line widths have a non-thermal contribution, which may be due
to turbulence. We impose a low level of turbulence (
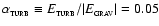 )
with a power spectrum
)
with a power spectrum
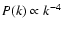 so as to mimic the observed scaling relation between
linear size and internal velocity dispersion (Larson 1981).
so as to mimic the observed scaling relation between
linear size and internal velocity dispersion (Larson 1981).
Collapse of the turbulent core leads to the formation of a single star
surrounded by a disc, and the material in the disc then slowly accretes
onto the star. A sink particle, representing the star and the inner
part of the disc, is created where the density first exceeds
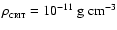 ,
and incorporating all
the matter within
,
and incorporating all
the matter within
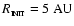 of this point (Bate et al. 1995). (The values of
of this point (Bate et al. 1995). (The values of
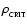 and
and
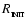 are
dictated by computational constraints. If
are
dictated by computational constraints. If
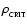 is
increased,
is
increased,
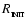 must be reduced, and more computational
time is needed.)
must be reduced, and more computational
time is needed.)
We use a newly developed type of sink called a smartie, which is a
rotating oblate spheroid with radius
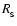 and half-thickness
and half-thickness
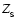 (Fig. 1). The star is a point mass
(Fig. 1). The star is a point mass
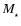 at the centre of the smartie, and the spheroid represents
the inner part of the accretion disc surrounding the star.
at the centre of the smartie, and the spheroid represents
the inner part of the accretion disc surrounding the star.
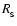 and
and
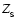 are calculated by assuming that the inner part of the
accretion disc (the part inside the spheroid) has uniform density,
temperature and angular speed, and that its internal energy and spin
angular momentum balance its self-gravity and the gravity of the central
star.
are calculated by assuming that the inner part of the
accretion disc (the part inside the spheroid) has uniform density,
temperature and angular speed, and that its internal energy and spin
angular momentum balance its self-gravity and the gravity of the central
star.
The SPH particles which enter the smartie during a timestep,
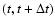 ,
are assimilated by it at the end of the timestep,
,
are assimilated by it at the end of the timestep,
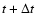 ,
and their
mass is initially added to the mass of the smartie,
,
and their
mass is initially added to the mass of the smartie,
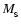 ,
i.e. to
the mass of the inner disc,
,
i.e. to
the mass of the inner disc,
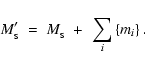 |
(2) |
At the same time, the centre of mass,
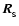 ,
and velocity,
,
and velocity,
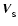 ,
of the smartie are adjusted to conserve linear momentum,
,
of the smartie are adjusted to conserve linear momentum,
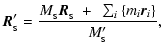 |
|
|
(3) |
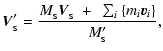 |
|
|
(4) |
and the intrinsic angular momentum (spin) of the smartie is adjusted
to conserve angular momentum,
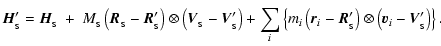 |
|
|
(5) |
In Eqs. (2) through (5), primed variables
(
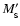 ,
,
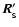 ,
,
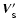 ,
,
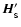 )
are used to denote sink parameters adjusted for
the addition of assimilated SPH particles.
)
are used to denote sink parameters adjusted for
the addition of assimilated SPH particles.
![\begin{figure}
{
\includegraphics[width=5cm,clip]{2952fig1.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg76.gif) |
Figure 1:
We use an oblate spheroidal sink particle, called a smartie,
which contains a central star and a disc, and launches a bipolar outflow. |
| Open with DEXTER |
The smartie mass evolves according to
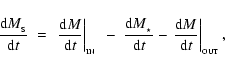 |
(6) |
where the first term on the right of Eq. (6) represents SPH particles
assimilated by the smartie, as discussed in the preceding paragraph.
The second term on the right of Eq. (6)
represents accretion onto the central star, and is given by
where
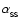 is the standard Shakura & Sunyaev (1973) turbulent
viscosity parameter and
is the standard Shakura & Sunyaev (1973) turbulent
viscosity parameter and
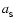 is the mean sound speed in the smartie.
The leading term represents turbulent viscosity, and the term in braces
adjusts this for angular momentum transport by gravitational torques in
a Toomre-unstable disc (cf. Lin & Pringle 1990).
is the mean sound speed in the smartie.
The leading term represents turbulent viscosity, and the term in braces
adjusts this for angular momentum transport by gravitational torques in
a Toomre-unstable disc (cf. Lin & Pringle 1990).
The third term on the right of Eq. (6) represents mass loss from
the smartie, which can occur in two ways. (i) SPH particles are created at
rate
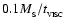 and launched along the rotation
axis with speed
and launched along the rotation
axis with speed
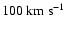 to form a bipolar outflow. These jets
push the surrounding material aside and create hourglass cavities about the
rotation axis. (ii) In the present model the outflow does not remove any angular
momentum. Therefore the redistribution of angular momentum which drives accretion
onto the central star causes the residual inner disc (which has to carry all
the angular momentum assimilated by the smartie) to expand. When this happens,
the smartie is allowed to expand until
to form a bipolar outflow. These jets
push the surrounding material aside and create hourglass cavities about the
rotation axis. (ii) In the present model the outflow does not remove any angular
momentum. Therefore the redistribution of angular momentum which drives accretion
onto the central star causes the residual inner disc (which has to carry all
the angular momentum assimilated by the smartie) to expand. When this happens,
the smartie is allowed to expand until
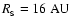 .
Thereafter,
.
Thereafter,
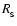 is held constant by excreting SPH particles - and
with them angular momentum - just outside the equator of the smartie.
is held constant by excreting SPH particles - and
with them angular momentum - just outside the equator of the smartie.
The luminosity of the star is given by
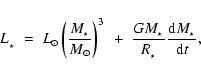 |
(9) |
where
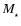 and
and
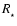 are the mass and radius of the star, and
we set
are the mass and radius of the star, and
we set
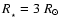 (Stahler 1988).
(Stahler 1988).
The mean smartie temperature, and hence also the mean smartie sound speed, are
determined by the balance between radiative cooling, heating by radiation from
the star and from the background radiation field, and viscous dissipation in
the inspiralling gas of the smartie. A full description of the implementation
of smarties is given in Boyd (2003), and the consequences of feedback from
bipolar outflows are explored in detail in Boyd et al. (in preparation).
For the radiative transfer simulations, we use a version of PHAETHON,
a Monte Carlo radiative transfer code which we have developed (Stamatellos
& Whitworth 2003) and optimised for radiative transfer simulations on SPH density fields (Paper I). The main developments of the optimised version
are (i) that it uses the tree structure inherent within the SPH code to
construct a grid of cubic radiative transfer (RT) cells, spanning the
entire computational domain, the global grid; and (ii) that in
addition it constructs a local grid of concentric spherical RT cells
around each star, a star grid, to capture the steep temperature
gradients that are expected in the vicinity of a star. The code
reemits luminosity packets as soon as they are absorbed (Lucy 1999) and
uses the frequency distribution adjustment technique developed by
Bjorkman & Wood (2000).
To construct RT cells for a given time-frame from an SPH simulation, we
take advantage of the fact that SPH uses an octal tree structure (to group
particles together when calculating gravity forces and also to find
neighbours; for details see Paper I). The SPH tree is a recursive
hierarchical division of the computational domain into cubic cells within
cubic cells (Barnes & Hut 1986). When the SPH tree is being built, we
record information about the size of each cell and the number of SPH particles it contains. The RT cells of the global grid are then the largest
SPH cells which contain 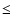
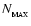 particles. This means that
the RT cells automatically have comparable mass. We choose
particles. This means that
the RT cells automatically have comparable mass. We choose
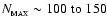 ,
i.e. somewhat larger than the mean number of SPH neighbours,
,
i.e. somewhat larger than the mean number of SPH neighbours,
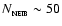 .
Consequently the size of the RT cells is on the order of the smoothing length, h, and so the temperature
resolution is similar to the density resolution of the SPH simulation.
.
Consequently the size of the RT cells is on the order of the smoothing length, h, and so the temperature
resolution is similar to the density resolution of the SPH simulation.
In order to increase the resolution of the radiative transfer simulation,
we use particle splitting (Kitsionas & Whitworth 2002). This method
replaces each SPH particle (parent particle) with a small group of 13 particles (children particles), each one having 1/13 of the mass of the
parent particle. The children are placed on an hexagonal close-packed
array, with one of them in the centre of the array and the other 12
equidistant from the first one. By doing this the smoothing length is
decreased by a factor of
13-1/3=0.425, and the average size of the
radiative transfer cells is reduced by the same factor.
In Paper I we discussed the need for a high-resolution grid of radiative
transfer cells - a star grid - in order to capture the steep
temperature gradients that are expected in the vicinity of a star. The star
grid discussed there was developed for treating the unresolved region inside
a spherically symmetric sink, and so a one-dimensional star grid consisting
of concentric spherical cells centred on the star was sufficient.
In the case we examine here the sinks are smarties, i.e. oblate spheroids,
and the unresolved region inside a smartie represents both the protostar and
the inner protostellar disc. Thus a spherically symmetric one-dimensional star grid
is inappropriate. Instead we adopt a similar approach to Kurosawa et al.
(2004) and represent the unresolved region near the star with a flared disc
(Fig. 2).
However, the properties of the inner disc are not imposed externally, as in
Kurosawa et al. (2004), but are determined by the properties of the smartie,
and therefore attempt to capture the physics of a protostellar disc accreting
onto a newly-formed protostar (as outlined in Sect. 2).
Specifically, we adopt an inner disc with inner radius
 ,
outer
radius
,
outer
radius
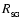 ,
and constant ratio of thickness, H, to radius, r,
,
and constant ratio of thickness, H, to radius, r,
 |
(10) |
The dust destruction radius is given by
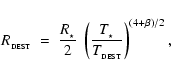 |
(11) |
where 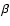 is the dust emissivity index (see Paper I). There is no dust
inside
is the dust emissivity index (see Paper I). There is no dust
inside
 .
.
We put
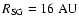 ,
since this is the maximum size of a
smartie, and it is comparable with the size of the local global RT cells
(the cubic cells constructed from the SPH tree).
,
since this is the maximum size of a
smartie, and it is comparable with the size of the local global RT cells
(the cubic cells constructed from the SPH tree).
For
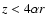 and
and
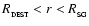 ,
the density
of the inner disc is given by
,
the density
of the inner disc is given by
![\begin{displaymath}\rho (z,r)= \rho_{_{\rm DEST}}~\left(\frac{r}{R_{_{\rm DEST}}...
...eft[ -~\frac{1}{2}\left( \frac{z}{\alpha r} \right)^2 \right],
\end{displaymath}](/articles/aa/full/2005/31/aa2952-05/img102.gif) |
(12) |
(cf. Wood et al. 2002a,b).
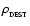 is fixed by equating
the mass of this inner disc to the mass of the disc inside the smartie. For
is fixed by equating
the mass of this inner disc to the mass of the disc inside the smartie. For
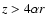 and
and
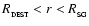 ,
the density
is set equal to the average density of the local global RT cells.
,
the density
is set equal to the average density of the local global RT cells.
The inner disc is then divided into RT cells by spherical and conical surfaces
(see Fig. 2). The spherical surfaces are evenly spaced in
logarithmic radius and there are typically 20 of them. The conical surfaces
are evenly spaced in polar angle and there are typically 30 of them.
![\begin{figure}
{
\includegraphics[width=8.5cm,clip]{2952fig2.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg106.gif) |
Figure 2:
The star grid consists of concentric spherical surfaces centred
on the star, with equal spacing in 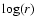 ,
and conical surfaces
symmetric about the angular momentum of the smartie, with equally spaced
opening angle ,
and conical surfaces
symmetric about the angular momentum of the smartie, with equally spaced
opening angle 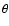 .
This grid takes account of the dust-free cavity
in the immediate vicinity of the star, and resolves the disc inside the
smartie. .
This grid takes account of the dust-free cavity
in the immediate vicinity of the star, and resolves the disc inside the
smartie. |
| Open with DEXTER |
3.3 Radiation sources
![\begin{figure}
{
\includegraphics[width=7.5cm,clip]{2952fig3.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg107.gif) |
Figure 3:
Dotted line: the external illumination field
(BISRF + emission from PAHs).
Solid line: the radiation scattered by the molecular cloud.
This is similar for all
the time-frames and viewing angles, for the models we examine here. |
| Open with DEXTER |
Table 1:
Model parameters.
The core is illuminated externally by the interstellar radiation field and
internally by the newly formed protostar (once it has formed).
For the external radiation field we adopt a revised version of the Black
(1994) interstellar radiation field (BISRF). The BISRF consists
of radiation from giant stars and dwarfs, thermal emission from dust grains,
cosmic background radiation, and mid-infrared emission from transiently heated
small PAH grains (André et al. 2003), as illustrated in Fig. 3.
Typically the BISRF is represented by
109-1010
L-packets.
The protostar luminosity,
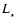 ,
and effective temperature,
,
and effective temperature,
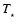 are given by Eq. (9); a blackbody spectrum at
are given by Eq. (9); a blackbody spectrum at
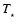 is assumed.
For the systems examined here, the accretion contribution to the luminosity
dominates, because the mass of the protostar is small (<
is assumed.
For the systems examined here, the accretion contribution to the luminosity
dominates, because the mass of the protostar is small (<
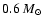 )
and the accretion rate is high (>
)
and the accretion rate is high (>
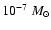 yr-1). Typically the
protostar is represented by
yr-1). Typically the
protostar is represented by
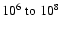 L-packets.
L-packets.
Like other studies of prestellar cores (e.g. Evans et al. 2001; Young et al. 2004) we use the Ossenkopf & Henning (1994) opacity for a standard
MRN interstellar grain mixture (53% silicate and 47% graphite) which has
coagulated and accreted thin ice mantles over a period of 105 yr at a
density of
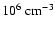 .
However, we emphasize that the opacity
of the dust in cores is very uncertain (e.g. Bianchi et al. 2003).
.
However, we emphasize that the opacity
of the dust in cores is very uncertain (e.g. Bianchi et al. 2003).
We perform radiative transfer simulations on 6 time-frames during the collapse
of a star-forming core. We focus our attention just before and just after the
formation of the first protostar in the core. The characteristics of each
time-frame are listed in Table 1. The simulations are
3-dimensional and provide dust temperature fields, SEDs and isophotal maps.
![\begin{figure}
\mbox{
\includegraphics[width=9.7cm]{2952fig4.eps}\hspace{-1cm}
\...
...1cm}
\includegraphics[width=9.7cm]{2952fig15.eps} }\vspace{-0.3cm}\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg133.gif) |
Figure 4:
Cross sections of density and dust temperature on a plane
parallel to the x=0 plane ( left two columns) and parallel to the
z=0 plane ( right two columns). Each row corresponds to a different
time frame from Table 1, top to bottom
t0 to t5. The planes are chosen so as to include the
maximum density region (t0 and t1) or the
protostar (t2 to t5). |
| Open with DEXTER |
In Fig. 4 we present the density fields and dust-temperature
fields for the 6 time-frames in Table 1. We plot the density
and the temperature on 2 cuts through the computational domain, one parallel to
the x=0 plane and one parallel to the z=0 plane. Each of these planes passes
through the protostar, or, if there is no protostar (as in the first 2 time-frames),
through the densest part of the core. The plots show only the central region of the
core (
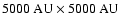 ). Additionally, in
Fig. 5, we plot the density and the temperature of each RT cell versus distance r from the centre of coordinates, on a logarithmic scale,
in order to depict better the regions very close to the protostar.
). Additionally, in
Fig. 5, we plot the density and the temperature of each RT cell versus distance r from the centre of coordinates, on a logarithmic scale,
in order to depict better the regions very close to the protostar.
Our results for the temperature are broadly similar to those of previous 1D and
2D studies of prestellar cores and Class 0 objects. Before the collapse, the
precollapse prestellar core is quite cold (
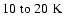 )
and it becomes even
colder (
)
and it becomes even
colder (
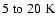 )
as the collapse proceeds and the central regions
become very dense and opaque. As soon as a protostar forms, the region around it
becomes very hot (up to the dust destruction temperature), but the temperature still
drops below
)
as the collapse proceeds and the central regions
become very dense and opaque. As soon as a protostar forms, the region around it
becomes very hot (up to the dust destruction temperature), but the temperature still
drops below 
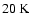 beyond a few
beyond a few
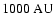 from the protostar,
because of the high optical depth in the dense accretion flow onto the protostar.
The luminosity of the protostar is dominated by the contribution from accretion.
Initially the accretion luminosity increases due to the increasing mass of the
protostar, but then it falls as the accretion rate declines.
from the protostar,
because of the high optical depth in the dense accretion flow onto the protostar.
The luminosity of the protostar is dominated by the contribution from accretion.
Initially the accretion luminosity increases due to the increasing mass of the
protostar, but then it falls as the accretion rate declines.
![\begin{figure}
\mbox{
\includegraphics[width=4.1cm]{2952fig16.eps}\includegraphi...
....2cm]{2952fig21.eps}\includegraphics[width=4.2cm]{2952fig27.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg139.gif) |
Figure 5:
Log-log plot of density ( left column) and dust temperature ( right column)
versus distance from the centre of coordinates, in a collapsing core which forms a
protostar; from top to bottom, time-frames t0 to t5 (see
Table 1). |
| Open with DEXTER |
The SEDs of the 6 time-frames in Table 1 are presented in
Fig. 6. These SEDs have been calculated assuming that the core is
at
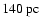 .
SEDs are plotted for 6 different viewing angles, i.e. 3 polar
angles (
.
SEDs are plotted for 6 different viewing angles, i.e. 3 polar
angles (
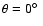 ,
,
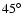 ,
,
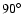 )
and 2 azimuthal angles
(
)
and 2 azimuthal angles
(
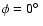 ,
,
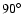 ). Hence on each graph there are 6 curves. However, in
several cases the SED is so weakly dependent on viewing angle that the curves
overlap. We plot only the thermal emission from the core, i.e. we neglect both
the long-wavelength background radiation that just passes through the cloud, and
the short-wavelength radiation that is scattered by the outer layers of the cloud.
). Hence on each graph there are 6 curves. However, in
several cases the SED is so weakly dependent on viewing angle that the curves
overlap. We plot only the thermal emission from the core, i.e. we neglect both
the long-wavelength background radiation that just passes through the cloud, and
the short-wavelength radiation that is scattered by the outer layers of the cloud.
The effective temperature of the core, as inferred from the peak of the SED, rises
and falls with the accretion luminosity of the protostar. For a prestellar core,
the SED peaks at 
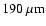 ,
implying
,
implying
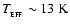 .
Once the protostar has formed and inputs energy into the system, the peak moves
steadily to shorter wavelengths, reaching
.
Once the protostar has formed and inputs energy into the system, the peak moves
steadily to shorter wavelengths, reaching 
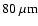 (
(
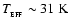 )
as the accretion luminosity reaches its maximum, and then moving back
to longer wavelengths again as the accretion luminosity declines. By the final frame
it has reached
)
as the accretion luminosity reaches its maximum, and then moving back
to longer wavelengths again as the accretion luminosity declines. By the final frame
it has reached 
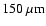 (
(
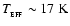 ).
).
The peak of the SED of a prestellar core is independent of viewing angle, since
the core is optically thin to the radiation it emits. In contrast, the peak of the
SED of a Class 0 object does depend on viewing angle, albeit weakly, because of the
presence of an optically thick disc around the protostar. However, even allowing for
variations in the viewing angle, the SED of a Class 0 object does not peak at the
wavelengths characteristic of prestellar cores (
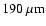 ).
).
Our model predicts that a young protostar embedded in a core
is not observable in the NIR, unless the protostar is displaced from
the central high-density region. This contradicts the recent results of
Whitney et al. (2003b) and Young et al. (2004). We attribute the difference
between our model and that of Young et al. to the density they use for the
region around the protostar (
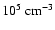 ), which may be too
low for a Class 0 objects and more appropriate for a prestellar core.
Whitney et al. use a higher density in the central region (
), which may be too
low for a Class 0 objects and more appropriate for a prestellar core.
Whitney et al. use a higher density in the central region (
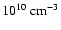 ), but it is still more than one order of magnitude lower
than the density produced by our SPH simulation (
), but it is still more than one order of magnitude lower
than the density produced by our SPH simulation (
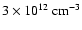 ). Additionally, they use different dust properties for the
different regions in their configuration (cloud, disc mid-plane, disc atmosphere,
outflow); in particular, the opacity of their dust in the disc midplane is smaller
than the opacity in our model, at wavelengths shorter than
). Additionally, they use different dust properties for the
different regions in their configuration (cloud, disc mid-plane, disc atmosphere,
outflow); in particular, the opacity of their dust in the disc midplane is smaller
than the opacity in our model, at wavelengths shorter than
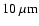 .
There
are also some differences in the properties of the discs used in the different
models, but these are less relevant to the escape of NIR radiation.
.
There
are also some differences in the properties of the discs used in the different
models, but these are less relevant to the escape of NIR radiation.
The models reported by Shirley et al. (2002) use central densities and dust
opacities similar to our models, but they confine their study to the FIR/mm
region of the spectrum, so a comparison is not possible.
Ultimately, the density distribution within
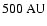 of the centre of
a core or protostar is not well constrained by observations, and therefore
radiative transfer calculations have to rely on theoretical models of core
collapse. Dust opacities are also poorly constrained (e.g. Bianchi et al.
2003). Comparison of our model with those of Whitney et al. (2003b) and Young
et al. (2004) suggests that the presence or absence of NIR emission from a
confirmed Class 0 object might be used to constrain the density profile within
a few
of the centre of
a core or protostar is not well constrained by observations, and therefore
radiative transfer calculations have to rely on theoretical models of core
collapse. Dust opacities are also poorly constrained (e.g. Bianchi et al.
2003). Comparison of our model with those of Whitney et al. (2003b) and Young
et al. (2004) suggests that the presence or absence of NIR emission from a
confirmed Class 0 object might be used to constrain the density profile within
a few
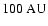 of the protostar and/or the opacity of the dust in the
same region.
of the protostar and/or the opacity of the dust in the
same region.
![\begin{figure}
\mbox{
\includegraphics[width=5cm]{2952fig28.eps}\includegraphics...
...th=5cm]{2952fig32.eps}\includegraphics[width=5cm]{2952fig33.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg160.gif) |
Figure 6:
SEDs of the 6 time-frames in Table 1, from 3 polar
angles (
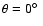 , ,
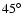 , ,
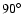 )
and 2 azimuthal angles ( )
and 2 azimuthal angles (
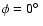 , ,
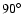 ); in several cases the SEDs from different viewing angles overlap. a) t0 - precollapse prestellar core. The SED peaks at ); in several cases the SEDs from different viewing angles overlap. a) t0 - precollapse prestellar core. The SED peaks at 
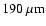 ,
which
implies an effective temperature ,
which
implies an effective temperature
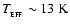 .
b) t1
- collapsing prestellar core. The SED appears the same as in (a) although the
collapse has started and the cloud is denser and colder at its centre. c)
t2 - Class 0 object. The emission of the system peaks at .
b) t1
- collapsing prestellar core. The SED appears the same as in (a) although the
collapse has started and the cloud is denser and colder at its centre. c)
t2 - Class 0 object. The emission of the system peaks at
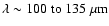 (depending on the observer's viewing angle), which implies
(depending on the observer's viewing angle), which implies
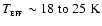 .
The total luminosity of the system is
higher than in b). d) t3 - Class 0 object. Similar to (c), but
the luminosity is even higher, and the SED peaks at .
The total luminosity of the system is
higher than in b). d) t3 - Class 0 object. Similar to (c), but
the luminosity is even higher, and the SED peaks at
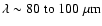 ,
implying ,
implying
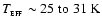 .
e) t4 - Class 0 object. Similar to (d), but the luminosity has started to decrease due to the falling
accretion rate, and the SED peaks at .
e) t4 - Class 0 object. Similar to (d), but the luminosity has started to decrease due to the falling
accretion rate, and the SED peaks at
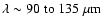 ,
implying ,
implying
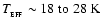 .
f) t5 - Class 0
object. The protostar has moved out of the central region by .
f) t5 - Class 0
object. The protostar has moved out of the central region by 
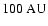 ,
and
the attenuated stellar emission can be seen at short wavelengths ( ,
and
the attenuated stellar emission can be seen at short wavelengths (
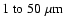 ).
The peak of the cloud emission is at ).
The peak of the cloud emission is at
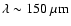 ,
implying ,
implying
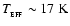 . . |
| Open with DEXTER |
![\begin{figure}
\mbox{
\includegraphics[width=6.5cm]{2952fig34.eps}\hspace{-.3cm}...
....eps}\hspace{-.3cm}
\includegraphics[width=6.5cm]{2952fig42.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg165.gif) |
Figure 7:
850
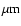 isophotal maps of 3 different time-frames ( first column:
t1 - collapsing prestellar core; second column: t3 -
Class 0 object;
isophotal maps of 3 different time-frames ( first column:
t1 - collapsing prestellar core; second column: t3 -
Class 0 object; third column: t5 - Class 0 object), and
from three different viewing angles (first row:
third column: t5 - Class 0 object), and
from three different viewing angles (first row:
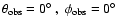 ;
second row: ;
second row:
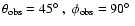 ;
third row: ;
third row:
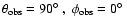 ). Cores with protostars ( second and third columns)
are more centrally condensed than prestellar cores ( first column).
We note that the axes (x,y) refer to the plane of sky
as seen by the observer. ). Cores with protostars ( second and third columns)
are more centrally condensed than prestellar cores ( first column).
We note that the axes (x,y) refer to the plane of sky
as seen by the observer. |
| Open with DEXTER |
![\begin{figure}
\mbox{
\includegraphics[width=6.5cm]{2952fig43.eps}\hspace{-.3cm}...
....eps}\hspace{-.3cm}
\includegraphics[width=6.5cm]{2952fig45.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg168.gif) |
Figure 8:
As Fig. 7, but after convolving with
a Gaussian beam having
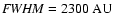 ,
(or equivalently ,
(or equivalently
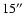 for a core at
for a core at
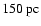 ). Cores with protostars ( middle
frame, t3; ). Cores with protostars ( middle
frame, t3; right-hand frame, t5) appear more circular,
but otherwise similar to the prestellar core ( left-hand frame, t1).
right-hand frame, t5) appear more circular,
but otherwise similar to the prestellar core ( left-hand frame, t1). |
| Open with DEXTER |
The shapes of prestellar cores and Class 0 objects depend on viewing angle.
In Fig. 7 we present isophotal maps at
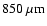 ,
for 3 different time-frames (t1, t3, t5), and from
3 different viewing angles. At
,
for 3 different time-frames (t1, t3, t5), and from
3 different viewing angles. At
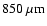 the core is optically thin,
and the temperature does not vary much (
the core is optically thin,
and the temperature does not vary much (
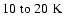 ,
apart from the region very close to the protostar in time-frames
t3 and t5), so the maps are effectively column density maps.
Class 0 objects are more centrally condensed than prestellar cores. They
also show more structure, due to bipolar outflows, which clear low-density
cavities (see images at
,
apart from the region very close to the protostar in time-frames
t3 and t5), so the maps are effectively column density maps.
Class 0 objects are more centrally condensed than prestellar cores. They
also show more structure, due to bipolar outflows, which clear low-density
cavities (see images at
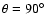 and
and
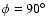 in
Fig. 7).
in
Fig. 7).
In Fig. 8 we present a selection of isophotal maps after
convolving them with a Gaussian beam having
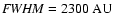 .
Assuming the cloud is 150 pc away, this corresponds to an angular resolution
of
.
Assuming the cloud is 150 pc away, this corresponds to an angular resolution
of
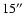 ,
which is similar to the beam size of current submm and mm
telescopes (e.g. SCUBA, IRAM). On these maps, Class 0 objects look very
similar to prestellar cores, apart from the fact that they tend to appear
more circular and featureless (cf. Fig. 7).
,
which is similar to the beam size of current submm and mm
telescopes (e.g. SCUBA, IRAM). On these maps, Class 0 objects look very
similar to prestellar cores, apart from the fact that they tend to appear
more circular and featureless (cf. Fig. 7).
The reason for this is that the emission from a core that contains a protostar is
concentrated in the central few hundred AU, and so, when it is convolved with
a
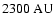 beam, it produces an image rather like the beam, i.e.
round and smooth. In contrast, the emission from a prestellar cores has structure
on scales of several thousand AU, much of which survives convolution with a
beam, it produces an image rather like the beam, i.e.
round and smooth. In contrast, the emission from a prestellar cores has structure
on scales of several thousand AU, much of which survives convolution with a
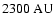 beam. Thus we should expect cores that contain protostars to
appear rounder than prestellar cores, and indeed this is what is observed
(Goodwin et al. 2002).
beam. Thus we should expect cores that contain protostars to
appear rounder than prestellar cores, and indeed this is what is observed
(Goodwin et al. 2002).
Time-frame t0, precollapse prestellar core. The core is
heated exclusively by the ambient radiation field, and so the outer
parts of the cloud are warmer (
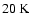 )
than the interior. The
temperature falls to
)
than the interior. The
temperature falls to 
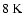 in the central
in the central 
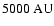 of the cloud, where the density is high,
of the cloud, where the density is high,  106 cm-3 (cf. Evans
et al. 2001; Zucconi et al. 2001; Stamatellos & Whitworth 2003;
Gonçalves et al. 2004; Stamatellos et al. 2004). The cloud emission
peaks at
106 cm-3 (cf. Evans
et al. 2001; Zucconi et al. 2001; Stamatellos & Whitworth 2003;
Gonçalves et al. 2004; Stamatellos et al. 2004). The cloud emission
peaks at 
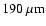 which implies
which implies
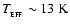 .
The SED is fairly typical for a prestellar core (e.g. Ward-Thompson et al.
2002), except that
.
The SED is fairly typical for a prestellar core (e.g. Ward-Thompson et al.
2002), except that
 is a little higher than for the majority
of prestellar cores (where it is
is a little higher than for the majority
of prestellar cores (where it is 
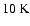 ). This is because the SED
plotted here includes the outer, warmer layers of the core, and this shifts
the peak of the SED to shorter wavelengths.
). This is because the SED
plotted here includes the outer, warmer layers of the core, and this shifts
the peak of the SED to shorter wavelengths.
Time-frame t1, collapsing prestellar core. The collapse
of the core results in a flattened, disc-like region in the centre of the cloud.
Heating is still provided only by the ambient radiation field. The
temperature at the centre of cloud is even lower (
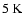 )
than
in time-frame t0, because the density - and hence the optical depth -
is even higher (>
)
than
in time-frame t0, because the density - and hence the optical depth -
is even higher (>
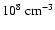 ). The SED looks very similar to time-frame
t0, even though the collapse has started and the cloud is denser
and colder at its centre. Thus the SED does not distinguish between a precollapse
prestellar core and a collapsing prestellar core.
). The SED looks very similar to time-frame
t0, even though the collapse has started and the cloud is denser
and colder at its centre. Thus the SED does not distinguish between a precollapse
prestellar core and a collapsing prestellar core.
Time-frame t2, Class 0 object. A protostar has formed at
the centre of the core, and started heating the core. The protostar has low mass
(
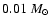 ), but the accretion rate onto it is high
(
), but the accretion rate onto it is high
(
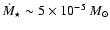 yr-1), and hence the
accretion luminosity is also quite high,
yr-1), and hence the
accretion luminosity is also quite high,
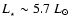 .
The dust temperature increases very close to the protostar, but drops down below
.
The dust temperature increases very close to the protostar, but drops down below
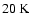 within a few
within a few
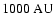 from the protostar, and then rises
towards the edge where the core is heated by the ambient radiation field (cf.
Shirley et al. 2002). Thus, at this early stage, it is necessary to probe the
inner
from the protostar, and then rises
towards the edge where the core is heated by the ambient radiation field (cf.
Shirley et al. 2002). Thus, at this early stage, it is necessary to probe the
inner
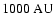 to infer the presence of the protostar. The peak of the
SED has moved to
to infer the presence of the protostar. The peak of the
SED has moved to 
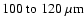 (depending on viewing angle),
which implies an effective temperature
(depending on viewing angle),
which implies an effective temperature
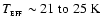 .
The dependence of the SED on viewing angle is due to the disc around
the protostar.
.
The dependence of the SED on viewing angle is due to the disc around
the protostar.
Time-frame t3, Class 0 object. The bipolar jets from the
protostar have created hourglass cavities, as can be seen on the density plots of
Fig. 4. As a consequence, the accretion rate onto the
protostar decreases to
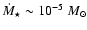 yr-1, but
its mass has increased (to
yr-1, but
its mass has increased (to 
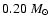 ), and so the luminosity
injected into the cloud increases (to
), and so the luminosity
injected into the cloud increases (to
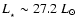 ).
As a result, the temperature is >
).
As a result, the temperature is >
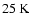 within
within
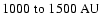 ,
and it does not fall below
,
and it does not fall below
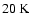 in the inner
in the inner
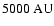 .
The SED peaks at
.
The SED peaks at 
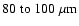 (depending on viewing angle),
which implies
(depending on viewing angle),
which implies
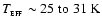 .
.
Time-frame t4, Class 0 object. The total luminosity injected
into the cloud is lower (
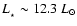 )
due to the reduced
accretion rate onto the protostar (
)
due to the reduced
accretion rate onto the protostar (
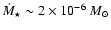 yr-1). The temperature distribution is similar to the previous
time-frame (time-frame t2), but slightly cooler due to the reduced
luminosity. The SED is also similar, but there is a slightly stronger dependence on
viewing angle. The SED now peaks at
yr-1). The temperature distribution is similar to the previous
time-frame (time-frame t2), but slightly cooler due to the reduced
luminosity. The SED is also similar, but there is a slightly stronger dependence on
viewing angle. The SED now peaks at 
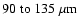 ,
implying
,
implying
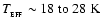 .
.
Time-frame t5, Class 0 object. Asymmetries in the pattern
of accretion onto the protostar have given it a small peculiar velocity, 
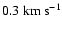 ,
and by t5 it is displaced from the dense
central region by
,
and by t5 it is displaced from the dense
central region by  100 AU. Consequently the accretion rate onto the
protostar is reduced (to
100 AU. Consequently the accretion rate onto the
protostar is reduced (to
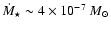 yr-1)
and with it the accretion luminosity (to
yr-1)
and with it the accretion luminosity (to
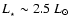 ).
As illustrated in the temperature cross section parallel to the x=0 plane in
Fig. 4, the upper half of the core is warmed to >
).
As illustrated in the temperature cross section parallel to the x=0 plane in
Fig. 4, the upper half of the core is warmed to >
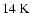 by the displaced protostar. In contrast, the lower half of the core is not affected
by the protostar, and the temperature here does not rise above
by the displaced protostar. In contrast, the lower half of the core is not affected
by the protostar, and the temperature here does not rise above 
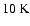 ,
apart from in the outer layers of the core, which are still heated by the ambient
radiation field. As a consequence of the reduced accretion luminosity, the peak of
the SED moves back to longer wavelengths (
,
apart from in the outer layers of the core, which are still heated by the ambient
radiation field. As a consequence of the reduced accretion luminosity, the peak of
the SED moves back to longer wavelengths (
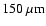 )
and cooler effective
temperature (
)
and cooler effective
temperature (
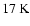 ). The displacement of the protostar also means that
it is now visible at shorter wavelengths (
). The displacement of the protostar also means that
it is now visible at shorter wavelengths (
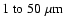 ), from viewing
angles close to the rotation axis.
), from viewing
angles close to the rotation axis.
We have simulated the collapse of a turbulent molecular core using SPH,
and performed 3-dimensional Monte Carlo radiative transfer simulations at
different stages of this collapse, to predict dust temperature fields,
SEDs and isophotal maps. We focus on the initial stages of protostar formation,
i.e. just before and just after the formation of a protostar, and derive
criteria for distinguishing between genuine prestellar cores and cores that contain
very young protostars. As pointed out by Masunaga et al. (1998), very young protostars
are difficult to observe directly, because they are deeply embedded, and may
be wrongly classified as prestellar cores. Hence it is important to consider
ways in which their presence might be inferred indirectly. The main results
of this study are as follows.
- (i)
- A starless core is heated only by the ambient interstellar radiation field.
Hence its outer regions are warm (

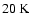 )
and the temperature drops
towards the centre of the core (to
)
and the temperature drops
towards the centre of the core (to 
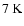 ). As the core collapses the
central region becomes denser and colder (
). As the core collapses the
central region becomes denser and colder (
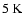 ), because the optical
depth to the centre increases. Thus, prestellar cores that are about to form a
protostar tend to be colder than precollapse prestellar cores.
), because the optical
depth to the centre increases. Thus, prestellar cores that are about to form a
protostar tend to be colder than precollapse prestellar cores.
- (ii)
- When a protostar first forms in a core, its luminosity vaporizes the dust
in its immediate vicinity, and heats the dust that survives up to the dust destruction
temperature (

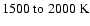 ). Initially, only the region
within
). Initially, only the region
within 
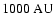 of the protostar is hotter than
of the protostar is hotter than
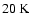 ,
but
as the collapse proceeds the accretion luminosity of the protostar increases and the
presence of the protostar affects the entire core. At this point, the heating of
the core is mainly due to the accretion luminosity of the
protostar, and the effect of the external radiation field is secondary.
,
but
as the collapse proceeds the accretion luminosity of the protostar increases and the
presence of the protostar affects the entire core. At this point, the heating of
the core is mainly due to the accretion luminosity of the
protostar, and the effect of the external radiation field is secondary.
- (iii)
- The effective temperature of the SED follows the variation of the accretion
luminosity, which initially increases due to the increase of the protostar mass
but then decreases due to the decline in the mass accretion rate onto the protostar.
Thus the SED of a prestellar core peaks at

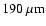 ,
corresponding to
an effective temperature
,
corresponding to
an effective temperature
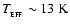 ,
but after a protostar has formed in the core, the
peak of the SED moves to shorter wavelengths (
,
but after a protostar has formed in the core, the
peak of the SED moves to shorter wavelengths (
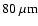 ,
corresponding to
,
corresponding to
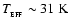 )
as the accretion luminosity increases, and then back
to longer wavelengths (
)
as the accretion luminosity increases, and then back
to longer wavelengths (
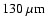 ,
corresponding to
,
corresponding to
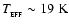 )
as the accretion luminosity decreases.
)
as the accretion luminosity decreases.
- (iv)
- The peak of the SED of a Class 0 object depends only weakly on viewing angle.
In general the peak is at longer wavelength when the Class 0 object is viewed in the
plane of the surrounding accretion disc. It varies by at most
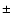
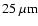 ,
and
is always
,
and
is always 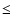
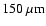 .
Thus, it should be straightforward to distinguish
Class 0 objects from prestellar cores, whose SEDs peak at
.
Thus, it should be straightforward to distinguish
Class 0 objects from prestellar cores, whose SEDs peak at 
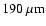 .
.
- (v)
- In our simulations, a newly-formed protostar cannot be observed in the NIR
because it is too deeply embedded. This result reflects the high densities which
our model predicts in the immediate surroundings of a newly-formed protostar.
Additionally, it depends on the dust opacity there. Thus, the presence or absence
of NIR emission from very young embedded protostars (confirmed by the presence
of molecular outflows or compact cm radio emission), could be used to constrain the model.
- (vi)
- At submm and mm wavelengths, isophotal maps of cores that contain protostars
(Class 0 objects) tend to have more structure than maps of prestellar cores, but
their emission also tends to be more strongly concentrated towards their centre.
Consequently, after convolving with the beams of current telescopes, most of this
central structure is lost and cores that contain protostars appear almost circular.
In contrast, prestellar cores tend to have more extended emission and tend to
maintain their shape after convolution.
Based on the above results we propose two criteria for identifying cores
which - despite appearing to be prestellar - may harbour very young
protostars:
- (a)
- They are warm (
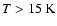 )
as indicated by the peak of the SED of the
core (
)
as indicated by the peak of the SED of the
core (
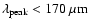 ). This criterion requires that the peak
of the SED can be measured to an accuracy of
). This criterion requires that the peak
of the SED can be measured to an accuracy of 
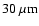 ,
which should be
feasible with observations in the far-IR from ISO (e.g. Ward-Thompson et al. 2002)
and the upcoming Herschel mission (André 2002), and in the mm/submm region from
SCUBA (Kirk et al. 2005) and IRAM (Motte et al. 1998). We have presumed that the
core is heated by the average interstellar radiation field, and the criterion
would have to be modified for a core irradiated by a stronger or weaker radiation
field.
,
which should be
feasible with observations in the far-IR from ISO (e.g. Ward-Thompson et al. 2002)
and the upcoming Herschel mission (André 2002), and in the mm/submm region from
SCUBA (Kirk et al. 2005) and IRAM (Motte et al. 1998). We have presumed that the
core is heated by the average interstellar radiation field, and the criterion
would have to be modified for a core irradiated by a stronger or weaker radiation
field.
- (b)
- Their submm/mm isophotal maps are circular, at least in the central
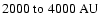 .
.
Using the above criteria, it is relatively easy to identify cores that may
contain young protostars. These warm, circular cores can then be probed by
other means (e.g. deep radio observations with the VLA, or sensitive NIR
observations with Spitzer), to ascertain whether they in fact contain very
young protostars.
Acknowledgements
We thank P. André for providing the revised version of the Black (1994)
ISRF, that accounts for the PAH emission. We also thank D. Ward-Thompson
for useful discussions and suggestions. This work was partly supported
from the EC Research Training Network "The Formation and Evolution of
Young Stellar Clusters'' (HPRN-CT-2000-00155), and partly by PPARC grant
PPA/G/O/2002/00497.
- Alves, J. F.,
Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] (In the text)
- André, P.,
Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] (In the text)
- André, P.,
Ward-Thompson, D., & Barsony, M. 2000, Protostars and Planets
IV, 59
(In the text)
- André, P.
2002, The Origins of Stars and Planets: The VLT View, Proc. of the
ESO Workshop held in Garching, Germany, 24-27 April 2001, 473
(In the text)
- André, P.,
Bouwman, J., Belloche, A., & Hennebelle, P. 2003, to appear
Proc. Chemistry as a Diagnostic of Star Formation, ed. C. L. Curry,
& M. Fich [arXiv:astro-ph/0212492]
(In the text)
-
Ballesteros-Paredes, J., Klessen, R. S., &
Vázquez-Semadeni, E. 2003, ApJ, 592, 188 [NASA ADS] [CrossRef] (In the text)
- Barnes, J.,
& Hut, P. 1986, Nature, 324, 446 [NASA ADS] [CrossRef] (In the text)
- Bate, M. R.,
Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [NASA ADS] (In the text)
- Beichman,
C. A., Myers, P. C., Emerson, J. P., et al. 1986, ApJ, 307,
337 [NASA ADS] [CrossRef] (In the text)
- Bertout, C.
1983, A&A, 126, L1 [NASA ADS] (In the text)
- Bianchi, S.,
Gonçalves, J., Albrecht, M., et al. 2003, A&A, 399,
L43 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Black, J. H.
1994, The First Symposium on the Infrared Cirrus and Diffuse
Interstellar Clouds, ASP Conf. Ser., 58, 355
(In the text)
- Bjorkman,
J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef]
- Bontemps,
S., André, P., & Ward-Thompson, D. 1995, A&A, 297,
98 [NASA ADS] (In the text)
- Boss, A. P., &
Yorke, H. W. 1990, ApJ, 353, 236 [NASA ADS] [CrossRef] (In the text)
- Boyd, D. F. A.
2003, Ph.D. Thesis (Cardiff University)
(In the text)
- Cassen, P.,
& Moosman, A. 1981, Icarus, 48, 353 [NASA ADS] [CrossRef] (In the text)
- Curiel, S.,
Canto, J., & Rodriguez, L. F. 1987, Rev. Mex. Astron.
Astrofis., 14, 595 [NASA ADS] (In the text)
- Evans, N. J.,
Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ,
557, 193 [NASA ADS] [CrossRef] (In the text)
- Gibb, A. G. 1999,
MNRAS, 304, 1 [NASA ADS] [CrossRef] (In the text)
- Gonçalves, J.,
Galli, D., & Walmsley, M. 2004, A&A, 415, 617 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Goodwin, S.
P., Ward-Thompson, D., & Whitworth, A. P. 2002, MNRAS, 330,
769 [NASA ADS] [CrossRef] (In the text)
- Goodwin, S.
P., Whitworth, A. P., & Ward-Thompson, D. 2004a, A&A, 414,
633 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Goodwin, S.
P., Whitworth, A. P., & Ward-Thompson, D. 2004b, A&A, 423,
169 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Jijina, J.,
Myers, P. C., & Adams, F. C. 1999, ApJS, 125, 161 [NASA ADS] [CrossRef] (In the text)
- Kirk, J. M.,
Ward-Thompson, D., & André, P. 2005, MNRAS, in press
(In the text)
-
Kitsionas, S., & Whitworth, A. P. 2002, MNRAS, 330, 129 [NASA ADS] [CrossRef] (In the text)
- Kurosawa,
R., Harries, T. J., Bate, M. R., & Symington, N. H. 2004,
MNRAS, 351, 1134 [NASA ADS] [CrossRef] (In the text)
- Larson, R. B.
1981, MNRAS, 194, 809 [NASA ADS] (In the text)
- Lin, D. N. C., &
Pringle, J. E. 1990, ApJ, 358, 515 [NASA ADS] [CrossRef] (In the text)
- Lucy, L. B. 1999,
A&A, 344, 282 [NASA ADS] (In the text)
- Masunaga,
H., Miyama, S. M., & Inutsuka, S. 1998, ApJ, 495, 346 [NASA ADS] [CrossRef] (In the text)
- Martin, S. C.
1996, ApJ, 473, 1051 [NASA ADS] [CrossRef] (In the text)
- Motte, F.,
André, P., & Neri, R. 1998, A&A, 336, 150 [NASA ADS] (In the text)
- Motte, F.,
André, P., Ward-Thompson, D., & Bontemps, S. 2001,
A&A, 372, L41 [EDP Sciences] [NASA ADS] (In the text)
- Myers, P. C.,
& Benson, P. J. 1983, ApJ, 266, 309 [NASA ADS] [CrossRef] (In the text)
- Myers, P. C.,
Linke, R. A., & Benson, P. J. 1983, ApJ, 264, 517 [NASA ADS] [CrossRef] (In the text)
- Neufeld, D.
A., & Hollenbach, D. J. 1994, ApJ, 428, 170 [NASA ADS] [CrossRef] (In the text)
- Neufeld, D.
A., & Hollenbach, D. J. 1996, ApJ, 471, L45 [NASA ADS] [CrossRef] (In the text)
-
Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] (In the text)
- Plummer, H.
C. 1915, MNRAS, 76, 107 [NASA ADS] (In the text)
- Shakura, N.
I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] (In the text)
- Shirley, Y.
L., Evans, N. J., & Rawlings, J. M. C. 2002, ApJ, 575, 337 [NASA ADS] [CrossRef] (In the text)
- Stahler, S.
W. 1988, ApJ, 332, 804 [NASA ADS] [CrossRef] (In the text)
-
Stamatellos, D. 2003, Ph.D. Thesis (Cardiff University)
(In the text)
-
Stamatellos, D., & Whitworth, A. P. 2003, A&A, 407,
941 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Stamatellos, D., & Whitworth, A. P. 2005, A&A, 439, 153 [EDP Sciences] [CrossRef]
(Paper I)
(In the text)
-
Stamatellos, D., Whitworth, A. P., André, P., &
Ward-Thompson, D. 2004, A&A, 420, 1009 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Steinacker, J., Lang, B., Burkert, A., Bacmann, A., & Henning,
T. 2004, ApJ, 615, L157 [NASA ADS] [CrossRef] (In the text)
- Ward-Thompson, D.,
Scott, P. F., Hills, R. E., & André, P. 1994, MNRAS, 268,
276 [NASA ADS] (In the text)
- Ward-Thompson, D.,
Motte, F., & André, P. 1999, MNRAS, 305, 143 [NASA ADS] [CrossRef] (In the text)
- Ward-Thompson, D.,
André, P., & Kirk, J. M. 2002, MNRAS, 329, 257 [NASA ADS] [CrossRef] (In the text)
- Whitney, B.
A., Wood, K., Bjorkman, J. E., & Wolff, M. J. 2003a, ApJ, 591,
1049 [NASA ADS] [CrossRef] (In the text)
- Whitney, B.
A., Wood, K., Bjorkman, J. E., & Cohen, M. 2003b, ApJ, 598,
1079 [NASA ADS] [CrossRef] (In the text)
-
Whitworth, A. P., & Ward-Thompson, D. 2001, ApJ, 547, 317 [NASA ADS] [CrossRef] (In the text)
- Winkler,
K.-H. A., & Newman, M. J. 1980, ApJ, 236, 201 [NASA ADS] [CrossRef] (In the text)
- Wood, K., Wolff,
M. J., Bjorkman, J. E., & Whitney, B. 2002a, ApJ, 564, 887 [NASA ADS] [CrossRef] (In the text)
- Wood, K., Lada,
C. J., Bjorkman, J. E., et al. 2002b, ApJ, 567, 1183 [NASA ADS] [CrossRef]
- Young, C. H.,
Jørgensen, J. K., Shirley, Y. L., et al. 2004, ApJS, 154,
396 [NASA ADS] [CrossRef] (In the text)
- Zucconi, A.,
Walmsley, C. M., & Galli, D. 2001, A&A, 376, 650 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
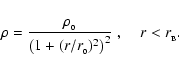
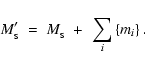
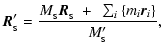
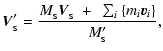
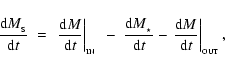
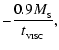
![$\displaystyle \frac{\left[G(M_{_\star} + M_{_{\rm S}})R_{_{\rm S}}\right]^{1/2}...
...}}^2}
{(M_{_\star} + M_{_{\rm S}}) R_{_{\rm S}} a_{_{\rm S}}^2} \right\}^{-1} ,$](/articles/aa/full/2005/31/aa2952-05/img81.gif)
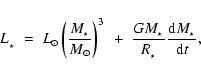

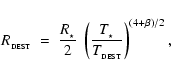
![\begin{displaymath}\rho (z,r)= \rho_{_{\rm DEST}}~\left(\frac{r}{R_{_{\rm DEST}}...
...eft[ -~\frac{1}{2}\left( \frac{z}{\alpha r} \right)^2 \right],
\end{displaymath}](/articles/aa/full/2005/31/aa2952-05/img102.gif)
![\begin{figure}
{
\includegraphics[width=8.5cm,clip]{2952fig2.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg106.gif)
![\begin{figure}
{
\includegraphics[width=7.5cm,clip]{2952fig3.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg107.gif)
![\begin{figure}
\mbox{
\includegraphics[width=9.7cm]{2952fig4.eps}\hspace{-1cm}
\...
...1cm}
\includegraphics[width=9.7cm]{2952fig15.eps} }\vspace{-0.3cm}\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg133.gif)
![\begin{figure}
\mbox{
\includegraphics[width=4.1cm]{2952fig16.eps}\includegraphi...
....2cm]{2952fig21.eps}\includegraphics[width=4.2cm]{2952fig27.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg139.gif)
![\begin{figure}
\mbox{
\includegraphics[width=5cm]{2952fig28.eps}\includegraphics...
...th=5cm]{2952fig32.eps}\includegraphics[width=5cm]{2952fig33.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg160.gif)
![\begin{figure}
\mbox{
\includegraphics[width=6.5cm]{2952fig34.eps}\hspace{-.3cm}...
....eps}\hspace{-.3cm}
\includegraphics[width=6.5cm]{2952fig42.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg165.gif)
![\begin{figure}
\mbox{
\includegraphics[width=6.5cm]{2952fig43.eps}\hspace{-.3cm}...
....eps}\hspace{-.3cm}
\includegraphics[width=6.5cm]{2952fig45.eps} }\end{figure}](/articles/aa/full/2005/31/aa2952-05/Timg168.gif)