1 - Institut für Physik, IGAM, Universitätsplatz 5, 8010 Graz, Austria
2 - Universitäts-Sternwarte, Geismarlandstraße 11, 37083 Göttingen, Germany

Abstract
We observe solar limb faculae at an unprecedented spatial resolution with the new 1 m Swedish Solar Telescope SST on La Palma. Speckle-reconstructed images are used to study 4475 limb facular grains simultaneously in the 430 nm G-band and the $587.5\pm1.5$ continuum up to only 1'' from the limb ( $\cos~\theta=0.05$ ). No systematic contrast decrease is found even a few arcsec from the solar limb. The facular grains appear to be "projected'' on the limb-side neighboring granules; approaching the disc center, the corresponding features occur as inter-granular G-band bright points. Independently, we took spectra with the French-Italian THEMIS telescope on Tenerife and find that the known "line-gap effect'' from disc center disappears near the limb. Here, the facular continuum is enhanced whereas the normalized profiles are unchanged with respect to the undisturbed neighborhood.

The solar surface is widely covered by small magnetic flux concentrations, even outside active regions and during the minimum of the solar cycle. They are identifiable by an intensity excess in the cores of absorption lines. These line-core brightenings are organized in "plages'' particularly visible in H $\alpha$ or Ca II K filtergrams. In the continuum they occur only at very high spatial resolution as tiny brightenings of the "solar filigree'' located in the inter-granular lanes (Dunn & Zirker 1973). At larger helio-centric angles, however, continuum structures become visible which consist of bright facular grains (e.g. Muller 1975). The spatial relation between these continuum (i.e. white light) facular regions and the H $\alpha$ or Ca II K plages (Beckers 1976; Spruit 1976) gives strong indication that the bright facular grains represent the limb occurrence of small-scale magnetic flux concentrations which, near solar disk center, are visible as bright points in the "G-band'' CH absorption bands (e.g., Muller & Roudier 1984).

The transition from the disc-center appearance of small-scale magnetic flux concentrations as G-band bright points (BP) to their limb appearance as facular grains will be of central importance for the understanding of their geometry. The facular contrast has been found to increase from disk center to heliocentric angles $\cos\theta \approx 0.3$ (Auffret & Muller 1991; Sánchez Cuberes et al. 2002); for $\cos\theta < 0.3$ these authors found the facular grains' intensity excess to decrease toward the limb. Okunev & Kneer (2004) found a monotonic decrease of the intensity contrast of polar faculae from $\cos\theta = 0.4$ towards the limb. Ortiz et al. (2002) found from MDI observations a contrast maximum near $\cos\theta = 0.3$ which, however, becomes less significant with increasing magnetic flux density. At the much higher spatial resolution of speckle reconstructed images, de Boer et al. (1997) as well as Sütterlin et al. (1999) found no indication for a contrast maximum up to $\cos\theta = 0.17$ ( $\theta=80^\circ$ ) which could fit Oritz et al. (2002) if the pronounced limb facular grains exhibit stronger magnetic fields. On the other side, Auffret & Muller (1991) found the contrast maximum near $\cos\theta = 0.3$ to be less pronounced for small features, this disagrees to some extent with Ortiz et al. (2002).

Spatially highly resolved images of plage regions (e.g. Fig. 1) readily give the qualitative impression that the number density of magnetic flux concentrations (e.g., BP per active region) markedly decreases from disk center to the limb. Indeed, Auffret & Muller (1991) found the number density to decrease by almost a factor of 10 from disk center to $\cos\theta \approx 0.3$ . Sánchez Cuberes et al. (2002) found a decrease of the number density of large facular grains with decreasing $\cos\theta$ . This seems to point to a selection effect of the visibility of small-scale magnetic flux concentrations near the limb, which may be due to the particular geometry.

Auffret & Muller (1991) found for the quiet network mean sizes which increase from $0\hbox{$.\!\!^{\prime\prime}$ }4$ (300 km) at disk center to $0\hbox{$.\!\!^{\prime\prime}$ }5$ at $\cos\theta = 0.2$ . However, Wiehr et al. (2004) found for the disk center most frequent BP diameters near 160 km with a clear decrease toward both, smaller and larger sizes. The upper diameter limit near 280 km as well as the absence of a marked drop of the brightness between 200 and 280 km does not indicate a transition to "invisible'' magnetic features of sizes between BP and pores.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{2789fig1.eps} \end{figure}$	Figure 1: Speckle reconstructed image of limb facular regions taken with the 1 m SST on July 15, 2003, in the 487.5 nm continuum; field of view: approximately $80^{\prime \prime }\times 80^{\prime \prime }$ .
Open with DEXTER

The finding that BP are smaller and more frequent than typical facular grains suggests that one should investigate their spectral signature. Plage regions near disk center show absorption lines with reduced central depression (i.e., enhanced line-core intensity; e.g., Stellmacher & Wiehr 1971) which, at sufficient spatial resolution, occur as "line gaps'' (Chapman & Sheeley 1977). This effect traces small-scale magnetic flux concentrations not only in strong chromospheric lines (as e.g. H $\alpha$ or Ca II K), but in any line-core. The reduced central line depression even occurs in ionized lines such as from Fe II (Stellmacher & Wiehr 1971), which might have been expected to become stronger (due to the enhanced ionization in the hot facular atmosphere). This apparent discrepancy has been explained (Stellmacher & Wiehr 1979) by a spatial smearing of a hot flux concentration with surrounding granules and intergranules in the spectra. The disappearance of that "residual intensity effect'' near the limb (Stellmacher & Wiehr 1973) is a hint for the dominant role of the geometry and the lateral radiation through the flux concentration for the visibility of facular grains near the limb. We thus also present spectra of magnetically insensitive lines in limb faculae.

2 Observations

2.1 Two-dimensional imaging

$\begin{figure} \par\includegraphics[width=17cm,clip]{2789fig2.eps} \end{figure}$	Figure 2: Faculae near a spot group (NOAA 0409) at $\theta \approx 61^{\circ }$ observed on July 14, 2003; left panel: 587.5 nm continuum, right panel: G-band. The images are oriented such that the solar radius vector points towards the right. Tickmarks are at distances of 1''. The white boxes give the sub-areas used for mean scans in Fig. 3.
Open with DEXTER

We used the new 1 m Swedish Solar Telescope on La Palma (SST; Scharmer et al. 2003) in July 2003 to observe facular regions near the solar limb. Images in the continuum at $587.5\pm1$ nm were taken simultaneously with "G-band'' images at $430.5\pm1$ nm. The pixel size is $0\hbox{$.\!\!^{\prime\prime}$ }042$ and the exposure time was varied between 4 ms and 10 ms to obtain optimal count numbers at all heliocentric angles. The tip-tilt mirror of the SST assured an effective correction for image motion. Bursts of some dozens of images were reconstructed using the speckle-masking method (Weigelt 1977; Pehlemann & von der Lühe 1989; de Boer 1996). An example is shown in Fig. 1.

The center-to-limb variation (CLV) of the continuum and the G-band intensities of the quiet Sun, $I^{\rm cont}_0(\theta )$ and $I^{G}_0(\theta )$ , have been determined from locations in-between the facular grains, and agree with the CLV of the photospheric LTE model by Holweger (1967). We finally remove that CLV from our images, thus obtaining a "flat'' intensity distribution up to the limb, allowing an easy determination of the intensity excess of facular grains:

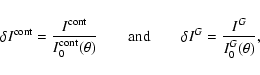$\begin{displaymath}\delta I^{\rm cont} = \frac{I^{\rm cont}}{I^{\rm cont}_0(\the... ...box{and} \qquad \delta I^{G} = \frac{I^{G}}{I^{G}_0(\theta )}, \end{displaymath}$

(1)

For an automatic recognition of the grains, a band-pass filter was applied and structures were selected which exceed a certain intensity threshold (Roudier & Muller 1987). Fourier filtering was carried out in order to remove residual noise (at high spatial wave-numbers k) and intensity fluctuations at scales much larger than the size of facular grains (low k). These large-scale intensity fluctuations can be clearly recognized in the original images (e.g. in that shown in Fig. 1) and might be caused by five minute oscillations. The Fourier filter F has the following analytical form:

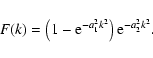2.2 Spectra

Independently, we took spectra at the French-Italian solar telescope THEMIS on Tenerife on May 23 through 25, 2001, of limb faculae and, for comparison, of disc center plage regions. In order to avoid magnetic line broadening, we observed the un-split lines Ti I 522.27, Fe II 722.45, Fe I 557.6, Fe I 543.45, and the small-split lines Fe II 526.48 ( $g_{\rm eff}=0.1$ ) and Ni I 543.58 ( $g_{\rm eff}=0.5$ ). These lines cover a large range of excitation potential and formation height and extend the observations by Stellmacher & Wiehr (1979) since taken simultaneously and at higher spatial resolution. The raw spectra were corrected for the dark and the gain matrices.

3 The brightness of limb facular grains

At the unprecedented high spatial resolution achieved in our speckle reconstructed images, limb facular grains appear to be "projected'' on the limb-side neighboring granules, whereas center-wards, a pronounced dark lane is visible (Fig. 2). This confirms the finding by Lites et al. (2004) and has been successfully modeled by Carlsson et al. (2004), Keller et al. (2004) and Steiner (2005). The brightening arises from the deep view into the atmosphere due to the depressed iso- $\tau$ surfaces in the quasi-evacuated flux concentration. The "dark lanes'' are explained by cool regions inside the flux concentration and above the center-ward granule (Keller et al. 2004; Steiner 2005) where the temperature gradient is smaller than at corresponding optical depths in the surroundings.

$\begin{figure} \par\includegraphics[width=8.0cm,clip]{2789fig3.eps} \par\end{figure}$

Figure 3: Mean spatial scans through facular grains at $\theta \approx 61^{\circ }$ in Fig. 2. The corresponding features have been aligned such that intensity minima of the "dark lanes'' are at the same spatial position (left-side boxes). The right panels show vertical averages in these boxes. The upper panels correspond to the 587.5 nm continuum, the lower ones to the G-band; solid lines give averages of all profiles in the boxes, dotted curves show only profiles where the maximum intensity exceeds 1.3.

Open with DEXTER

3.1 Spatial intensity scans along the radius vector

For quantitative comparison with model calculations (e.g., Steiner 2005), we determine spatial scans through bright "projected'' facular grains and their adjacent dark lanes along the direction perpendicular to the solar limb. For this purpose, the respective structures (see Fig. 2) were spatially aligned such that the intensity minima of the "dark lanes'' occur at the same x-position (left panels of Fig. 3). In the right panels of Fig. 3, averages of these scans are plotted in units of the average intensity $I_{\rm phot}$ of the surrounding quiet photosphere.

The spatial scans in Fig. 3 show intensity distributions with a maximum and rather flat limb-ward decrease indicating a smooth transition from the granular hot walls to the quiet photosphere, in agreement with Steiner (2005). The various intensity maxima yield average values over all scans in the subfield of $\langle\delta I^{\rm cont}\rangle = 1.33$ and $\langle\delta I^{G}\rangle = 1.42$ for the 587.5 nm continuum and the G-band, respectively. In order to exclude intergranular surroundings, we additionally distinguish features of brightness excess $\delta I^{\rm cont} > 1.3$ for which $\langle\delta I^{\rm cont}\rangle = 1.36$ and $\langle\delta I^{G}\rangle = 1.45$ , respectively, establish the above values. The spatial extension of the whole brightening is larger than $1^{\prime \prime }$ .

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{2789fig4.eps} \par\end{figure}$	Figure 4: Facular regions at $\theta =38^{\circ }$ in the light of the 430 nm G-band; limb direction is to the right. The insertion in the upper right corner shows a separate part of the rather large total image, which was located $\approx$ $30^{\prime \prime }$ below its current position. Tickmarks are spaced by $1^{\prime \prime }$ .
Open with DEXTER

The "dark lanes'' appear as significant minima with average intensities of $\langle\delta I^{\rm cont}\rangle = 0.81$ and $\langle\delta I^{G}\rangle = 0.82$ . Center-wards of the "dark lanes'' (i.e., leftwards in Fig. 3) the intensity increases rather steeply up to $0\hbox{$.\!\!^{\prime\prime}$ }2$ from the intensity minimum, then flattens markedly, eventually reaching $I^{\rm cont}_{0}$ and I^G₀. The observed width of the intensity depression is not larger than twice the width of the strong intensity gradient, i.e. $0\hbox{$.\!\!^{\prime\prime}$ }4$ . The inflection points, however, occur about $0\hbox{$.\!\!^{\prime\prime}$ }09$ limb-wards and $0\hbox{$.\!\!^{\prime\prime}$ }13$ center-wards from the minimum, suggesting an average width of the dark lane near $0\hbox{$.\!\!^{\prime\prime}$ }22$ . According to Steiner (2005) the dark lane "samples the deep cool layers''; Keller et al. (2004) present a sketch showing that the maximum contribution stems from colder material "above the centerward granule and inside the flux concentration''.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{2789fig5.eps} \end{figure}$	Figure 5: Same as Fig. 3, but for different structures at $\theta =38^{\circ }$ ; increasing abscissa = limb direction; panel labels correspond to the boxes in Fig. 4. Dotted curves show averages of profiles with maximum intensities larger than 1.2.
Open with DEXTER

At smaller angles, however, "projected'' and non-"projected'' structures occur in close spatial proximity. Box-a in Fig. 4 gives an example of a chain of several BP without pronounced "brightness projection'' onto the limbside neighboring granule. The corresponding spatial scans in Fig. 5 show "dark lanes'' with $\langle\delta I^{G}\rangle = 0.8$ and $\langle\delta I^{\rm cont}\rangle = 0.85$ in the G-band and the continuum, respectively. The intensity excess in the G-band amounts to $\langle\delta I^{G}\rangle = 1.3$ . In the continuum, however, the intensity does not exceed that of the neighboring granules.

The middle panels in Fig. 5 (box-b in Fig. 4) show spatial scans across bright structures which, unlike BP, are not completely separated from the limb-sided granule. However, they also do not show a clear "projection'' onto the limbside granule. The lower panels of Fig. 5 give spatial scans across structures with a clear "projection effect'' (box c in Fig. 4).

$\begin{figure} \par\includegraphics[width=8.0cm,clip]{2789fig6.eps} \end{figure}$	Figure 6: Maximum (solid and dotted lines) of faculae and minimum (dashed and dot-dot-dot-dashed lines) intensities of facular "dark lanes'' from averaged profiles vs. the heliocentric angle.
Open with DEXTER

Figure 6 shows the variation of the spatial scans with the heliocentric angle $\theta$ . The data points have been derived from selected facular areas (as e.g. in Fig. 2) and do not denote a statistical mean. The intensity maxima increase up to $\theta\approx~70^{\circ}$ and remain constant or slightly decrease towards larger $\theta$ . The minimum intensities of the facular lanes exhibit an opposite behavior so that the contrast of the maximum relative to the adjacent lanes achieves a maximum at $\theta\approx~70^{\circ}$ . This trend is quite clear for the 587.5 nm continuum but is not that pronounced in the G-band. The distances between the intensity minima of the "dark lanes'' and the maxima of the hot wall effect are approximately $0\hbox{$.\!\!^{\prime\prime}$ }3$ at $\theta = 61^{\circ}$ (see Fig. 3). We find no systematic variation of these distances with $\theta$ .

3.2 Statistical behavior

Figure 7 shows scatter plots of the 4475 facular grains detected by means of the algorithm described in Sect. 2.1. The maximum sizes (Fig. 7a) reach A=199 pixel which corresponds to a projected area of 0.185 Mm² (each pixel being equivalent to 0.00176 arcsec²). The maximum continuum intensity excess occurs at $1.18 \le \langle\delta I^{\rm cont}\rangle \le 2.39$ (Fig. 7b). Most of the facular grains are located in an interval $1.3<\delta I^{\rm cont}<1.7$ which is in agreement with findings by Sütterlin et al. (1999).

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{2789fig7.eps} \end{figure}$	Figure 7: Scatter plots of all 4475 facular grains detected in the $\lambda =587.5$ nm continuum images. The upper panel shows the relative areas A vs. cos $\theta$ , the lower panel represents the maximum intensity excess of the facular grains.
Open with DEXTER

In Fig. 8 we display the CLV of various quantities averaged in bins of width $\Delta \cos \theta = 0.02$ . The over-plotted error bars denote standard deviations in each bin. The maximum and the mean intensity excesses of the entire sample of 4475 facular grains (Fig. 8, middle) show no significant variation with the heliocentric angle. This is in contrast to earlier measurements (e.g. Lawrence 1988; Auffret & Muller 1991; Sánchez Cuberes et al. 2002; Okunev & Kneer 2004), but confirms the findings by de Boer et al. (1997) and by Sütterlin et al. (1999) extending them from $\theta\le82^\circ$ to $\theta\le88^\circ$ . We do not find indication for a substantial change in the smooth CLV for $45^\circ<\theta<60^\circ$ as reported by Topka et al. (1997) who, however, refer to conglomerates of magnetic structures considerably larger than those revealed in the present observations.

The areas (measured in pixel squares) remain remarkably constant with $\theta$ (upper left panel). This closely agrees with Steiner (2005; solid dots in the right hand in his Figs. 2 and 4), but it disagrees with Auffret & Muller (1991). Simple correction for geometric foreshortening (dividing by $\cos\theta$ ) would yield an increase of the "true'' areas toward the very limb (upper right panel of our Fig. 8) and thus contradict to some extent the results of Sánchez Cuberes et al. (2002) who found a decrease of the number of large de-projected areas towards the limb. However, it seems doubtful whether a division by $\cos\theta$ yields reasonable information, since the facular brightening occurs at the "hot wall'' rather than on the solar surface.

The sizes of the limb facular grains show a clear dependence on their brightness (Fig. 8; lower right panel) in the sense that larger limb facular grains are brighter. This may yield a selection effect which favors the detection of larger grains near the limb, and may partly explain the abovementioned discrepancies.

$\begin{figure} \par\includegraphics[width=8.5cm,clip]{2789fig8.eps} \end{figure}$	Figure 8: CLV of the facular grain areas, de-projected areas ( upper), maximum and mean continuum intensity excesses, averaged in bins of $\Delta \cos \theta = 0.02$ width ( middle), together with the corresponding number of grains and the area dependence of the maximum intensity excesses ( lower panels).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{2789fig9.ps} \end{figure}$

Figure 9: Profiles of absorption lines with zero or negligible Zeeman effect in a limb facular grain at $\theta \approx 70^\circ$ (upper full lines) compared to a neighboring undisturbed location at equal $\theta$ (dotted); the dashed line gives the facular profile normalized to have the same continuum intensity as the undisturbed region profile: the "residual intensity effect'' from disk center disappears almost entirely. Ordinate in units of continuum =100; abscissa in CCD-pixels.

Open with DEXTER

4 The intensity excess in the line-cores

The spectral signature of the facular grains is of importance for a realistic theoretical modelling. In Fig. 9 we give typical profiles of the non-magnetic lines taken simultaneously in an isolated limb facular grain at $\theta \approx 70^\circ$ . It shows the pronounced continuum excess, but almost no change of the line depression when normalized to the adjacent continuum. This finding supports the results by Stellmacher & Wiehr (1979) at higher spatial resolution and with more confidence since observed simultaneously.

For comparison, we show in Fig. 10 the same line profiles as in Fig. 9, but for a disk center plage region showing a pronounced "line gap'' in the spectrum. The significant residual intensity enhancement is positive for all lines independent of their excitation or equivalent width; however, its amount increases with the line strength, in good agreement with Stellmacher & Wiehr (1979). The corresponding continua do not show any excess, as to be expected for the finite spatial resolution achieved in the spectra (about $0\hbox{$.\!\!^{\prime\prime}$ }8$ ) as compared to the extremely small size of the tiny magnetic structures (see, e.g., Wiehr et al. 2004).

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{2789fig10.ps} \end{figure}$	Figure 10: The "residual intensity effect'' of a "line gap'' at disc center in absorption lines with zero or negligible Zeeman effect; line profiles from the "gap'' location (full) compared with a neighboring non-magnetic region (dotted lines).
Open with DEXTER

5 Conclusions

The disappearance of the "residual intensity effect'' in the continuum-normalized line profiles of limb facular grains can be explained by the spatial displacement of the line-cores with respect to their corresponding continuum (Stellmacher & Wiehr 1991, 2001) originating from the formation height of the line-core above that of the continuum seen at an oblique line-of-sight. This "geometric elevation'' of the line-cores in regions very close to the limb has the result that a wavelength scan starting at the spatial location of the bright facular continuum misses the "corresponding'' line-core location since the latter is spatially displaced toward the limb. In turn, a spectral scan that crosses the facular location of the line-core gives a continuum limb-wards of the maximum facular intensity. This spatial offset has so far not been considered in modelling line profiles of facular grains near the limb.

Our two-dimensional images at unprecedented spatial resolution show that limb facular grains are clearly visible up to $\theta=87^\circ$ , i.e., cos $\theta>0.05$ . This extends former results by de Boer et al. (1997) and by Sütterlin et al. (1999) which excluded a contrast decrease at cos $\theta > 0.17$ , to cos $\theta>0.05$ .

The spatial scans through the two-dimensional images yield profiles and maximum values which agree with model calculations by Steiner (2005), which, however, do not make predictions for large helio-centric angles up to $\theta=87^\circ$ . In particular, the question of whether the models yield a constant intensity excess down to cos $\theta=0.05$ is uncertain; this equally holds for the model calculations by Keller et al. (2004) and by Carlsson et al. (2004). Steiner & Stenflo (1990) find for a "hot cloud'' in upper layers, fed by the lateral radiation of the hot walls, a "secondary'' contrast maximum in close proximity to the limb. Our data, however, indicate a smooth variation of the CLV.

On the other hand, such a "hot cloud'' (Rogerson 1961) was used to explain measurements of an enhanced solar oblateness in presence of pronounced facular plages (e.g., Chapman & Ziegler 1996; Bruls & Solanki 2002). Also the "hillock model'' by Schatten et al. (1986), predicting elevated iso- $\tau$ surfaces in the flux concentration, might offer a possible explanation of the substantial contrast at the extreme limb.

Still more critical than the intensity excess at the extreme limb is the occurrence of "dark lanes'' even at very large helio-centric angles, where the cold "bottom'' of a small-scale flux concentration is barely visible. Steiner (2005) calculates that these lanes do not arise exclusively from the "bottom'' of the flux concentration but to a large extent from the immediate vicinity where photon escape towards the flux sheet occurs. Compared to the models, the smaller lanes observed might point to remaining problems with the accurate treatment of (lateral) radiative transfer.

The co-existence of "projected'' (i.e., facular grain type) and roundish (i.e., BP type) structures at $\theta =38^{\circ }$ may be explained by a large variety of magnetic field inclinations which could either counterbalance the "projection on the hot wall'' or enhance it. The required field inclinations up to $38^{\circ}$ agree with Beck et al. (2005) who found a large variety of field inclinations. Much earlier, Wiehr (1978) found spatial displacements at disc center between maxima of field strengths and corresponding Ca II K brightness excesses of up to 2'', indicating for Ca II K formation at h=1250 km an inclination of as much as $55^{\circ}$ . Stangl & Hirzberger (2005) found spatial displacements up to $0\hbox{$.\!\!^{\prime\prime}$ }21$ for a formation height distance of 200 km; this corresponds to inclinations of $37^{\circ}$ . A comprehensive treatment of the inclination of plage fields was given by Martinez Pillet et al. (1997).

The nature of facular grains at the extreme limb should be studied in more detail by both very high resolution observations and model calculations at largest helio-centric angles.

Solar limb faculae

1 Introduction