F. Pont1 - F. Bouchy2,3 - C. Melo4 - N. C. Santos5 - M. Mayor1 - D. Queloz1 - S. Udry1
1 - Observatoire de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland
2 -
Laboratoire d'Astrophysique de Marseille,
Traverse du Siphon, 13013 Marseille, France
3 -
Observatoire de Haute Provence, 04870 St Michel l'Observatoire, France
4 -
ESO, Casilla 19001, Santiago 19, Chile
5 -
Lisbon Observatory, Tapada da Ajuda, 1349-018 Lisboa, Portugal
Received 26 January 2005 / Accepted 23 March 2005
Abstract
We present the results of our high-resolution spectroscopic follow-up of 42 planetary transit candidates in Carina from the OGLE survey. This follow-up has already allowed the discovery of three new transiting exoplanets, OGLE-TR-111, 113 and 132. Here we analyse the data for the remaining 39 candidates. The radial velocity data show that most of them are eclipsing binaries, in very varied configurations. Precise radial velocity orbits were derived for 15 binaries, revealing 9 transits of small stars (generally M-dwarfs) in front of F-G dwarfs, 1 grazing equal-mass eclipsing binary, 4 triple and 1 quadruple systems. A further 14 systems appear binary, but the exact orbit is uncertain or was not determined. 2 objects do not show any radial velocity variations in phase with the transit signal, and 6 do not possess spectral lines strong enough for a reliable cross-correlation function to be measured. Among these last two categories, up to 6 objects are suspected false positives of the photometric transit detection. 2 objects are unsolved cases that deserve further observations.
Our study illustrates the wide variety of cases that can mimic photometric planetary transits, and the importance of spectroscopic follow-up. Multi-fiber capacities and an optimized follow-up strategy, which we present here, can help deal with the high number of candidates that are likely to be found in the near future.
An important by-product of this study is the determination of exact masses and radii for five very low-mass stars, including two at the very edge of the stellar domain, OGLE-TR-106 (
![]() )
and OGLE-TR-122 (
)
and OGLE-TR-122 (
![]() ). The radius of these objects is consistent with theoretical expectations. Two further objects, OGLE-TR-123 and OGLE-TR-129, may harbour transiting companions near the brown-dwarf/stellar limit (
). The radius of these objects is consistent with theoretical expectations. Two further objects, OGLE-TR-123 and OGLE-TR-129, may harbour transiting companions near the brown-dwarf/stellar limit (
![]() ), whose confirmation requires further high-resolution spectroscopic monitoring.
), whose confirmation requires further high-resolution spectroscopic monitoring.
No transiting massive planets (
![]() )
were detected, confirming the rarity of such systems at short period as indicated by Doppler surveys. No light (
)
were detected, confirming the rarity of such systems at short period as indicated by Doppler surveys. No light (
![]() ), large (
), large (
![]() )
planets were found either, indicating that "hot Saturns'' generally have smaller radii than hot Jupiters. Three short period binaries with a M-dwarf companion show definite orbital eccentricities, with periods ranging from 5.3 to 9.2 days. This confirms theoretical indications that orbital circularisation in close binaries is less efficient for smaller companion masses.
)
planets were found either, indicating that "hot Saturns'' generally have smaller radii than hot Jupiters. Three short period binaries with a M-dwarf companion show definite orbital eccentricities, with periods ranging from 5.3 to 9.2 days. This confirms theoretical indications that orbital circularisation in close binaries is less efficient for smaller companion masses.
We also discuss the implications of our results for the statistical interpretation of the OGLE planetary transit survey in Carina in terms of planet frequency and detection efficiency. We find that the actual transit detection threshold is considerably higher than expected from simple estimates, and very strongly favours the detection of planets with periods shorter than about 2 days. The apparent contradition between the results of the OGLE transit survey and Doppler surveys can be resolved when this detection bias is taken into account.
Key words: stars: planetary systems - stars: low-mass, brown dwarfs - stars: binaries: eclipsing
Since the groundbreaking discovery of 51 Pegasi (Mayor & Queloz 1995), more that one hundred planets have been detected around other stars, the vast majority of them by radial velocity surveys.
Transiting planets are especially valuable in the study of exoplanets, because the presence of a transit allows the determination of the exact mass and radius - and therefore mean density - of the planet. These are obviously very important parameters in the physical understanding of exoplanet structure and evolution. Data from transits are thus an important complement to radial velocity planet searches which provide only an estimate of
![]() in addition to orbital parameters.
in addition to orbital parameters.
The first exoplanet transit was detected around HD 209458 by Charbonneau et al. (2000) and Henry et al. (2000), the planet having been previously discovered in radial velocity by Mazeh et al. (2000). This planet has turned out to have a radius much larger than Jupiter,
![]()
![]() (Brown et al. 2001), and to be undergoing significant evaporation (Vidal-Madjar et al. 2003; Brown et al. 2002; Charbonneau et al. 2002; Vidal-Madjar et al. 2004).
(Brown et al. 2001), and to be undergoing significant evaporation (Vidal-Madjar et al. 2003; Brown et al. 2002; Charbonneau et al. 2002; Vidal-Madjar et al. 2004).
In the wake of the first exoplanet detection, Gilliland et al. (2000) have monitored several thousand stars in the globular cluster 47 Tuc with the HST in search of photometric planetary transits, but none were found. This result is now attributed to the paucity of short-period planets around metal-poor stars (Sackett et al. 2005).
In recent years, increasing telescope automation and the capacity to process large amounts of CCD photometric data have make possible several ambitious ground-based searches for planetary transits: e.g. STARE (Brown & Charbonneau 2000), WASP (Kane et al. 2001), PLANET (Sackett et al. 2004). The most successful of these searches to date has been the OGLE survey, which monitored 3 fields in the direction of the Galactic bulge and 3 fields in Carina during 2001/2002, annoucing 137 possible transiting candidates (Udalski et al. 2002c,a,b,2003). After these candidates were announced, several spectroscopic follow-up programmes were initiated (Gallardo et al. 2005; Konacki et al. 2003b; Dreizler et al. 2002), including our own follow-up of 17 candidates in the Galactic bulge field (Bouchy et al. 2005, hereafter Paper I). It was found that the vast majority of transiting candidates were eclipsing binaries, as predicted by the simulations of Brown (2003).
In this context, Konacki et al. (2003a) announced the first exoplanet discovered by photometric transit surveys, OGLE-TR-56b (confirmed by Bouchy et al. 2005). This planet was found to orbit with the unexpectedly short period of 1.2-days, much shorter than the observed pile-up of periods above 3 days in radial velocity surveys.
In March 2004, using the FLAMES/UVES multi-fiber spectrograph on the VLT, we acquired high-resolution spectroscopic information for 42 of the most promising candidates in the OGLE Carina fields, up to 8 spectra per object. Three planets were discovered in this way: OGLE-TR-111b (Pont et al. 2004), OGLE-TR-113b and OGLE-TR-132b (Bouchy et al. 2004). Two of them are very short-period planets, revealing that the case of OGLE-TR-56b was not uncommon. OGLE-TR-113b was subsequently confirmed by independent radial velocity measurements (Konacki et al. 2004) and a high-accuracy photometric transit curve was obtained for OGLE-TR-132 by Moutou et al. (2004). One more object in the OGLE survey, OGLE-TR-10, has gradually emerged as a solid transiting planet detection (Konacki et al. 2005,2003b; Bouchy et al. 2005).
The only other transiting planet discovered to date by transit searches is TrES-1 (Alonso et al. 2004). The total of known transiting planets is now seven, and they have already spurred several interesting studies (e.g. Burrows et al. 2004; Chabrier et al. 2004; Lecavelier des Etangs et al. 2004; Mazeh et al. 2005; Sasselov 2003).
In Paper I, we showed that most of the OGLE transiting candidates are actually eclipsing binaries. These binaries can be interesting in their own right, especially since in many of them the eclisping body is a very small star. Because the mass and radius of the transiting body can be obtained from the transit and radial velocity data, an important by-product of the radial velocity follow-up is to provide constraints on the mass-radius relation for low-mass stars (see Paper I). These data augment those from brighter eclipsing binaries and from interferometric studies of nearby M-dwarfs.
The present paper gives the results of our spectroscopic follow-up of OGLE transiting candidates in Carina (Candidates number 60-132 described in Udalski et al. 2002b,2003). Section 2 presents the spectroscopic data and reduction, Sect. 3 explains the tools used in the analysis of the light curve and spectroscopic data, Sect. 4 presents the resolution of all cases by category, and Sect. 5 discusses some implications of this study, notably on the stellar mass-radius relation for low-mass stars and the statistical implications of the planet detections.
The observations were acquired in 8 half-nights (32 h) on FLAMES on 13 to 21 March 2004 (Prog. 72.C-0191). FLAMES is a multi-fiber link which allows feeding the high-resolution spectrograph UVES with up to 7 targets on a field of view of 25 arcmin diameter, in addition to a simultaneous thorium calibration (Pasquini et al. 2002). In a previous run on this instrument (Paper I), we have shown that FLAMES was able to measure radial velocities with an accuracy of about 30 m s-1 on stars down to the 16th mag in I. Some trials with HARPS and UVES in slit mode (see Paper I) led to the conclusion that FLAMES was a very efficient instrument for the radial velocity follow-up of OGLE transit candidates.
For the 73 OGLE transit candidates in the Carina field (OGLE-TR-60 to TR-132), the most promising candidates in terms of planetary transits were selected according to three main criteria:
In order to optimize the use of telescope time, we used a real-time replacement strategy throughout the observing run: as soon as an object was detected as a binary (i.e. photometric transit signal not caused by a planet but by an eclipsing binary), the object was marked for possible re-allocation of the corresponding FLAMES fiber to another target. The objects were also marked if no signal was detected in the cross-correlation function (indicating a fast-rotating star, an early-type star or a heavily blended system). In the following night, the fiber corresponding to the objects marked was re-allocated to a new target, if allowed by the distribution of the targets in the sky. In that way, we could observe and characterise 42 objects with four fields of 7 fibers and make a highly efficient use of the multiplex facility. We could observe all first-priority targets, and 11 of the 16 second-priority targets (OGLE-TR-70, 71, 73, 74 and 115 were left unobserved because of their inconvenient position in the field).
Most OGLE candidates are eclipsing binaries rather than planets. We used three criteria to identify eclipsing binaries from the spectroscopic measurements: (i) presence of more than one set of lines in the spectrum (double- or triple-lined binaries); (ii) rotational broadening of the lines corresponding to tidal synchronisation; (iii) large variations of the radial velocity. Figure 1 shows examples of spectral cross-correlation function (CCF) illustrating the different cases.
Note that criteria (i) and (ii) require only one spectroscopic measurement. Criterion (ii) is based on the fact that binaries with periods smaller than about 10 days are expected to be tidally locked to their companions in synchronous rotation. The increased rotation velocity is observed as a broadening of the correlation dip in the cross-correlation function. See Sect. 3 for more details.
The spectra obtained from FLAMES/UVES were extracted using
the standard ESO-pipeline with bias, flat-field and background correction. Wavelength
calibration was performed with the ThAr spectra. The radial velocities were obtained by
cross-correlation with a numerical template constructed from the Sun spectrum atlas.
The ThAr spectrum was used in order to compute
the instrumental drift by cross-correlation with a thorium template (see Paper I for details).
Radial velocity uncertainties were computed as in Paper I.
The most precise of our measurements (![]() m s-1) are not photon-noise limited and
we added quadratically an uncertainty of 30 m s-1 in order to take into the account
systematic errors probably due to wavelength calibration errors, fiber-to-fiber
contamination, and residual cosmic rays. This value was ajusted on
the O-C residuals of the non-rotating star without significant radial velocity variations OGLE-TR-131 (Bouchy et al. 2004).
m s-1) are not photon-noise limited and
we added quadratically an uncertainty of 30 m s-1 in order to take into the account
systematic errors probably due to wavelength calibration errors, fiber-to-fiber
contamination, and residual cosmic rays. This value was ajusted on
the O-C residuals of the non-rotating star without significant radial velocity variations OGLE-TR-131 (Bouchy et al. 2004).
In the case of double-lined and triple-lines spectra, the radial velocities of each component were calculated with standard techniques for spectroscopic binaries. Iterative solutions were often necessary to disentangle the components when the multiple line systems are blended with each other. We note that the radial velocity uncertainties were calculated assuming single-lined spectra and in the case of blended spectra they may be underestimated.
Our radial velocity measurements and cross-correlation function parameters are listed in Table 8 (available in electronic form) and analysed in Sect. 4.
Rotational velocities were computed from the observed cross-correlation function using rotationally broadened line profiles convolved with a Gaussian instrumental profile of width 4.0 km s-1 (found suitable for our instrumental setup in Paper I). The profiles were fitted to the CCF simultaneously with the radial velocity to determine the projected rotation velocity v sin i of the target objects.
A quadratic limb-darkening with coefficients
![]() was assumed
(the computations of Barban et al. 2003 find that such a coefficient is a suitable approximation for a wide range of spectral types in wavelengths corresponding to the V filter).
was assumed
(the computations of Barban et al. 2003 find that such a coefficient is a suitable approximation for a wide range of spectral types in wavelengths corresponding to the V filter).
For the slowly-rotating stars in our sample, the stellar parameters (temperatures, gravities and metallicities) were obtained from an analysis of a set of Fe I and Fe II lines, following the procedure used in Santos et al. (2004). The precision of the derived atmospheric parameters is limited by the relatively low S/N of the combined spectra (30-50), together with some possible contamination coming from the ThAr spectrum.
For the stars in our sample rotating with v sin i ![]() 20 km s-1, or multiple-lined spectra,
the method described in Santos et al. (2004) is not applicable,
because the measurement of individual equivalent widths is
not accurate enough due to line blending. The majority of the objects in our sample are actually in this case.
When necessary for the resolution of the case, we have determined very rough estimates of the spectral type by visual comparison of the observed spectra with a grid of synthetic spectra.
20 km s-1, or multiple-lined spectra,
the method described in Santos et al. (2004) is not applicable,
because the measurement of individual equivalent widths is
not accurate enough due to line blending. The majority of the objects in our sample are actually in this case.
When necessary for the resolution of the case, we have determined very rough estimates of the spectral type by visual comparison of the observed spectra with a grid of synthetic spectra.
For close binaries, with rotation periods of the order of a few days, we expect the
rotation axis to be aligned with the orbital axis and the system
to be tidally locked (e.g. Hut 1981; Levato 1976). For known close binaries, the alignment of the axes and the tidal locking is fast. In that case,
![]() and the rotation velocity is
directly related to the radius of the primary. In Paper I, we could indeed verify this hypothesis in all the targets observed, and we shall use it here both to estimate the primary radius R and as an indication that the companion is massive when we have only one spectroscopic measurement.
and the rotation velocity is
directly related to the radius of the primary. In Paper I, we could indeed verify this hypothesis in all the targets observed, and we shall use it here both to estimate the primary radius R and as an indication that the companion is massive when we have only one spectroscopic measurement.
Figure 2 shows, for the Carina sample, the rotation velocity of the primary target as a function of the period of the transit signal (for transiting objects,
![]() and therefore
and therefore
![]() ). Most objects have a rotation velocity compatible with synchronisation for reasonable values of the primary radius (1-2
). Most objects have a rotation velocity compatible with synchronisation for reasonable values of the primary radius (1-2 ![]() ), indicating that eclipsing binaries dominate the sample. The only exceptions are the three planet hosts OGLE-TR-111, 113 and 132, and the objects OGLE-TR-97, 124 and 131. OGLE-TR-97 has a triple-lined spectrum and the last two are suspected false transit detections (see Sect. 4.4).
), indicating that eclipsing binaries dominate the sample. The only exceptions are the three planet hosts OGLE-TR-111, 113 and 132, and the objects OGLE-TR-97, 124 and 131. OGLE-TR-97 has a triple-lined spectrum and the last two are suspected false transit detections (see Sect. 4.4).
The radial velocity data, obtained two years after the photetric data, generally allow a significant improvement of the determination of the orbital periods. Some systems turn out to be grazing, equal-mass eclipsing binaries where both the eclipse and anti-eclipse were visible in the light curve. In these cases the real orbital period of the system is double the period in Udalski et al. (2002b,2003).
Unlike in Paper I, there were no cases where the radial velocity indicated a completely different period than the photometry. This reflects the fact that fewer candidates with only two or three measured transits were accepted in the OGLE Carina sample than in the Galactic bulge sample.
The depth, width and general shape of the transit signal depend on a combination of
physical variables, mainly the radius ratio qR (noted
![]() in Paper I), the primary radius R and the impact
parameter b (or, equivalently for circular orbits, the angle i of the normal of the
orbital plane with the line-of-sight) and the orbital eccentricity. It is also more weakly
dependent on the total mass (m+M) - via the orbital period and semi-major axis for a
Keplerian orbit - and the limb darkening coefficients. The parameter qR is mainly
constrained by the transit depth, b by the transit shape and the factor
R (m+M)-1/3 by the transit duration.
in Paper I), the primary radius R and the impact
parameter b (or, equivalently for circular orbits, the angle i of the normal of the
orbital plane with the line-of-sight) and the orbital eccentricity. It is also more weakly
dependent on the total mass (m+M) - via the orbital period and semi-major axis for a
Keplerian orbit - and the limb darkening coefficients. The parameter qR is mainly
constrained by the transit depth, b by the transit shape and the factor
R (m+M)-1/3 by the transit duration.
The light curves were fitted by non-linear least square fitting with analytic transit curves
computed according to Mandel & Agol (2002), using a
quadratic limb darkening model with
![]() .
Note that this is
different to the coefficients used for the determination of the rotational velocity,
because the wavelengths are different. The OGLE data was
obtained with an I filter while the spectra are centered on the visible. The fitted
parameters were qR, VT/R and b, where VT is the transversal orbital velocity
at the time of the transit. The uncertainties on these parameters were estimated using a method that
takes into account the covariance of the photometric residuals (see Paper I for details).
.
Note that this is
different to the coefficients used for the determination of the rotational velocity,
because the wavelengths are different. The OGLE data was
obtained with an I filter while the spectra are centered on the visible. The fitted
parameters were qR, VT/R and b, where VT is the transversal orbital velocity
at the time of the transit. The uncertainties on these parameters were estimated using a method that
takes into account the covariance of the photometric residuals (see Paper I for details).
For convenience, the six relations
used to infer the system parameters from the observables are repeated below from Paper I:
| (1) | |||
| (2) | |||
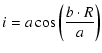 |
(3) | ||
| (4) | |||
| qR= r/R | (5) | ||
| (6) |
where v sin i is the projected rotation velocity in km s-1, i the orbital inclination, P the period in days, R, r, M and m the radii and masses of the eclipsed and eclipsing bodies in solar units, K the primary radial-velocity semi-amplitude in km s-1, and a the orbital semi-major axis in units of ![]() .
The function f in the last equation is the relation given by the theoretical stellar evolution models of Girardi et al. (2002).
.
The function f in the last equation is the relation given by the theoretical stellar evolution models of Girardi et al. (2002).
We assumed that all orbits were circular (e=0) unless the radial velocity data clearly indicated otherwise.
Very close binaries are expected to be circularized on a timescale shorter than typical stellar ages. However, the circularisation timescale
increases with decreasing companion mass (Zahn 1989), so that some of the low-mass companions in our sample may still have eccentric orbits.
Four objects show definite indications of ![]() in the velocity curve. For eccentric orbits, Eqs. (2)-(4) above must be slightly modified. The distribution of eccentricities are discussed in Sect. 5.2.
For eccentric orbits, the synchronisation may also still be in progress. Eccentric orbits are expected to evolve towards "pseudo-synchronisation'', i.e. synchronisation of the rotation with the orbital velocity at periastron. For the two objects with the most eccentric orbits in our sample, OGLE-TR-120 and OGLE-TR-122, the rotation velocity does not seem compatible with either synchronisation or pseudo-synchronisation. We therefore do not use the synchronisation constraint in these two cases.
in the velocity curve. For eccentric orbits, Eqs. (2)-(4) above must be slightly modified. The distribution of eccentricities are discussed in Sect. 5.2.
For eccentric orbits, the synchronisation may also still be in progress. Eccentric orbits are expected to evolve towards "pseudo-synchronisation'', i.e. synchronisation of the rotation with the orbital velocity at periastron. For the two objects with the most eccentric orbits in our sample, OGLE-TR-120 and OGLE-TR-122, the rotation velocity does not seem compatible with either synchronisation or pseudo-synchronisation. We therefore do not use the synchronisation constraint in these two cases.
The analysis of the 42 objects measured in spectroscopy is presented below, divided for convenience according to categories reflecting the treatment of the data and the nature of the systems: single-lined spectroscopic binaires (eclipsing binaries with small companion), multiple-lined spectroscopic binaries (grazing eclipsing binaries, multiple systems, line-of-sight blends), transiting planets, suspected false transit detections, and objects without CCF signal. Table 7 summarizes the conclusions of the analysis.
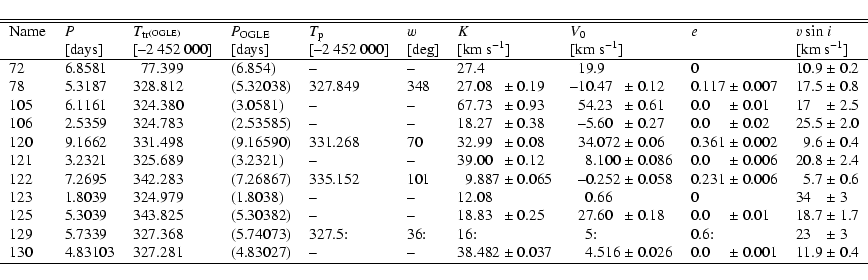
Objects OGLE-TR-72, 78, 105, 106, 120, 121, 122, 125 and 130 show single-lined spectra with radial velocity variations compatible with orbital motion at the period given by the photometric transits. They are eclipsing binaries, with a fainter, unseen companion causing the observed photometric signal. The radial velocity data were fitted with Keplerian orbits. Figure 3 shows the resulting radial velocity orbits. The spectroscopic and light-curve data were then combined as described briefly above and more fully in Paper I to determine the mass and radius of both components. The target stars are assumed to be tidally locked to their companion in synchronous rotation, which implies that the rotation velocity derived from the broadening of the cross-correlation function is directly related to the star's radius (Eq. (1)).
Contrarily to Paper I, for most of the objects in this study we have no precise spectroscopic estimate of the temperature, because of the rotational line broadening and the low signal-to-noise of the spectra. When necessary to constrain the solution, the existence of a signal in the cross-correlation function was used to give a broad upper limit to the temperature,
![]() K. This improves the solution for m by eliminating very high values of M in cases when R is large (namely for OGLE-TR-78 and 125).
K. This improves the solution for m by eliminating very high values of M in cases when R is large (namely for OGLE-TR-78 and 125).
![\begin{figure}
\par\includegraphics[angle=-90,width=5.7cm,clip]{2771f3a.ps}\hspa...
...space*{2mm}
\includegraphics[angle=-90,width=5.7cm,clip]{2771f3h.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg43.gif) |
Figure 3: Radial velocity data and orbits for single-lined spectroscopic binaries. The orbital periods and epochs are constrained in combination with the photometric signal. The corresponding parameters are given in Table 1. The measurements uncertainties are smaller than the symbols. |
|
The results for the radial velocity orbit and the rotation velocity are given in Table 1. The parameters obtained from the combination of the light curve and spectroscopy are given in Table 7.
Two different methods were used to combine the constraints (1)-(6): if the impact parameter was low, the solution was obtained by ![]() minimisation as in Paper I. For higher values of the impact parameter, the radius ratio is partly degenerate with the orbital angle. In these cases (OGLE-TR-72, 105, 121), we first obtained an estimate of the primary mass using the approximate relation
minimisation as in Paper I. For higher values of the impact parameter, the radius ratio is partly degenerate with the orbital angle. In these cases (OGLE-TR-72, 105, 121), we first obtained an estimate of the primary mass using the approximate relation
![]() ,
then fitted the light curve with VT/R fixed and only the radius ratio and impact parameters as free parameters. Obviously, in that case some values obtained can have higher uncertainties, as indicated in Table 7 with colons.
,
then fitted the light curve with VT/R fixed and only the radius ratio and impact parameters as free parameters. Obviously, in that case some values obtained can have higher uncertainties, as indicated in Table 7 with colons.
For OGLE-TR-105, the radial velocity data show that the period needs to be doubled, and that both transit and anti-transit were visible in the photometric data.
OGLE-TR-122 is the smallest stellar object in our sample, with a planet-like radius, and as such is highly interesting. It is analysed in more details in a separate article (Pont et al. 2005).
![\begin{figure}
\par\includegraphics[angle=-90,width=5.7cm,clip]{2771f4a.ps}\hspace*{2mm}\includegraphics[angle=-90,width=5.7cm,clip]{2771f4b.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg47.gif) |
Figure 4: Radial velocity data and tentative orbital solution for OGLE-TR-123 and OGLE-TR-129. The orbital periods and epochs are constrained in combination with the photometric signal. The corresponding parameters are given in Table 1. The measurements uncertainties are plotted only when larger than the symbols. |
OGLE-TR-123 was measured only three times and the solution proposed in Table 1 is only tentative. Our three spectra for this objects show a wide CCF signal, with v sin i ![]() 34.5 km s-1, and small velocity variations to the level of a few km s-1. The rotation is compatible with synchronisation, and would indicate
34.5 km s-1, and small velocity variations to the level of a few km s-1. The rotation is compatible with synchronisation, and would indicate
![]() .
A circular orbit fitted on the velocity points with the epoch of the transit signal gives K=12.08 km s-1, V0= 0.66 km s-1and P=1.8038 days. These are tentative values because the number of free parameters is equal to the number of points. If the period is fixed to the OGLE value as well, the orbit fit yields
.
A circular orbit fitted on the velocity points with the epoch of the transit signal gives K=12.08 km s-1, V0= 0.66 km s-1and P=1.8038 days. These are tentative values because the number of free parameters is equal to the number of points. If the period is fixed to the OGLE value as well, the orbit fit yields
![]() km s-1 and
km s-1 and
![]() km s-1. This implies
km s-1. This implies
![]() and
and
![]() for the transiting body, making OGLE-TR-123 an extremely interesting candidate of transiting brown dwarf or low-mass star near the hydrogen-burning limit (see Fig. 10). However, the transit duration is longer than would be predicted by this scenario. More data is needed to confirm the period and exclude more complex blend scenarios
for the transiting body, making OGLE-TR-123 an extremely interesting candidate of transiting brown dwarf or low-mass star near the hydrogen-burning limit (see Fig. 10). However, the transit duration is longer than would be predicted by this scenario. More data is needed to confirm the period and exclude more complex blend scenarios![]() .
.
OGLE-TR-129 has a wide and very shallow signal in the CCF, and the radial velocities have large uncertainties. The projected rotation velocity is v sin i ![]() 23 km s-1, which implies
23 km s-1, which implies
![]() in case of synchronised rotation. The spectrum indicates a high temperature,
in case of synchronised rotation. The spectrum indicates a high temperature,
![]() ,
compatible with this radius value. The radial velocity data phased on the period of the photometric transit signal are compatible with a markedly eccentric orbit. There is some degeneracy between the eccentricity and K, and orbits with lower eccentricity and lower values of K are also marginally compatible with the data. Possible values for K would imply
,
compatible with this radius value. The radial velocity data phased on the period of the photometric transit signal are compatible with a markedly eccentric orbit. There is some degeneracy between the eccentricity and K, and orbits with lower eccentricity and lower values of K are also marginally compatible with the data. Possible values for K would imply
![]() for the transiting body. A transiting M-dwarf scenario is not coherent, however, with the transit shape and depth if the primary is synchronised: the amplitude of the radial velocity variation indicates
for the transiting body. A transiting M-dwarf scenario is not coherent, however, with the transit shape and depth if the primary is synchronised: the amplitude of the radial velocity variation indicates
![]() ,
but the transit depth indicates
,
but the transit depth indicates
![]() ,
therefore with a synchronised primary
,
therefore with a synchronised primary
![]() for the secondary. Such a mass-radius relation for a M-dwarf is not expected. Moreover, the transit is clearly V-shaped, indicating a grazing transit with
for the secondary. Such a mass-radius relation for a M-dwarf is not expected. Moreover, the transit is clearly V-shaped, indicating a grazing transit with ![]() ,
which would imply an even larger secondary. The position of OGLE-TR-129 in Fig. 11 indicates that it lies near the transit detection threshold, with
,
which would imply an even larger secondary. The position of OGLE-TR-129 in Fig. 11 indicates that it lies near the transit detection threshold, with
![]() .
Comparison with other similar cases (see Sect. 4.4) suggest that it may be a false positive. In that case, the radial velocity variation may be unrelated to the photometric transit signal. Alternatively, the radial velocity variations may be explaind by a blend of more than one set of lines. The radial velocities are not precise enough to distinguish a Keplerian orbit from other types of variations. In summary, a possible scenario for OGLE-TR-129 is that of a
.
Comparison with other similar cases (see Sect. 4.4) suggest that it may be a false positive. In that case, the radial velocity variation may be unrelated to the photometric transit signal. Alternatively, the radial velocity variations may be explaind by a blend of more than one set of lines. The radial velocities are not precise enough to distinguish a Keplerian orbit from other types of variations. In summary, a possible scenario for OGLE-TR-129 is that of a
![]() transiting M-dwarf with a hot, fast-rotating primary that is not yet synchronised, but other scenarios cannot be entirely excluded.
transiting M-dwarf with a hot, fast-rotating primary that is not yet synchronised, but other scenarios cannot be entirely excluded.
The proposed orbits for these two objects are displayed in Fig. 4.
OGLE-TR-63 was measured three times in spectroscopy. Its rotation velocity is compatible with orbital synchronisation. Because the rotational broadening is very large (v sin i ![]() 74 km s-1), the radial velocities have high uncertainties. Moreover, the period near 1 day causes an unfavourable phase sampling. As a consequence, the radial velocity data is compatible with both a small M-dwarf transiting companion and with a constant velocity. This case remains unsolved.
74 km s-1), the radial velocities have high uncertainties. Moreover, the period near 1 day causes an unfavourable phase sampling. As a consequence, the radial velocity data is compatible with both a small M-dwarf transiting companion and with a constant velocity. This case remains unsolved.
OGLE-TR-94, 98, 99 and 126 were measured only once in spectroscopy. Their rotational line broadening is compatible with tidal synchronisation at the period of the observed transit signal (see Table 1 and Fig. 2), so that these objects are very likely to be eclipsing binaries. Note that even if by chance the high rotation velocity were not due to orbital synchronisation, it would make the detection of a planet orbital motion very challenging anyway, because the large width of the spectral lines significantly increases the uncertainty on the derived radial velocities. The resulting radial velocity uncertainties would be too high to reveal a planetary orbit with our FLAMES/VLT observational setup and reasonable exposure times. Moreover, if the rapid rotation were not due to synchronisation, it would most probably indicate an early-type primary. In that case, the large radius of the primary would imply a secondary radius too large for a planet. Therefore, we do not expect to miss any planet detection by rejecting these fast rotators.
For these objects, a tentative value of the primary radius can be obtained from the rotation velocity and Eq. (1), and the secondary radius can be estimated through the radius ratio obtained by a fit of the lightcurve. No mass estimate can be derived. Table 2 gives v sin i, R and r for these objects. These values are tentative estimates and no uncertainties are derived.
In the case of OGLE-TR-94, the lightcurve indicates a grazing transit, so that the radius ratio is degenerate with the impact parameter. Only a lower limit can be assigned to r. It is also possible that both the eclipse and anti-eclipse are seen, and in that case the period has to be doubled and the secondary radius is comparable to the primary radius, so that the value of r given in the table is really a lower limit.
| Name | N | v sin i | R | r |
|
| [km s-1] | [ |
[ |
[days] | ||
| OGLE-TR-63 | 3 | 74 | 1.6 | 0.15 | 1.06698 |
| OGLE-TR-94 | 1 | 28 | 1.7 | >0.2 | 3.09222 |
| OGLE-TR-98 | 1 | 18 | 2.2 | 0.34 | 6.39800 |
| OGLE-TR-99 | 1 | 51 | 1.1 | 0.19 | 1.10280 |
| OGLE-TR-126 | 1 | 18 | 1.8 | 0.25 | 5.11080 |
| Name | Comp. | P |
|
|
K | V0 | v sin i |
| [days] | [-2 452 000] | [days] | [km s-1] | [km s-1] | [km s-1] | ||
OGLE-TR-64 |
a | 5.434691 | 78.569 | (2.71740) | 62.43 |
-1.17 |
12 |
| b | 96.46 |
9: | |||||
OGLE-TR-65 |
a | 1.720390 | 76.319 | (0.86013) | 114.53 |
-2.18 |
43.6 |
| b | 119.09 |
43.9 |
|||||
| c | -6: | <5 | |||||
OGLE-TR-76 |
a | 2.12725 | 323.545 | (2.12678) | 74.1 |
11.8 |
29: |
| c | -11: | 20:: | |||||
OGLE-TR-85 |
a | 2.11481 | 324.440 | (2.11460) | 48.62 |
4.48 |
31 |
| c | -1: | 60: | |||||
OGLE-TR-112 |
a | 3.8754 | 327.532 | (3.87900) | 29.8 |
-3.3 |
40:: |
| c | - | - | 80.9 |
-11.32 |
<5 | ||
| d | 90.6 |
<5 | |||||
OGLE-TR-114 |
a | 3.4218 | 323.249 | (1.71213) | 80 |
5 |
10.8 |
| b | 80 |
10.6 |
|||||
| c | 7 (drifting) | <5 |
![\begin{figure}
\par\resizebox{15cm}{!}{\includegraphics[angle=-90]{2771f5a.ps}\i...
...cs[angle=-90]{2771f5e.ps}\includegraphics[angle=-90]{2771f5f.ps}} %
\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg65.gif) |
Figure 5:
Radial velocity data and resulting orbits for double-lined and triple-lined spectroscopic binaries. The transit epoch is derived from the photometric data. The corresponding parameters are given in Table 3. The different components identified in the spectra are identified with different symbols. In all plots the black dots indicate the object undergoing the eclipse at
|
| Name | Comp. | N | v sin i | R |
|
| [km s-1] |
|
[days] | |||
OGLE-TR-69 |
a | 2 | 15.6 | 1.44 | 2 |
| b | 11.5 | 1.06 | |||
OGLE-TR-81 |
a | 1 | 21: | 1.4 | 3.21650 |
| b | <5 | - | |||
OGLE-TR-93 |
a | 1 | 45: | 2.0 | 2.20674 |
| b | <5 | - | |||
OGLE-TR-95 |
a | 1 | 65:: | 1.8 | 1.39358 |
| b | 12 | - | |||
OGLE-TR-96 |
a | 1 | 11: | 1.4 | 2 |
| b | 9: | 1.2 | |||
| c | 71: | - | |||
OGLE-TR-97 |
a | 1 | 10.7 | - | 2 |
| b | 9.4 | - | |||
| c | <5 | - | |||
OGLE-TR-110 |
a | 1 | 11.7 | 1.32 | 2 |
| b | 11.4 | 1.28 |
Such systems range across a wide variety of cases: grazing eclipsing binaries, triple and quadruple systems. The resolution of the cases in this section necessitates the full arsenal of spectroscopic binaries analysis, that we will not repeat in detail here. The CCF components are often blended with each other and their separation requires a global, iterative treatment of all the measurements. When an orbit could be determined, the orbital solution is given in Table 3 and illustrated in Fig. 5. Estimates of masses and radii are given in Table 7. Other cases are presented in Table 4. The radius of probably synchronised components is estimated from the rotation velocity.
OGLE-TR-64 shows two dips in the cross-correlation function varying in anti-phase. The mass of both components can be determined precisely from the orbit. Both radii can be determined from the rotation velocities derived from the line broadening in the CCF. The ![]() factor can be calculated from the a posteriori fit of the light curve with both radii fixed. The period is the double of that given by Udalski et al. (2002b), because both the eclipse and anti-eclipse are seen in the light curve.
factor can be calculated from the a posteriori fit of the light curve with both radii fixed. The period is the double of that given by Udalski et al. (2002b), because both the eclipse and anti-eclipse are seen in the light curve.
OGLE-TR-69 and 110, with only one or two measurements showing two sets of lines with a large radial velocity difference and rotational broadening compatible with orbital synchronisation, are also probable grazing eclipsing binaries. The masses of the components could be estimated from the velocities using the period and epoch of the photometric transits, but the time interval between the two sets of measurements is too large to provide reliable values.
OGLE-TR-76 and 85 are triple systems with two sets of lines in the spectrum, an eclipsing binary blended with a third body. In these cases the CCF shows one set of lines with orbital motion, broadened by synchronous rotation, and the other without radial velocity change. Therefore the body causing the eclipse is an unseen third body in orbit around the first. The second body seen in the CCF is either gravitationally bound to the two others in a triple system, or an unrelated star along the same line-of-sight. The treatment of these cases is the same as for single-lined spectroscopic binaries, except that the lightcurve also contains an unknown contamination from the third body, so that the radius ratio cannot be determined from the transit signal. OGLE-TR-81, 93 and 95, with one measurement only, show one broad and one narrow component in the CCF and are probably similar systems.
Note that for all triple systems, the radial velocity of the third component is near enough to the systemic velocity of the eclipsing binary for the systems to be gravitationally bound multiple systems rather than line-of-sight contamination.
OGLE-TR-65 and 114 show three sets of lines in the CCF. These targets are equal-mass eclipsing binaries in triple systems. OGLE-TR-96, with only one measurement, appears to be a similar system with two synchronised components and a wider component (a fast-rotating F-dwarf).
OGLE-TR-112 is a truly involved case with three dips in the CCF, all varying in radial velocity on short timescales. It is a quadruple system, with three components visible in the spectra. Two of them describe an eccentric orbit around each other with a period unrelated to the photometric signal (
![]() days). The third has an orbit with the period of the transit signal, revealing that it is eclipsed by a fourth, unseen companion. Therefore OGLE-TR-112 is a system of two close binaries.
days). The third has an orbit with the period of the transit signal, revealing that it is eclipsed by a fourth, unseen companion. Therefore OGLE-TR-112 is a system of two close binaries.
For some multiple objects with only one spectroscopic measurement, the broadening of some of the spectral components are compatible with synchronous rotation with a massive eclipsing companion, but there is not enough information to determine the exact parameters of the system. Table 4 gives, for these objects, the rotation velocities indicated by the CCF components, and the corresponding radius if the rotation velocity is compatible with the period of the photometric transit signal, or with double that period for suspected grazing binaries.
For OGLE-TR-69, 81, 93, 96 and 110, the rotation velocities allows a tentative scenario to be proposed. OGLE-TR-69, 96 and 110 appear to be grazing equal-mass binaries with twice the OGLE period (Sect. 4.2.1). OGLE-TR-81 and 93 appear to be spectroscopic binaries blended with a non-rotating third body (Sect. 4.2.2).
For OGLE-TR-97, several scenarios are possible and none is clearly favoured. The CCF shows three clear dips, but none of the calculated rotation velocities are compatible with synchronisation with the (very short) period indicated with the photometry. More measurements would be needed to determine the nature of this system. However, since the presence of three sets of lines in its spectrum show that it is a blended system, it loses its interest in the context of planetary transit search, which was the main objective of our study.
Transiting exoplanets were securely detected around three of the objects: OGLE-TR-111, OGLE-TR-113 and OGLE-TR-132. A detailed account has been previously published in Bouchy et al. (2004) and Pont et al. (2004). The orbits are included in Fig. 6 for completeness.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{2771f6.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg70.gif) |
Figure 6: Radial velocity data and orbit for the three detected transiting planets. Adapted from Pont et al. (2004); Bouchy et al. (2004); Moutou et al. (2004). |
Two objects, measured 8 times each, with very high-accuracy radial velocity data, show no radial velocity variation in phase with the transit signals to the level of less than 50 m s-1(see Fig. 7). OGLE-TR-124 shows a constant drift of the radial velocity throughout the observation period, and OGLE-TR-131 shows radial velocity residuals consistent with the noise around a constant velocity. A third object, OGLE-TR-109, shows no significant radial velocity variations either, but with larger uncertainties due to a large rotational broadening. These objects are discussed in some detail here. They are interesting in the context of planet search because the absence of detected short-period radial velocity orbit is compatible with the explanation of the photometric data in terms of planetary transit if the planet mass is smaller than some upper limit. Spectroscopic information for these objects is given in Table 5. For the reasons exposed below however, we estimate that these objects are probably false positives of the transit detection procedure.
OGLE-TR-109:
The spectral lines of OGLE-TR-109 show a large rotational broadening, indicating v sin i =
![]() km s-1. The radial velocity uncertainties are correspondingly higher, and our 8 measurements show no significant variation within these uncertainties. The radial velocity data is displayed in Fig. 7. Fitting a circular orbit at the period of the transit gives
km s-1. The radial velocity uncertainties are correspondingly higher, and our 8 measurements show no significant variation within these uncertainties. The radial velocity data is displayed in Fig. 7. Fitting a circular orbit at the period of the transit gives
![]() km s-1. The temperature of the target is
km s-1. The temperature of the target is
![]() K according to our estimation,
K according to our estimation,
![]() K according to Gallardo et al. (2005). Synchronisation with the transiting companion would imply
K according to Gallardo et al. (2005). Synchronisation with the transiting companion would imply
![]() ,
which is incompatible with the temperature observed. Even if both eclise and anti-eclipse were seen, the primary radius would only be
,
which is incompatible with the temperature observed. Even if both eclise and anti-eclipse were seen, the primary radius would only be
![]() ,
still much too low to match the spectral type. Therefore the target is a non-synchronised, fast-rotating F-star, which leaves three scenario open:
,
still much too low to match the spectral type. Therefore the target is a non-synchronised, fast-rotating F-star, which leaves three scenario open:
OGLE-TR-124:
this object exhibits a linear drift in the radial velocity across eight nights of measurements,
![]() m s-1day-1. The measured rotational velocity, v sin i = 6.3
m s-1day-1. The measured rotational velocity, v sin i = 6.3 ![]() 0.1 km s-1, is not compatible with tidal synchronisation. That the radial velocity drift is indeed a long-term drift and not part of a short-period orbit was verified with a single later measurement on this objects with the ESO HARPS spectrometer on
0.1 km s-1, is not compatible with tidal synchronisation. That the radial velocity drift is indeed a long-term drift and not part of a short-period orbit was verified with a single later measurement on this objects with the ESO HARPS spectrometer on
![]() with
with
![]() km s-1. The residuals around a linear relation (90 m s-1, 29 m s-1 without the discrepant point at JD = 53 083) put an upper limit of around 0.1
km s-1. The residuals around a linear relation (90 m s-1, 29 m s-1 without the discrepant point at JD = 53 083) put an upper limit of around 0.1
![]() on a putative planet.
on a putative planet.
OGLE-TR-131:
this object shows no velocity variations, with residuals of 60 m s-1. Ajusting an orbital solution gives K = 16![]() 17 m s-1, which implies
17 m s-1, which implies
![]() for a possible planet. The shape of the transit is quite remote from a typical central-transit shape, and the lightcurve fit yields b>0.79 for the impact parameter.
for a possible planet. The shape of the transit is quite remote from a typical central-transit shape, and the lightcurve fit yields b>0.79 for the impact parameter.
For both OGLE-TR-124 and OGLE-TR-131, the best fit to the light curve is given by a grazing transit with a large impact parameter. Therefore the explanation in terms of transiting planet is much less likely than in terms of blend with a background eclipsing binary contributing a few percent of the light and not seen in the CCF, or in terms of false positive of the transit detection procedure.
We note that all three objects in this section belong to a category where the existence of the transit signal itself is not beyond doubt - see Sect. 5.4 and Fig. 11, where we try to estimate the actual detection threshold of this OGLE transit survey in Carina. The position of OGLE-TR-109, 124 and 131 in Fig. 11 shows that they stand out below the other confirmed candidates in terms of significance of the transit detection. The position of these objects without detected velocity variations near or below the detectability threshold is unlikely to be a coincidence. Some or all of them may simply be false positives of the transit detection procedure, a suspicion reinforced by their non-square shape for OGLE-TR-124 and OGLE-TR-131.
| |
Figure 7:
Radial velocity data for the objects without radial velocity variations in phase with the transit signal. The dotted line indicates the orbit corresponding to a transiting 1 |
The likelihood of OGLE-TR-109 being a false transit detection is difficult to evaluate because OGLE-TR-109 is situated in a magnitude range where the sensitivity limit of the OGLE transit search is not easy to define. The sensitivity limit has two regimes: for
![]() mag, the photon noise dominates, which makes the errors uncorrelated and produces a detection limit dependent on the
mag, the photon noise dominates, which makes the errors uncorrelated and produces a detection limit dependent on the ![]() parameter. For brighter magnitudes, the systematic drifts in the photometry become the dominant obstacle to the detection. The covariance of the residuals on timescales of a few hours - comparable to the duration of the transit signal - makes the actual transit detection threshold much higher than in the case of white noise. This effect is clearly reflected in Figure 11 by the absence of low-
parameter. For brighter magnitudes, the systematic drifts in the photometry become the dominant obstacle to the detection. The covariance of the residuals on timescales of a few hours - comparable to the duration of the transit signal - makes the actual transit detection threshold much higher than in the case of white noise. This effect is clearly reflected in Figure 11 by the absence of low-![]() detections below
detections below
![]() .
In this second regime, the detection threshold can be modelled with an "effective''
.
In this second regime, the detection threshold can be modelled with an "effective''
![]() that does not reduce below a certain value, even when the nominal individual errors on the photometric data decrease. The limits resulting from this assumption are displayed on Fig. 11 for floor values
that does not reduce below a certain value, even when the nominal individual errors on the photometric data decrease. The limits resulting from this assumption are displayed on Fig. 11 for floor values
![]() and 6 mmag.
and 6 mmag.
The general behaviour of the transit detection threshold is clear from the position of the OGLE data relative to these two detectability regimes, but the transition from one regime to the other is difficult to locate. Indeed, the status of OGLE-TR-109 is critical to the localisation of this threshold, since it is the only object in the relevant zone.
A finer analysis of the detectability threshold, which is beyond the scope of this discussion, would be necessary to ascertain whether OGLE-TR-109 is a likely false positive or bona fide transit system. Given that OGLE-TR-109 is in absolute terms the shallowest of all OGLE transit detections (![]() mmag), we would tend to lean towards the first explanation. In the second case, higher accuracy photometric coverage of the transit would be useful to determine if the duration and shape is coherent with the planet scenario. That would make it the first planet detected around a fast-rotating F-star. Nevertheless, even with better photometry, radial velocity confirmation would be out of reach of present observational means.
mmag), we would tend to lean towards the first explanation. In the second case, higher accuracy photometric coverage of the transit would be useful to determine if the duration and shape is coherent with the planet scenario. That would make it the first planet detected around a fast-rotating F-star. Nevertheless, even with better photometry, radial velocity confirmation would be out of reach of present observational means.
Figure 11 is discussed further in Sect. 5, where we reflect on the characteristics of the actual OGLE transit detection threshold.
| Name | N | v sin i |
|
rms | |
| [km s-1] | [km s-1] | [km s-1] | [
|
||
| OGLE-TR-109 | 8 | 35.4 |
1.0 | 1.9 | 45 |
| OGLE-TR-124 | 8 | 6.3 |
0.055 | 0.090 | 0.1 |
| OGLE-TR-131 | 8 | <5 | 0.035 | 0.037 | 0.2 |
Some objects showed no unambiguous signal in the CCF, namely OGLE-TR-68, 82, 84, 89, 107, 118 and 127. The absence of signal can be due to several causes: (i) the target is an early-type star (earlier than about F2) and fast-rotating, with few narrow metallic lines; (ii) synchronous rotation broadens the lines below the detection threshold (iii) the target is a multiple-line spectroscopic binary, with the flux from each components damping the depth of the CCF of the other component. (iv) the signal-to-noise ratio of the spetrum was too low even to detect a narrow CCF dip.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{2771f8.ps} %
\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg92.gif) |
Figure 8: Lower limit for the rotation velocity as a function of period for objects without detected signal in the CCF, if they are single stars of spectral type later than F2. Lines as in Fig. 2. |
Only in case (iv) does the target remain a plausible planetary transit candidate. In case (i), the primary has a large radius, and therefore the eclipse depth implies a secondary radius larger than expected for planets. In case (ii), the same arguments as in Sect. 2.1 indicate that the eclipsing companion is likely to be of stellar mass. In case (iii), the flux of the other components dilutes the transit, so that the minimum radius of the transiting body also becomes larger than expected for a planet.
For each of the objects without a detected CCF signal, we calculated the lower limit of the rotation velocity compatible with the absence of detection in the case of a late-type primary. We assume that the detection threshold of a CCF signal is five times the rms of the CCF continuum, and use a lower limit of 1.8 km s-1 for the surface of the CCF signal, suitable for stars later than F2 and not too metal-poor.
Table 6 gives the resulting rotation velocity lower limit for objects in this section. Figure 8 displays the results as a function of period, to be compared with Fig. 2. This calculation shows that all targets except OGLE-TR-82 cannot be isolated, slowly rotating late-type stars, and therefore the transiting object is most probably not a planet. All but OGLE-TR-127 have minimum rotational velocites compatible with an explanation in terms of single eclipsing binaires, albeit with
![]() .
OGLE-TR-127 cannot be a single synchronised binary with a late-type primary, and may be either a multiple-lined binary or a hot star. Its spectrum shows strong
.
OGLE-TR-127 cannot be a single synchronised binary with a late-type primary, and may be either a multiple-lined binary or a hot star. Its spectrum shows strong
![]() compared to
compared to
![]() which may indicate an A-type star. For OGLE-TR-82, our spectrum does not have high enough signal to detect any CCF (
which may indicate an A-type star. For OGLE-TR-82, our spectrum does not have high enough signal to detect any CCF (
![]() ,
,
![]() ).
).
The position of these objects in the detectability plot (Fig. 11) show that they fall into two categories:
Three of the objects, OGLE-TR-89, 118 and 127, are also markedly lower than confirmed eclipse/transit cases in terms of reliability of the photometric transit detection. Therefore they may well be false positives, and in that case the absence of CCF signal would indicate hot stars (stars earlier than about F2 do not produce a detectable CCF signal). They would be the early-type complement of the false detection group constituted by OGLE-TR-124 and 131. Indeed, very hot temperatures (T>8000 K) were found for OGLE-TR-89 and OGLE-TR-118 by Gallardo et al. (2005) from infrared photometry.
The other group, OGLE-TR-68, 82, 84 and 107, are objects situated above the detectability threshold, but near the faint end of the sample in terms of magnitudes. They are probably bona fide eclipsing binaries with large or early-type primaries, with synchronised rotation braodening the CCF below the detectability limit, with the exception of OGLE-TR-82. The spectrum of OGLE-TR-82 shows very little signal, 16 times less than OGLE-TR-84, which was measured on the same exposure and is 0.4 mag fainter in I. This may be due to an incorrect centering of the FLAMES fiber. If the fiber was correctly centered on the object, the weakness of the signal (the spectrum flux is centered in the V filter) implies that OGLE-TR-82 is at least 3 mag redder in V-I than OGLE-TR-84. The best solution for the light curve of OGLE-TR-82 is of a ![]()
![]() body transiting across a
body transiting across a ![]()
![]() star. In this scenario the primary would be a K7/M0 dwarf. Such objects are extremely rare in a magnitude-selected sample, but the fact that the spectrum favors a very red object is intriguing. OGLE-TR-82 is therefore an interesting object that would deserve further observations. It may be a unique example of very small star or planet transiting in front of a late K dwarf on a very close orbit (P=0.76 days). Multi-colour photometry or low-resolution spectroscopy would indicate if the primary is indeed such a late-type object.
star. In this scenario the primary would be a K7/M0 dwarf. Such objects are extremely rare in a magnitude-selected sample, but the fact that the spectrum favors a very red object is intriguing. OGLE-TR-82 is therefore an interesting object that would deserve further observations. It may be a unique example of very small star or planet transiting in front of a late K dwarf on a very close orbit (P=0.76 days). Multi-colour photometry or low-resolution spectroscopy would indicate if the primary is indeed such a late-type object.
| Name | N | rms
|
|
|
| [%] | [km s-1] | |||
| OGLE-TR-68 | 1 | 0.9 | 3 | 19 |
| OGLE-TR-82 | 1 | 1.2 | <1 | - |
| OGLE-TR-84 | 1 | 0.6 | 4 | 34 |
| OGLE-TR-89 | 1 | 0.5 | 7 | 49 |
| OGLE-TR-107 | 1 | 0.6 | 4 | 32 |
| OGLE-TR-118 | 3 | 0.4 | 6 | 53 |
| OGLE-TR-127 | 1 | 0.2 | 15 | 119 |
Table 7 summarizes the conclusions of the spectroscopic follow-up for our 42 targets in terms of mass and radius of the eclipsed and eclipsing body, and of the nature of the systems. Specific notes on some systems are included below the table.
| Name | R | r | M | m | i | Nature | Section |
| [ |
[ |
[
|
[
|
[ |
|||
| OGLE-TR-63 | (1.6) | (0.15) | M eclipsing binary? | [4.1.3] | |||
| OGLE-TR-64 | 1.29 |
0.97: | 1.37 |
0.87 |
83 | grazing eclipsing binary | [4.2.1] |
| OGLE-TR-65 | 1.58 |
1.59 |
1.15 |
1.11 |
70 | triple system | [4.2.3] |
| OGLE-TR-68 | eclipsing binary? | [4.5] | |||||
| OGLE-TR-69 | 1.44 |
1.06 |
82 | grazing eclipsing binary | [4.2.5] | ||
| OGLE-TR-72 | 1.49 |
0.31: | 0.26: | 86-87 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-76 | 1.2 |
0.64: | >77 | triple system | [4.2.2] | ||
| OGLE-TR-78 | 1.51 |
0.24 |
0.243 |
>85 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-81 | (1.4) | triple system? | [4.2.5] | ||||
| OGLE-TR-82 | unsolved | [4.5] | |||||
| OGLE-TR-84 | eclipsing binary? | [4.5] | |||||
| OGLE-TR-85 | 1.30 |
0.39: | >77 | triple system | [4.2.2] | ||
| OGLE-TR-89 | false transit detection? | [4.5] | |||||
| OGLE-TR-93 | (2.0): | triple system? | [4.2.5] | ||||
| OGLE-TR-94 | (1.7) | (>0.2) | M eclipsing binary? | [4.1.3] | |||
| OGLE-TR-95 | (1.8) | multiple system | [4.2.2] | ||||
| OGLE-TR-96 | (1.4) | (1.2) | 84 | grazing eclipsing binary | [4.2.5] | ||
| OGLE-TR-97 | multiple system | [4.2.5] | |||||
| OGLE-TR-98 | (2.2) | (0.34) | M eclipsing binary? | [4.1.3] | |||
| OGLE-TR-99 | (1.1) | (0.19) | M eclipsing binary? | [4.1.3] | |||
| OGLE-TR-105 | 2.06 |
1.05: | 82 | G eclipsing binary | [4.1.1] | ||
| OGLE-TR-106 | 1.31 |
0.181 |
0.116 |
>85 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-107 | eclipsing binary ? | [4.5] | |||||
| OGLE-TR-109 | unsolved | [4.4] | |||||
| OGLE-TR-110 | (1.32) | (1.28) | 84 | grazing eclipsing binary | [4.2.5] | ||
| OGLE-TR-111 |
|
|
|
0.00050 |
planet | [4.3] | |
| OGLE-TR-112 | 3.5:: | 0.4:: | >70 | quadruple system | [4.2.4] | ||
| OGLE-TR-113 | 0.765 |
0.111 |
0.77 |
0.00130 |
planet | [4.3] | |
| OGLE-TR-114 | 0.73 |
0.72 |
0.82 |
0.82 |
83 | triple system | [4.2.3] |
| OGLE-TR-118 | false transit detection? | [4.5] | |||||
| OGLE-TR-120 | 1.62 |
0.42 |
0.47 |
>88 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-121 | 1.33 |
0.33: | 0.35: | 85 (fixed) | M eclipsing binary | [4.1.1] | |
| OGLE-TR-122 |
|
|
0.092 |
>88 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-123 | (0.1) | (0.07) | M eclipsing binary? | [4.1.2] | |||
| OGLE-TR-124 | false transit detection? | [4.4] | |||||
| OGLE-TR-125 | 1.94 |
0.211 |
0.209 |
>86 | M eclipsing binary | [4.1.1] | |
| OGLE-TR-126 | (1.8) | (0.25) | M eclipsing binary? | [4.1.3] | |||
| OGLE-TR-127 | false transit detection? | [4.5] | |||||
| OGLE-TR-129 | M eclipsing binary? | [4.1.2] | |||||
| OGLE-TR-130 | 1.13 |
0.25: | 0.39: | 85 (fixed) | M eclipsing binary | [4.1.1] | |
| OGLE-TR-131 | false transit detection? | [4.4] | |||||
| OGLE-TR-132 | 1.43 |
0.116 |
1.35 |
0.00113 |
planet | [4.3] |
|
Individual notes:
OGLE-TR-64:
the period is twice the OGLE estimate. With the new period, the even transits are clearly shallower than the odd transits (0.030 and 0.018 mag respectively), reflecting the luminosity difference between the two components.
OGLE-TR-85:
the spectra consist of a broad component superimposed on an even broader component. We assumed that the wide-lined system had a constant radial velocity, which yields a much better orbital solution for the other component than allowing it to vary. The parameters of the second component somewhat depend on the choice of fixed parameters for the first.
OGLE-TR-89:
the CCF shows the possible presence of a second, very wide component, but the signal-to-noise ratio is not high enough to measure it with confidence.
OGLE-TR-93:
The transit depth and ellipsoidal modulation amplitude (Sirko & Paczynski 2003) are compatible with a
|
The detection and characterisation of transiting extrasolar planets is the main result of this study, but mass and radius measurements for very small stars is an important by-product. Stellar structure models predict a nearly proportional relation between mass and radius down to the stellar/brown dwarf transition, then a slightly increasing radius throughout the brown dwarf domain down to the planet domain, with an age-dependent connection between the two domains (Chabrier et al. 2000). Few radii are known yet for stars lighter than 0.5
![]() ,
some from eclipsing binaries (CM Dra, Metcalfe et al. 1996; CU Cnc, Ribas 2003), some from interferometric radius measurements (Ségransan et al. 2003; Lane et al. 2001), and some from the previous OGLE transiting candidates (Paper I).
,
some from eclipsing binaries (CM Dra, Metcalfe et al. 1996; CU Cnc, Ribas 2003), some from interferometric radius measurements (Ségransan et al. 2003; Lane et al. 2001), and some from the previous OGLE transiting candidates (Paper I).
Figure 9 shows the results of the present study in the mass-radius plot. It adds 9 new low-mass stars to the list of objects with direct mass and radius determinations, together with three new planets. Moreover, two of our objects skirt the lower mass limit for stellar objects (![]()
![]() )
and their radius measurements are especially interesting because they explore the mass domain where the models predict a change of regime between solar-like behaviour and a degenerate equation of state.
)
and their radius measurements are especially interesting because they explore the mass domain where the models predict a change of regime between solar-like behaviour and a degenerate equation of state.
Figure 10 zooms on the stellar region below 0.5
![]() ,
and compares the OGLE data from this paper and Paper I to other known stellar radii. The OGLE transit survey is seen to provide comparable constraints on the lower stellar mass-radius relation as all other studies combined, a very remarkable by-product of the planet search. Our mass-radius data for stellar objects confirm the general adequacy of the models. In fact the agreement of the results from independent methods is excellent and indicates that at the level of a few percent there is no "second parameter'' in the mass-radius relation for M dwarfs down to the stellar limit, as predicted by the models. OGLE-TR-106 is about 2-sigma away from the theoretical relation and may indicate a departure from the models near
,
and compares the OGLE data from this paper and Paper I to other known stellar radii. The OGLE transit survey is seen to provide comparable constraints on the lower stellar mass-radius relation as all other studies combined, a very remarkable by-product of the planet search. Our mass-radius data for stellar objects confirm the general adequacy of the models. In fact the agreement of the results from independent methods is excellent and indicates that at the level of a few percent there is no "second parameter'' in the mass-radius relation for M dwarfs down to the stellar limit, as predicted by the models. OGLE-TR-106 is about 2-sigma away from the theoretical relation and may indicate a departure from the models near
![]() ,
that needs to be confirmed with further data. OGLE-TR-122 is situated near the expected transition to a completely degenerate dependence of radius on mass. The uncertainty on its radius is still too high to constrain the models, but it does show that stars can reach smaller radii than planets, as predicted.
,
that needs to be confirmed with further data. OGLE-TR-122 is situated near the expected transition to a completely degenerate dependence of radius on mass. The uncertainty on its radius is still too high to constrain the models, but it does show that stars can reach smaller radii than planets, as predicted.
Figure 10 also plots the position of OGLE-TR-123 with the tentative solution derived from our three measurements. These would place it on the expected locus of young objects (![]() Gyr), near or below the Hydrogen-burning limit and potentially within the brown-dwarf domain. This tantalizing result underlines the interest of collecting further spectroscopic data on this object, as well as a finer measurement of its photometric transit.
Gyr), near or below the Hydrogen-burning limit and potentially within the brown-dwarf domain. This tantalizing result underlines the interest of collecting further spectroscopic data on this object, as well as a finer measurement of its photometric transit.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2771f9.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg115.gif) |
Figure 9: Mass-radius relation for low-mass stars and planets. Black dots show the objects in this study with well-determined mass and radius, crosses the objects with higher uncertainties. Diamonds show Jupiter and Saturn, open circles the results of the OGLE bulge fields from Paper I, the hexagons are the three other transiting planets HD 209458 (Brown et al. 2001), OGLE-TR-56 (Konacki et al. 2003a) and TrES-1 (Alonso et al. 2004). The lines show the models of Girardi et al. (2002) for Solar-type stars, for ages 0, 3 and 10 Gyr, and of Baraffe et al. (1998) and Chabrier et al. (2000) for low-mass stars, brown dwarfs and planets for ages 0.5 and 5 Gyr. |
It is worth commenting on the absence of detection of transiting companions in four zones of the mass-radius plane:
The absence of heavy (2-10
![]() )
gas giants is more significant, since these are expected to have radii comparable or larger than hot Jupiters. Their absence is in agreement with indications from Doppler surveys that heavy gas giants are not found on tight orbits (Pätzold & Rauer 2002; Zucker & Mazeh 2002; Udry et al. 2002) except in binary systems (Eggenberger et al. 2004).
)
gas giants is more significant, since these are expected to have radii comparable or larger than hot Jupiters. Their absence is in agreement with indications from Doppler surveys that heavy gas giants are not found on tight orbits (Pätzold & Rauer 2002; Zucker & Mazeh 2002; Udry et al. 2002) except in binary systems (Eggenberger et al. 2004).
The absence of
![]() hot Jupiters like HD 209458 in the OGLE Carina survey is a strong constraint, since such objects would have been much easier to detect in a transit survey than the three detected planets (see Sect. 5.4 below). This indicates that cases such as HD 209458 are relatively rare.
hot Jupiters like HD 209458 in the OGLE Carina survey is a strong constraint, since such objects would have been much easier to detect in a transit survey than the three detected planets (see Sect. 5.4 below). This indicates that cases such as HD 209458 are relatively rare.
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{2771f10.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg122.gif) |
Figure 10: Mass-radius relation for M-dwarfs. Black dots show the objects in this study with well-determined mass and radius, open circles the results of the OGLE bulge fields from Paper I. Triangles are data from equal-mass eclipsing binaries (Ribas 2003; Metcalfe et al. 1996) and crosses from interferometry (Ségransan et al. 2003; Lane et al. 2001). The lines show the models of Baraffe et al. (1998) and Chabrier et al. (2000) for low-mass stars and brown dwarfs for ages 0.5 and 5 Gyr. The vertical line shows the brown dwarf limit. The crossed circle is the position of our tentative solution for OGLE-TR-123. |
Finally, the absence of credible candidates for light transiting planets in our sample (OGLE-TR-109, 124 and 131 could in principle harbour such objects, but as discussed in Sect. 4.4 an explantion in terms of false transit positive is found to be more likely) indicates that "hot Saturns'' generally have smaller radii, or are less numerous than hot Jupiters. Some models of pure H-He close-in gas giants (Guillot 2005) show that light close-in planets could be inflated to 1
![]() or higher by the incident flux of the star. Catastrophic evaporation scenarios like that of Baraffe et al. (2004) also predict a light, expanded but very transient state. The non-detection of
or higher by the incident flux of the star. Catastrophic evaporation scenarios like that of Baraffe et al. (2004) also predict a light, expanded but very transient state. The non-detection of
![]() light planets in transit surveys needs to be confirmed with higher statistics but could indicate that hot Saturns have smaller radii than more massive gas giants, possibly indicating the presence of heavier material in their composition (Guillot 2005).
light planets in transit surveys needs to be confirmed with higher statistics but could indicate that hot Saturns have smaller radii than more massive gas giants, possibly indicating the presence of heavier material in their composition (Guillot 2005).
There are several objects for which we obtained only one measurement indicating a probable small eclipsing companion. Further radial velocity monitoring of these objects would be useful in the context of the low-mass stellar mass-radius relation. These are OGLE-TR-98, 99, 126 (and to a lesser degree OGLE-TR-94 with a probable grazing eclipse). As mentioned above, OGLE-TR-123 is especially interesting as a potential transiting brown dwarf.
Binaries with periods smaller than about 10 days are observed to be circularised by tidal interaction, except when a third body can pump eccentricity into the orbit (Udry et al. 2000). In several cases our radial velocity measurements are numerous and precise enough compared to the orbital amplitude for a precise determination of the orbital eccentricity, the value of the period being fixed by the transit signal. Simple models predict a 1/(1+q)q dependence of the orbital circularisation timescale (Zahn 1989), where q is the mass ratio, and therefore the circularisation is expected to take longer for lighter companions. This is indeed what we observed. From this data we conclude that the typical circularisation period for small M-dwarf reach down to 5 days, i.e. as low as for hot Jupiters.
If we adopt for each system the resolution considered most likely in Sect. 4, the result of our follow-up is the following breakdown by type of system:
Transit by a small stellar companion |
16 |
Grazing binary |
3 |
Multiple systems |
10 |
Transiting planets |
3 |
False positives |
6 |
Unspecified binary |
2 |
Unsolved |
2 |
Among the binary systems therefore, about half are transiting small stellar companions, a tenth are grazing binaries and the rest are triple or blended systems. The objects in this last category can be gravitationally bound systems or line-of-sight alignements. The observed velocity differences between the close binary and the third body are compatible with both scenarios.
We compared these results to the prediction of a Monte Carlo simulation based on Brown (2003). The simulation predicts, for a transit signal depth of 0.02, 40% small eclipsing companions, 35% grazing eclipses, 18% physical triples and 7% line-of-sight blends, in good agreement with the observed proportions. The only difference is the lower number of grazing binaries in the observed sample, which probably reflects the fact that many such cases were rejected by eye by Udalski et al. (2002c,2003) because of obviously V-shaped transit.
All three planets discovered in the OGLE Carina survey are peculiar in some way compared to the hot Jupiters found by radial velocity searches. OGLE-TR-113 and OGLE-TR-132 are "very hot Jupiters'' with periods much shorter than any planet from Doppler surveys, and OGLE-TR-111 has a period of almost exactly 4 days. Here we try to understand the properties of the OGLE detection procedure and the statistical implications of the results for planet properties.
Udalski et al. (2002c,2003) have used a threshold of ![]() for transit candidate selection, where
for transit candidate selection, where ![]() is the criteria defined by Kovács et al. (2002),
is the criteria defined by Kovács et al. (2002),
![]() (d is the transit depth,
(d is the transit depth,
![]() the mean photometric uncertainty, N the number of data points and q the length of the transit in phase - therefore N q is the average number of points expected in the transit). With figures typical of the OGLE Carina data (N=1150,
the mean photometric uncertainty, N the number of data points and q the length of the transit in phase - therefore N q is the average number of points expected in the transit). With figures typical of the OGLE Carina data (N=1150,
![]() mag), this implies that a planet with
mag), this implies that a planet with
![]() with
with ![]() days could be detected in front of a
days could be detected in front of a
![]() star, and a
star, and a
![]() in front of a
in front of a
![]() star. The OGLE Carina fields contain several tens of thousands of objects with
star. The OGLE Carina fields contain several tens of thousands of objects with
![]() or better. Using a frequency of 1% for hot Jupiters and a geometric transit probability of 10%, several dozen detection of transiting hot Jupiters could be expected, while only three were detected up to now.
or better. Using a frequency of 1% for hot Jupiters and a geometric transit probability of 10%, several dozen detection of transiting hot Jupiters could be expected, while only three were detected up to now.
There are two explanations for this apparent paradox: first, planets are smaller and target stars are larger than usually assumed; second, the actual detection threshold is generally much higher than indicated by an ![]() criteria.
criteria.
All three transiting planets detected in Carina have radii comparable to Jupiter, contrasting with the high radius (
![]() )
and very low density of HD 209458. This shows that HD 209458 is not a typical hot Jupiter in terms of size, and that most hot Jupiters probably have smaller radii. Moreover, in a magnitude-limited sample in a Galactic disc field, the median radius of the target stars is about 1.4
)
and very low density of HD 209458. This shows that HD 209458 is not a typical hot Jupiter in terms of size, and that most hot Jupiters probably have smaller radii. Moreover, in a magnitude-limited sample in a Galactic disc field, the median radius of the target stars is about 1.4 ![]() (see e.g. Besançon Model of the Galaxy, Robin et al. 2003). Therefore typical hot Jupiter transits produce a signal of depth only
(see e.g. Besançon Model of the Galaxy, Robin et al. 2003). Therefore typical hot Jupiter transits produce a signal of depth only ![]() 0.5%, which is significantly below the detection capabilities of the OGLE survey.
0.5%, which is significantly below the detection capabilities of the OGLE survey.
Secondly, although the OGLE detection used a ![]() threshold, Udalski et al. (2002c) also state that to avoid many obviously spurious detections, a further cut was also imposed in terms of the significance of the signal in the BLS periodogram (the "SDE'' criteria of Kovács et al. 2002). This criteria expresses the significance of the detection of a periodic transit signal in the lightcurve. For a given
threshold, Udalski et al. (2002c) also state that to avoid many obviously spurious detections, a further cut was also imposed in terms of the significance of the signal in the BLS periodogram (the "SDE'' criteria of Kovács et al. 2002). This criteria expresses the significance of the detection of a periodic transit signal in the lightcurve. For a given ![]() ,
the SDE criteria is enhanced if
,
the SDE criteria is enhanced if
![\begin{figure}
\par\includegraphics[angle=-90,width=7.2cm,clip]{2771f11.ps}\end{figure}](/articles/aa/full/2005/30/aa2771-05/Timg137.gif) |
Figure 11:
Transit signal-to-noise ratio (
|
Figure 11 shows that at magnitudes brighter than about I=15.3 mag, the detection threshold is even much higher. This can be expected because at these magnitude the systematic drifts in the photometry start dominating the photon noise (Udalski et al. 2005). These drifts (due to varying atmospheric conditions and airmass) operate on timescales similar to the transit duration, a few hours. They therefore produce an additional noise in the periodogram. We model this effect by assuming that below a certain value
![]() ,
the effective
,
the effective
![]() for transit detection no longer decreases, even if the nominal photometric uncertainty gets smaller. The detection limits for two possible values of
for transit detection no longer decreases, even if the nominal photometric uncertainty gets smaller. The detection limits for two possible values of
![]() ,
4.5 mmag and 6 mmag, is plotted in Fig. 11. There is not enough data to decide which of these two values is more appropriate, but it does seem that our scheme provides a correct approximation of the selection limits.
,
4.5 mmag and 6 mmag, is plotted in Fig. 11. There is not enough data to decide which of these two values is more appropriate, but it does seem that our scheme provides a correct approximation of the selection limits.
With this caveat, we can model the behaviour of the detection threshold as a function of transit depth and period. We simulated sets of data with a time sampling typical of the OGLE Carina survey, and applied the
![]() selection criteria with various periods, and Monte Carlo realisations of a random phase shift. Figure 12 plots, for three values of
selection criteria with various periods, and Monte Carlo realisations of a random phase shift. Figure 12 plots, for three values of
![]() relevant for planetary transits, the proportion of detected transits in the simulations as a function of periods. Near the detection threshold, a strong dependence of detectability on period is observed. This effect typical of ground-based, mono-site transit surveys was already discussed by Gaudi et al. (2005) in the same context (cf. their Fig. A4). The detection of transit signals with periods resonant with 1 day are slightly less favoured for deep transits, and greatly favoured for very shallow transits, compared with non-resonant periods. The lower panel of Fig. 12 shows that near the detection threshold, only transits with very short periods or periods very close to integer number of days can be detected.
relevant for planetary transits, the proportion of detected transits in the simulations as a function of periods. Near the detection threshold, a strong dependence of detectability on period is observed. This effect typical of ground-based, mono-site transit surveys was already discussed by Gaudi et al. (2005) in the same context (cf. their Fig. A4). The detection of transit signals with periods resonant with 1 day are slightly less favoured for deep transits, and greatly favoured for very shallow transits, compared with non-resonant periods. The lower panel of Fig. 12 shows that near the detection threshold, only transits with very short periods or periods very close to integer number of days can be detected.
These elements make the peculiar characteristics of the OGLE planets look more reasonable. OGLE-TR-113 has a very short period (P=1.43 days), OGLE-TR-111 has a strongly resonant period (P=4.02 days) and OGLE-TR-132 has both but to a weaker degree (
![]() days). (Note that the same effects are visible in the OGLE bulge field, with OGLE-TR-56 at a very short period and OGLE-TR-10 near a resonance). This also provides a qualitative understanding of the surprising abundance of "very hot Jupiters'' and scarcity of normal hot Jupiters in the OGLE survey: most P<1.5 day planets can be detected, but only a few percent of 3-4 day hot Jupiters near resonances. Gaudi et al. (2005), from scaling arguments only, estimate that the detection of P=1-2 days planets is enhanced by a factor 6 compared to 3-10 days planets. By revealing that some OGLE candidates were probable false positives, correspondingly increasing the effective detection threshold, our study indicates that this selection bias could even be higher, further increasing the marging for compatibility between the radial velocity surveys and the OGLE survey. Thus we can state that at this point there is no significant incompatibility between the results of the OGLE survey and the radial velocity survey in terms of planet frequencies. More quantitative estimates would require more detailed modelling of the detection threshold and a better knowledge of the actual selection procedure than described in Udalski et al. (2002c).
days). (Note that the same effects are visible in the OGLE bulge field, with OGLE-TR-56 at a very short period and OGLE-TR-10 near a resonance). This also provides a qualitative understanding of the surprising abundance of "very hot Jupiters'' and scarcity of normal hot Jupiters in the OGLE survey: most P<1.5 day planets can be detected, but only a few percent of 3-4 day hot Jupiters near resonances. Gaudi et al. (2005), from scaling arguments only, estimate that the detection of P=1-2 days planets is enhanced by a factor 6 compared to 3-10 days planets. By revealing that some OGLE candidates were probable false positives, correspondingly increasing the effective detection threshold, our study indicates that this selection bias could even be higher, further increasing the marging for compatibility between the radial velocity surveys and the OGLE survey. Thus we can state that at this point there is no significant incompatibility between the results of the OGLE survey and the radial velocity survey in terms of planet frequencies. More quantitative estimates would require more detailed modelling of the detection threshold and a better knowledge of the actual selection procedure than described in Udalski et al. (2002c).
The absence of detection of large transiting hot Jupiters in Carina is also a strong contraint on the radius distribution of hot Jupiters, because the transit depth has a square dependence on the planetary radius. Inflated hot Jupiters with
![]() give rise to transits almost two times deeper and would be much easier to detect (compare the upper and lower panels of Fig. 12). Given the fact that hot Jupiters are near the detectability threshold, the absence of detection indicates that inflated hot Jupiters do not constitute more than a minor fraction of the total number of hot Jupiters. The detection of OGLE-TR-10 in the OGLE bulge sample, on the other hand, shows that they are not totally absent.
On the small-radius side, it is possible that some hot Jupiters have substiantially smaller radii than 1.1
give rise to transits almost two times deeper and would be much easier to detect (compare the upper and lower panels of Fig. 12). Given the fact that hot Jupiters are near the detectability threshold, the absence of detection indicates that inflated hot Jupiters do not constitute more than a minor fraction of the total number of hot Jupiters. The detection of OGLE-TR-10 in the OGLE bulge sample, on the other hand, shows that they are not totally absent.
On the small-radius side, it is possible that some hot Jupiters have substiantially smaller radii than 1.1
![]() ,
and therefore the OGLE survey may have sampled only the high-radius end of the actual radius distribution.
,
and therefore the OGLE survey may have sampled only the high-radius end of the actual radius distribution.
Much was learned with this study concerning exoplanet transit surveys and the associated Doppler follow-up.
First, with FLAMES on the VLT we could extend the limit of planet detection down to I=16.5 (
![]() ). It is probably impractical at present to go beyond this value, at least with fiber-fed instruments, because even if a CCF signal can be obtained, it is unlikely to be measured with the precision necessary to detect a planetary orbit, even with an 8-m telescope. A slit spectrograph could gather more signal, but at the loss of radial velocity accuracy because of the difficulty of controlling the position of the object in the slit with sufficient precision (see the UVES measurements for OGLE-TR-8, 10 and 12 in Paper I). This implies that the OGLE survey is near the upper limiting magnitude for spectroscopic follow-up with ground-based facilities, and that deeper photometric transit surveys - such as for instance with the HST - would run into the difficulty of having no possibility of confirmation with the velocity orbit for most of their candidates. This is a major difficulty, because Paper I and this study amply confirm that low-mass companions can perfectly mimic the signal of a transiting planet in photometry.
). It is probably impractical at present to go beyond this value, at least with fiber-fed instruments, because even if a CCF signal can be obtained, it is unlikely to be measured with the precision necessary to detect a planetary orbit, even with an 8-m telescope. A slit spectrograph could gather more signal, but at the loss of radial velocity accuracy because of the difficulty of controlling the position of the object in the slit with sufficient precision (see the UVES measurements for OGLE-TR-8, 10 and 12 in Paper I). This implies that the OGLE survey is near the upper limiting magnitude for spectroscopic follow-up with ground-based facilities, and that deeper photometric transit surveys - such as for instance with the HST - would run into the difficulty of having no possibility of confirmation with the velocity orbit for most of their candidates. This is a major difficulty, because Paper I and this study amply confirm that low-mass companions can perfectly mimic the signal of a transiting planet in photometry.
Another conclusion is that the list of possible configurations of the photometric and spectroscopic data is almost endless. The bestiary of cases encountered in our sample is even more varied than that of Paper I. It illustrates the range of contaminations expected in a planetary transit survey, and the complexity of the subsequent spectroscopic follow-up. The systems fall in three broad categories: (i) bona fide planets; (ii) eclipsing binaries in various configurations; and (iii) false transit detections. Case (ii), in turn, can be divided in many subcases. For practical purposes there are two very different types of eclipsing binaries mimicking a planetary transit: either a grazing or blended eclipse of two large (
![]() )
stars, or the transit of a small M-dwarf in front of a solar-type star. The duration and shape of the transit, as well as the presence of light-curve modulations outside the transit (Sirko & Paczynski 2003), can be useful to reject these. Note that the main source of confusion (transiting M-dwarfs) does not produce a detectable colour signature in the transit signal. Therefore colour information (see e.g. Charbonneau et al. 2004) is not a very strong discriminator for ground-based transit surveys.
)
stars, or the transit of a small M-dwarf in front of a solar-type star. The duration and shape of the transit, as well as the presence of light-curve modulations outside the transit (Sirko & Paczynski 2003), can be useful to reject these. Note that the main source of confusion (transiting M-dwarfs) does not produce a detectable colour signature in the transit signal. Therefore colour information (see e.g. Charbonneau et al. 2004) is not a very strong discriminator for ground-based transit surveys.
All transiting candidates with a good CCF signal and sufficiently high transit signal-to-noise (![]() )
turned out to be eclipsing binaries or transiting planets, and it is worth noting that our follow-up did not reveal any intrinsic source of false positives, such as stellar spots or unusual variability patterns.
)
turned out to be eclipsing binaries or transiting planets, and it is worth noting that our follow-up did not reveal any intrinsic source of false positives, such as stellar spots or unusual variability patterns.
This study illustrated the very high potential of FLAMES/UVES on the VLT for follow-up of transit candidates in medium-deep fields. In only 8 half-nights (32 h) of observations, we have followed 42 transit candidates including all the most promising candidates revealed by the photometric survey, detecting three planets among a much larger sample of eclipsing binaries, as well as collecting valuable data on very low-mass stars. As a comparison, for the OGLE bulge field it has taken several observation runs for three different teams to cover only a fraction of the candidates (see references in the Introduction). Our strategy for the spectroscopic follow-up, detailed in Sect. 2.1, has therefore proved its efficiency. Note however that it is designed to uncover planet cases among a large number of transiting candidates, and does not aim to be 100% complete. Because fast rotation is used as a telltale signal of orbital synchronisation, planets orbiting a fast-rotating star would not be detected. However, in such a case the detection of a planet would be made very difficult by the decreased accuracy of the radial velocity determination due to rotational line broadening. Planets orbiting stars too hot for precise radial velocities would also be missed.
Recently, Udalski et al. (2005) have announced a new list of 40 transiting candidates in six fields monitored during 2002 and 2003, using an improved candidate selection procedure taking into account the lessons of the high-resolution follow-up. If the resulting list provides comparable results to the Carina fields presented in this paper, the OGLE survey would be supported as a very effective tool for ground-based transiting planet detection.
Acknowledgements
We thank the OGLE team for making their list of transiting candidates publicly available for spectroscopic follow-up and accessible in a very user-friendly way.
| BJD | RV | Depth | FWHM | SNR |
|
| [ -2 453 000 d] | [km s-1] | [%] | [km s-1] | [km s-1] | |
| OGLE-TR-63 | |||||
| 78.63476 | -29.141 | 2.23 | 82.4 | 3.9 | 3.131 |
| 79.57336 | -24.663 | 2.61 | 90.8 | 6.3 | 1.739 |
| 80.58924 | -25.147 | 2.68 | 86.4 | 6.3 | 1.652 |
| OGLE-TR-64a | |||||
| 78.63475 | 4.373 | 10.00 | 18.0 | 4.0 | 0.320 |
| 79.57336 | 56.232 | 11.78 | 18.4 | 6.5 | 0.172 |
| 80.58923 | 43.547 | 11.79 | 18.5 | 6.1 | 0.183 |
| OGLE-TR-64b | |||||
| 78.63475 | -10.012 | 2.40 | 13.9 | 4.0 | 1.166 |
| 79.57336 | -89.975 | 2.62 | 17.3 | 6.5 | 0.734 |
| 80.58923 | -70.125 | 2.31 | 14.7 | 6.1 | 0.817 |
| OGLE-TR-65a | |||||
| 78.63475 | 72.265 | 1.60 | 53.6 | 4.5 | 3.051 |
| 79.57336 | -99.104 | 2.98 | 49.1 | 7.6 | 0.929 |
| 80.58923 | 111.614 | 2.73 | 43.9 | 7.3 | 0.998 |
| 81.68999 | -76.895 | 2.73 | 52.0 | 6.8 | 1.166 |
| 84.57980 | -45.244 | 2.60 | 66.9 | 9.7 | 0.974 |
| 85.67894 | 107.523 | 2.33 | 40.2 | 7.8 | 1.047 |
| OGLE-TR-65b | |||||
| 78.63475 | -82.835 | 2.98 | 47.8 | 4.5 | 1.547 |
| 79.57336 | 97.622 | 2.66 | 38.2 | 7.6 | 0.918 |
| 80.58923 | -119.194 | 2.79 | 53.2 | 7.3 | 1.075 |
| 81.68999 | 75.493 | 1.70 | 37.9 | 6.8 | 1.598 |
| 84.57980 | 44.270 | 2.26 | 41.5 | 9.7 | 0.882 |
| 85.67894 | -116.179 | 2.74 | 51.3 | 7.8 | 1.006 |
| OGLE-TR-65c | |||||
| 78.63475 | -7.327 | 2.22 | 12.2 | 4.5 | 1.049 |
| 79.57336 | -5.425 | 2.63 | 12.1 | 7.6 | 0.523 |
| 80.58923 | -5.002 | 2.29 | 10.0 | 7.3 | 0.569 |
| 81.68999 | -5.827 | 2.69 | 10.6 | 6.8 | 0.535 |
| 84.57980 | -5.676 | 2.22 | 10.9 | 9.7 | 0.461 |
| 85.67894 | -6.383 | 2.14 | 13.7 | 7.8 | 0.666 |
| OGLE-TR-68 | |||||
| 81.69000 | - | - | - | 3.1 | - |
OGLE-TR-69a |
|||||
| 84.579811 | -14.988 | 3.14 | 27.1 | 4.1 | 1.214 |
| 85.678947 | 87.732 | 2.76 | 20.5 | 3.7 | 1.331 |
| OGLE-TR-69b | |||||
| 84.579811 | 51.167 | 1.73 | 14.5 | 4.1 | 1.611 |
| 85.678947 | -68.270 | 2.82 | 20.6 | 3.7 | 1.305 |
| OGLE-TR-72 | |||||
| 81.68998 | 9.599 | 15.73 | 17.8 | 3.6 | 0.226 |
| 84.57979 | 41.057 | 21.28 | 16.5 | 5.5 | 0.110 |
| 85.67893 | 16.490 | 19.60 | 17.2 | 4.7 | 0.140 |
| OGLE-TR-76a | |||||
| 78.659480 | -11.0 | 1.80 | 28.0 | 18.6 | 0.475 |
| 79.607748 | -11.0 | 1.80 | 28.0 | 19.6 | 0.451 |
| 80.624408 | -11.0 | 1.80 | 28.0 | 18.5 | 0.478 |
| 81.631519 | -11.0 | 1.80 | 28.0 | 19.6 | 0.451 |
| 82.676072 | -11.0 | 1.80 | 28.0 | 19.2 | 0.461 |
| 83.593052 | -11.0 | 1.80 | 28.0 | 15.6 | 0.566 |
| 84.686852 | -11.0 | 1.80 | 28.0 | 18.9 | 0.468 |
| 85.571295 | -11.0 | 1.80 | 28.0 | 20.6 | 0.430 |
| OGLE-TR-76b | |||||
| 78.659480 | 18.294 | 0.60 | 34.6 | 18.6 | 1.582 |
| 79.607748 | -30.235 | 0.70 | 33.6 | 19.6 | 1.268 |
| 80.624408 | 53.437 | 0.30 | 36.2 | 18.5 | 3.252 |
| 81.631519 | -38.871 | 0.60 | 43.3 | 19.6 | 1.679 |
| 82.676072 | 76.459 | 0.40 | 31.0 | 19.2 | 2.175 |
| 83.593052 | -57.686 | 0.60 | 52.7 | 15.6 | 2.327 |
| 84.686852 | 83.450 | 0.60 | 28.2 | 18.9 | 1.405 |
| 85.571295 | -55.996 | 0.60 | 44.9 | 20.6 | 1.627 |
| OGLE-TR-78 | |||||
78.65948 |
6.133 | 8.69 | 27.2 | 8.8 | 0.208 |
| 79.60775 | -21.430 | 9.51 | 24.6 | 10.4 | 0.154 |
| 80.62441 | -34.631 | 8.81 | 26.6 | 11.9 | 0.152 |
| 81.63152 | -22.449 | 9.98 | 23.9 | 11.9 | 0.128 |
| 82.67607 | 10.708 | 8.58 | 25.9 | 9.8 | 0.185 |
| 83.59305 | 16.285 | 7.15 | 24.5 | 5.7 | 0.366 |
| 84.68685 | -15.866 | 10.03 | 24.7 | 12.3 | 0.126 |
| 85.57130 | -32.386 | 9.05 | 25.9 | 10.0 | 0.172 |
| OGLE-TR-81a | |||||
| 78.684263 | -17.175 | 2.24 | 9.3 | 9.4 | 0.436 |
| OGLE-TR-81b | |||||
| 78.684263 | 14.555 | 1.30 | 31.6 | 9.4 | 1.380 |
| OGLE-TR-82 | |||||
| 78.684264 | - | - | - | 2.0 | - |
| OGLE-TR-84 | |||||
| 78.684266 | - | - | - | 4.1 | - |
OGLE-TR-85a |
|||||
| 78.659504 | -1.0 | 1.00 | 90.0 | 6.2 | 4.591 |
| 79.607771 | -1.0 | 1.00 | 90.0 | 9.1 | 3.128 |
| 80.624432 | -1.0 | 1.00 | 90.0 | 8.5 | 3.348 |
| 81.631542 | -1.0 | 1.00 | 90.0 | 9.5 | 2.996 |
| 82.676095 | -1.0 | 1.00 | 90.0 | 6.7 | 4.248 |
| 83.593075 | -1.0 | 1.00 | 90.0 | 4.6 | 6.187 |
| 84.686875 | -1.0 | 1.00 | 90.0 | 8.0 | 3.558 |
| 85.571317 | -1.0 | 1.00 | 90.0 | 6.9 | 4.125 |
| OGLE-TR-85b | |||||
| 78.659504 | 42.924 | 2.00 | 39.9 | 6.2 | 1.529 |
| 79.607771 | -20.555 | 2.90 | 49.3 | 9.1 | 0.799 |
| 80.624432 | 23.797 | 2.80 | 44.5 | 8.5 | 0.842 |
| 81.631542 | -7.581 | 3.10 | 43.1 | 9.5 | 0.670 |
| 82.676095 | 14.049 | 2.30 | 49.4 | 6.7 | 1.369 |
| 83.593075 | 9.384 | 1.60 | 45.4 | 4.6 | 2.747 |
| 84.686875 | 0.020 | 2.60 | 50.1 | 8.0 | 1.021 |
| 85.571317 | 32.024 | 2.50 | 36.0 | 6.9 | 1.044 |
| OGLE-TR-89 | |||||
| 82.603122 | - | - | - | 7.4 | - |
| OGLE-TR-93a | |||||
| 82.603127 | 41.872 | 7.63 | 12.1 | 8.6 | 0.163 |
| OGLE-TR-93b | |||||
| 82.603127 | 9.492 | 3.05 | 55.6 | 8.6 | 0.854 |
| OGLE-TR-94 | |||||
| 82.60312 | -28.875 | 6.06 | 36.8 | 15.9 | 0.192 |
| OGLE-TR-95a | |||||
| 82.603116 | -0.332 | 2.93 | 18.1 | 5.4 | 0.807 |
| OGLE-TR-95b | |||||
| 82.603116 | -90.494 | 1.25 | 127.0 | 5.4 | 5.009 |
| OGLE-TR-96a | |||||
| 82.603113 | -85.557 | 2.37 | 16.3 | 11.2 | 0.458 |
| OGLE-TR-96b | |||||
| 82.603113 | -3.783 | 1.80 | 94.6 | 11.2 | 1.448 |
| OGLE-TR-96c | |||||
| 82.603113 | 55.246 | 3.73 | 15.9 | 11.2 | 0.288 |
| OGLE-TR-97a | |||||
| 83.628839 | 56.177 | 7.81 | 17.7 | 10.0 | 0.165 |
| OGLE-TR-97b | |||||
| 83.628839 | -48.176 | 3.55 | 16.1 | 10.0 | 0.341 |
| OGLE-TR-97c | |||||
| 83.628839 | 13.911 | 1.73 | 11.9 | 10.0 | 0.599 |
| OGLE-TR-98 | |||||
| 83.62884 | -0.210 | 7.71 | 24.6 | 4.8 | 0.404 |
| OGLE-TR-99 | |||||
| 83.62884 | -24.145 | 3.27 | 70.2 | 5.7 | 1.349 |
| OGLE-TR-105 | |||||
| 78.60418 | -8.707 | 2.02 | 22.0 | 8.3 | 0.840 |
| 79.64234 | 50.273 | 1.85 | 26.2 | 9.3 | 0.893 |
| 81.59491 | 117.739 | 1.63 | 17.5 | 7.3 | 1.055 |
| 82.71279 | 57.870 | 2.37 | 22.5 | 8.7 | 0.691 |
| 83.66467 | 2.705 | 1.77 | 23.9 | 8.2 | 1.011 |
| 84.65148 | -9.314 | 2.13 | 20.9 | 10.6 | 0.608 |
| 85.60720 | 37.973 | 1.75 | 20.3 | 9.2 | 0.840 |
| OGLE-TR-106 | |||||
| 78.60418 | -24.828 | 4.59 | 42.1 | 3.2 | 1.326 |
| 79.64234 | 9.532 | 5.89 | 33.9 | 3.8 | 0.781 |
| 80.65956 | -13.450 | 4.93 | 35.1 | 3.0 | 1.202 |
| 81.59491 | -12.040 | 5.22 | 33.5 | 2.9 | 1.148 |
| 82.71279 | 6.894 | 5.20 | 35.5 | 3.4 | 1.012 |
| 83.66467 | -23.908 | 5.97 | 39.0 | 3.4 | 0.924 |
| 84.65148 | 9.035 | 5.66 | 39.2 | 3.8 | 0.874 |
| 85.60720 | -6.853 | 6.22 | 34.2 | 4.0 | 0.706 |
| OGLE-TR-107 | |||||
| 82.603106 | - | - | - | 4.1 | - |
| OGLE-TR-109 | |||||
| 78.60420 | -11.963 | 1.77 | 53.5 | 12.2 | 1.017 |
| 79.64235 | -12.455 | 1.82 | 59.3 | 14.2 | 0.895 |
| 80.65958 | -13.858 | 1.65 | 60.9 | 11.4 | 1.245 |
| 81.59492 | -15.263 | 1.69 | 56.5 | 10.9 | 1.225 |
| 82.71280 | -11.850 | 1.62 | 56.5 | 13.7 | 1.017 |
| 83.66469 | -13.758 | 1.75 | 61.1 | 13.4 | 1.001 |
| 84.65149 | -12.460 | 1.72 | 52.9 | 14.6 | 0.870 |
| 85.60721 | -8.818 | 1.74 | 54.8 | 14.6 | 0.875 |
| OGLE-TR-110a | |||||
| 80.659567 | -39.425 | 5.45 | 19.7 | 6.7 | 0.366 |
| OGLE-TR-110b | |||||
| 80.659567 | 56.957 | 5.00 | 16.0 | 6.7 | 0.360 |
| OGLE-TR-111 | |||||
| 78.60420 | 25.111 | 31.14 | 10.4 | 6.9 | 0.045 |
| 79.64235 | 25.163 | 30.56 | 10.4 | 6.9 | 0.046 |
| 80.65958 | 25.220 | 27.78 | 10.1 | 5.0 | 0.069 |
| 81.59492 | 25.106 | 25.23 | 10.8 | 4.3 | 0.091 |
| 82.71280 | 25.029 | 31.08 | 10.4 | 7.4 | 0.042 |
| 83.66469 | 25.175 | 29.02 | 10.3 | 5.9 | 0.056 |
| 84.65149 | 25.219 | 33.48 | 10.2 | 8.6 | 0.033 |
| 85.60721 | 25.149 | 32.78 | 10.2 | 7.8 | 0.037 |
| OGLE-TR-112a | |||||
| 78.604197 | -49.156 | 3.29 | 12.1 | 22.5 | 0.145 |
| 79.642351 | -41.946 | 3.45 | 12.8 | 25.4 | 0.127 |
| 80.659577 | -8.420 | 3.72 | 14.5 | 21.8 | 0.145 |
| 81.594925 | 86.548 | 3.23 | 11.3 | 19.3 | 0.166 |
| 82.712800 | 58.124 | 3.15 | 12.6 | 25.9 | 0.135 |
| 83.664686 | 9.111 | 3.56 | 12.4 | 24.0 | 0.129 |
| 84.651492 | -14.857 | 3.50 | 12.5 | 24.8 | 0.127 |
| 85.607208 | -30.259 | 3.30 | 11.8 | 24.4 | 0.133 |
OGLE-TR-112b |
|||||
| 78.604197 | 31.991 | 2.16 | 11.3 | 22.5 | 0.210 |
| 79.642351 | 22.937 | 2.53 | 11.9 | 25.4 | 0.165 |
| 80.659577 | -15.744 | 2.70 | 10.6 | 21.8 | 0.170 |
| 81.594925 | -119.516 | 2.36 | 14.2 | 19.3 | 0.251 |
| 82.712800 | -89.284 | 2.29 | 11.7 | 25.9 | 0.177 |
| 83.664686 | -33.716 | 2.35 | 11.9 | 24.0 | 0.187 |
| 84.651492 | -4.470 | 2.48 | 13.2 | 24.8 | 0.181 |
| 85.607208 | 10.060 | 2.35 | 11.3 | 24.4 | 0.179 |
| OGLE-TR-112c | |||||
| 78.604197 | 22.192 | 1.55 | 59.3 | 22.5 | 0.663 |
| 79.642351 | -11.342 | 1.40 | 59.0 | 25.4 | 0.649 |
| 80.659577 | -37.596 | 1.23 | 53.9 | 21.8 | 0.822 |
| 81.594925 | 20.250 | 1.06 | 54.5 | 19.3 | 1.083 |
| 82.712800 | 13.662 | 1.14 | 51.4 | 25.9 | 0.729 |
| 83.664686 | -17.880 | 1.40 | 54.0 | 24.0 | 0.657 |
| 84.651492 | -28.478 | 1.44 | 49.2 | 24.8 | 0.590 |
| 85.607208 | 18.729 | 1.38 | 59.1 | 24.4 | 0.686 |
| OGLE-TR-113 | |||||
78.60419 |
-7.883 | 39.95 | 11.7 | 14.1 | 0.039 |
| 79.64235 | -8.302 | 39.77 | 11.8 | 14.4 | 0.039 |
| 80.65957 | -7.972 | 39.39 | 11.6 | 13.0 | 0.040 |
| 81.59492 | -7.887 | 38.73 | 11.6 | 11.5 | 0.042 |
| 82.71279 | -8.120 | 39.89 | 11.7 | 14.7 | 0.039 |
| 83.66468 | -8.120 | 39.29 | 11.6 | 13.1 | 0.040 |
| 84.65149 | -7.641 | 40.60 | 11.6 | 16.1 | 0.038 |
| 85.60720 | -8.082 | 40.12 | 11.6 | 15.0 | 0.039 |
| OGLE-TR-114a | |||||
| 78.604187 | -72.952 | 6.50 | 16.7 | 9.6 | 0.200 |
| 79.642340 | 34.714 | 5.70 | 18.7 | 8.1 | 0.283 |
| 80.659566 | 69.960 | 6.20 | 15.9 | 7.5 | 0.260 |
| 81.594914 | -61.504 | 5.90 | 16.1 | 6.6 | 0.311 |
| 82.712790 | -32.185 | 6.43 | 17.0 | 10.0 | 0.196 |
| 83.664676 | 84.788 | 5.66 | 17.3 | 8.0 | 0.278 |
| 84.651481 | -4.038 | 7.19 | 18.8 | 11.5 | 0.161 |
| 85.607198 | -68.153 | 6.22 | 16.8 | 10.1 | 0.199 |
OGLE-TR-114b |
|||||
| 78.604187 | 84.598 | 5.94 | 16.3 | 9.6 | 0.215 |
| 79.642340 | -24.713 | 6.38 | 17.8 | 8.1 | 0.247 |
| 80.659566 | -59.671 | 6.15 | 16.6 | 7.5 | 0.267 |
| 81.594914 | 71.205 | 5.84 | 14.9 | 6.6 | 0.302 |
| 82.712790 | 42.987 | 6.31 | 17.2 | 10.0 | 0.200 |
| 83.664676 | -73.867 | 6.10 | 17.9 | 8.0 | 0.262 |
| 84.651481 | 13.530 | 7.44 | 19.5 | 11.5 | 0.159 |
| 85.607198 | 77.476 | 6.55 | 16.8 | 10.1 | 0.189 |
| OGLE-TR-114c | |||||
| 78.604187 | 7.166 | 8.57 | 9.4 | 9.6 | 0.117 |
| 79.642340 | 7.358 | 7.81 | 10.3 | 8.1 | 0.156 |
| 80.659566 | 7.183 | 7.84 | 9.4 | 7.5 | 0.160 |
| 81.594914 | 7.232 | 7.49 | 9.0 | 6.6 | 0.185 |
| 82.712790 | 7.110 | 8.49 | 10.0 | 10.0 | 0.117 |
| 83.664676 | 6.915 | 7.72 | 9.5 | 8.0 | 0.154 |
| 84.651481 | 6.943 | 8.20 | 9.5 | 11.5 | 0.104 |
| 85.607198 | 6.897 | 8.17 | 9.3 | 10.1 | 0.116 |
| OGLE-TR-118 | |||||
| 78.574215 | - | - | - | 3.3 | - |
| 79.692810 | - | - | - | 6.7 | - |
| 80.695892 | - | - | - | 5.1 | - |
| OGLE-TR-120 | |||||
| 78.57422 | 29.764 | 10.28 | 16.6 | 4.4 | 0.272 |
| 79.69282 | 42.857 | 15.48 | 16.2 | 10.7 | 0.081 |
| 80.69590 | 56.690 | 14.24 | 15.9 | 8.1 | 0.109 |
| 81.72915 | 69.946 | 14.28 | 15.9 | 8.2 | 0.108 |
| 82.64057 | 60.727 | 14.11 | 15.8 | 7.2 | 0.122 |
| 83.70041 | 15.286 | 14.89 | 16.1 | 9.1 | 0.095 |
| 84.61587 | 5.387 | 13.36 | 16.0 | 6.0 | 0.154 |
| 85.64256 | 9.553 | 13.55 | 16.2 | 6.6 | 0.139 |
| OGLE-TR-121 | |||||
| 78.57422 | 22.508 | 7.85 | 28.3 | 5.5 | 0.371 |
| 79.69282 | -30.078 | 9.90 | 30.7 | 12.1 | 0.143 |
| 80.69590 | 29.621 | 9.37 | 29.7 | 10.1 | 0.176 |
| 81.72916 | 28.150 | 9.41 | 29.2 | 9.8 | 0.179 |
| 82.64057 | -28.573 | 9.43 | 31.4 | 9.1 | 0.199 |
| 83.70041 | 13.803 | 9.64 | 30.2 | 10.4 | 0.168 |
| 84.61587 | 45.009 | 8.42 | 28.7 | 6.9 | 0.279 |
| 85.64256 | -19.195 | 9.26 | 29.9 | 8.1 | 0.221 |
| OGLE-TR-122 | |||||
| 78.63477 | -7.720 | 17.54 | 11.2 | 3.7 | 0.159 |
| 79.57337 | -2.620 | 21.85 | 11.4 | 5.3 | 0.094 |
| 80.58925 | 2.930 | 19.22 | 11.8 | 4.7 | 0.119 |
| 81.69001 | 7.820 | 21.48 | 11.9 | 5.3 | 0.097 |
| 84.57982 | -9.535 | 26.78 | 12.2 | 7.5 | 0.063 |
| 85.67896 | -8.809 | 25.92 | 12.1 | 7.3 | 0.065 |
| OGLE-TR-123 | |||||
| 81.68998 | 0.234 | 5.97 | 44.9 | 10.7 | 0.317 |
| 84.57979 | -6.208 | 6.13 | 43.4 | 15.2 | 0.215 |
| 85.67893 | 12.276 | 6.14 | 43.9 | 11.9 | 0.274 |
| OGLE-TR-124 | |||||
| 78.65948 | -5.308 | 23.50 | 12.0 | 10.0 | 0.056 |
| 79.60775 | -5.385 | 24.00 | 12.1 | 12.0 | 0.050 |
| 80.62441 | -5.458 | 24.15 | 12.0 | 13.4 | 0.048 |
| 81.63152 | -5.545 | 24.35 | 12.2 | 13.2 | 0.048 |
| 82.67608 | -5.594 | 23.78 | 12.1 | 10.7 | 0.054 |
| 83.59306 | -5.446 | 20.55 | 11.9 | 6.4 | 0.086 |
| 84.68686 | -5.810 | 24.59 | 12.0 | 14.0 | 0.046 |
| 85.57130 | -5.880 | 23.48 | 12.1 | 10.8 | 0.054 |
| OGLE-TR-125 | |||||
| 78.65949 | 32.731 | 3.68 | 22.7 | 7.5 | 0.519 |
| 79.60776 | 46.168 | 3.72 | 23.8 | 8.8 | 0.448 |
| 80.62442 | 37.267 | 3.56 | 26.3 | 9.1 | 0.476 |
| 81.63153 | 16.405 | 3.64 | 25.2 | 10.3 | 0.403 |
| 82.67608 | 9.185 | 3.33 | 26.6 | 7.1 | 0.655 |
| 83.59306 | 25.120 | 2.19 | 19.4 | 5.1 | 1.184 |
| 84.68686 | 45.041 | 3.62 | 23.5 | 8.9 | 0.453 |
| 85.57130 | 42.347 | 3.35 | 21.3 | 7.5 | 0.552 |
| OGLE-TR-126 | |||||
| 78.68427 | 5.519 | 4.40 | 24.9 | 7.4 | 0.461 |
| OGLE-TR-127 | |||||
| 82.603117 | - | - | - | 16.8 | - |
| OGLE-TR-129 | |||||
| 78.57423 | 28.954 | 1.18 | 29.1 | 4.2 | 3.266 |
| 79.69283 | -1.838 | 2.37 | 37.3 | 10.2 | 0.759 |
| 80.69591 | -3.341 | 2.09 | 34.2 | 7.6 | 1.105 |
| 81.72916 | 1.110 | 2.14 | 33.8 | 8.3 | 0.983 |
| 82.64058 | 5.068 | 1.91 | 35.5 | 7.4 | 1.265 |
| 83.70042 | 14.841 | 1.83 | 42.1 | 8.7 | 1.223 |
| 84.61588 | 15.003 | 1.00 | 51.9 | 5.6 | 3.860 |
| 85.64257 | -3.476 | 1.83 | 39.9 | 6.4 | 1.618 |
| OGLE-TR-130 | |||||
| 78.57422 | 7.894 | 12.60 | 17.6 | 6.8 | 0.151 |
| 79.69281 | 43.016 | 14.62 | 17.9 | 13.3 | 0.074 |
| 80.69589 | 15.732 | 14.47 | 17.3 | 10.6 | 0.089 |
| 81.72915 | -28.779 | 13.47 | 17.9 | 10.1 | 0.100 |
| 82.64056 | -25.896 | 13.49 | 17.5 | 8.7 | 0.113 |
| 83.70040 | 21.937 | 13.93 | 17.6 | 10.6 | 0.092 |
| 84.61586 | 42.805 | 14.05 | 17.5 | 9.1 | 0.104 |
| 85.64255 | 10.091 | 13.50 | 17.6 | 9.3 | 0.106 |
| OGLE-TR-131 | |||||
| 78.57421 | 18.879 | 19.59 | 10.7 | 3.2 | 0.160 |
| 79.69280 | 18.937 | 35.15 | 10.4 | 7.4 | 0.051 |
| 80.69588 | 18.937 | 32.13 | 10.7 | 5.9 | 0.062 |
| 81.72914 | 18.997 | 32.19 | 10.4 | 6.0 | 0.061 |
| 82.64055 | 18.988 | 29.93 | 10.2 | 4.8 | 0.075 |
| 83.70039 | 18.935 | 32.65 | 10.4 | 6.3 | 0.059 |
| 84.61585 | 18.934 | 27.08 | 10.6 | 4.5 | 0.087 |
| 85.64254 | 18.918 | 27.46 | 10.7 | 4.7 | 0.084 |
| OGLE-TR-132 | |||||
| 81.72913 | 39.690 | 30.61 | 10.5 | 9.3 | 0.049 |
| 82.64054 | 39.676 | 28.80 | 10.6 | 7.9 | 0.055 |
| 83.70038 | 39.517 | 30.88 | 10.6 | 10.0 | 0.047 |
| 84.61585 | 39.760 | 29.89 | 10.4 | 8.5 | 0.052 |
| 85.64253 | 39.491 | 30.32 | 10.5 | 9.2 | 0.049 |