A&A 438, 1083-1097 (2005)
DOI: 10.1051/0004-6361:20052695

On the effect of the inhomogeneous subsurface flows on the high degree solar p-modes

B. M. Shergelashvili[*] - S. Poedts

Centre for Plasma Astrophysics, Katholieke Universiteit Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium

Received 28 May 2002 / Accepted 5 April 2005

Abstract
The observed power spectrum of high-degree solar p-modes ($\ell>200$) shows discrepancies with the power spectrum predicted by the stochastic excitement and damping theory. In an attempt to explain these discrepancies, the present paper is concerned with the influence of the observed subsurface flows on the trapped acoustic modes (p-modes). The effect of these inhomogeneous background flows is investigated by means of a non-modal analysis and a multi-layer model. It is shown that the rotational and meridional components of the velocity field change the wavelengths of the oscillation modes which, in turn, results in modifications of the corresponding modal frequencies. The magnitudes of the frequency residuals depend on the spatial scales of the modes and on the gradients of the different components of the flow velocity. Together with other mechanisms (e.g. the scattering of modes by the large-scale convection), the non-modal effect of the variation of the frequencies in time may contribute: 1) to the observed widening of the corresponding peaks in the observed power spectrum with increasing angular degree; 2) to the partial dissipation of spectral power, and, as a result; 3) to the discrepancies between the predicted and the observed power spectrum of solar p-modes.

Key words: Sun: oscillations - Sun: rotation - hydrodynamics - waves

1 Introduction

One of the main goals of helioseismology is to understand the excitation and damping mechanisms that yield the observed power spectrum of the solar oscillation modes. The theory of the random generation of modes by convective turbulence has been developed by Goldreich et al. (1994) and Goldreich & Kumar (1990) in an attempt to quantitatively understand the structure of mode sources and the generation rate of the oscillation modes. Observations show (see e.g. Libbrecht, 1988; Woodard et al. 2001) that the energy of the p-modes with frequencies below the photospheric cut-off grows with the angular degree $\ell$ for intermediate values of $\ell$, i.e.  $100<\ell<200$. This observational fact is in good agreement with the predictions from the theory of turbulent excitement and damping of p-modes mentioned above. However, for $\ell>200$there are substantial discrepancies between the theory and the observations. Recent observations by Woodard et al. (2001) show that for $\ell>200$ the wave energy distribution function decreases rapidly with increasing angular degree $\ell$. The latter authors remark that the discovered decline in mode energy at high $\ell$ values may indicate the existence of some "unmodeled mechanism of damping''. In the present paper, the viability of such a mechanism is studied, viz. mode damping due to a sheared background flow. There exist numerous helioseismological measurements of solar subsurface flows (see González Hernández et al. 1999; González Hernández & Patrón 2000). These observations show that the velocity field of these flows has both rotational and meridional components and that the gradients of these flow velocity components depend on the spatial coordinates. We will present a multi-layer model for these flows that allows us to quantify their effect on the solar p-modes.

Several other candidate mechanisms for non-turbulent wave damping have been suggested, e.g. the nonlinear coupling between trapped and propagating modes (Kumar & Goldreich 1989) or mode scattering by convective motions (Goldreich & Murray 1994). Moreover, the direct influence of the inhomogeneous temperature, the magnetic field, and/or the velocity fields on the solar p-modes and f-modes have been studied intensively Murawski & Roberts (1993a,b); Murawski & Goossens (1993); Vanlommel & Cadez (1998), Vanlommel & Goossens (1999), while "resonant absorption'' (or "continuum damping'') has been introduced as a candidate damping mechanism for p-modes by Tirry et al. (1998). Clearly, the physical characteristics of the solar medium affect and systematically distort the main frequencies and the travel times of the modes. This insight has led to the development of the time-distance technique in helioseismology (Duval et al. 1993) which became a powerful tool for the observation of 3D structures with inhomogeneous magnetic and temperature profiles.

As pointed out by Goldreich et al. (1994), when the widths of the frequency peaks in the power spectrum are greater than the inverse of the observation time, these peaks contain information about the damping rates of the modes. These authors also indicated that the excess width of the peaks (with respect to the inverse observation time) can result from a variation of either the frequency or the amplitude of the modes and that it is reasonable to assume that both these types of velocity modulation yield comparable contributions in the line width. Observations show that the line widths of the oscillation modes increase with increasing frequency and angular degree. Goldreich & Murray (1994) suggested the scattering of modes by turbulent velocity fluctuations as a possible mechanism supporting this observational fact.

The main properties of the solar oscillation modes are well described by the standard normal mode analysis. For a static equilibrium and for appropriate boundary conditions, the linear MHD (magnetohydrodynamics) operator is self-adjoint. However, in neutral fluids and in plasmas with nonuniform background flows there are often discrepancies between the analytical results of the standard modal analysis and experimental data. These discrepancies are usually ascribed to the mathematical incompleteness of the normal mode spectrum due to the non-self-adjoint nature of the governing equations (Trefethen et al. 1993; Criminale & Drazin 2000, 1990). One of the alternative and complementary methods to solve the initial value problem in sheared plasma flows is the non-modal analysis. In this formalism a transformation of the variables is performed and, as a result, the spatially inhomogeneous terms in the governing equations are replaced by time-dependent terms. Therefore, in general, this method enables one to study the non-exponential temporal evolution of linear perturbations of sheared flows. The non-modal analysis was introduced originally by Lord Kelvin (1887) and the theoretical basis for studying the wave dynamics in hydrodynamical and plasma flows has been developed by Goldreich & Linden-bell (1965), Craik & Criminale (1986); Chagelishvili et al. (1997); Rogava et al. (2000,2001). Many authors showed that the shear in the flow velocity field can have substantial effects on the wave dynamics, e.g. causing time-dependent frequencies and wave numbers (Butler & Farrell 1992; Chagelishvili et al. 1994) and coupling of different wave modes (Chagelishvili et al. 1996; Rogava & Mahajan 1997). The non-modal approach has also been applied to the study of several aspects of the excitement of gravitational and acoustic waves on the Sun Chagelishvili et al. (2000); Pataraya & Pataraya (1997).

The significant discrepancies between the observed and predicted power spectra of trapped modes with high angular degree $\ell>200$may be due to sheared flow effects. These modes mostly propagate in the thin cavity below the photosphere ( $r>0.95~R_{\odot}$) in which plasma flows with strongly pronounced velocity gradients have been observed. Hence, the aim of our study was to investigate the possible role of the non-exponential temporal evolution of the modes (due to the nonuniform flows) in the formation of the observed power spectra. We applied a non-modal analysis to study the effect of the observed sub-photospheric shear flows on the frequencies and the propagation characteristics of the solar p-modes. In order to distinguish the effect of velocity shear from all other effects, we adopt a very simple model and consider the modes locally, in plane slab geometry. Our model allows us to separate the effects related to the spatial inhomogeneity of the background flow from the inhomogeneity coming from the gravitational stratification and the temperature gradient and enables us to focus on the evolution of the wave characteristics associated with the flow inhomogeneity itself.

In the next section, we present the model we applied to investigate the interaction between the inhomogeneous flows beneath the photosphere and trapped acoustic modes. In the third section, we describe and analyze our theoretical results. In the fourth section, we discuss the obtained numerical results and we present and discuss some phenomenological points of view in the framework of the obtained results. Then, we discuss the possible observational consequences of the shear flow effects on the p-modes. In the final section, we formulate our conclusions.

2 Physical model and equations

The aim is to study the temporal evolution of small perturbations in a stratified medium with a non-uniform two-dimensional "background'' flow. The problem is considered in plane-parallel geometry and is described in Cartesian coordinates. The x-axis denotes the "toroidal'' direction and its positive direction is chosen as the direction in which the Sun rotates. The y-axis coincides with the "meridional'' direction and is directed towards the north pole. The z-axis covers the "radial'' direction and is directed outwardly, to the solar atmosphere. We study the properties of modes with small amplitudes which are considered as linear perturbations of the equilibrium state.

2.1 The equilibrium model

In this subsection, the main parameters characterizing the equilibrium are introduced, in particular the parameters characterizing the equilibrium flow velocity. These parameters are determined in such a way that they yield a good approximation of the above-mentioned measurements of the solar subsurface flow profiles. In general, the subsurface flows can be very complicated. In the non-modal analysis, the nine components describing the shear rates of the background flow velocity  $\vec V_{0}$ components in the three spatial directions are collected in the so-called "Shear Matrix'' S (for details e.g. see Mahajan & Rogava (1999)). In its most general form this matrix reads:

 \begin{displaymath}% S\equiv \left( \begin{array}{ccc} V_{0x,x} & V_{0x,y} & V_{... ...{0y,z} \\ V_{0z,x} & V_{0z,y} & V_{0z,z} \end{array}\right ), \end{displaymath} (1)

where the index after the comma denotes the derivative with respect to the corresponding spatial coordinate. We want to study the joint influence of the rotational and the meridional subsurface flows on the solar p-modes. Hence, the equilibrium velocity field includes both rotational (x-) and meridional (y-) components. In our general model we consider the x-component of the equilibrium flow velocity as a function of both the y- and z-coordinates, V0x=V0x(y,z). Further, we also take into consideration the meridional component of the flow velocity and its dependence on the radial coordinate, i.e. V0y=V0y(z). Consequently, in the equilibrium state we have an inhomogeneous velocity field $\vec{V}_0 = (V_{0x}(y,z),V_{0y}(z),0)$.

In Sect. 4 we will model the subsurface flows with a linear approximation of the velocity profiles measured by González Hernández & Patrón (2000). Hence, in the local frame of reference the components of the flow velocity read as:

 
V0x=V01+ay+bz, (2)

and

 
V0y=V02+cz, (3)

where, V01 and V02 represent the constant parts of the rotational and meridional components of the flow velocity and the parameters a=V0x,y, b=V0x,z and c=V0y,z are the local spatial derivatives of the corresponding velocity component. Note, that the considered background flow is incompressible $\nabla\cdot\vec{V}_0=0$.


  \begin{figure} \par\includegraphics[width=7cm,clip]{2695fig1.eps}\end{figure} Figure 1: Schematic view of the modelled subsurface spherical shell (in plain slab geometry). The dashed horizontal lines schematically represent the boundaries of the thin layers considered in our multi-layer model. Within each of these thin layers the sound speed is assumed to be approximately constant corresponding to the piecewise constant temperature profiles shown in Figs. 3 or 7.
Open with DEXTER

In order to consider the propagation of small perturbations in the gravitationally stratified medium we adopt a local analysis, similar to the formalism used by Whittaker (1963) and Ulrich (1970). It should be noted, however, that we here focus on the effects of the inhomogeneous background flow and thus we excluded the effects related to the magnetic field, radiative flux and convective motions. The latter issue has already been addressed by several authors (e.g. see Swisdak & Zweibel 1999). In addition, the influence of the random velocity fields on f-modes has been studied by Murawski & Roberts (1993a,b) and by Murawski & Goossens (1993) also including the effect of the chromospheric magnetic field. Within each of the thin shells in our model (schematically shown by the horizontal dashed lines in Fig. 1 the temperature (i.e. sound speed) is assumed to be constant. Hence, the temperature profile of the standard solar model is approximated by a step-function. In other words, locally, in each thin layer we have an equilibrium density and pressure profile of the form $\rho _0(z),p_0(z)\propto \exp{\left (-z/H \right )}$, where H is the local scale height, so that in each layer the temperature is constant.

2.2 The temporal evolution of the p-modes

Let us now study the propagation of small perturbations in the considered plasma shell and focuss on the effects related to the inhomogeneity of the background flow(s). We consider the waves as linear perturbations of the stationary equilibrium described in the previous section. The following set of linearized equations then governs the dynamics of the small disturbances in a gravitationally stratified isentropic gas:

 \begin{displaymath}% \frac{\partial\rho_{1}}{\partial t}+(\vec{V}_{0}{\bf\cdot}\... ...a})\rho_{0}(z)+\rho_{0}(z)(\vec{\nabla}{\bf\cdot}\vec{v}_1)=0, \end{displaymath} (4a)
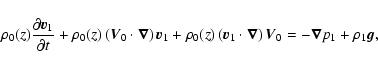\begin{displaymath}% \rho_{0}(z)\frac{\partial\vec{v}_1}{\partial t}+\rho_{0}(z)... ...abla}\right) \vec{V}_{0}= -\vec{\nabla}p_{1}+\rho_{1}\vec{g}, \end{displaymath} (4b)
 \begin{displaymath}% \frac{\partial p_{1}}{\partial t}+\left( \vec{V}_{0}\cdot\v... ...\rho_{1}+(\vec{v}_1{\bf\cdot}\vec{\nabla})\rho _{0}(z)\right), \end{displaymath} (4c)

where $\vec{g}$ denotes the gravitational acceleration and $\gamma$ is the ratio of specific heats, symbols with index 0 denote the equilibrium quantities and those with index 1 the perturbations.

Clearly, in the case of a static medium, i.e. without the background flows, we get a simplified set of equations without the inhomogeneous terms coming from the convective derivatives. In this case, the normal-mode solution of this set of equations takes the form:

 \begin{displaymath}% \psi \sim \exp \left[ {\rm i}\left(\omega t + k_xx+k_yy +\left( k_{z}-\frac{{\rm i}}{2H}\right)z \right) \right], \end{displaymath} (5)

where, $\psi $ represents the quantities $\rho _{1}/\rho _{0}$, $p_{1}/\rho_{0}$ and the components of the velocity perturbation. However, we want to know what happens to these solutions when the non-uniform equilibrium flows are taken into account. Notice that Eqs. (4) contain convective derivatives, which also take into account the spatial inhomogeneity of the initial (equilibrium) velocity field. These spatially inhomogeneous terms complicate the analysis considerably. For small magnitudes of the background flow and of its gradients the problem has been studied in the standard framework of the normal modal analysis and the influence of the flow on the eigenfrequencies has been treated as a small perturbation of the basic frequencies. This perturbation technique is applied in Backus & Gilbert (1961) and Ulrich et al. (1979). The methods of inversion of the solar internal rotation rate, from the frequency splitting observations of the solar non-radial oscillations, are based on a similar theoretical formalism. These methods allow us to determine the internal rotational velocity profile of the Sun with high accuracy.

However, due to the inhomogeneous background flow the governing equations have a non-self-adjoint character. Hence, we apply the non-modal technique, which enables us to find an additional class of "non-normal'' solutions of the above set of Eqs. (4). These solutions describe the evolution of the perturbations in time which, in general, can be non-exponential.

Following the non-modal technique we represent the perturbation quantities $\rho _{1}/\rho _{0}$, $p_{1}/\rho_{0}$, and $\vec{v}_1$ in the following form:

 \begin{displaymath}% \psi(x,y,z;t)=\hat{\psi} (k_x,k_y,k_z;t)\exp{\left ( {\rm i... ...ft (\varphi_1-\varphi_2-\frac{{\rm i} z}{2H}\right )\right )}, \end{displaymath} (6)

where,

 \begin{displaymath}% \varphi_1 (x,y,z;t)=k_x(t)x+k_y(t)y+k_z(t)z, \end{displaymath} (7)

and

 \begin{displaymath}% \varphi_2 (k_x(t),k_y(t);t)= V_{01}\int{k_x(t)dt}+V_{02}\int{k_y(t){\rm d}t}. \end{displaymath} (8)

In these expressions kx(t), ky(t) and kz(t) are the (in general) time dependent components of the wavevector satisfying the following set of ODEs:

 \begin{displaymath}% \frac{{\rm d}\vec{k}}{{\rm d}t}+S^{\rm T}\cdot \vec{k}=0, \end{displaymath} (9)

where $S^{\rm T}$ is the transposed shear matrix. In this general formalism, the substitution of expressions (6)-(8) in the governing equations results in a set of ordinary differential equations (ODEs) in time in which the spatial inhomogeneity is replaced by a temporal one (for details see e.g. Rogava et al. 2001). These ODEs govern the temporal evolution of the spatial Fourier harmonics with time-dependent components of the wave vector. In the case of the two dimensional non-uniform flow considered here, one gets:

 \begin{displaymath}% \frac {{\rm d}k_x}{{\rm d}t}=0, \end{displaymath} (10a)
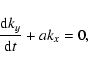\begin{displaymath}% \frac {{\rm d}k_y}{{\rm d}t}+ak_x=0, \end{displaymath} (10b)
 \begin{displaymath}% \frac {{\rm d}k_z}{{\rm d}t}+bk_x + ck_y=0. \end{displaymath} (10c)

Consequently, for the considered flow velocity profiles the x-component of the wave vector remains constant in time, kx=kx0, but

 
ky(t)=ky0-akxt. (11)

Integrating Eq. (10c), we find for the temporal evolution of the radial (z-) component of wavevector:

 \begin{displaymath}% k_z(t) = k_{z0} - \left(bk_{x0}+ck_{y0}\right)~t+\frac{ack_{x0}}{2}~t^2. \end{displaymath} (12)

In this case a combination of the solutions of the Eqs. (10a)-(10c) that is preserved in time can be written Rogava (2002), viz.

 \begin{displaymath}% \Delta \equiv ck_y ^2+2\left(bk_yk_x-ak_zk_x\right)=\hbox{const}. \end{displaymath} (13)

Using the representation (6) in Eqs. (4) and rewriting the equations for the components of the velocity perturbations, normalized density perturbation $D=\rho_1/\rho_0$and the enthalpy perturbation $Q=p_1/\rho_0$we get the following set of ODEs for the perturbed quantities:

 \begin{displaymath}% \frac{{\rm d}\hat{D}}{{\rm d}t}+{\rm i}\left( k_{x}\hat{v}_{x}+k_{y}(t)\hat {u}_{y}+\tilde{k}_{z}(t)\hat{v}_{z}\right) =0, \end{displaymath} (14a)
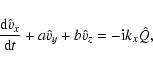\begin{displaymath}% \frac{{\rm d}\hat{v}_{x}}{{\rm d}t}+a\hat{v}_{y}+b\hat{v}_{z}=-{\rm i}k_{x}\hat{Q}, \end{displaymath} (14b)
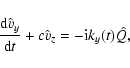\begin{displaymath}% \frac{{\rm d}\hat{v}_{y}}{{\rm d}t}+c\hat{v}_{z}=-{\rm i}k_{y}(t)\hat{Q}, \end{displaymath} (14c)
 \begin{displaymath}% \frac{{\rm d}\hat{v}_{z}}{{\rm d}t}=-{\rm i}\tilde{k}_{z}(t)\hat{Q}+g\hat{D}, \end{displaymath} (14d)
 \begin{displaymath}% \frac{{\rm d}\hat{Q}}{{\rm d}t}=C_{s}^{2}\left( \frac{{\rm ... ...{D}}{{\rm d}t} +\frac{(\gamma-1)\hat{v}_{z}}{\gamma H}\right), \end{displaymath} (14e)

where $\tilde{k}_{z}(t)=k_{z}(t)+{\rm i}/2H$. Hence, the presence of shear flows causes a transformation of the wave solutions in time. The rate of this transformation strongly depends on the initial orientation of the wave vector and on the values of the shear parameters included in the shear matrix.

Our first aim is to qualitatively understand the temporal behavior of the p-modes driven by the joint effect of the inhomogeneous rotation and the meridional flow appearing in the thin shell just below the photosphere. Therefore, in the next section we will introduce some simplifying assumptions. This will enable us to derive an approximate analytical "dispersion relation'' which governs the temporal evolution of the "effective frequencies'' of the modes. We will also demonstrate the shear flow effect in a simple model with a linear velocity profile, viz. for a mode with l = 951 which is confined within a very thin cavity above the fractional radius 0.997. In Sect. 4 we then try to quantify this effect in first order with a multi-layer model. The measured velocity profiles are approximated linearly in each layer and the cumulative effect of the layers is calculated taking into account the time spent by the modes in each layer.

3 Approximative analysis

In general, the application of the non-modal approach means that, in the governing equations, the spatial inhomogeneity (related to the terms containing the nonuniform background flows) is replaced by a temporal one. After this transformation of the perturbation variables the temporal behavior of the spatial Fourier harmonics (containing the time-dependent wavenumbers) can be studied. In most cases, the solution of the resulting ODEs (in time) requires the application of numerical techniques. In this particular case of trapped acoustic-gravity modes, the initial value problem has a specific feature. On one hand, the time dependence of the wavevector results in a variation of the phase speed and the direction of the wave propagation, in time. On the other hand, the temperature gradient refracts the propagating mode. Formally speaking, the local approach outlined in the previous section is the "non-modal equivalent'' of the so-called ray approximation, commonly used for the local description of p-modes (Whitaker 1963; Ulrich 1970). But, in this case we do not perform a Fourier transform with respect to time. Instead, one has to study the propagation of the modes by solving the governing Eqs. (14) in each layer separately and then matching the solutions at the interfaces between the different layers. However, at this stage we aim to qualitatively estimate the characteristic changes in the modal properties in order to understand the principle of the mechanism of these changes induced by the inhomogeneity of the background flows. Therefore, we adopt an approximative analysis to study the propagation properties of the modes and to construct the shape of their ray paths. The part of the ray path confined within a given layer with constant temperature is locally linear (a schematic view of this kind of piecewise straight ray path is shown in Fig. 2) and within this layer the equations governing the motion of a point of the wave front can be written as follows:

 \begin{displaymath}% \left ( \frac {\delta x}{\delta t} \right ) _i=v_{{\rm ph}}... ...rt}= \frac{\omega (t)k_{x_i}(z_i,t)}{\vert k_i(z_i,t)\vert^2}, \end{displaymath} (15a)
 \begin{displaymath}% \left ( \frac {\delta y}{\delta t} \right ) _i=v_{{\rm ph}}... ...t}= \frac{\omega (t)k_{y_i}(z_i,t)}{\vert k_i(z_i,t)\vert^2}, \end{displaymath} (15b)
 \begin{displaymath}% \left ( \frac {\delta z}{\delta t} \right ) _i=v_{{\rm ph}}... ...}= \frac{\omega (t)k_{z_i}(z_i,t)}{\vert k_i (z_i,t)\vert^2}, \end{displaymath} (15c)

where index i denotes a given layer between horizontal planes located at z1i=zi and $z_{2i}=z_i+(\delta z) _i$; ki, kxi, kyi and kzi are the module and components of wavevector, respectively. In these equations we introduce the time dependent "effective'' frequency  $\omega (t)$. We will turn to the issue of validity of such a description in the following subsection. Because of the temperature gradient the local values of the sound speed in each neighboring layer are different. Therefore, the components of the wavevector should be adjusted accordingly, in order to keep the "effective'' frequency unchanged through the interface between the layers. One can easily see that in the case without a shear flow the "effective'' frequencies should be replaced by the usual constant modal frequencies. In this latter case the problem always can be reduced to two dimensions (as it is usually done under the normal mode formalism). In our case, however, the trajectories (ray paths) of the modes are 3D curves. From this point our problem is reduced to the determination of the "effective'' frequency and how it relates to the time dependent components of the wavevector.


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{2695fig2.eps} \end{figure} Figure 2: Schematic view of the piecewise straight ray path.
Open with DEXTER

3.1 The "effective'' frequency

Generally speaking, the effect of an inhomogeneous flow on waves manifests itself in a temporal variation of the modal properties. Using different analytical methods (among which the non-modal approach) it has been shown that strong gradients in the background flow velocity can cause very rapid changes of the modal frequency and the amplitude, even in time intervals as short as an oscillation period. As a result, the power spectrum of the waves is affected in such a way that it may become impossible to distinguish the individual peaks in the spectrum.

In the Sun, however, such strong gradients of the flow velocity are not observed. Therefore, in this first attempt to model this "small'' effect qualitatively, we assume that the sheared flows below the surface of the Sun just slightly transform the oscillation modes and that this transformation is represented by a small deviation of the mode properties found by the standard modal analysis. As a result of the flow inhomogeneity there appear terms of the form  Sijui (where a summation over repeated indices is meant) in the Eqs. (14b)-(14c). Here the indices i,j=1,2,3 represent the x-, y-, and z-direction, respectively, and S is the shear matrix. From Table 1 it is clear that the gradients of the flow velocity components are two to four orders smaller than the characteristic angular frequencies of the oscillation modes. Hence, we expect that the contribution from the Sijui terms in the solution of the governing equations is very small. Therefore, at this stage we neglect these terms, at least in Eqs. (14b)-(14c).


  \begin{figure} \par\includegraphics[width=16.3cm,clip]{2695fig3.eps} \end{figure} Figure 3: Piecewise constant radial profile of the temperature (panel A) and scale height (panel B) corresponding to the case of the simple velocity profile addressed in Sect. 3.2.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=16cm,clip]{2695fig4.eps} \end{figure} Figure 4: The variation of the modal frequency in time. The curves correspond to the mode $\ell =951$, n=2 and with the basic modal frequency $\nu _0 =4.5243$ mHz. The calculations have been done for a simple, linear profile of the flow velocity with the shear parameters equal to a=-1 $\times $ 10-6 s-1, b=2.5 $\times $ 10-5 s-1 and c=2.0 $\times $ 10-5 s-1. Panel A: curve a corresponds to ky0>0 (angle $\beta = 45^{\circ }$) and curve b corresponds to ky0<0 (angle $\beta = -45^{\circ }$). The points denoted by 1a and 1b correspond to the frequency of the respective mode close to its upper turning points (i.e. the frequencies observable on the surface!) while the inner turning points are denoted by 2a and 2b. Panel B: curves of the frequency variation corresponding to the upper turning points for different directions of the horizontal wavevector kh (i.e. for different values of the angle $\beta $). The curves are denoted respectively as: a1 and a2 - $\beta = \pm 5^{\circ }$ (crossed lines), b1 and b2 - $\beta = \pm 30^{\circ }$ (dashed lines), c1 and c2 - $\beta = \pm 45^{\circ }$ (solid lines), d1 and d2 - $\beta = \pm 60^{\circ }$ (dotted lines), e1 and e2 - $\beta = \pm 85^{\circ }$ (dash-dotted lines).
Open with DEXTER

The above approximation results in a mathematical simplification of the problem as it makes the frequency purely real, i.e. oscillatory. In other words, it is equivalent to the assumption that the amplitude of the mode varies much slower in time than the rapid oscillation itself so that the amplitude remains approximately constant. This approximation thus results in perturbations of the form $\hat \psi \approx \hat \psi(t_0)\exp({\rm i}\varphi(t))$. The set of Eqs. (14) then leads the dispersion equation for ${\partial\varphi(t)}/{\partial t}$, which has a similar form as the one given by Whitaker (1963) for waves propagating in a static medium:

 \begin{displaymath}% \left( \frac{\partial\varphi(t)}{\partial t}\right) ^{4}-\l... ...^{2}\right) +\omega_{\rm b}^{2}C_{\rm s}^{2} k_{\rm h}^{2} =0, \end{displaymath} (16)

where, $k_{\rm h}^2=k_{x}^2+k_{y}^2$, $\omega_{\rm a}=\gamma g/2C_{\rm s}$ is the local acoustic cutoff frequency, and $\omega_{\rm b}=\sqrt{g(\gamma-1)/\gamma H}$ is the local Brunt-Väisälä frequency. The difference between Eq. (16) and the dispersion equation for "homogeneous'' (in the sense of flows) waves is that now the coefficients in the equation are time dependent. Thus by using Eq. (6) we can write the approximate "effective frequency'' as the time derivative of the time dependent phase:
 
                                 $\displaystyle % \omega$ = $\displaystyle V_{01}k_{x} +V_{02}k_{y}-y\frac{\partial k_{y}}{\partial t} -z\frac{\partial k_{z}}{\partial t} - \frac{\partial \varphi(t)}{\partial t}$  
  = $\displaystyle (\vec k\cdot \vec V_{0})- \frac{\partial \varphi(t)}{\partial t},$ (17)

where,

 \begin{displaymath}% \frac{\partial \varphi(t)}{\partial t}=-\sqrt{\frac{1}{2} W... ...qrt{W^{2}-4\omega_{\rm b}^{2} C_{\rm s}^{2}k_{\rm h}^{2}(t)}}, \end{displaymath} (18)


 \begin{displaymath}% W=C_{\rm s}^{2}\left(k_{\rm h}^{2}(t)+k_{z}(t)^{2}\right) +\omega_{\rm a}^{2}. \end{displaymath} (19)

In Eq. (18) we chose the "-'' sign before the square root without loss of generality. It can easily be shown that the first four terms in the RHS of Eq. (17) in fact represent the expression  $(\vec k\cdot \vec V_{0})$. It is well-known that this scalar product of the wavevector and the background flow velocity represents the effect of the Doppler shift of the frequencies due to the fact that the waves are advected by the flow. Hence, this term is analogous to the one given for example by Ulrich et al. (1979). However, here the components of the wavevector (and thus the characteristic frequency) are time dependent. This time dependency represents the deviation from a purely exponential ($\sim$ $\exp ({\rm i}\omega t)$) temporal evolution of the small disturbances.

3.2 Effect of a simple (linear) velocity profile

In order to numerically calculate the changes of the modal frequencies purely due to the non-modal effects we developed a numerical code making use of a spatial discretisation on the basis of the Standard solar model (www.ap.stmarys.ca/~guenther/solar/ssm455.sink) and the approximate "dispersion relation'' (Eq. (17)). In our calculations we used also the observed p-mode frequency data (published online by Libbrecht et al. and Bachmann et al., see the web page http://www.gong.noao.edu/teams/data/jwl_freqs.html). As an example we examined the mode with $\ell =951$. In Fig. 3 we show the piecewise constant radial profiles of the temperature (panel A) and scale height (panel B). The shown range of the fractional radius includes the very thin cavity in which the $\ell =951$ mode is confined.

Notice that these illustrative calculations involve a sample mode with $\ell =951$, n=2 and $\nu _0 =4.5243$ mHz. The curves in Fig. 4 correspond to a simple velocity profile. In particular, it was assumed that the profiles of both the rotational and the meridional flows are linear in the entire (narrow) cavity in which the mode is confined. As one can see from Eq. (17) the non-modal change in wavelength directly manifests itself in a variation of the effective frequency in time. However, the problem we are considering here has one specific feature: the modes are trapped in the acoustic cavity between the upper and inner turning points. As a result, if the modal frequency increases (decreases), when it propagates from the upper turning point to the inner one, then the frequency decreases (increases) when mode propagates in the backward direction. Therefore, any observable changes in modal frequencies (on the surface) can only arise when the net influence of the flow, during the propagation of the mode in the inward and outward directions, is nonzero. Hence, the nonzero residuals in Fig. 4 result from the asymmetry of the background flow. The example shown in Fig. 4 corresponds to a case with a simple flow velocity profile: for this calculation we assumed linear rotational and meridional flow profiles in the entire cavity. This simple profile is appropriate for the modes with very high angular degree. The total residual during the observed modal lifetimes is thus the sum of the net frequency changes appearing during each passage from the upper turning point to the inner one and backward as shown in Fig. 4 (panel A). The curve a (solid line) corresponds to the mode with kx>0 and ky0>0 and the curve b to the kx>0 and ky0<0 (dashed line). The points 1a and 2a correspond to the moments when the mode areaches its upper and inner turning points, respectively. Similarly we have points 1b and 2b for the curve b. The panel B in Fig. 4 illustrates the changes in modal frequency for different ratios kx/ky(0), i.e. for different directions of the horizontal wavevector in the initial momentum. The curves in this panel in fact are the lines connecting the residuals in frequencies corresponding to the moments when the considered mode is close to its upper turning points. We denote the curves for modes with ky0>0 by the characters with the index 1 and for the modes with ky0<0 by characters with index 2. If we represent the ky0 components of the wavevector as $k_{y0}=k_{\rm h}\sin(\beta)$, where $\beta $ is the angle between the  $\vec k_{\rm h}$ and x-axis, then the curves on panel B correspond to the values of $\beta $ in the following order: curves a1 and a2 (crossed lines) correspond to $\beta = \pm 5^{\circ }$, b1 and b2 (dashed lines) correspond to $\beta = \pm 30^{\circ }$, c1 and c2 (solid lines) correspond to $\beta = \pm 45^{\circ }$, d1 and d2 (doted lines) correspond to $\beta = \pm 60^{\circ }$ and e1 and e2(dash-dotted lines) correspond to $\beta = \pm 85^{\circ }$. Clearly, the residuals in modal frequency due to the non-modal effects are greater for modes propagating in an oblique direction with respect to the both rotational and meridional flows and the effect is maximal for the angle $\beta = \pm 45^{\circ }$ (i.e. kx=ky0) (the angle corresponding to maximum rates of the frequency residuals can differ from this, it can be $\pm$ $30^{\circ}$ or $\pm$ $60^{\circ}$, depending on the values of shear rates and wavevector components).


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{2695fig5.eps} \end{figure} Figure 5: Results of the calculations for the same mode as in Fig. 4 for a smaller value of the shear parameter a=-0.1 $\times $ 10-6 s-1. The value of the shear parameter b has been taken the same as in Fig. 4 (b=2.5 $\times $ 10-5 s-1). In panel A we show the curve of the frequency variation in time, for the angle $\beta = 45^{\circ }$, within the first three evolution hours. The solid line corresponds to c=2.0 $\times $ 10-5 s-1 and the dashed line to c=3.0 $\times $ 10-5 s-1. Similar curves are plotted in panel B for the angle  $\beta =30^{\circ }$, where the dashed-dotted line corresponds to the smaller value of the parameter c and the dotted line to the larger one. Panel C shows the resulting modal frequency evolution over a time interval of 10 h. The different line styles correspond to the line styles in the previous panels.
Open with DEXTER

In Fig. 5 we show results for a rather small value of the parameter a (a=-0.1 $\times $ 10-6 s-1) obtained for the same mode as in Fig. 4. The curves in panel A correspond to the angle $\beta = 45^{\circ }$. The solid curve corresponds to the shear rate c=2.0 $\times $ 10-5 s-1 and the dashed line corresponds to c=3.0 $\times $ 10-5 s-1. Similarly, we show the results for the angle $\beta =30^{\circ }$ in panel B, where the dashed-dotted curve corresponds to the smaller value of parameter c and the dotted line to the larger one. From both panels A and B one can easily see that the amplitude of the frequency variation along the ray path increases as c increases. Finally, we combine the results for both angle values $\beta = 45^{\circ }$(solid and dashed lines) and $\beta =30^{\circ }$ (dashed dotted and dotted lines) calculated for a 10 h period. In this panel the line styles correspond to the same values of the shear parameter c as in the previous panels. From this panel we conclude that the rate of the overall frequency residuals drops down by a factor of 10 compared with the case shown in Fig. 4 since now the value of parameter a is 10 times smaller. This seems to indicate that the frequency residual rates depend nearly linearly on the value of this parameter. We will come back on this point in the next section.

We adopted a simplified velocity profile with fixed constant values of the shear parameters within the entire cavity (above the fractional radius 0.997), in which the examined oscillation mode with $\ell =951$ is confined. This simple model yields the following main conclusions: (1) The joint effect of the non-uniform rotational and meridional flows can yield finite differences between the normal mode frequencies and the "effective frequencies''; (2) These "residuals'' can be of the order of a few tens of $\mu$Hz. It is thus worthwhile to improve the model in an attempt to better "quantify'' the effect of the shear flows. This is done in the next section, where we consider a more advanced model including observed (not simplified) velocity profiles, and perform calculations for different sample modes including the one considered in the current subsection.

4 Numerical results for observed velocity profiles

In this section we consider cases of modes with different angular degrees. For these purposes, in general more complicated, the observed velocity profiles should be taken into account in the model. Modes with $\ell$ significantly lower than that considered in the previous subsection penetrate deeper in the solar interior and correspondingly we expand the width of cavity as is shown in Figs. 6 and 7, where we consider the propagation of modes. We explain the model in detail.

4.1 Modelling the subsurface flows

As a basis for the present study we use the results of helioseismological measurements of the subsurface velocity profiles (see e.g. González Hernández et al. 1999; González Hernández & Patrón 2000). These observations show that the gradients of the flow velocity components are functions of position. This is why we present our results for a number of magnitudes of the shear parameters confined within some ranges of values. The model "shear parameters'' included in the shear matrix are estimated as follows. The photospheric latitudinal variation of the rotation rate is usually modelled as:

 \begin{displaymath}% \Omega (\theta) = \sum _{k=0,2,4}a_k\cos^k (\theta)+s_0, \end{displaymath} (20)

where $\theta$ denotes the colatitude and a0=452.0 nHz, a2=-49.0 nHz, a4=-84.0 nHz, and s0=-31.7 nHz (Snodgrass 1984; González Hernández & Patrón 2000). As the parameter a=V0x,y included in the shear matrixes corresponds to the derivative with respect to the y-coordinate of the x-component of the equilibrium flow velocity. Thus, this parameter represents the latitudinal variation of the rotational velocity in the considered local plane-parallel slab. We performed the calculations assuming that this parameter is of the order of $a \simeq -0.01$ $\times $ 10-6, -0.1 $\times $ 10-6, -0.3 $\times $ 10-6, -0.6 $\times $ 10-6, or -1.0 $\times $ 10-6 s-1.

To estimate the values of the parameter b=V0x,z, which locally represents the radial variation of the rotational component of the flow velocity, and the radial shear c of the meridional (y-) component of the velocity field, we used results of helioseismic inversions given in Gonsález Hernández et al. (1999), González Hernández & Patrón (2000). In Fig. 6 we show the rotational profile for latitude  $15^{\circ }$ taken from González Hernández & Patrón (2000) (dotted line). We provide a linear approximation of the observed profile. The approximate profile is also plotted in Fig. 6 (solid line). This approximate profile corresponds to specific values of the shear parameter b. The results of our estimates, for different fractional distances from the solar center, are shown in the Table 1. At depths below the thin sub-photospheric layer, i.e. for $r<0.95~R_{\odot}$, we assume the radial gradient of the rotational velocity to be negligibly small. We only consider oscillation modes with angular degree $\ell \geq 95$, which have their lower turning points far above the solar tachocline. These parameters a, b, and c determine the inhomogeneity of the background flow. Together with the spatial scales of the waves themselves and with the timescales of the interaction between the modes and the flows, they determine the strength of the influence of the inhomogeneous flow on the waves.


  \begin{figure} \par\includegraphics[width=7.3cm,clip]{2695fig6.eps}\end{figure} Figure 6: Profile of the rotational velocity in the solar subsurface layers. The solid line shows the sample profile for latitude angle  $15^{\circ }$ given by González Hernández & Patrón (2000). The dotted curve is the observed rotational profile. The solid lines show the modelled linear approximations of the observed profile for different fractional radii.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=7.6cm,clip]{2695fig7.eps} \end{figure} Figure 7: As in Fig. 3 corresponding to the range of the fractional radius values r=0.95-1.00. The squares in the right bottom corners show the areas plotted in respective panels of Fig. 3.
Open with DEXTER

Table 1: Values of the shear parameters b and cat different fractional radii.

4.2 Determination of the timescales of influence

We now address the timescales of the interaction between the flow and the oscillation modes. One of the basic temporal parameters characterizing the solar p-modes is the lifetime. Several observational methods have been used by numerous authors to estimate the lifetimes TL of the solar p-modes, see e.g. the work of of Chou et al. (2001) and Chen et al. (1996). There exists a discrepancy between the observational measurements of the modal lifetimes. Nevertheless, from the above-mentioned measurements one can estimate the range of the lifetimes as 2-10 h.

Another characteristic temporal parameter of an oscillation mode is its travel time $\tau$ along the ray path, from one reflection in the upper turning point to another one (see Fig. 1). These travel times are observable by methods of local helioseismology.

The radial gradient of the temperature and, therefore, of the sound speed inside the Sun leads to the refraction of waves. Hence, to properly calculate the changes in the modal frequencies as the modes propagate along their ray path, we radially discretize the plain-parallel slab. We thus consider a set of very thin shells so that within each of these thin plasma layers the local sound speed, the cut-off frequency and the Brünt-Väisäla frequency can be assumed to be constant. Therefore, the spatial orientation of the wavevector also approximately remains constant when the waves propagate within the given layer. In our calculations we use the equilibrium parameters taken from the standard solar model (see e.g. www.ap.stmarys.ca/~guenther/solar/ssm455.sink). We denote the part of the total ray path confined within the given layer by ${\rm d}s={v_{{\rm ph}}} {\rm d}t$ where, $v_{{\rm ph}}=\omega /k$ is the modal phase velocity and ${\rm d}t$ is the time interval during which the wave front stays within the given layer. This distance is related to the distance between the top and bottom boundaries of the layer ${\rm d}z$as follows:

 \begin{displaymath}% {\rm d}z={\rm d}s \cos \alpha, \end{displaymath} (21)

where $\alpha$ is the angle between the vector ${\vec ds}$ and the vertical (see the schematic view in Fig. 1). The cosine of this angle can be written in terms of the components of the wavevector. In particular, $\cos \alpha =k_z/k$ where kz and k are the radial component and length of the wavevector, respectively. Finally according to the above expressions we can write:

 \begin{displaymath}% {\rm d}t = \frac {k^2}{\omega k_z} {\rm d}z. \end{displaymath} (22)

This last expression determines the time interval during which the wave undergoes an influence from the inhomogeneous flow within the given thin layer. Hence, in our model we consider the influence of the inhomogeneous flows on the oscillation modes as the accumulation of the effects in the different layers reached by the given mode as it propagates from its upper to its lower turning point and back. Now, as we have parameterized the effective time of influence of the nonuniform flows on the p-modes, the question that remains is: "how strong is this influence?''. Is the total time interval of influence large enough for significant changes in the modal properties? Below, we discuss this issue.


  \begin{figure} \par\includegraphics[width=12.8cm,clip]{2695fig8.eps} \end{figure} Figure 8: The variation of the modal frequencies in time calculated in the case of the velocity shear profile described in Sect. 4.1 (see Table 1). The direction of the horizontal wavevector is taken as $\beta = \pm 45^{\circ }$. Curves a1 and a2 (dashed lines) correspond to the sample mode with $\ell =95$, n=4 and with basic modal frequency $\nu _0=2.3761$ mHz. Similarly, the b1-b2(dashed dotted lines) and c1-c2 (dotted lines) respectively are curves for the modes $\ell =263$, n=6, $\nu _0=4.2336$ mHz and $\ell =673$, n=2, $\nu _0=3.8202$ mHz. The curves d1-d2(solid lines) correspond to the same mode with $\ell =951$considered in Sect. 3.2. Different panels show results of calculations in the three different cases of the latitudinal gradient of the rotational velocity: panel  A) the parameter a=-1 $\times $ 10-8 s-1; panel  B) a=-1 $\times $ 10-7 s-1; panel  C) a=-3 $\times $ 10-7 s-1; panel  D) a=-6 $\times $ 10-7 s-1; panel  E) a=-1 $\times $ 10-6 s-1. Note that the ordinate axes in panels  A)- E) have different scales. In panel  F) the frequency residuals arising after a 10 h period are plotted as functions of the shear parameter |a|absolute values.
Open with DEXTER

4.3 Modes with angular degree ${\ell < 200}$

In this subsection, results of calculations are presented based on the model discussed in the previous subsections, i.e. the more general case with realistic approximations of the velocity profiles. The shear parameters used for these calculations depend on depth and are given in Table 1. In Fig. 8 the results of these calculations are shown for different values of the shear parameter a. The panels A, B, C, D and E correspond to $\beta = \pm 45^{\circ }$ and to the values a=-1 $\times $ 10-8 s-1, a=-1 $\times $ 10-7 s-1, a=-3 $\times $ 10-7 s-1, a=-6 $\times $ 10-7 s-1 and a=-1 $\times $ 10-6 s-1, respectively. Again the curves labelled with characters with index 1 correspond to modes with ky0>0, while the labels with index 2 correspond to modes with ky0<0. The curves a1 and a2 (dashed lines) correspond to the mode with angular degree $\ell =95$, n=4 and a basic modal frequency $\nu _0=2.3761$ mHz. Clearly, the influence of shear flow is more pronounced as time proceeds. It yields changes in the frequency of the order of a few $\mu$Hz to, at most, 5 to $20~\mu$Hz after 10 h (the maximal life time of the mode). The values of the shear parameter a used in the calculations correspond approximately to the latitudes $1^{\circ}$, $10^{\circ}$, $25^{\circ}$, $40^{\circ}$ and  $60^{\circ}$, respectively. The overall frequency residual (after 10 h) for the considered mode is plotted in panel F of Fig. 8 (dashed line) as a function of the parameter a.

4.5 Modes with angular degree ${\ell \geqslant 200}$

From Eqs. (10) and (17)-(19) it is clear that the rate of change of the modal wavelength in time strongly depends on the modulus (and consequently on the angular degree of modes as $k_{\rm h} ^2 \propto \ell (\ell +1)$) and the direction of the wavevector, i.e. on its horizontal ($k_{\rm h}$) and radial (kz) components. In particular, the larger the component $k_{\rm h}$ of the wavevector is, the more substantial the changes of the modal properties are. Therefore, we can expect that the deviation of the modal properties (from those of normal modes) increases with angular degree. Our calculations show larger residuals from the basic modal frequency for the sample modes (see Fig. 8): $\ell =263$, n=6, $\nu _0=4.2336$ mHz (curves b1 and b2 (dash-dotted lines)), $\ell =673$, n=2, $\nu _0=3.8202$ mHz (curves c1 and c2 (dotted lines)), and the mode considered in Sect. 3.2 (curves d1 and d2 (solid lines)). These plots demonstrate that the residuals of the modal frequency due to the non-modal effects increase with growth of the angular degree. The overall residuals after 10 h versus parameter a are also plotted for these sample modes in panel F in the respective order of line styles. This confirms that the frequency residuals depend on the values of the parameter a, and this dependence has a nearly linear character.

In addition, the modes experience a more substantial influence of the flow when they are closer to their inner turning points. As a result, modes with inner turning points within the area with strongly pronounced gradients of the flow velocity (i.e. mostly the modes with ${\ell \geqslant 200}$) change more effectively in time. This also contributes to the appearance of more significant non-modal effects for modes with higher angular degree. Comparing the results shown in Fig. 8 for the sample mode with $\ell =951$ (solid lines in panels B and E) with those obtained with the simplified velocity shear profiles (see panel B in Fig. 4 and panel C in Fig. 5) it is easily seen that our preliminary estimates given in Sect. 3.2 that frequency residuals up to values of a few tens of $\mu$Hz should be expected were true. For a=-1 $\times $ 10-7 s-1 the solid line d1 in panel B in Fig. 8 should be compared with the solid and dashed lines in panel C of Fig. 5, which correspond to the angle $\beta = 45^{\circ }$. On the other hand, from the panel E of Fig. 8 one can see that (comparing the solid curves d1 and d2 with the similar curves in panel B of Fig. 4) the characteristic frequency residuals with the observed velocity profiles are somewhat smaller than those obtained with the constant shear rates in Sect. 3.2. This is due to the complicated radial profile of the observed rotational and meridional flows leading to alternating signs of the shear rates along the radial direction.

5 Discussion

Non-uniform flows can influence the linear wave modes in fluids and plasmas in two different ways. On one hand the flow advects the wave front producing a Doppler shift of the modal frequencies (the scalar product on the RHS of the Eq. (17)). On the other hand, the shear background flow causes (in general) changes in the modal wavelength, which in turn results in a temporal variation of the characteristic frequencies and/or amplitudes of the linear disturbances (for the case of modes considered here see the last term in RHS of Eq. (17)). Under the standard normal mode formalism it is a priori assumed that the perturbations evolve as purely exponential ($\sim$ $\exp ({\rm i}\omega t)$) functions of time. The Doppler shift of the modal frequencies can be described under the normal mode analysis very well. On the other hand, as we have shown, the temporal changes in wave characteristics related to the time dependence of the wavenumbers can be studied as well. The normal mode decomposition of the perturbations neglects this latter characteristic of the temporal evolution of the wave modes. For the particular case of p-modes trapped in the solar interior this assumption is true in most cases. Indeed, there are no sharp flow velocity gradients observed in the solar interior. Even in narrow shells below the convection zone and just beneath the photosphere, where significant gradients of the flow velocity are observed, the shear rates still are by several orders of magnitude lower than the characteristic frequencies of the oscillation modes. Therefore, we expected that the inhomogeneous flows in the subsurface shell, which is under consideration here, could only slightly deviate (non-modally) the temporal behavior of the modes from that described under the standard normal mode approach. The approximative analysis performed in this work leads to the conclusion that these expectations were true. Nevertheless, the considered non-modal effects still turn out to be "strong'' enough to support different observational evidence. In particular, from the global point of view the non-modal effects can cause the "blurring'' of the global p-mode power spectra and the mixing of the modal power with the noise. On the other hand, these effects contribute to a slight "deformation'' of the modal ray paths. We address these observational aspects of the non-modal effects in details in the following subsections.

5.1 The observational aspects of the non-modal effects - global view


  \begin{figure} \par\includegraphics[width=11cm,clip]{2695fig9.eps} \end{figure} Figure 9: Schematic view of the peak(s) in the power spectrum corresponding to the oscillation mode with a given angular degree. a) In static medium; b) in the case of uniform flow; c) inhomogeneous flow without the non-modal effects; d) inhomogeneous flow including the non-modal effects.
Open with DEXTER

How do the effects related to the flow velocity gradients manifest in the observed power spectrum of the solar p-modes? It is believed that the solar oscillations are excited by the stochastic motions in the upper part of the convection zone. From the global point of view, the solar p-modes are observed as global oscillation modes of the Sun by measuring the characteristic frequencies of the intensity or the velocity field oscillations. The observational data are then concentrated in the power spectrum which enables the identification of different oscillation modes by fitting the peaks arising in the spectrum with the peaks in the analytically obtained Fourier power spectrum. The formation of each peak involves the contribution of many modes with similar properties. The oscillation modes are characterized by their frequency, their radial order n, their angular degree $\ell$ and their azimuthal order m. As is well known from the theory of stellar non-radial oscillations (Unno et al. 1989), in the case of a spherically symmetric star the eigenfrequencies are degenerate with respect to the azimuthal order. This means that it is not possible to distinguish modes (in the observed power spectrum) with the same radial order and angular degree but propagating in different horizontal directions. In Fig. 9, panel a schematically shows one peak corresponding to a given radial order and angular degree and containing the power of all modes with azimuthal order $m=-\ell,-\ell+1, ..., 0, ..., \ell-1,\ell$.

Any phenomenon that breaks the spherical symmetry (for example the axi-symmetric rotation of the star, magnetic field etc.) results in lifting of the degeneracy with respect to m. In the non-spherically symmetric case, instead of one peak several peaks appear in the power spectrum corresponding to the different orientations of the horizontal wave vector. In panel b of Fig. 9 this is illustrated schematically by two peaks in the power spectrum corresponding to two modes with the same radial order and angular degree, but with horizontal wave vectors directed in opposite directions. This effect is the well-known phenomenon of "frequency splitting''. Clearly, frequency splitting observations allow us to perform the inversion of the observational data into the rotational profile inside the Sun. However, the eigenfrequency splitting can also be caused by any other factor breaking the spherical symmetry such as, for example, the meridional flows.

The effect of inhomogeneous flows on the power spectrum can be complicated. The flow velocity gradients contribute to the frequency splitting just as a uniform flow would do. On the other hand, we have shown above that the influence of the flow inhomogeneity can be important, able to serve as a mechanism causing changes in the modal properties which can contribute to the observed deficit of modal power for very high degree p-modes. In the non-modal approach we have described these changes by a time dependent wavevector and a time dependent modal frequency. Hence, to describe the effect of inhomogeneous flows on the power spectrum we need to use additional characteristic temporal parameters: viz. the widths of the peaks in the power spectra  $\Delta \nu$ and the observation time, which relates to the resolution of the observations. If the changes in the modal frequencies  $\delta \nu$ occurring due to the non-modal effects during the lifetime of the mode are much smaller than the half-width of the corresponding peak in the power spectrum, then one can assume that the changes in frequency are negligible. In this case the background flow only contributes to the observed frequency splitting. This is the case considered under the formalism of the standard modal analysis by Ulrich et al. (1979). A schematic view of this situation is given in panel c in Fig. 9.

When $\delta \nu \simeq \Delta \nu$ the changes in frequency contribute to the line width (along with different damping mechanisms causing a variation of the mode amplitudes). When $\delta \nu > \Delta \nu$ the frequencies of the individual modes "drift'' along the frequency axis. In this case a part of their power is mixed with the acoustic noise (leading to a decrease of the signal to noise ratio) and a part of their power contributes to the neighboring peaks. Under these circumstances, even in the conservative case where we assume that the average power exchanged by two neighboring peaks are approximately equal to each other (in the real situation this cannot be true, see Goldreich et al. 1994), the non-modal effects could be the cause of the partial dissipation of the power because of mixing with noise. The last two situations are schematically displayed in panel d in Fig. 9. The modes that contribute to a given peak in the power spectrum are randomly excited by different convective sources at different time intervals. But, as the flow velocity gradients are small on the Sun, the changes in frequencies of the particular mode by the non-modal effects need a significant time to occur. That is why the peaks in the power spectrum remain concentrated around the basic central frequency and why the frequency splitting is still observable.

5.2 The observational aspects of the non-modal effects - local view


  \begin{figure} \par\includegraphics[width=13.4cm,clip]{2695fig10.eps} \end{figure} Figure 10: Schematic view of the modal ray paths: A) without non-modal effects; B) same as panel A (solid line) and the non-modal deformation of the ray path due to the temporal evolution of the radial component kz of the wavevector, which first increases and then decreases in length (dashed line) and vice versa (dash-dotted lines); C) the non-modal deformation of the ray path because of the temporal evolution of the meridional component ky of the wavevector (dashed and dash-dotted lines). The modes do not stay in one plane; the trajectories become 3D curves.
Open with DEXTER

How do the non-modal changes in modal properties affect the observational data obtained by using local helioseismology (such as time-distance techniques, ring diagrams, etc.)? The expressions (15) determine the shape of the trajectory of a point with a constant phase, within the framework of our model with a piecewise constant temperature. In the shearless (zero shear matrix) limit the horizontal components (kx and ky) remain constant. Therefore, in this case the modes propagate in the horizontal direction along straight lines (x and y coordinates of the point are linear functions of time) and the ray path is confined in one plane (the problem is two dimensional). The variation of the radial component of the wavenumber kz arises from the refraction of waves by the temperature gradient along the radius. The schematic view of a given modal ray path between two neighboring reflections at the upper turning points is shown in Fig. 10 (panel A). The effects that can systematically distort the ray paths (when we exclude non-modal changes) relate only to the inhomogeneous temperature and/or magnetic field profiles and Doppler shift of frequencies due to the advection of modes by the flows (this effect is represented by the scalar product on the RHS of Eq. (17)). These systematic distortions are immediately detectable by using local methods of helioseismology. On the one hand, observations detect changes in modal travel times and distances. On the other hand, changes of modal frequencies result in a transformation of the so-called acoustic ring shape from a ring to an elliptical one.

For the case of nonzero shear rates, it can be seen from Eq. (15) that the components of the wavevector are time dependent, in general. The character of this dependence is determined by the profiles of the background non-uniform velocity field. In the particular case which we consider in this paper (rotational velocity depending on y and z coordinates and the meridional flow varying only radially) we get the "dispersion relation'' (17) by introducing an "effective frequency'' because of the rather small shear rates and, consequently, a very slow and small variation of the wavenumbers and frequencies in time. The non-modal changes of the "effective frequency'' and wavevector result in a slight deformation of the ray path. In particular, the radial component of the wavevector kz now varies along the ray path for two reasons. The first one is the usual variation due to the temperature gradient. The second reason is related to the non-modal variation (see Eq. (12)). If kz increases (decreases) within a given layer, when the mode propagates from the upper turning point to the lower one, then the non-modal variation of the radial wavenumber turns and extends (shortens) the wavevector. The wavevector behaves oppositely when the mode propagates from the lower turning point to the upper one: within the same layer it turns in the opposite direction and its length decreases (increases) resulting in a compensation of the residual of the "effective frequency'' produced within the same layer before. Therefore, the combined action of the refraction and non-modal effects produces the shape of the ray path in the kh0-kz0 plane schematically shown in Fig. 10 (panel B).

The uncompensated finite residuals in modal wavelength (frequency) can arise only in the case of nonzero a and c coefficients. This is the reason why the slight non-modal evolution of the p-modes occurs only under the joint effect of the gradients of the rotational (parameter a) and meridional (parameter c) flows. The nonzero value a leads to variation of ky(Eq. (11)) in time. Because of this, the ray paths do not stay in the kh0-kz0 plane, but instead they become 3D curves. The schematic view of these curves are shown in Fig. 10 (panel C).

The residuals occurring during two neighboring reflections are very small and they can not be detected in the observational data of the modal travel times and distances. The non-modal variation of the modal properties is a cumulative effect in the case of trapped modes, occurring only after a significant number of reflections, while the effect related to the Doppler shift of the frequencies is immediately detectable as it systematically shifts all frequencies at once. Formally, the non-modal variation of the frequency is a "second order'' effect and it only becomes significant some time after the modal excitation. The effect considered in this paper cannot be detected by the ring diagram method either. The acoustic rings represent slices of the 3D local power spectrum at a given fixed frequency and deformation of the ring demonstrates the shift of frequencies due to advection (for example see Hill 1988). Because of the non-modal variation the "effective frequency'' slowly migrates along and/or across the corresponding ridge. This is why we do not expect that the non-modal variation will cause any additional deformation of the slices of the spectrum by fixed frequency planes. However, some signature of non-modal variation can arise because of the azimuthal variation of the height (or width of the ridges). This issue is become the subject of a separate study to verify whether the order of magnitude of the mentioned azimuthal variation is compatible with the resolution of the employed method (in this case a FFT). To detect the non-modal effects efficiently, it is convenient to develop a different kind of multidimensional spectral method involving different methods of data analysis with variable temporal and spatial scales (such as a window Fourier transform or a wavelet analysis). This latter issue is out of the scope of the current work.

6 Conclusions

The influence of the observed subsurface flow inhomogeneity on solar p-modes has been studied in the framework of a non-modal analysis. Particular attention was given to the possible role of the non-modal time-dependent effects in the formation of the observed p-mode power spectra. We suggest that several properties of the high-degree p-modes could be attributed to the slight ("non-modal'') deviation of the temporal behavior of this kind of mode from a purely ("modal'') exponential ($\sim$ $\exp ({\rm i}\omega t)$) evolution. This effect is related to the non self-adjointness of the governing equations which leads to the existence of alternative solutions for these equations describing the temporal evolution (in general non-exponential) of perturbations. This statement is based on the fact that high degree p-modes are mostly confined in the upper thin subsurface shell with strongly pronounced inhomogeneous flows. It was found that:

a) It is a well-established observational fact that the line widths of the peaks in the p-mode power spectrum increase with the angular degree of modes. In the previous section we have discussed the observational aspects of the flow inhomogeneity-related phenomena. Our results show that the non-uniform flows can contribute to the excess line widths (compared to the inverse observational time) in the observed power spectrum. Clearly, the effect addressed in this paper acts along with other damping mechanisms. As the frequencies in the spectrum are concentrated in the peaks around some central frequencies, the temporal rates of stochastic excitement of the modes by different convective sources are greater than the characteristic time of the significant changes in the modal properties. That is why the effect discussed here cannot be observed as a shift of the peak in the power spectrum. Although some shifts can appear because of the different values of residuals in frequency of modes propagating in different horizontal directions with respect to the meridional flow. However, it is much less significant than the changes of the particular wave frequency excited by a given convective source. Another finding supporting this scenario is that the residuals appear due to the asymmetry of the considered velocity field. When the terms in the approximate "dispersion relation'' containing information about the meridional flow are negligibly small, the modes undergo a much smaller net effect from the flow non-uniformity during the propagation in the inward and outward directions.

b) We considered the effect of the inhomogeneous background flows on the lower degree (${\ell < 200}$) modes. These modes have their turning points deeper in the convection zone, where we have only latitudinal differential rotation. In this case, the effect of inhomogeneous flows is of the order of 6-12 $\mu$Hz and this fact is in agreement with (and confirms) the observational evidence that the theory of mode excitement/damping explains the observed energetic spectrum very well for values of the angular degree ${\ell < 200}$.

c) The joint effect of the differential rotation and the inhomogeneous meridional flow on the oscillation modes with very high angular degree ( $\ell \gg 200$) causes significant changes of the mode frequencies in time. This may mean that the evolution of the p-modes due to the background velocity shear takes part in the distribution of the wave energy over frequencies and angular degrees. Together with several other possible damping mechanisms, this effect can explain or contribute to the observed energetic spectrum of the modes that shows a systematic lack of contributions from high degree modes. This may be caused by partial mixing of power related to the given mode with the acoustic noise. Hence, the suggested mechanism may be the cause of the discrepancies between theoretical predictions from the model of turbulent exitation/damping of oscillations on the sun on the one hand, and helioseismic observations of very high degree p-modes on the other hand. Additionally, the changes of modal frequency due to the non-modal effects might be a possible reason for the increase of the wide line widths of very high degree solar p-modes.
The assumptions we made during the analysis of our theoretical results enable us to study the main features of the modes propagating in the nonuniform flow. However, they only allow us to understand the "principle'' of the process and to estimate the possible changes of the modal properties related to the non-modal effects. In order to study this problem quantitatively more systematically, (i) The analytical model should be further developed and probably multidimensional spectra should be constructed (analogous to the ring diagrams) involving different methods of data analysis (e.g. wavelets); (ii) Direct numerical simulations of the governing equations in real space and time should be carried out; (iii) The results of these simulations should be analyzed and compared with the new observational data.

Acknowledgements
The authors thank Dr. A. D. Rogava for informative discussions and suggestions. This work has been developed in the doctoral program of B. M. Shergelashvili at the Centre for Plasma Astrophysics, K. U. Leuven (scholarship OE/02/20). These results were obtained in the projects OT/02/57 (K. U. Leuven) and 14815/00/NL/SFe(IC) (ESA Prodex 6). We express our gratitude to Prof. K. G. Libbrecht for allowing us to use the p-mode frequency data. We are also grateful to the anonymous referee whose comments and suggestions led to significant improvement of the manuscript.

References

 
Copyright ESO 2005