A&A 438, 1163-1173 (2005)
DOI: 10.1051/0004-6361:20042523

Astrophysical parameters of Galactic open clusters

N. V. Kharchenko ^1,2,3 - A. E. Piskunov ^1,2,4 - S. Röser ¹ - E. Schilbach ¹ - R.-D. Scholz ²

1 - Astronomisches Rechen-Institut, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
2 - Astrophysikalisches Institut Potsdam, An der Sternwarte 16, 14482 Potsdam, Germany
3 - Main Astronomical Observatory, 27 Academica Zabolotnogo Str., 03680 Kiev, Ukraine
4 - Institute of Astronomy of the Russian Acad. Sci., 48 Pyatnitskaya Str., Moscow 109017, Russia

Received 13 December 2004 / Accepted 31 January 2005

Abstract
We present a catalogue of astrophysical data for 520 Galactic open clusters. These are the clusters for which at least three most probable members (18 on average) could be identified in the ASCC-2.5, a catalogue of stars based on the Tycho-2 observations from the Hipparcos mission. We applied homogeneous methods and algorithms to determine angular sizes of cluster cores and coronae, heliocentric distances, mean proper motions, mean radial velocities, and ages. For the first time we derive distances for 200 clusters, radial velocities for 94 clusters, and ages of 196 clusters. This homogeneous new parameter set is compared with earlier determinations, where we find, in particular, that the angular sizes were systematically underestimated in the literature.

Key words: techniques: photometric - catalogs - astrometry - stars: kinematics - open clusters and associations: general - Galaxy: stellar content

1 Introduction

Although open clusters are typical representatives of the Galactic disk population, systematic investigation of their nature, size, number of members, and age is hampered by the inhomogeneity of the data. On one hand, general bibliographic catalogues derived from reviews of the literature are available, e.g. Lyngå (1987), Ruprecht et al. (1981), Dias et al. (2004), and the data base WEBDA of Mermilliod. In these collections general parameters of the clusters are simply taken from the published literature. These collections are indispensable sources for further work in this field; however, their parameters cannot be used for systematic studies or for comparisons between clusters. On the other hand, there are uniform lists of a few hundred clusters, the parameters of which were derived either from coherent photometric studies (e.g. Becker & Fenkart 1971; Janes & Adler 1982; Loktin et al. 2001; Tadross 2001) or from their kinematics (e.g. Baumgardt et al. 2000; Dias et al. 2001, 2002).

A few years ago we started a project to determine membership and principal parameters of open clusters by use of objective methods and algorithms. In order to get such an unbiased view of the whole system of open clusters of our Galaxy, one has to start with a homogeneous sky survey obtained with no particular emphasis on open clusters. One result of ESA's Hipparcos mission, the Tycho-2 catalogue (Høg et al. 2000), fulfills this necessary criterion, but its contents alone were not sufficient for our purpose.

As a first step, therefore, a catalogue of 2.5 million stars with proper motions in the Hipparcos system and B, V magnitudes in the Johnson photometric system was compiled and supplemented with spectral types and radial velocities when available. The resulting All-Sky Compiled Catalogue of 2.5 Million Stars (ASCC-2.5, Kharchenko 2001) can be retrieved from the CDS, a detailed description of the catalogue can be found in that paper or in the corresponding ReadMe file at the CDS.

In a second step, we used the ASCC-2.5 to identify known open clusters and compact associations listed in the Lund Catalogue of Open Clusters (Lyngå 1987), the Optically Visible Open Clusters Catalog (Dias et al. 2004, hereafter DLAM), and the Catalogue of Star Clusters and Associations (Ruprecht et al. 1981). Applying an iterative procedure for cluster membership determination based on proper motion, photometric, and spatial criteria to the ASCC-2.5 data, we could identify 520 of about 1700 known clusters. After re-estimating the positions of cluster centres and cluster sizes, about 150 000 ASCC-2.5 stars were selected in these 520 cluster areas, and membership probabilities were computed for each star in this list, which we called the Catalogue of Stars in Open Cluster Areas (CSOCA). The procedure for determining cluster membership is briefly described below, but a detailed information is given in Kharchenko et al. (2004b), hereafter Paper I. The CSOCA is a catalogue of stars that now gives us the basis for deriving uniform structural (location, size), kinematic (proper motions and spatial velocities), and evolutionary (age) parameters for open clusters in the wider neighbourhood of the Sun. The results are published in the Catalogue of Open Cluster Data (COCD) and the Open Cluster Diagrams Atlas (OCDA).

The present paper, the third step in our long-term project, is structured as follows: in Sect. 2 we briefly describe the basic data and our procedure of member selection. In Sect. 3 parameters describing the spatial-structure of the clusters are discussed, while Sect. 4 is devoted to the kinematics of the clusters. In Sect. 5 we describe the method applied for deriving ages of the clusters. Concluding remarks are given in Sect. 6, and in the appendices we describe the format of the COCD and OCDA.

  
2 Cluster list and membership criteria

Input data for this study come from the ASCC-2.5 and cover 513 open clusters and 7 compact associations, i.e. the associations with sufficiently high projected density of stars, so that the developed general procedure of member selection works properly. Due to a relatively bright limiting magnitude ( $V\approx 14$ mag) of the ASCC-2.5, our sample does not include faint and generally remote or highly obscured open clusters. Also, the two nearest extended clusters, the Hyades and Cr 285 (the UMa cluster), are missing in our list since they require a special and more sophisticated technique of membership determination. However, from comparison with DLAM, our sample is sufficiently complete for clusters up to 1 kpc, and it can be used for the study of cluster parameters and of the properties of the local population of open clusters.

For each cluster, membership determination is based on a comprehensive common analysis of several diagrams derived with ASCC-2.5 data: a sky chart referring to the cluster, radial distribution F(r) of the projected stellar density, a vector point diagram (VPD) of the proper motions, the magnitude dependence of the proper motion components, and a colour-magnitude diagram (CMD).

Figure 1: Illustration of the member-selection algorithm for the open cluster Stock 2. Arrows show the sequence of the basic selection phases presented by rectangles. Panel  a) is a sky map of the cluster neighbourhood. Panel  b) shows radial profiles of the projected density; panel  c) is the colour-magnitude diagram; panel  d) is vector point diagram; and panels  e) and f) are "magnitude equations'' ( $\mu _{x,y}-V$ relations). Additional explanations for each panel are given in Appendix B.

Open with DEXTER

As a first approximation of the member selection algorithm applied, we consider all ASCC-2.5 stars within an area of $1\times1$ sq. deg around the cluster centre with coordinates taken from DLAM. Using proper motion and photometric criteria, we then separate field stars and cluster members and adopt the point of maximum surface density for cluster members as the new approximation for locating the cluster centre. After analyzing surface cluster density F(r), a projected radius of the cluster is derived, and the resulting spatial parameters are used for the next steps in the iteration, which are stopped when the cluster member list no longer changes. As a rule, two iterations are sufficient to establish cluster membership and determine the structural and kinematic parameters. However, some clusters with sparse structure or initially erroneous central coordinates require three and more iterations. The member selection pipeline is illustrated in Fig. 1 for the case of open cluster Stock 2 (see Paper I, for more details).

For a star, the probability of belonging to a cluster is calculated as a measure of deviation either from the cluster mean proper motion (kinematical probability) or from the Main Sequence (MS) edges (photometric probability). Stars deviating from the reference values by less than one $\sigma$ rms are classified as most probably being cluster members (1$\sigma$-members, i.e., with a membership probability $P \ge 61$%). Those falling in semi intervals [1$\sigma$, 2$\sigma$) or [2$\sigma$, 3$\sigma$) are considered as possible members (P=14-61%) or possible field stars (P=1-14%), respectively. Stars with deviations larger than 3$\sigma$ are regarded as definite field stars (P < 1%). As a rule, all cluster parameters were determined using data on the most probable cluster members.

   
3 Spatial structure parameters of the clusters

  
3.1 Distance and extinction

Although about 9700 of the CSOCA stars with cluster membership probabilities higher than 14 % (i.e. 1$\sigma$- or 2$\sigma$-members) have trigonometric parallaxes measured by Hipparcos/Tycho, the parallaxes are significant (i.e. $\pi > 3\sigma_{\pi}$) for only 640 of these stars. Reliable Hipparcos-based distances to a few nearby clusters have already been determined by Robichon et al. (1999). But for the vast majority of the clusters under study, trigonometric parallaxes are not sufficiently accurate or not available at all. Therefore, we are forced to use indirect distance estimates.

The photometric approach to simultaneous determination of distance and interstellar extinction requires at least 3-colour photometry lacking in the ASCC-2.5. Therefore, for 255 clusters we took the data from a list derived and newly revised by Loktin et al. (2001, LGM hereafter) and Loktin (2004), who estimated distances and interstellar extinctions from homogeneous photometric parameters. Further, we include data of Robichon et al. (1999) - 8 clusters, Lyngå (1987) - 19 clusters, DLAM - 31 clusters, de Zeeuw et al. (1999) - 1 association, Ruprecht et al. (1981) - 6 associations.

For the remaining 200 clusters we determined or revised cluster distances and reddening by use of supplementary data on spectral classes of the most probable members available from the ASCC-2.5 and the Tycho-2 Spectral Type Catalog (Wright et al. 2003). Beyond this, we adopted Schmidt-Kaler's (1982) Zero Age Main Sequence (ZAMS) for the Main Sequence (MS) fitting and $A_{\rm V} =3.1 \times E(B-V)$ for computing the total interstellar extinction and colour-excess. The spectral class-colour/absolute magnitude calibration was based on Straizys (1992). The references for adopted extinction and distances are provided in the COCD for each cluster.

	Figure 2: Comparison of distance d and colour-excess E(B-V) derived by Loktin et al. (2001) and Loktin (2004) from 3-colour photometry with values determined on the basis of spectral classification.
Open with DEXTER

In order to check the reliability of determined distances and extinction, we applied our procedure to a few clusters selected arbitrarily from LGM and distributed over a wide range of distances. The results are compared with the original LGM data and given in Fig. 2. We may conclude that distances and colour excesses derived by the spectral method coincide well with the published LGM data based on 3-colour photometry.

3.2 Angular sizes

Spatial parameters of the clusters were determined from profiles of stellar density derived from star counts. For each cluster, the counts were carried out in concentric circles around the cluster centre, which was determined as the point of maximum surface density of the cluster members (see Sect. 2).

As a rule, differences between the determined coordinates of cluster centres and those listed in DLAM are small. Only for 21 clusters do they exceed $0~\hbox{$.\!\!^\circ$ }3$ either due to errors in the cluster coordinates in old catalogs (particularly in the Collinder list) or due to problematic definition of centres of large open clusters like Mel 20 ($\alpha$ Per), Mel 111 (Coma Berenicis), poor stellar groups (some objects from Platais et al. 1998), and cluster-like associations as, for example, Sco OB4.

A general model describing the structural parameters of clusters was developed by King (1962) and successfully applied to globular clusters. Since a typical open cluster has a relatively small number of members and the spatial distribution of members is not regular, it is difficult to find a formal model which would, on one hand, describe structural details of a given cluster and, on the other, would be valid in general. As a compromise, we assumed a centrally symmetric distribution of the cluster members and considered only two structural components, a core with a radius r₁, and a corona with a radius r₂. The core radius corresponds to a distance where the decrease of stellar surface density stops abruptly. The corona radius (i.e. the actual radius of a cluster) is defined as the distance from the cluster centre where the surface density of stars becomes equal to the average density of the surrounding field (see Fig. 1b). For each cluster, core and corona radii were checked by visual inspection, and the constraints set by the corresponding VPD and CMD were always taken into account. Even though this approach is somehow subjective and time-consuming, it can be applied to poorer clusters and thereby considerably expand the sample studied.

For each cluster, the surface density was computed in concentric strips of $0~\hbox{$.\!\!^\circ$ }05$ up to 10 degrees from the cluster centre and for three different stellar samples: (i) all stars; (ii) cluster members with probabilities $P \ge 1$%; and (iii) cluster members with probabilities $P \ge 61$%. Nevertheless, the distribution of $1\sigma$ members ($P \ge 61$%) was the decisive factor for determining the cluster radius. On average, a core radius is about 2.5 times smaller than a corona radius. Figure 1b illustrates the degree of variation of F(r) with radial distance in the case of open cluster Stock 2.

For 515 clusters in common, Fig. 3 compares the angular radii of cluster coronas determined in this paper and the corresponding data compiled by DLAM. Independent of distance, the published radii are on average lower (by about a factor of 1.5 for "large'' clusters and by a factor of 2.5 for "small'' clusters). There can be several reasons for this bias. Often, cluster sizes are empirically derived from star counts or even from visual inspection of cluster areas without previous membership determination. The area of concentration of the brightest stars usually defines the cluster size, and fainter cluster members are lost in the rich fore - or background. In this case, one should instead speak of a "core radius'' than of a "cluster radius''. Sometimes, a cluster size is estimated from dedicated observations in small sky fields. The investigations are limited by the detector used in the study (e.g., photographic plate or CCD frame) enough to give rather underestimated cluster radii. Finally, adopting the cluster sizes from the Lund catalogue, one should not forget that Lyngå (1987) himself aimed to publish the sizes of the cluster cores.

Our determinations of cluster sizes are not restricted by limited sky areas, and the information on membership is used. Nevertheless, the sizes derived are based on counts of relatively bright stars ( $V \lesssim 12$), and thus they can be influenced by the mass segregation effect (see e.g. Raboud & Mermilliod 1998; or Kharchenko et al. 2003). Therefore our data should be considered as lower limits of the actual cluster sizes.

	Figure 3: Comparison of derived angular radii with data compiled by Dias et al. (2004). The solid line is the locus of equal radii. Crosses mark clusters with distances $d \ge 1$ kpc, whereas the dots are nearer clusters. The dashed line separates "large'' and "small'' clusters.
Open with DEXTER

  
4 Cluster kinematic parameters

Figure 4: Comparison of cluster proper motions derived in this study from ASCC-2.5 data with results of a) Robichon et al. (1999); b) Baumgardt et al. (2000); and c) Dias et al. (2001, 2002). Bars show rms-errors. The straight lines are the loci of equal proper motion components. The upper lines and left axes refer to clusters included in our sample and in the comparison samples. The lower lines and right axes are for 35 clusters common to all samples.

Open with DEXTER

4.1 Proper motions

For each cluster, the mean components $\overline{\mu}_{x,y}$ of common proper motion were computed from proper motions of the most probable members ($P \ge 61$%). The number of such stars varies from 3 to 178 with an average of 18 stars per cluster. For 91% of the clusters, the proper-motion components $\overline{\mu}_{x,y}$ are determined with standard errors of less than $\pm 1$ mas/yr (for 42% - less than $\pm$0.5 mas/yr). The proper motions are derived directly in the Hipparcos system, for 301 clusters - for the first time (see also Kharchenko et al. 2003).

Figure 4 compares the cluster proper motions derived in this study with the corresponding findings of Robichon et al. (1999), Baumgardt et al. (2000), and Dias et al. (2001, 2002), which are all based on the data from the Hipparcos and Tycho-2 catalogues. Although different techniques of member selection were applied, the mean proper motions of the common clusters agree quite well. Even clusters with small proper motions coincide within a few mas/yr. This is remarkable because in these cases cluster members are difficult to separate from field stars.

4.2 Radial velocities

It is well known that our knowledge of radial velocities (RV) of open clusters is much poorer than of proper motions. According to DLAM, RVs have been published for only 240 of about 1700 known clusters. Moreover, these data are very inhomogeneous: sometimes the RV of a cluster is taken from measurements of only one star; sometimes the rms errors reach 30 km s^-1; and some authors did not give any information on accuracy at all. Fortunately, the situation will be considerably improved when the RAVE programme (Steinmetz 2003) will have been completed in the next years, including some dedicated observations in the Galactic plane.

Radial velocities for only 196 clusters of our sample are listed in DLAM, the Lund Catalogue, and Ruprecht et al. (1981). In order to update the RVs of these clusters, we cross-identified (Kharchenko et al. 2004a) the ASCC-2.5 with the General Catalogue of Radial Velocities (Barbier-Brossat & Figon 2000). On the basis of our membership determination, we were able to revise the RVs for 159 clusters. Additionally, for 94 clusters RVs have been determined for the first time. So, we can now publish RVs of 290 open clusters of our sample.

In Fig. 5 the revised RVs for 160 clusters are compared with the published data collected in DLAM. The mean difference between the "old'' and "new'' RVs of these clusters is $\overline{RV_ {\rm ref} - RV}= 0.36 \pm 0.88$ km s^-1.

	Figure 5: Comparison of cluster radial velocities derived in this study with data published in Lyngå (1987), Ruprecht et al. (1981), and DLAM. If the mean RV of a cluster is determined from more than two members, error bars are shown.
Open with DEXTER

  
5 Cluster ages

In the preliminary version of the COCD (Kharchenko et al. 2003), cluster ages were taken from the literature. Since different authors used different methods of estimating age, these ages represent an inhomogeneous set of data in contrast with the homogeneity of other cluster parameters in the catalogue of Kharchenko et al. (2003). In the current version of the COCD we implement our own isochrone-based procedure of age determination, which provides a uniform scale of ages for all clusters.

The contents of the COCD catalogue put several constraints on the theoretical models that can be used for the age estimates. Since a wide span of cluster ages is expected, the CMDs of many clusters in our sample should present the evolved portions of the upper Main Sequence. On the other hand, the Pre-MS branches, observed at relatively faint absolute magnitudes should be seen in the COCD cluster diagrams only in rare cases of young and nearby clusters. Taking the above into account, we have been concentrating on the Post-MS isochrones. Due to the rather bright limiting magnitude of the ASCC-2.5, our sample is biased towards local clusters with typical distances less than 1.5 kpc from the Sun. This means that for our sample, no considerable metallicity trends due to the radial gradient of [Fe/H] in the Galactic disk are expected, and we can limit ourselves to considering only solar metallicity isochrones.

5.1 Input data

There are three recently published data sets of Post-MS isochrones suitable for our purposes: Lejeune & Schaerer (2001), called the Geneva grid hereafter; Girardi et al. (2002) or the Padova grid; and Yi et al. (2001), Kim et al. (2002), and Yi et al. (2003), known as the Y² grid. Although the isochrones of the Geneva grid provide the widest range of ages, they do not show agreement with present-day observed MSs of open clusters, whereas the two others do (see Grocholski & Sarajedini 2003). The Y²-isochrones agree well with cluster MSs, and integrate both Pre- and Post-MS stages. Unfortunately, they are limited to small and moderate mass models ( $m \la 5 ~m_\odot$), and cannot be applied to the youngest clusters with massive and bright stars. Thus we are left with the Padova Post-MS isochrones, which show good agreement with cluster MSs for $M_V \la 7$ mag and are finely spaced over the age scale ( $\Delta\log t = 0.05$). The major inconvenience of the Padova grid is the relatively high lower limit of the age scale ( $\log t =6.6$), which restricts a proper dating of young clusters. We implement the Padova overshooting isochrone grid with the following parameters: $m=0.15...66~ m_\odot, Z=0.019, Y=0.273$.

The Pre-MS isochrones were derived with the Grenoble Pre-MS tracks Internet-server of Siess et al. (2000). We computed a grid of the Pre-MS isochrones which covers the same scale of ages as the Post-MS grid. Their agreement with the Padova models is acceptable and suits our purposes, so in this paper we use models with overshooting for a mass range $0.1...7.0~ m_\odot$ and Z=0.02, Y=0.28.

Since the turn-on points are observed only in a few clusters of our sample, we do not use the Pre-MS isochrones for cluster age determination but show them in the cluster CMDs to illustrate the degree of conformity to the nuclear and thermal age scales. Furthermore, the Pre-MS grid was already used in this study for photometric selection of cluster members (see Paper I, for details).

Figure 6: Illustration of the adopted algorithm for determination of cluster ages. In Panel  a), the thin curves are isochrones for three different ages ( $\log t = 8.30$; 8.60; 9.00). The dotted curve is the locus of unresolved binaries with mass ratio q=1 for the age $\log t = 8.60$. The thick dashed curve is the adopted ZAMS where the dots mark the empirical ZAMS of Schmidt-Kaler (1982). The thick curves to the right of the ZAMS are the blue (s=0.15) and red (i.e., TAMS, s=1.00) borders of the evolved MS. Horizontal lines indicate the EMS spread at MV = 0; 1; 2. Age variations along these lines are shown in Panel  b) as functions of the evolutionary status s, while the blue edge of the evolved MS is marked by the vertical line at s=0.15. Photometric errors in (B-V) of 0.01 mag are converted to corresponding errors in s and shown as bars. Stars marked by letters B,C,D,E are hypothetical cluster members, where B is the brightest MS star. X marks the isochrone base point defined as the cross-section of the corresponding isochrone with the blue edge of the evolved MS. $\Delta M_V$ is the magnitude range adopted for the cluster age evaluation. While stars Band C will be included by the algorithm in the age determination, stars Dand E will be rejected.

Open with DEXTER

5.2 The method

We applied a simple logic for evaluating cluster ages: the average age of individual MS cluster members. In contrast to the standard method of isochrone fitting, this approach yields objective estimates not only of the cluster age but also of its uncertainty (the standard deviation). Moreover, the algorithm is coded easily and can be used in the data processing pipeline. The age evaluation procedure can be run in parallel with the iterations of membership determination. This is an important feature because one is confronted with hundreds of clusters in a wide range of ages.

The individual ages of stars are derived from their locations in the CMD with respect to the isochrone grid (see Fig. 6). Only the most probable kinematic members are considered. Likewise, in order to avoid additional uncertainties that could be introduced by age estimates of red giants (e.g., due to the treatment of convection, mass loss, or insecure conversion to the observed passbands), we restrict the age evaluation to MS stars. Thus, we choose a red border defined by the Termination Age Main Sequence (TAMS) which is shown in Fig. 6a as the thick curve farthest to the right. On the other hand, a relatively slow evolution close to the ZAMS leads to high density of the isochrones in this region of the CMD and, consequently, to a low accuracy of the interpolation. This forces us to use only an evolutionary advanced region of the MS where the isochrone crowding effect is much weaker. This "blue'' border is shown as the curve to the right of the ZAMS and is defined below. We call the region of the cluster MS between the red and blue borders the Evolved Main Sequence (EMS).

In order to define the blue border of the EMS, we introduce parameter s as a measure of the evolutionary advancement of a given star, called hereafter the evolutionary status of the star. For a star with absolute magnitude M_V and colour index (B-V)₀, the parameter s is defined as

$$s=\frac{(B-V)_0-(B-V)_{\rm ZAMS}}{(B-V)_{\rm TAMS}-(B-V)_{\rm ZAMS}},$$

where $(B-V)_{\rm ZAMS}$ and $(B-V)_{\rm TAMS}$ are the colour indices of stars of the same magnitude M_V on the ZAMS and TAMS, respectively. Since the ZAMS is not explicitly present in the Padova grid, we adopt the youngest isochrone of $\log t =6.6$ to represent the ZAMS. At M_V > -3 this isochrone coincides well with the empirical ZAMS of Schmidt-Kaler (1982).

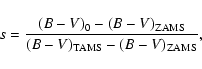
Table 1: Distribution of clusters according to the number of members (N_t) used for age determination. Typically, the more stars used, the more reliable the age determination. Cases i to iii are explained in the text.

In Fig. 6b we show age profiles of MS stars for three different absolute magnitudes. The profiles have been constructed by spline interpolations along the isochrones of different ages. As one can see, at small s (near the ZAMS) the profiles steepen considerably, making the age uncertainties due to typical photometric errors unacceptably large. Analysis of the MS band over its full length ( M_V =-8...+5) has shown that for a relatively safe age determination one should consider stars with s > 0.15. For these stars, the ages are determined from age profiles that correspond to their absolute magnitude M_V and evolutionary status s.

In order to define a range of absolute magnitudes $\Delta M_V$ where the age evaluation seems to be reasonable for a given cluster, we estimate the age of the brightest member among the evolved MS cluster stars and consider the corresponding isochrone. Then the bright limit of $\Delta M_V$ is the absolute magnitude of this member, and the faint limit is defined as the cross-point between the corresponding isochrone and the blue edge of the evolved MS. If the brightest member falls just in the TAMS, then the full spread of the evolved MS is available for the age calculation. On the other hand, if the brightest member is located near the blue edge (i.e., $\Delta M_V \approx 0$), no other stars are included in the cluster age determination. The distribution of clusters over the number of the most probable kinematic members used for the computing of cluster ages is given in Table 1.

In Table 1, there are three special cases marked by i, ii, or iii where the applied procedure of age determination does not work. The first two groups include young clusters whereas the third one consists mainly of old clusters. For a remote young cluster, the ASCC-2.5 contains only the top of the cluster MS that is generally badly populated due to IMF depletion in the domain of massive stars. For these clusters the Padova grid could not be used for our purpose, because for stars with $M_V \la -3$ mag, the computed strip of the evolved MS becomes artificially narrow. On the other hand, different effects like variable extinction, stellar binarity, rotation, etc. increase the observed spread of stars around the MS. Therefore, even small photometric effects could lead to a situation where no members of remote young clusters would be present in the narrowed EMS area. In total, 53 of the young clusters do not fulfill the criteria set by the procedure. As a compromise, we considered the brightest proper motion members approaching the EMS-area either from the blue (Group i in Table 1) or from the red (ii) direction and treated them in the procedure of age determination as if they were located at the EMS borders; usually a shift of less than 0.05 mag parallel to the (B-V)₀ axis is considered acceptable. This attribution means that the cluster ages can be overestimated for Group i or underestimated for Group ii. Wherever it is possible, we prefer the red-edge ages as less affected by random errors.

For 14 old clusters of the third group (iii) we found that their turn-off points are fainter than the limiting magnitude of the ASCC-2.5. Since only sub-giants or red giants in these clusters are present in the ASCC-2.5, we are not able to determine their age, so we accept, instead, the published values. For 11 other clusters, the turn-off points are still seen at the faint ASCC-2.5 limit, but due to large photometric errors at these magnitudes, the observed CMDs are very shallow. Therefore, ages were estimated manually by isochrone fitting. Both cases fall into Group (iii). Remarks on these special cases and decisions made in estimating cluster ages are given in the notes file added to the COCD. In order to illustrate the conformance of the derived ages with the structures of observed CMDs, the corresponding isochrones are shown in the CMDs of the Cluster Diagram Atlas.

In total, the ages were determined for 506 out of 520 clusters of our sample, and for 196 of them age estimates are given for the first time.

5.3 Accuracy of the results and comparison with another scale of cluster ages

Although the proposed method of individual age determination is sufficiently flexible and can be applied to poorly populated and sparse CMDs, there are several sources of uncertainty which could considerably affect the results. We can divide them into random errors and biases. Random errors create scattering in a cluster CMD and stem from random photometric errors, variable extinction, stellar spots, etc. Some biases like stellar rotation or unresolved multiplicity have strong random parts such as the orientation of rotation axes or the actual distribution of the component masses. They produce a quasi-random scattering of stars in the CMDs. The biases due to the adopted cluster distance and average reddening systematically affect the age estimates of one particular cluster, but they act more or less randomly if we consider a large sample of clusters. Finally, there are purely systematic effects that influence the age estimates of all clusters in the same way, e.g. uncertainties of the model grid which arise basically from the underlying physics or from neglecting particular evolutionary phases.

The uncertainty of a random or quasi-random impact on the cluster age determination can be estimated from the age-absolute magnitude relation (AMR) at the red edge of the EMS. Since the general shape of the AMR is similar at the red and blue edges, one could, in theory, consider the blue AMR edge, too. But due to technical reasons like insufficient accuracy of published input data and slow evolution near the ZAMS, the red edge of the AMR suits our purposes better. From rms errors in absolute magnitude $\sigma_{M_V}$, age uncertainty $\sigma_{\log t}$ can be evaluated as $\sigma^2_{\log t} = \gamma^2~\sigma^2_{M_V}$. Here $\gamma$ is the AMR slope $\gamma = {\rm d}\log t/{\rm d}M_V$. For the Padova isochrones, this slope varies from 0.1 to 0.4 within the complete MS range (M_V=-8,+4 mag). In further estimates we use an averaged slope of $\gamma_{\rm MS}=0.26\pm0.10$.

Let us first estimate the impact of uncertainties in cluster distances onto the derived cluster ages. The effects we consider include uncertainties in distance modulus and reddening. Generally, the clusters of our sample are located within 1.5 kpc from the Sun, i.e. at galactocentric distances where no substantial radial metallicity gradient has been detected (see e.g. Andrievsky et al. 2002). Thus, we can adopt the solar abundance of heavy elements in clusters of our sample and neglect metallicity corrections. A spread of cluster metallicity could only arise from a Galactic disk inhomogeneity that, according to Vereshchagin & Piskunov (1992), is about $\Delta{\rm [Fe/H]}\approx 0.1$, or $\sigma_{M_V} \approx 0.1$ mag if converted to absolute magnitudes. Furthermore, a typical accuracy of about 0.2 mag is expected for a cluster distance modulus (Subramaniam & Sagar 1999), and a reddening uncertainty of a few hundredths of a magnitude is derived from the LGM data. Then, the total rms error due to uncertainties in metallicity, interstellar extinction, and distance modulus does not exceed 0.3 mag. The corresponding age error is $\sigma_{\log t} \approx 0.08$.

The unresolved multiplicity of MS stars is another effect that may influence age determination. For close unresolved binaries (UBs) an offset of up to $\Delta M_V= 0.75$ mag exists compared to single stars. At first glance, the displacement produced by an unresolved component introduces systematic errors in the cluster age determination because it always shifts the UB up and to the right in the CMD. For the adopted technique of averaging individual ages it could be regarded as a random effect, though with no strong bias component. Indeed, in the vicinity of the MS turn-off/turn-on points, the loci of single stars and UBs of the same age do cross. This produces a symmetry in the UBs spread around the isochrone of a single star (see Fig. 6a). In the plot we compare two isochrones corresponding to populations of single stars and UBs in a cluster with an age of $\log t= 8.6$. To show the effect at its largest amplitude we use the extreme case of components of equal mass. The resulting symmetry of the UB locus with respect to the crossing-point (B) in Fig. 6a is evident. One can see that treating unresolved binaries as single stars produces ages both lower than the cluster age (those residing above point B) and higher than the true cluster age (below point B). Since in our approach we consider only the range of evolved stars (those brighter than M_V(X)), the mentioned symmetry is not violated by fainter unevolved UBs. Thus, no systematic age bias is expected from the unresolved binaries effect in our dating technique. On the contrary, for isochrone-based dating, this effect contains a potential danger: ages are underestimated when evolved bright binaries are treated as single stars. Since $\Delta M_V= 0.75$ is the maximum magnitude spread produced by UBs in the vicinity of the single-star turn-off point, we estimate that this effect introduces $\sigma_{\log t} < 0.19$to the average cluster age.

We do not consider the impact of mass loss on the age determination since this effect is implicitly taken into account by the isochrones involved. Although stellar rotation can change the observed absolute magnitude of the MS stars, the effect is less important than the one introduced by unresolved multiples. According to Maeder & Peyntremann (1970), for critically rotating stars (near the break-up velocity) with masses of $1.4{-}5~ m_\odot$, the offset in brightness is less than $\pm$0.6 mag (i.e. $\sigma_{\log t} \le 0.16$). This effect decreases rapidly when rotation slows down, while at a rotation velocity of 0.8 of the critical value, the offset is $\vert\Delta M_V\vert \la 0.2$ ( $\sigma_{\log t} \le 0.05$). Due to the random orientation of the aspect angle it has a random character.

Also, uncertainties in age calibration due to the hooks of the isochrones near the red border of the EMS are small, since the time of overall contraction after the hydrogen core exhaustion is relatively short. According to the simulations that take this evolutionary phase into account, $\log t$ of an individual star within the hook area changes by less than 0.02.

We conclude that the accuracy of age determination for clusters in our sample is about $\sigma_{\log t} = 0.20 {-} 0.25$ and compare results with uniform data on cluster ages recently published by LGM. The cluster ages in LGM are derived via the method of isochrone fitting and have the same theoretical basis (i.e. the Padova grid). The authors make use of photoelectric $\it UBV$observations without explicit selection of cluster members. In total, the LGM and our samples have 255 clusters in common, with 52 of them in Groups (i) and (ii) (cf. Table 1). Since both methods use the same isochrone grid, the ages of a single cluster differ only due to the algorithms applied and the selected observations.

The results of the comparison are presented in Fig. 7. As both coordinates are subject to rms errors, a simple linear regression analysis is inappropriate. A least square bisector solution as proposed by Isobe et al. (1990) should be adopted instead. For all clusters in common, this solution of the equation

$$\log t = c_0 + c_1\cdot\log t_{\rm LGM}, %$$

yields $(c_0,c_1)=(-0.48\pm0.18,1.07\pm 0.02)$. It is shown in Fig. 7 as a solid line.

Figure 7: Comparison of the derived cluster ages with data published in LGM. Dots indicate clusters where only one star (Nt=1) is used for the age determination, whereas crosses and filled circles are for clusters with Nt=2and Nt>2, respectively. The circle sizes are scaled by the number of stars used for the age determination of a given cluster (cf. Table 1). For clusters with Nt>2, the bars show rms-errors of the averaged ages derived in this paper. For clusters with Nt=2, the bars indicate the scatter and are shown without hats. Triangles are the clusters of group (i), whereas the upside-down triangles mark the group (ii). The dashed line is the locus of equal ages. The solid line shows a regression solution obtained for the complete sample.

Open with DEXTER

The mean age difference turns out to be $\overline{\Delta\log t}=-0.06\pm0.02$, which is small compared to the standard deviation of $\sigma_{\Delta\log t}=0.32$. According to Fig. 7, a relatively large spread is caused by 27 outstanding clusters above the regression line and 4 clusters below this line. Checking these clusters in detail, we found that only for a few very distant clusters the large deviations can be explained by low accuracy of the cluster CMDs near the limiting magnitude of the ASCC-2.5. For the majority, the different stellar content (i.e. adopted members) between LGM and this paper is the decisive factor. In the case of clusters above the regression line, bright stars in the cluster areas are considered by LGM as cluster members, but according to their kinematics we found that they are non-members. Therefore, we may assume underestimation of the true ages for these clusters by LGM rather than overestimation by us. In the case of the clusters below the regression line, the effect is reversed; bright stars within the central cluster area were rejected by LGM as non-members, although they fulfill all selection criteria we adopt for members.

Excluding these 31 clusters from consideration, we obtain for the mean age difference and its standard deviation $\overline{\Delta\log t}=0.01\pm0.01$and $\sigma_{\Delta\log t}=0.20$, respectively. We may conclude that the applied technique allows us to derive age estimates with an accuracy comparable to the accuracy of the classical method of isochrone fitting. According to the discussion above, the small but significant systematic bias (c₁=1.07) can be explained by slight underestimation of the LGM isochronic ages of older ( $\log t > 8.3$) clusters due to the UB effect. On the other hand, since the lower limit of the Padova isochrones is set at $\log t =6.6$, this yields a bias by somewhat "compressing'' the left side of the above relation and might increase c₁, too.

  
6 Conclusions

Starting from a homogeneous sky-survey, we determined a number of astrophysical parameters of Galactic open clusters. This sky survey, i.e. the ASCC-2.5, allowed us to perform an unbiased rediscussion of cluster membership (Kharchenko et al. 2004b), a necessary requirement for characterisation of the clusters. The results of this paper are published in the form of an open cluster catalogue, that, for all of the 520 clusters investigated, contains: heliocentric distance, interstellar extinction along the line of sight, angular size, mean proper motion, radial velocity, and age.

For 200 clusters heliocentric distances have been newly determined via MS-fitting. We calibrated our results by a comparison with a subset of clusters in Loktin's (Loktin et al. 2001; Loktin 2004) sample, distributed over a wide range of distances.

For 301 clusters mean proper motions in the Hipparcos system have been derived for the first time, based on the individual proper motions of the most probable members. For the remaining clusters, proper motions are compared with the results of Robichon et al. (1999), Baumgardt et al. (2000), and Dias et al. (2001, 2002) and good agreement within a few mas/year has been found.

For 290 clusters in our sample, mean radial velocities could be determined based on identifications of our members in the catalogue of Barbier-Brossat & Figon (2000) or retrieved from the literature. For 94 clusters radial velocities are determined for the first time; for others our findings were compared with Lyngå (1987), Ruprecht et al. (1981), and DLAM, and good agreement was found. On the other hand, there are 230 clusters in our sample, for which not even a single radial velocity measurement of any member is available so far.

Considerable effort has been put into determining cluster ages. In the end, ages could be determined for 506 out of 520 clusters, of which 196 are first estimates. We compared our determinations with the work of Loktin et al. (2001) and Loktin (2004) and found good agreement. For 31 cases with large discrepancies between this paper and LGM, these can be explained by the difference in membership criteria between the two papers.

Angular sizes of the cluster cores and coronas have been newly determined. This is the area where the full-sky coverage of the ASCC-2.5 is very helpful. It frees size determination from selection effects such as limited field, star counts, or visual inspection of the sky without taking membership criteria into account, and others. Despite the relatively bright limiting magnitude of the sky survey we used (ASCC-2.5 with a completeness limit at V = 11.5 and a limiting magnitude at V = 14.0), we find that the angular sizes of the cluster coronas are systematically larger than in earlier determinations in the literature. If mass segregation in open clusters is an important issue (see e.g. de Grijs et al. 2002), our cluster corona determinations are probably only lower limits of the true sizes.

To improve this situation, a homogeneous sky survey with fainter limiting magnitude is needed. Although such surveys are available in infrared photometry (e.g. 2MASS), a survey is missing in the optical and ultraviolet regimes, just as it is missing for proper motions, and it certainly cannot be expected soon for radial velocities. More than a decade from now, the ESA project GAIA is supposed to provide a survey that will fulfill all the requirements stated above, but in the meantime, progress has to be made in the field of ground-based astronomy in order to derive a homogeneous, bias-free survey in multicolour photometry (SEGUE in the Galactic plane), in proper motions (beyond UCAC), and in radial velocities (RAVE).

Acknowledgements

This work was supported by DFG grant 436 RUS 113/757/0-1, RFBR grant 03-02-04028, and by the FCNTP "Astronomy''. We acknowledge use of the Simbad database and the VizieR Catalogue Service operated at the CDS, France, and WEBDA facility at the Observatory of Geneva, Switzerland. We thank the referee, J.-C. Mermilliod, whose comments helped us to improve the paper.

  
Appendix A: The Catalogue of open cluster data

Table A.1: Contents of the COCD main table.

The Catalogue of Open Cluster Data (COCD) exists only in machine readable form and can be retrieved from the CDS online archive. The catalogue consists of three files: format description (ReadMe), the main table with derived parameters and literature data, and a notes file. In order to inform the reader of the scope of data included in the catalogue, we describe the main table here. It contains data on 520 clusters and consists of 520 lines and 30 columns, which are described in Table A.1.

  
Appendix B: The open cluster diagrams atlas

Figure B.1: An example of the atlas: a plot for the open cluster Coma Berenicis.

The Atlas (OCDA) presents visual information about (i) data used to determine cluster parameters; (ii) the quality of member selection; and (iii) the accuracy of the derived parameters. The OCDA consists of 520 PostScript plots stored as gzipped files (i.e. one file per cluster), which will be available in electronic form only via the CDS. In order to get easy access to the catalogue data, the file name includes the sequential number of the corresponding cluster in COCD and the cluster name (Col. 2 in the main table). Each plot contains a header and five diagrams used in the reduction pipeline. An example is given in Fig. B.1 for the Coma Berenicis cluster.

In the header we provide the equatorial coordinates of the newly determined cluster center, the cluster number in the COCD and the most common designation of the cluster. The panels present spatial, kinematic, and evolutionary information. The upper row: the left panel is a sky map of the cluster neighbourhood constructed with stars from the ASCC-2.5 and the right panel is the colour-magnitude diagram. The bottom row: the left panel shows radial profiles of the projected density; the middle panel is the vector point diagram of proper motions; and the two right panels are "magnitude equation'' ( $\mu _{x,y}-V$ relation) diagrams.

The sky map: A blue cross marks the adopted cluster centre. Pluses are centres of all clusters located within the displayed area and taken from the literature, i.e. the large plus in blue is for the given cluster, while the smaller magenta ones (absent in the example) are for other clusters. The large circles are the borders of the cluster core (solid curve) and of the corona (dashed curve). The small circles are stars with size indicating (only in this panel) stellar magnitude. The bold circles are $1\sigma$ cluster members ( $P_{\rm c} \ge 61$%), i.e. black circles are the members in the core area, and red circles members in the corona. Stars located outside the corona are displayed in cyan.

The colour-magnitude diagram: In this and the following diagrams stars are marked as coloured dots. $1\sigma$-members are shown with error bars. Stars used for age determination are marked as bold magenta circles. Colours of the curves: magenta for the adopted Post-MS and Pre-MS isochrones, cyan for the borders of the Evolved Main Sequence and the "mean'' location of the Hertzsprung gap, and blue for the borders used in the photometric selection (see Paper I for details). Additionally, cluster parameters selected from the COCD are plotted where the rms errors are given in parentheses, with references to the published data in brackets. The symbol (#) in the line with the average age (log t) indicates the number of stars used for age determination.

The density profiles diagram: The curves show distributions of stars with angular distance from the cluster center. The green curve shows all stars in the cluster area, while the magenta and black curves are for $3\sigma$- and $1\sigma$-members, respectively. The adopted core and corona radii are shown by solid and dashed lines.

The vector point diagram shows the proper motion distribution of ASCC-2.5 stars in this sky area. Error bars are shown for the cluster members.

The magnitude equation diagrams show distribution of the proper motions versus magnitudes. They are useful as a proper motion check since proper motions of cluster members should not depend on their magnitudes. The horizontal lines correspond to the average proper motion of the cluster, and the bars indicate the rms errors of proper motions for the cluster members.

References

• Andrievsky, S. M., Bersier, D., Kovtyukh, V. V., et al. 2002, A&A, 384, 140 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Barbier-Brossat, M., & Figon, P. 2000, General catalogue of averaged stellar radial velocities for Galactic stars, A&AS, 142, 217 (GCRV, Cat. III/213) (In the text)
• Baumgardt, H., Dettbarn, C., & Wielen, R. 2000, A&AS, 146, 251 [EDP Sciences] [NASA ADS] (In the text)
• Becker, W., & Fenkart, R. 1971, A&AS, 4, 241 [NASA ADS] (In the text)
• Dias, W. S., Lépine, J. R. D., & Alessi, B. S. 2001, A&A, 376, 441 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dias, W. S., Lépine, J. R. D., & Alessi, B. S. 2002, A&A, 388, 168 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dias, W. S., Lépine, J. R. D., Alessi, B. S., & Moitinho, A. 2004, Open clusters and Galactic structure, Version 2.0, http://www.astro.iag.usp.br/~wilton (In the text)
• Girardi, L., Bertelli, G., Bressan, A., et al. 2002, A&A, 391, 195 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• de Grijs, R., Gilmore, G. F., Mackey, A. D., et al. 2002, MNRAS, 337, 597 [NASA ADS] [CrossRef]. (In the text)
• Grocholski, A. J., & Sarajedini, A. 2003, MNRAS, 345, 1015 [NASA ADS] [CrossRef] (In the text)
• Høg, E., Fabricius, C., Makarov, V. V., et al. 2000, The Tycho-2 Catalogue: Positions, proper motions and two-colour photometry of the 2.5 million brightest stars, Copenhagen, CD-ROM distribution (In the text)
• Isobe, T., Feigelson, E., Akritas, M. G., & Babu, G. B. 1990, ApJ, 364, 104 [NASA ADS] [CrossRef] (In the text)
• Janes, K. A., & Adler, D. 1982, ApJS, 49, 425 [NASA ADS] [CrossRef] (In the text)
• Kim, Y. C., Demarque, P., Yi, S. K., & Alexander, D. R. 2002, ApJS, 143, 499 [NASA ADS] [CrossRef] (In the text)
• Kharchenko, N. V. 2001, Kinematics and Physics of Celestial Bodies, 17, 409 (In the text)
• Kharchenko, N. V., Pakulyak, L. K., & Piskunov, A. E. 2003, Astron. Rep., 47, 263 [NASA ADS] [CrossRef] (In the text)
• Kharchenko, N. V., Piskunov, A. E., & Scholz, R.-D. 2004a, Astron. Nachr., 325, 439 [NASA ADS] [CrossRef] (In the text)
• Kharchenko, N. V., Piskunov, A. E., Röser, S., Schilbach, E., & Scholz, R.-D. 2004b, Astron. Nachr., 325, 743 [NASA ADS] (Paper I) (In the text)
• King, I. 1962, AJ, 67, 471 [NASA ADS] [CrossRef] (In the text)
• Loktin, A. V. 2004, private communication (In the text)
• Loktin, A. V., Gerasimenko, T. P., & Malysheva, L. K. 2001, Astron. Astrophys. Trans., 20, 607 (In the text)
• Lejeune, T., & Schaerer, D. 2001, A&A, 366, 538 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Lyngå, G. 1987, Catalogue of open clusters data, Fifth edition (Strasbourg: CDS, VII/92) (In the text)
• Maeder, A., & Peytremann, E. 1970, A&A, 7, 120 [NASA ADS] (In the text)
• Platais, I., Kozhurina-Platais, V., & van Leeuwen, F. 1998, AJ, 116, 2423 [NASA ADS] [CrossRef] (In the text)
• Raboud, D., & Mermilliod, J.-C. 1998, A&A, 333, 897 [NASA ADS] (In the text)
• Robichon, N., Arenou, F., Mermilliod, J.-C., & Turon, C. 1999, A&A, 345, 471 [NASA ADS] (In the text)
• Ruprecht, J., Balazs, B., & White, R. E. 1981, Catalogue of Star Clusters and Associations, Supplement 1, Associations, Akademiai Kiado (Budapest: Publ. House Hungarian Acad. Sciences) (In the text)
• Schmidt-Kaler, Th. 1982, in Landolt-Börnstein Numerical Data and Functional Relationships in Science and Technology, New Series, Group IV, ed. K. Schafer, & H. H. Voigt (Berlin-Heidelberg, New York: Springer-Verlag Press), 2, 15 (In the text)
• Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 358, 593 [NASA ADS] (In the text)
• Steinmetz, M. 2003, in GAIA Spectroscopy: Science and Technology, ASP Conf. Proc., 298, ed. U. Munari, 381 (In the text)
• Straizys, V. 1992, Multicolour stellar photometry (Tucson, Arizona: Pachart Publishing House) (In the text)
• Subramaniam, A., & Sagar, R. 1999, AJ, 117, 937 [NASA ADS] [CrossRef] (In the text)
• Tadross, A. L. 2001, New Astr., 6, 293 [NASA ADS] (In the text)
• Vereschagin, S. V., & Piskunov, A. E. 1992, in Chemical evolution of stars and the Milky Way galaxy, ed. A. G. Massevich (Moscow: Kosmoinform Publ.), 5 (In the text)
• Yi, S., Demarque, P., Kim, Y. C., et al. 2001, ApJS, 136, 417 [NASA ADS] [CrossRef] (In the text)
• Yi, S. K., Kim, Y. C., & Demarque, P. 2003, ApJS, 144, 259 [NASA ADS] [CrossRef] (In the text)
• de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] (In the text)
• Wright, C. O., Egan, M. P., Kraemer, K. E., & Price, S. D. 2003, AJ, 125, 359 [NASA ADS] [CrossRef] (In the text)