1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str.1, Postfach 1317, 85741 Garching, Germany
2 - Instituto de Astrofísica de Canarias, 38200 La Laguna, Tenerife, Spain
3 - Space Research Institute (IKI), Russian Academy of Sciences, Moscow, Russia

Abstract
We explore the imprint of the cosmological hydrogen recombination lines on the power spectrum of the cosmic microwave background (CMB). In particular, we focus on the three strongest lines for the Balmer, Paschen and Brackett series of hydrogen. We expect changes in the angular power spectrum due to these lines of about $0.3~\mu{\rm K}$ for the H $\alpha$ line, being maximum at small angular scales ( $\ell \approx 870$ ). The morphology of the signal is very rich. It leads to relatively narrow spectral features ( $\Delta \nu / \nu \sim 10^{-1}$ ), with several regions in the power spectrum showing a characteristic change of sign of the effect as we probe different redshifts or different multipoles by measuring the power spectrum at different frequencies. It also has a very peculiar dependence on the multipole scale, connected with the details of the transfer function at the epoch of scattering. In order to compute the optical depths for these transitions, we have numerically evolved the populations of the levels of the hydrogen atom during recombination, simultaneously treating the evolution of helium. For the hydrogen atom, we follow each angular momentum state separately, up to the level n=10. Foregrounds and other frequency dependent contaminants such as Rayleigh scattering may be a important limitation for these measurements, although the peculiar frequency and angular dependences of the effect that we are discussing might permit us to separate it. Detection of this signal using future narrow-band spectral observations can give information about the details of how the cosmic recombination proceeds, and how Silk damping operates during recombination.

Key words: cosmic microwave background - cosmology: theory - early Universe - atomic processes

Existing and planned experiments devoted to the measurements of Cosmic Microwave Background (CMB) angular fluctuations will reach an unprecedent high sensitivity of measurements. Planck, SPT, ACT and QUEST will achieve sensitivities several orders of magnitude higher than the amplitude of the acoustic peaks which were the dream of theorists in the seventies (Peebles & Yu 1970; Doroshkevich et al. 1978; Sunyaev & Zeldovich 1970), and are observed with good precision now by Boomerang, Maxima, DASI, VSA, CBI, and more recently with very high accuracy by WMAP (Bennett et al. 2003).

The experimental progress demonstrates that we are entering the era of "precision cosmology'', and many of the effects that were obvious for theoreticians but of small amplitude become now accessible to experimentalists.

One of such problems is the direct detection of the hydrogen or helium lines from the epoch of recombination of hydrogen in the Universe at redshift $z \sim 1000$ . In Russia, all the study of cosmological recombination grew up from the question of Vladimir Kurt: "where are the Ly- $\alpha$ line photons from recombination in the Universe?''. This question forced Zeldovich et al. (1968, hereafter ZKS68) to study the detailed physics of recombination, and to show that two-photon decay of 2s level of hydrogen is more important than the escape of redshifted Ly- $\alpha$ photons due to expansion of the Universe in determining the rate at which recombination occurs. It was shown that there are strong distortions of the CMB spectrum due to two-photon decay, but unfortunately these distortions are practically unobservable because they lie in the distant Wien region of the CMB spectrum. Peebles (1968, hereafter P68), and Seager et al. (1999,2000) came to the same conclusion. Dubrovich (1975) proposed to look for CMB spectral distortions due to transitions between higher levels (Balmer, Paschen and higher series), which should be broadened due to the delayed recombination, and many papers were devoted to the computation of these very small but extremely interesting effects (Grachev & Dubrovich 1991; dell'Antonio & Rybicki 1993; Dubrovich & Shakhvorostova 2004). Although several computations of the intensity of these lines gave contradictory results (see e.g. dell'Antonio & Rybicki 1993 and Dubrovich & Shakhvorostova 2004), it is obvious that the corresponding distortions of the CMB spectrum are extremely weak, and that $\Delta I/B_\nu$ does not exceeds the level of 10^-7, which is two orders of magnitude below the sensitivity of COBE-FIRAS experiment, but certainly will be the goal of future more precise experiments.

Another physical process with information about the epoch of recombination is Rayleigh scattering on neutral hydrogen and helium atoms (Yu et al. 2001). This process, due to the characteristic dependence of the scattering cross-section on wavelength ( $\sigma_{\rm R} \propto \nu^4$ ), has a very strong frequency dependence of the power spectrum, $C_\ell$ . Unfortunately, this frequency dependence is rather similar to the spectrum of dust emission from local dust and bright extragalactic star-forming galaxies, and the amplitude of the effect becomes important in frequencies where the dust emission is significant ( $\nu \ga 200$ GHz). This will make a rather difficult task to separate it from nearby and bright foreground dust contribution.

In this paper, we concentrate on the detection of hydrogen lines, and we propose a different method to detect the consequences of the overpopulated levels of hydrogen atom at the epoch of recombination. We propose to look for frequency dependent angular fluctuations of the CMB in different angular scales and at frequencies in the vicinity of the redshifted Balmer (and higher series) lines. Here, we estimate how the small optical depths connected with these transitions influences the angular distribution of the CMB, arising mainly due to Thomson scattering on free electrons. We show that one should expect changes in the angular power spectrum due to these lines of about 0.3 $\mu {\rm K}$ , being maximum at small angular scales ( $\ell \approx 870$ ). These numbers are at the level of the planned sensitivity of the Planck satellite but for large angular scales, and certainly should be achieved by future ground-based instruments looking for polarization of the CMB, and future space missions like CMBPol. It is important to mention that present day technology permits one to achieve sensitivities at least 50 times better than that of Planck (Church 2002). The maximum signal that we are discussing corresponds to the redshifted H $\alpha$ recombination line, which unfortunately is located in a frequency region where the contribution from dust emission is very important, and where the Rayleigh scattering is 100 times larger in $C_\ell$ (10 times in temperature).

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig1.ps}\end{figure}$

Figure 1: Distortion of the power spectrum due to coherent scattering in the H $\alpha$ line, as a function of the observing frequency today. The maximum distortion (in absolute value) is obtained at $\nu =452$ GHz for $\ell =873$ . We show that shifting the observing multipole in a region of $\Delta \ell = \pm 70$ around the maximum, we still have the signal within the 70% of the peak intensity.

Coherent scattering in the H $\alpha$ line produces a $\Delta T/T_0 \approx 10^{-7}$ signal in the angular distribution of the CMB, whereas spectral distortions in the same line are close to 10^-8-10^-7. Currently, experimentalists put their main effort in observing angular fluctuations. Therefore, the signal under discussion in this paper might be observed sooner or later.

This effect is small, but it leads to relatively narrow spectral features in the power spectrum ( $\Delta \nu / \nu \sim 10^{-1}$ ). In addition, there are several regions in the angular power spectrum at high multipoles where the sign of $\delta C_\ell$ (= $C_\ell^{\rm line} - C_\ell$ ) connected with this process depends on the wavelength, i.e. it changes from positive to negative when the frequency is shifted from 350 GHz to 450 GHz (Fig. 1). The effect also has a very peculiar dependence on $\ell$ at all frequencies (Fig. 2), and these peculiarities in frequency and angular scale dependence might permit future observers to separate coherent scattering on $\rm H\alpha$ during the epoch of recombination from foregrounds and even from the cosmic variance of the effect of Rayleigh scattering.

The discovery of these spectral features in the CMB angular distribution will permit us to measure directly the tail of the recombination process and its position with good precision, and may give additional information about cosmological parameters of the Universe and their evolution with time.

This may also give direct spectroscopic evidence of recombination. If Rayleigh scattering probes the existence of neutral hydrogen immediately after the peak of the visibility function, the profile of the Balmer lines features in the power spectrum gives us the possibility to check the dynamics of recombination when the electron density changes from $n_{\rm e}/n_{\rm H}\approx 1$ to 10^-2, and correspondingly, the optical depth in H $\alpha$ and the population of the second level are traced. The characteristic physical length producing fluctuations in H $\alpha$ in that epoch corresponds to smaller scales than those for Rayleigh scattering. It is also important that for the hydrogen lines, each observed frequency corresponds to a given redshift z, but the "picture'' from Rayleigh scattering is the same for all frequencies (there is only a change in amplitude). Thus, when the line is placed inside recombination, the shape of the angular power spectrum for these two effects differs strongly.

Computations of the $\delta C_\ell$ connected with recombinational lines are direct, because detailed estimates of the recombination process show (SSS99) that the assumption of ZKS68 about the Saha equilibrium of all levels above level two is valid with good precision. This gives us the possibility to find the optical depth in each line of interest, and include it as an additional opacity coefficient in the CMBFast code (Seljak & Zaldarriaga 1996), as it was done for the lines in the case of resonant scattering by Zaldarriaga & Loeb (2002) (lithium doublet), and Basu et al. (2004, hereafter BHMS04) for fine structure lines of neutral atoms and ions of carbon, nitrogen and oxygen. Let us mention here that the computations of the line intensities (i.e. spectral distortions of CMB) require the detailed calculation of tiny deviations from Saha equilibrium, which are connected to the process of recombination controlled by 2s-level decay. For our purposes, it is enough to use the equilibrium distribution because the generation of new angular fluctuations is connected with just re-distribution of radiation over angles, so it has no relation to the difference between excitation temperature and color temperature of radiation. Optical depths in all lines, including Balmer lines, is very small (e.g. $\tau \sim 5$ $\times$ 10^-5 for H $\alpha$ line at z=1000). But as it was shown by Hernández-Monteagudo & Sunyaev (2005, hereafter HMS05) and BHMS04, correlation effects with the existing radiation fluctuation field amplifies the effect in such a way that $\delta C_\ell$ s are effectively proportional to $\tau_\nu$ , instead of $\tau_\nu^2$ . It should be noted that the signal that we are discussing is smaller than the cosmic variance level, but as is explained by HMS05 and BHMS04, multi-frequency observations permit one to avoid the limit imposed by the cosmic variance associated with the intrinsic CMB fluctuations, and reveal signals below this threshold.

Finally, it is important to mention that these detections strongly rely on a accurate cross-calibration between different channels of a given experiment. However, there is a possibility to use the thermal SZ effect (Sunyaev & Zeldovich 1972) on clusters of galaxies and sum of blackbodies approach for such a calibration. Both methods are discussed by Chluba & Sunyaev (2004).

The outline of the paper is as follows. In Sect. 2, we review the basic equations which describe the cosmic recombination process, and we present a code that we have developed to compute the optical depths in the lines for the required transitions. In Sect. 3, we show how to derive the $\delta C_\ell$ quantities for a given line, and present our results for the considered transitions. Section 4 presents a discussion about the foreground contamination and the amplitude of the effect compared to Rayleigh scattering. Conclusions are given in Sect. 5.

2 Cosmological recombination process

In this section, we review the basic equations describing the process of cosmic recombination of hydrogen and helium, and we show how to use them to infer the optical depths for the recombination lines. Since the first computations by ZKS68 and P68, many refinements have been introduced (for a review, see SSS00). SSS00 has the most detailed calculations to date, including 300 levels for the hydrogen atom, 200 for HeI and 100 for HeII. When compared with the standard "effective three-level computation'', their calculation results in a roughly 10% change in the electron fraction at low redshift for most of the cosmological models, plus a delay in HeI recombination. All these results were incorporated in the RECFAST code (SSS99), which consists in a modification of the effective three-level model to reproduce the new values.

For this paper, we are interested in computing the optical depths associated with the hydrogen recombination lines of the Balmer, Paschen and Brackett series. We will not discuss here the helium lines (see Dubrovich & Stolyarov 1997, for a discussion on the spectrum of primordial HeI and HeII recombination lines). In order to obtain the optical depths, we need to know the populations for all levels in the hydrogen atom which contribute to the transitions we want to study. We will do this following two different approaches.

On the one hand (method I), we will follow SSS00 and we will evolve the level populations for a hydrogen atom with 10 levels, separating levels both by principal quantum number n and angular momentum l. In method II, we will adopt the ionisation fraction from RECFAST and compute, using the Saha equation relative to the continuum, the population of the excited levels (e.g. Liubarskii & Sunyaev 1983). This method is a valid approximation for those levels above the second one and for redshifts $z\ga900$ , but as we will see, this is indeed our range of interest because at lower redshifts the visibility function is very small.

2.1 Method I: Detailed follow-up of level population

The detailed formalism and the equations describing the evolution of the population of the levels of hydrogen and helium atoms with cosmic time is presented in SSS00. Here, we enumerate the assumptions of our work and the differences to that paper.

Values for the physical constants for hydrogen and helium were taken from SSS99 and SSS00. The values for the oscillator strengths and the corresponding Einstein coefficients for instantaneous emission were computed following Green et al. (1957). The value for the two photon decay transition $A_{{\rm 2s,1s}}$ is essential, given that this is the dominant mechanism driving the cosmological recombination. We adopt here the latest value, $8.22458~{\rm s}^{-1}$ , from Goldman (1989).

The photoionization/recombination rates were computed in two different ways. The first one was by using the photoionization cross-sections from Storey & Hummer (1991); Hummer (1994). The second one uses the analytical expressions from Burgess (1958), which are valid for small values of the energy of the ejected electron. In both cases, radiative recombination rates included spontaneous and induced transitions. Our final results were obtained using the second method, which is computationally faster than the first one. Nevertheless, we checked that both methods give similar results for the populations of the levels.

Once the populations of all levels are obtained at all redshifts, the optical depth associated with any permitted transition $j \rightarrow i$ connecting the levels i=(n,l) and j=(m,l') (with m>n) can be computed using the Sobolev formula as

In Fig. 3 we show our result for the electron density evolution ( $x_{\rm e} = n_{\rm e}/n_{\rm H}$ ) as a function of redshift, compared with the standard calculation using RECFAST. These results are consistent with those obtained by SSS00 when they use n=10 levels, but it should be noted that in our calculation we do a detailed follow-up of the population of the different angular momentum states. When more levels are included in the computation, SSS00 show that the residual electron density at low redshifts becomes smaller, and for $n\ga 50$ it converges as the atom becomes complete in terms of energy levels. However, for the purposes of this paper, it is enough to consider a 10-level hydrogen atom to achieve good precision in the region of interest.

$\begin{figure} \par\includegraphics[width=8cm,clip]{fig3.eps}\end{figure}$

Figure 3: Multilevel hydrogen recombination as computed in this paper (using 10 levels for quantum number n, and following independently all the states of angular momentum), compared with the standard "effective three level'' computation from RECFAST. It is shown $x_{\rm e}$ (= $n_{\rm e}/n_{\rm H}$ ) as a function of redshift in the vicinity of the epoch of cosmic recombination for the cosmological model with parameters $\Omega _{\rm b}=0.044$ , $\Omega _{{\rm tot}}=1$ and h=0.71 (Bennett et al. 2003).

2.2 Method II: Saha equation from the continuum

As suggested by ZKS68, and confirmed with the computations of SSS00, the approximation of equilibrium of all levels above the second one yields very good results, and deviations greater than 10% are only found at redshifts $z \la 800$ . Thus, we can derive (to a good approximation) the population of the level in two steps. We first use the standard RECFAST computation, and derive the evolution of the electron density. From here, and using the Saha equation relative to the continuum, we can derive the population of all levels above the second one, and can compute all the optical depths for Balmer lines and higher series. It should be noted that this approximation fails for redshifts below $z\sim900$ because most of the atoms have recombined and the transition rates are not enough to keep equilibrium between high levels.

Table 1: List of the strongest hydrogen recombination lines studied in this paper. We present the three strongest lines for the first three series of hydrogen atom between excited states: Balmer ( $m\rightarrow 2$ ), Paschen ( $m\rightarrow 3$ ) and Brackett ( $m\rightarrow 4$ ). For each transition $m\rightarrow n$ , we show its name, the rest frame wavelength, and the oscillator strength (these values have been taken from Green et al. 1957). For illustration, we also present in the fifth column the redshifted frequency observed today if emission took place at z=1000. The last column shows the optical depth in the line at that redshift (z=1000), as computed using our code.
Transition m $\lambda_{nm}$ ( $\AA$ ) f_nm $\nu_0(z=1000)$ (GHz) $\tau _{nm}(z=1000)$

Balmer lines (n=2)

H $\alpha$ 3 6562.8 0.6407 456.3 4.53 $\times$ 10^-5

H $\beta$ 4 4861.3 0.1193 616.1 6.14 $\times$ 10^-6

H $\gamma$ 5 4340.5 0.0447 690.0 2.09 $\times$ 10^-6

Paschen lines (n=3)

P $\alpha$ 4 18751.0 0.8421 159.7 1.17 $\times$ 10^-7

P $\beta$ 5 12818.1 0.1506 233.6 1.47 $\times$ 10^-8

P $\gamma$ 6 10938.1 0.0558 273.8 4.75 $\times$ 10^-9

Brackett lines (n=4)

B $\alpha$ 5 40512.0 1.0377 73.9 2.57 $\times$ 10^-8

B $\beta$ 6 26252.0 0.1793 114.1 3.42 $\times$ 10^-9

B $\gamma$ 7 21655.0 0.0655 138.3 1.09 $\times$ 10^-9

**Table 1:** List of the strongest hydrogen recombination lines studied in this paper. We present the three strongest lines for the first three series of hydrogen atom between excited states: Balmer ( $m\rightarrow 2$ ), Paschen ( $m\rightarrow 3$ ) and Brackett ( $m\rightarrow 4$ ). For each transition $m\rightarrow n$ , we show its name, the rest frame wavelength, and the oscillator strength (these values have been taken from Green et al. 1957). For illustration, we also present in the fifth column the redshifted frequency observed today if emission took place at z=1000. The last column shows the optical depth in the line at that redshift (z=1000), as computed using our code.
Transition	m	$\lambda_{nm}$ ( $\AA$ )	f_nm	$\nu_0(z=1000)$ (GHz)	$\tau _{nm}(z=1000)$
Balmer lines (n=2)
H $\alpha$	3	6562.8	0.6407	456.3	4.53 $\times$ 10^-5
H $\beta$	4	4861.3	0.1193	616.1	6.14 $\times$ 10^-6
H $\gamma$	5	4340.5	0.0447	690.0	2.09 $\times$ 10^-6
Paschen lines (n=3)
P $\alpha$	4	18751.0	0.8421	159.7	1.17 $\times$ 10^-7
P $\beta$	5	12818.1	0.1506	233.6	1.47 $\times$ 10^-8
P $\gamma$	6	10938.1	0.0558	273.8	4.75 $\times$ 10^-9
Brackett lines (n=4)
B $\alpha$	5	40512.0	1.0377	73.9	2.57 $\times$ 10^-8
B $\beta$	6	26252.0	0.1793	114.1	3.42 $\times$ 10^-9
B $\gamma$	7	21655.0	0.0655	138.3	1.09 $\times$ 10^-9

2.3 Optical depth in the hydrogen recombination lines

Although we have computed many more transitions, in this paper we shall concentrate on those lines whose expected contribution is largest. Thus, we investigate here the three first transitions (labelled as $m\rightarrow n$ ) for the Balmer (n=2), Paschen (n=3) and Brackett (n=4) series. Table 1 presents the wavelengths and oscillator strengths for these lines. For illustration, we show in the last two columns the redshifted frequency and the optical depth in the line evaluated at redshift z=1000, and for a cosmological model with parameter values taken from Bennett et al. (2003), i.e. $\Omega _{{\rm tot}}=1$ , $\Omega _{\rm b}=0.044$ and reduced Hubble constant h=0.71. Throughout this paper we have used these values, unless otherwise stated.

$\begin{figure} \par\includegraphics[width=7.8cm,clip]{fig4.eps}\end{figure}$

Figure 4: Optical depths for several lines considered in this paper, as a function of redshift z. All values were computed using method I. For the H $\alpha$ line, it is also shown the computation using the Saha approximation (method II), to show that with this method, deviations with respect to the detailed calculation (method I) only appear when the Universe is practically transparent, which corresponds to the high frequency wing of the line and where the expected effect is not important.

Figure 4 shows the optical depth in the lines ( $\tau _{nm}$ ) derived with our method I, and for this cosmological model. Using the method II, we obtain these same values for the optical depths, but only for redshifts above $z\approx900$ . To illustrate this point, we also display in Fig. 4 the optical depth for the H $\alpha$ line using the method II (dotted line). Method II reproduces the non-equilibrium computation above $z\approx900$ , but fails below this point, showing a divergent behaviour. The reason for this was pointed out above. At these redshifts, the radiation field has not enough photons to maintain the equilibrium of the second level with the continuum. The photoionization rates become smaller than the photorecombination rates, and the Saha equilibrium between the second level and the continuum is no longer valid (e.g. ZKS68). Moreover, the populations of $\rm 2s$ and $\rm 2p$ levels start to show strong departures from their equilibrium ratio. Given that the cosmological recombination is proceeding much more slowly than expected from a Saha recombination, method II (which uses the Saha equation relative to a continuum level which has been computed using the effective three level calculation) predicts very high values for the population of the second level in this redshift range. This is the reason for the divergent behaviour at $z\la 900$ of the H $\alpha$ optical depth computed with method II. Although we have used the exact (non-equilibrium) computation for all the results presented in this paper, we wanted to show that using a very simple approximation (method II) it is possible to correctly estimate the values for the optical depths in the range of interest (as we show below, the peak of the effect we are investigating occurs at $z\sim 1010$ ).

In Fig. 4, we finally note that for Balmer transitions, the shape of the optical depth as a function of frequency is similar for all lines. This can be easily understood because the population of the second level is much larger than the population of higher levels, and thus the optical depth is directly proportional to this population ( $n_{{\rm 2s}}+n_{{\rm 2p}}$ ) for all Balmer lines.

Figure 5 shows the optical depth in the H $\alpha$ line, together with the Thomson visibility function (Sunyaev & Zeldovich 1970), $\mathcal{V}_{\rm T}(\eta) = ({\rm d}\tau_{\rm T}/{\rm d}\eta) \exp(-\tau_{\rm T})$ , and the function $\exp(-\tau_{\rm T})$ . Here, $\tau_{\rm T}$ is the Thomson optical depth and $\eta$ is the conformal time. As we can see from this figure, the maximum optical depth for this transition is reached beyond the peak of the visibility function, around $z\approx1400$ , but there the Thomson optical depth is very large. This is why the maximum contribution to the effect we are discussing comes from lower redshifts ( $z \sim 1000$ ). As we show in the next section, the generation of new anisotropies is conected to the term $\tau_{{\rm H}\alpha} \exp(-\tau_{\rm T})$ , also shown in Fig. 5.

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{fig5.eps}\end{figure}$

Figure 5: Dependence of the optical depth with the redshift for the H $\alpha$ line. For comparison, we also show the Thomson visibility function ( $\mathcal{V}_{\rm T}(\eta) = ({\rm d}\tau_{\rm T}/{\rm d}\eta) \exp(-\tau_{\rm T})$ ), the function $\exp(-\tau_{\rm T})$ , and the function $\tau_{{\rm H}\alpha} \exp(-\tau_{\rm T})$ . To display all of them on the same scale, they were rescaled by the indicated factors.

3 Imprint of hydrogen recombination lines on the CMB

The imprint of line transitions on the CMB spectrum has been examined by Zaldarriaga & Loeb (2002) for the case of lithium recombination, and for other ions and atoms in BHMS04. We extend these works here and we consider the case in which the coherent scattering occurs inside recombination.

The drag force induced on CMB photons by the scattering in the hydrogen recombination lines was already discussed by Loeb (2001). They showed that due to the low population of the excited levels, the characteristic time over which the peculiar velocity of the gas is damped due to the drag force on the hydrogen atoms is much longer than the Hubble time at that epoch. We repeated this computation and found that it is at least five orders of magnitude longer. Thus the drag force can be safely neglected when computing the effect of coherent scattering in these lines on the power spectrum of the CMB, as it was done in Zaldarriaga & Loeb (2002) and BHMS04.

3.1 Widths of the recombination lines

Before hydrogen is significantly recombined in the Universe, the optical depth for electron scattering is very high, so every scattering leads to a broadening of the line. For z=1000, the thermal (Doppler) width of the lines is close to $(\Delta \nu/\nu)_{{\rm th}} \approx 4$ $\times$ 10^-5. Subsequent electron scattering of these photons might increase this width up to $(\Delta \nu/\nu)_{\rm e} \approx 2$ $\times$ 10^-3. The characteristic width of recombination in redshift space, $(\delta z/z)_{\rm rec}$ , is much bigger than this electron broadening (from Fig. 5, the visibility function has a width of $\delta z \approx 80$ , so $(\delta z/z)_{\rm rec} \approx 1/14$ ). On the other hand, the optical depths in the lines under discussion are also changing slowly. The redshift interval $(\delta z/z)_{{\rm H}\alpha}$ in which $\tau_{{\rm H}\alpha}$ changes significantly (i.e. $\delta \tau_{{\rm H}\alpha}/\tau_{{\rm H}\alpha} \approx 1$ ) is about 0.07 for z=1000. Thus, we expect that both Doppler and electron broadening of the lines will not change our effect significantly. We have checked this point by repeating the computations of this paper for different widths for the lines.

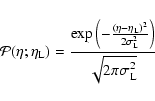
One important consequence that can be determined from here is that every frequency observed today corresponds to a given redshift z. With electron scattering, we are averaging all the effects well before the peak of the visibility function, and we are losing information about the redshift in which a given part of the signal was produced. However, the study of these lines will permit us to check the velocities and optical depths at any stage of recombination. In order to do this, it will be necessary to optimise the observing frequencies of the detectors, and to have observing bandwidths narrower than the widths of the features (we will see below that typical widths are $\Delta \nu/\nu \approx 0.1$ ). Unfortunately, present day and planned experiments (like Planck) have widths of the channels broader than this, and even broader than the width of recombination, so these effects are averaged inside the observing bandwidths. But in principle, future ground based experiments or experiments like CMBPol might be adapted to the width and frequency dependence of the features that we are discussing, and it could be possible to trace using this tomography the overall behavior of recombination.

3.2 Coherent scattering in hydrogen lines during recombination

In this subsection, we present the equations and the method of computation of the effect of coherent scattering in hydrogen lines. To perform the computations for this paper, we have used the code from BHMS04, which was a modification of CMBFAST including the presence of a resonant line at a given redshift. We will follow here their notation.

In the conformal Newtonian gauge, the Boltzmann equation for the evolution of the k-mode of the photon temperature fluctuation can be formally integrated to give (Seljak & Zaldarriaga 1996)

Using this modification inside the CMBFAST code, and neglecting the drag force induced by this process on the CMB photons, it is possible to compute the effect of the coherent scattering on the power spectrum. The important point for us is that, as shown by HMS05, the effect of lines on the CMB spectrum is amplified due to correlation with the existing radiation field. The presence of coherent scattering in lines produces an angular redistribution of the CMB photons. For the lines considered in BHMS04, the net effect is generation of anisotropies at large scales due to Doppler motion of scattering atoms, and suppression of power at small scales. Summarizing, the amplification effect consists in that the change in the power spectrum ( $\delta C_\ell \equiv C_\ell^{{\rm line}} -C_\ell$ ) due to a given transition $m\rightarrow n$ is proportional to $\tau _{nm}$ (and not to $\tau_{nm}^2$ ) for small values of the optical depths. Thus, in the optically thin limit we have

Equation (5) can be used in our problem, in which the scattering line is embedded inside recombination, although there are some differences to the case in which the line is placed between recombination and us. As was shown in BHMS04, the generation and blurring terms tend to cancel each other at a multipole value $\ell \sim (\eta_0-\eta_{{\rm cs}})/(\eta_{{\rm cs}}-\eta_{{\rm rec}})$ , with $\eta_{{\rm cs}}$ , $\eta_{{\rm dec}}$ and $\eta_0$ the conformal times at the coherent scattering, at recombination and the present day, respectively. From this, one can expect that if coherent scattering takes place not far from recombination, both generation and blurring will cancel over a wider range of multipoles. We illustrate this in Fig. 6, where we show the dependence of the linear term ( $\mathcal{C}_1(\ell)$ ) for four different cases of a hypothetical line placed at redshifts z=850, 950, 1050 and 1150. Thus, in other words, the presence of this strong decrease in the power at angular scales $\ell \la 200$ is direct evidence that the line is located at the epoch of recombination in the Universe. Unfortunately, because of this decrease, the detection at large angular scales of this signal will be more difficult.

Only at redshifts lower than the redshift of recombination is the blurring term dominant at high multipoles: when the line is well within the peak of the Thomson visibility function, both blurring and generation terms cancel each other, at least to a level of a few percent. This is seen in Fig. 6, so for redshifts in the tail of the visibility function (z=850) the linear term is equal to $-2 C_\ell$ at high multipoles. But if we move to higher redshifts, this behavior disappears.

$\begin{figure} \par\includegraphics[width=7.4cm,clip]{fig6.ps}\end{figure}$

Figure 6: Linear term of the correction to the angular power spectrum originated from coherent scattering in a line located at the specified redshift. These curves have to be multiplied by the optical depth in the line to obtain the first order correction to $\delta C_\ell$ . Thick lines correspond to positive values, and thin lines to negative ones. For comparison, it is also shown the primary CMB power spectrum (dotted lines). Note that at high- $\ell$ , the correction is roughly $-2 C_\ell$ for the case z=850 or z=950, as we would expect for a line located between us and recombination. This property disappears when we go to higher redshifts, because in that case the line is located inside recombination where radiative viscosity and thermal conductivity are important. (See movie in the electronic version.)

For illustrational purposes, we discuss how the visibility function is modified when we consider coherent scattering in the hydrogen lines. In the optically thin limit, we can write to first order in the optical depth ( $\tau _{nm}$ ) that

$\displaystyle % \mathcal{V}\left(\eta ; \eta_{\rm L}\right)$	=	$\displaystyle \dot{\tau} {\rm e}^{\textstyle -\tau }$
	$\textstyle \approx$	$\displaystyle \left[1 - \tau_{nm} \mathcal{A}(\eta)\right] \mathcal{V}_{\rm T} ... ...\eta) {\rm e}^{\textstyle -\tau_{\rm T} } + \mathcal{O}\left(\tau_{nm}^2\right)$	(6)

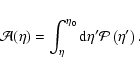
$\begin{figure} \par\includegraphics[width=7.8cm,clip]{fig7.eps}\end{figure}$

Figure 7: Correction to the visibility function in the presence of coherent scattering in the H $\alpha$ line. To first order in the optical depth of the line ( $\tau _{nm}$ ), there are two terms. One is associated with suppression (Eq. (7)), and the other one with the generation of new anisotropies (Eq. (8)). Both terms are plotted (dot-dashed and dashed lines, respectively) together with their sum (solid line), for the case of observing the H $\alpha$ line placed at z=1000. For comparison, we also show the Thomson visibility function (dotted line).

Table 2: Maximum signal (in absolute value) obtained for each of the lines within the considered cosmological model. It is shown the angular multipole, the redshift and the observed frequency (today) at which we have maximum effect. We also present the (full) widths $\Delta \ell$ and $\Delta \nu _0$ around the peak value, defined as the regions where the signal is greater than 70% of the maximum value. The last two columns show the amplitude of the effect in temperature ( $\mu {\rm K}$ ) and the relative value of the temperature to the primordial CMB power spectrum. All these maximum deviations are negative (i.e. the correction to the power spectrum $\delta C_\ell$ at those maxima is negative).
Line $\ell_{{\rm max}}$ $\Delta \ell$ $z_{{\rm max}}$ $\nu_0$ $\Delta \nu _0$ $\sqrt{ \ell (\ell+1)\vert\delta C_\ell\vert /2\pi}$ $\sqrt{ \vert\delta C_\ell\vert/C_\ell}$

[GHz] [GHz] [ $\mu {\rm K}$ ]

H $\alpha$ 873 140 1010 452 56 0.28 $5.8\times 10^{-3}$

H $\beta$ 873 140 1010 610 76 0.10 $2.1\times 10^{-3}$

H $\gamma$ 873 140 1010 683 85 0.06 $1.2\times 10^{-3}$

P $\alpha$ 888 121 1050 152 16 $1.6\times 10^{-2}$ $3.5\times 10^{-4}$

P $\beta$ 888 121 1050 223 24 $5.7\times 10^{-3}$ $1.2\times 10^{-4}$

P $\gamma$ 888 121 1050 261 28 $3.3\times 10^{-3}$ $7.1\times 10^{-5}$

B $\alpha$ 891 116 1060 70 7 $8.1\times 10^{-3}$ $1.8\times 10^{-4}$

B $\beta$ 891 116 1060 108 11 $2.9\times 10^{-3}$ $6.4\times 10^{-5}$

B $\gamma$ 891 116 1060 130 13 $1.7\times 10^{-3}$ $3.6\times 10^{-5}$

**Table 2:** Maximum signal (in absolute value) obtained for each of the lines within the considered cosmological model. It is shown the angular multipole, the redshift and the observed frequency (today) at which we have maximum effect. We also present the (full) widths $\Delta \ell$ and $\Delta \nu _0$ around the peak value, defined as the regions where the signal is greater than 70% of the maximum value. The last two columns show the amplitude of the effect in temperature ( $\mu {\rm K}$ ) and the relative value of the temperature to the primordial CMB power spectrum. All these maximum deviations are negative (i.e. the correction to the power spectrum $\delta C_\ell$ at those maxima is negative).
Line	$\ell_{{\rm max}}$	$\Delta \ell$	$z_{{\rm max}}$	$\nu_0$	$\Delta \nu _0$	$\sqrt{ \ell (\ell+1)\vert\delta C_\ell\vert /2\pi}$	$\sqrt{ \vert\delta C_\ell\vert/C_\ell}$
				[GHz]	[GHz]	[ $\mu {\rm K}$ ]
H $\alpha$	873	140	1010	452	56	0.28	$5.8\times 10^{-3}$
H $\beta$	873	140	1010	610	76	0.10	$2.1\times 10^{-3}$
H $\gamma$	873	140	1010	683	85	0.06	$1.2\times 10^{-3}$
P $\alpha$	888	121	1050	152	16	$1.6\times 10^{-2}$	$3.5\times 10^{-4}$
P $\beta$	888	121	1050	223	24	$5.7\times 10^{-3}$	$1.2\times 10^{-4}$
P $\gamma$	888	121	1050	261	28	$3.3\times 10^{-3}$	$7.1\times 10^{-5}$
B $\alpha$	891	116	1060	70	7	$8.1\times 10^{-3}$	$1.8\times 10^{-4}$
B $\beta$	891	116	1060	108	11	$2.9\times 10^{-3}$	$6.4\times 10^{-5}$
B $\gamma$	891	116	1060	130	13	$1.7\times 10^{-3}$	$3.6\times 10^{-5}$

$\begin{figure} \par\includegraphics[width=7.5cm,clip]{fig8.ps}\end{figure}$

Figure 8: Correction to the power spectrum due to coherent scattering in the H $\alpha$ line. We plot three curves for three different redshifts, namely z=900, 1150 (which correspond to 507 GHz and 397 GHz, respectively), and also z=1010 (452 GHz), which is the redshift (frequency) at which we have the maximum amplitude for signal, at multipole $\ell =873$ . Note how the z=900 case mimics the shape of the power spectrum at high multipoles, but with negative sign, and how this behavior disappears as we go to higher redshifts. Observing at different frequencies with sufficiently narrow spectral bands, we can perform tomography of the recombination epoch using the H $\alpha$ line.

3.3 Results for the considered lines

Our main result for the nine transitions under discussion can be summarized in Table 2, where we present the angular scale and the redshift at which we obtain the maximum signal for each of the lines. From these values, we see that the best angular scale to look for this effect is placed in the region of the third acoustic peak, and that the maximum signal comes from redshifts $z\sim 1010{-}1060$ . These values lie close to the peak of the visibility function, but in the low-redshift tail. We also present the full widths of the regions around the maxima where the signal is within 70% of the peak value, both in multipole ( $\Delta \ell$ ) and frequency ( $\Delta \nu _0$ ). We note that $\Delta \nu_0/\nu_0$ is of the order of 10%, which is hundreds of times larger than the Doppler broadening of the lines. This will help in the detection of these features. We also show that the width of the feature in multipole space is of the order of 140, so a full sky coverage is not necessary to detect the signal.

$\begin{figure} \par\includegraphics[width=7.2cm,clip]{fig9.ps}\end{figure}$

Figure 9: Relative correction ( $\vert\delta C_\ell \vert / C_\ell$ ) to the power spectrum due to scattering in the H $\alpha$ line, as a function of angular scale ( $\ell$ ). Thick lines correspond to positive values whereas thin lines represent negative ones. The distortions are larger at small angular scales, approaching the asymptotics of $-2\tau _{{\rm H}\alpha }$ (dotted line) for redshifts before the peak of the visibility function. The region where this asymptotic behavior is valid changes with redshift, and for redshifts well inside the recombination, it disappears. This behavior could give us information about the process of dissipation of short wavelength adiabatic perturbations due to radiative viscosity and thermal conductivity during recombination.

The last two columns in Table 2 show the amplitude of the signals at these maxima, both in temperature and the fractional change in temperature with respect to the intrinsic CMB power spectrum. Although the values for $\sqrt{ \vert\delta C_\ell\vert/C_\ell}$ are small, the present day sensitivity for the detection of angular fluctuations is better than that for spectral measurements, so in principle these features should be easier to detect than the distortions of the spectrum. We now investigate in more detail the angular and frequency dependences of this effect. We will concentrate here on the H $\alpha$ line, which gives the strongest signal. Predictions for the other transitions can be derived in a similar way.

Figure 8 shows the angular dependence of the effect, for the case of H $\alpha$ line, and for redshift values z=900, 1010 and 1150, which correspond to (redshifted) present day frequencies of 507, 452 and 397 GHz, respectively. Given the small values of the optical depth, the linear term gives the dominant contribution to the effect, so the shape of the plot is similar to Fig. 6, but the amplitude is modulated by the optical depth for the transition at every redshift. As shown in Table 2, the maximum signal is obtained at redshift z=1010. Prior to this redshift, the shape of the $\delta C_\ell$ mimics that of the primordial $C_\ell$ at high multipoles, because the suppression term dominates here (and hence the $\delta C_\ell$ are negative). When the line is placed at higher redshifts, well inside the recombination, the cancellation of the generation and blurring terms at high multipoles produces a number of regions where the $\delta C_\ell$ quantities have different signs. The exact position of the zeros strongly depends on the particular cosmological model, and as pointed above, it could be used to investigate in detail the shape of the transfer function at all redshifts.

In Fig. 9 we present the same redshift slices as in Fig. 6, but now showing $\vert\delta C_\ell \vert / C_\ell$ for the H $\alpha$ transition. The relative value of the distortion of the power spectrum is of the order of 10^-5-10^-4 in band power ( $\sim$ 10^-2 in temperature). It should be also noted that $\vert\delta C_\ell \vert / C_\ell$ is growing at large multipoles, and approaches the asymptotic value of $-2\tau _{{\rm H}\alpha }$ (shown here as a dotted line), although the multipole region where we reach this behavior depends on the considered redshift slice. When the line is placed at higher redshifts inside recombination, the asymptotic behavior is reached at higher multipoles in the damping tail region of the spectrum. Moreover, when the redshift is high enough, this asymptotic region disappears, and we find a complicated structure of positive/negative features due to the aforementioned cancellation. Thus, this method could give us information about the "Silk damping'' (Silk 1968), or processes of dissipation of short wavelength adiabatic perturbations due to radiative viscosity and thermal conductivity during the recombination.

$\begin{figure} \par\includegraphics[width=6.2cm,clip]{fig10a.eps}\vspace*{2mm} \... ...10b.eps}\vspace*{2mm} \includegraphics[width=6.2cm,clip]{fig10c.eps}\end{figure}$

Figure 10: Angular power spectrum arising from the Balmer recombination lines of hydrogen during cosmological recombination, as a function of the redshifted (observed) frequency. We plot the values at $\ell =20$ ( top panel), at $\ell =300$ ( middle panel), and at $\ell =800$ ( bottom panel). Thick lines corresponds to region where the $\delta C_\ell$ are positive, whereas thin lines correspond to negative values.

$\begin{figure} \par\includegraphics[width=8.1cm,clip]{fig11.ps}\end{figure}$

Figure 11: Same as Fig. 10, but only for the H $\alpha$ line which gives the maximum contribution. The vertical axis is now presented in a linear scale so we can explicitly see the change of sign. We plot values for five multipole scales, $\ell =100, 350, 750, 1200$ , and also $\ell =873$ , which is the multipole at which we have the maximum signal at $\nu =452$ GHz. (See movie in the electronic version.)

We now consider the frequency dependence of the effect. Figure 10 shows the relative change in the power spectrum due to the presence of the hydrogen recombination lines of Balmer series, as a function of the present day redshifted frequency. For each Balmer line, we show three different panels corresponding to three different angular scales ( $\ell = 20, 300$ and 800). As pointed above, the signal has a very peculiar frequency dependence, and for example at angular scales of $\ell =20$ and $\ell =800$ , we can see a characteristic change of sign of the effect, related to the positions of the cancellations of the generation and blurring terms. For the most intense line, H $\alpha$ , we show five more angular scales in Fig. 11, where we explicitly use a linear scale in the vertical axis to show the change of sign. The case of $\ell =873$ , which is giving the maximum signal (in absolute value) is shown as a solid line in that figure. The frequency dependence of the effect is unique and completely different from that of foregrounds (e.g. dust emission), and thus it might be used to separate these signals from other contaminants, as we will see below.

$\begin{figure} \par\includegraphics[height=5.2cm,width=7.6cm,clip]{fig12a.eps}\i... ...g12c.eps}\includegraphics[height=5.2cm,width=7.4cm,clip]{fig12d.eps}\end{figure}$

Figure 12: Angular power spectrum arising from the P $\alpha$ ( top row) and B $\alpha$ ( bottom row) hydrogen lines during recombination, as a function of the redshifted frequency ( left column) and the angular multipole ( right column). The solid lines in all panels refer to the cases in which the signal is maximum, according to Table 2.

The figures for the Paschen and Brackett lines are similar to those for Balmer lines. For illustration, in Fig. 12 we present the angular and frequency dependence for the B $\alpha$ and the P $\alpha$ lines. The amplitude of the signal for all the transitions considered in this paper is presented in Table 2.

Summarizing this subsection, we conclude that the best strategy to observe these features and perform this tomography would be to use bandwidths ( $\Delta \nu/\nu$ ) of the order of 10%, although bandwidths of 1% would trace this signal much better. These values are narrower than the width of the visibility function in the line, but still wide enough to keep enough photons. It is clear that the major contribution to the effect during the epoch of recombination is coming from high $\ell$ multipoles, and that the widths of the features is of the order of $\Delta \ell \sim 140$ , so this opens the possibility to use not only satellites but balloons or ground based experiments to look for this signal.

4 Contamination from other effects

In this section we discuss how the presence of foregrounds and the effect associated with Rayleigh scattering might affect the study of the lines. We shall adopt the middle-of-the-road model of Tegmark et al. (2000, hereafter T00), and we consider the contribution of five foreground sources, namely synchrotron radiation, free-free emission, dust emission, thermal SZ effect associated with filaments and superclusters of galaxies, and Rayleigh scattering. Point sources are not considered here, so we assume that resolved sources can be extracted from the maps, and that the contribution of unresolved sources can be lowered down to roughly the noise level of the observing instrument.

For the first three components, synchrotron, free-free and dust, the angular dependence of the power spectra was approximated by a power law. The frequency dependence for free-free and synchrotron was taken to be a power law, whereas a modified black-body spectrum was used for the dust component. For the SZ effect, the frequency dependence is well-known. Details of the modeling of the angular dependence can be found in T00. This neglects the contribution from the SZ effect generated by resolved clusters of galaxies, which we assume can be removed from the maps. For the Rayleigh scattering effect modeling, we follow BHMS04. As discussed above, the scattering cross-section of this process has a very strong dependence on the frequency,

$\begin{figure} \par\includegraphics[height=8.6cm,width=15cm,clip]{fig13.eps}\end{figure}$

Figure 13: a) Maximum contribution of the coherent scattering in the H $\alpha$ line to the angular CMB power spectrum, as seen by an hypothetical experiment measuring at 430 GHz and 130 GHz. The upper thick solid line gives the reference power spectrum. b) Contribution of foregrounds at these frequencies. All thin lines refer to the foreground model as quoted in T00: free-free emission is shown as dotted line; synchrotron emission as solid line; the thermal SZ effect produced in filaments as dot-dashed line and the thermal dust emission is shown by dashed lines. Rayleigh scattering contribution is shown as a thick long-dashed line, whereas the cosmic variance contribution associated to this effect is shown as a thin long-dashed line.

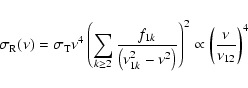
Figure 13 shows the expected level, prior to any removal, of the discussed foregrounds when looking for the maximum of the H $\alpha$ line. We considered here the case of an ideal experiment measuring at 430 GHz and 130 GHz, and with an instrumental bandwidth of $\Delta \nu/\nu=10^{-2}$ , which is comparable to the electron width of the line under discussion. It is clear that the main diffuse contamination will come from dust emission, but there are other two signals which will be larger than the H $\alpha$ contribution, namely the thermal SZ emission from filaments and the Rayleigh scattering. For the first one, the signal has a completely different frequency and angular behavior from the one we are considering, so these peculiarities could be used to separate both components.

For the case of Rayleigh scattering, the frequency behavior is also completely different from the case of resonant scattering. The angular dependence has some similarities in the high multipole range (damping tail) if we probe a line in the low redshift tail of recombination, because here both effects are proportional to $-2\tau C_\ell$ . However, as we probe higher redshifts, the behaviors become different also in this domain. In addition to this, there is another difference between the Rayleigh scattering and the coherent scattering in lines, which is related to the different evolution of the optical depth of each process during recombination, and which is superimposed on the previous effect. To illustrate it, we show in Fig. 14 the redshift dependence of the population of electrons, neutral hydrogen atoms and the population of hydrogen atoms in the level 2p, all computed using our code. These three variables ( $n_{\rm e}$ , $n_{{\rm HI}}$ and $n_{{\rm 2p}}$ ) are proportional to the differential optical depth $\dot{\tau}$ for the Thomson, Rayleigh and coherent scatterings, respectively. From this, it is clear that the redshift interval $\delta z/z$ in which the optical depth for Rayleigh scattering changes significantly is much larger than the corresponding one of the H $\alpha$ line scattering. Thus, instruments with broad bandwidths will dilute the signal from the lines, but add up the signal from Rayleigh scattering. This also could be used to separate them, because using a broad-band instrument we can isolate the Rayleigh scattering component, and then subtract it.

One interesting physical remark is that the evolution of the population of the 2p level in Fig. 14 is practically proportional to the electron density in this redshift range. This is what we expected, as we can immediately see from Eq. (2) ( $n_{{\rm 2p}} \propto n_{\rm e}^2 \exp \{ \chi_2/(k_{\rm B} T_{\rm e}) \}$ ) and from the evolution of the electron density ( $x_{\rm e} \propto (1/z) \exp \{ -\chi_2 / (k_{\rm B} T_{\rm e}) \}$ , see ZKS68).

$\begin{figure} \par\includegraphics[width=7.75cm,clip]{fig14.eps}\end{figure}$

Figure 14: Multilevel hydrogen recombination computed in this paper. It is presented the evolution of the relative fraction of electrons ( $x_{\rm e}$ ), neutral hydrogen atoms ( $x_{{\rm HI}}=n_{{\rm HI}}/n_{\rm H}$ ) and the population of the 2p level ( $x_{{\rm 2p}}=n_{{\rm 2p}}/n_{\rm H}$ ), as a function of the redshift z in the vicinity of the epoch of recombination (near the peak of the visibility function). The $x_{{\rm 2p}}$ values were multiplied by 10¹⁰ to display all lines in the same scale. The cosmological model adopted here is the same as in Fig. 3.

5 Discussion and conclusions

We have studied here the imprint of cosmological hydrogen recombination lines on the power spectrum of the CMB. To this end, we have developed a code that follows the evolution of the population of the levels of the hydrogen atom, separately treating those levels with different angular momentum. From here, we have obtained the optical depths associated with coherent scattering in these lines during the epoch of recombination, and these numbers were used to compute the effect on the angular power spectrum of the CMB.

These changes are small ( $0.1~\mu{\rm K}$ - $0.3~\mu{\rm K}$ ), but could be separated from other effects due to their peculiar frequency and angular dependence. Unfortunately, the line giving the maximum signal (the H $\alpha$ line) is placed in a frequency domain where the contribution from dust emission, the tSZ effect produced in filaments and Rayleigh scattering are important, so it will be necessary either to look for regions with low contamination (for the case of dust), or to use component separation techniques to reach this signal. The important point here is that the signal under discussion has a very characteristic behavior, both in frequency and in angular scale, which is completely different from any of the above contaminants.

One of the most important properties of this signal is that each observing frequency is associated with one redshift, so observations of these signals at different frequencies might give information about the amplitude of the fluctuations and corresponding peculiar velocities of matter at different redshifts during the epoch of recombination.

In this paper, the best-fit cosmological model to the WMAP 1st-year data (Bennett et al. 2003) was adopted to make predictions about the shape and the intensity of the signal we expect to measure. With the announced sensitivities of future experiments, these signals should be detected, and thus we could try to infer some information on the values of the cosmological parameters. The inferred constraints from the detection of these lines will be clearly independent of those obtained using the model-fitting to the power spectrum of the CMB. This additional information could be used to break some degeneracies in the parameters in two ways. First, as pointed out above, observations in narrow spectral bands of these signals can give us information about specific redshift slices during the process of recombination in the Universe. The shape and positions of the peaks and zeros of the signal presented in Figs. 8 and 9 reveal the details of the baryon transfer function at each considered epoch, so they could be used as an additional test of the cosmological model. For a given experiment with a given bandwidth, it is straight-forward to derive the prediction for $\delta C_\ell$ , so model fitting could be used here, in the same way as it is used today to extract parameters from the power spectrum. Secondly, the determination of the amplitude of this effect at a given redshift could also be used to set an independent constraint on $\Omega_{\rm b} h^2$ .

Using this signal, future narrow-band spectral observations might permit one to study all the details of the transfer function describing the evolution and viscous damping of perturbations in the epoch of recombination.

Contents

The imprint of cosmological hydrogen recombination lines on the power spectrum of the CMB

1 Introduction