A&A 438, 757-767 (2005)
DOI: 10.1051/0004-6361:20052890
G. Cresci 1,2 - R. I. Davies 2 - A. J. Baker 3,4 - M. D. Lehnert 2
1 - Dipartimento di Astronomia, Universitá di Firenze,
Largo E. Fermi 5, 50125 Firenze, Italy
2 - Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, 85741 Garching, Germany
3 - Jansky Fellow, National Radio Astronomy Observatory
4 - Department of Astronomy, University of Maryland, College
Park, MD 20742-2421, USA
Received 16 February 2005 / Accepted 20 April 2005
Abstract
In this paper we present the approach we have used to determine and
account for the anisoplanatic point spread function (PSF) in deep adaptive optics (AO) images
for the Survey of a Wide Area with NACO (SWAN) at the ESO VLT.
The survey comprises adaptive optics observations in the
![]() band totaling
band totaling ![]()
![]() ,
assembled from 42 discrete fields centered on different
bright stars suitable for AO guiding.
We develop a parametric model of the PSF variations across the field of view
in order to build an accurate model PSF for every galaxy detected in each of
the fields. We show that this approach is particularly convenient, as it uses only easily
available data and makes no uncertain assumptions about the stability of the
isoplanatic angle during any given night.
The model was tested using simulated galaxy profiles to check its performance
in terms of recovering the correct morphological parameters; we find that the
results are reliable up to
,
assembled from 42 discrete fields centered on different
bright stars suitable for AO guiding.
We develop a parametric model of the PSF variations across the field of view
in order to build an accurate model PSF for every galaxy detected in each of
the fields. We show that this approach is particularly convenient, as it uses only easily
available data and makes no uncertain assumptions about the stability of the
isoplanatic angle during any given night.
The model was tested using simulated galaxy profiles to check its performance
in terms of recovering the correct morphological parameters; we find that the
results are reliable up to
![]() (
(
![]() )
in a typical SWAN field.
Finally, the model obtained was used to derive the first results from five SWAN fields, and to obtain the AO morphology of 55 galaxies brighter than
)
in a typical SWAN field.
Finally, the model obtained was used to derive the first results from five SWAN fields, and to obtain the AO morphology of 55 galaxies brighter than
![]() .
These preliminary results demonstrate the unique power of
AO observations to derive the details of faint galaxy morphologies and to
study galaxy evolution.
.
These preliminary results demonstrate the unique power of
AO observations to derive the details of faint galaxy morphologies and to
study galaxy evolution.
Key words: instrumentation: adaptive optics - galaxies: fundamental parameters - galaxies: statistics - infrared galaxies
In recent years an increasing number of adaptive optics
(AO) systems have become available, which are capable of obtaining
near-infrared images at the diffraction limits of 8-m class
telescopes. The scientific potential of such instrumentation is evident, but careful
analysis of the resulting data is necessary to take account of the
effects introduced by the method and the limitations of wavefront sensing
and correction.
A key point in the detailed analysis of AO images is the determination
of the point spread function (PSF) across the whole field of view.
However, this task is made more difficult because the performance and
correction of the AO system are strongly anisoplanatic, and depend on
many parameters such as the brightness of the reference guide star and
the structure (height, size-scale, velocity) of the often quickly
changing atmospheric turbulence.
As a result, the PSF produced by an AO system can change rapidly in
both time and position on the frame.
For natural guide star (NGS) wavefront sensing, an extragalactic science
target will typically be offset from the guide star by
![]() 10
10
![]() -30
-30
![]() at best. As a result,
the on-axis PSF no longer provides a suitable
reference model for the off-axis PSF at the position
of the scientific target.
Until the advent of multi-conjugate adaptive optics systems on 8-m
class telescopes (e.g., Le Louarn et al. 2002) full
correction over a wide (1-2
at best. As a result,
the on-axis PSF no longer provides a suitable
reference model for the off-axis PSF at the position
of the scientific target.
Until the advent of multi-conjugate adaptive optics systems on 8-m
class telescopes (e.g., Le Louarn et al. 2002) full
correction over a wide (1-2![]() )
field will not be possible, and even
then there will still be some PSF variation across the field
(e.g., Vérinaud et al. 2003).
Therefore, a simple and generally applicable technique to model the
variations in the PSF across a given science field would be of benefit
to all wide-field adaptive optics data.
)
field will not be possible, and even
then there will still be some PSF variation across the field
(e.g., Vérinaud et al. 2003).
Therefore, a simple and generally applicable technique to model the
variations in the PSF across a given science field would be of benefit
to all wide-field adaptive optics data.
In this paper we present the approach we have used to account for the anisoplanatic PSF in deep adaptive optics images for the Survey of a Wide Area with NACO (SWAN). In the following section SWAN will be briefly described and motivated. In Sect. 3 some different proposed methods for PSF reconstruction will be analyzed, while in Sect. 4 our method will be explained and discussed. Computer simulations were used to validate the model, and their results are shown in Sect. 5. The first application of the model to five of the deep science fields will be presented in Sect. 6, and our conclusions follow in Sect. 7.
In order to make full use of the new generation of telescopes, it is
necessary to overcome the blurring effects of the atmosphere through
the use of AO systems. These can allow ground-based telescopes to operate
at or near the diffraction limit in the near infrared (![]()
![]() in K-band for an 8 m telescope), resulting in high
angular resolution and a low background in each pixel. In principle,
such capabilities should offer important benefits for studying how galaxies
form and evolve in the early universe. In practice, however, reaping the
expected rewards has proved difficult, due to the small number of
extragalactic sources known lying at distances
in K-band for an 8 m telescope), resulting in high
angular resolution and a low background in each pixel. In principle,
such capabilities should offer important benefits for studying how galaxies
form and evolve in the early universe. In practice, however, reaping the
expected rewards has proved difficult, due to the small number of
extragalactic sources known lying at distances
![]() from bright (
from bright (![]() ) stars suitable for AO guiding.
) stars suitable for AO guiding.
The prospects for AO cosmology will undoubtedly improve with the
widespread adoption of laser guide star (LGS) systems, since these impose less
stringent requirements on the brightness and nearness of stars used for
tip-tilt correction. In the mean time, to overcome the current shortage of
extragalactic AO targets for NGS wavefront sensing, we have undertaken a
program to identify and characterize faint field galaxies lying close to
bright, blue stars at high Galactic latitudes (see, e.g., Larkin et al.
1999; Davies et al. 2001). Our own 42 southern bright
star fields were initially imaged at seeing-limited resolution in ![]() with SOFI at the ESO New Technology Telescope (Baker et al. 2003), were followed up with optical imaging (Davies et al. 2005), and are now targets for VIMOS optical spectroscopy at the
ESO Very Large Telescope (VLT).
with SOFI at the ESO New Technology Telescope (Baker et al. 2003), were followed up with optical imaging (Davies et al. 2005), and are now targets for VIMOS optical spectroscopy at the
ESO Very Large Telescope (VLT).
SWAN is the AO-assisted payoff of these seeing-limited preliminaries.
Having already characterized large samples of objects in our bright star
fields, we targeted them with NACO on the VLT in order to exploit the present
generation of AO technology for galaxy evolution studies. NACO comprises the
NAOS Shack-Hartmann AO module (Rousset et al. 2003) mated with the
CONICA near-infrared camera (Lenzen et al. 1998). Our choice of NACO
observing mode was dictated by our desire to differentiate SWAN from previous
HST/NICMOS surveys. First, we chose to prioritize survey area over depth,
thereby improving SWAN's sensitivity to rare objects and its robustness against
cosmic variance. Second, we chose to image in ![]() ,
where NICMOS is
less sensitive than in J and H, thus making SWAN preferentially sensitive
to red objects. Use of NACO's
,
where NICMOS is
less sensitive than in J and H, thus making SWAN preferentially sensitive
to red objects. Use of NACO's
![]() pixel scale (to maximize field
of view) and the Strehl ratios of 30-60% typically achieved in
pixel scale (to maximize field
of view) and the Strehl ratios of 30-60% typically achieved in ![]() thus result in images that are undersampled. Each NACO
pointing provides only a usable
thus result in images that are undersampled. Each NACO
pointing provides only a usable ![]()
![]() of the full
of the full
![]()
![]()
![]() detector area, due to losses from dithering and the
central star (see, e.g., Fig. 1). Nevertheless, the anticipated
survey area that will result from assembling 42 such images will be - at
detector area, due to losses from dithering and the
central star (see, e.g., Fig. 1). Nevertheless, the anticipated
survey area that will result from assembling 42 such images will be - at
![]()
![]() - some six times larger than the NICMOS survey
of the HDF and flanking fields in J and H (Dickinson 1999;
Dickinson et al. 2000).
In the ecology of near-IR surveys, SWAN aims to occupy a niche combining the
high angular resolution of a space-based survey with the shallower depth and
wider area of a ground-based survey, thereby probing sources that are compact,
faint, red, and rare more effectively than any other survey to date.
First results from an initial analysis of nine SWAN AO fields are presented
in Baker et al. (2005), where NACO imaging is seen to
detect a population of compact galaxies that cannot be identified as such in
seeing-limited data.
- some six times larger than the NICMOS survey
of the HDF and flanking fields in J and H (Dickinson 1999;
Dickinson et al. 2000).
In the ecology of near-IR surveys, SWAN aims to occupy a niche combining the
high angular resolution of a space-based survey with the shallower depth and
wider area of a ground-based survey, thereby probing sources that are compact,
faint, red, and rare more effectively than any other survey to date.
First results from an initial analysis of nine SWAN AO fields are presented
in Baker et al. (2005), where NACO imaging is seen to
detect a population of compact galaxies that cannot be identified as such in
seeing-limited data.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2890fig1.eps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg33.gif) |
Figure 1:
Example of a SWAN field: SBSF 18. The circles are the extended
objects detected by SExtractor (SExtractor stellarity index
|
| Open with DEXTER | |
To extract full information about the morphology of the sources detected in
the SWAN images by taking into account the effects introduced by the PSF, it
is necessary to develop a reliable model of the off-axis PSF in each of the
fields. This task is not easy, however, as the AO PSF changes quickly in both
time and position on the frame; in our case it is made even more difficult by
the distinctive attributes of the SWAN observing strategy. First,
because of their high Galactic latitudes, relatively few point sources
are present in each of the fields, so that very few objects can be used as
references to constrain how the PSF varies off-axis. In addition, in order to
be background-limited so that the aim of the survey to detect faint galaxies
can be realized, the on-axis star is always saturated on the science frames,
meaning the on-axis PSF has to be obtained with separate unsaturated
exposures. Finally, NACO has only very rarely been used to image
stellar fields with the (undersampled)
![]() pixel scale and the
visible wavefront sensor; as a result, the VLT archive contains no suitable
stellar fields that can help characterize the properties of the PSF as far
off-axis as the SWAN images extend.
pixel scale and the
visible wavefront sensor; as a result, the VLT archive contains no suitable
stellar fields that can help characterize the properties of the PSF as far
off-axis as the SWAN images extend.
Given the above considerations, our data obviously pose several challenges for the recovery of intrinsic source parameters. Indeed, the same challenges will be faced by any extragalactic AO survey that relies on NGS or LGS wavefront sensing, and that efficiently builds up statistical samples of faint field galaxies by including a wide area around each bright star position. It is thus of general interest to devise a strategy to account for anisoplanaticism in deep, wide-field AO imaging.
There have been several methods proposed in the literature for estimating or calculating the off-axis PSF in an AO field. In this section we summarize these methods, and explain why they are not ideal for deep wide-field AO imaging with current instrumentation.
A theoretical analytical expression to model PSF variation and anisoplanaticism has been derived by Fusco et al. (2000), who validated their method on both simulated and experimental data, leading to a reduction in the error on the magnitude estimation in stellar fields from more than 30% to only 1%. They showed that the total optical transfer function (OTF) is simply the product of the on-axis OTF with an anisoplanatic OTF. The on-axis OTF can be readily obtained, for example from real-time data accumulated by the AO system or a measurement of the on-axis PSF. The anisoplanatic OTF, however, requires an independent measurement of how the turbulence in the atmosphere depends on altitude, as quantified by the atmospheric refractive index structure constant C2n. In their example case this was obtained by balloon probes, but similar measurements are not usually available.
In a similar vein, the possibility of using AO measurements together with simultaneous scintillation detection and ranging (SCIDAR) measurements to reconstruct the C2n profile and hence the off-axis PSF, was investigated by Weiß et al. (2002a,b). While such measurements were made and analyzed, the idea was never brought to fruition and no such system has been installed as a permanent facility instrument.
An alternative semi-empirical approach was proposed by
Steinbring et al. (2002), based on calibration images of
dense stellar fields to determine the change in PSF with field position.
Their results showed that this simple method reduces the error
in the prediction of the FWHM of the PSF at large distances off-axis
from 60% to only ![]()
![]() .
However, obtaining a suitable calibration field is not an easy task
as atmospheric conditions can change rapidly.
Steinbring et al. were able to complete the observations necessary to
construct their mosaic images in less than 10 min.
However, this approach is not practicable for even moderately
deep-field observations. Our SWAN observations, for example, typically
have integration time (without overheads) of 60 min.
The additional time needed to switch continually between science and
calibration fields would be prohibitive - even assuming that a suitable
stellar field with a guide star of comparable brightness can be found not
too far from the science field and also at a similar airmass.
Furthermore, the authors point out that variations of up to 50% in
the measured on-axis Strehl ratio ultimately limit the accuracy of the
results.
.
However, obtaining a suitable calibration field is not an easy task
as atmospheric conditions can change rapidly.
Steinbring et al. were able to complete the observations necessary to
construct their mosaic images in less than 10 min.
However, this approach is not practicable for even moderately
deep-field observations. Our SWAN observations, for example, typically
have integration time (without overheads) of 60 min.
The additional time needed to switch continually between science and
calibration fields would be prohibitive - even assuming that a suitable
stellar field with a guide star of comparable brightness can be found not
too far from the science field and also at a similar airmass.
Furthermore, the authors point out that variations of up to 50% in
the measured on-axis Strehl ratio ultimately limit the accuracy of the
results.
A third approach to the problem was investigated by Tristram & Prieto (2005). They parameterized the PSF using an elliptical Gaussian and a decaying elliptical exponential function. Starting with 11 parameters, they were able to eliminate all but four, which would need to be derived from stars in the science field. At high Galactic latitudes, the difficulty is that the number of point sources will be very limited in any science fields. To constrain 4 parameters reliably, the authors used 20 point sources, while our SWAN images always have fewer point sources per field - in a number of cases there are fewer than four - that are usually too faint for a detailed PSF fitting as is required here.
Given that it is not practical to apply any of these methods to SWAN or similar data, in the next section we propose an alternative method suited to cases where there are very few unresolved sources in the science field (and those which do exist are often rather faint), and where one does not necessarily need a highly precise estimate of the PSF.
To tackle the issue of anisoplanaticism in the SWAN data and to model an accurate PSF for every galaxy we detect we have developed a parametric model of the variations of the PSF across the field of view. This kind of approach is particularly convenient, as it uses only easily available data and makes no uncertain assumptions about the stability of the isoplanatic angle during any given night. Although the PSF reconstruction is not perfect, we will show that it is accurate enough for our purpose of measuring galaxy morphologies.
According to a theoretical analysis of the anisoplanatic effect in AO systems (e.g., Fusco et al. 2000; Voitsekhovich & Bara 1999), the off-axis PSF can be expressed as a convolution
between the on-axis PSF of the guide star with a spatially variable
kernel, i.e.,
| (1) |
Table 1: Observations of PSF calibration fields. The Strehl ratio is that measured on-axis in the short exposure frames taken before and after the deep science exposures.
We will make the extreme assumption that the model of the kernel
![]() is sufficiently well
constrained that the difference in the kernel from one science field to
the next is reduced to a single parameter, namely the isoplanatic
angle. This is the most convenient solution for fields with
sparse point source populations and, as we show, is able to reproduce a
reasonable approximation to the PSF at any given location in
the field of view using just the the on-axis PSF and a few reference point
sources in the science field as calibration.
is sufficiently well
constrained that the difference in the kernel from one science field to
the next is reduced to a single parameter, namely the isoplanatic
angle. This is the most convenient solution for fields with
sparse point source populations and, as we show, is able to reproduce a
reasonable approximation to the PSF at any given location in
the field of view using just the the on-axis PSF and a few reference point
sources in the science field as calibration.
For each SWAN field the on-axis PSF was monitored by taking short
unsaturated images of the bright star both before and after (and in
some cases half-way through) the deep science exposure.
These short exposure frames were taken in the ![]() band,
IB_2.21 (
band,
IB_2.21 (
![]() ,
FWHM = 0.060
,
FWHM = 0.060 ![]() m) or
NB_2.17 (
m) or
NB_2.17 (
![]() ,
FWHM = 0.023
,
FWHM = 0.023 ![]() m) filters.
The integration time varied in the range 0.5-2.0 s depending on
the filter used. In addition, observations of galactic star cluster fields were planned
periodically in order to build up a database of anisoplanatic PSFs.
At the time of writing only two such calibration fields had been
observed (see Table 1), but between them and the 7 SWAN fields
with the highest numbers of point sources (see end of this section),
included in Fig. 2, they still provide nearly 80 different point sources.
These fields will be used in the following analysis as a test bench to
derive a suitable parametric model for the off-axis PSF.
m) filters.
The integration time varied in the range 0.5-2.0 s depending on
the filter used. In addition, observations of galactic star cluster fields were planned
periodically in order to build up a database of anisoplanatic PSFs.
At the time of writing only two such calibration fields had been
observed (see Table 1), but between them and the 7 SWAN fields
with the highest numbers of point sources (see end of this section),
included in Fig. 2, they still provide nearly 80 different point sources.
These fields will be used in the following analysis as a test bench to
derive a suitable parametric model for the off-axis PSF.
The images were reduced using PC-IRAF version 2.11.3. The presence of the bright star in the center of a field less than 1' across made the data reduction a little more complex then usual, requiring two iterations of object masking and sky subtraction to avoid over-subtraction from very extended faint scattering around bright objects. For further details about data reduction see Cresci et al. (2005).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2890fig2.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg40.gif) |
Figure 2:
Isoplanatic angle scaling. The Strehl ratios of point
sources in the two calibration fields and 7 SWAN fields
(SBSF 14, SBSF 15, SBSF 18, SBSF 24, SBSF 27, SBSF 28, SBSF 41)
are plotted against their radial distance |
| Open with DEXTER | |
The isoplanatic angle of these fields was measured by considering - independently for each field -
the Strehl ratio of the detected stars as a function of radius from the guide star.
To these data we fit the theoretically expected function (e.g., Beckers
1993; Roddier 1999):
![\begin{figure}
\par\includegraphics[width=11.6cm,clip]{2890fig3.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg43.gif) |
Figure 3:
Upper panels: FWHM fits to the kernel. The radial
( left panel) and tangential ( right panel) FWHMs of the kernel to
be convolved with the on-axis PSF to reproduce the observed PSF for
the point sources in the calibration fields (diamonds)
and in the seven SWAN fields of Fig. 2 (pluses),
along with the best
fitting second order polynomial. Lower panels:
the total FWHMs of the observed point sources (radial at left,
tangential at right) as a function of radial distance |
| Open with DEXTER | |
Our model is motivated by the fact that the wavefront error in the
anisoplanatic kernel is dominated by the tip-tilt terms.
This is borne out in practice, since the major degradation of the PSF
observed in the calibration field images is an increasing radial elongation
towards the guide star as one moves further off-axis.
This suggests that, as a first approximation, one can represent the
anisoplanatic kernel
![]() with an
elliptical Gaussian elongated towards the guide star.
For each of the point sources in both of the calibration
fields, we therefore derived the best fitting radial and tangential FWHMs
of the elliptical Gaussian kernel to be convolved with the
on-axis PSF in order to reproduce the observed off-axis PSF (see
Fig. 3).
with an
elliptical Gaussian elongated towards the guide star.
For each of the point sources in both of the calibration
fields, we therefore derived the best fitting radial and tangential FWHMs
of the elliptical Gaussian kernel to be convolved with the
on-axis PSF in order to reproduce the observed off-axis PSF (see
Fig. 3).
The fit was obtained by minimizing the sum of the squared difference between the observed star and models with different kernel FWHMs, weighted by the flux in each pixel of the star frame (in order to optimize the fit in the PSF core) and including all pixels brighter than 1% of the star peak. As the noise is dominated by the background, which is constant over each star, a noise term was not included in the expression, because it would have added just a constant scaling factor.
The residuals of the fitting are shown in Fig. 4 as a
function of separation from the guide star. The residuals are defined as follows:
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{2890fig4.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg45.gif) |
Figure 4: Residuals from the PSF fitting with the elliptical kernel for the point sources in the two calibration fields, NGC 6752 (triangles) and NGC 6809 (squares), and in the 7 SWAN fields of Fig. 2 (stars). The residuals plotted are defined in Eq. (3). |
| Open with DEXTER | |
The FWHMs obtained along the radial and tangential directions were then fitted empirically as functions of the radial distance from the AO guide star. The function chosen was a second order polynomial, which was forced to a constant after reaching a maximum. Using higher order polynomials (or other analytical functions) just increased the number of free parameters without improving the fit. The final best fitting functions obtained are
for the radial axis:
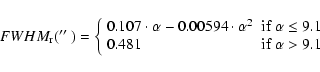 |
(4) |
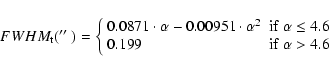 |
(5) |
The variation of the total FWHM - i.e., the kernel convolved with the on-axis PSF - along both radial and tangential directions for the point sources in the calibration field is shown in the lower panels of Fig. 3. It can be seen how the total FWHM has a behavior consistent with what is observed for other AO PSFs (e.g., Flicker & Rigaut 2002).
Using the derived parametric model for the kernel, it is now possible
to build the model PSF for any position in any of the
SWAN fields with only an estimate of the isoplanatic angle in the
respective field.
The isoplanatic angle is derived by fitting the Strehl ratio of the
few point sources detected in each science frame as a function of
radius with Eq. (2).
We have used SExtractor (Bertin & Arnouts 1996)
to identify the sources in our SWAN NACO images, and
as reference point sources for fitting the Strehl ratio, we use those
with SExtractor
stellarity index
![]() (see Fig. 1).
The derived isoplanatic angle is then used to rescale
the radial distance from the guide star and to build the model PSF.
(see Fig. 1).
The derived isoplanatic angle is then used to rescale
the radial distance from the guide star and to build the model PSF.
| |
Figure 5:
Comparison between the true and model PSFs for a point
source in NGC 6752.
The left panel shows the original star, the central panel the
model for the corresponding position on the detector, and the right panel the
residuals after subtracting the two. The star is located at
26.8
|
| Open with DEXTER | |
We additionally compared these results to those that could be obtained using PSFs generated by the PAOLA software (http://cfao.ucolick.org/software/paola.php), with an appropriate isoplanatic angle. PAOLA (Performance of Adaptive Optics for Large Apertures) is a set of functions and procedures written in IDL for calculating the performance of an AO system installed at the focus of an astronomical telescope. It relies on an analytic expression of the power spectrum of the corrected phase and its relation to the AO OTF. It therefore assumes that the AO system is "perfect'', failing to reproduce second order effects due to imperfections of the system. A set of PSFs were generated at different distances from the guide star, using in the model average parameters for the VLT and NACO. The radial distances of the PSFs were then rescaled to match the isoplanatic angle observed in the different fields. However, the match with the true PSFs was no better - and often worse - than that obtained with our parametric model, in particular worsening for increasing distances from the guide star.
![\begin{figure}
\par\mbox{\includegraphics[width=8cm,clip]{2890fig6.ps}\hspace{1.15cm}
\includegraphics[width=8cm,clip]{2890fig7.ps} }
\end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg50.gif) |
Figure 6:
The left panels show the rms of the magnitude, Sérsic index and effective radius obtained from the GALFIT fits of the simulated profiles with Sérsic index n = 1 as a function of the input magnitude. For each point, 100 galaxies with 10 different PSF were used (see text for details). The solid lines are the rms obtained using the model PSF as an input for GALFIT, while the dashed ones are obtained with the original NACO PSF. The right panels show the results obtained for simulated profiles with Sérsic index n = 4. In both cases it is clear that the parameters can be reliably recovered up to
|
| Open with DEXTER | |
The PSF model developed in the previous section was carefully tested
to see how well it performs in terms of recovering the correct morphological
parameters of simulated galaxy profiles.
The galaxy models were built by convolving a Sérsic (1968) profile,
![\begin{displaymath}%
I(R) = I(R_{\rm e}) \times {\rm e}^{\left( -b_n \times \left[\left(R/R_{\rm e}\right)^{1/n} - 1\right]\right)}
\end{displaymath}](/articles/aa/full/2005/29/aa2890-05/img51.gif) |
(6) |
We used Sérsic index n = 1 for disk-like galaxies and
n = 4 for elliptical-like galaxies.
For both types we ran several sets of simulations, each including 100 galaxies, at fixed magnitudes ranging from 17-22 mag in the ![]() band, with the same pixel scale used in the SWAN images.
The noise was set to the level expected for NACO integration time
of 60 min for all the galaxies, since this is the typical integration
time for a SWAN field. The inclination and position angle
were random for each simulated profile, while the distribution of
effective radii
band, with the same pixel scale used in the SWAN images.
The noise was set to the level expected for NACO integration time
of 60 min for all the galaxies, since this is the typical integration
time for a SWAN field. The inclination and position angle
were random for each simulated profile, while the distribution of
effective radii ![]() was chosen to roughly reproduce that observed in
the real data - i.e. 40% of the objects having
was chosen to roughly reproduce that observed in
the real data - i.e. 40% of the objects having
![]() ,
20% each with
,
20% each with
![]() and
and
![]() ,
and 10% each with
,
and 10% each with
![]() and
and
![]() .
Ten different PSFs extracted from point sources in the calibration or
SWAN fields were used for each set of 100 galaxies.
.
Ten different PSFs extracted from point sources in the calibration or
SWAN fields were used for each set of 100 galaxies.
To recover the galaxy morphological parameters, we used GALFIT (Peng et al. 2002), a widely used software package which fits an image of a galaxy and/or point source with one or more analytic functions. For our simulations we used GALFIT to fit a single Sérsic profile, leaving as free parameters the center of the galaxy, the Sérsic index n, the effective radius, the magnitude, the position angle and the axis ratio. The software needs an image of the PSF as input in order to fit the galaxy profile, both to deconvolve the original galaxy image and to convolve the derived model. For each simulated galaxy we ran GALFIT using both the true PSF from the NACO data - i.e., that which had been used to create the profile - and the corresponding model PSF, in order to compare the results.
The results of the simulations are shown in Fig. 6, where the uncertainties in the derived magnitude, Sérsic index, and effective radius are plotted as a function of magnitude for both disk-like and elliptical-like profiles. The results obtained using both the model PSF (solid lines) and true PSF (dashed lines) as input to GALFIT are shown, and it can be seen that these are in general very similar. Since using the true PSF is the best that can be done, we conclude that - in the application here of deriving the morphological parameters of galaxies - our model is a reasonable and valid approximation to the true PSF.
The most significant discrepancy between the two sets of results is a
larger rms in the Sérsic index for the simulated disk galaxies when
the model PSF was used in GALFIT.
In addition, the rms for the Sérsic index is quite large (![]() 1)
for elliptical galaxies, but this time for both the model and true PSFs.
In principle this rather large uncertainty on the Sérsic index could
restrict our ability to separate the two populations of disk-like and
elliptical-like galaxies.
However, in practice, the large variance for the ellipticals is due to
a long tail to high values of n, as apparent in Fig. 7.
We have found that starting with two populations of simulated
galaxies with Sérsic index n = 1 and n = 4 respectively, only a small
fraction (that increases with the magnitude of the galaxies, see
Fig. 8) of disks was recovered with n > 2, and few ellipticals
were recovered with n < 2.
The two classes can be clearly distinguished up to
1)
for elliptical galaxies, but this time for both the model and true PSFs.
In principle this rather large uncertainty on the Sérsic index could
restrict our ability to separate the two populations of disk-like and
elliptical-like galaxies.
However, in practice, the large variance for the ellipticals is due to
a long tail to high values of n, as apparent in Fig. 7.
We have found that starting with two populations of simulated
galaxies with Sérsic index n = 1 and n = 4 respectively, only a small
fraction (that increases with the magnitude of the galaxies, see
Fig. 8) of disks was recovered with n > 2, and few ellipticals
were recovered with n < 2.
The two classes can be clearly distinguished up to
![]() ,
where
90% of the disks are recovered with Sérsic index n < 2 and 90% of the
ellipticals are recovered with Sérsic index n > 2, using the model PSF
in GALFIT (see Fig. 7).
As a result, it is possible to set a threshold of n = 2 that is able to
discriminate between the two populations with a high degree of success.
The fraction of disks recovered with a Sérsic index n < 2 and the
fraction of ellipticals recovered with n > 2 are shown in Fig. 8
as a function of the magnitude, using both the model and true PSF.
As the correct fitting of the Sérsic index is limited by the signal to noise
of the sources, in order to correctly discriminate between disks and
ellipticals at a fainter magnitude
,
where
90% of the disks are recovered with Sérsic index n < 2 and 90% of the
ellipticals are recovered with Sérsic index n > 2, using the model PSF
in GALFIT (see Fig. 7).
As a result, it is possible to set a threshold of n = 2 that is able to
discriminate between the two populations with a high degree of success.
The fraction of disks recovered with a Sérsic index n < 2 and the
fraction of ellipticals recovered with n > 2 are shown in Fig. 8
as a function of the magnitude, using both the model and true PSF.
As the correct fitting of the Sérsic index is limited by the signal to noise
of the sources, in order to correctly discriminate between disks and
ellipticals at a fainter magnitude ![]() ,
the integration time should
be scaled as
,
the integration time should
be scaled as
![]() .
.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2890fig8.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg58.gif) |
Figure 7:
Disk/elliptical separation using GALFIT measurement of Sérsic
index for simulated profiles with
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{2890fig9.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg59.gif) |
Figure 8: The fraction of ellipticals recovered with n>2 (left panel) and the fraction of disks recovered with a Sérsic index n < 2 (right panel) as a function of the input magnitude. The dashed lines show the results obtained using the true NACO PSF, while the solid lines the ones obtained with the model PSF. |
| Open with DEXTER | |
As an additional check of the usefulness of the model
PSF, we repeated the experiment described above but giving GALFIT the
observed on-axis PSF instead of either the model or true PSF.
The outcome was that, even at relatively bright magnitudes
![]() ,
all the galaxies with a Sérsic index n = 4 were actually
recovered with an index of n < 2, making it impossible to discriminate
between the two populations.
This emphasizes the important result of our simulations that it is only
possible to discriminate between disk galaxies and elliptical
galaxies using an anisoplanatic PSF, and that using our very simple PSF model is nearly as good as using the true PSF.
,
all the galaxies with a Sérsic index n = 4 were actually
recovered with an index of n < 2, making it impossible to discriminate
between the two populations.
This emphasizes the important result of our simulations that it is only
possible to discriminate between disk galaxies and elliptical
galaxies using an anisoplanatic PSF, and that using our very simple PSF model is nearly as good as using the true PSF.
Prompted by the results on the simulated galaxy profiles, we have begun using our PSF model coupled with GALFIT to derive morphological parameters of the galaxies detected in a few of the SWAN survey fields in order to gain some insight into what we should expect, although clearly a full analysis requires the results of the dedicated redshift survey currently underway. In this paper we present the first results obtained from the first five fields, SBSF 14, SBSF 15, SBSF 18, SBSF 24 and SBSF 41, all of them already included in the preliminary discussion in Baker et al. (2005). The observations are summarized in Table 2, and the data were reduced using the same procedure adopted for the calibration fields (see Sect. 4).
Table 2:
Observations of the five SWAN fields included
in the analysis here. CE is the encircled energy
reported by the adaptive optics system in real time.
The isoplanatic angle ![]() is that derived by the fit using point sources in the
fields (see Sect. 4).
is that derived by the fit using point sources in the
fields (see Sect. 4).
The performance obtained in these first SWAN fields compares
favorably with that obtained by previous AO observations of faint field
galaxies, e.g., Larkin et al. (2000) and
Glassman et al. (2002). They obtained
12 H-band (
![]() )
images of disk galaxies at
)
images of disk galaxies at
![]() using the AO system on the Keck II telescope.
They obtain FWHMs ranging from 0.050
using the AO system on the Keck II telescope.
They obtain FWHMs ranging from 0.050
![]() to 0.15
to 0.15
![]() ,
and Strehl ratios of 1%-20%. Due to the very small
field of view (4.5
,
and Strehl ratios of 1%-20%. Due to the very small
field of view (4.5
![]() )
only one galaxy could be observed for each
frame. The PSF was reconstructed using dedicated observations of
faint off-axis stars with comparable offset, but different position
angle, from the guide star.
Due to the very low S/N obtained, the extraction of morphological
parameters was run under several assumptions to limit the number
of free parameters in the fit of a bulge and a disk to each galaxy.
In addition, the AO galaxy profiles only had reasonable S/N out to
1
)
only one galaxy could be observed for each
frame. The PSF was reconstructed using dedicated observations of
faint off-axis stars with comparable offset, but different position
angle, from the guide star.
Due to the very low S/N obtained, the extraction of morphological
parameters was run under several assumptions to limit the number
of free parameters in the fit of a bulge and a disk to each galaxy.
In addition, the AO galaxy profiles only had reasonable S/N out to
1
![]() -2
-2
![]() radius, thus limiting the constraints on the outer
portions of the disks.
Steinbring et al. (2004) imaged with the same AO system
three galaxies selected because they had been observed previously
with Hubble Space Telescope at optical wavelengths. However they
conclude that higher S/N was needed in the AO images in order
to match the HST data, and the results were limited
due to poor constraints on the AO PSF.
radius, thus limiting the constraints on the outer
portions of the disks.
Steinbring et al. (2004) imaged with the same AO system
three galaxies selected because they had been observed previously
with Hubble Space Telescope at optical wavelengths. However they
conclude that higher S/N was needed in the AO images in order
to match the HST data, and the results were limited
due to poor constraints on the AO PSF.
![\begin{figure}
\par\includegraphics[width=14.3cm,clip]{2890fig10.eps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg63.gif) |
Figure 9:
Examples of single and multiple component fits by GALFIT of
SWAN galaxies using the model PSF. In all images North is up and East
is left. The distance of the galaxy from the guide star is shown in the
upper right corner of each panel. For both galaxies, the |
| Open with DEXTER | |
In each SWAN field, sources were detected using SExtractor, with the
appropriate parameters set to provide a positive detection for objects
brighter than ![]() per pixel over an area of more then
3 pixels.
To improve the detection of faint sources we used a Gaussian
filter (
per pixel over an area of more then
3 pixels.
To improve the detection of faint sources we used a Gaussian
filter (
![]() pixels) to smooth the image.
False detections at the noisy borders
of the mosaic and on the spikes and the ghost of the bright guide star
were removed.
For the former, a mask which indicated the fraction of
the total integration time spent on each pixel was used; objects detected in
pixels below a specified threshold were rejected.
For the latter appropriate object masks were created.
The resulting coverage of these 5 fields was
pixels) to smooth the image.
False detections at the noisy borders
of the mosaic and on the spikes and the ghost of the bright guide star
were removed.
For the former, a mask which indicated the fraction of
the total integration time spent on each pixel was used; objects detected in
pixels below a specified threshold were rejected.
For the latter appropriate object masks were created.
The resulting coverage of these 5 fields was
![]() ,
within
which a total of 178 sources were detected down to a magnitude of
,
within
which a total of 178 sources were detected down to a magnitude of
![]() (
(
![]() ).
Of these, 146 were allocated a stellarity index
).
Of these, 146 were allocated a stellarity index
![]() by
SExtractor, and hence classified as galaxies.
The SExtractor classifications should be treated with caution
since they assume a constant PSF across each field. However,
all the objects classified as stars by SExtractor lie on an upper
envelope in a Strehl versus radial distance plot, i.e., they have the
highest Strehl ratio among the sources at the same distance from
the guide star,
supporting their classification as point sources.
by
SExtractor, and hence classified as galaxies.
The SExtractor classifications should be treated with caution
since they assume a constant PSF across each field. However,
all the objects classified as stars by SExtractor lie on an upper
envelope in a Strehl versus radial distance plot, i.e., they have the
highest Strehl ratio among the sources at the same distance from
the guide star,
supporting their classification as point sources.
We again used GALFIT to derive the morphological parameters of the detected galaxies. We used single component Sérsic profiles, providing the output from SExtractor as the initial guesses for magnitude, position, position angle, and axis ratio. For the deconvolution, a model PSF was created using the position of the center according to SExtractor and scaled according to the isoplanatic angle, which is shown for each field in Table 2. For each object, GALFIT was run twice, using as initial guesses for the second iteration the outputs of the first iteration.
Some of the sources still showed bumps in the center or disk-like structures in the residuals after the single component fit. These objects were re-fitted using either two Sérsic components (bulge + disk) or a Sérsic component with an additional point source, to improve the fit and minimize the residuals.
A second iteration was also performed for close pairs or interacting galaxies; we fit both of them simultaneously to avoid incorrect background estimation or contamination from the companion. Some examples of single and multiple component fits are shown in Fig. 9. For galaxies fitted using multiple components, we report only the values for the larger scale component; the nuclear properties will be discussed elsewhere.
The results obtained for the effective radii of
the 55 galaxies brighter than
![]() are shown in
Fig. 10.
While the redshifts of these objects are presently unknown,
the magnitude-redshift relation of Cowie et al. (1996)
and the K20 survey (Cimatti et al. 2002)
indicate that at K = 20 the median redshift is
are shown in
Fig. 10.
While the redshifts of these objects are presently unknown,
the magnitude-redshift relation of Cowie et al. (1996)
and the K20 survey (Cimatti et al. 2002)
indicate that at K = 20 the median redshift is
![]() .
At this redshift, our spatial resolution of
.
At this redshift, our spatial resolution of
![]() ,
which also
corresponds to the smallest effective radius bin, is equivalent to
only 500 pc for typical cosmologies, hinting at the exciting
potential of this work.
,
which also
corresponds to the smallest effective radius bin, is equivalent to
only 500 pc for typical cosmologies, hinting at the exciting
potential of this work.
Using n = 2 to discriminate between disks and ellipticals, we find there are 24 elliptical-like and 31 disk-like galaxies, with uncertainties below 10% on both numbers (see Sect. 5). In fact, with similar numbers of each type found, the number of ellipticals scattered into the disk-like category should roughly compensate the number of disks scattered out of it, and vice-versa.
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{2890fig11.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg71.gif) |
Figure 10:
Distribution of effective radii |
| Open with DEXTER | |
The distribution of effective radii is strongly peaked towards very
compact sources, even down to scales of 0.1
![]() .
To check if this is due to a selection effect introduced by the AO correction - since adaptive optics data are inherently most sensitive
to compact sources - we ran GALFIT on the same five fields, but using
the seeing limited observations made with SOFI (Baker et al. 2003).
The same procedure was used, but a fixed PSF derived from the
unsaturated guide star in each SOFI science field was provided to GALFIT
instead of the model PSFs.
Not all the galaxies detected in the NACO images are present in the
SOFI data, but on the other hand the SOFI spatial coverage is
.
To check if this is due to a selection effect introduced by the AO correction - since adaptive optics data are inherently most sensitive
to compact sources - we ran GALFIT on the same five fields, but using
the seeing limited observations made with SOFI (Baker et al. 2003).
The same procedure was used, but a fixed PSF derived from the
unsaturated guide star in each SOFI science field was provided to GALFIT
instead of the model PSFs.
Not all the galaxies detected in the NACO images are present in the
SOFI data, but on the other hand the SOFI spatial coverage is ![]() 5 times larger, so that in the end we detected a comparable number of
objects: 181 in total, 92 brighter than
5 times larger, so that in the end we detected a comparable number of
objects: 181 in total, 92 brighter than
![]() .
The obtained
distribution is shown in Fig. 10 as a gray histogram.
The distribution of
.
The obtained
distribution is shown in Fig. 10 as a gray histogram.
The distribution of ![]() shows similar behavior in both AO and seeing
limited data, suggesting that the observed distribution of
shows similar behavior in both AO and seeing
limited data, suggesting that the observed distribution of ![]() in the SWAN
fields is real and not due to selection effects.
Nevertheless, the NACO distribution shows an excess of sources in the
range
in the SWAN
fields is real and not due to selection effects.
Nevertheless, the NACO distribution shows an excess of sources in the
range
![]() with respect to SOFI, indicating that the better
resolution of NACO is able to resolve many sources that in the SOFI data
appear merely "compact'' (e.g., a bright elliptical galaxy that NACO correctly
recovers with n=4 and
with respect to SOFI, indicating that the better
resolution of NACO is able to resolve many sources that in the SOFI data
appear merely "compact'' (e.g., a bright elliptical galaxy that NACO correctly
recovers with n=4 and
![]() is recovered by SOFI for a seeing of
is recovered by SOFI for a seeing of
![]() as a compact source with
as a compact source with
![]() ,
while a disky galaxy
with n=1 and the same effective radius is correctly recovered by both).
,
while a disky galaxy
with n=1 and the same effective radius is correctly recovered by both).
Finally, the axis ratio distribution shows the co-sinusoidal distribution expected from random inclinations, except for a peak at b/a = 0 due to very compact galaxies for which GALFIT could not calculate the axis ratio, and hence which were arbitrarily assigned to this bin.
We have derived a first estimate of the completeness
limit in our images using simulated galaxy profiles convolved with true
NACO PSFs.
This is a difficult task, as the completeness depends not only on the
brightness and morphology of the source, but even on the distance from
the guide star and the position on the frame.
Therefore we derived a first estimate using only one reference PSF, a
star at
![]() from the guide star in SBSF 15.
Fields with simulated galaxies of fixed magnitude and
different
from the guide star in SBSF 15.
Fields with simulated galaxies of fixed magnitude and
different ![]() (from
(from
![]() to
to
![]() )
were created, and the sources
were recovered using the same SExtractor parameters as used for the
SWAN fields. We find that at
)
were created, and the sources
were recovered using the same SExtractor parameters as used for the
SWAN fields. We find that at
![]() all the simulated elliptical-like galaxies were
detected, while the disk-like galaxies were only 100% complete for
effective radii smaller than
all the simulated elliptical-like galaxies were
detected, while the disk-like galaxies were only 100% complete for
effective radii smaller than
![]() .
An average 50% completeness limit - i.e., the 50% limit for
galaxies with
.
An average 50% completeness limit - i.e., the 50% limit for
galaxies with
![]() - is
- is
![]() (
(
![]() )
for disk-like galaxies and
)
for disk-like galaxies and
![]() (
(
![]() )
for elliptical-like ones.
A more detailed analysis of completeness will
be presented in a forthcoming paper (Cresci et al. 2005).
)
for elliptical-like ones.
A more detailed analysis of completeness will
be presented in a forthcoming paper (Cresci et al. 2005).
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{2890fig12.ps} \end{figure}](/articles/aa/full/2005/29/aa2890-05/Timg80.gif) |
Figure 11:
The difference
|
| Open with DEXTER | |
The recovered position angle distribution can be used to indicate whether we are
indeed correcting for the anisoplanatic PSF in an effective manner,
and to evaluate possible biases
in the results due to contributions by the wavefront correction that are still
uncorrected by our PSF model.
We have divided our sample in two subsets with separations
![]() and
and
![]() .
This separation was chosen empirically as the approximate
radius beyond which the PSF distortion becomes
noticeable (see Baker et al. 2005), but also corresponds
to the average isoplanatic angle of the five fields in our analysis here.
If no radial stretch due to PSF anisoplanaticism is present (or if
this effect is fully taken into account by a PSF model) we would
expect the distribution of
.
This separation was chosen empirically as the approximate
radius beyond which the PSF distortion becomes
noticeable (see Baker et al. 2005), but also corresponds
to the average isoplanatic angle of the five fields in our analysis here.
If no radial stretch due to PSF anisoplanaticism is present (or if
this effect is fully taken into account by a PSF model) we would
expect the distribution of
![]() ,
i.e., the difference between the radial vector from the star to the
source at offset (
,
i.e., the difference between the radial vector from the star to the
source at offset (
![]() )
and the source's own major
axis position angle
)
and the source's own major
axis position angle ![]() ,
to be uniform over the interval
,
to be uniform over the interval
![]() for both
for both
![]() subsamples.
subsamples.
The distribution derived using SExtractor with no PSF anisoplanaticism correction (see Fig. 11, left panel) shows
a clear peak at
![]() for objects at large radial distances
from the guide star, i.e., these objects appear to be preferentially
oriented towards the guide star.
The right panel of Fig. 11 shows the same distribution as measured
by GALFIT using the model PSF.
As one would expect, in this case the peak is greatly reduced due to
the model PSF. The small remaining overcounts could easily be due to random chance
rather than a systematic effect.
Indeed, analysis of this effect in the simulated galaxies indicates
that it is completely removed.
for objects at large radial distances
from the guide star, i.e., these objects appear to be preferentially
oriented towards the guide star.
The right panel of Fig. 11 shows the same distribution as measured
by GALFIT using the model PSF.
As one would expect, in this case the peak is greatly reduced due to
the model PSF. The small remaining overcounts could easily be due to random chance
rather than a systematic effect.
Indeed, analysis of this effect in the simulated galaxies indicates
that it is completely removed.
In this paper we have presented a new approach to account for the PSF variations across the field of view in deep AO images, developed to correct the anisoplanaticism in SWAN images obtained with NACO at the ESO VLT, but also more generally applicable to other wide-field adaptive optics data. The survey is intended to overcome the current shortage of extragalactic AO targets and to study faint and compact field galaxies with unprecedented resolution in the near-IR. The observing strategy fully exploits the present capabilities of AO instrumentation, so that our method for PSF modeling may be broadly useful for AO cosmology.
We have described the PSF as the convolution between the on-axis PSF and a spatially varying kernel, an elliptical Gaussian elongated towards the AO guide star. We find that even adopting the most extreme case in which the the difference between the kernels in two different fields is given by a single parameter, namely the isoplanatic angle, the PSF can still be described with enough accuracy to extract reliable morphological parameters of field galaxies. This approach is particularly convenient, as it uses only easily available data and makes no uncertain assumptions about the stability of the isoplanatic angle during any given night. In addition, just a few point sources are required in each field to derive the isoplanatic angle and therefore compute the kernel.
Our simulations demonstrate that the model is able to recover reliably
morphological parameters in a typical SWAN field with an integration time of
one hour up to
![]() (
(
![]() ), and that our
very simple model is nearly as good as using the true PSF to account for
anisoplanaticism.
), and that our
very simple model is nearly as good as using the true PSF to account for
anisoplanaticism.
Finally, we have presented the first morphological results for five SWAN fields, using the GALFIT package coupled with our model PSF. The recovered source parameters confirm that we are indeed accounting for anisoplanaticism, and show the unique power of AO observations to derive the details of morphology in faint galaxies. These results pave the way for the forthcoming analysis of all the obtained SWAN fields, which will combine for the first time the high angular resolution of a space-based survey with the shallower depth and wider area of a ground-based survey.
Acknowledgements
The authors are grateful to the staff at Paranal Observatory for their hospitality and support during the observations. We thank Rainer Schödel for obtaining the observations of SBSF 41, Nancy Ageorges and Chris Lidman for helping us sift through the NACO data archive; and our collaborators on SWAN (Reinhard Genzel, Reiner Hofmann, Sebastian Rabien, Niranjan Thatte, and W. Jimmy Viehhauser); Christophe Verinaud, Miska Le Louarn, Emiliano Diolaiti and Thierry Fusco for their assistance. Some of the data included in this paper were obtained as part of the MPE guaranteed time programme. G.C. and A.J.B. acknowledge MPE for supporting their efforts on this project; A.J.B. further acknowledges support from the National Radio Astronomy Observatory, which is operated by Associated Universities, Inc., under cooperative agreement with the National Science Foundation.