- ... clustering
![[*]](/icons/foot_motif.gif)
- Appendices A-C are only available in electronic form at http://www.edpsciences.org
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... density
![[*]](/icons/foot_motif.gif)
- We have disregarded the infinities arising from the evaluation of the field
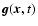 at the particles' positions. These are artifacts of using point particles and are treated by smearing the particles over an infinitesimal size. For our formal manipulations, it suffices with the implicit understanding that the infinities can be dropped when they appear.
at the particles' positions. These are artifacts of using point particles and are treated by smearing the particles over an infinitesimal size. For our formal manipulations, it suffices with the implicit understanding that the infinities can be dropped when they appear.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... fields
![[*]](/icons/foot_motif.gif)
- Notice that this closure
requires one to consider the energy or, equivalently, the
thermodynamic temperature as another fundamental field on equal
footing with
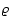 and
and 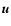 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
![[*]](/icons/foot_motif.gif)
- According to Eq. (13b),
the same model is recovered if
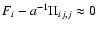 ,
i.e.,
when the corrections to the mean field are counterbalanced by velocity
dispersion - we have not explored the physical meaning of such a
balance condition.
,
i.e.,
when the corrections to the mean field are counterbalanced by velocity
dispersion - we have not explored the physical meaning of such a
balance condition.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... length
![[*]](/icons/foot_motif.gif)
- The denomination "large-scale expansion''
used in Domínguez (2000) may lead to confusion.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...2001)
![[*]](/icons/foot_motif.gif)
- Bharadwaj (1996)
extended this claim to the case of multi-streamed initial conditions
in the simplified model of free particles. This conclusion is, however,
false because of a mathematical mistake in his Eq. (34).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...1999)
![[*]](/icons/foot_motif.gif)
- In that work, only the particular case of a polytropic
dependence,
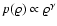 ,
in an Einstein-de
Sitter cosmological background was considered, but it can be checked
that Eq. (35) holds generally. Also in that work,
a minor mistake was made and the coefficient
,
in an Einstein-de
Sitter cosmological background was considered, but it can be checked
that Eq. (35) holds generally. Also in that work,
a minor mistake was made and the coefficient
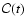 quoted there
is missing an extra time-dependent factor when
quoted there
is missing an extra time-dependent factor when
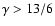 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field
![[*]](/icons/foot_motif.gif)
- If such conditions
are imposed on the problem,
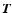 becomes a harmonic vector function
which can be set to zero for periodic boundary conditions of the
cosmological fields on some large scale (since then the only
harmonic functions are spatially constant and can be set to zero due
to the invariance of the basic equations with respect to spatially
constant translations).
becomes a harmonic vector function
which can be set to zero for periodic boundary conditions of the
cosmological fields on some large scale (since then the only
harmonic functions are spatially constant and can be set to zero due
to the invariance of the basic equations with respect to spatially
constant translations).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
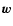
![[*]](/icons/foot_motif.gif)
- For details on the
possibility and advantage of this choice, see Adler & Buchert (1999, Appendix A).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...J
![[*]](/icons/foot_motif.gif)
- Of course,
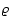 solves Eq. (48), if
solves Eq. (48), if 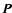 solves Eq. (47).
solves Eq. (47).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... time
![[*]](/icons/foot_motif.gif)
- In this work we are
not concerned with more general (non-Lagrangian) singularities in the
velocity-gradient field, such as those that may occur in
incompressible flows.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model
![[*]](/icons/foot_motif.gif)
- The weak solutions can be
interpreted equivalently as solutions of the integral form of
the balance equations for mass and momentum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... variable
![[*]](/icons/foot_motif.gif)
- As in the case of deriving Eq. (4), the
formal definitions of the fields
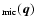 ,
,
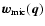 can be regularized by smearing Dirac's delta function.
can be regularized by smearing Dirac's delta function.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
state''
![[*]](/icons/foot_motif.gif)
- This notion as well as the names attached to the
different polytropic models (with the polytropic index n defined through
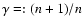 )
is borrowed from thermodynamics. We emphasize that here we refer to dynamical stresses and do not imply thermal equilibrium.
)
is borrowed from thermodynamics. We emphasize that here we refer to dynamical stresses and do not imply thermal equilibrium.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.