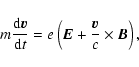 |
(1) |
Y. Kuramitsu - V. Krasnoselskikh
Laboratoire Physique et Chimie de l'Environnement, CNRS, 45071 Orléans, France
Received 29 October 2004 / Accepted 15 March 2005
Abstract
We discuss an acceleration mechanism of charged particles by magnetohydrodynamic (MHD) structures, such as quasi-parallel shocks and short-large amplitude magnetic structures (SLAMS).
In the presence of electromagnetic waves and an electrostatic electric field, particles are accelerated efficiently in the perpendicular direction to the background magnetic field by the combination of two effects, the trapping of particles by the wave and the dragging by the electrostatic field to keep the resonance condition.
This allows particles to propagate downstream even when they initially have smaller kinetic energy than the potential.
We show the fundamental properties of this mechanism, referred to as gyroresonant surfing.
Key words: acceleration of particles - shock waves - diffusion
It is widely accepted that diffusive shock acceleration (DSA) is a major cosmic ray acceleration mechanism in astrophysical and solar system plasmas (Blandford & Ostriker 1978; Krymskii 1977; Bell 1978; Axford et al. 1978). It is essentially the first order Fermi acceleration, and predictions of DSA agree well with the observed cosmic ray spectra. Since it is necessary for particles to cross the shock front back and forth many times, the particles should have high initial energy and be well separated from the thermal background, that is, the so called "seed'' population should exist. An important issue is related to the injection problem; the formation of this population still remains controversial (see for reviews Forman & Webb 1985; Jones & Ellison 1991; Scholer et al. 1998).
Malkov & Voelk (1995) and Malkov (1998) discussed the injection problem of DSA assuming ion leakage from downstream of the parallel shock. In their models particles are accelerated directly from the thermal population in the same way as the DSA. In this sense, there is no need for the seed population, and the injection problem becomes the question of how to produce backstreaming particles. The formation of leakage particles from downstream thermal plasma might be considered as a solution of the injection problem if such a process would supply a significant particle flux. This is the key assumption of Malkov & Voelk (1995) and they further assumed that this population can be described as a "warm beam''. Such a wide-spread beam will excite waves with a wide spectrum that can be described by quasi-linear theory, but not quasi-monochromatic waves as often detected in in situ observations (Hoppe et al. 1981; Hoppe & Russell 1983). Moreover, in the standard quasi-linear theory, there is no pitch angle diffusion over 90 degrees when the waves propagate parallel to the background magnetic field (e.g., Ng & Reames 1995; Schlickeiser 1989). This problem does not exist for the finite amplitude waves. When the wave amplitude is finite, particle simulations show that particles can diffuse over 90 degrees because of nonlinearity in the particle dynamics (e.g., Tsurutani et al. 2002). Nonlinear interaction between particles and finite amplitude waves is essential for acceleration and transport processes in the presence of large amplitude waves often observed in situ at the quasi-parallel shocks.
Performing particle simulations, Scholer et al. (1998) pointed out that incoming particles gain considerable energy at the first encounter with the shock. This cannot result from the leakage process. Sugiyama et al. (2001) proposed a simple idea to explain this; they found that particles are trapped at the shock front by large amplitude waves resulting in rapid acceleration. This process is the same as the first order Fermi acceleration, i.e., the particles are scattered back and forth in shock front. In order to accelerate particles efficiently, therefore, the shock must have a sharp transition in their model. While the quasi-perpendicular shocks can have a sharp transition, however, the quasi-parallel shocks have a rather broader spatial scale. Recent electric and magnetic field measurements gave clear evidence that the quasi-parallel shock front structure can be presented as a patchwork of short large amplitude magnetic structures (SLAMS) rather than a continuous transition (Schwartz et al. 1992; Schwartz & Burgess 1991). The first measurements obtained from Cluster satellites of the shock electrostatic potential (Behlke et al. 2004) are often ignored in the context of ion acceleration since the electrostatic fields of shocks are considered to decelerate ions.
The direct in-situ observations of particles and related wave activities are impossible in astrophysical plasmas. Therefore, revealing the relation between observed ion populations and shock structure with various wave activities by using in-situ observations of the Earth's bow shock is essential to understand the acceleration of energetic particles or cosmic rays from thermal plasmas. Recent satellite programs have carried out detailed studies of the Earth's bow shock, a relatively small and weak nonrelativistic version of astrophysical shocks. In situ studies of particle distribution functions have allowed identification of several suprathermal ion populations and their relationship to different forms of wave activity in the vicinity of the quasi-parallel shock front (Hoppe et al. 1981; Paschmann et al. 1981). Generation of different ion populations is often explained by the following scenario. Some portion of solar wind ions is specularly reflected at the shock front, the reflected population then excites low-frequency quasi-monochromatic waves via Doppler shifted cyclotron resonance, and these waves in turn scatter particles, forming a diffuse distribution (Hoshino & Terasawa 1985). In this scenario, another population, the intermediate ions, is trapped by the waves and sometimes observed as phase bunched or "gyrating'' ions (Meziane et al. 2001). The other possible scenario is the direct production of gyrating ions as a result of a specularly reflection of the solar wind at the shock (Gosling et al. 1982). Since He2+/H+ density ratios in the field aligned beams show significantly smaller values than those of diffuse ions, the evolution from beam to diffuse distribution is unlikely to take place (Ipavich et al. 1984; Fuselier 1995; Ipavich et al. 1988; Fuselier et al. 1995). It is more probable that the diffuse ion distributions evolve from ring beam populations produced by direct reflection from the solar wind (Fuselier 1995; Fuselier et al. 1995). In both scenarios, ions must have been reflected before they are observed in the foreshock region. However, if there is no acceleration, the specularly reflection results in a strong underestimate of particles perpendicular velocity and predicts narrower velocity distributions than observed.
In this paper, we study ion motion in the vicinity of shock type structures or SLAMS in the presence of an electromagnetic circularly polarized wave, as often observed in in-situ observations. In Sect. 2, we describe the basic idea of gyroresonant surfing acceleration. We start from a simplified model where an electromagnetic wave and an electrostatic field act on a particle resulting in strong and efficient acceleration under a certain condition, namely, when a particle is in resonance with the propagating wave. In Sect. 3, we show that the acceleration operates for a wide class of potentials. Before discussing the gyroresonant surfing in the presence of the potential at the shock, we consider the upstream particle motion where the electrostatic field is absent and the electromagnetic field is present. We discuss the finite amplitude effects on particle trapping by the monochromatic wave. Then, we start with the resonant particles to investigate fundamental properties of gyroresonant surfing. We show that the acceleration occurs only for certain polarizations of electromagnetic waves, while for the others the action of fields results in deceleration. Next, we use the more realistic parameters often observed in situ measurement or in computer simulations. We show that for a shock-like profile of the potential with a monochromatic wave excited by the specularly reflected portion of the solar wind, the acceleration occurs efficiently for reflected particles. In Sect. 4, we summarize our results and discuss the injection problem for cosmic rays.
We introduce gyroresonant surfing (Kuramitsu & Krasnoselskikh 2005) focusing on a resonant particle in an ideal situation.
We consider a parallel shock geometry where a monochromatic electromagnetic wave propagates parallel to a background magnetic field with
a certain velocity with respect to the upstream plasma.
We assume an electrostatic potential profile of the shock varying along the same direction.
The basic equations are the equations of motion,
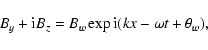 |
(2) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2283f1.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg32.gif) |
Figure 1:
Resonant particle (solid lines) trajectories are shown a) in x-vx space with electrostatic potential (dotted line); b) in the perpendicular plane; and c) the time evolution of |
| Open with DEXTER | |
We show in Fig. 1 the particle trajectories obtained by numerical integration of Eq. (1), where the electrostatic field is given by Eq. (5).
All the variables are normalized using B0,
![]() ,
and
,
and ![]() .
Figure 1 shows the trajectories of a resonant particle (solid lines) in x-vx space together with the electrostatic field (dotted line) (a), in perpendicular velocity space (b), and the time evolution of the ion perpendicular velocity (c).
The parameters are b=0.3, k=2,
.
Figure 1 shows the trajectories of a resonant particle (solid lines) in x-vx space together with the electrostatic field (dotted line) (a), in perpendicular velocity space (b), and the time evolution of the ion perpendicular velocity (c).
The parameters are b=0.3, k=2,
![]() ,
,
![]() ,
v=1, and
,
v=1, and
![]() .
In Fig. 1a, the particle propagates against the electrostatic potential, which is calculated from Eq. (5) for this ion, keeping the parallel velocity constant. From panels b and c, one can see that the particle is accelerated monotonically in the perpendicular direction satisfying the cyclotron resonance condition along the trajectory.
.
In Fig. 1a, the particle propagates against the electrostatic potential, which is calculated from Eq. (5) for this ion, keeping the parallel velocity constant. From panels b and c, one can see that the particle is accelerated monotonically in the perpendicular direction satisfying the cyclotron resonance condition along the trajectory.
Figure 2a shows the time evolution of relative phases ![]() (solid lines) with the same parameters as in Fig. 1 except
(solid lines) with the same parameters as in Fig. 1 except ![]() ranges
ranges
![]() .
The relative phases approach
.
The relative phases approach ![]() (dotted line) asymptotically.
Since the particles have a
(dotted line) asymptotically.
Since the particles have a ![]() phase difference with the magnetic field, they are in phase with the electric field of the electromagnetic wave.
The trajectories are unstable when
phase difference with the magnetic field, they are in phase with the electric field of the electromagnetic wave.
The trajectories are unstable when ![]() is close to 0 and
is close to 0 and ![]() ,
which corresponds to the separatrix when
,
which corresponds to the separatrix when
![]() .
Figure 2b shows the time evolution of vy (solid lines) and Ey (dotted line).
Particles begin to oscillate in phase with the wave electric field with time resulting in efficient acceleration.
This phase synchronization can be understood as follows.
From Eq. (4) the y component of the particle velocity is written as
.
Figure 2b shows the time evolution of vy (solid lines) and Ey (dotted line).
Particles begin to oscillate in phase with the wave electric field with time resulting in efficient acceleration.
This phase synchronization can be understood as follows.
From Eq. (4) the y component of the particle velocity is written as
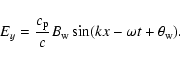 |
(7) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2283f2.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg45.gif) |
Figure 2:
a) Time evolution of |
| Open with DEXTER | |
We show another example in Fig. 3 where an electrostatic field attempts to accelerate a particle.
The parameters are k=0.5, v=2,
![]() ,
and the others are the same as Fig. 1.
From Eq. (5), the electrostatic potential decreases along the trajectory, thus the particle will be accelerated in the parallel direction.
However, the particle keeps the resonant condition in panel a and is accelerated efficiently in the perpendicular direction in panel b and c, similar to the situation when the electrostatic field attempts to decelerate particles.
Since the wave number is smaller than in the previous run, the rate of perpendicular velocity gain is higher.
The ratio of rates corresponds to the wave number ratio.
The energy that a particle gets is much larger than the potential energy difference.
Thus, the acceleration is not a simple transformation from parallel to perpendicular energy, but rather is due to the electromagnetic electric fields as we described above.
We will return to this point later.
,
and the others are the same as Fig. 1.
From Eq. (5), the electrostatic potential decreases along the trajectory, thus the particle will be accelerated in the parallel direction.
However, the particle keeps the resonant condition in panel a and is accelerated efficiently in the perpendicular direction in panel b and c, similar to the situation when the electrostatic field attempts to decelerate particles.
Since the wave number is smaller than in the previous run, the rate of perpendicular velocity gain is higher.
The ratio of rates corresponds to the wave number ratio.
The energy that a particle gets is much larger than the potential energy difference.
Thus, the acceleration is not a simple transformation from parallel to perpendicular energy, but rather is due to the electromagnetic electric fields as we described above.
We will return to this point later.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2283f3.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg46.gif) |
Figure 3:
Same as Fig. 1, except k=0.5, v=1, and
|
| Open with DEXTER | |
The above ideal situation is useful to understand the basic feature of the gyroresonant surfing.
The gyroresonant surfing acceleration can take place not only for resonant particles but also non-resonant or near-resonant particles (Kuramitsu & Krasnoselskikh 2005).
It follows then that the acceleration operates in the presence of a wider class of potential fields.
This flexibility comes from the trapping of particles by the wave, since there is little difference in dynamics between resonant and trapped particles.
As we see below, in the presence of finite amplitude wave particles close to resonance are trapped by the wave in repeated acceleration and deceleration around the trapping center that is out of phase with the wave electric field.
Thus, there is no net energization of particles in the wave frame when the other external forces are absent.
Therefore, if the trapping center can be shifted to be in-phase with the wave electric field, i.e., if the particle gyrophase is synchronized to the phase of the wave electric field, there will be a net energy change of the particle.
Importantly, this phase shift does not need to be exactly in-phase, but even a slight shift can make the net energy change; this is valid only for trapped particles.
In this section we apply our model to parallel shock fronts, including SLAMS, which generally grow from upstream to downstream.
Thus, we assume a model electric field of the form
Let us define the reference frame where the electrostatic field profile is at rest as the S-system and the upstream plasma frame as the P-system.
We consider a shell distribution with a thermal spread corresponding to ![]() as a part of upstream plasmas.
We choose the system such that both the wave and the particles are convected towards the electrostatic potential profile.
In solar wind plasma the bulk velocity is often much larger than the thermal velocity
as a part of upstream plasmas.
We choose the system such that both the wave and the particles are convected towards the electrostatic potential profile.
In solar wind plasma the bulk velocity is often much larger than the thermal velocity
![]() ,
and the monochromatic wave, which is associated with the intermediate or gyrating ions, is considered to be excited via cyclotron resonance by the backstreaming component of the solar wind.
We assume here specularly reflection, i.e.,
,
and the monochromatic wave, which is associated with the intermediate or gyrating ions, is considered to be excited via cyclotron resonance by the backstreaming component of the solar wind.
We assume here specularly reflection, i.e.,
![]() in the S-system (e.g., Fuselier et al. 1990).
Thus, the wave should be a right-hand polarized anti-parallel propagating wave (R-), and the wave number has to satisfy the relation
in the S-system (e.g., Fuselier et al. 1990).
Thus, the wave should be a right-hand polarized anti-parallel propagating wave (R-), and the wave number has to satisfy the relation
![]() ,
where the factor two comes from the particle velocity in the P-system.
Such a low frequency MHD wave, here an Alfvén wave, can have a larger amplitude as is often detected by in-situ observations (Hoppe & Russell 1983).
Moreover, the electrostatic potential energy difference between the upstream and downstream is believed to be comparable to that of the upstream plasma flow, (
,
where the factor two comes from the particle velocity in the P-system.
Such a low frequency MHD wave, here an Alfvén wave, can have a larger amplitude as is often detected by in-situ observations (Hoppe & Russell 1983).
Moreover, the electrostatic potential energy difference between the upstream and downstream is believed to be comparable to that of the upstream plasma flow, (
![]() )
(Scholer et al. 2003).
)
(Scholer et al. 2003).
Some important external parameters are: the electric field amplitude a, spatial scale l, the wave amplitude b, the wave number k, the upstream plasma velocity ![]() ,
and the particle thermal velocity
,
and the particle thermal velocity ![]() .
We define the wave and the particle parameters in the P-system, then transform all the variables to the S-system.
Injecting the particles from far upstream of the profile, we solve Eq. (1) in the S-system numerically.
.
We define the wave and the particle parameters in the P-system, then transform all the variables to the S-system.
Injecting the particles from far upstream of the profile, we solve Eq. (1) in the S-system numerically.
Before discussing the combined effects of the electromagnetic wave and the electrostatic potential on a particle, we study the upstream particle motion where the role of the electrostatic field is still negligible.
The description of such motion was studied in detail by many authors (see for instance, Matsumoto 1979; Karpman 1974).
In the presence of a finite amplitude electromagnetic wave, particles having a velocity around resonant velocity are trapped by the wave.
To describe this, we define the phase relation of particle and wave in the perpendicular plane to the background magnetic field as shown in Fig. 4, where
![]() is the particle gyrophase,
is the particle gyrophase,
![]() is the wave phase, and
is the wave phase, and ![]() is their difference.
Now we use a coordinate moving with the wave phase velocity (W-system), namely
is their difference.
Now we use a coordinate moving with the wave phase velocity (W-system), namely
![]() ,
where
,
where
![]() is the wave phase velocity.
In this system particle energy is conserved.
We rewrite
is the wave phase velocity.
In this system particle energy is conserved.
We rewrite ![]() and
and
![]() ,
where
,
where ![]() is the pitch angle cosine defined in the W-system.
We can reduce the equation of motion to
is the pitch angle cosine defined in the W-system.
We can reduce the equation of motion to
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{2283f4.eps}
\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg65.gif) |
Figure 4: Definition of the phase relation in the perpendicular plane is shown. |
| Open with DEXTER | |
| (13) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2283f5.eps}
\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg85.gif) |
Figure 5:
Particle trajectories are shown in the |
| Open with DEXTER | |
Figure 5 shows the particle trajectories in the ![]() phase space when
phase space when ![]() with wave amplitude
b=0.01,0.1,1,10.
When the wave amplitude is small (b=0.01), particles are trapped around the linear cyclotron resonant velocity,
with wave amplitude
b=0.01,0.1,1,10.
When the wave amplitude is small (b=0.01), particles are trapped around the linear cyclotron resonant velocity,
![]() ,
which is equivalent to
,
which is equivalent to
![]() using the original variables.
As the wave amplitude becomes larger, the trapping region also becomes larger.
A new trapping region is born in a location far from the linear cyclotron resonance condition.
We refer to this trapping as the "non-resonant trapping''.
In the very large amplitude limit, the non-resonant trapping region has almost the same size as the trapping region from the linear resonance (b=10).
using the original variables.
As the wave amplitude becomes larger, the trapping region also becomes larger.
A new trapping region is born in a location far from the linear cyclotron resonance condition.
We refer to this trapping as the "non-resonant trapping''.
In the very large amplitude limit, the non-resonant trapping region has almost the same size as the trapping region from the linear resonance (b=10).
Figure 6 shows the particle trajectories in the case
![]() with the same amplitude as Fig. 5.
Since
with the same amplitude as Fig. 5.
Since
![]() ,
we can see no trapping region when the wave amplitude is small, b=0.01.
However, as the wave amplitude becomes larger, the (non-resonant) trapping regions appear around the beam velocity as we saw in the previous case; the resonant and the non-resonant trapping regions occupy almost the same areas of the phase space.
When a large amplitude wave exists, particles can be trapped regardless of the linear cyclotron resonance condition.
,
we can see no trapping region when the wave amplitude is small, b=0.01.
However, as the wave amplitude becomes larger, the (non-resonant) trapping regions appear around the beam velocity as we saw in the previous case; the resonant and the non-resonant trapping regions occupy almost the same areas of the phase space.
When a large amplitude wave exists, particles can be trapped regardless of the linear cyclotron resonance condition.
As mentioned above, since the monochromatic waves are excited by the backstreaming particles, the incoming solar wind particles do not satisfy the resonance condition, and the wave is R- in the P-system. In spite of this, to study the fundamental aspects of gyroresonant surfing, we start by considering resonant particle motion under the influence of each of the wave families, i.e., either right or left-hand polarization, and either parallel or anti-parallel velocity with respect to the background magnetic field in the P-system. Thus, the parameters we applied here are not realistic in terms of intermediate or gyrating ions associated with the monochromatic wave.
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2283f6.eps} %
\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg88.gif) |
Figure 6:
Same as Fig. 5 except the
|
| Open with DEXTER | |
Let us start with the dependence of acceleration on the wave families.
In the presence of R- or the left-hand polarized parallel propagating wave (L+), ions parallel velocity must be negative to resonate with the wave
![]() in the P-system.
On the other hand, in the presence of the left-hand polarized anti-parallel (L-) or the right-hand polarized parallel propagating wave (R+), the resonant velocity is positive
in the P-system.
On the other hand, in the presence of the left-hand polarized anti-parallel (L-) or the right-hand polarized parallel propagating wave (R+), the resonant velocity is positive
![]() in the P-system.
We keep parameters equal for all runs as a=1, l=10, b=0.2,
in the P-system.
We keep parameters equal for all runs as a=1, l=10, b=0.2,
![]() ,
,
![]() ,
except k=0.4,
,
except k=0.4,
![]() for R-, k=0.4,
for R-, k=0.4,
![]() for L+, k=-0.4,
for L+, k=-0.4,
![]() for L-, and k=-0.4,
for L-, and k=-0.4,
![]() for R+.
We choose the wave numbers and the thermal velocity so that the shell includes the resonant velocity.
From the resonance condition Eq. (12) the resonant velocities are
for R+.
We choose the wave numbers and the thermal velocity so that the shell includes the resonant velocity.
From the resonance condition Eq. (12) the resonant velocities are
![]() and 3.5 (7.5), respectively in the P (S)-system.
and 3.5 (7.5), respectively in the P (S)-system.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2283f7.eps} %
\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg95.gif) |
Figure 7: Initial pitch angle and phase dependence of gyroresonant surfing acceleration is shown in the presence of a) R-; b) L+; c) L-; and d) R+, respectively. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2283f8.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg96.gif) |
Figure 8: Trajectories of upstream particles in the same phase space shown using the same parameters as Fig. 7. Note that these are projections of trajectories from higher dimensional phase space. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.1cm,clip]{2283f9.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg97.gif) |
Figure 9: Dependence of acceleration efficiency on wave number. a) Ensemble averages and b) maximum values of perpendicular velocity after interaction with the profile against the absolute value of wave number. In c) and d) the same values as a) and b) are plotted against the resonant velocity and absolute value in the S-system. Except for the abscissa of c), all panels are plotted in the logarithmic scale. In all panels circles, squares, triangles and inverse triangles represent the presence of R-, L+, L- and R+, respectively. |
| Open with DEXTER | |
Figure 7 shows the difference of perpendicular velocity of particles between before and after the interaction
![]() with the profile as a function of the initial pitch angle and the phase in the presence (red dots) of R- (a), L+ (b), L- (c), and R+ (d), respectively.
Here
with the profile as a function of the initial pitch angle and the phase in the presence (red dots) of R- (a), L+ (b), L- (c), and R+ (d), respectively.
Here
![]() is the pitch angle cosine in the P-system.
In (a) acceleration is most efficient, in (b) we still see efficient acceleration, although we cannot see it in (c) and (d).
is the pitch angle cosine in the P-system.
In (a) acceleration is most efficient, in (b) we still see efficient acceleration, although we cannot see it in (c) and (d).
Figure 8 shows ion trajectories upstream of the profile, i.e., Ex=0, in the same phase space as Fig. 7.
Note that a shell in the P-system is different from that of the W-system; the group of particles having a constant value of the velocity (
![]() )
in one reference frame does not satisfy the same condition in another reference frame (
)
in one reference frame does not satisfy the same condition in another reference frame (
![]() ).
Thus in the P-system we cannot write Eq. (1) in a form like Eq. (9).
Some trajectories can cross in the phase space since they have the same H but different
).
Thus in the P-system we cannot write Eq. (1) in a form like Eq. (9).
Some trajectories can cross in the phase space since they have the same H but different ![]() .
However, this is not essential to gyroresonant surfing.
Comparing Figs. 7 and 8, we can see that the gyroresonant surfing is efficient around trapping regions.
While for (a) and (b) (
.
However, this is not essential to gyroresonant surfing.
Comparing Figs. 7 and 8, we can see that the gyroresonant surfing is efficient around trapping regions.
While for (a) and (b) (
![]() in the P-system) the trapped particles are accelerated efficiently, for (c) and (d) (
in the P-system) the trapped particles are accelerated efficiently, for (c) and (d) (
![]() in the P-system) trapped particles are decelerated.
in the P-system) trapped particles are decelerated.
Keeping the parameters for the particles and potential the same as Fig. 7, we change the wave numbers over wide range.
As we previously noted, to apply our theory to the parallel shock environment, the wave frequency must be smaller than the ion gyrofrequency. However, it is always useful to know what happens in the limits where the governing parameters are small or large.
Figure 9 shows the wave number dependence of perpendicular acceleration using a wide parameter space of the wave number, where circles, squares, triangles and inverse triangles represent the presence of
R-, L+, L- and R+, respectively.
In (a) the ensemble average of the particle perpendicular velocity after interaction with the profile is plotted against the absolute value of the wave number.
The ensemble averages are taken over all the particles, for example, in Fig. 7a, and so on.
In (b) the maximum values of perpendicular velocity out of the same ensemble are plotted in the same coordinates as (a).
When the wave number is very large, that is, at the high frequency limit, both the ensemble averages and maximum values approach constants;
![]() and the maximum
and the maximum
![]() .
Those are the average and maximum values of the initial distribution.
Thus nothing happens in this limit in the perpendicular direction regardless of the wave family.
When the wave number is very small, the effects of waves are also small. The maxima are larger than
.
Those are the average and maximum values of the initial distribution.
Thus nothing happens in this limit in the perpendicular direction regardless of the wave family.
When the wave number is very small, the effects of waves are also small. The maxima are larger than ![]() ;
however, the averages are still close to
;
however, the averages are still close to
![]() ,
suggesting that the waves scatter particles in the perpendicular direction but that the net acceleration is still small.
When
0.03<|k|<1, efficient acceleration takes place for R- and L+, on the other hand for L- and R+ no efficient acceleration is observed.
Comparing (a) and (b), peak values are reversed for R- and L+, since
,
suggesting that the waves scatter particles in the perpendicular direction but that the net acceleration is still small.
When
0.03<|k|<1, efficient acceleration takes place for R- and L+, on the other hand for L- and R+ no efficient acceleration is observed.
Comparing (a) and (b), peak values are reversed for R- and L+, since
![]() depends on how many particles are accelerated and this is dependent on the trapping width in the
depends on how many particles are accelerated and this is dependent on the trapping width in the ![]() phase space (for instance Figs. 8a and 8b).
There is a large difference in low frequency waves (|k|<1) between k>0 (R-, L+) and k<0 (L-, R+), namely
phase space (for instance Figs. 8a and 8b).
There is a large difference in low frequency waves (|k|<1) between k>0 (R-, L+) and k<0 (L-, R+), namely
![]() and
and
![]() in the P-system.
In (c) and (d) the abscissa of (a) and (b) are converted to resonant velocity (in a linear scale) and its absolute value in the S-system, respectively.
While the resonant velocity for L-, R+ in the P-system is always positive, for R-, L+ it can be positive or negative because of the Doppler shift.
It is clear that the acceleration is efficient around
in the P-system.
In (c) and (d) the abscissa of (a) and (b) are converted to resonant velocity (in a linear scale) and its absolute value in the S-system, respectively.
While the resonant velocity for L-, R+ in the P-system is always positive, for R-, L+ it can be positive or negative because of the Doppler shift.
It is clear that the acceleration is efficient around
![]() ,
since the acceleration time is proportional to l/vx, i.e. the time for a particle to cross the potential.
Another reason is that particles are initially distributed
,
since the acceleration time is proportional to l/vx, i.e. the time for a particle to cross the potential.
Another reason is that particles are initially distributed
![]() ,
in this case
,
in this case
![]() ,
and if particles are specularly reflected by the potential, they are distributed as
,
and if particles are specularly reflected by the potential, they are distributed as
![]() .
As a natural consequence of the gyroresonant surfing, particles are accelerated when resonant waves exist.
.
As a natural consequence of the gyroresonant surfing, particles are accelerated when resonant waves exist.
Focusing on R- and L+, the acceleration is more efficient when
![]() than
than
![]() .
This is understood from Eq. (4); the ideal perpendicular acceleration is inversely proportional to k, and k is smaller when
.
This is understood from Eq. (4); the ideal perpendicular acceleration is inversely proportional to k, and k is smaller when
![]() than
than
![]() .
This is clear in (d), where in the large |k| limits the resonant velocity approach
.
This is clear in (d), where in the large |k| limits the resonant velocity approach
![]() in the P (S)-system since
in the P (S)-system since
![]() ,
and maximum values of
,
and maximum values of ![]() approach
approach
![]() 4).
From these limits as k becomes smaller, the maximum value of
4).
From these limits as k becomes smaller, the maximum value of ![]() becomes larger when
becomes larger when
![]() becomes smaller.
From the peaks, as
becomes smaller.
From the peaks, as
![]() increases the maxima become smaller, where the sign of resonant velocity is negative.
Reflected particles can be accelerated in a similar way, as was shown in Fig. 3.
We will discuss this further later.
increases the maxima become smaller, where the sign of resonant velocity is negative.
Reflected particles can be accelerated in a similar way, as was shown in Fig. 3.
We will discuss this further later.
On the other hand, in the presence of L- and R+ the larger ![]() has a larger maximum.
As seen in Figs. 7c and 7d, the trapped particles are decelerated rather than accelerated.
At some point
has a larger maximum.
As seen in Figs. 7c and 7d, the trapped particles are decelerated rather than accelerated.
At some point
![]() ,
,
![]() is smaller than the asymptotic value, i.e., there is a net deceleration.
To confirm this, we perform test runs using the same resonant velocity in the S-system and the same absolute value of wave number with different signs.
We set
is smaller than the asymptotic value, i.e., there is a net deceleration.
To confirm this, we perform test runs using the same resonant velocity in the S-system and the same absolute value of wave number with different signs.
We set
![]() ,
,
![]() ,
then
,
then ![]() for L+ and L-, respectively.
The other parameters are b=0.5, a=-1, l=20,
for L+ and L-, respectively.
The other parameters are b=0.5, a=-1, l=20,
![]() ,
and
,
and
![]() for
for
![]() .
.
Figure 10 shows the particle trajectories in the presence of L+ (solid lines) and in the presence of L- (dashed lines) in
![]() space (a), in vx-x space (b) and in the perpendicular velocity space (c).
In the presence of L+ the particle is accelerated efficiently around the profile in the perpendicular direction (a) keeping the parallel velocity constant on average (b).
In (c) we can see the typical trajectory of gyroresonant surfing acceleration, which is spiral.
On the other hand, in the presence of L-, even though the initial velocity is the same, the particle is decelerated in the profile in the perpendicular direction (a), keeping vx constant on average (b) before reflection.
After reflection, while
space (a), in vx-x space (b) and in the perpendicular velocity space (c).
In the presence of L+ the particle is accelerated efficiently around the profile in the perpendicular direction (a) keeping the parallel velocity constant on average (b).
In (c) we can see the typical trajectory of gyroresonant surfing acceleration, which is spiral.
On the other hand, in the presence of L-, even though the initial velocity is the same, the particle is decelerated in the profile in the perpendicular direction (a), keeping vx constant on average (b) before reflection.
After reflection, while ![]() is almost constant (a), in the parallel direction the particle is accelerated efficiently.
In (c) we can see a similar trajectory to the red one, however this is a deceleration process.
Thus, there exists a gyroresonant surfing deceleration.
Since the perpendicular deceleration ends when
is almost constant (a), in the parallel direction the particle is accelerated efficiently.
In (c) we can see a similar trajectory to the red one, however this is a deceleration process.
Thus, there exists a gyroresonant surfing deceleration.
Since the perpendicular deceleration ends when
![]() ,
it is impossible to keep on decelerating monotonically.
This results in the reflection of the particle by the profile.
The parallel acceleration after reflection is explained as follows.
The gyroresonant surfing can transport a particle to a higher potential than the parallel energy of the particle, however, the particle cannot continue gyroresonant surfing because of the above limits.
After reflection, particle are accelerated in the parallel direction by the potential.
In (c) the particle is reflected (vx=0) at
,
it is impossible to keep on decelerating monotonically.
This results in the reflection of the particle by the profile.
The parallel acceleration after reflection is explained as follows.
The gyroresonant surfing can transport a particle to a higher potential than the parallel energy of the particle, however, the particle cannot continue gyroresonant surfing because of the above limits.
After reflection, particle are accelerated in the parallel direction by the potential.
In (c) the particle is reflected (vx=0) at ![]() ,
thus the potential difference between here and upstream is about half of the total potential difference.
If this potential energy (
,
thus the potential difference between here and upstream is about half of the total potential difference.
If this potential energy (![]() 20) is converted into particle parallel energy,
20) is converted into particle parallel energy,
![]() ,
this is consistent with the numerical result.
,
this is consistent with the numerical result.
Up to now we used ideal parameters to show the fundamental properties of gyroresonant surfing.
Here we choose a more realistic set of parameters corresponding to typical in situ observations.
To this end, we choose the upstream bulk velocity to be larger than the thermal velocity (
![]() ,
,
![]() ), the wave amplitude is moderately large (b=0.5), and the wave frequency is small (
), the wave amplitude is moderately large (b=0.5), and the wave frequency is small (
![]() ), which is typical of in situ observations.
The other parameters are the same as in Fig. 7a.
Now flow energy of the upstream particles is comparable to the potential difference across the shock and the resonant velocity is close to
), which is typical of in situ observations.
The other parameters are the same as in Fig. 7a.
Now flow energy of the upstream particles is comparable to the potential difference across the shock and the resonant velocity is close to
![]() .
All the particles do not satisfy the resonance condition Eq. (12),
.
All the particles do not satisfy the resonance condition Eq. (12),
![]() in the S (P)-system.
in the S (P)-system.
Figure 11a shows the dependence of the perpendicular acceleration on the initial pitch angle and phase.
We can see a quite efficient acceleration and a clear separation between accelerated and non-accelerated particles in the phase space.
Figure 11b shows the particle parallel position after interaction with the profile in the same phase space as in Fig. 11a.
We also see the clear separation in particle positions and the considerable acceleration corresponding to reflected particles x<0.
Figure 11c shows the distribution of the particles before (blue crosses) and after (red dots) interaction.
The green circles represent the distribution when the wave is absent b=0 for reference.
In this case, upstream particles with
![]() cannot propagate downstream resulting in "specularly'' reflection,
cannot propagate downstream resulting in "specularly'' reflection,
![]() .
These reflected particles are considered to excite the monochromatic wave via cyclotron resonance.
On the other hand, particles with
.
These reflected particles are considered to excite the monochromatic wave via cyclotron resonance.
On the other hand, particles with
![]() go through the potential losing the parallel energy by an amount of the potential difference,
go through the potential losing the parallel energy by an amount of the potential difference,
![]() .
On the contrary, when the wave exists, there are two distinct components; one is thermal, low energy particles, and the other is non-thermal, high energy particles.
Some of thermal particles have a parallel velocity less than zero.
However, from (b) this is simply because of oscillations by the large wave amplitude.
All the thermal particles are downstream particles and all the non-thermal particles are reflected upstream ones.
The non-thermal particles are not distributed around the resonant velocity, and have a smaller absolute value of the parallel velocity than the resonant one.
As we see in Fig. 6, when the wave amplitude is large, particles can be trapped by the wave regardless of the resonance condition.
.
On the contrary, when the wave exists, there are two distinct components; one is thermal, low energy particles, and the other is non-thermal, high energy particles.
Some of thermal particles have a parallel velocity less than zero.
However, from (b) this is simply because of oscillations by the large wave amplitude.
All the thermal particles are downstream particles and all the non-thermal particles are reflected upstream ones.
The non-thermal particles are not distributed around the resonant velocity, and have a smaller absolute value of the parallel velocity than the resonant one.
As we see in Fig. 6, when the wave amplitude is large, particles can be trapped by the wave regardless of the resonance condition.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2283f10.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg135.gif) |
Figure 10:
Particle trajectories in the presence of L- (solid lines) and L+ (dashed lines) using the same |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2283f11.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg136.gif) |
Figure 11: a) Difference of perpendicular velocity; and b) parallel position after the interaction of particles in the same phase space as Fig. 7. c) The distribution of particles in velocity space are shown with the resonant velocity (dotted line). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2283f12.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg137.gif) |
Figure 12:
Particle trajectories are shown a) in
|
| Open with DEXTER | |
Figure 12 shows trajectories of particles from those in Fig. 11 in
![]() space (a), in
space (a), in ![]() space (b) and in velocity space (c).
The initial parameters are chosen as
space (b) and in velocity space (c).
The initial parameters are chosen as
![]() ,
,
![]() and 0.9, represented with red, black, and blue lines, respectively.
The first two particles have a smaller initial parallel energy than the potential, however, the particle with
and 0.9, represented with red, black, and blue lines, respectively.
The first two particles have a smaller initial parallel energy than the potential, however, the particle with ![]() goes through the potential.
This is due to the transport property of gyroresonant surfing.
In (a), the reflected particles (red) are accelerated efficiently before and after reflection by the potential; on the contrary, the particle with
goes through the potential.
This is due to the transport property of gyroresonant surfing.
In (a), the reflected particles (red) are accelerated efficiently before and after reflection by the potential; on the contrary, the particle with ![]() propagating to the downstream (black) is slightly accelerated.
From panel b, the reflected particles are trapped before and after reflection.
The transmitted particle with
propagating to the downstream (black) is slightly accelerated.
From panel b, the reflected particles are trapped before and after reflection.
The transmitted particle with ![]() is trapped when it goes through the potential, although one with
is trapped when it goes through the potential, although one with
![]() is not trapped through the trajectory.
Thus, non-thermal particles are accelerated on approaching and coming back from the potential; on the other hand, thermal particles can be accelerated only when they go through the potential.
There is no efficient acceleration in the parallel direction, unlike in Fig. 10b, where the particle is accelerated about four times more efficiently than by specularly reflection.
Furthermore, the particles have smaller
is not trapped through the trajectory.
Thus, non-thermal particles are accelerated on approaching and coming back from the potential; on the other hand, thermal particles can be accelerated only when they go through the potential.
There is no efficient acceleration in the parallel direction, unlike in Fig. 10b, where the particle is accelerated about four times more efficiently than by specularly reflection.
Furthermore, the particles have smaller
![]() than that of specularly reflection,
than that of specularly reflection,
![]() .
This is also because of the transport property of gyroresonant surfing; even when a potential attempts to accelerate particles in the parallel direction, particles can keep the parallel velocity constant while they are accelerated in the perpendicular direction.
We have already illustrated this in Fig. 3.
.
This is also because of the transport property of gyroresonant surfing; even when a potential attempts to accelerate particles in the parallel direction, particles can keep the parallel velocity constant while they are accelerated in the perpendicular direction.
We have already illustrated this in Fig. 3.
Finally, we discuss the dependence of perpendicular acceleration on the spatial scale of the potential and the wave amplitude.
Although the potential difference is believed to be comparable to the upstream plasma kinetic energy, there are not many observations of shock or SLAMS potential, moreover the estimates of spatial scales are still controversial.
Thus, it is interesting to study the dependence of the characteristics of acceleration on the spatial scale of the potential, keeping the potential difference across the layer constant.
These characteristics are determined by the combination of two effects, trapping of a particle by the electromagnetic wave and dragging or pushing by the electrostatic potential.
Therefore, the balance of these two forces is of special importance here.
We also focus on the wave amplitude since the theoretical electric field Eq. (5) is proportional to b2.
We change a, l and b keeping
![]() and the other parameters the same as in Fig. 11.
and the other parameters the same as in Fig. 11.
Figure 13 shows the ensemble average of the perpendicular velocity difference of particles before and after interaction with the profile (a), and those of the maximum values (b) in the b-l parameter space.
Note that the potential spatial scale is directly related to the amplitude of electrostatic field, because we keep the potential difference constant.
From Fig. 13a, looking at a certain l, one can see that
![]() has a maximum in terms of b, and when the l is large, the b tends to be small.
The larger wave amplitude naturally needs the larger electrostatic field to accelerate particles efficiently.
However, the b2 dependence is not clear; this may come from the functional difference between Eqs. (5) and (8).
In (a), when b=1 and l=1, the net acceleration is most efficient, and when b=0.1 and
has a maximum in terms of b, and when the l is large, the b tends to be small.
The larger wave amplitude naturally needs the larger electrostatic field to accelerate particles efficiently.
However, the b2 dependence is not clear; this may come from the functional difference between Eqs. (5) and (8).
In (a), when b=1 and l=1, the net acceleration is most efficient, and when b=0.1 and ![]() ,
acceleration is efficient in a relatively wider parameter space.
In (b), when
,
acceleration is efficient in a relatively wider parameter space.
In (b), when
![]() is large, the maximum is also large.
However, when the wave amplitude is very large and the potential scale is very small, i.e., the electric field amplitude is very large, we can see very efficient acceleration.
Even a very thin shock can produce high energy particles when a large amplitude wave exists.
is large, the maximum is also large.
However, when the wave amplitude is very large and the potential scale is very small, i.e., the electric field amplitude is very large, we can see very efficient acceleration.
Even a very thin shock can produce high energy particles when a large amplitude wave exists.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2283f13.eps}\end{figure}](/articles/aa/full/2005/29/aa2283-04/Timg147.gif) |
Figure 13:
a) Dependence of
|
| Open with DEXTER | |
We have discussed the gyroresonant surfing operating by the combination of trapping of particles by the electromagnetic wave and the parallel force of the electrostatic field. One important aspect of this process is the efficient acceleration in the perpendicular direction. In the presence of a finite amplitude wave, particles are trapped by the wave, repeating acceleration and deceleration as we see in Fig. 5, while they keep the energy constant in the wave frame. When an electrostatic field is introduced here, the parallel force tunes the particle gyrophase to the phase of the wave electric field, resulting in monotonic acceleration in the perpendicular direction. This acceleration mechanism is similar to the conventional surfing acceleration (Lee et al. 1996; Katsouleas & Dawson 1983; Zank et al. 1996; Sagdeev & Shapiro 1973; Sagdeev 1966), where particles "surf'' on the electrostatic field. In our theory, particles surf on the rotating perpendicular electromagnetic wave spirally as seen in Figs. 1b, 3b, and 10c. The acceleration is most efficient in the presence of a right hand polarized anti-parallel propagating wave and a left hand polarized parallel propagating wave in the plasma frame. On the other hand, in the presence of a left hand polarized anti-parallel propagating wave and a right hand polarized parallel propagating wave, particles are decelerated rather than accelerated. Gyroresonant surfing deceleration also exists.
Another important aspect of gyroresonant surfing is transportation of particles downstream even when the particle energy is less than the potential. This is very important since the transport of particles from upstream to downstream of shocks is quite often discussed only in terms of parallel energy balance. Moreover, if a particle is transported to a high potential position then the gyroresonant surfing is terminated; this leads to parallel acceleration of reflected particle due to the electrostatic field as seen in Fig. 10b. The reflection of particles transported to high potential fields by gyroresonant surfing can accelerate particles much more than the specularly reflection, which is simple mirroring of the parallel velocity of particles. Although we have discussed the in-coming particle, it is possible to transport downstream particles upstream without gaining energy of amount of the electrostatic potential difference. The same mechanism can also accelerate or decelerate electrons. The major difference will consist of the scales and characteristics of waves needed to provide a similar efficiency. For electrons, we have to consider the electron scale, high frequency wave, such as whistler waves, instead of the Alfvén waves or MHD waves considered here. Such high frequency waves are also common in the shock environments, for example, whistler precursor of SLAMS (Dudok de Wit et al. 1995). One interesting application to electron transport at collisionless shocks is the so-called de Hoffman-Teller gap (Gedalin 1999). All the electrons passing the shock potential must be accelerated by the amount of the potential difference. Thus, from this idea there should be a hole in the electron distribution, however, such a hole distribution has not been observed in in situ measurements. The gyroresonant surfing can potentially transport electrons without gaining energy from the electrostatic field, and can also decelerate them in the perpendicular direction.
Since the monochromatic waves often observed are excited by backstreaming ions, the wave must be R- in the plasma frame. When we apply the appropriate parameters as often observed in situ measurements, ions are accelerated efficiently and are separated into two populations, one thermal, low-energy downstream particles, and another non-thermal, high-energy upstream particles with a ring beam distribution (Fuselier 1995; Fuselier et al. 1995) or like gyrating ions often associated with the quasi-monochromatic waves (Meziane et al. 2001). Furthermore, the typical energy of accelerated particles by this mechanism can be estimated to be 4-5 times greater than the potential difference of the electrostatic potential. Thus, it is 4-5 times greater than the energy of the upstream particles. This can be much larger than the thermal energy of particles. This particular feature makes this mechanism an excellent candidate to operate as an injection mechanism for DSA acceleration in quasi-parallel shocks. Incoming upstream particles do not satisfy the resonance condition initially, as indicated in Fig. 11c; the resonant velocity (dotted line) is far away from the initial distribution of ions (blue crosses). Thus, those particles are simply decelerated by the potential, then, some of them are trapped by the wave because of the large wave amplitude effects. Among such trapped particles, some can be reflected by the potential and accelerated by gyroresonant surfing, where the potential field attempts to accelerate particles, resulting in clear separation of non-thermal reflected and thermal transmitted particles.
In this paper, we have neglected the wavelength, the wave amplitude, the wave phase velocity, and the plasma flow changes through the shock crossing.
In general, the plasma is compressed by the shock, thus, within linear theory, the wavelength becomes shorter, the wave amplitude becomes larger, the Alfvén velocity becomes larger, and the plasma flow is decelerated downstream of the shock.
A change of wavelength can be crucial for cyclotron resonance; however, as we have shown in Fig. 9, the gyroresonant surfing has a large flexibility, about one order of wavelength, to accelerate particles efficiently.
The amplification of wave amplitude and Alfvén velocity makes the acceleration more efficient, and the deceleration of plasma can decrease the efficiency because of the diminishing of the wave electric field in the S-system.
Further, neglecting those changes corresponds to excluding the possibilities of first and second order Fermi acceleration.
Thus, we have discussed the pure effect of a combination of wave and potential, that is, gyroresonant surfing.
Comparing Fig. 2b or Fig. 10b of Sugiyama et al. (2001) and our Fig. 12c one can see clear difference; the first order Fermi accelerated particle crosses
![]() several times with (approximately) two scattering centers, on the other hand, in our case particle are accelerated monotonically in the perpendicular direction.
While the particle is accelerated by gyroresonant surfing, there is no scattering center.
While the particle is downstream and upstream (
several times with (approximately) two scattering centers, on the other hand, in our case particle are accelerated monotonically in the perpendicular direction.
While the particle is accelerated by gyroresonant surfing, there is no scattering center.
While the particle is downstream and upstream (![]() ), there is only one scattering center.
Furthermore, unlike to their model, where the shock transition has to be sharp, the gyroresonant surfing has a large flexibility of wave amplitude and shock potential width as seen in Fig. 13.
Moreover, since the reflected particles are accelerated substantially, the downstream plasma state is not crucial for those particles.
), there is only one scattering center.
Furthermore, unlike to their model, where the shock transition has to be sharp, the gyroresonant surfing has a large flexibility of wave amplitude and shock potential width as seen in Fig. 13.
Moreover, since the reflected particles are accelerated substantially, the downstream plasma state is not crucial for those particles.
The gyroresonant surfing is efficient in a wider range of parameter space. Importantly it is not an exclusive process. When the field inhomogeneity exists and/or at the oblique shocks, gyroresonant surfing is still efficient (not shown here, details will be published elsewhere). Furthermore, in the presence of elliptically and linearly polarized waves, which are often observed in situ in association with diffuse ions, particles are accelerated efficiently and diffuse in pitch angle at the same time as diffuse ions (submitted to J. Geophys. Res.). We can conclude that gyroresonant surfing provides an efficient injection mechanism; the particles are accelerated from the thermal background and form a non-thermal population to be further accelerated by the DSA. The model electric field Eq. (8) used here is considered to roughly correspond to the shock potential or SLAMS potential. The electrostatic potential of quasi-parallel shocks was not directly measured until recent Cluster attempts (Behlke et al. 2004). Further comparison between our model and observations needs more detailed data of electrostatic fields at shock, together with the parameter changes we mentioned above.
Acknowledgements
The authors would like to thank B. Lefebvre, V. Lobzin, T. Hada, H. Kucharek and M. Scholer for their helpful comments. This work was supported by the STUDIUM program of the Centre region in France.