A&A 438, 721-726 (2005)
DOI: 10.1051/0004-6361:20042212
W. Rammacher1 - M. Cuntz2,3
1 - Kiepenheuer-Institut für Sonnenphysik, Schöneckstr. 6,
79104 Freiburg, Germany
2 -
Department of Physics, Science Hall, University of Texas at Arlington (UTA),
Arlington, TX 76019-0059, USA
3 -
Institut für Theoretische Astrophysik, Universität Heidelberg,
Albert Überle Str. 2, 69120 Heidelberg, Germany
Received 19 October 2004 / Accepted 22 March 2005
Abstract
We assess different types of average temperatures in time-dependent
solar chromosphere models. They include the conventional definition
of mean and median temperature, and a formal definition related to
the model-dependent hydrogen ionization degree, referred to as ionization
temperature. It is found that the latter is always higher than the mean
and median temperatures, except in the photosphere,
and that the mean temperatures are always higher than the median temperatures,
especially in models with frequency spectra. The most dramatic differences
are attained in the topmost portion of one of our models with the ionization
temperatures up to a factor 150 higher than the mean and median
temperatures. The differences between the mean, median, and ionization temperatures
are a direct consequence of nonlinearities ("spikyness'') of the temperatures
in the models mostly due to strong shocks. The main results hold
for both acoustic and magnetic models despite significant differences in the
initial wave energy fluxes, densities, and geometrical settings.
Key words: hydrodynamics - methods: numerical - methods: statistical - magnetohydrodynamics (MHD) - Sun: chromosphere - waves
A key element in the description of solar and stellar chromospheres is the assessment and interpretation of time-averaged temperatures, which are typically given through the analysis of spectral information or evaluation of detailed chromospheric heating simulations (e.g., Schrijver & Zwaan 2000). Theoretical models of solar and stellar chromospheres have been obtained based on acoustic waves and/or different types of magnetic waves as discussed in recent reviews by Ulmschneider & Musielak (2003), Roberts (2004), and Musielak (2004). These models take into account the generation, propagation, and dissipation of the waves, as well as the description of emergent emission. Recent models for the Sun have been given by Rammacher & Ulmschneider (2003), Bogdan et al. (2003), and Wedemeyer et al. (2004). Simulations of chromospheric heating for stars other than the Sun by our group include models by Cuntz et al. (1999), Fawzy et al. (2002), and Rammacher & Cuntz (2003).
A common feature of these models is the strong temperature fluctuation with time at different atmospheric heights. These fluctuations are due to shock heating and are particularly pronounced if the ionization of hydrogen is described in a self-consistent, time-dependent manner (e.g., Carlsson & Stein 1994; Rammacher & Cuntz 2005; Carlsson & Stein 1995; Rammacher & Ulmschneider 2003), as in this case very high temperature jumps occur immediately behind strong shocks. Other types of models used to derive time-averaged temperatures in the solar chromosphere are semi-empirical models, which interpret spectral information ranging from UV to the optical and infrared regimes. Early models by Vernazza et al. (1981), Maltby et al. (1986), Fontenla et al. (1993), as well as more recent models, assume a smooth increase in temperature as function of height, which is now considered highly unrealistic.
In order to illustrate some of the underlying aspects, we pursue a
quantitative analysis of different types of time-averaged temperatures
taking up-to-date theoretical solar chromosphere models as examples.
The different types of average temperatures include the mean temperature
![]() ,
the median temperature
,
the median temperature
![]() ,
and the
ionization temperature
,
and the
ionization temperature
![]() inferred from
the hydrogen ionization degree. Our paper is
structured as follows. In Sect. 2, we describe the basics of the
(magneto-)hydrodynamic code and provide different definitions of
average temperature. In Sect. 3, we give our results and discussion.
The summary and conclusions are given in Sect. 4.
inferred from
the hydrogen ionization degree. Our paper is
structured as follows. In Sect. 2, we describe the basics of the
(magneto-)hydrodynamic code and provide different definitions of
average temperature. In Sect. 3, we give our results and discussion.
The summary and conclusions are given in Sect. 4.
The solar chromospheric models based on acoustic waves or longitudinal flux-tube waves are calculated using the numerical code by Rammacher & Ulmschneider (2003) and Cuntz & Rammacher (2005). This code allows one to compute one-dimensional time-dependent wave propagation in solar and stellar atmospheres, while incorporating the treatment of hydrogen ionization through solving the time-dependent statistical rate equations (see also Carlsson & Stein 1995,1992, for another version of that method). The solutions of the (magneto-)hydrodynamic equations are obtained together with the radiative transfer equation considering departures from local thermodynamic equilibrium (NLTE). Furthermore, the code also considers ionization of magnesium and calcium. The thermodynamical relationships, as well as the Rankine-Hugoniot relations across the shocks, are solved in a self-consistent time-dependent manner. The inner boundary condition allows the treatment of upward propagating waves, whereas the outer boundary condition allows the waves to be transmitted.
The code is suitable for the treatment of monochromatic waves and frequency spectra. With respect to monochromatic wave models, the dynamic structure of the acoustic and magnetic chromosphere models is found to be given by a time-dependent balance among shock heating, radiative and hydrodynamic cooling, and ionization. As expected, the ionization balance of H+/H, Ca II/Ca, and Mg II/Mg is essentially unaffected by the localized energy dissipation behind the shocks as already found in previous models for the Sun (Rammacher & Ulmschneider 2003). This allows the post-shock temperatures to increase beyond the values typically attained in models with time-independent (i.e., instantaneous) ionization. In fact, the formation of Ca II and Mg II emission does not occur immediately behind the shocks and is thus considerably reduced compared to previous models.
The concept of average temperatures is highly problematic in shock-dominated atmospheres. In empirical models, temperatures are typically derived from other quantities such as element ionization stages and electron densities. These quantities are, however, not unambiguously dependent on temperature, thus yielding different types of average temperatures. An observed electron density, for instance, can correspond to radically different temperatures depending on the adopted chromospheric model.
In the following, we introduce three different types of average temperatures to demonstrate the effect of ambiguity. In the existing literature, average quantities are frequently defined at given mass column densities, which is highly appropriate for those observed spectral diagnostics that tend to be formed at a given optical depth. In the present paper, time averages are calculated at a given geometric height (Eulerian frame).
The first type is the "classical'' arithmetic mean temperature,
defined as
![]() .
Here
.
Here ![]() is given by the weights of the N contributions of Ti.
In case of nonequidistant time-spacing, the values of
is given by the weights of the N contributions of Ti.
In case of nonequidistant time-spacing, the values of ![]() will be different, which may occur both in theoretical and observational
studies. In theoretical models,
will be different, which may occur both in theoretical and observational
studies. In theoretical models, ![]() is often chosen differently to
resolve temperature jumps associated with the spiky structure of the
atmosphere.
is often chosen differently to
resolve temperature jumps associated with the spiky structure of the
atmosphere.
The second type of average temperature is the median temperature
![]() ,
which during the timespan of averaging
is defined as temperature where half of the time the instant temperature
is higher and half of the time the instant temperature is lower than that
temperature. The difference between
,
which during the timespan of averaging
is defined as temperature where half of the time the instant temperature
is higher and half of the time the instant temperature is lower than that
temperature. The difference between
![]() and
and
![]() is
a measure of the skewness of the time-dependent temperature fluctuation at
a given height as, e.g., introduced by strong shocks.
is
a measure of the skewness of the time-dependent temperature fluctuation at
a given height as, e.g., introduced by strong shocks.
The third type of average temperature can be obtained from the reanalysis
of the (model-dependent) time-averaged hydrogen ionization degree. In
principle, we find that
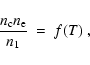 |
(1) |
| (2) | |||
| (3) |
| (4) |
The departure coefficients b1 and b2 for the first and second level,
normalized to the continuum, are
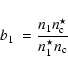 |
(5) |
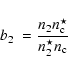 |
(6) |
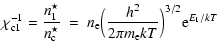 |
(7) | ||
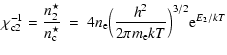 |
(8) |
Due to the nonlinearities and the time-dependent behavior of the relevant
variables (see Fig. 1), Eqs. (2) to (8) cannot hold simultaneously if
![]() ,
,
![]() ,
b1, b2, and T are represented by their mean values.
On the other hand, if mean values are selected for those variables except T,
Eqs. (2) to (8) can be utilized to recalculate T, which shall be defined as
"ionization temperature''
,
b1, b2, and T are represented by their mean values.
On the other hand, if mean values are selected for those variables except T,
Eqs. (2) to (8) can be utilized to recalculate T, which shall be defined as
"ionization temperature''
![]() ,
a new type of "average temperature''.
The fact that
,
a new type of "average temperature''.
The fact that
![]() deviates from
deviates from
![]() ,
as well as from
,
as well as from
![]() in most cases, is a direct consequence of the behavior of the
various particle densities, as well as b1 and b2. This is particularly
evident in models with strong shocks and noninstantaneous ionization.
in most cases, is a direct consequence of the behavior of the
various particle densities, as well as b1 and b2. This is particularly
evident in models with strong shocks and noninstantaneous ionization.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{2212fi1.ps}\end{figure}](/articles/aa/full/2005/29/aa2212-04/Timg25.gif) |
Figure 1:
Time-step of the model representing stochastic
longitudinal flux-tube waves after 2366 s. Shown are
temperature T (thick-solid) and particle densities
n1 (thin-solid), n2 (dashed), and |
| Open with DEXTER | |
Note that
![]() is largely affected by the time-averaged
electron number density, which is chiefly determined by the
increased ionization degree in the post-shock regions, although there are
significant modifications of this picture due to noninstantaneous
ionization. This will result in
is largely affected by the time-averaged
electron number density, which is chiefly determined by the
increased ionization degree in the post-shock regions, although there are
significant modifications of this picture due to noninstantaneous
ionization. This will result in
![]() being higher than
being higher than
![]() and
and
![]() .
Nonetheless, the above given
definition of
.
Nonetheless, the above given
definition of
![]() is only one of several possibilities.
Theoretically, for any ionized stage of an element (e.g., Ca II,
Mg II) such a ionization temperature could be defined. Undisputably,
however, hydrogen is by far the most abundant element in stellar
atmospheres, and furthermore ionization of hydrogen is by far the most
important process for determining the electron density particularly
in the upper solar chromosphere, making the above choice of
is only one of several possibilities.
Theoretically, for any ionized stage of an element (e.g., Ca II,
Mg II) such a ionization temperature could be defined. Undisputably,
however, hydrogen is by far the most abundant element in stellar
atmospheres, and furthermore ionization of hydrogen is by far the most
important process for determining the electron density particularly
in the upper solar chromosphere, making the above choice of
![]() most appropriate.
most appropriate.
In empirical models, a further type of "average temperature''
arises that is not directly related to any of the temperatures
discussed here. This temperature is defined as reproducing quantities
as close as possible to the observed temporal means. How this
semi-empirical temperature relates to any physical temperature in a
dynamic model is not clear and will depend on the observable(s) used in
the semi-empirical model. If the observable is the mean intensity in
the UV (as is the case in VAL3C), the semi-empirical temperature will
always sample the higher temperatures exhibited in the dynamic model
rather than temperatures close to
![]() or
or
![]() .
.
In the following, we consider three different models: a monochromatic acoustic model (model 1), a monochromatic longitudinal flux-tube model (model 2), and a stochastic longitudinal flux-tube model (model 3). The construction of these models requires the computation of input parameters. They include wave energy fluxes for each of those models, the wave frequency spectrum for the stochastic model, and the representative wave period in the monochromatic models.
The computation of the acoustic energy flux follows the work by
Ulmschneider et al. (1996), who incorporated an improved description of the spatial
and temporal spectrum of the turbulent flow. These models utilize
an extended Kolmogorov spectrum with a modified Gaussian frequency factor.
The acoustic energy flux is found to be dependent on the mixing-length
parameter ![]() ,
for which we use
,
for which we use ![]() as indicated by solar
studies (Steffen 1993; Robinson et al. 2003). Similar investigations in the case of
longitudinal flux-tube waves have been presented by Ulmschneider & Musielak (1998).
The initial wave energy flux for our acoustic model is thus given as
as indicated by solar
studies (Steffen 1993; Robinson et al. 2003). Similar investigations in the case of
longitudinal flux-tube waves have been presented by Ulmschneider & Musielak (1998).
The initial wave energy flux for our acoustic model is thus given as
![]() erg cm-2 s-1, whereas the
initial wave energy flux for the longitudinal flux-tube models is given as
erg cm-2 s-1, whereas the
initial wave energy flux for the longitudinal flux-tube models is given as
![]() erg cm-2 s-1. The work by
Ulmschneider & Musielak (1998) also provides information on the frequency spectrum for
polychromatic longitudinal waves. The wave period at the maximum of the
energy distribution for both the acoustic and longitudinal frequency
spectrum is found to be close to 60 s. Therefore, this value will be
used for the two monochromatic wave computations in this study.
erg cm-2 s-1. The work by
Ulmschneider & Musielak (1998) also provides information on the frequency spectrum for
polychromatic longitudinal waves. The wave period at the maximum of the
energy distribution for both the acoustic and longitudinal frequency
spectrum is found to be close to 60 s. Therefore, this value will be
used for the two monochromatic wave computations in this study.
Furthermore, we must also define the geometrical setting. Model 1 is based on plane-parallel geometry, while for model 2 and model 3 flux-tube geometry is assumed. The flux-tube geometry is based on the idea that at very low atmospheric heights, unobstructed spreading occurs, whereas at larger heights, the influence of neighboring flux tubes (e.g., Schrijver & Title 2003; Frutiger & Solanki 2001) dominates, thus leading to reduced spreading. Eventually, a distinct tube opening radius is reached (see Rammacher & Ulmschneider 1989; Fawzy et al. 2002; Rammacher & Ulmschneider 2003; Fawzy et al. 1998, for earlier work). For the flux-tube model in this paper, the bottom opening radius is set as 55 km, corresponding to half of the photospheric density scale-height. The top opening radius of the flux tube is assumed to be 175 km. Therefore, the top opening area of the tube is about ten times larger than its bottom area. At relatively low heights, exponential spreading occurs. Full spreading is attained at a height of 620 km.
![\begin{figure}
\par\includegraphics[angle=-90,width=11cm,clip]{2212fi2a.ps}\par\includegraphics[angle=-90,width=11cm,clip]{2212fi2b.ps}\end{figure}](/articles/aa/full/2005/29/aa2212-04/Timg30.gif) |
Figure 2: Temperature contour maps for the monochromatic longitudinal wave model (model 2) ( top) and stochastic longitudinal wave model (model 3) ( bottom) based on the data also taken for the calculation of the different types of time-averaged temperatures. |
| Open with DEXTER | |
Temperature contour maps of the monochromatic and stochastic longitudinal wave models based on the data used for the calculation of the different types of time-averaged temperatures are given in Fig. 2.
In the following, we discuss results for the different types of average temperatures obtained for our acoustic and magnetic wave models. In that respect, we focus on timespans where the switch-on phase of the wave entering the undisturbed atmosphere has completely subsided. In the case of the monochromatic acoustic and magnetic wave model (models 1 and 2, respectively), this status has been achieved after 50 wave periods entered the atmospheric computational domain. Note that due to the inclusion of time-dependent ionization, this timespan is longer than in previous models with time-independent ionization where dynamic equilibrium was typically reached after 20 wave periods.
Figure 3 shows the behavior of the pre-shock and post-shock temperatures of model 1, T1 and T2, respectively. Evidently, only very small variations of T1 and T2 exist - unequivocal evidence of dynamical equilibrium. In the case of the stochastic longitudinal wave model (model 3), no dynamic equilibrium persists. Nevertheless, time-averaged temperatures were calculated after a sufficiently long elapsed time to ensure that the dynamics of the wave is determined by the employed frequency spectrum rather than switch-on effects. The timespans for the calculation of time-averaged temperatures for models 1-3 have been 1021 s, 1861 s, and 909 s, respectively.
Figure 4 shows the behavior of
![]() ,
,
![]() ,
and
,
and
![]() for models 1-3. It is found that
for models 1-3. It is found that
![]() is higher than both
is higher than both
![]() and
and
![]() ,
and
,
and
![]() is higher than
is higher than
![]() at all heights except in the photosphere.
For model 1,
at all heights except in the photosphere.
For model 1,
![]() ,
,
![]() ,
and
,
and
![]() at 1000 km are 3810 K, 4140 K, and 6100 K; they are
3790 K, 4270 K, and 6690 K at 1500 km, and
5310 K, 5840 K, and 8050 K at 2000 km, respectively. In model 2,
those temperatures are generally higher, but it is found that the
differences between the different types of average temperatures at a
given height are about the same, irrespective of the different
initial wave energy fluxes, densities, and geometries of the two models.
This phenomenon is an intimate consequence of the limiting shock strength
behavior of those waves as previously discussed by Ulmschneider (1970), Cuntz & Ulmschneider (1988), and
Cuntz (2004). For further results on the propagation of longitudinal tube
waves with the consideration of time-dependent ionization see Rammacher & Cuntz (2005).
at 1000 km are 3810 K, 4140 K, and 6100 K; they are
3790 K, 4270 K, and 6690 K at 1500 km, and
5310 K, 5840 K, and 8050 K at 2000 km, respectively. In model 2,
those temperatures are generally higher, but it is found that the
differences between the different types of average temperatures at a
given height are about the same, irrespective of the different
initial wave energy fluxes, densities, and geometries of the two models.
This phenomenon is an intimate consequence of the limiting shock strength
behavior of those waves as previously discussed by Ulmschneider (1970), Cuntz & Ulmschneider (1988), and
Cuntz (2004). For further results on the propagation of longitudinal tube
waves with the consideration of time-dependent ionization see Rammacher & Cuntz (2005).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{2212fi3.ps}\end{figure}](/articles/aa/full/2005/29/aa2212-04/Timg31.gif) |
Figure 3: Minimum and maximum temperature values for the pre-shock and post-shock temperatures T1 and T2(solid lines) given by the monochromatic acoustic wave model (model 1) after dynamic equilibrium has been attained. The average values are given as dotted lines. Note that shock formation occurs near 570 km. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{2212fi4a.ps}\par\i...
...2fi4b.ps}\par\includegraphics[angle=-90,width=7cm,clip]{2212fi4c.ps}\end{figure}](/articles/aa/full/2005/29/aa2212-04/Timg32.gif) |
Figure 4:
Comparison of
|
| Open with DEXTER | |
Table 1: Time-averaged b1 and b2 values.
A drastically different picture concerning the different types of average
temperatures emerges for model 3. Here it is found that
![]() ,
,
![]() ,
and
,
and
![]() at 1000 km are given as 3250 K, 3450 K,
and 7000 K; at 1500 km, they are given as 2440 K, 3330 K, and 8650 K; and
at 2000 km, they are given as 1835 K, 2890 K, and 19200 K, respectively.
These extremely large differences between
at 1000 km are given as 3250 K, 3450 K,
and 7000 K; at 1500 km, they are given as 2440 K, 3330 K, and 8650 K; and
at 2000 km, they are given as 1835 K, 2890 K, and 19200 K, respectively.
These extremely large differences between
![]() and
and
![]() ,
on one hand, and
,
on one hand, and
![]() ,
on the other hand,
particularly at large chromospheric heights, are due to the highly nonlinear
behavior of the temperature that is a consequence of the occurrence of
strong shocks formed by merging of shocks in the stochastic wave field.
,
on the other hand,
particularly at large chromospheric heights, are due to the highly nonlinear
behavior of the temperature that is a consequence of the occurrence of
strong shocks formed by merging of shocks in the stochastic wave field.
Very low temperatures are attained for
![]() ,
especially at
large chromospheric heights, a consequence of the presence of strong shocks,
which noticeably affect
,
especially at
large chromospheric heights, a consequence of the presence of strong shocks,
which noticeably affect
![]() ,
but barely
,
but barely
![]() .
In model 3,
.
In model 3,
![]() ranges between 1600 and 1850 K at heights
beyond 2000 km, thus constituting absurdly low values for any type
of chromospheric structure. On the other hand,
ranges between 1600 and 1850 K at heights
beyond 2000 km, thus constituting absurdly low values for any type
of chromospheric structure. On the other hand,
![]() is found
to reach 254 000 K at 2480 km, the outermost point of our model, thus
becoming a factor of more than 150 higher than
is found
to reach 254 000 K at 2480 km, the outermost point of our model, thus
becoming a factor of more than 150 higher than
![]() .
An important property affecting
.
An important property affecting
![]() is the extreme NLTE effect impacting the degree of hydrogen
ionization (see Table 1); e.g., at 2000 km in model 3, b1 and b2are identified as
is the extreme NLTE effect impacting the degree of hydrogen
ionization (see Table 1); e.g., at 2000 km in model 3, b1 and b2are identified as
![]() and
and
![]() ,
respectively.
The fact that in the stochastic magnetic wave model, contrary to the
monochromatic magnetic wave model, very low temperatures are reached
at large heights most of the time is also visible from the temperature
contour maps (Fig. 2).
,
respectively.
The fact that in the stochastic magnetic wave model, contrary to the
monochromatic magnetic wave model, very low temperatures are reached
at large heights most of the time is also visible from the temperature
contour maps (Fig. 2).
The uppermost portion of the chromosphere heated by stochastic longitudinal flux-tube waves is the most drastic case of differences in average temperatures, according to the adopted definitions. A cool chromosphere, identified by its mean temperature, can thus show the same mean degree of hydrogen ionization as a "classical'' chromosphere with a relatively high mean temperature. The customary definition of mean and median temperature therefore seems inappropriate for describing shock-heated atmospheres - assuming that such strong shocks as in model 3 (see Fig. 1) exist in reality. This pivotal issue is part of an ongoing debate that will be briefly visited in the next section.
We have discussed the significance of different types of average
temperatures with respect to time-dependent solar chromosphere
models. Specifically, we considered a monochromatic acoustic model,
a monochromatic longitudinal flux-tube model, and a stochastic
longitudinal flux-tube model. The different definitions of
average temperature include its conventional definition (
![]() ),
the median of the time-dependent temperature (
),
the median of the time-dependent temperature (
![]() ),
and a formal definition given by the analysis of the time-averaged
hydrogen ionization degree (
),
and a formal definition given by the analysis of the time-averaged
hydrogen ionization degree (
![]() ).
).
For all three models, we found that beyond photospheric levels,
![]() is always higher than
is always higher than
![]() ,
and
,
and
![]() is
always higher than
is
always higher than
![]() .
In the stochastic wave model, the differences
between the three different average temperatures are found to increase
with height. This result is a direct consequence of the nonlinearities
and time fluctuations exhibited by the wave simulations. For instance,
in the stochastic wave model
.
In the stochastic wave model, the differences
between the three different average temperatures are found to increase
with height. This result is a direct consequence of the nonlinearities
and time fluctuations exhibited by the wave simulations. For instance,
in the stochastic wave model
![]() is found to exceed 40 000 K
beyond 2200 km, whereas
is found to exceed 40 000 K
beyond 2200 km, whereas
![]() is found to stay below 4500 K
at all heights above the photosphere. On the other hand,
is found to stay below 4500 K
at all heights above the photosphere. On the other hand,
![]() is as low as 1600 K as reached at heights above 2000 km in the stochastic
longitudinal flux-tube model. It is also found that in monochromatic
wave simulations,
is as low as 1600 K as reached at heights above 2000 km in the stochastic
longitudinal flux-tube model. It is also found that in monochromatic
wave simulations,
![]() gradually increases with height, as
previously noted by Rammacher & Ulmschneider (2003); whereas in the stochastic wave
simulation,
gradually increases with height, as
previously noted by Rammacher & Ulmschneider (2003); whereas in the stochastic wave
simulation,
![]() decreases with height, consistent with
earlier results by Carlsson & Stein (1994,1995) and Rammacher & Ulmschneider (2003).
decreases with height, consistent with
earlier results by Carlsson & Stein (1994,1995) and Rammacher & Ulmschneider (2003).
An important question closely related to the topic of this paper
concerns the realistic behavior of the "real'' time-averaged
temperature
![]() exhibited by the magnetic and nonmagnetic
solar chromosphere for the different atmospheric heights. This
is the focus of an ongoing debate with a wide variety of views.
On one hand, it has been argued that
exhibited by the magnetic and nonmagnetic
solar chromosphere for the different atmospheric heights. This
is the focus of an ongoing debate with a wide variety of views.
On one hand, it has been argued that
![]() increases with
height to account for the variety of UV diagnostics
(e.g., Kalkofen et al. 1999). On the other hand, Carlsson & Stein (1994,1995)
originally proposed that
increases with
height to account for the variety of UV diagnostics
(e.g., Kalkofen et al. 1999). On the other hand, Carlsson & Stein (1994,1995)
originally proposed that
![]() decreases with height
in stark contrast to "classical'' solar chromosphere models.
In fact, Ayres (2002) argued that this type of model is
"not even cold enough'', as suggested by the off-limb solar
CO emission. An intermediate possibility is given by the concept
of thermal bifurcation and radiative instability, which points to
high and low temperatures occurring at the same mass column density
within the outer solar atmosphere
(e.g., Ayres 1981; Cuntz & Muchmore 1994; Muchmore & Ulmschneider 1985; Solanki et al. 1994, and others).
decreases with height
in stark contrast to "classical'' solar chromosphere models.
In fact, Ayres (2002) argued that this type of model is
"not even cold enough'', as suggested by the off-limb solar
CO emission. An intermediate possibility is given by the concept
of thermal bifurcation and radiative instability, which points to
high and low temperatures occurring at the same mass column density
within the outer solar atmosphere
(e.g., Ayres 1981; Cuntz & Muchmore 1994; Muchmore & Ulmschneider 1985; Solanki et al. 1994, and others).
A different type of approach consists in considering effects due to 3-D propagation of the waves as discussed by Wedemeyer et al. (2004), Kalkofen (2004), and Ulmschneider et al. (2005), among others. Ulmschneider et al. (2005) argue that acoustic waves are expected to propagate in cone-shaped channels, thus avoiding significant shock overtaking and the formation of strong shocks (as obtained in model 3), but generating a weak quasi-steady level of background heating. If correct, acoustic and magnetic waves may therefore be able to produce a quasi-monotonic increase in temperature with height, consistent with previous semi-empirical models.
Acknowledgements
This work has been supported by the German Research Foundation DFG through grant UL57/33-1 (W. R.) and by NSF through grant ATM-0087184 (M. C.). We also appreciate comments by an anonymous referee on the temperature definition in empirical chromosphere models.