A&A 438, 349-363 (2005)
DOI: 10.1051/0004-6361:20052765
Spherical harmonic decomposition of solar magnetic fields
R. Knaack1 - J. O. Stenflo1,2
1 - Institute of Astronomy, ETH-Zentrum, 8092 Zürich, Switzerland
2 - Faculty of Mathematics and Science, University of Zurich, 8057 Zürich, Switzerland
Received 25 January 2005 / Accepted 5 April 2005
Abstract
We have investigated the temporal evolution of large-scale magnetic fields in the solar photosphere during the time interval 1966-2004 by means of spherical harmonic decomposition and subsequent time series analysis. Two data sets of daily magnetograms recorded at the Mt. Wilson and Kitt Peak observatories were used to calculate the spherical harmonic coefficients of the radial magnetic field for axisymmetric (m=0) and non-axisymmetric (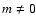 )
modes. Time series analysis was then applied to deduce their temporal variations. A third data set of synoptic Carrington rotation maps from Kitt Peak was also analyzed for completeness. Besides the obvious
)
modes. Time series analysis was then applied to deduce their temporal variations. A third data set of synoptic Carrington rotation maps from Kitt Peak was also analyzed for completeness. Besides the obvious
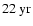 magnetic cycle, we have found evidence for intermittent oscillations with periods of
magnetic cycle, we have found evidence for intermittent oscillations with periods of
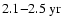 ,
,
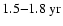 and
and
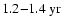 .
The biennial oscillation occurred during the solar maxima of cycles 20-22 (and likely also during the current cycle 23) and was most pronounced for modes that resemble non-linear dynamo waves (Stix 1972, A&A, 20, 9).
The
.
The biennial oscillation occurred during the solar maxima of cycles 20-22 (and likely also during the current cycle 23) and was most pronounced for modes that resemble non-linear dynamo waves (Stix 1972, A&A, 20, 9).
The
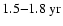 period was stronger during the odd cycles 21 and 23 than during the even cycles 20 and 22, whereas the opposite was the case for the
period was stronger during the odd cycles 21 and 23 than during the even cycles 20 and 22, whereas the opposite was the case for the
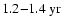 period. Similar variations of
period. Similar variations of
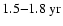 have recently been detected in the north-south asymmetry of the magnetic flux
(Knaack et al. 2004, A&A, 418, L17),
while quasi-periodicities of
have recently been detected in the north-south asymmetry of the magnetic flux
(Knaack et al. 2004, A&A, 418, L17),
while quasi-periodicities of  1.3 yr have been observed in the rotation rate near the base of the convection zone (Howe et al. 2000, Science, 287, 2456),
in the heliosphere and geomagnetic activity (Lockwood 2001, J. Geophys. Res., 106, 16 021)
in sunspot areas (Krivova & Solanki 2002, A&A, 394, 701),
and in the large-scale photospheric magnetic field (Knaack et al. 2005, A&A, in press).
In agreement with the latter study, we have found additional quasi-periodicities in the range
1.3 yr have been observed in the rotation rate near the base of the convection zone (Howe et al. 2000, Science, 287, 2456),
in the heliosphere and geomagnetic activity (Lockwood 2001, J. Geophys. Res., 106, 16 021)
in sunspot areas (Krivova & Solanki 2002, A&A, 394, 701),
and in the large-scale photospheric magnetic field (Knaack et al. 2005, A&A, in press).
In agreement with the latter study, we have found additional quasi-periodicities in the range
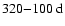 and rotational periods of
and rotational periods of
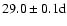 ,
,
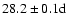 ,
and
,
and
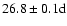 .
Compared to earlier decompositions by Stenflo & Vogel (1986, Nature, 319, 285)
and Stenflo & Güdel (1988, A&A, 191, 137),
we can confirm the main features of their results, although several modifications need to be considered.
.
Compared to earlier decompositions by Stenflo & Vogel (1986, Nature, 319, 285)
and Stenflo & Güdel (1988, A&A, 191, 137),
we can confirm the main features of their results, although several modifications need to be considered.
Key words: Sun: activity - Sun: magnetic fields - Sun: photosphere - Sun: rotation
1 Introduction
Stenflo:Vogel:1986Paper I
Stenflo:Guedel:1988Paper II
The decomposition of the radial component of large-scale solar magnetic fields in terms of spherical harmonics Ylm by Stenflo & Vogel (1986) and Stenflo & Güdel (1988) revealed a modal structure of resonance frequencies for the rotationally symmetric zonal modes (m=0). Their analysis of a
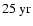 long data set of synoptic magnetic field maps from 1959 to 1984 showed that modes with odd degree l, which are antisymmetric with regard to the equatorial plane of the Sun, were dominated by the
long data set of synoptic magnetic field maps from 1959 to 1984 showed that modes with odd degree l, which are antisymmetric with regard to the equatorial plane of the Sun, were dominated by the
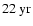 magnetic cycle. This Hale cycle was absent for even (symmetric) modes. Instead, a ridge-like pattern of resonance frequencies increasing with l was detected for
magnetic cycle. This Hale cycle was absent for even (symmetric) modes. Instead, a ridge-like pattern of resonance frequencies increasing with l was detected for
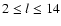 ,
which was interpreted as a possible sign of constructive and destructive interference of global magnetic waves in the solar interior.
,
which was interpreted as a possible sign of constructive and destructive interference of global magnetic waves in the solar interior.
The dominance of the
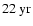 magnetic cycle for odd modes was corroborated by an analysis of zonal distributions of magnetic polarities inferred from H
magnetic cycle for odd modes was corroborated by an analysis of zonal distributions of magnetic polarities inferred from H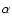 data for the period
1941-1984 (Stenflo & Weisenhorn 1987). The pattern of resonance frequencies for the even modes, however, could not be verified, which was attributed to the low signal-to-noise ratio of the data. An analysis of Greenwich sunspot data from 1874-1976 by Gokhale et al. (1992) confirmed again the
data for the period
1941-1984 (Stenflo & Weisenhorn 1987). The pattern of resonance frequencies for the even modes, however, could not be verified, which was attributed to the low signal-to-noise ratio of the data. An analysis of Greenwich sunspot data from 1874-1976 by Gokhale et al. (1992) confirmed again the
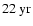 period for odd modes, but the authors concluded that there was no evidence of any other
period for odd modes, but the authors concluded that there was no evidence of any other 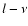 relation (
relation (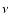 denotes frequency). From the theoretical point of view, model calculations of a 1D axisymmetric mean-field dynamo by Hoyng et al. (1994) accounted for the
denotes frequency). From the theoretical point of view, model calculations of a 1D axisymmetric mean-field dynamo by Hoyng et al. (1994) accounted for the
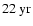 cycle in the odd modes and the phase relations in terms of rapid random fluctuations in the dynamo parameter
cycle in the odd modes and the phase relations in terms of rapid random fluctuations in the dynamo parameter 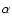 .
However, a modal structure for the even modes could not be reproduced.
.
However, a modal structure for the even modes could not be reproduced.
Given the conflicting observational evidence and the important constraints which a possible modal structure of the global magnetic fields may introduce on solar dynamo theories, we have continued the earlier work and decomposed three different data sets in spherical harmonics. Compared to Stenflo & Vogel (1986) and Stenflo & Güdel (1988), where solely synoptic magnetic field maps from the Mt. Wilson and Kitt Peak observatories were used, we have focused this time mainly on daily magnetograms. Unlike synoptic maps, which represent the solar disk near the central meridian as a function of Carrington longitude over a full Carrington rotation (27.2753 days) and thus mix longitude and time coordinates, magnetograms allow a straightforward expansion of the radial magnetic field not only for the rotationally symmetric modes (m=0) but also for the non-axisymmetric modes (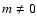 ). The first data set that we have analyzed consists of daily magnetograms recorded at the Mount Wilson observatory from 1966 to 2004, the second one of daily magnetograms recorded at the Kitt Peak Vacuum Telescope from 1976 to 2003. Since additional data have become available for synoptic charts as well, we have again considered the Kitt Peak synoptic charts from 1975 to 2003 to complete the present analysis. We subsequently used the Lomb-Scargle method as well as Fourier and wavelet analysis to deduce the variations of the spherical harmonic coefficient time series. A more detailed description of the data and the reduction procedure is given in Sect. 2.
). The first data set that we have analyzed consists of daily magnetograms recorded at the Mount Wilson observatory from 1966 to 2004, the second one of daily magnetograms recorded at the Kitt Peak Vacuum Telescope from 1976 to 2003. Since additional data have become available for synoptic charts as well, we have again considered the Kitt Peak synoptic charts from 1975 to 2003 to complete the present analysis. We subsequently used the Lomb-Scargle method as well as Fourier and wavelet analysis to deduce the variations of the spherical harmonic coefficient time series. A more detailed description of the data and the reduction procedure is given in Sect. 2.
The results of our present analysis support in principle the earlier findings of Stenflo & Vogel (1986) and Stenflo & Güdel (1988). However, the extended data sets together with improved time series analysis have provided a clearer picture of the temporal behavior of the large-scale solar magnetic fields, and several modifications therefore need to be taken into account. As far as the axisymmetric modes with odd l are concerned, they do show the dominant
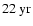 magnetic cycle, but additionally a pronounced biennial oscillation with a period of
magnetic cycle, but additionally a pronounced biennial oscillation with a period of
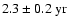 has become evident for l=5,7,9 during the maxima of solar cycles 20-22 and possibly also during the current cycle 23. The shape of these time series resembles, with exception of the biennial oscillation, closely the non-linear dynamo wave for the azimuthal vector potential A derived by Stix (1972). The modes with l=11,13 show a shorter periodicity of
has become evident for l=5,7,9 during the maxima of solar cycles 20-22 and possibly also during the current cycle 23. The shape of these time series resembles, with exception of the biennial oscillation, closely the non-linear dynamo wave for the azimuthal vector potential A derived by Stix (1972). The modes with l=11,13 show a shorter periodicity of
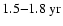 that was present during all four cycles 20-23 but stronger during the odd cycles 21 and 23. This is in good agreement with the distinct periodicities of
that was present during all four cycles 20-23 but stronger during the odd cycles 21 and 23. This is in good agreement with the distinct periodicities of
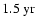 and
and
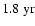 that we have recently found in the north-south asymmetry of the (unsigned) magnetic flux for the time intervals 1978-1984 and 1995-2001, respectively (Knaack et al. 2004). The biennial oscillation and the
that we have recently found in the north-south asymmetry of the (unsigned) magnetic flux for the time intervals 1978-1984 and 1995-2001, respectively (Knaack et al. 2004). The biennial oscillation and the
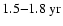 periodicity have also been detected in our time series analysis of longitudinally averaged synoptic maps (Knaack et al. 2005). The even modes also show the biennial oscillation for l=6,8,10, whereas the
periodicity have also been detected in our time series analysis of longitudinally averaged synoptic maps (Knaack et al. 2005). The even modes also show the biennial oscillation for l=6,8,10, whereas the
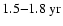 period is rather faint for higher l. Instead, a
period is rather faint for higher l. Instead, a
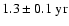 oscillation occurs for l=12,14, and it was apparently strongest during the maxima of the even cycles 20 and 22. Variations with a period of
oscillation occurs for l=12,14, and it was apparently strongest during the maxima of the even cycles 20 and 22. Variations with a period of 
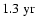 have recently been observed in the rotation rate near the base of the convection zone (Howe et al. 2000), in the heliosphere and geomagnetic activity (Lockwood 2001, and references therein; see also Mursula et al. 2003), in sunspot numbers and sunspot areas (Krivova & Solanki 2002) and in the large-scale photospheric magnetic field (Knaack et al. 2005). In the latter paper we have suggested that the
have recently been observed in the rotation rate near the base of the convection zone (Howe et al. 2000), in the heliosphere and geomagnetic activity (Lockwood 2001, and references therein; see also Mursula et al. 2003), in sunspot numbers and sunspot areas (Krivova & Solanki 2002) and in the large-scale photospheric magnetic field (Knaack et al. 2005). In the latter paper we have suggested that the
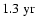 period is related to large-scale magnetic surges towards the poles described for instance by Howard & Labonte (1981) and Wang et al. (1989). Finally, our present analysis has revealed several intermediate periodicities in the range of
period is related to large-scale magnetic surges towards the poles described for instance by Howard & Labonte (1981) and Wang et al. (1989). Finally, our present analysis has revealed several intermediate periodicities in the range of
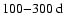 and rotational periods of
and rotational periods of
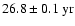 ,
,
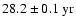 and
and
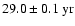 ,
which is in accordance with Knaack et al. (2005).
,
which is in accordance with Knaack et al. (2005).
Evidence for several of the above mentioned periodicities was already provided by Stenflo & Vogel (1986) and Stenflo & Güdel (1988). In conjunction with our results in Knaack et al. (2005,2004), we are therefore convinced that the solar magnetic fields exhibit (quasi-) periodic variations on time scales shorter than the
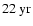 magnetic cycle (or
magnetic cycle (or
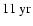 sunspot cycle) that are not random but clearly structured. Whether these variations can be explained in terms of dynamo theory, with the interference of magnetic waves in the solar interior as suggested by Stenflo & Vogel (1986) and Stenflo & Güdel (1988) or possibly with Rossby-like modes as proposed by Dzhalilov et al. (2002) remains to be seen. We present the results for the axisymmetric modes in Sect. 3.1, and for non-axisymmetric modes in Sect. 3.2. The discussion of the detected periods is given in Sect. 4.
sunspot cycle) that are not random but clearly structured. Whether these variations can be explained in terms of dynamo theory, with the interference of magnetic waves in the solar interior as suggested by Stenflo & Vogel (1986) and Stenflo & Güdel (1988) or possibly with Rossby-like modes as proposed by Dzhalilov et al. (2002) remains to be seen. We present the results for the axisymmetric modes in Sect. 3.1, and for non-axisymmetric modes in Sect. 3.2. The discussion of the detected periods is given in Sect. 4.
2 Data and reduction procedure
In this section a detailed explanation of the data and the data analysis is given. Firstly, we focus on the three data sets and the modifications that were applied to the raw data. Secondly, we outline the analysis methods, which use concepts from helioseismology.
2.1 Data
Three data sets were used. The main emphasis was on daily magnetograms because of their, compared to synoptic maps, favorable properties concerning the decomposition into non-axisymmetric modes 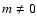 .
However, we also used one data set of synoptic charts for the decomposition into axisymmetric modes m= 0 for the sake of completeness.
.
However, we also used one data set of synoptic charts for the decomposition into axisymmetric modes m= 0 for the sake of completeness.
2.1.1 Mt. Wilson magnetograms
The first data set consists of  55 000 magnetograms recorded at the Mount Wilson Observatory from September 1966 to September 2004, covering approximately
55 000 magnetograms recorded at the Mount Wilson Observatory from September 1966 to September 2004, covering approximately 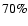 of the days in this time interval. Multiple records per day exist from December 1985 onwards. Each magnetogram is originally a
of the days in this time interval. Multiple records per day exist from December 1985 onwards. Each magnetogram is originally a
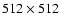 full-disk image of the Sun in image plane coordinates, each pixel gives the line-of-sight component of the magnetic field vector (measured in the spectral line Fe I 525.02 nm) of the respective surface element. A detailed description of the magnetograph is given by Howard et al. (1983). Instead of the original raw magnetograms we used reduced magnetograms that had been mapped into a
full-disk image of the Sun in image plane coordinates, each pixel gives the line-of-sight component of the magnetic field vector (measured in the spectral line Fe I 525.02 nm) of the respective surface element. A detailed description of the magnetograph is given by Howard et al. (1983). Instead of the original raw magnetograms we used reduced magnetograms that had been mapped into a
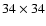 grid of heliographic sine longitude and sine latitude coordinates. They were kindly provided by J. E. Boyden (UCLA). We preferred low-resolution data in order to be consistent with the synoptic maps applied in Stenflo & Vogel (1986) and Stenflo & Güdel (1988), which had 36 sectors in longitude and 30 zones in sine latitude. The question of resolution, however, has some undesired numerical effects on the spherical harmonic decomposition, which will be discussed briefly in Sect. 2.2.3.
grid of heliographic sine longitude and sine latitude coordinates. They were kindly provided by J. E. Boyden (UCLA). We preferred low-resolution data in order to be consistent with the synoptic maps applied in Stenflo & Vogel (1986) and Stenflo & Güdel (1988), which had 36 sectors in longitude and 30 zones in sine latitude. The question of resolution, however, has some undesired numerical effects on the spherical harmonic decomposition, which will be discussed briefly in Sect. 2.2.3.
The spectral line Fe I 525.02 nm exhibits considerable Zeeman saturation (nonlinearity in the polarization signal when the Zeeman splitting is large) and temperature sensitivity (weakening of the line in magnetic regions). These effects and their center-to-limb variation have been calibrated (Stenflo 1972; Howard & Stenflo 1972) and the magnetograms were adjusted accordingly. The line-of-sight component of the magnetic field vector was converted into the approximate flux density under the assumption that magnetic fields are radial in the photosphere, which is incorrect in strong active regions but is a close approximation in quieter areas (Bernasconi 1997; Wang & Sheeley 1992).
2.1.2 Kitt Peak magnetograms
The second data set consists of  7700 full-disk magnetograms recorded at the National Solar Observatory at Kitt Peak (NSO/KP) from February 1974 to September 2003. The observations were made in the spectral line Fe I 868.8 nm with a short interlude from April to November 1992 when the line was Fe I 550.7 nm. The data coverage before August 1976 was rather poor and thus we considered only data after this date. Prior to 1992, a 512-channel magnetograph (Livingston et al. 1976) was used to produce
7700 full-disk magnetograms recorded at the National Solar Observatory at Kitt Peak (NSO/KP) from February 1974 to September 2003. The observations were made in the spectral line Fe I 868.8 nm with a short interlude from April to November 1992 when the line was Fe I 550.7 nm. The data coverage before August 1976 was rather poor and thus we considered only data after this date. Prior to 1992, a 512-channel magnetograph (Livingston et al. 1976) was used to produce
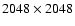 full-disk images of the Sun. It was then replaced with a spectromagnetograph (Jones et al. 1992), and the resolution was reduced to
full-disk images of the Sun. It was then replaced with a spectromagnetograph (Jones et al. 1992), and the resolution was reduced to
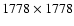 .
.
Again we did not use the raw magnetograms but a remapped set of radial magnetic flux maps in heliographic longitude and sine latitude coordinates with a constant resolution of
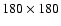 .
They were compiled using codes kindly made available by J. Harvey (NSO). A description of the data reduction, including the transformation into radial magnetic flux density, is given in Harvey & Worden (1998) and Worden & Harvey (2000). The older magnetograms recorded with the 512-channel magnetograph showed a radial and an east-west trend of the zero point, which had to be individually fitted and removed.
The magnetograms recorded with the new spectromagnetograph did not seem to be influenced by similar effects and were therefore not corrected.
.
They were compiled using codes kindly made available by J. Harvey (NSO). A description of the data reduction, including the transformation into radial magnetic flux density, is given in Harvey & Worden (1998) and Worden & Harvey (2000). The older magnetograms recorded with the 512-channel magnetograph showed a radial and an east-west trend of the zero point, which had to be individually fitted and removed.
The magnetograms recorded with the new spectromagnetograph did not seem to be influenced by similar effects and were therefore not corrected.
Unlike the Mount Wilson observations, the Kitt Peak magnetograms are not significantly affected by Zeeman saturation or temperature sensitivity. Therefore, these effects have not been accounted for. However, we rejected approximately 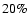 of the remapped Kitt Peak magnetograms due to observational or numerical artefacts. A pronounced decrease in quality occurred during the year 1991, before the new spectromagnetograph became operational. The overall data coverage of the Kitt Peak data set was thus reduced to
of the remapped Kitt Peak magnetograms due to observational or numerical artefacts. A pronounced decrease in quality occurred during the year 1991, before the new spectromagnetograph became operational. The overall data coverage of the Kitt Peak data set was thus reduced to 
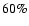 of the days in the considered time interval.
of the days in the considered time interval.
2.1.3 Kitt Peak synoptic maps
Finally, the third data set consists of 377 NSO/KP synoptic maps that cover Carrington rotations 1625-2007 (corresponding to the period February 1975-September 2003). Data gaps are Carrington rotations 1640-1644 and 1854. Each synoptic map has a resolution of
 pixels in longitude
pixels in longitude  sine latitude. Using the Carrington coordinate system, the maps represent an estimate of the magnetic flux near the central meridian of the solar disk as a function of Carrington longitude (Worden & Harvey 2000, and references therein). The maps were compiled from daily NSO/KP magnetograms and can therefore be seen as an additional supplement to our second data set described above. A highly desirable property of synoptic maps is that they offer an evenly spaced time series with (almost) no data gaps, which is preferable for time series analysis. A point against is that they mix longitude and time coordinates, which complicates the spherical harmonic decomposition into non-axisymmetric modes (Stenflo & Güdel 1988). We used them therefore only for the decomposition into axisymmetric modes (m=0).
sine latitude. Using the Carrington coordinate system, the maps represent an estimate of the magnetic flux near the central meridian of the solar disk as a function of Carrington longitude (Worden & Harvey 2000, and references therein). The maps were compiled from daily NSO/KP magnetograms and can therefore be seen as an additional supplement to our second data set described above. A highly desirable property of synoptic maps is that they offer an evenly spaced time series with (almost) no data gaps, which is preferable for time series analysis. A point against is that they mix longitude and time coordinates, which complicates the spherical harmonic decomposition into non-axisymmetric modes (Stenflo & Güdel 1988). We used them therefore only for the decomposition into axisymmetric modes (m=0).
2.2 Data analysis
The data analysis consists of two parts. Firstly, each remapped magnetogram or synoptic map is decomposed into the spherical harmonic coefficients by means of the Legendre transform. Secondly, the time series of each coefficient is analyzed by means of the Lomb-Scargle method, Fourier and wavelet analysis.
2.2.1 Spherical harmonic decomposition
Spherical harmonics Ylm with degree l and azimuthal order m form a complete orthonormal basis set on a spherical surface and satisfy the orthonormality condition
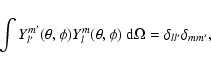 |
(1) |
where
![$\theta\in[0,\pi]$](/articles/aa/full/2005/28/aa2765-05/img77.gif) denotes colatitude,
denotes colatitude,
![$\phi\in[-\pi,\pi]$](/articles/aa/full/2005/28/aa2765-05/img78.gif) longitude and
longitude and 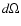 the surface element (for the definition of the Ylm, see Appendix A in Stenflo & Güdel 1988). The azimuthal order m defines the number of longitudinal node cycles of Ylm, while l-m gives the number of latitudinal node circles. Modes with m=0 are axisymmetric with respect to the rotation axis of the Sun, modes with
the surface element (for the definition of the Ylm, see Appendix A in Stenflo & Güdel 1988). The azimuthal order m defines the number of longitudinal node cycles of Ylm, while l-m gives the number of latitudinal node circles. Modes with m=0 are axisymmetric with respect to the rotation axis of the Sun, modes with 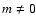 are non-axisymmetric. Modes with even l-m are symmetric with respect to the equatorial plane of the Sun, modes with odd l-m are antisymmetric.
are non-axisymmetric. Modes with even l-m are symmetric with respect to the equatorial plane of the Sun, modes with odd l-m are antisymmetric.
Due to Eq. (1), the radial component of the magnetic field B at a given time t can be expanded as
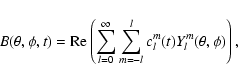 |
(2) |
where Re() denotes the real part of a complex number (the
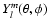 and the respective spherical harmonic coefficients clm(t) are complex if
and the respective spherical harmonic coefficients clm(t) are complex if 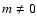 ).
).
The spherical harmonic coefficients are given by
| cml(t) |
= |
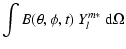 |
(3) |
| |
= |
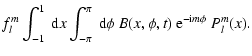 |
(4) |
Asterisk in upper case denotes complex conjugation, fml is the factor of proportionality, Pml(x) the associated Legendre function, and
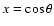 .
The phase
.
The phase
![$\varphi\equiv\arctan[{\rm Im}(c_l^m)/{\rm Re}(c_l^m)]\in[-\pi,+\pi]$](/articles/aa/full/2005/28/aa2765-05/img85.gif) of a spherical coefficient clm gives the angle of the rotated spherical harmonic Ylm with respect to the central meridian (
of a spherical coefficient clm gives the angle of the rotated spherical harmonic Ylm with respect to the central meridian (
 denotes the imaginary part). See Fig. 7 for an example.
denotes the imaginary part). See Fig. 7 for an example.
Each remapped magnetogram or each synoptic chart provides the distribution of the radial magnetic field component B of the visible surface as a function of 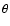 and
and 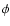 at a specific
time t. Therefore, Eq. (3) offers a straightforward method to calculate the time series clm(t) for a given mode (l,m). When several magnetograms were available per day (as for the Mt. Wilson data), we used the daily average of the spherical coefficients. Note that we subtracted the "unphysical'' monopole contribution
at a specific
time t. Therefore, Eq. (3) offers a straightforward method to calculate the time series clm(t) for a given mode (l,m). When several magnetograms were available per day (as for the Mt. Wilson data), we used the daily average of the spherical coefficients. Note that we subtracted the "unphysical'' monopole contribution
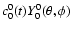 from
from
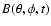 before calculating the other spherical harmonic coefficients. This is equivalent to forcing the average magnetic field of each remapped magnetogram (or synoptic map) to zero. Observational and numerical limitations that complicate the computation of Eq. (3) are briefly discussed in Sect. 2.2.3.
before calculating the other spherical harmonic coefficients. This is equivalent to forcing the average magnetic field of each remapped magnetogram (or synoptic map) to zero. Observational and numerical limitations that complicate the computation of Eq. (3) are briefly discussed in Sect. 2.2.3.
2.2.2 Time series analysis
The classic approach to deduce the temporal variations of a time series clm(t) is to calculate the Fourier transform
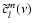 and then to estimate the power spectral density F by taking the modulus squared:
and then to estimate the power spectral density F by taking the modulus squared:
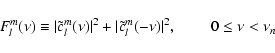 |
(5) |
where
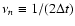 is the Nyquist frequency and
is the Nyquist frequency and 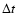 the sampling interval (
the sampling interval (
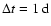 for magnetograms and
for magnetograms and
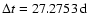 for synoptic maps). If clm(t) is real, the two terms in Eq. (5) are equal and we have
for synoptic maps). If clm(t) is real, the two terms in Eq. (5) are equal and we have
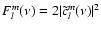 .
The power density should be normalized according to Parseval's theorem, i.e. the integrated power should equal the variance of the time series. This kind of power spectrum estimator is generally called a periodogram.
.
The power density should be normalized according to Parseval's theorem, i.e. the integrated power should equal the variance of the time series. This kind of power spectrum estimator is generally called a periodogram.
The Fast Fourier Transform (FFT), which was used to calculate
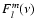 ,
requires evenly spaced time series. As long as the data gaps are much shorter than the periodicities one is looking for, these gaps can be filled with zeroes. In our case, the data gaps are usually in the range of one to several days. Since we are mainly interested in periodicities in the range
,
requires evenly spaced time series. As long as the data gaps are much shorter than the periodicities one is looking for, these gaps can be filled with zeroes. In our case, the data gaps are usually in the range of one to several days. Since we are mainly interested in periodicities in the range
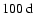 -
-
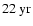 ,
filling the gaps with zeroes introduces high-frequency noise that can be ignored. However, even for rotational periods around
,
filling the gaps with zeroes introduces high-frequency noise that can be ignored. However, even for rotational periods around
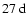 zero-filling yields acceptable results.
zero-filling yields acceptable results.
A more elegant way to deal with unevenly spaced time series is to use the Lomb-Scargle periodogram (Press & Rybicki 1989; Scargle 1982; Lomb 1976; Horne & Baliunas 1986). This method evaluates the data only at times it was actually measured. However, the Lomb-Scargle periodogram can be applied only to real time series, and therefore we used it mainly for the axisymmetric modes (m=0). For non-axisymmetric modes (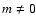 ), either the time series of the real and imaginary part of the spherical coefficients need to be considered separately, or Eq. (5) is used after the data gaps were filled with zeros, since the FFT can handle complex time series.
), either the time series of the real and imaginary part of the spherical coefficients need to be considered separately, or Eq. (5) is used after the data gaps were filled with zeros, since the FFT can handle complex time series.
Besides the Lomb-Scargle and the FFT periodograms, we also applied the continuous wavelet transform, which decomposes a one-dimensional time series into the two-dimensional time-frequency space. Thus it is possible to determine not only the frequency of (quasi-) periodic oscillations but also how these oscillations vary in time (Torrence & Compo 1998, and references therein).
2.2.3 Observational and numerical limitations
Spherical harmonics Ylm do not form a complete orthonormal basis set over only a portion of a sphere, and magnetograms cover even less than a hemisphere of the Sun. Therefore, Eq. (3) cannot give the exact value for the spherical coefficient of a given mode (l,m). This means that the spherical harmonic decomposition of magnetograms leads to so-called "spatial leakage'', i.e. each time series is contaminated by power from neighboring spherical harmonics (Hill & Howe 1998). As a consequence, the power of a (quasi-) periodic oscillation in a periodogram
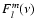 leaks into periodograms with nearby l' and m'. We will return to this point later in the paper.
leaks into periodograms with nearby l' and m'. We will return to this point later in the paper.
Another problem which concerns mainly the Mt. Wilson data is caused by the resolution of the magnetograms. The resolution in latitude numerically defines the number of sampling points of the Legendre polynomials Plm(x). The orthonormality condition given in Eq. (1) does not hold if the number of sampling points is too small. The Mt Wilson magnetograms used here have a resolution of 34 bins in
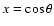 .
This is close to the synoptic charts used in Stenflo & Vogel (1986) and Stenflo & Güdel (1988), which had a resolution of 30 bins. However, Fig. 1 shows that the cross products in Eq. (1) (for m=m'=0 and
.
This is close to the synoptic charts used in Stenflo & Vogel (1986) and Stenflo & Güdel (1988), which had a resolution of 30 bins. However, Fig. 1 shows that the cross products in Eq. (1) (for m=m'=0 and
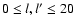 )
may deviate from the expected values
)
may deviate from the expected values
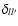 if the resolution is too small. Interpolating the magnetograms to a higher resolution did not improve the results perceivably. For the Kitt Peak data, which have 180 bins in x, this effect is negligeable.
if the resolution is too small. Interpolating the magnetograms to a higher resolution did not improve the results perceivably. For the Kitt Peak data, which have 180 bins in x, this effect is negligeable.
![\begin{figure}
\par\includegraphics[width=4.2cm,clip]{2765fg1a.eps}\hspace*{2mm}
\includegraphics[width=4.2cm,clip]{2765fg1b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2765-05/Timg101.gif) |
Figure 1:
Cross products according to Eq. (1) for m=m'=0 and
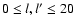 .
The diagram to the left was calculated for a resolution of 34 bins in .
The diagram to the left was calculated for a resolution of 34 bins in
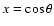 ,
the diagram to the right for 180 bins. ,
the diagram to the right for 180 bins. |
| Open with DEXTER |
Although spatial leakage and the sampling problem impose a bias on the spherical harmonic decomposition of daily magnetograms, the analysis of the derived power spectra nevertheless provides valuable information about (quasi-) periodic oscillations in the solar magnetic field, as we are going to show in the next section.
3 Results
3.1 Time series and power spectra for axisymmetric modes m = 0
The time series clm(t) derived from the daily Mt. Wilson (MWM) and Kitt Peak magnetograms (KPM) are displayed in Fig. 2 for m=0 and
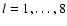 .
Also shown are the corresponding Lomb-Scargle power spectra. The nominal frequency resolution for the MWM data is
.
Also shown are the corresponding Lomb-Scargle power spectra. The nominal frequency resolution for the MWM data is
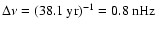 ,
and for the KPM data
,
and for the KPM data
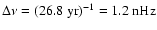 .
The error
.
The error 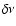 is taken to be half the frequency resolution, i.e.
is taken to be half the frequency resolution, i.e.
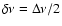 .
The power spectra are oversampled by a factor of 4 to obtain a smoother distribution. In the following, frequencies (and periods) usually refer to the MWM data. The corresponding frequencies for the KPM data are only discussed if they differ significantly.
.
The power spectra are oversampled by a factor of 4 to obtain a smoother distribution. In the following, frequencies (and periods) usually refer to the MWM data. The corresponding frequencies for the KPM data are only discussed if they differ significantly.
The modes with odd l=1,3,5,7 (Figs. 2a-d), which are antisymmetric with respect to the equatorial plane, exhibit a strong 
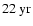 modulation caused by the solar magnetic cycle. In the power spectra, this is seen as the dominant peak at
modulation caused by the solar magnetic cycle. In the power spectra, this is seen as the dominant peak at
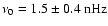 (corresponding to a period of
(corresponding to a period of
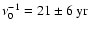 ). The MWM time series of the dipole coefficient c10 in Fig. 2a shows the most pronounced sinusoidal behavior. Its yearly running mean reaches maximum amplitude during solar activity minimum when the large scale magnetic field configuration is closest to a dipole. This sinusoid is increasingly distorted for growing l=3,5,7 in the MWM time series, and a biennial oscillation becomes evident for l=5,7 during the maxima of all four cycles 20-23 (Fig. 2c,d). The corresponding double peak occurs in the power spectra at the frequencies
). The MWM time series of the dipole coefficient c10 in Fig. 2a shows the most pronounced sinusoidal behavior. Its yearly running mean reaches maximum amplitude during solar activity minimum when the large scale magnetic field configuration is closest to a dipole. This sinusoid is increasingly distorted for growing l=3,5,7 in the MWM time series, and a biennial oscillation becomes evident for l=5,7 during the maxima of all four cycles 20-23 (Fig. 2c,d). The corresponding double peak occurs in the power spectra at the frequencies
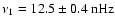 (
(
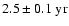 )
and
)
and
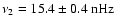 (
(
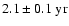 ). The frequency splitting
). The frequency splitting
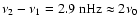 is twice the frequency of the 22 yr cycle. This indicates that the amplitude of the biennial oscillation is modulated by the magnetic cycle itself and that the "true'' frequency is close to
is twice the frequency of the 22 yr cycle. This indicates that the amplitude of the biennial oscillation is modulated by the magnetic cycle itself and that the "true'' frequency is close to
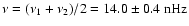 (
(
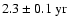 ). Interestingly, the shape of the l=5,7 modes in Figs. 2c and 2d resemble, with exception of the biennial oscillation, the non-linear dynamo wave for the vector potential A derived by Stix (1972) using a one-dimensional
). Interestingly, the shape of the l=5,7 modes in Figs. 2c and 2d resemble, with exception of the biennial oscillation, the non-linear dynamo wave for the vector potential A derived by Stix (1972) using a one-dimensional
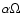 dynamo model with
dynamo model with 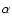 quenching. We will return to this point in Sect. 4.
quenching. We will return to this point in Sect. 4.
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,height=5cm,clip]{2765fg6a....
...\includegraphics[width=8.8cm,height=5cm,clip]{2765fg6h.eps} }
\par\end{figure}](/articles/aa/full/2005/28/aa2765-05/Timg124.gif) |
Figure 2:
Time series and Lomb-Scargle power spectra for the axisymmetric modes with m=0,
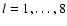 .
a) l=1. The top panel shows the time series c10(t) (in Gauss) calculated according to Eq. (5) for the Mt. Wilson magnetogram data (MWM). Each dot represents one day, the yearly running mean is overplotted (heavy line). The time series for the Kitt Peak magnetogram data (KPM) is shown in the middle panel. The lower two panels show the power spectra in the frequency ranges 0- .
a) l=1. The top panel shows the time series c10(t) (in Gauss) calculated according to Eq. (5) for the Mt. Wilson magnetogram data (MWM). Each dot represents one day, the yearly running mean is overplotted (heavy line). The time series for the Kitt Peak magnetogram data (KPM) is shown in the middle panel. The lower two panels show the power spectra in the frequency ranges 0-
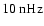 and 0-
and 0-
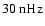 .
The power for the MWM data (heavy line) is given on the left axis in arbitrary but constant units, the power for the KPM data (dotted) is given on the right axis. Both panels were scaled to the height of the peak at .
The power for the MWM data (heavy line) is given on the left axis in arbitrary but constant units, the power for the KPM data (dotted) is given on the right axis. Both panels were scaled to the height of the peak at 
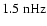 (
(
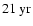 ). b)-d) The same for the odd modes l=3,5,7. Nicely seen is the distortion of the sinusoid in the MWM data with growing l and the amplification of the biennial oscillation during solar activity maxima. The biennial oscillation occurs in the power spectra as a double peak at ). b)-d) The same for the odd modes l=3,5,7. Nicely seen is the distortion of the sinusoid in the MWM data with growing l and the amplification of the biennial oscillation during solar activity maxima. The biennial oscillation occurs in the power spectra as a double peak at
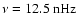 (
(
 )
and )
and
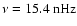 (
(
 ). e)-h) The same for the even modes l=2,4,6,8. The strong annual variations are artefacts. Power is plotted in a single diagram for each mode. ). e)-h) The same for the even modes l=2,4,6,8. The strong annual variations are artefacts. Power is plotted in a single diagram for each mode. |
| Open with DEXTER |
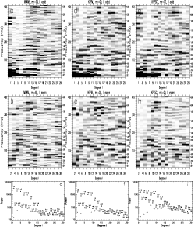 |
Figure 3:
Comparison of the Lomb-Scargle power spectra as functions of frequency 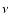 (in nHz) and spherical harmonic degree l (m=0), calculated for Mount Wilson magnetograms (MWM, left column), Kitt Peak magnetograms (KPM, middle column) and Kitt Peak synoptic charts (KPSC, right column). Periods
(in nHz) and spherical harmonic degree l (m=0), calculated for Mount Wilson magnetograms (MWM, left column), Kitt Peak magnetograms (KPM, middle column) and Kitt Peak synoptic charts (KPSC, right column). Periods 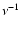 (in yr) are indicated to the right. a) MWM data, odd
l=1,...,29. The grey scale is linear with 16 steps and runs for each l from zero (white) to a maximum value (full black) that is indicated in the bottom panel c. b) MWM data, even modes
l=2,...,30. c) Grey scale normalization factors for panels a and b. The squares give the power maxima for odd and even l in the frequency range
(in yr) are indicated to the right. a) MWM data, odd
l=1,...,29. The grey scale is linear with 16 steps and runs for each l from zero (white) to a maximum value (full black) that is indicated in the bottom panel c. b) MWM data, even modes
l=2,...,30. c) Grey scale normalization factors for panels a and b. The squares give the power maxima for odd and even l in the frequency range
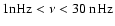 ,
the numbers above indicate the frequency (in nHz) where the maxima are located. These maxima correspond to maximum darkness for the even modes in panel b. The crosses give the power maxima for the odd l between ,
the numbers above indicate the frequency (in nHz) where the maxima are located. These maxima correspond to maximum darkness for the even modes in panel b. The crosses give the power maxima for the odd l between
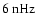 and
and
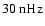 . They were used as normalization factors in panel a, i.e. power amplitudes equaling or exceeding these levels appear black. This was necessary to accentuate the faint features. d)- f) The same for the KPM data. g)- i) The same for the KPSC data.
. They were used as normalization factors in panel a, i.e. power amplitudes equaling or exceeding these levels appear black. This was necessary to accentuate the faint features. d)- f) The same for the KPM data. g)- i) The same for the KPSC data. |
| Open with DEXTER |
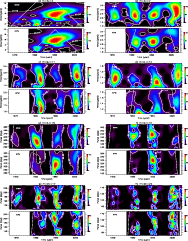 |
Figure 4:
Wavelet power spectra for axisymmetric modes (m=0) that show concurrent periodic oscillations in the Mt. Wilson magnetogram (MWM) and Kitt Peak magnetogram (KPM) data. The periods decrease from panel a) to h). The raw time series were divided by their variance, data gaps were filled with zeros. Quasi-periodic variations appear as regions of increased power. The corresponding periodicity is given on the y-axis (in years or days), time is on the x-axis. Contour lines indicate the 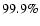 significance level according to Torrence & Compo (1998), the "cone of influence'' is also shown as straight lines near the left and right margin of each diagram. Morlet wavelets with nondimensional frequencies 6 (panels a, b, c), 9 (panels d, e), 12 (panels f, g) and 15 (panel h) were applied (for details see Torrence & Compo 1998).
significance level according to Torrence & Compo (1998), the "cone of influence'' is also shown as straight lines near the left and right margin of each diagram. Morlet wavelets with nondimensional frequencies 6 (panels a, b, c), 9 (panels d, e), 12 (panels f, g) and 15 (panel h) were applied (for details see Torrence & Compo 1998). |
| Open with DEXTER |
The KPM data qualitatively supports the behavior of the MWM modes. However, an obvious inconsistency occurs in the KPM time series for l=1 and l=3 around 1992 (Figs. 2a,b), when the 512-channel magnetograph was replaced with the new spectromagnetograph (cf. Sect. 2.1.2). Before this date, the KPM and MWM time series of the two modes agree reasonably well, thereafter the amplitude of the two KPM modes is reduced. This inconsistency disappears for l>3.
The modes with even l=2,4,6,8 (Figs. 2e-f) are symmetric relative to the equatorial plane. They are obviously much less influenced by the 22 yr magnetic cycle, although both the MWM and KPM modes l=2,4 show increased power around
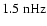 .
Strong annual variations at
.
Strong annual variations at
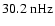 (
(
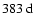 )
and
)
and
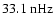 (
(
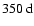 )
are visible in all the even modes (note that
)
are visible in all the even modes (note that
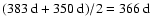 ). They are an artefact due to the inclination of the solar rotation axis relative to the ecliptic, which periodically leaves one of the poles poorly observed. Generally, the even modes seem to contain less information than the odd modes and their power spectra appear noisy. They do, however, also show some kind of biennial oscillations during the activity maxima.
). They are an artefact due to the inclination of the solar rotation axis relative to the ecliptic, which periodically leaves one of the poles poorly observed. Generally, the even modes seem to contain less information than the odd modes and their power spectra appear noisy. They do, however, also show some kind of biennial oscillations during the activity maxima.
An overview of the power spectra of the axisymmetric modes is given for all three data sets for
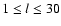 and
and
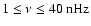 (
(
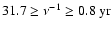 )
in Fig. 3, including the Kitt Peak synoptic charts (KPSC). The grey scale diagrams show power as function of frequency
)
in Fig. 3, including the Kitt Peak synoptic charts (KPSC). The grey scale diagrams show power as function of frequency 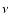 and degree l separately for odd and even modes. The grey scale is linear and varies from white for zero power to black when the power is equal or larger than the normalization factor, which is given for each l in the bottom diagrams (cf.
Figs. 3c,f,i). The factors were chosen to bring out the weaker features for each mode and are therefore different for different l, which retains the information on relative amplitudes within each mode but not between modes. Due to the spatial leakage problem discussed in Sect. 2.2.3, power usually appears at the same frequency for several nearby modes, leading to black bands in the grey scale diagrams.
and degree l separately for odd and even modes. The grey scale is linear and varies from white for zero power to black when the power is equal or larger than the normalization factor, which is given for each l in the bottom diagrams (cf.
Figs. 3c,f,i). The factors were chosen to bring out the weaker features for each mode and are therefore different for different l, which retains the information on relative amplitudes within each mode but not between modes. Due to the spatial leakage problem discussed in Sect. 2.2.3, power usually appears at the same frequency for several nearby modes, leading to black bands in the grey scale diagrams.
The odd modes with l<13 are clearly dominated by the solar magnetic cycle
(cf. Figs. 3a,d,g), visible as a black band around 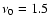 -
-
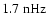 (21.1-
(21.1-
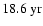 ,
the hyphen indicates the range given by different modes and data sets), followed by the overtone at 4.4-
,
the hyphen indicates the range given by different modes and data sets), followed by the overtone at 4.4-
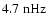 (7.2-
(7.2-
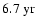 ). This overtone, which corresponds to
). This overtone, which corresponds to 
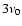 ,
is likely due to the anharmonic shape of the
,
is likely due to the anharmonic shape of the

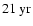 oscillation and may even become the strongest peak for
oscillation and may even become the strongest peak for 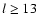 .
Increased power is also seen around 7.1-
.
Increased power is also seen around 7.1-
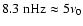 (4.5-
(4.5-
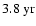 ), particularly for the modes
l=13,15,17 and
), particularly for the modes
l=13,15,17 and
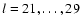 .
The double peak around
.
The double peak around
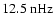 (
(
 )
and
)
and
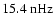 (
(
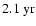 )
is again visible for the modes l=5,7,9 and corresponds to the amplitude modulated biennial oscillation discussed above. Interestingly, another double peak occurs at 17.7-
)
is again visible for the modes l=5,7,9 and corresponds to the amplitude modulated biennial oscillation discussed above. Interestingly, another double peak occurs at 17.7-
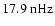 (
(
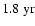 )
and
)
and
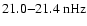 (
(
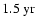 )
for l=11,13.
)
for l=11,13.
While the results for odd modes agree qualitatively well, the grey scale diagrams for the even modes (Figs. 3 b,e,h) apparently show a more noisy picture. The MWM mode l=2 exhibits increased power at
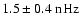 (
(
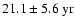 ), which agrees well with the peak in he KSPC power spectrum at
), which agrees well with the peak in he KSPC power spectrum at
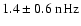 (
(
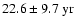 ). The KPM l=2 mode shows power at the shifted frequency
). The KPM l=2 mode shows power at the shifted frequency
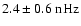 (
(
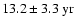 ). The reason for this shift is not clear, but it seems reasonable to assume that the l=2 mode is mainly influenced by the
). The reason for this shift is not clear, but it seems reasonable to assume that the l=2 mode is mainly influenced by the 
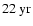 periodicity of the magnetic cycle, possibly through spatial leakage from the odd l=1,3 modes. The l=4 mode shows for all three data sets power at 4.7-
periodicity of the magnetic cycle, possibly through spatial leakage from the odd l=1,3 modes. The l=4 mode shows for all three data sets power at 4.7-
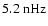 (6.7-
(6.7-
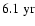 ), which is again close to the overtone
), which is again close to the overtone

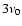 ,
and at 9.2-
,
and at 9.2-
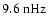 (3.4-
(3.4-
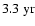 ). The l=6,8,10 modes then show increased power around the double peak at 12.4-
). The l=6,8,10 modes then show increased power around the double peak at 12.4-
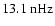 (2.6-
(2.6-
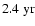 )
and 15.6-
)
and 15.6-
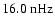 (
(
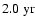 ), similar to the odd modes l=5,7,9. As already mentioned, most even modes show a pronounced annual variation, which is an observational artefact and leads to peaks in the power spectra at
), similar to the odd modes l=5,7,9. As already mentioned, most even modes show a pronounced annual variation, which is an observational artefact and leads to peaks in the power spectra at
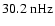 (
(
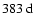 )
and
)
and
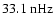 (
(
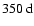 ). However, modes l=12,14 also show for all three data sets a peak at 36.4-
). However, modes l=12,14 also show for all three data sets a peak at 36.4-
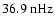 (318-
(318-
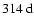 ), which might possibly be real. Note that the odd modes
l=15,21,23 show peaks at the same frequency.
), which might possibly be real. Note that the odd modes
l=15,21,23 show peaks at the same frequency.
Given the rather high noise level in the grey scale power diagrams in Fig. 3, we select in the following MWM and KPM modes that show (quasi-) periodic oscillations with good agreement not only in frequency (period) but also in time. The wavelet power spectra for these modes are displayed in Fig. 4. However, we would like to emphasize that also other modes may show concurrent oscillations, but then usually at similar frequencies and less pronounced than the modes discussed below.
The mode l=4 in Fig. 4a shows enhanced power at the 
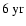 periodicity in the time interval around 1990. Comparison with the time series in Fig. 2f shows a pronounced bump-like oscillation with side lobes at this time. During the preceding activity maximum around 1980, a similar oscillation with a shorter periodicity of
periodicity in the time interval around 1990. Comparison with the time series in Fig. 2f shows a pronounced bump-like oscillation with side lobes at this time. During the preceding activity maximum around 1980, a similar oscillation with a shorter periodicity of  2-
2-
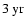 occurred. The biennial oscillation for the odd mode l=7 is nicely seen in Fig. 2b during the maxima of the sunspot cycles 20, 21 and 22. The wavelet coefficients for the maximum of the current cycle 23 lie in the so-called "cone of influence'' (cf. Torrence & Compo 1998) and are therefore less reliable, but it seems that a shift towards a somewhat longer periodicity of
occurred. The biennial oscillation for the odd mode l=7 is nicely seen in Fig. 2b during the maxima of the sunspot cycles 20, 21 and 22. The wavelet coefficients for the maximum of the current cycle 23 lie in the so-called "cone of influence'' (cf. Torrence & Compo 1998) and are therefore less reliable, but it seems that a shift towards a somewhat longer periodicity of 
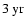 may have occurred. Another interesting behavior is seen for the
may have occurred. Another interesting behavior is seen for the
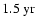 and
and
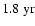 periodicities for the mode l=11 (Fig. 4c). While the former periodicity is prominent during the maximum of cycle 21, the latter occurs during the maximum of cycle 23. These periodicities seem to have occurred also during the maxima of cycles 20 and 21, but less pronounced. This may possibly be a hint that the 1.5-
periodicities for the mode l=11 (Fig. 4c). While the former periodicity is prominent during the maximum of cycle 21, the latter occurs during the maximum of cycle 23. These periodicities seem to have occurred also during the maxima of cycles 20 and 21, but less pronounced. This may possibly be a hint that the 1.5-
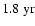 periodicities show strongest power during odd numbered cycles. This is in agreement with the two pronounced
periodicities show strongest power during odd numbered cycles. This is in agreement with the two pronounced
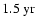 and
and
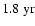 periodicities recently detected in the north-south asymmetry of the photospheric magnetic flux for the time intervals 1978-1984 and 1995-2001, respectively (Knaack et al. 2004).
periodicities recently detected in the north-south asymmetry of the photospheric magnetic flux for the time intervals 1978-1984 and 1995-2001, respectively (Knaack et al. 2004).
Enhanced power appears also at shorter periodicities than
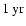 .
The mode l=15 shows a periodicity around 300-
.
The mode l=15 shows a periodicity around 300-
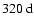 during cycles 20-22 (Fig. 4d), the mode l=10 around 225-
during cycles 20-22 (Fig. 4d), the mode l=10 around 225-
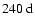 during cycles 21 and 22 (Fig. 4e). A more complicated structure appears for l=15. Enhanced power can be seen around
during cycles 21 and 22 (Fig. 4e). A more complicated structure appears for l=15. Enhanced power can be seen around
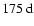 during the maximum of cycles 20 and 21, around
during the maximum of cycles 20 and 21, around
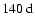 and
and
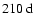 during cycle 22, and around
during cycle 22, and around
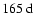 during cycle 23. Finally, mode l=23 shows periodicities around
during cycle 23. Finally, mode l=23 shows periodicities around
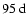 during cycle 21, around 100-
during cycle 21, around 100-
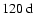 during cycle 22, and around 105-
during cycle 22, and around 105-
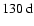 during cycle 23. Similar periodicities have been observed in the photospheric magnetic field by Knaack et al. (2005).
during cycle 23. Similar periodicities have been observed in the photospheric magnetic field by Knaack et al. (2005).
3.2 Time series and power spectra for non-axisymmetric modes m>0
The MWM time series and power spectra for m=1,
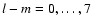 are displayed in Fig. 5. The KPM time series are not shown but agree reasonably well. Unlike the axisymmetric modes discussed above, the non-axisymmetric coefficients are complex and the phase
are displayed in Fig. 5. The KPM time series are not shown but agree reasonably well. Unlike the axisymmetric modes discussed above, the non-axisymmetric coefficients are complex and the phase
![$\varphi(t)=\arctan[{\rm Im}(c_l^m(t))/{\rm Re}(c_l^m(t))]$](/articles/aa/full/2005/28/aa2765-05/img179.gif) provides additional information about the temporal evolution of the modes (also shown in Fig. 5). The real part of the m=1 modes behaves, apart from a sign change, very similar to the corresponding m=0 modes with the same l-m (cf. Fig. 2). This is at least partly due to the spatial leakage problem discussed in Sect. 2.2.3. The real part of the modes with odd l-m therefore shows again the increasingly distorted sinusoid for growing l-m and the amplifying biennial oscillation. The latter is best seen for l-m=5,7 in Fig. 5d and occurs again as double peak at
provides additional information about the temporal evolution of the modes (also shown in Fig. 5). The real part of the m=1 modes behaves, apart from a sign change, very similar to the corresponding m=0 modes with the same l-m (cf. Fig. 2). This is at least partly due to the spatial leakage problem discussed in Sect. 2.2.3. The real part of the modes with odd l-m therefore shows again the increasingly distorted sinusoid for growing l-m and the amplifying biennial oscillation. The latter is best seen for l-m=5,7 in Fig. 5d and occurs again as double peak at
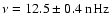 (
(
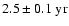 )
and
)
and
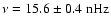 (
(
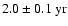 )
in the power spectrum. The imaginary part exhibits for all odd modes a quite distinct periodic but asymmetric shape. The corresponding power spectra show mainly two peaks, one at
)
in the power spectrum. The imaginary part exhibits for all odd modes a quite distinct periodic but asymmetric shape. The corresponding power spectra show mainly two peaks, one at
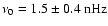 (
(
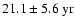 )
and the other at the overtone
)
and the other at the overtone
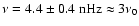 (
(
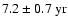 ). The latter is thus primarily a consequence of the asymmetric cycle shape. This is nicely seen for both the real and imaginary parts of the l-m=5 mode in Fig. 5c.
). The latter is thus primarily a consequence of the asymmetric cycle shape. This is nicely seen for both the real and imaginary parts of the l-m=5 mode in Fig. 5c.
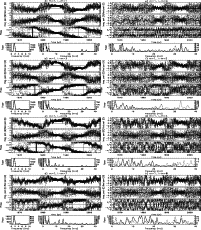 |
Figure 5:
Time series and Lomb-Scargle power spectra for the non-axisymmetric modes clm(t) with m=1,
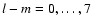 calculated for the Mt. Wilson magnetogram data according to Eq. (5). Modes with odd l-m ( left column) are antisymmetric with respect to the equatorial plane, modes with even l-m ( right column) are symmetric. a) l-m=1. The top panel shows the real part of c21(t) (in Gauss) vs. time, the imaginary part is given in the second panel. Each dot represents one day, the yearly running mean is overplotted (heavy line). The third panel shows the phase
calculated for the Mt. Wilson magnetogram data according to Eq. (5). Modes with odd l-m ( left column) are antisymmetric with respect to the equatorial plane, modes with even l-m ( right column) are symmetric. a) l-m=1. The top panel shows the real part of c21(t) (in Gauss) vs. time, the imaginary part is given in the second panel. Each dot represents one day, the yearly running mean is overplotted (heavy line). The third panel shows the phase
![$\varphi=\arctan[{\rm Im}(c_2^1)/{\rm Re}(c_2^1)]$](/articles/aa/full/2005/28/aa2765-05/img185.gif) .
The heavy line here was calculated with the yearly means of .
The heavy line here was calculated with the yearly means of
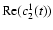 and
and
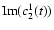 .
The lower two panels show the power spectra in the frequency ranges 0- .
The lower two panels show the power spectra in the frequency ranges 0-
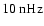 and 0-
and 0-
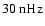 .
The power for the real part (solid curve) is given on the left axis in arbitrary but constant units, the power for the imaginary part (dotted) is given on the right axis. Both panels were scaled to the height of the peak at .
The power for the real part (solid curve) is given on the left axis in arbitrary but constant units, the power for the imaginary part (dotted) is given on the right axis. Both panels were scaled to the height of the peak at 
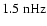 (
(
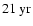 ). b)-d) The same for the odd modes l-m=3,5,7. e)-d) The same for the even modes
l-m=0,2,4,6. Power spectra are given in a single diagram. ). b)-d) The same for the odd modes l-m=3,5,7. e)-d) The same for the even modes
l-m=0,2,4,6. Power spectra are given in a single diagram. |
| Open with DEXTER |
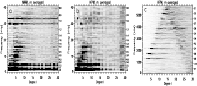 |
Figure 6:
Fourier power spectra 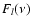 as functions of
as functions of 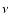 and spherical harmonic degree l (1<l<40), summed over
and spherical harmonic degree l (1<l<40), summed over
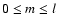 .
The frequency range is .
The frequency range is
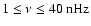 for panels a) (MWM data) and b) (KPM data), while it is
for panels a) (MWM data) and b) (KPM data), while it is
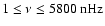 for panel c) (KPM data). Periods are indicated on the right axis in years for panels a) and b), in days for panel c). The grey scale is linear and runs in 16 steps from zero (white) to an upper cut off (full black) that is constant within each panel and has been chosen as
for panel c) (KPM data). Periods are indicated on the right axis in years for panels a) and b), in days for panel c). The grey scale is linear and runs in 16 steps from zero (white) to an upper cut off (full black) that is constant within each panel and has been chosen as
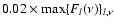 for panel a and as
for panel a and as
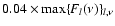 for panels b) and c).
for panels b) and c). |
| Open with DEXTER |
The phase 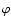 of the odd modes shows a rather unexpected behavior. Not surprising is that
of the odd modes shows a rather unexpected behavior. Not surprising is that 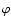 clusters either around 0 or
clusters either around 0 or 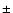
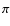 during the solar activity minima. The imaginary part of the spherical harmonic coefficients vanishes then and the configuration
during the solar activity minima. The imaginary part of the spherical harmonic coefficients vanishes then and the configuration
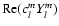 on the visible surface is most similar to a dipole, in particular for the
m=1, l-m=1 mode. During solar maximum, one would expect that the phase alternates periodically and equally between plus and minus due to the rotation of the magnetic field pattern over the solar surface. This would cause an "x-like'' structure in the phase diagram (where the intersection between the ascending and the descending branch of the "x'' corresponds to
on the visible surface is most similar to a dipole, in particular for the
m=1, l-m=1 mode. During solar maximum, one would expect that the phase alternates periodically and equally between plus and minus due to the rotation of the magnetic field pattern over the solar surface. This would cause an "x-like'' structure in the phase diagram (where the intersection between the ascending and the descending branch of the "x'' corresponds to 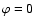 ). This structure is indeed seen in Figs. 5a-5d, but either the ascending or the descending branch seems to be preferred. Figure 7 is an enlargement of the phase diagram in Fig. 5a for the quadrupole mode
m=1, l-m=1 during 1980-1982. Visible are the expected short term variations caused by the solar rotation and the unexpected long term trend, which is gradually decreasing. Positive phases are apparently preferred, which is reversed during the following cycle (Fig. 5a). We do not yet have a physical explanation for this behavior.
). This structure is indeed seen in Figs. 5a-5d, but either the ascending or the descending branch seems to be preferred. Figure 7 is an enlargement of the phase diagram in Fig. 5a for the quadrupole mode
m=1, l-m=1 during 1980-1982. Visible are the expected short term variations caused by the solar rotation and the unexpected long term trend, which is gradually decreasing. Positive phases are apparently preferred, which is reversed during the following cycle (Fig. 5a). We do not yet have a physical explanation for this behavior.
In contrast to the odd modes, the modes with even l-m seem to show no obvious regularities (Figs. 5e-h). Note that the mode c11 (i.e. l-m=0) corresponds to the "equatorial dipole''. For an observer on earth, it resembles the monopole c00 if
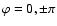 .
The spatial leakage between these two modes is large. Since we removed the monopole contribution from the magnetograms before calculating all other coefficients, the amplitude of
.
The spatial leakage between these two modes is large. Since we removed the monopole contribution from the magnetograms before calculating all other coefficients, the amplitude of
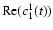 is suppressed and the phase of c11(t) is artificially concentrated around
is suppressed and the phase of c11(t) is artificially concentrated around
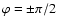 .
.
What does the picture look like for modes with m>1? In Fig. 6, the grey-scale diagrams of Fourier power spectra 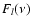 are shown as functions of
are shown as functions of 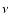 and l, summed over
and l, summed over
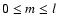 .
An upper cut-off was used for the grey-scale normalization to emphasize the faint features for frequencies larger than
.
An upper cut-off was used for the grey-scale normalization to emphasize the faint features for frequencies larger than
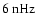 .
Both the MWM and KPM data exhibit a roughly linear increase in the
.
Both the MWM and KPM data exhibit a roughly linear increase in the 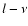 plane in Figs. 6a,b. The dominating features are again the magnetic cycle visible as the horizontal band at
plane in Figs. 6a,b. The dominating features are again the magnetic cycle visible as the horizontal band at
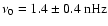 (
(
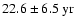 )
and the overtone around
)
and the overtone around
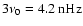 (
(
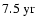 ). Increased power is also seen at higher overtones near
). Increased power is also seen at higher overtones near
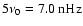 (
(
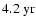 )
and
)
and
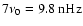 (
(
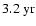 ). The double peak discussed previously is clearly visible at
). The double peak discussed previously is clearly visible at
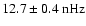 (
(
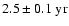 )
and
)
and
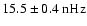 (
(
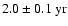 )
for
)
for
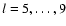 .
This is close to
.
This is close to 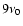 and
and 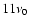 .
Thus it seems that the low-frequency range for
.
Thus it seems that the low-frequency range for
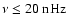 is mainly dominated by odd multiples of the fundamental frequency
is mainly dominated by odd multiples of the fundamental frequency 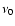 ,
although some modes also show power at
,
although some modes also show power at 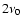 (
(
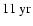 ,
cf. Figs. 2a,b). Since the overtone at
,
cf. Figs. 2a,b). Since the overtone at 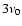 is likely due to the anharmonic shape of the time series for coefficients with odd l-m, this might also be the reason for the overtones at
is likely due to the anharmonic shape of the time series for coefficients with odd l-m, this might also be the reason for the overtones at 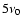 and
and 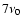 .
In contrast, the biennial variation (near
.
In contrast, the biennial variation (near 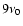 and
and 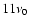 )
appears to be a pronounced oscillatory process that is associated with solar activity maxima.
)
appears to be a pronounced oscillatory process that is associated with solar activity maxima.
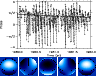 |
Figure 7:
Upper panel: phase 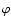 of the quadrupole mode m=1, l=2 during 1980-1982 (enlargement of portion of Fig. 5a). Crosses indicate daily measurements. Visible are short-term variations due to solar rotation and a gradually decreasing long-term trend (heavy line, calculated from the yearly running mean of the real and imaginary parts of c21(t)). Lower panel: geometric sketch of the real part of
c21Y21 for phases
of the quadrupole mode m=1, l=2 during 1980-1982 (enlargement of portion of Fig. 5a). Crosses indicate daily measurements. Visible are short-term variations due to solar rotation and a gradually decreasing long-term trend (heavy line, calculated from the yearly running mean of the real and imaginary parts of c21(t)). Lower panel: geometric sketch of the real part of
c21Y21 for phases
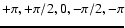 ( from left to right). Bright shades indicate positive, dark shades negative amplitudes. The node lines are given in black. The rotation axis is inclined by
( from left to right). Bright shades indicate positive, dark shades negative amplitudes. The node lines are given in black. The rotation axis is inclined by
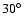 towards the observer.
towards the observer. |
| Open with DEXTER |
As far as the high frequency range is concerned (Fig. 6c), the modes are dominated by harmonics of the (synodic) solar rotation frequency
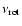 that ranges from
that ranges from 
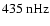 (
(
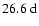 )
at the equator to
)
at the equator to 
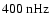 (
(
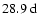 )
at latitudes
)
at latitudes
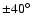 .
For a given order m most power is concentrated at the harmonic
.
For a given order m most power is concentrated at the harmonic
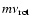 ,
followed by
,
followed by
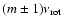 .
Modes with m>13 thus exceed the Nyquist critical frequency
.
Modes with m>13 thus exceed the Nyquist critical frequency
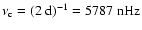 ,
which is the highest possible frequency that can be resolved with Fourier analysis for daily sampled data. Power of these modes is aliased down to lower frequencies and finally compromises the low frequency range for modes with m>26 before it is "reflected'' back again to higher frequencies. This aliasing explains the "
,
which is the highest possible frequency that can be resolved with Fourier analysis for daily sampled data. Power of these modes is aliased down to lower frequencies and finally compromises the low frequency range for modes with m>26 before it is "reflected'' back again to higher frequencies. This aliasing explains the " ''-like structure in Fig. 6c and can also be seen at the right margin of Fig. 6b. Interestingly, Fig. 8 shows that the power for low-degree modes with l=1,2 and
''-like structure in Fig. 6c and can also be seen at the right margin of Fig. 6b. Interestingly, Fig. 8 shows that the power for low-degree modes with l=1,2 and
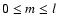 has maxima at
has maxima at
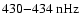 (
(
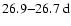 )
and
)
and
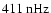 (
(
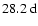 )
for l-m=0, at
)
for l-m=0, at
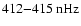 and
and
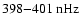 (
(
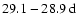 )
for l-m=1, and again at
)
for l-m=1, and again at
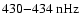 for l-m=2.
for l-m=2.
These findings agree well with the results in our previous paper (Knaack et al. 2005), where we have shown that the rotational power for the large-scale magnetic fields was concentrated at discrete frequencies during cycles 21-23. We found that a 26.7-
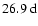 period was prominent in the northern hemisphere during cycle 21, while a
period was prominent in the northern hemisphere during cycle 21, while a 
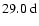 period occured during cycle 22. A 28.0-
period occured during cycle 22. A 28.0-
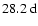 period dominated in the south during cycles 21 and 22. The
period dominated in the south during cycles 21 and 22. The
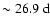 period was also detected by Antonucci et al. (1990) and interpreted as a four sector pattern (m=2). Bai (2003a) reported a "double-hot-spot'' system with a rotation period of
period was also detected by Antonucci et al. (1990) and interpreted as a four sector pattern (m=2). Bai (2003a) reported a "double-hot-spot'' system with a rotation period of
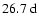 in the northern hemisphere during cycles 20 and 21, while a single "hot-spot'' with a rotation period of
in the northern hemisphere during cycles 20 and 21, while a single "hot-spot'' with a rotation period of
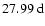 occurred in the southern hemisphere during cycles 19-22. The term hot-spot refers to a region of enhanced flare activity, a double-hot-spot system consists of two hot-spots that are separated by
occurred in the southern hemisphere during cycles 19-22. The term hot-spot refers to a region of enhanced flare activity, a double-hot-spot system consists of two hot-spots that are separated by
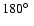 in longitude and rotate with the same period. Similar structures of two activity centers separated by
in longitude and rotate with the same period. Similar structures of two activity centers separated by
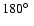 were found in sunspot records by Berdyugina & Usoskin (2003) in both north and south. The average rotation period of these structures was estimated to be
were found in sunspot records by Berdyugina & Usoskin (2003) in both north and south. The average rotation period of these structures was estimated to be
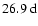 .
Periodicities of
.
Periodicities of
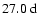 have also been detected in the solar wind speed and the interplanetary magnetic field (Neugebauer et al. 2000) as well as in the photospheric magnetic field (Ruzmaikin et al. 2001; Henney & Harvey 2002). As pointed out by these authors, such discrete rotation periods are likely due to long-lived complexes of active regions, often referred to as "active/preferred longitudes'' (see, for example, Bumba & Howard 1969; Brouwer & Zwaan 1990; Gaizauskas et al. 2001; Bogart 1982; Trotter & Billings 1962; Gaizauskas et al. 1983). We therefore assume, in agreement with our conclusions in Knaack et al. (2005), that the periodicities of 26.7-
have also been detected in the solar wind speed and the interplanetary magnetic field (Neugebauer et al. 2000) as well as in the photospheric magnetic field (Ruzmaikin et al. 2001; Henney & Harvey 2002). As pointed out by these authors, such discrete rotation periods are likely due to long-lived complexes of active regions, often referred to as "active/preferred longitudes'' (see, for example, Bumba & Howard 1969; Brouwer & Zwaan 1990; Gaizauskas et al. 2001; Bogart 1982; Trotter & Billings 1962; Gaizauskas et al. 1983). We therefore assume, in agreement with our conclusions in Knaack et al. (2005), that the periodicities of 26.7-
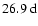 ,
28.0-
,
28.0-
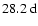 and
and 
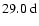 in the power spectra of Fig. 8 are the consequence of the existence of such activity complexes.
in the power spectra of Fig. 8 are the consequence of the existence of such activity complexes.
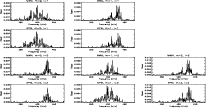 |
Figure 8:
Fourier power spectra
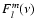 of the MWM and KPM time series for l=1,2 ( from top to bottom) and
of the MWM and KPM time series for l=1,2 ( from top to bottom) and
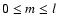 ( from left to right). The (synodic) frequency range is
( from left to right). The (synodic) frequency range is
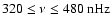 ,
which corresponds to periods ,
which corresponds to periods
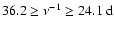 .
The modes with l-m=0 show dominant peaks at .
The modes with l-m=0 show dominant peaks at 
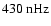 (
(
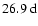 )
and )
and 
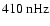 (
(
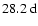 ), modes with l-m=1 at ), modes with l-m=1 at 
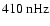 and
and 
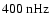 (
(
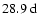 ), modes with l-m=2 again at ), modes with l-m=2 again at 
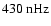 . . |
| Open with DEXTER |
4 Discussion
The present analysis of daily magnetograms through spherical harmonic decomposition partly supports the results of Stenflo & Vogel (1986), Stenflo & Weisenhorn (1987) and Stenflo & Güdel (1988). However, the use of extended data sets covering solar cycles 20-23 and of the continuous wavelet transform have now provided a clearer picture of the possible modal structure of the solar magnetic field, and several modifications therefore need to be considered.
Firstly, the odd axisymmetric modes show a richer spectrum than initially assumed. Besides the generally dominant 
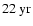 magnetic cycle and its second and third harmonics at
magnetic cycle and its second and third harmonics at 
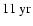 and
and 
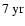 ,
a pronounced
,
a pronounced
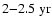 oscillation is evident for l=5,7,9 during the activity maxima of solar cycles 20-23 (Fig. 4b). The amplitude of this biennial oscillation is modulated by the
oscillation is evident for l=5,7,9 during the activity maxima of solar cycles 20-23 (Fig. 4b). The amplitude of this biennial oscillation is modulated by the
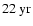 cycle. The modes l=11,13 show shorter periodicities of
cycle. The modes l=11,13 show shorter periodicities of
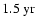 and
and
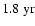 .
The former was present during the maximum of cycle 21, the latter during the maximum of cycle 23 (Fig. 4c). For cycles 20 and 22, the power of this
.
The former was present during the maximum of cycle 21, the latter during the maximum of cycle 23 (Fig. 4c). For cycles 20 and 22, the power of this
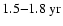 periodicity was noticeably reduced, which might indicate that it is generally stronger during odd-numbered cycles. Moreover, we have shown that the dipole mode l=1 exhibits a nearly sinusoidal behavior, but that this sinusoid is increasingly distorted for odd modes with higher degree l (Figs. 2a-d). The anharmonic shape of the l=5,7 modes resembles, with exception of the biennial oscillation, closely the non-linear dynamo wave of the azimuthal vector potential A derived by Stix (1972, his Fig. 2). This vector potential basically describes the poloidal field and was calculated for a one-dimensional
periodicity was noticeably reduced, which might indicate that it is generally stronger during odd-numbered cycles. Moreover, we have shown that the dipole mode l=1 exhibits a nearly sinusoidal behavior, but that this sinusoid is increasingly distorted for odd modes with higher degree l (Figs. 2a-d). The anharmonic shape of the l=5,7 modes resembles, with exception of the biennial oscillation, closely the non-linear dynamo wave of the azimuthal vector potential A derived by Stix (1972, his Fig. 2). This vector potential basically describes the poloidal field and was calculated for a one-dimensional
 dynamo model allowing for
dynamo model allowing for 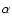 -quenching. The resemblence between A and our time series appears to be qualitatively even better for the the real part of the m=1, l-m=5 mode (Fig. 5c). The circumstance that the amplitude of the biennial oscillation is modulated by the magnetic cycle and that it is strongest for modes that resemble non-linear dynamo waves possibly indicates that the biennial oscillation might be a feature of the dynamo that has not yet been accounted for in dynamo models.
-quenching. The resemblence between A and our time series appears to be qualitatively even better for the the real part of the m=1, l-m=5 mode (Fig. 5c). The circumstance that the amplitude of the biennial oscillation is modulated by the magnetic cycle and that it is strongest for modes that resemble non-linear dynamo waves possibly indicates that the biennial oscillation might be a feature of the dynamo that has not yet been accounted for in dynamo models.
Secondly, the qualitative behavior of the odd and even axisymmetric modes in the 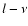 plane does not appear to be completely different. This is valid for the spherical coefficients derived from magnetograms as well as from synoptic maps. The even modes are certainly much less influenced by the
plane does not appear to be completely different. This is valid for the spherical coefficients derived from magnetograms as well as from synoptic maps. The even modes are certainly much less influenced by the 
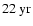 cycle, but the l=2,4 modes also show power near or at
cycle, but the l=2,4 modes also show power near or at
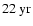 and
and
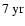 .
The biennial oscillation is evident for l=6,8,10 (Fig. 3b,e,h), while a
.
The biennial oscillation is evident for l=6,8,10 (Fig. 3b,e,h), while a 
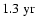 periodicity occurs mainly in the Mt. Wilson data for l=12,14 (Fig. 4d). The latter was apparently strongest during cycles 20 and 22, which is the opposite behavior to the
periodicity occurs mainly in the Mt. Wilson data for l=12,14 (Fig. 4d). The latter was apparently strongest during cycles 20 and 22, which is the opposite behavior to the
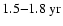 oscillation seen for the odd l=11,13 modes. Whether or not it is a coincidence that the
oscillation seen for the odd l=11,13 modes. Whether or not it is a coincidence that the 
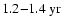 periodicity in the l=12,14 mode is approximately half the
periodicity in the l=12,14 mode is approximately half the 
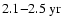 periodicity seen for l=7 (Fig. 4b) is an open question.
periodicity seen for l=7 (Fig. 4b) is an open question.
Thirdly, most of the above mentioned oscillations with
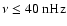 have frequencies that are close to (odd) integer multiples of the fundamental frequency
have frequencies that are close to (odd) integer multiples of the fundamental frequency
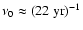 .
This is particularly well seen as an increasing pattern in the
.
This is particularly well seen as an increasing pattern in the  plane when the power spectra are summed over
plane when the power spectra are summed over
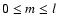 (Figs. 6a,b). The power around
(Figs. 6a,b). The power around 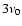 is likely due to the anharmonic shape of the magnetic cycle, and this might also explain the peaks at
is likely due to the anharmonic shape of the magnetic cycle, and this might also explain the peaks at 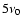 and
and 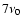 (although the cause for these two peaks is not yet really understood). However, the biennial oscillation, which appears as a double peak at
(although the cause for these two peaks is not yet really understood). However, the biennial oscillation, which appears as a double peak at 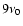 and
and 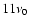 ,
is clearly discernible in the time series as an independent oscillation.
,
is clearly discernible in the time series as an independent oscillation.
Finally, we have found quasi-periodicities of
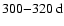 (l=15),
(l=15),
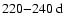 (l=10),
(l=10), 
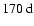 (l=17) and
(l=17) and
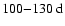 (l=23, cf. Figs. 3e-h). In the high-frequency range, rotational power has been found to be concentrated at (synodic) periods of
(l=23, cf. Figs. 3e-h). In the high-frequency range, rotational power has been found to be concentrated at (synodic) periods of
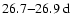 ,
,
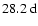 and
and
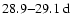 .
These periodicities agree well with our results in Knaack et al. (2005). A detailed analysis of the rotation of large-scale magnetic fields (which often appears to be nearly rigid) during cycles 21-23 is given there.
.
These periodicities agree well with our results in Knaack et al. (2005). A detailed analysis of the rotation of large-scale magnetic fields (which often appears to be nearly rigid) during cycles 21-23 is given there.
In the following, we will discuss the detected frequencies and compare them to previous studies. Evidence for biennial oscillations in the photospheric magnetic field has been provided earlier by Stenflo & Vogel (1986), Stenflo & Güdel (1988), Erofeev (2001), Obridko & Shelting (2001), and Knaack et al. (2005). In the latter paper we have performed a time series analysis of the longitudinally averaged Kitt Peak synoptic maps for cycles 21-23 and showed that the biennial oscillations occurred predominantly in the southern hemisphere. Benevolenskaya (1998) proposed a model of a double magnetic cycle of solar activity based on the assumption of two dynamo sources separated in space. In this model, a low-frequency component operates at the bottom of the convection zone and generates the 
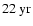 magnetic cycle, while a high-frequency component near the top causes the biennial oscillations. The radial component Br of the poloidal field was described as the superposition of two dynamo waves, i.e.
magnetic cycle, while a high-frequency component near the top causes the biennial oscillations. The radial component Br of the poloidal field was described as the superposition of two dynamo waves, i.e.
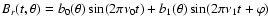 ,
where b0 and b1 are the amplitudes of the low and high-frequency components,
,
where b0 and b1 are the amplitudes of the low and high-frequency components,
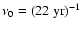 and
and
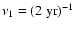 the corresponding frequencies, while
the corresponding frequencies, while 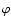 denotes the phase (see Eq. (2) in Benevolenskaya 1998). However, as already mentioned in Sect. 3.1, the power spectra of the l=5,7 modes in Figs. 3b,d clearly show that the biennial oscillation occurs as a double peak at the frequencies
denotes the phase (see Eq. (2) in Benevolenskaya 1998). However, as already mentioned in Sect. 3.1, the power spectra of the l=5,7 modes in Figs. 3b,d clearly show that the biennial oscillation occurs as a double peak at the frequencies
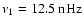 (
(
 )
and
)
and
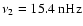 (
(
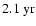 ), the frequency splitting being
), the frequency splitting being
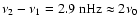 .
This indicates that the amplitude of the biennial oscillation is modulated by the
.
This indicates that the amplitude of the biennial oscillation is modulated by the
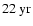 magnetic cycle and that the time evolution of these modes can be approximated by
magnetic cycle and that the time evolution of these modes can be approximated by
![\begin{displaymath}
c_{l=5,7}^{0}(t)=\sin^n(2\pi\nu_0t)\left[x_l+y_l\sin\left(2\pi\frac{\nu_1+\nu_2}{2}t+\varphi\right)\right] +z_l(t)
\end{displaymath}](/articles/aa/full/2005/28/aa2765-05/img259.gif) |
(6) |
where xl and yl are constant, while zl(t) depends on time. We have introduced the power n since the sometimes quite pronounced peak at 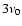 ,
which also appears in the power spectra of the l=5,7 and most other odd modes, can be empirically better reproduced for n=3 than for n=1. However, Eq. (6) cannot account for the distinct anharmonic shape of the time series in Figs. 2c,d or Figs. 5c,d and should be seen only as a crude estimate. To fully allow for the time evolution of the l=5,7 modes, non-linear effects (like
,
which also appears in the power spectra of the l=5,7 and most other odd modes, can be empirically better reproduced for n=3 than for n=1. However, Eq. (6) cannot account for the distinct anharmonic shape of the time series in Figs. 2c,d or Figs. 5c,d and should be seen only as a crude estimate. To fully allow for the time evolution of the l=5,7 modes, non-linear effects (like 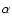 quenching) must be considered.
quenching) must be considered.
As far as the shorter periodicity of 
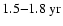 for the l=11,13 modes is concerned, we have recently reported two pronounced
for the l=11,13 modes is concerned, we have recently reported two pronounced
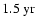 and
and
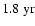 oscillations in the north-south asymmetry of the (unsigned) magnetic flux (Knaack et al. 2004). The former was present from 1978 to 1984, the latter from 1995 to 2001. This is in good agreement with the present analysis. For the 1978-1984 interval, periods of
oscillations in the north-south asymmetry of the (unsigned) magnetic flux (Knaack et al. 2004). The former was present from 1978 to 1984, the latter from 1995 to 2001. This is in good agreement with the present analysis. For the 1978-1984 interval, periods of 
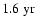 and
and 
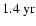 were also found in the variation of southern coronal hole areas (McIntosh et al. 1992) and in the occurrence of H
were also found in the variation of southern coronal hole areas (McIntosh et al. 1992) and in the occurrence of H flares, the numbers of which varied in anti-phase between the northern and southern hemisphere (Ichimoto et al. 1985). We have subsequently shown that the
flares, the numbers of which varied in anti-phase between the northern and southern hemisphere (Ichimoto et al. 1985). We have subsequently shown that the
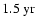 oscillation occurred in the unsigned flux in both hemispheres at latitudes
oscillation occurred in the unsigned flux in both hemispheres at latitudes 
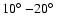 during the maximum of cycle 21, while variations of
during the maximum of cycle 21, while variations of
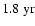 were present predominantly in the southern hemisphere at latitudes
were present predominantly in the southern hemisphere at latitudes 
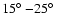 during cycle 23 (Knaack et al. 2005). The circumstance that the
during cycle 23 (Knaack et al. 2005). The circumstance that the
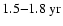 periodicity appears to be related to north-south asymmetries explains why it mainly occurs for odd and not for even modes.
periodicity appears to be related to north-south asymmetries explains why it mainly occurs for odd and not for even modes.
On the other hand, the 
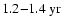 periodicity for the even l=12,14 modes is likely related to the
periodicity for the even l=12,14 modes is likely related to the
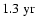 period detected in the unsigned flux at intermediate latitudes
period detected in the unsigned flux at intermediate latitudes 
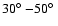 in both hemispheres (Knaack et al. 2005). This
in both hemispheres (Knaack et al. 2005). This
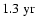 oscillation occurred during the maxima of all three cycles 21-23, but it was most pronounced during cycle 22. Comparison with butterfly diagrams indicated that it may be related to the large-scale magnetic surges towards the poles described by Howard & Labonte (1981) and Wang et al. (1989). Quasi-periodic variations of
oscillation occurred during the maxima of all three cycles 21-23, but it was most pronounced during cycle 22. Comparison with butterfly diagrams indicated that it may be related to the large-scale magnetic surges towards the poles described by Howard & Labonte (1981) and Wang et al. (1989). Quasi-periodic variations of
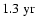 have previously been reported in the rotation rate at the bottom of the convection zone (Howe et al. 2000), in the interplanetary magnetic field (IMF) and geomagnetic activity (Lockwood 2001, and references therein), in sunspot areas and in sunspot numbers (Krivova & Solanki 2002). Lockwood (2001) found that this periodicity has largest powers around the maxima of even-numbered cycles, which is in agreement with our results in Knaack et al. (2005) and the present analysis.
have previously been reported in the rotation rate at the bottom of the convection zone (Howe et al. 2000), in the interplanetary magnetic field (IMF) and geomagnetic activity (Lockwood 2001, and references therein), in sunspot areas and in sunspot numbers (Krivova & Solanki 2002). Lockwood (2001) found that this periodicity has largest powers around the maxima of even-numbered cycles, which is in agreement with our results in Knaack et al. (2005) and the present analysis.
Wang & Sheeley (2003) have shown that quasi-periodicities in the range 
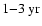 may be due to stochastic processes associated with the emergence of active regions. However, since our results indicate that the biennial oscillation has been a recurrent phenomenon with constant period over at least solar cycles 20-22 and that also the
may be due to stochastic processes associated with the emergence of active regions. However, since our results indicate that the biennial oscillation has been a recurrent phenomenon with constant period over at least solar cycles 20-22 and that also the 
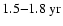 and
and 
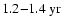 periodicities apparently show certain regularities (the former being more pronounced during odd numbered, the latter during even numbered cycles), it appears unlikely that these periodicities are of random occurrence.
periodicities apparently show certain regularities (the former being more pronounced during odd numbered, the latter during even numbered cycles), it appears unlikely that these periodicities are of random occurrence.
Another approach is given by Dzhalilov et al. (2002), who have proposed that Rossby-like modes depending on the inner structure of the Sun may cause the
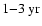 oscillations. Dzhalilov et al. named these resonant cavity modes R-modes to distinguish them from the common r-modes, which are independent of the inner structure and mainly caused by geometrical effects (Wolff 2000; Provost et al. 1981; Wolff & Blizard 1986; Smeyers et al. 1981; Papaloizou & Pringle 1978; Saio 1982; Wolff 1998). There have been suggestions by Sturrock et al. (1999), Lou (2000) and Sturrock (2004) that the Rieger period of
oscillations. Dzhalilov et al. named these resonant cavity modes R-modes to distinguish them from the common r-modes, which are independent of the inner structure and mainly caused by geometrical effects (Wolff 2000; Provost et al. 1981; Wolff & Blizard 1986; Smeyers et al. 1981; Papaloizou & Pringle 1978; Saio 1982; Wolff 1998). There have been suggestions by Sturrock et al. (1999), Lou (2000) and Sturrock (2004) that the Rieger period of 
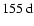 (Rieger et al. 1984; Bogart & Bai 1985; Kiplinger et al. 1984) and similar "Rieger-type'' periodicities of
(Rieger et al. 1984; Bogart & Bai 1985; Kiplinger et al. 1984) and similar "Rieger-type'' periodicities of  129,
129,  104,
104,  78 and
78 and 
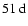 (Bai & Sturrock 1991) may be due to r-modes or equatorially-trapped Rossby waves (Lou 2000).
(Bai & Sturrock 1991) may be due to r-modes or equatorially-trapped Rossby waves (Lou 2000).
Rieger-type periodicities empirically seem to hint at subharmonics (multiples) of a fundamental period around
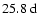 (Bai & Sturrock 1991), which is close to the sidereal solar rotation period at the equator (
(Bai & Sturrock 1991), which is close to the sidereal solar rotation period at the equator (
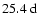 ,
Schou et al. 1998). Such periodicities have been found in various solar activity indices (e.g. Rieger et al. 1984; Bai & Sturrock 1991; Delache et al. 1985; Wolff 1983; Pap et al. 1990; Lou et al. 2003; Lean & Brueckner 1989; Bai 2003b). Recently, we have reported that the photospheric magnetic field exhibits a whole series of Rieger-type periodicities in the range
,
Schou et al. 1998). Such periodicities have been found in various solar activity indices (e.g. Rieger et al. 1984; Bai & Sturrock 1991; Delache et al. 1985; Wolff 1983; Pap et al. 1990; Lou et al. 2003; Lean & Brueckner 1989; Bai 2003b). Recently, we have reported that the photospheric magnetic field exhibits a whole series of Rieger-type periodicities in the range
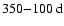 ,
which are close to the period estimates for Rossby waves with even
,
which are close to the period estimates for Rossby waves with even
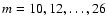 (Knaack et al. 2005). We also pointed out that the possible long-period r-mode signature with
(Knaack et al. 2005). We also pointed out that the possible long-period r-mode signature with
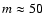 reported by Kuhn et al. (2000), who used MDI data from 1996.3 to 1998.5, might be related to the
reported by Kuhn et al. (2000), who used MDI data from 1996.3 to 1998.5, might be related to the
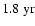 periodicity in the photospheric magnetic field, since the period estimate for such a sectoral r-mode is close to
periodicity in the photospheric magnetic field, since the period estimate for such a sectoral r-mode is close to
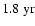 .
Our present analysis has again yielded several Rieger-type periodicities at
.
Our present analysis has again yielded several Rieger-type periodicities at
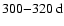 (l=15),
(l=15),
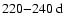 (l=10),
(l=10), 
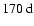 (l=17) and
(l=17) and
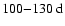 (l=23, cf. Fig. 3e-h). However, the degree l and azimuthal order m=0 where we have detected these periodicities does not correspond to the r-modes or equatorially-trapped Rossby waves that have similar periods. This does not exclude the possibility that r-modes or Rossby waves may trigger Rieger-type (or longer) periodicities, but the way in which the waves interact with the magnetic field would need to be clarified. In any case, the observational evidence for Rieger-type periods in solar indices is increasing. Whether they can be explained by r-modes, Rossby-type waves or another effect remains to be seen.
(l=23, cf. Fig. 3e-h). However, the degree l and azimuthal order m=0 where we have detected these periodicities does not correspond to the r-modes or equatorially-trapped Rossby waves that have similar periods. This does not exclude the possibility that r-modes or Rossby waves may trigger Rieger-type (or longer) periodicities, but the way in which the waves interact with the magnetic field would need to be clarified. In any case, the observational evidence for Rieger-type periods in solar indices is increasing. Whether they can be explained by r-modes, Rossby-type waves or another effect remains to be seen.
Acknowledgements
We are indebted to Jack Harvey (NSO) and Frank Hill (NSO) for their comprehensive support in compiling the NSO/Kitt Peak data used here, which have been produced cooperatively by NSF/NOAO, NASA/GSFC, and NOAA/SEL. This study also includes data from the synoptic program at the 150-Foot Solar Tower of the Mt. Wilson Observatory, which were compiled and kindly made available by J. Boyden (UCLA). The Mt. Wilson 150-Foot Solar Tower is operated by UCLA, with funding from NASA, ONR and NSF, under agreement with the Mt. Wilson Institute. Wavelet software was provided by C. Torrence and G. Compo, and is available at URL: http://paos.colorado.edu/research/wavelets/
- Antonucci, E., Hoeksema,
J. T., & Scherrer, P. H. 1990, ApJ, 360, 296 [NASA ADS] [CrossRef] (In the text)
- Bai, T. 2003a,
ApJ, 585, 1114 [NASA ADS] [CrossRef] (In the text)
- Bai, T. 2003b,
ApJ, 591, 406 [NASA ADS] [CrossRef]
-
Bai, T., & Sturrock, P. A. 1991, Nature, 350, 141 [NASA ADS] [CrossRef] (In the text)
- Benevolenskaya, E. E. 1998,
ApJ, 509, L49 [NASA ADS] [CrossRef] (In the text)
- Berdyugina, S. V., &
Usoskin, I. G. 2003, A&A, 405, 1121 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Bernasconi, P. N. 1997, Stokes Vector Polarimetry: Observation
and Analysis of Solar Magnetic Fields, Ph.D. Thesis (ETH
Zurich)
- Bogart,
R. S. 1982, Sol. Phys., 76, 155 [NASA ADS] [CrossRef]
-
Bogart, R. S., & Bai, T. 1985, ApJ Lett., 299, L51 [NASA ADS]
-
Brouwer, M. P., & Zwaan, C. 1990, Sol. Phys., 129,
221 [NASA ADS] [CrossRef]
-
Bumba, V., & Howard, R. 1969, Sol. Phys., 7, 28 [NASA ADS] [CrossRef]
-
Delache, P., Laclare, F., & Sadsaoud, H. 1985, Nature, 317,
416 [NASA ADS] [CrossRef]
- Dzhalilov, N. S., Staude, J.,
& Oraevsky, V. N. 2002, A&A, 384, 282 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Erofeev,
D. V. 2001, Sol. Phys., 198, 31 [NASA ADS] [CrossRef] (In the text)
- Gaizauskas, V., Harvey,
K. L., Harvey, J. W., & Zwaan, C. 1983, ApJ, 265,
1056 [NASA ADS] [CrossRef]
- Gaizauskas, V., Mackay,
D. H., & Harvey, K. L. 2001, ApJ, 558, 888 [NASA ADS] [CrossRef]
-
Gokhale, M. H., Javaraiah, J., Kutty, K. N., &
Varghese, B. A. 1992, Sol. Phys., 138, 35 [NASA ADS] [CrossRef] (In the text)
-
Harvey, J., & Worden, J. 1998, in Synoptic Solar Physics, ASP
Conf. Ser., 140, 155
(In the text)
-
Henney, C. J., & Harvey, J. W. 2002, Sol. Phys., 207,
199 [NASA ADS] [CrossRef]
- Hill,
F., & Howe, R. 1998, in Structure and Dynamics of the Interior
of the Sun and Sun-like Stars SOHO 6/GONG 98 Workshop, 6, 225
(In the text)
- Horne, J. H., & Baliunas,
S. L. 1986, ApJ, 302, 757 [NASA ADS] [CrossRef]
-
Howard, R., Boyden, J. E., Bruning, D. H., et al.
1983, Sol. Phys., 87, 195 [NASA ADS] [CrossRef] (In the text)
- Howard, R., & Labonte,
B. J. 1981, Sol. Phys., 74, 131 [NASA ADS] [CrossRef] (In the text)
- Howard, R., & Stenflo,
J. O. 1972, Sol. Phys., 22, 402 [NASA ADS] [CrossRef]
- Howe,
R., Christensen-Dalsgaard, J., Hill, F., et al. 2000, Science,
287, 2456 [NASA ADS] [CrossRef] (In the text)
-
Hoyng, P., Schmitt, D., & Teuben, L. J. W. 1994, A&A,
289, 265 [NASA ADS] (In the text)
-
Ichimoto, K., Kubota, J., Suzuki, M., Tohmura, I., & Kurokawa,
H. 1985, Nature, 316, 422 [NASA ADS] [CrossRef] (In the text)
-
Jones, H. P., Duvall, T. L., Harvey, J. W.,
et al. 1992, Sol. Phys., 139, 211 [NASA ADS] [CrossRef] (In the text)
- Kiplinger, A. L., Dennis,
B. R., & Orwig, L. E. 1984, BAAS, 16, 891 [NASA ADS]
-
Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2004,
A&A, 418, L17 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2005,
A&A, in press
(In the text)
- Krivova, N. A., &
Solanki, S. K. 2002, A&A, 394, 701 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kuhn,
J. R., Armstrong, J. D., Bush, R. I., &
Scherrer, P. 2000, Nature, 405, 544 [NASA ADS] [CrossRef] (In the text)
- Lean, J. L., & Brueckner,
G. E. 1989, ApJ, 337, 568 [NASA ADS] [CrossRef]
- Livingston, W. C., Harvey,
J., Slaughter, C., & Trumbo, D. 1976, Appl. Opt., 15, 40 [NASA ADS] (In the text)
- Lockwood,
M. 2001, J. Geophys. Res., 106, 16 021
(In the text)
- Lomb, N. R.
1976, Ap&SS, 39, 447 [NASA ADS]
- Lou, Y. 2000, ApJ,
540, 1102 [NASA ADS] [CrossRef] (In the text)
- Lou, Y.,
Wang, Y., Fan, Z., Wang, S., & Wang, J. X. 2003, MNRAS,
345, 809 [NASA ADS] [CrossRef]
-
McIntosh, P. S., Thompson, R. J., & Willock,
E. C. 1992, Nature, 360, 322 [NASA ADS] [CrossRef] (In the text)
-
Mursula, K., Zieger, B., & Vilppola, J. H. 2003, Sol.
Phys., 212, 201 [NASA ADS] [CrossRef]
- Neugebauer, M., Smith,
E. J., Ruzmaikin, A., Feynman, J., & Vaughan, A. H.
2000, J. Geophys. Res., 2315
(In the text)
- Obridko, V. N., &
Shelting, B. D. 2001, Astron. Rep., 45, 1012 [NASA ADS] [CrossRef] (In the text)
- Pap, J.,
Bouwer, S. D., & Tobiska, W. K. 1990, Sol. Phys.,
129, 165 [NASA ADS] [CrossRef]
- Papaloizou, J., & Pringle,
J. E. 1978, MNRAS, 182, 423 [NASA ADS]
-
Press, W. H., & Rybicki, G. B. 1989, ApJ, 338,
277 [NASA ADS] [CrossRef]
-
Provost, J., Berthomieu, G., & Rocca, A. 1981, A&A, 94,
126 [NASA ADS]
-
Rieger, E., Kanbach, G., Reppin, C., et al. 1984, Nature, 312,
623 [NASA ADS] [CrossRef]
- Ruzmaikin, A., Feynman, J.,
Neugebauer, M., & Smith, E. J. 2001, J. Geophys. Res.,
8363
- Saio, H. 1982,
ApJ, 256, 717 [NASA ADS] [CrossRef]
- Scargle,
J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef]
-
Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505,
390 [NASA ADS] [CrossRef] (In the text)
-
Smeyers, P., Craeynest, D., & Martens, L. 1981, Ap&SS, 78,
483 [NASA ADS]
- Stenflo,
J. O. 1972, Sol. Phys., 23, 307 [NASA ADS] [CrossRef]
- Stenflo, J. O., &
Güdel, M. 1988, A&A, 191, 137 [NASA ADS] (In the text)
-
Stenflo, J. O., & Vogel, M. 1986, Nature, 319, 285 [NASA ADS] [CrossRef] (In the text)
- Stenflo, J. O., &
Weisenhorn, A. L. 1987, Sol. Phys., 108, 205 [NASA ADS] [CrossRef] (In the text)
- Stix, M. 1972,
A&A, 20, 9 [NASA ADS] (In the text)
- Sturrock,
P. A. 2004, ApJ, 605, 568 [NASA ADS] [CrossRef] (In the text)
-
Sturrock, P. A., Scargle, J. D., Walther, G., &
Wheatland, M. S. 1999, ApJ, 523, L177 [NASA ADS] [CrossRef] (In the text)
- Torrence, C., & Compo,
G. P. 1998, Bull. Am. Met. Soc., 79, 61 [NASA ADS] (In the text)
- Trotter, D. E., &
Billings, D. E. 1962, ApJ, 136, 1140 [NASA ADS]
- Wang,
Y.-M., Nash, A. G., & Sheeley, N. R. 1989, ApJ, 347,
529 [NASA ADS] [CrossRef] (In the text)
-
Wang, Y.-M., & Sheeley, N. R. 1992, ApJ, 392, 310 [NASA ADS] [CrossRef]
-
Wang, Y.-M., & Sheeley, N. R. 2003, ApJ, 590, 1111 [NASA ADS] [CrossRef] (In the text)
- Wolff,
C. L. 1983, ApJ, 264, 667 [NASA ADS] [CrossRef]
- Wolff,
C. L. 1998, ApJ, 502, 961 [NASA ADS] [CrossRef]
- Wolff,
C. L. 2000, ApJ, 531, 591 [NASA ADS] [CrossRef]
-
Wolff, C. L., & Blizard, J. B. 1986, Sol. Phys., 105,
1 [NASA ADS] [CrossRef]
-
Worden, J., & Harvey, J. 2000, Sol. Phys., 195, 247 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
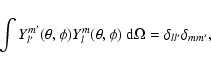
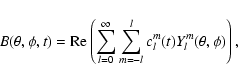
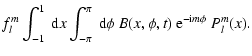
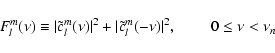
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,height=5cm,clip]{2765fg6a....
...\includegraphics[width=8.8cm,height=5cm,clip]{2765fg6h.eps} }
\par\end{figure}](/articles/aa/full/2005/28/aa2765-05/Timg124.gif)






![\begin{displaymath}
c_{l=5,7}^{0}(t)=\sin^n(2\pi\nu_0t)\left[x_l+y_l\sin\left(2\pi\frac{\nu_1+\nu_2}{2}t+\varphi\right)\right] +z_l(t)
\end{displaymath}](/articles/aa/full/2005/28/aa2765-05/img259.gif)