A&A 438, 201-209 (2005)
DOI: 10.1051/0004-6361:20042335
P. Lampens 1 - Y. Frémat 1 - R. Garrido 2 - J. H. Peña 3 - L. Parrao 3 - P. Van Cauteren 4 - J. Cuypers 1 - P. De Cat 5,1 - K. Uytterhoeven 5 - T. Arentoft 1,6 - M. Hobart 7
1 - Koninklijke Sterrenwacht van België, Ringlaan 3, 1180 Brussel, Belgium
2 -
Instituto de Astrofísica de Andalucía, CSIC,
Camino Bajo de Huetor, 18008 Granada, Spain
3 -
Instituto de Astronomía, UNAM Apartado Postal 70-264
México 04510, DF, Mexico
4 -
Beersel Hills Observatory, Laarheidestraat 166, 1650 Beersel, Belgium
5 -
Institute of Astronomy, KULeuven Celestijnenlaan 200B, 3001 Leuven, Belgium
6 -
Department of Physics and Astronomy, Aarhus University, 8000 Aarhus C., Denmark
7 -
Facultad de Física, Universidad Veracruzana, Veracruz, Mexico
Received 8 November 2004 / Accepted 14 November 2005
Abstract
Multi-site and multi-year differential photometry of the triple star DG Leo reveals
a complex frequency spectrum that can be modelled as the combination of at least three ![]() Scuti type frequencies in the range 11.5-13 c/d (with semi-amplitudes of 2-7 mmag) and a superimposed slow variability of larger amplitude.
The period of the slow variation fits very well with half the orbital period of the inner spectroscopic binary indicating the presence of ellipsoidal variations caused by the tidally deformed components in a close configuration. These findings, together with the results of a recent spectroscopic analysis (showing that the system consists of a pair of mild Am stars and one A-type component of normal solar composition), infer that DG Leo is an extremely interesting asteroseismic target. Identification of which component(s) of this multiple system is (or are) pulsating and determination of the excited pulsation modes will both contribute to a much better understanding of the non-trivial link between multiplicity, chemical composition, rotation, and pulsation in the lower part of the classical Cepheid instability strip.
Scuti type frequencies in the range 11.5-13 c/d (with semi-amplitudes of 2-7 mmag) and a superimposed slow variability of larger amplitude.
The period of the slow variation fits very well with half the orbital period of the inner spectroscopic binary indicating the presence of ellipsoidal variations caused by the tidally deformed components in a close configuration. These findings, together with the results of a recent spectroscopic analysis (showing that the system consists of a pair of mild Am stars and one A-type component of normal solar composition), infer that DG Leo is an extremely interesting asteroseismic target. Identification of which component(s) of this multiple system is (or are) pulsating and determination of the excited pulsation modes will both contribute to a much better understanding of the non-trivial link between multiplicity, chemical composition, rotation, and pulsation in the lower part of the classical Cepheid instability strip.
Key words: stars: binaries: visual - stars: binaries: spectroscopic - stars: variables: ![]() Sct - stars: individual: DG Leo - technique: photometric
Sct - stars: individual: DG Leo - technique: photometric
A "bonus'' of studying stellar pulsations in binary and multiple systems is that one can exploit
the dynamical information to obtain independent constraints on the pulsational models via the
determination of the physical properties of the components. Multi-year photometry with a good
phase coverage of the beat periods of the oscillations, on the one hand, allows accurate frequency analyses of the combined light. A careful spectroscopic analysis will, on the other hand,
provide information on the mass and the luminosity ratios, the effective temperature, the chemical composition, and the surface gravity of each component given that the spectrum is composite. If dynamically determined masses of the system can be obtained with sufficiently good accuracy, these can be directly confronted with the pulsation masses. By comparing the frequency and modal content of the components that originate from the same protostellar environment, one may realistically hope to improve understanding of pulsation physics, since a difference in pulsational behaviour between each can only be attributed to a limited number of (differing) stellar parameters. Binarity/multiplicity may thus lead to an explanation of the so-far unknown amplitude and mode selection mechanism operating in ![]() Scuti stars, and to a refined characterization of the pulsations of variable stars in general.
Scuti stars, and to a refined characterization of the pulsations of variable stars in general.
In a review of pulsating ![]() Scuti stars in known double or multiple stars, Lampens & Boffin (2001) discussed several potentially interesting objects, one of which was DG Leonis which appears to be a triple system whose components are nearly identical.
Scuti stars in known double or multiple stars, Lampens & Boffin (2001) discussed several potentially interesting objects, one of which was DG Leonis which appears to be a triple system whose components are nearly identical.
DG Leo (HR 3889, HIP 48218, Kui 44 AB) is an hierarchical triple system which consists of a close
double-lined spectroscopic binary (components Aa and Ab) and one distant companion (component B)
forming the wider visual binary. It has V = 6.085 mag and (B-V) = 0.25 mag (Mermilliod
& Mermilliod 1998). The orbital period of the Aa,b system is 4.147 days,
while the orbital period of the visual pair AB is roughly 200 years (Fekel & Bopp 1977).
The visual component B, observed by HIPPARCOS with an angular separation of 0.17
![]() and a magnitude difference of 0.69 mag with respect to Aa,b (ESA 1997), was monitored by means of micrometric observations and speckle interferometry from 1935 till 1997 (Hartkopf et al. 2000). The existing astrometric data indicate a highly inclined and possibly eccentric orbit. Both Barnes et al. (1977) and Rosvick & Scarfe (1991) presented evidence for possible shallow eclipses with an inclination of
and a magnitude difference of 0.69 mag with respect to Aa,b (ESA 1997), was monitored by means of micrometric observations and speckle interferometry from 1935 till 1997 (Hartkopf et al. 2000). The existing astrometric data indicate a highly inclined and possibly eccentric orbit. Both Barnes et al. (1977) and Rosvick & Scarfe (1991) presented evidence for possible shallow eclipses with an inclination of ![]() 75
75![]() for the Aa,b system.
for the Aa,b system.
Both close components have spectral type A8 IV (Hoffleit & Jaschek 1982), while the composite spectrum was classified as type F0 IIIn (Cowley 1976) and type A7 III with
enhanced Sr (Cowley & Bidelman 1979). All three components of the system are located
in the ![]() Scuti instability strip and are therefore potential candidates for pulsations.
Danziger & Dickens (1967) first reported the short-period variability in the system but were inconclusive about its nature. The claims for short-period oscillations seem to concern mainly one component: component B was classified both as an ultra-short period Cepheid (Eggen 1979, with a period <0.275 days) and as a
Scuti instability strip and are therefore potential candidates for pulsations.
Danziger & Dickens (1967) first reported the short-period variability in the system but were inconclusive about its nature. The claims for short-period oscillations seem to concern mainly one component: component B was classified both as an ultra-short period Cepheid (Eggen 1979, with a period <0.275 days) and as a ![]() Scuti star (Elliot 1974, with a mean periodicity of
Scuti star (Elliot 1974, with a mean periodicity of
![]() ). Possible amplitude and phase changes were also reported (Antonello & Mantegazza 1982; Rosvick & Scarfe 1991). Since these previous studies are based on very limited photometric data sets, little was known about the pulsational characteristics. A first report on the multiperiodicity of the variations was recently presented after performing a preliminary frequency analysis of newly acquired photometric data (Lampens et al. 2004). In the following sections, we will present the complete and updated photometric analysis of this interesting asteroseismic target, where metallicity as well as binarity effects may influence pulsational behaviour.
). Possible amplitude and phase changes were also reported (Antonello & Mantegazza 1982; Rosvick & Scarfe 1991). Since these previous studies are based on very limited photometric data sets, little was known about the pulsational characteristics. A first report on the multiperiodicity of the variations was recently presented after performing a preliminary frequency analysis of newly acquired photometric data (Lampens et al. 2004). In the following sections, we will present the complete and updated photometric analysis of this interesting asteroseismic target, where metallicity as well as binarity effects may influence pulsational behaviour.
During 2002 and 2003, we performed photoelectric photometry campaigns of DG Leo at two prime
sites located at different longitudes and equipped with identical instrumentation and standard
Strömgren filters in a near simultaneous mode. New uvby data were collected with the 1.5 m
telescopes at San Pedro Martír (OAN), México, between Feb. 4-11, 2002 and at Sierra
Nevada (OSN), Spain, between Feb. 11-17, 2002. More uvby data were collected at OAN between
January 8-14, 2003. We used C1 = HD 84497 = HIP 47946 = GSC 1416-210 (G8 III, V = 7.42, b-y = 0.581) and C2 = HD 84739 = HIP 48051 = Cou 284 (F0, V = 7.39, b-y = 0.290, also a close visual double star) as comparison stars. The check star was C3 = HD 86516 = HIP 48977 = GSC1418-1085 (Am, V = 6.74, b-y = 0.109). The magnitude differences in the sense (C1-C3) were shown by Rosvick & Scarfe (1991) to be constant at their level of precision. The HIPPARCOS CATALOGUE (ESA 1997) mentions that C1 showed no detectable variability throughout the mission, while the comparison stars C2 and C3 carry the flag "Duplicity-induced variability''. The standard deviations of the uvby data of the OSN 2002 and OAN 2003 campaigns show that C1 and C2 remained constant at the level of a few mmag, except in filter u for which the noise level is larger (cf. values between brackets in Table 2 introduced later in this section).
On the other hand, C3 might be variable on a long-term scale, even though it was used for a
short time as a comparison star by Jerzykiewicz (1993). We found a difference of
more than 2![]() on index m1 and more than 6
on index m1 and more than 6![]() on index c1 when comparing our
mean indices with the standard indices published by Maitzen et al. (1998; based on 6 measurements, see below).
on index c1 when comparing our
mean indices with the standard indices published by Maitzen et al. (1998; based on 6 measurements, see below).
Table 1: OAN errors in the instrumental system and colour indices of the comparison stars in the standard system (season 2003).
The observations at OAN were performed according to the sequence "variable sky C1 variable C2 (variable C3)''. Five successive 10-s integrations per filter were used for the stars, while only one 10-s integration per filter was used for the sky. The observations at OSN were performed according to the sequence "variable C1 C2 sky'' using 30-s integrations in each filter for all objects. During the OAN 2003 campaign the check star (C3) was also included in the observational sequence.
Table 2: Mean differences between variable/comparison 2 and comparison 1 star per season and per filter.
All OAN data were reduced according to the same reduction method as applied to the OSN data. First, the dead-time correction was applied to all counts. Then, subtraction of the (average) sky measurement from the average value of the target star was carried out for each cycle. The atmospheric extinction was calculated from the comparison star data following the method of Grønbech et al. (1976) and the corresponding corrections were subsequently applied to the magnitude differences. The OAN instrumental errors computed for each season using the standard stars are shown in Table 1. As can be seen from this table, the OAN instrumental errors were larger for the 2002 than for the 2003 season. The reason for the smaller errors in 2003 was the implementation of new phototubes for the uvby photometric system in 2002 followed by a debugging phase which lead to more precise determination of the dead-time corrections for the 2003 OAN season.
The photometric data discussed here represent magnitude differences in the instrumental system between the variable and the comparison star (C1 or C2) interpolated to the observation time of the variable star. As the mean differences were not exactly the same for both observatories, we applied small corrective shifts for each of the three campaigns (see Table 2). Note that the OAN 2003 campaign was held at an epoch closely matching that of the the high-resolution spectroscopic run conducted at the Observatoire de Haute-Provence (Frémat et al. 2004b). In this way we obtained a homogeneous data set consisting of 1590 epochs and multi-colour differential magnitudes of DG Leo. The new material represents about 110 h of high-quality photoelectric photometry (Data Set 1).
In order to increase the amount of data and extend the time basis of the previous data set,
we also performed complementary observations with a small telescope at Beersel Hills Observatory (BHO), Belgium, during the year 2003. Since the target is very bright, we used a 10 cm telescope with an SBIG ST10XMe camera to additionally collect differential CCD data, and we adopted C4 = HD 85017 = HIP 48197 = GSC1417-315 as the comparison star and C5 = HD 85215 = HIP 48303 = GSC1417-312 as the check star. We also defocused slightly in order to improve the photometric precision. These frames were reduced with the aperture photometry procedure of the Mira AP software package![]() . 1071 differential (stacked) V measurements were thus obtained between Jan. 9 and March 14, 2003 representing a total of 59 h of differential CCD photometry in the instrumental system. Though the equipment and the filters are not exactly the same and the comparison stars were obviously different, we combined all differential V and Strömgren y measurements into one large set (Data Set 2 containing 2661 differential magnitudes in a "single'' filter), which will serve the purposes of a) providing a different time distribution with a distinct alias pattern and b) verifying the frequency solution that will be presented in the following section. To perform such data combination, we needed to apply small corrective shifts of order 0.01 mag on the CCD differential data computed from the shifts between the nightly means of the two comparison stars in the field. The averaged V and Strömgren y magnitude
differences were subsequently subtracted for both data types. No other transformation was applied.
Table 3 shows the log of the observational runs performed between January 2002 and March 2004.
. 1071 differential (stacked) V measurements were thus obtained between Jan. 9 and March 14, 2003 representing a total of 59 h of differential CCD photometry in the instrumental system. Though the equipment and the filters are not exactly the same and the comparison stars were obviously different, we combined all differential V and Strömgren y measurements into one large set (Data Set 2 containing 2661 differential magnitudes in a "single'' filter), which will serve the purposes of a) providing a different time distribution with a distinct alias pattern and b) verifying the frequency solution that will be presented in the following section. To perform such data combination, we needed to apply small corrective shifts of order 0.01 mag on the CCD differential data computed from the shifts between the nightly means of the two comparison stars in the field. The averaged V and Strömgren y magnitude
differences were subsequently subtracted for both data types. No other transformation was applied.
Table 3 shows the log of the observational runs performed between January 2002 and March 2004.
Table 3: Log of photometric observational campaigns.
We performed the frequency analysis with two different codes that are based on computation of the Fourier Tranform and/or on the technique of least-squares fitting.
At first, we used P ERIOD98 (Sperl 1998), a programme which determines the frequencies one by one by computing the classical Fourier Transform followed by adjustment of the parameters of the periodic functions (zero point, amplitudes, and phases) using least-squares fitting. Next, the computed frequency solution is refined through simultaneous adjustment of all the parameters, including the frequencies in the course of a (local) minimization process. Since we are dealing with multiperiodic signals, we used the empirical criterion that a frequency is significant as long as the signal-to-noise ratio of the corresponding semi-amplitude is greater than 4 (Kuschnig et al. 1997).
Secondly, a multi-parameter fitting code that scans a wide range in frequency and searches
to minimize the residuals by simultaneously adjusting multiple periodic functions was used
(global minimization). In this way accurate, alternative multi-frequency solutions can be found
that might be overlooked by the previous code (Schoenaers & Cuypers 2004).
This is especially useful when an alternative solution due to the ambiguity of some aliasing pattern is also probable. In this case both computations gave identical results in all filters except for filter u which was of lower quality. Table 4 lists the results for Data Set 1 for each filter of the Strömgren system. Listed are the frequency (in c d-1), the semi-amplitude (in mmag), the phase (in 2![]() rad), and the total fraction of the variance that is removed from the signal (R). In addition we list the signal-to-noise ratio, with respect to the mean noise level in the residual periodogram computed within a box of width 5c d-1 centered on the relevant frequency, as well as the standard deviation of the residual signal,
rad), and the total fraction of the variance that is removed from the signal (R). In addition we list the signal-to-noise ratio, with respect to the mean noise level in the residual periodogram computed within a box of width 5c d-1 centered on the relevant frequency, as well as the standard deviation of the residual signal,
![]() ,
which would correspond if P ERIOD98 were used; and a succession of prewhitenings with the previous frequency
would be performed at each step.
,
which would correspond if P ERIOD98 were used; and a succession of prewhitenings with the previous frequency
would be performed at each step.
The dominant frequency F1, the one of largest amplitude found at about 0.48 c d-1, corresponds to a slow periodic change of the mean intensity linked to the orbital variations of the short-period pair
![]() .
It is very close to one half of
.
It is very close to one half of
![]() days, which is the orbital period derived from the published spectroscopic analyses (Fekel & Bopp 1977; Frémat et al. 2004a). Note that the orbital frequency itself (F0) is not significant, as its signal-to-noise ratio remains far below 4 in all the passbands. However, we considered its contribution, since omitting it would affect the other frequency values very slightly, particularly in the u passband. Four more frequencies between 11.9 and 12.8 c d-1 (F2-F5) were detected in each filter. In fact, two of these are located about 0.08 c d-1 apart, which caused some caution in the preliminary study where T was only about 12 days (Lampens et al. 2004). Their presence is undoubtedly confirmed as the new time base of 767 days corresponds to a formal resolution of 0.0013 c d-1. Also note that F3 and F4 could be subject to the n year-1 ambiguity (with n equal to 1 or 3). Obviously, there is excellent agreement between the solutions in all four passbands. We point out the high R-value in filters b and v, but also the poorer match of the same solution in the u passband (R
days, which is the orbital period derived from the published spectroscopic analyses (Fekel & Bopp 1977; Frémat et al. 2004a). Note that the orbital frequency itself (F0) is not significant, as its signal-to-noise ratio remains far below 4 in all the passbands. However, we considered its contribution, since omitting it would affect the other frequency values very slightly, particularly in the u passband. Four more frequencies between 11.9 and 12.8 c d-1 (F2-F5) were detected in each filter. In fact, two of these are located about 0.08 c d-1 apart, which caused some caution in the preliminary study where T was only about 12 days (Lampens et al. 2004). Their presence is undoubtedly confirmed as the new time base of 767 days corresponds to a formal resolution of 0.0013 c d-1. Also note that F3 and F4 could be subject to the n year-1 ambiguity (with n equal to 1 or 3). Obviously, there is excellent agreement between the solutions in all four passbands. We point out the high R-value in filters b and v, but also the poorer match of the same solution in the u passband (R ![]() 33%). From a comparison of the R-values for nearby alias frequency sets, we verified that no other combination was as significant as the one listed for the y passband. As an illustration of this analysis we present Fig. 2, which is entirely based on the computations performed in parallel with P ERIOD98 and derived in successive steps for the data in filter b.
33%). From a comparison of the R-values for nearby alias frequency sets, we verified that no other combination was as significant as the one listed for the y passband. As an illustration of this analysis we present Fig. 2, which is entirely based on the computations performed in parallel with P ERIOD98 and derived in successive steps for the data in filter b.
The expected error in frequency in the case of uncorrelated observations can be computed using the equation
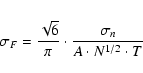
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2335fig2.eps} \end{figure}](/articles/aa/full/2005/28/aa2335-04/Timg20.gif) |
Figure 1: Residual standard deviation as a function of the number of removed sinusoids (Set 1 - filter b). |
| Open with DEXTER | |
Table 4: Multi-parameter fits and solutions (Data Set 1).
Data Set 2 spans the same time base as the former data set but consists of 2661 combined measurements in the filters y and V. While the time base is identical, the increased number of measurements should improve the accuracy of the analysis. However, because the site for the CCD data is located near an industrialized area and a smaller telescope was used, the accuracy of a single measurement is lower. We therefore assigned a relative weight of about 5-1 for each CCD measurement with respect to a photoelectric one. The inverse ratio of the variances of the differential magnitudes between the comparison stars C4 and C5 (BHO) and C1 and C2 (OSN, OAN) was used to compute this factor. The main asset of these data is that the spectral window is different, largely due to the fact that the CCD observations spanned several months in the 2003 season (cf. Fig. 3).
We again performed the same analysis twice: first with P ERIOD98, then with the method of multi-parameter fitting. We list the best set of parameters when adopting a six-frequency model with the latter method in Table 5. From a comparison of the R-values for close sets of aliased frequencies, we also verified that no other combination was as significant as this one. In particular, the frequency at 12.1145 c d-1 (F4) is slightly more convincing than its year-1 alias at 12.1172 c d-1. Note that the 3 year-1 ambiguity no longer affects the solution. In theory, the formal errors in frequency would be improved by
![]() (with N1 and N2 the number of data in the first and last set respectively). However, considering the use of a relative weight of 5-1 for the V data, we will adopt the same conservative errors as before (i.e. errors of 2.-10
(with N1 and N2 the number of data in the first and last set respectively). However, considering the use of a relative weight of 5-1 for the V data, we will adopt the same conservative errors as before (i.e. errors of 2.-10 ![]() 10-5 c/d respectively on frequencies F1-F5). From here on, we will adopt the frequency solution of the v data (Data Set 1) as the final solution since it is based on homogeneous data of very high quality and since it is furthermore fully consistent with the solution derived for Data Set 2 within the quoted error bars.
10-5 c/d respectively on frequencies F1-F5). From here on, we will adopt the frequency solution of the v data (Data Set 1) as the final solution since it is based on homogeneous data of very high quality and since it is furthermore fully consistent with the solution derived for Data Set 2 within the quoted error bars.
Table 5: Multi-parameter fit and solution (weighted Data Set 2).
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2335fig1new.eps} \end{figure}](/articles/aa/full/2005/28/aa2335-04/Timg23.gif) |
Figure 2: Successive frequency searches and spectral window of the Fourier analysis (Set 1 - filter b). |
| Open with DEXTER | |
| |
Figure 3: Spectral windows showing the difference in aliasing between Set 1 and Set 2. |
| Open with DEXTER | |
As mentioned, the frequency of highest amplitude has a value close to
![]() and corresponds to a slow periodic variability of the daily mean intensity due to the geometrical variations of the inner binary
and corresponds to a slow periodic variability of the daily mean intensity due to the geometrical variations of the inner binary
![]() .
With an orbital period as short as 4 days, both components of
.
With an orbital period as short as 4 days, both components of
![]() must have their shapes distorted by tidal interaction. We adopted the spectroscopic orbital period (
must have their shapes distorted by tidal interaction. We adopted the spectroscopic orbital period (
![]() days) and used the following model of the light curve of an ellipsoidal binary:
days) and used the following model of the light curve of an ellipsoidal binary:
| (1) |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.5cm,clip]{2335fig4.eps} \end{figure}](/articles/aa/full/2005/28/aa2335-04/Timg32.gif) |
Figure 4: Individual OAN light curves showing the ellipsoidal variation of DG Leo (filter y). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.5cm,clip]{2335fig5.eps} \end{figure}](/articles/aa/full/2005/28/aa2335-04/Timg33.gif) |
Figure 5: Individual OSN light curves showing the ellipsoidal variation of DG Leo (filter y). Note the different orbital phase coverage. |
| Open with DEXTER | |
The other frequencies detected in the light variations may be associated to pulsations of the type ![]() Scuti in one (possibly more) component(s) of DG Leo. Adopting a unique frequency solution (the final one derived in Sect. 3.2) for all passbands, we recomputed the semi-amplitudes and the phases with their standard errors through least squares fitting (Table 6). Note the tiny colour effect in frequencies F1 and F0 as the amplitude in filter u for F0 =
Scuti in one (possibly more) component(s) of DG Leo. Adopting a unique frequency solution (the final one derived in Sect. 3.2) for all passbands, we recomputed the semi-amplitudes and the phases with their standard errors through least squares fitting (Table 6). Note the tiny colour effect in frequencies F1 and F0 as the amplitude in filter u for F0 =
![]() becomes larger. The amplitude ratios and phase shifts between the different colours displayed in this table contain information that will be helpful for identifying the modes of the excited pulsations (Garrido 2000). Note, however, that the true semi-amplitudes will be larger than observed since three almost equally luminous stars were observed jointly. Given that
becomes larger. The amplitude ratios and phase shifts between the different colours displayed in this table contain information that will be helpful for identifying the modes of the excited pulsations (Garrido 2000). Note, however, that the true semi-amplitudes will be larger than observed since three almost equally luminous stars were observed jointly. Given that
![]() is the true semi-amplitude,
is the true semi-amplitude,
![]() the observed one, and f the additional light source with respect to the maximum light of the variable component B, we derive:
the observed one, and f the additional light source with respect to the maximum light of the variable component B, we derive:
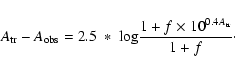 |
(2) |
Table 6: Comparison of amplitudes and phases in various passbands.
We next computed the OAN mean magnitudes and colours of the triple star in the Strömgren standard system (for the 2002 season) in order to derive the global atmospheric parameters of the system through application of the calibration procedure (Lester et al. 1986). The absolute magnitude, effective temperature, surface gravity, and metallicity of DG Leo Aab, B and their standard errors are presented in Table 7.
Table 7: Mean standard colours and global atmospheric parameters of DG Leo in two photometric systems.
We also started to collect absolute data in all seven filters of the Geneva photometric system with the MERCATOR telescope![]() . We determined the mean colours and standard deviations of the 90 measurements acquired between February and March 2002 (cf. Table 1). Intrinsic colours of B2 to M0 stars in the Geneva system have been estimated by Meylan et al. (1980) and Hauck (1993). The global colours of DG Leo seem to match an unreddened MK spectral type of A7 III, except for filter U where the system is less luminous (cf. Table 2 in Hauck 1993). We next made use of the CALIB code developed by Künzli et al. (1997) which allows the atmospheric parameters from the Geneva colour indices to be derived for B to mid-G stars on or just above the main sequence. With this code it is also possible to treat metallic-line stars. Using a zero colour excess, we obtained the atmospheric properties listed in Table 7. From the reddening-free parameter d = 1.283 (measuring the Balmer discontinuity), we next derived
. We determined the mean colours and standard deviations of the 90 measurements acquired between February and March 2002 (cf. Table 1). Intrinsic colours of B2 to M0 stars in the Geneva system have been estimated by Meylan et al. (1980) and Hauck (1993). The global colours of DG Leo seem to match an unreddened MK spectral type of A7 III, except for filter U where the system is less luminous (cf. Table 2 in Hauck 1993). We next made use of the CALIB code developed by Künzli et al. (1997) which allows the atmospheric parameters from the Geneva colour indices to be derived for B to mid-G stars on or just above the main sequence. With this code it is also possible to treat metallic-line stars. Using a zero colour excess, we obtained the atmospheric properties listed in Table 7. From the reddening-free parameter d = 1.283 (measuring the Balmer discontinuity), we next derived ![]() = 0.107 (measuring how much the star is evolved away from the main sequence) and MV = 1.51
= 0.107 (measuring how much the star is evolved away from the main sequence) and MV = 1.51 ![]() 0.30 mag following Hauck (1973). However, North et al. (1997) re-examined the existing calibrations of the Strömgren and Geneva systems in terms of MV for Am stars. Their conclusion was that the previous calibrations were not reliable and that the Geneva photometry underestimates the luminosity of the hottest Am stars. Applying the new relation on the Strömgren indices from Table 7 and using V sin i
0.30 mag following Hauck (1973). However, North et al. (1997) re-examined the existing calibrations of the Strömgren and Geneva systems in terms of MV for Am stars. Their conclusion was that the previous calibrations were not reliable and that the Geneva photometry underestimates the luminosity of the hottest Am stars. Applying the new relation on the Strömgren indices from Table 7 and using V sin i ![]() 30 km s-1 as an appropriate value (Frémat et al. 2004b), we derived the somewhat lower absolute magnitude
MV = 1.08
30 km s-1 as an appropriate value (Frémat et al. 2004b), we derived the somewhat lower absolute magnitude
MV = 1.08 ![]() 0.31 mag.
0.31 mag.
We might compare these calibrated mean values with those that can be directly derived on the basis of the Hipparcos parallax (ESA 1997). In Sect. 3.3 we showed that both components of the close binary, Aa and Ab, have similar colours since no net reflection effect is observed in the light curve. We therefore assume that the difference in magnitude between these components is very small (neither one is evolved). On the other hand, we know that the (Hp) magnitude difference between components Aab and B is 0.69 mag (ESA 1997). Adopting V = 6.085 mag, we then obtain
![]() = 6.546 mag and VB = 7.236 mag. Similarly we also have
= 6.546 mag and VB = 7.236 mag. Similarly we also have
![]()
![]()
![]() = 7.299 mag. Converting to absolute visual magnitudes gives
= 7.299 mag. Converting to absolute visual magnitudes gives
![]()
![]()
![]() = 1.31 mag and MVB = 1.25 mag. The relative parallax error of 15% contributes the most to the error in such a way that none of the above calibrations can be rejected (
= 1.31 mag and MVB = 1.25 mag. The relative parallax error of 15% contributes the most to the error in such a way that none of the above calibrations can be rejected (
![]()
![]() = 0.33 mag).
= 0.33 mag).
The listed errors were increased by 50% with respect to the nominal accuracies to take the fact into account that three stars were observed jointly. Since the three components are not very different, these derived properties will correspond to approximate values of the physical parameters of the components, whereas the high-resolution spectroscopic analysis allowed us to perform a detailed study of the differences between each of the components (cf. Table 6 in Frémat et al. 2004b). A comparison between these component properties and the global values based on photometric calibrations shows that the agreement in effective temperature is reasonably good (mean of 7500 K), while the agreement in surface gravity is concordant with the value derived from the Geneva photometry (mean of 3.8). Both [M/H] determinations suggest enhanced metallicity of the combined light, an observational fact already mentioned by Fekel & Bopp (1977) and Cowley & Bildelman (1979), but only recently quantified (Frémat et al. 2004b).
Acquisition of absolute multi-colour photometry in the Geneva photometric system was pursued during 2004 with the aim of obtaining well-sampled colour curves for each of the pulsation frequencies. The reduction of these observations is presently taking place.
The multi-colour time series of DG Leo recently collected on two continents at the same epoch were merged together and frequency-analysed. Both time series contain high-quality data in the Strömgren instrumental system. Their combination furthermore presents the advantage of largely suppressed day-1 aliasing effects which made the frequency-analyses straightforward and lead (a) to an improved interpretation of (the light curve of) the close binary system and (b) to the detection of multiperiodic oscillations in the combined flux. Monitoring during a few successive years (2002-2004) procured reasonably good accuracy and also permitted verification of the stability of the new frequency solution.
Up to four ![]() Scuti frequencies in the range 11.5-13 c d-1 (with semi-amplitudes of 2-7 mmag in the v passband), as well as a slow variation (with a semi-amplitude of 9 mmag in the v passband) were identified with high confidence. The frequency solution as derived from the Strömgren v data appeared to fit the data very well in all other passbands, as well as the more extended data set which is, however, less homogeneous. This unique frequency solution was shown to remain stable over a period of a few years. We further concluded that the period of the slow variation fits very well with half the spectroscopic orbital period of the close binary and that its presence can be explained by continuous ellipsoidal variations supplemented by a tiny colour effect. Despite these efforts, the full frequency content of the pulsations in DG Leo has not yet been identified as still more peaks are present in the same range of the periodogram of the residuals. A far more extended time series would be needed to determine them with good reliability.
Scuti frequencies in the range 11.5-13 c d-1 (with semi-amplitudes of 2-7 mmag in the v passband), as well as a slow variation (with a semi-amplitude of 9 mmag in the v passband) were identified with high confidence. The frequency solution as derived from the Strömgren v data appeared to fit the data very well in all other passbands, as well as the more extended data set which is, however, less homogeneous. This unique frequency solution was shown to remain stable over a period of a few years. We further concluded that the period of the slow variation fits very well with half the spectroscopic orbital period of the close binary and that its presence can be explained by continuous ellipsoidal variations supplemented by a tiny colour effect. Despite these efforts, the full frequency content of the pulsations in DG Leo has not yet been identified as still more peaks are present in the same range of the periodogram of the residuals. A far more extended time series would be needed to determine them with good reliability.
As the triple system cannot be resolved photometrically, this analysis is valid for the combined light of all three components. Previous studies indicate that the components have similar characteristics. Therefore, the true semi-amplitudes of the pulsations are diluted by a factor of about 3. The semi-amplitudes and the phases were determined in each of the four Strömgren colour indices and will - after finalising the reduction of the M ERCATOR data - also be known in the Geneva photometric system. These will be important diagnostics when identifying the degree ![]() of the excited pulsation modes. Of course, such analysis depends on correct identification of the component(s) in which the pulsations originate. Only a detailed spectroscopic analysis can provide reliable and accurate information at the component level. Frémat et al. (2004b) thus revealed that the close binary consists of two mild Am stars and that line-profile variations on the photometric time-scales of the pulsations were detected in the time-series spectra of the distant companion. The in-depth analysis of DG Leo - a triple system with three almost identical components - should put strict empirical constraints on the development of this type of pulsations in stars of the same mass and age, but of different chemical
composition in the outer layers.
of the excited pulsation modes. Of course, such analysis depends on correct identification of the component(s) in which the pulsations originate. Only a detailed spectroscopic analysis can provide reliable and accurate information at the component level. Frémat et al. (2004b) thus revealed that the close binary consists of two mild Am stars and that line-profile variations on the photometric time-scales of the pulsations were detected in the time-series spectra of the distant companion. The in-depth analysis of DG Leo - a triple system with three almost identical components - should put strict empirical constraints on the development of this type of pulsations in stars of the same mass and age, but of different chemical
composition in the outer layers.
Our intention is to postpone the modal interpretation until the frequency analysis of the line profile variations detected in the high-resolution spectra can be presented as well. Reliable conclusions on this issue should indeed come from evidence based on both photometric and spectroscopic diagnostics (both types of data were acquired quasi-simultaneously for a better understanding of this triple system). Only then will we be able to consider the exact origin of the pulsations and to establish the link between multiplicity, chemical composition, and pulsation in this extremely interesting ![]() Scuti star. A modelling of the pulsations should finally be attempted, in the same way as the preliminary one by Grigahcène et al. (2005).
Scuti star. A modelling of the pulsations should finally be attempted, in the same way as the preliminary one by Grigahcène et al. (2005).
Acknowledgements
P. Lampens, Y. Frémat, and T. Arentoft gratefully acknowledge financial support from the Belgian Science Policy (through project MO/33/007). R. Garrido aknowledges financial support from the project ESP2001-4528-EP. L. Parrao and J. H. Peña thank the OAN staff for assistance during the observations, Dr. J. P. Sareyan for measuring the OAN dead-time corrections, and PAPIIT IN110102 for the funds provided. Some support from the Fund for Scientific Research - Flanders (Belgium) through project G.0178.02 is also acknowledged. Part of these data was acquired with equipment purchased thanks to a research fund financed by the Belgian National Lottery (1999). Extensive use was made of the ADS and Simbad (operated by the Centre de Données Astronomiques, Strasbourg, France) data bases.