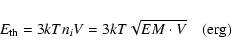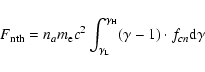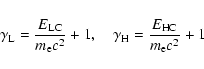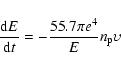A&A 438, 325-339 (2005)
DOI: 10.1051/0004-6361:20042128
Thermal and non-thermal effects driven by magnetic reconnections observed in a confined flare
H. Li1 - A. Berlicki2,3 - B. Schmieder2,4
1 - Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008, PR China
2 -
Observatoire de Paris, Section de Meudon, LESIA, 92195 Meudon Principal Cedex,
France
3 - Astronomical Institute of the Wroc aw University, ul. Kopernika 11, 51-622
Wroc
aw University, ul. Kopernika 11, 51-622
Wroc aw, Poland
aw, Poland
4 -
Institute of Theoretical Astrophysics, University of Oslo, Blindern, 0315 Oslo,
Norway
Received 7 October 2004 / Accepted 9 March 2005
Abstract
In order to better understand the energy processes occurring during the impulsive phase of solar flares we compare observations with our magnetic model calculations. We study the 1N/M1.9 confined flare of 20 October 2003 observed during a Joint Observation Program (JOP157), and concentrate on the spectral analysis of the Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI). These X-ray observations are combined with those from the Solar and Heliospheric Observatory (SOHO) instruments, the French Italian magnetograph (THEMIS), and the Multi-channel Infrared Solar Spectrograph (MISS). The flare occurred in a complex active region, NOAA 10484, with a 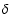 configuration. For model calculations we extrapolate magnetic field lines, which allows us to understand the magnetic topology of the region. This topology and the long impulsive phase of the flare with numerous peaks (GOES, RHESSI) suggest multiple magnetic field reconnection processes. The RHESSI images show a bright structure in hard X-rays (HXR) that could be the tops of the loops. We measure a significant displacement of this structure between the two main maxima of emission, which infers different sites for the reconnection process. The energy release processes can be understood by analyzing the RHESSI spectra using different models. First, using the thermal plus broken power law non-thermal component, we derive the low energy cutoff for the power law distribution of the high-energy electrons (
configuration. For model calculations we extrapolate magnetic field lines, which allows us to understand the magnetic topology of the region. This topology and the long impulsive phase of the flare with numerous peaks (GOES, RHESSI) suggest multiple magnetic field reconnection processes. The RHESSI images show a bright structure in hard X-rays (HXR) that could be the tops of the loops. We measure a significant displacement of this structure between the two main maxima of emission, which infers different sites for the reconnection process. The energy release processes can be understood by analyzing the RHESSI spectra using different models. First, using the thermal plus broken power law non-thermal component, we derive the low energy cutoff for the power law distribution of the high-energy electrons (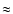 25 keV). Then, we apply two models (thermal plus thick-target and thermal plus thin-target non-thermal component) that allow us to fit the observations. These two models lead to similar results; non-thermal energy contributes a significant amount (approximately 20%) of the total flare energy only during the first peak of the impulsive phase. This suggests that the energy that heats the chromosphere is transported mainly by thermal conduction. The temperature of the thermal plasma is 34 MK and 20 MK at the first and second peaks, respectively.
25 keV). Then, we apply two models (thermal plus thick-target and thermal plus thin-target non-thermal component) that allow us to fit the observations. These two models lead to similar results; non-thermal energy contributes a significant amount (approximately 20%) of the total flare energy only during the first peak of the impulsive phase. This suggests that the energy that heats the chromosphere is transported mainly by thermal conduction. The temperature of the thermal plasma is 34 MK and 20 MK at the first and second peaks, respectively.
Key words: Sun: flares - Sun: X-rays, gamma-rays - Sun: magnetic fields - Sun: activity
1 Introduction
Between 19 October and 4 November 2003, twelve X-class solar flares and many smaller (lower class) flares were observed. Other events are associated with these flares, including coronal mass ejections and increased flux of accelerated particles (electrons, protons and neutrons). This extremely high level of activity resulted from the formation of three complex active regions (NOAA 10484, 10486, 10488). Various aspects of this activity have been investigated previously in a special issue of J. Geophys. Res. (2005).
We are presently interested in the changes of magnetic configuration of the active regions leading to flares and in the processes that heat the low level atmosphere (chromosphere and transition region). There are a number of conditions that are necessary for the production of flares: (i) complex magnetic topology of the active region, such as the so-called 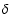 configuration in which umbrae of opposite polarity share a common penumbra; (ii) a high level of stored energy by shear, twist, or emerging flux; and (iii) strength of the magnetic field that will influence the strength of the X-ray flare. Magnetic field changes can occur on a large scale (shear, see as an example the paper of Hagyard et al. 1984) and small scale (emergence of a small bipole, see Berlicki et al. 2004). The source of energy released in solar flares is generally believed to be the energy stored in non-potential magnetic structures. This energy is then rapidly released leading to acceleration of particles, plasma heating, and plasma motion. The question remains about the trigger of this reconstruction process and its diagnostics from available observations, while final aim of such studies is to be able to predict the flaring activity.
configuration in which umbrae of opposite polarity share a common penumbra; (ii) a high level of stored energy by shear, twist, or emerging flux; and (iii) strength of the magnetic field that will influence the strength of the X-ray flare. Magnetic field changes can occur on a large scale (shear, see as an example the paper of Hagyard et al. 1984) and small scale (emergence of a small bipole, see Berlicki et al. 2004). The source of energy released in solar flares is generally believed to be the energy stored in non-potential magnetic structures. This energy is then rapidly released leading to acceleration of particles, plasma heating, and plasma motion. The question remains about the trigger of this reconstruction process and its diagnostics from available observations, while final aim of such studies is to be able to predict the flaring activity.
To understand the mechanism of active region activity, different methods could be applied: statistics or systematic detection of shear or other parameters
(Li et al. 2000; Leka & Barnes 2003a,b; Zharkova et al. 2005), or else studies of details of the magnetic configuration of one active region in the context of a multi-wavelength analysis. To infer a large-scale three-dimensional (3D) structure over the active region, we can either extrapolate the measured photospheric longitudinal field (Alissandrakis 1981; Sakurai 1982; Démoulin et al. 1997) or use a variety of more elaborate methods. If any current in the region is confined to heights at or below the photosphere, the field above is a potential field; if not, a force-free field configuration (
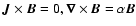 )
is commonly assumed because of the low plasma
)
is commonly assumed because of the low plasma 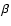 (
(
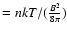 ,
where n is the plasma density, k the Boltzmann constant, T the plasma temperature, and B the magnetic field strength), corresponding to
,
where n is the plasma density, k the Boltzmann constant, T the plasma temperature, and B the magnetic field strength), corresponding to 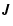 parallel to
parallel to 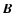 (Metcalf et al. 1995). Magnetic modelling will give us information about the complexity of the active region and indicate the location of possible reconnection sites, the so-called separatrix layers, or quasi-separatrix layers (QSLs) where the distance between the field lines of different connectivities is not exactly zero. Démoulin et al. (1997) demonstrated that in 3D such QSLs are important locations for reconnection of magnetic field lines.
(Metcalf et al. 1995). Magnetic modelling will give us information about the complexity of the active region and indicate the location of possible reconnection sites, the so-called separatrix layers, or quasi-separatrix layers (QSLs) where the distance between the field lines of different connectivities is not exactly zero. Démoulin et al. (1997) demonstrated that in 3D such QSLs are important locations for reconnection of magnetic field lines.
It is well documented that solar flares result from the rapid release of free magnetic energy near the reconnection site of active region loops. The dissipation of this energy in the coronal release sites leads to acceleration of particles, to direct heating of the plasma, and to plasma motions. The so-called thermal and non-thermal models concern two extreme cases of flare models. Thermal models assume that most of the released energy goes into the impulsive heating of the plasma near the release site (Brown et al. 1979). Conduction fronts are formed in the loops and move at fast speed (typically 100-1000 km s-1) towards the chromosphere in a few seconds (10 s). On the contrary, the non-thermal thick target models assume that most of the released energy goes into the acceleration of particles (Brown 1971). Precipitating electrons or ions heat the chromosphere plasma, and the H line is emitted in less than one second.
line is emitted in less than one second.
These two mechanisms can be dissociated only with very high cadence observations (less than 1 s; Trottet et al. 2000; Ji et al. 2004). In these two papers using high time resolution H observations, a fast evolution of the chromospheric brightening has been found comparable to hard X-ray time evolution and the two mechanisms have been shown to depend on the energy of the flares.
observations, a fast evolution of the chromospheric brightening has been found comparable to hard X-ray time evolution and the two mechanisms have been shown to depend on the energy of the flares.
On the other hand, it is known that the temporal response of the chromosphere also has a slowly varying component (Trottet et al. 2000), which is not well understood, because it could be interpreted in various ways: continuous heating by accelerated electrons (Brown 1971), by electric field, turbulence, and thermal conduction. The physical processes that heat the chromosphere and the transition region (within flare ribbons) during the gradual phase are still debated, is the chromosphere heated by thermal or non-thermal mechanisms? Non-thermal mechanisms could be due to the trapped particles at the reconnection site.
The evaporation and soft X-ray heating of the chromosphere, the cooling of hot coronal plasma by radiative losses, and thermal conduction are parts of the thermal mechanisms that should be considered in the modelling of energy transport from the corona towards the chromosphere. Interpretation of the chromosphere brightening also requires analysis of the formation of the chromospheric lines, using non-LTE radiative transfer methods with an energy equation including these various phenomena (e.g. Berlicki & Heinzel 2004).
We had an opportunity to observe the flare ribbons in three different chromospheric lines. The temporal evolution of these three lines compared to the RHESSI curves at different energies gives some constraints for future modelling.
Table 1:
Observational information for the 1N/M1.9 flare of 20 October 2003.
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2128f01a.eps}\hspace*{4mm}
\includegraphics[width=8.4cm,clip]{2128f01b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg17.gif) |
Figure 1:
a) GOES X-ray flux in 0.5-4 Å and 1-8 Å. The two dashed vertical bars indicate the start and end time of RHESSI light curves in b) and the numbers (1-2) mark the two peaks of GOES 0.5-4 Å flux in the time range of RHESSI observation. b) RHESSI light curves in the energy range of 3-12 keV, 12-25 keV, and 25-50 keV retrieved from the RHESSI data of collimators and detectors 3F-8F with a time bin of 4 s. The numbers (1-2) mark the two peaks of RHESSI light curve that temporally correspond to the two GOES 0.5-4 Å peaks marked in Frame a). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f02.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg18.gif) |
Figure 2:
a), b) Magnetogram at 07:59:03 UT and c) intensity image at 06:46:00 UT observed by SOHO/MDI. d) and e) magnetogram and intensity image observed by THEMIS in the MSDP mode at Na I 5896 Å 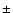 0.1 Å. The image size of b)- e) is
130 0.1 Å. The image size of b)- e) is
130
  130 130
 .
North is on the top and east to the left for all the images shown in this paper. Many fine thread-like structures are observed in the negative polarity in the THEMIS magnetogram shown in d). The spatial resolution of THEMIS images is estimated to be better than 0.8 .
North is on the top and east to the left for all the images shown in this paper. Many fine thread-like structures are observed in the negative polarity in the THEMIS magnetogram shown in d). The spatial resolution of THEMIS images is estimated to be better than 0.8
 . . |
| Open with DEXTER |
The Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI, Lin et al. 2002) observations allow us to reconstruct the spectra in the X-ray energy range of 3-100 keV. These observed spectra can be reproduced by calculations based on different theoretical models. In general, we apply two types of models: thermal and non-thermal. The thermal component represents the flare energy contained in the thermal plasma, while the non-thermal component can give us some suggestions about the importance of non-thermal particles in the overall energy budget of solar flares. The ratio of the non-thermal and thermal energies calculated for different flares can be different (McDonald et al. 1999; Berlicki et al. 2004), and its value determines the dominant heating mechanism during the flare.
We focus our present paper on analyzing the M 1.9 flare (20 October 2003 at 07:10 UT) in the active region NOAA 10484 observed during a coordinated observation campaign between space-borne and ground-based instruments. The multi-wavelength observations of this flare cover the impulsive, as well as the gradual phase. In our analysis we emphasize on the X-ray data from the RHESSI instrument. In the second section we describe the observations, and in the third the flare and the magnetic topology of the region. The RHESSI spectral analysis is reported in Sect. 4, where we also compute the ratio between non-thermal and thermal energy according to the chosen flare models (thin- or thick target). Section 5 summarizes the analysis and discusses our results.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f03.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg19.gif) |
Figure 3:
A selection of reconstructed RHESSI images (not normalized) from collimators and detectors 3F-8F using the CLEAN image algorithm with a time interval of 60 s. The observation times and energy bands are indicated in each image. The image size is 128
  128 128
 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2128f04a.eps}\hspace*{3mm}
\...
...4c.eps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{2128f04d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg20.gif) |
Figure 4:
Coalignment of RHESSI images of different energy bands and times: a) contour of the image of 25-50 keV at 07:13 UT is superposed on the image of 12-25 keV at 07:13 UT; b) contour of the image of 25-50 keV at 07:21 UT is superposed on the image of 12-25 keV at 07:21 UT; c) contour of the image of 12-25 keV at 07:21 UT is superposed on the image of 12-25 keV at 07:13 UT; d) contour of the image of 25-50 keV at 07:21 UT is superposed on the image of
25-50 keV at 07:13 UT. The RHESSI images are reconstructed from collimators and detectors 3F-8F using the CLEAN image algorithm with a time interval of 60 s. The contour levels of RHESSI image are 60%, 70%, 80%, 90%, and 95% of the maximum value of the image. |
| Open with DEXTER |
The 1N/M1.9 flare of 20 October 2003 was located at N03E48 and occurred in the active region NOAA 10484, one of the three flare-productive active regions that appeared in late October 2003. This flare was observed during a multi-wavelength observation campaign (JOP 157) by space-borne and ground-based instruments, including GOES, RHESSI, the Solar and Heliospheric Observatory (SOHO) (Domingo et al. 1995), THEMIS on the Canary Islands in the MSDP (Multichannel Subtractive Double Pass) observing mode (Mein 2002), and the Multi-channel Infrared Solar Spectrograph (MISS) at Purple Mountain Observatory (PMO) (Li et al. 19992002). Table 1 summarizes the observational information about this flare.
The Solar Geophysical Data (SGD)registration indicates that the X-ray flare started at 06:45 UT, peaked at 07:22 UT, and ended at 07:43 UT, and the H flare peaked at 07:23 UT and ended at 08:51 UT (Fig. 1a). The EUV data of this flare in 195 Å and 304 Å are from observations of the Extreme-ultraviolet Imaging Telescope (EIT) (Delaboudinière et al. 1995) onboard SOHO, which observed this flare with a cadence of about 12 min. The full-disk intensity images, which are used to coalign the ground-based and space-borne observations, and the longitudinal magnetic field were observed by the Michelson Doppler Imager (MDI) (Scherrer et al. 1995) onboard SOHO.
flare peaked at 07:23 UT and ended at 08:51 UT (Fig. 1a). The EUV data of this flare in 195 Å and 304 Å are from observations of the Extreme-ultraviolet Imaging Telescope (EIT) (Delaboudinière et al. 1995) onboard SOHO, which observed this flare with a cadence of about 12 min. The full-disk intensity images, which are used to coalign the ground-based and space-borne observations, and the longitudinal magnetic field were observed by the Michelson Doppler Imager (MDI) (Scherrer et al. 1995) onboard SOHO.
The spectro-polarimetric observations of the flare were made by the THEMIS telescope with the MSDP spectrograph observing mode in the period of 08:13-15:30 UT, partially covering the gradual phase of the flare. THEMIS is a polarization-free telescope, designed especially for polarimetric observations. The polarization analyzer provides the Stokes parameters 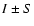 (S=V, Q or U) successively without differential blurring due to seeing effects. A detailed description of the specific instrumental set-up of THEMIS in the MSDP observing mode is published in Mein (2002). Figure 2 shows both the location of the AR 10484 and the longitudinal magnetograms and intensity images of this active region observed by THEMIS in MSDP mode in the Na I 5896 Å line in 25 min and by MDI in the Ni I 6768 Å line for comparison. The active region consists of one leading sunspot of positive polarity and several following sunspots of negative polarity. In the southern part of the region, penumbrae of positive polarity surround the negative sunspot group. With all these polarities the active region NOAA 10484 presents a
(S=V, Q or U) successively without differential blurring due to seeing effects. A detailed description of the specific instrumental set-up of THEMIS in the MSDP observing mode is published in Mein (2002). Figure 2 shows both the location of the AR 10484 and the longitudinal magnetograms and intensity images of this active region observed by THEMIS in MSDP mode in the Na I 5896 Å line in 25 min and by MDI in the Ni I 6768 Å line for comparison. The active region consists of one leading sunspot of positive polarity and several following sunspots of negative polarity. In the southern part of the region, penumbrae of positive polarity surround the negative sunspot group. With all these polarities the active region NOAA 10484 presents a 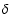 configuration (Fig. 2). Zharkova et al. (2005) identified 17 umbrae in this active region, among them 2 large umbrae of positive polarity and 3 with negative polarity; these positive polarities do not balance the negative ones.
configuration (Fig. 2). Zharkova et al. (2005) identified 17 umbrae in this active region, among them 2 large umbrae of positive polarity and 3 with negative polarity; these positive polarities do not balance the negative ones.
MISS observations started at 06:47 UT and ended at 07:58 UT, covering the full impulsive and gradual phases of this flare. MISS observations consist of spectra in three lines - H ,
Ca II 8542 Å, and He I 10 830 Å - and H
,
Ca II 8542 Å, and He I 10 830 Å - and H images obtained simultaneously with the spectra by the slit-jaw system of MISS, which uses a Daystar filter with 0.5 Å passband. The integration times of H
images obtained simultaneously with the spectra by the slit-jaw system of MISS, which uses a Daystar filter with 0.5 Å passband. The integration times of H ,
Ca II 8542 Å, and He I 10 830 Å spectra are, respectively, 0.06 s, 0.06 s, and 0.4 s, while the spectral dispersions are 0.05453 Å, 0.05113 Å, and 0.04776 Å per pixel, respectively. The spatial resolution is 1.34
,
Ca II 8542 Å, and He I 10 830 Å spectra are, respectively, 0.06 s, 0.06 s, and 0.4 s, while the spectral dispersions are 0.05453 Å, 0.05113 Å, and 0.04776 Å per pixel, respectively. The spatial resolution is 1.34
 along the slit after 4-row binning, while the temporal resolution is about 2.8 s. The observed spectral data were first corrected for the dark-current, flat-field, scattered light, and instrument profile, and then were absolutely calibrated using the continuum intensity near these wavelengths. The calibration was done by comparing the observed profiles in the nearby quiet region with theoretical mean profiles for H
along the slit after 4-row binning, while the temporal resolution is about 2.8 s. The observed spectral data were first corrected for the dark-current, flat-field, scattered light, and instrument profile, and then were absolutely calibrated using the continuum intensity near these wavelengths. The calibration was done by comparing the observed profiles in the nearby quiet region with theoretical mean profiles for H (David 1961) and Ca II 8542 Å (Linsky et al. 1970), and with an observed standard profile for He I 10 830 Å (http://bass2000.obspm.fr/).
(David 1961) and Ca II 8542 Å (Linsky et al. 1970), and with an observed standard profile for He I 10 830 Å (http://bass2000.obspm.fr/).
GOES X-ray flux curves indicate an impulsive phase with two bumps before the maximum of the flare (Fig. 1a). The maximum is flat with 2 peaks in the 0.5-4 Å flux that are
labelled "1'' and "2'' in Fig. 1a. This flare was observed by RHESSI with attenuator A1 placed before the detectors (the attenuator was changed to A0 three times for a short period at around 07:28 UT, 07:34 UT, and 07:56 UT, respectively) in the period of 07:04-08:00 UT, covering the 2 peaks of GOES 0.5-4 Å X-ray flux (Fig. 1a). Using collimators and detectors
3F-8F, we retrieved the X-ray light curves and reconstructed X-ray images from RHESSI observational data. RHESSI light curves show that the X-ray emissions above 80 keV are negligible.
Figure 1b presents a part of the light curves. The first two peaks of the RHESSI light curves are coincident with the two peaks of GOES X-ray flux. A careful comparison of RHESSI light curves shows that the first peak of the light curve in the low energy channel is delayed with respect to that in the high energy channel. We also noticed from Fig. 1b that the count rate ratio of the 25-50 keV light curve around the second peak to the first peak is much smaller than that of 12-25 keV. The third peak of the 25-50 keV light curve near 07:45 UT is produced by charged particles at high geomagnetic latitude. The jumps of the light curves in Fig. 1b around 07:28 UT, 07:34 UT, and 07:56 UT are due to the change of the attenuator from A1 to A0.
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f05.eps}\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg22.gif) |
Figure 5:
a)- e) Normalized SOHO/EIT/304 Å images and f) SOHO/EIT/195 Å image. The contours in Frame d) represent the longitudinal magnetic field observed by SOHO/MDI at 07:59:03 UT (the solid line stands for positive field and the dotted for negative field). The letters "R1a'', "R1b'', "R2'' and "R3'' in Frame b) correspond to the H flare ribbons in Fig. 6f. The observation times and wavelengths are shown in each image. The image size is 286
flare ribbons in Fig. 6f. The observation times and wavelengths are shown in each image. The image size is 286
  286 286
 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f06.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg23.gif) |
Figure 6:
Normalized slit-jaw H images observed by MISS at PMO. The observation times are shown in the upper-left corner of each image. The image size is 170
images observed by MISS at PMO. The observation times are shown in the upper-left corner of each image. The image size is 170
  128 128
 .
The letters "R1a'', "R1b'', "R2'', and "R3'' in frame f) mark the H .
The letters "R1a'', "R1b'', "R2'', and "R3'' in frame f) mark the H flare ribbons. Contours in frame f) represent the longitudinal magnetic field observed by SOHO/MDI at 07:59:03 UT (solid line for positive field and dotted line for negative field). The arrows labelled "FL'' and "QS'' in e) indicate the points where we computed the line center intensities shown in Fig. 10 for the flare and quiet sun, respectively. "FL'' corresponds to a point in ribbon R1b.
flare ribbons. Contours in frame f) represent the longitudinal magnetic field observed by SOHO/MDI at 07:59:03 UT (solid line for positive field and dotted line for negative field). The arrows labelled "FL'' and "QS'' in e) indicate the points where we computed the line center intensities shown in Fig. 10 for the flare and quiet sun, respectively. "FL'' corresponds to a point in ribbon R1b. |
| Open with DEXTER |
Figure 3 shows a selection of the reconstructed RHESSI images in 12-25 keV and
25-50 keV energy bands (not normalized). Most of these images displayed a single loop-top source. Meanwhile, two sources are visible in the images of 12-25 keV in the period of 07:06-07:10 UT (cf. Fig. 3); the north-east one is only seen in these images. Some of the 25-50 keV images showed three HXR sources (e.g., images at 07:08-07:09 UT and 07:15-07:16 UT in Fig. 3), but they are too weak to be taken as certain. The reconstructed RHESSI images demonstrate that the maximum emission in 25-50 keV occurred at 07:11-07:12 UT, while that in 12-25 keV at
07:12-07:13 UT, which is consistent with the above statement about the delay of the light curve in the low energy channel with respect to that in the high energy channel.
We coaligned RHESSI images in two energy bands (12-25 keV and 25-50 keV) near the first two peak times of the RHESSI light curve (namely 07:13 UT and 07:21 UT) and display them in Fig. 4. The coalignments show source motions in both 12-25 keV and 25-50 keV images. Similar results are reported by other authors (e.g. Gallagher et al. 2002; Liu et al. 2004; Li et al. 2005) and attributed to the rise of flaring loops due to continuous magnetic reconnection. The figure also demonstrates that the sources in the two energy bands at the same time are spatially consistent and the sources at 07:21 UT moved to the north east with respect to that at 07:13 UT. This implies that the corresponding magnetic field reconnection site moved to the north east and, accordingly, took place between different magnetic loops.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2128f07a.eps}\hspace*{3mm}
\...
...7c.eps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{2128f07d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg24.gif) |
Figure 7:
RHESSI 25-50 keV image at 07:11-07:12 UT (contour) is superposed on a) EIT/304 Å image at 07:19:34 UT, b) SOHO/MDI magnetogram at 07:59:03 UT, and c) MISS/H image at 07:23:00 UT. d) EIT/195 Å image at 07:19:23 UT (contour) is superposed on the MISS/H
image at 07:23:00 UT. d) EIT/195 Å image at 07:19:23 UT (contour) is superposed on the MISS/H image at 07:23:00 UT. The contour levels of the RHESSI image are 60%, 70%, 80%, 90%, and 95% of the maximum value of the image.
image at 07:23:00 UT. The contour levels of the RHESSI image are 60%, 70%, 80%, 90%, and 95% of the maximum value of the image. |
| Open with DEXTER |
We used the EUV observational data from SOHO/EIT because there is no high resolution EUV observation from Transition Region and Coronal Explorer (TRACE) for this flare. Selected EUV images in 304 Å and 195 Å are shown in Fig. 5. During the flare, 304 Å images were obtained with a cadence of
12 min, and only one 195 Å image was recorded at 07:13:29 UT. From Fig. 5, we see the evolution of the flare in 304 Å. The flare shows two different "low temperature'' (
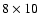 4
4 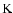 ,
Delaboudinière et al. 1995) bright features in 304 Å wavelength, which underwent different changes in area and intensity versus time. There were already two ribbons at 06:48:14 UT (R1 and R2). At 07:19:23 UT two structures (R1a and R1b) can be distinguished in the northern ribbon, and the ribbon R2 is reduced to one kernel and a new bright "J-shape'' structure appeared that we named R3 (Figs. 5a,b,c). The intensity and area of these ribbons decreased after 07:25 UT (Figs. 5c,d,e). The ribbon R1 overlays the negative polarity, and the ribbons R2 and R3 the positive polarity (Fig. 5d).
,
Delaboudinière et al. 1995) bright features in 304 Å wavelength, which underwent different changes in area and intensity versus time. There were already two ribbons at 06:48:14 UT (R1 and R2). At 07:19:23 UT two structures (R1a and R1b) can be distinguished in the northern ribbon, and the ribbon R2 is reduced to one kernel and a new bright "J-shape'' structure appeared that we named R3 (Figs. 5a,b,c). The intensity and area of these ribbons decreased after 07:25 UT (Figs. 5c,d,e). The ribbon R1 overlays the negative polarity, and the ribbons R2 and R3 the positive polarity (Fig. 5d).
The 195 Å image in Fig. 5f shows the high temperature (
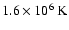 ,
Delaboudinière et al. 1995) flare. We see small 195 Å loops connecting the two 304 Å ribbons (R1 and R2). We will show in the next subsection that they also connect the two H
,
Delaboudinière et al. 1995) flare. We see small 195 Å loops connecting the two 304 Å ribbons (R1 and R2). We will show in the next subsection that they also connect the two H ribbons.
ribbons.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2128f08a.ps}\hspace*{3mm}
\i...
...e*{4cm}\includegraphics[width=6cm,clip]{2128f08c.ps}\hspace*{4cm}}\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg28.gif) |
Figure 8:
Extrapolated magnetic field lines using the longitudinal magnetic field observed by THEMIS at 09:13:15 UT for the active region NOAA 10484. The THEMIS magnetogram has been inserted in a large MDI map obtained at 09:35:04 UT (303
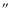  230 230
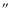 ). The extrapolation was performed in a current-free field configuration. a) observer view, b) radial ( top) view and c) 3D perspective view. The letters "R1a'', "R1b'', "R2'', and "R3'' indicate the locations of the H ). The extrapolation was performed in a current-free field configuration. a) observer view, b) radial ( top) view and c) 3D perspective view. The letters "R1a'', "R1b'', "R2'', and "R3'' indicate the locations of the H flare ribbons. Thick lines indicate the lines where the change of connectivity is drastic.
flare ribbons. Thick lines indicate the lines where the change of connectivity is drastic. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{2128f09.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg29.gif) |
Figure 9:
Profiles of a) H ,
b) Ca II 8542 Å, and c) He I 10 830 Å lines observed by MISS at 07:11:14 UT. The solid lines stand for the profiles in the flaring region (marked "FL'' (in the ribbon R1b) in Fig. 6e) and dotted lines for those in the nearby quiet region (marked "QS'' in Fig. 6e). ,
b) Ca II 8542 Å, and c) He I 10 830 Å lines observed by MISS at 07:11:14 UT. The solid lines stand for the profiles in the flaring region (marked "FL'' (in the ribbon R1b) in Fig. 6e) and dotted lines for those in the nearby quiet region (marked "QS'' in Fig. 6e). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2128f10.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg30.gif) |
Figure 10:
Temporal evolution of the line-center intensities of H ,
Ca II 8542 Å, and He I 10 830 Å lines observed by MISS at PMO for the point indicated in Fig. 6e by the arrow labelled "FL''. The symbols ,
Ca II 8542 Å, and He I 10 830 Å lines observed by MISS at PMO for the point indicated in Fig. 6e by the arrow labelled "FL''. The symbols
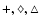 stand for the observed line-center intensities of H
stand for the observed line-center intensities of H ,
Ca II 8542 Å, and He I 10 830 Å, respectively, and the corresponding solid lines for the smoothed ones. The horizontal short bars on the left side of the plot indicate the line-center intensities of the three lines observed in the nearby quiet-sun region (marked "QS'' in Fig. 6e). Also plotted is the RHESSI 25-50 keV light curve. ,
Ca II 8542 Å, and He I 10 830 Å, respectively, and the corresponding solid lines for the smoothed ones. The horizontal short bars on the left side of the plot indicate the line-center intensities of the three lines observed in the nearby quiet-sun region (marked "QS'' in Fig. 6e). Also plotted is the RHESSI 25-50 keV light curve. |
| Open with DEXTER |
3.2 Optical analysis
Optical observations of this flare were made by THEMIS, and MISS. THEMIS observed the line-of-sight (LOS) magnetic field of the active region during the gradual phase and after the flare at 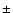 0.1 Å of Na I 5896 Å line center. One example observed at 07:59 UT is given in Fig. 2, which shows more fine structure than the MDI/SOHO image. The THEMIS image has a better resolution (0.6
0.1 Å of Na I 5896 Å line center. One example observed at 07:59 UT is given in Fig. 2, which shows more fine structure than the MDI/SOHO image. The THEMIS image has a better resolution (0.6
 )
than the MDI image.
)
than the MDI image.
Nine normalized slit-jaw H images obtained by MISS are shown in Fig. 6, which cover the whole flare period. From these images, we clearly see two H
images obtained by MISS are shown in Fig. 6, which cover the whole flare period. From these images, we clearly see two H flare ribbons that correspond to R1, R2, and partly R3 of the EUV 304 Å ribbons. The coalignment with magnetograms and intensity images of THEMIS and MDI indicated that the ribbons stride over the measured magnetic neutral line and are located in the penumbrae of two sunspots separately (Fig. 6f). R1 is larger and stronger than R2. At 06:47:12 UT, the two ribbons are very weak (Fig. 6a). And then R1 began to increase its intensity and area (Fig. 6b). We can distinguish two bright parts of R1 in the image at 07:06:42 UT (Fig. 6c), which are co-spatial with the EUV ribbon R1a and R1b in Fig. 5. R2 started to increase its intensity near 07:06 UT
(Fig. 6c). The intensities and areas of R1 and R2 kept increasing
(Fig. 6d and 6e) and reached their maximum around 07:23 UT (Fig. 6f).
flare ribbons that correspond to R1, R2, and partly R3 of the EUV 304 Å ribbons. The coalignment with magnetograms and intensity images of THEMIS and MDI indicated that the ribbons stride over the measured magnetic neutral line and are located in the penumbrae of two sunspots separately (Fig. 6f). R1 is larger and stronger than R2. At 06:47:12 UT, the two ribbons are very weak (Fig. 6a). And then R1 began to increase its intensity and area (Fig. 6b). We can distinguish two bright parts of R1 in the image at 07:06:42 UT (Fig. 6c), which are co-spatial with the EUV ribbon R1a and R1b in Fig. 5. R2 started to increase its intensity near 07:06 UT
(Fig. 6c). The intensities and areas of R1 and R2 kept increasing
(Fig. 6d and 6e) and reached their maximum around 07:23 UT (Fig. 6f).
We coaligned the RHESSI HXR (25-50 keV) image at 07:11-07:12 UT, the slit-jaw H image at 07:23:00 UT, the EIT/304 Å image at 07:19:34 UT and the SOHO/MDI magnetogram at 07:59:03 UT. The results are given in Fig. 7. We infer from the coalignments that the RHESSI HXR source is a loop-top source. The ribbons R1 (R1a and R1b) and R2 observed in H
image at 07:23:00 UT, the EIT/304 Å image at 07:19:34 UT and the SOHO/MDI magnetogram at 07:59:03 UT. The results are given in Fig. 7. We infer from the coalignments that the RHESSI HXR source is a loop-top source. The ribbons R1 (R1a and R1b) and R2 observed in H and 304 Å would be the footpoints.
and 304 Å would be the footpoints.
3.3 Magnetic topology
The presence of the three ribbons observed in H and 304 Å can be interpreted by analyzing the magnetic topology of the active region.
and 304 Å can be interpreted by analyzing the magnetic topology of the active region.
We extrapolated the measured photospheric magnetic field obtained by THEMIS to infer the large scale 3D structure over the region. Before the extrapolation we inserted the THEMIS magnetogram at 09:13:15 UT in a large MDI magnetogram at 09:35:04 UT to take advantage of the enhanced spatial resolution of THEMIS. We interpolated the non computed values of the magnetic field over the ribbons. The extrapolation of the magnetic field lines in the corona was performed with the assumption of a current-free field configuration (
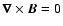 )
and by using the code developed by Démoulin et al. (1997) (code base of FROMAGE).
)
and by using the code developed by Démoulin et al. (1997) (code base of FROMAGE).
Figure 8 represents the result of the extrapolation. The ribbons are located in regions where the field lines change their connectivity (see mainly field lines starting from R1); this suggests that these regions correspond to the places where quasi-separatrix layers intersect the chromosphere (see Démoulin et al. 1997, and references therein). There are several sites of possible reconnections. The ribbons R1 and R2 appear first and then the ribbon R3. Multiple reconnections are possible. A further analysis should be done to confirm this scenario.
3.4 Response of the chromosphere to hard X-ray flux
During MISS observations, the observer may put the slit at different positions of the flare by shifting the solar image. We can follow some points of interest by carefully coaligning the MISS slit-jaw H image using the SOHO/MDI intensity image. In order to investigate the time evolution of chromospheric and X-ray emission in all the MISS observations, we selected spectra corresponding to the point marked "FL'' (in ribbon R1b) in Fig. 6e with a spatial resolution
of 1.34
image using the SOHO/MDI intensity image. In order to investigate the time evolution of chromospheric and X-ray emission in all the MISS observations, we selected spectra corresponding to the point marked "FL'' (in ribbon R1b) in Fig. 6e with a spatial resolution
of 1.34
 .
.
We present a sample set of the H ,
Ca II 8542 Å, and He I 10 830 Å profiles at this point observed by MISS in the impulsive phase at 07:11:14 UT in Fig. 9. In this figure the solid lines stand for the profiles in the flaring region and dotted lines for those in a nearby quiet-sun region.
Figure 9 shows that the profiles in all three lines display red-asymmetry.
,
Ca II 8542 Å, and He I 10 830 Å profiles at this point observed by MISS in the impulsive phase at 07:11:14 UT in Fig. 9. In this figure the solid lines stand for the profiles in the flaring region and dotted lines for those in a nearby quiet-sun region.
Figure 9 shows that the profiles in all three lines display red-asymmetry.
To study their temporal variations, we plotted all the H ,
Ca II 8542 Å, and He I 10 830 Å profiles at the selected point and computed the line-center intensities from absolutely calibrated spectral data (see Sect. 2 for details about the calibration). The flare occurred over the sunspot group and therefore the continuum intensities in all "FL'' profiles were less than those corresponding to the quiet region. The derived line-center intensity curves are plotted in Fig. 10 together with the RHESSI X-ray flux in 25-50 keV for comparison. The time profiles of line-center intensities shown in solid lines are the 7-point average of the observed ones shown as "+'', "
,
Ca II 8542 Å, and He I 10 830 Å profiles at the selected point and computed the line-center intensities from absolutely calibrated spectral data (see Sect. 2 for details about the calibration). The flare occurred over the sunspot group and therefore the continuum intensities in all "FL'' profiles were less than those corresponding to the quiet region. The derived line-center intensity curves are plotted in Fig. 10 together with the RHESSI X-ray flux in 25-50 keV for comparison. The time profiles of line-center intensities shown in solid lines are the 7-point average of the observed ones shown as "+'', "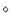 '', and "
'', and "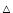 '' for H
'' for H ,
Ca II 8542 Å, and He I 10 830 Å, respectively. In Fig. 10, for comparison, we also denoted the line-center intensities of the three lines in a quiet region of the Sun that were computed from the data of the point marked "QS'' in Fig. 6e.
,
Ca II 8542 Å, and He I 10 830 Å, respectively. In Fig. 10, for comparison, we also denoted the line-center intensities of the three lines in a quiet region of the Sun that were computed from the data of the point marked "QS'' in Fig. 6e.
Figure 10 shows that the temporal variations of the line-center intensities of H ,
Ca II 8542 Å, and He I 10 830 Å have the same trend and peak almost simultaneously within the measurement uncertainties. The MISS spectrograms were taken with a cadence of 2.8 s. However, the average time interval for the spectrograms selected to compute the intensities in Fig. 10 is
,
Ca II 8542 Å, and He I 10 830 Å have the same trend and peak almost simultaneously within the measurement uncertainties. The MISS spectrograms were taken with a cadence of 2.8 s. However, the average time interval for the spectrograms selected to compute the intensities in Fig. 10 is 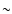 40 s due to the seeing and image shift by the observer during the observation. The intensities of the three analyzed lines increased already before the flare at the location of the ribbons. It could be due to a pre-flare event. The intensity time profiles show a steep slope at 07:10 UT corresponding to the rising phase of the hard X-ray emission in the 25-50 keV range. After this steep slope we observe a plateau and then again an intensity increase, until a smooth maximum slightly after the second peak of the 25-50 keV emission.
40 s due to the seeing and image shift by the observer during the observation. The intensities of the three analyzed lines increased already before the flare at the location of the ribbons. It could be due to a pre-flare event. The intensity time profiles show a steep slope at 07:10 UT corresponding to the rising phase of the hard X-ray emission in the 25-50 keV range. After this steep slope we observe a plateau and then again an intensity increase, until a smooth maximum slightly after the second peak of the 25-50 keV emission.
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{2128f11a.eps}\par\vspace*...
...\par\vspace*{3mm}
\includegraphics[width=13.8cm,clip]{2128f11d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg35.gif) |
Figure 11:
RHESSI spectral fit results for data retrieved from collimators and detectors 1F,
3F-6F and 8F-9F with a 20 s time interval. The energy range is set to 12-80 keV for 07:06:00-07:22:00 UT and 12-60 keV for other times. The background order is taken to be 1 for 3-50 keV and 3 for energy ranges higher than 50 keV. Time profiles of the broken energy
( left of the first panel) and normalization factor ( right of the first panel) from the fitting with the "vth+bpow'' method (cf. Sect. 4.1). The second panel shows the fitted photon spectra with this model for the time interval of 07:11:00-07:11:20 UT ( left) and 07:21:00-07:21:20 UT ( right). The third and the fourth panels are the same as the second panel but with the "vth+thin'' and "vth+thick'' model, respectively (please see the text in
Sect. 4.1 for details about the models). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2128f12a.eps}\includegraphics[width=8.3cm,clip]{2128f12b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg36.gif) |
Figure 12:
Time profile of a) temperature and b) emission measure derived from GOES-10 (solid line) and RHESSI spectral analysis with "vth+thin'' (dashed line) and "vth+thick'' (dotted line) model. |
| Open with DEXTER |
4 RHESSI spectral analysis
4.1 Spectral analysis
The flare was well observed by RHESSI, even though it had already started when RHESSI came out of orbit night and began to observe. The RHESSI spectra were generated every 20 s from collimators and detectors 1F, 3F-6F and 8F-9F for the period of 07:04-07:28 UT. During the fitting process, the time bin was set to 20 s. The background model was selected for each energy range to allow for variation with time. We chose linear extrapolations between the nighttime count rates (before and after the flare) for the lower energy ranges (3-50 keV) and higher order (order 3) fits for the energy bands above 50 keV. The attenuator A1 was placed before the detectors during the observations, therefore the spectra below 12 keV are not reliable due to the absorption of passive material in front of the detectors (thermal blankets, beryllium detector window, aluminum attenuator, etc.). Meanwhile, HXR emission in the energy channel >70 keV is quite weak and ignorable. Therefore, in our fitting process, we set the energy range to 12-80 keV for the period of 07:06-07:22 UT and 12-60 keV for other time intervals.
The low energy cutoff for the power-law distribution of non-thermal electrons has been disputed for many years and is generally set to 15-25 keV (e.g. Hudson & Canfield 1978; Canfield & Gunkler 1985; Zarro & Canfield 1989; Mariska & Zarro 1991; Hawley & Fisher 1994; Wülser et al. 1994; McDonald et al. 1999). Here we try to estimate the low energy cutoff of the non-thermal electron distribution for this flare. To do this, we fit the count spectra with a thermal plus broken power-law component in the above-mentioned energy range. As generally, the negative power-law index below the break energy is fixed to 1.5 in order to avoid an unrealistic flux value at low energy range. In such cases, the break energy is the low energy cutoff. If this model can fit the observed spectra well, we can get the low energy cutoff from the spectral fitting. Two examples that show a good fit to the observed spectra around the two RHESSI light-curve peaks are given in Fig. 11 (second panel). The resulting break energy and normalization factor are shown in the first panel of Fig. 11. The normalization factor in this case is the extrapolated flux at 50 keV for the component below the break energy. Its impulsive behavior, as shown in the right of the first panel in Fig. 11 at around 07:11 UT, generally indicates the existence of non-thermal emission. The break energy falls in the range of 22-30 keV with an average of about 25 keV. Therefore, in our later spectral fitting, we will set the low energy cutoff to 25 keV.
Now we will use different models to fit the observed RHESSI spectra. We note that RHESSI images show the HXR source as mainly near the loop tops (Fig. 3). Thus we first invoke a model comprising a thermal bremsstrahlung function plus a thin-target non-thermal broken power-law function with low- (25 keV) and high-energy (32 MeV) cutoffs (hereafter called "vth+thin'' model). Then, for comparison we also invoke a model comprised of a thermal bremsstrahlung function plus a thick-target non-thermal broken power-law function with low- (25 keV) and high-energy (1 MeV) cutoffs (hereafter called "vth+thick'' model). For the "vth+thick'' model we used a high-energy cutoff of 1 MeV instead of 32 MeV to save computer time because the corresponding function is rather slow to run. The estimated error of this change is less than 2% in our case. The chi-square values for all the fittings are in the range of 0.3-1.8. Two examples of the fit results around the two RHESSI light-curve peaks are presented in the third and fourth panels of Fig. 11 for the "vth+thin'' and "vth-thick'' models, respectively.
We derived the plasma temperature and emission measure (EM) from the fit parameters and plotted them in Figs. 12a and 12b, respectively. In this figure, we also plotted the temperature and EM derived from the GOES-10 X-ray observation. Figure 12 tells us that the temperatures from RHESSI spectral analysis are two or even three times higher than the GOES temperatures, while the emission measures are about 1-2 orders of magnitude lower than that of GOES. The maximum computed temperature is about
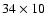
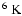 at 07:11 UT (the main HXR peak in Fig. 1b and SXR peak in Fig. 1a). It is worth mentioning that the "vth+thin'' and "vth+thick'' models give similar time profiles of temperature and EM.
at 07:11 UT (the main HXR peak in Fig. 1b and SXR peak in Fig. 1a). It is worth mentioning that the "vth+thin'' and "vth+thick'' models give similar time profiles of temperature and EM.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2128f13a.eps}\hspace*{4mm}
\includegraphics[width=7.5cm,clip]{2128f13b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg39.gif) |
Figure 13:
a) Temporal variations of thermal energy (
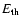 ,
thick line) and non-thermal energy ( ,
thick line) and non-thermal energy (
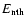 ,
thin line) computed from the fit parameters with the "vth+thick'' (solid line) and "vth+thin'' models (dashed line). b) Time profile of the ratio of non-thermal energy to thermal energy ( ,
thin line) computed from the fit parameters with the "vth+thick'' (solid line) and "vth+thin'' models (dashed line). b) Time profile of the ratio of non-thermal energy to thermal energy (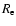 )
for the studied flare calculated from RHESSI spectral analysis with the "vth+thick'' (solid line) and "vth+thin'' (dashed line) models. The low energy cutoff for the non-thermal electron beam was set to 25 keV based on our estimation. The mean lifetime of non-thermal electrons is set to 1 s. )
for the studied flare calculated from RHESSI spectral analysis with the "vth+thick'' (solid line) and "vth+thin'' (dashed line) models. The low energy cutoff for the non-thermal electron beam was set to 25 keV based on our estimation. The mean lifetime of non-thermal electrons is set to 1 s. |
| Open with DEXTER |
4.2 Thermal and non-thermal energy estimation
From the fit parameters of the preceding spectral analysis, we can estimate the thermal and non-thermal energy in the flare. The thermal energy was computed from the temperature and emission measure for the thermal portion of the spectral fit by (cf. McDonald et al. 1999; Berlicki et al. 2004; Ji et al. 2004)
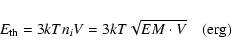 |
(1) |
where k, T, EM, and V are the Boltzmann constant, the plasma temperature (K), the emission measure (cm-3), and source volume (cm3), respectively. Here a homogeneous plasma target was assumed so that equation
EM=ni2V is applicable. The source volume was estimated using
the 50% contour of the reconstructed 12-25 keV RHESSI images (Emslie et al. 2004) and assuming a cylinder structure of the flare loop.
The thick-target and thin-target models that are used to fit the non-thermal portion of the RHESSI spectra allow us to compute the energy flux of non-thermal electrons by integrating above the low energy cutoff. The energy flux of non-thermal electrons is calculated by the following equation:
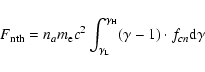 |
(2) |
where na (electron s-1) is the normalization factor (electron flux), 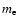 the electron mass, and c the speed of light.
the electron mass, and c the speed of light.
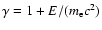 is the electron gamma. fcn is the value of the electron distribution function, which is computed using functions provided in RHESSI analysis software. And
is the electron gamma. fcn is the value of the electron distribution function, which is computed using functions provided in RHESSI analysis software. And
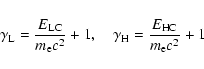 |
(3) |
where
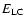 and
and
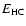 are, respectively, the low-energy and high-energy cutoffs set in the spectral fitting process. The total non-thermal energy injected into the flaring plasma is computed by integrating the energy flux of non-thermal electrons over the flaring time. We can compute the non-thermal energy in the flare at a given time by equation
are, respectively, the low-energy and high-energy cutoffs set in the spectral fitting process. The total non-thermal energy injected into the flaring plasma is computed by integrating the energy flux of non-thermal electrons over the flaring time. We can compute the non-thermal energy in the flare at a given time by equation
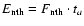 if we know the mean lifetime ta of the non-thermal electrons. Brown (1971) provided an approximate formula for the average energy loss rate of high-energy electrons by collision
if we know the mean lifetime ta of the non-thermal electrons. Brown (1971) provided an approximate formula for the average energy loss rate of high-energy electrons by collision
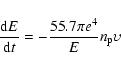 |
(4) |
where E is the energy of the energetic electrons, e the electronic charge (esu), 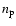 the total number density of the ambient protons, and
the total number density of the ambient protons, and 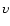 the supersonic electron velocity. X-ray emissions in less than 10 keV are generally taken to be of thermal nature. From Eq. (4) we calculated the time required for an electron of 80 keV (the maximum observed in our case) to lose its energy by collisions to 10 keV. This time is approximately 0.72 s with
the supersonic electron velocity. X-ray emissions in less than 10 keV are generally taken to be of thermal nature. From Eq. (4) we calculated the time required for an electron of 80 keV (the maximum observed in our case) to lose its energy by collisions to 10 keV. This time is approximately 0.72 s with
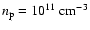 ,
and is consistent with other estimations. Emslie (1983) showed that for a thick target, HXR emissions produced by instantaneously injected high-energy electrons decrease to
,
and is consistent with other estimations. Emslie (1983) showed that for a thick target, HXR emissions produced by instantaneously injected high-energy electrons decrease to 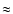 20% of the maximum value within 1 s. Therefore, in our computation of the non-thermal energy in the flare, we take
20% of the maximum value within 1 s. Therefore, in our computation of the non-thermal energy in the flare, we take
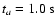 .
We will discuss this point in next section. The time profiles of the calculated non-thermal energy (
.
We will discuss this point in next section. The time profiles of the calculated non-thermal energy (
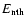 )
and thermal energy (
)
and thermal energy (
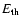 )
in the flare are plotted in Fig. 13a for the two models, and the corresponding non-thermal to thermal energy ratio (
)
in the flare are plotted in Fig. 13a for the two models, and the corresponding non-thermal to thermal energy ratio (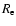 )
in Fig. 13b.
)
in Fig. 13b.
It can be seen from Fig. 13 that during most of the analyzed period the non-thermal component can be ignored as compared with the thermal component (Fig. 13a). During the RHESSI flare maximum (07:10-07:13 UT) (Fig. 13a) the non-thermal component is significant. This is confirmed by the impulsive behavior of the normalization factor from the spectral fitting (Fig. 11, right of the first panel). The maximum portion of the non-thermal energy represents approximately 20% of the total flare energy (
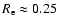 )
around 07:11 UT.
)
around 07:11 UT.
5 Discussion and conclusion
We studied the 1N/M1.9 flare of 20 October 2003 that occurred in active region NOAA 10484 during a coordinated observation program (JOP157) with space-borne and ground-based instruments including RHESSI, SOHO, GOES, THEMIS/MSDP, and MISS of Nanjing (China). It was a relatively confined flare because no CME (SOHO/LASCO) was reported. In the optical (H with the slit-jaw of MISS) and UV domain images (304 Å with SOHO/EIT), the flare consisted of several bright regions that corresponded to the three flare ribbons R1, R2, and R3. The magnetic topology of the region was investigated by extrapolating the photospheric longitudinal magnetic field observed by THEMIS/MSDP using a current-free field approximation. The ribbons were located in regions where the field lines changed connectivities, which suggests that they correspond to the intersections of magnetic separatrices or quasi-separatrices with the chromosphere. In particular, ribbon R1 is so wide that it could correspond to a quasi-separatrix region. Separatrix regions are locations where magnetic reconnections are possible (Démoulin et al. 19961997), and the three ribbons are the signatures of such magnetic reconnections. They did not flare at the same time; but instead we observed first the brightening of R1 and R2, then a few minutes later ribbon R3 brightened and again R1. This infers that we observed successive reconnections. The RHESSI images show a hard X-ray emission (HXR) structure that could correspond to the loop top joining R1 and R2 according to the overlay between RHESSI images and the extrapolated magnetic field lines. We noticed a significant displacement of the HXR source during the impulsive phase, which implies different reconnection sites.
with the slit-jaw of MISS) and UV domain images (304 Å with SOHO/EIT), the flare consisted of several bright regions that corresponded to the three flare ribbons R1, R2, and R3. The magnetic topology of the region was investigated by extrapolating the photospheric longitudinal magnetic field observed by THEMIS/MSDP using a current-free field approximation. The ribbons were located in regions where the field lines changed connectivities, which suggests that they correspond to the intersections of magnetic separatrices or quasi-separatrices with the chromosphere. In particular, ribbon R1 is so wide that it could correspond to a quasi-separatrix region. Separatrix regions are locations where magnetic reconnections are possible (Démoulin et al. 19961997), and the three ribbons are the signatures of such magnetic reconnections. They did not flare at the same time; but instead we observed first the brightening of R1 and R2, then a few minutes later ribbon R3 brightened and again R1. This infers that we observed successive reconnections. The RHESSI images show a hard X-ray emission (HXR) structure that could correspond to the loop top joining R1 and R2 according to the overlay between RHESSI images and the extrapolated magnetic field lines. We noticed a significant displacement of the HXR source during the impulsive phase, which implies different reconnection sites.
GOES X-ray flux shows a long rising phase of this flare and a broad double-peaked maximum. RHESSI light curves confirm the appearance of the two main peaks during the flare maximum (marked "1''
and "2'' in Fig. 1a) and thus multiple reconnection processes.
HXR emission is recorded up to 80 keV for this flare near the flare maximum and to less than 60 keV for the other periods. We analyzed the HXR emission using different models. First, using the "thermal with broken power law'' component, we could derive the low energy cutoff. Then we used a thin- and a thick-target model to compute the non-thermal component of the emission. During the main phase of the flare, the value of the energy cutoff is found to be between 22 and
30 keV (Fig. 11 - upper left panel). Then, we again fitted the RHESSI spectra using a constant energy cutoff (25 keV) and the two models (the "vth+thin'' and "vth+thick'' models). The fit results showed that the first RHESSI HXR peak is "harder'' than the second peak, and during most of the computed period, the non-thermal component is negligible compared with the thermal component except during the first peak (cf. Fig. 13). It is worth mentioning that both the "vth+thin'' and "vth+thick'' models can fit the observed RHESSI spectra and yield similar results (cf. Sect. 4), but we cannot tell which one is more reasonable so far.
Based on the fit parameters, we estimated the thermal and non-thermal energy of the flare and the ratio of the non-thermal to the thermal energy (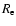 )
at different times, always adopting the estimated low energy cutoff of 25 keV and a mean lifetime of 1.0 s for the high-energy electrons. The computation indicates that during the first peak (07:09 and 07:13 UT), the non-thermal energy contributes significantly to the total energy with an amount reaching
)
at different times, always adopting the estimated low energy cutoff of 25 keV and a mean lifetime of 1.0 s for the high-energy electrons. The computation indicates that during the first peak (07:09 and 07:13 UT), the non-thermal energy contributes significantly to the total energy with an amount reaching 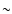 20%; while during the second peak the contribution of the non-thermal electrons is negligible. The non-thermal nature of hard X-ray radiation for E>50 keV is also confirmed by the behaviour of the X-ray flux at around 07:11 UT. The estimated thermal and non-thermal energies and
20%; while during the second peak the contribution of the non-thermal electrons is negligible. The non-thermal nature of hard X-ray radiation for E>50 keV is also confirmed by the behaviour of the X-ray flux at around 07:11 UT. The estimated thermal and non-thermal energies and 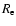 are in agreement with the spectral fitting shown in Fig. 11. Therefore, we could infer that most of the time the HXR emission in this flare is mainly of thermal origin, and thermal conduction transports most of the energy released during the flare to the chromosphere and subsequently heats it. Only during the first peak around 07:11 UT are the non-thermal processes significant. The estimated values of thermal energy, non-thermal energy, and the ratio are consistent with the previous results of McDonald et al. (1999); and the ratio is larger than that computed for an M 1.0 flare in its gradual phase (Berlicki et al. 2004), where the non-thermal effect was negligible.
are in agreement with the spectral fitting shown in Fig. 11. Therefore, we could infer that most of the time the HXR emission in this flare is mainly of thermal origin, and thermal conduction transports most of the energy released during the flare to the chromosphere and subsequently heats it. Only during the first peak around 07:11 UT are the non-thermal processes significant. The estimated values of thermal energy, non-thermal energy, and the ratio are consistent with the previous results of McDonald et al. (1999); and the ratio is larger than that computed for an M 1.0 flare in its gradual phase (Berlicki et al. 2004), where the non-thermal effect was negligible.
The non-thermal energy estimation is very sensitive to the value of the low energy cutoff 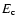 due to the power-law property of the high energy electron distribution. Increasing or reducing
due to the power-law property of the high energy electron distribution. Increasing or reducing 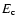 by only a few keV can substantially reduce or increase the amount of non-thermal energy in the system (McDonald et al. 1999). However, it is quite difficult to determine the low energy cutoff
by only a few keV can substantially reduce or increase the amount of non-thermal energy in the system (McDonald et al. 1999). However, it is quite difficult to determine the low energy cutoff 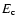 from observations, so in our analysis, we tried to estimate the low energy cutoff and got a value of about 25 keV. The inaccuracy of
from observations, so in our analysis, we tried to estimate the low energy cutoff and got a value of about 25 keV. The inaccuracy of 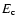 could introduce uncertainties in our analysis. Other factors affecting the energy estimation are the measurement accuracy of the
HXR source volume V and the value of ta. We estimate the source volume based on the 50% contour of
12-25 keV RHESSI image. In this case, the volume may differ by a factor of 2, resulting in about
a 40% uncertainty for the estimated thermal energies and 20% uncertainty for the ratio
could introduce uncertainties in our analysis. Other factors affecting the energy estimation are the measurement accuracy of the
HXR source volume V and the value of ta. We estimate the source volume based on the 50% contour of
12-25 keV RHESSI image. In this case, the volume may differ by a factor of 2, resulting in about
a 40% uncertainty for the estimated thermal energies and 20% uncertainty for the ratio 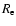 .
We notice from Eq. (4) that the average energy loss rate is proportional to
.
We notice from Eq. (4) that the average energy loss rate is proportional to
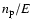 .
In other words, while the high-energy electrons move towards the chromosphere along the field lines from the reconnection site, with
.
In other words, while the high-energy electrons move towards the chromosphere along the field lines from the reconnection site, with 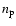 increasing and E decreasing, the energy loss rate increases rapidly. The value we used in the non-thermal energy estimation (ta=1.0 s) may be larger than the actual value, which leads to a larger portion of non-thermal energy. To be more accurate, more detailed and precise computations are required.
increasing and E decreasing, the energy loss rate increases rapidly. The value we used in the non-thermal energy estimation (ta=1.0 s) may be larger than the actual value, which leads to a larger portion of non-thermal energy. To be more accurate, more detailed and precise computations are required.
We also computed the emission measure and plasma temperature from GOES and RHESSI X-ray observations. The results indicate that the temperature of the flare plasma peaks at 34 MK around the main RHESSI hard X-ray emission peak and remains above 20 MK during the full analyzed time. The temperature determined from the GOES channels is lower (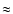 14 MK) and almost constant during the same time period. Large discrepancies between the calculated values of temperatures are probably due to the different sensitivity and response of these two satellites. Such difference can also support the fact that the observed plasma is multi-temperature.
14 MK) and almost constant during the same time period. Large discrepancies between the calculated values of temperatures are probably due to the different sensitivity and response of these two satellites. Such difference can also support the fact that the observed plasma is multi-temperature.
The analysis of H ,
Ca II 8542 Å, and He I 10 830 Å lines emission for the selected points of the flare shows a slow time evolution compared to the hard X-ray emission (cf. Fig. 10). But the maximum emission of the chromosphere is observed
,
Ca II 8542 Å, and He I 10 830 Å lines emission for the selected points of the flare shows a slow time evolution compared to the hard X-ray emission (cf. Fig. 10). But the maximum emission of the chromosphere is observed 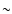 15 min after the maximum of hard X-rays. The steep slope of chromospheric intensity time profiles observed at 07:10 UT could be interpreted as due to heating of the chromosphere by accelerated particles within time scales, typically <1 s, as well as due to fast conduction front with time scales on the order of 10 s. Even though MISS took one spectrogram every 2.8 s, due to the seeing and image shift by the observer in the observation, the averaged time interval for the spectrograms used to derive the time profiles of the chromospheric lines is about 40 s. With the low temporal resolution it is not possible to distinguish between these two processes.
15 min after the maximum of hard X-rays. The steep slope of chromospheric intensity time profiles observed at 07:10 UT could be interpreted as due to heating of the chromosphere by accelerated particles within time scales, typically <1 s, as well as due to fast conduction front with time scales on the order of 10 s. Even though MISS took one spectrogram every 2.8 s, due to the seeing and image shift by the observer in the observation, the averaged time interval for the spectrograms used to derive the time profiles of the chromospheric lines is about 40 s. With the low temporal resolution it is not possible to distinguish between these two processes.
On the other hand, it is interesting to analyze the slowly varying response of the chromosphere and compare it to the hard and soft X-ray emissions observed by RHESSI. The trend of the time profiles of chromospheric lines emission suggests that it could correspond to the accumulation of energy. Trottet et al. (2000) find that the slow component evolves like the time integral of HXR count rates. We also have a similar behavior in our observations. This slow response of the chromosphere could be due to different phenomena: i.e. continuous heat flux from the hot corona or trapped particles. However, the spectral analysis of X-ray emission observed by RHESSI suggests that thermal conduction is dominant (see Sect. 4).
The long-duration brightening of the chromospheric flare ribbons can be explained in terms of the cooling time of hot coronal loops. Schmieder et al. (1995) estimated that the time necessary to cool down the hot flaring loops is on the order of 1000-2000 s, which means that during this time thermal conduction efficiently transports energy and heats the chromosphere causing its brightening. This time is consistent with our observations of enhanced chromospheric emission.
Nevertheless, for better understanding the chromospheric emission, non-LTE radiative transfer methods needed to be used. Up to now some preliminary computations have been done incorporating bombardment of electrons in the chromosphere (Heinzel & Karlický 1992; Kasparova & Heinzel 2002) and soft X-ray radiation (Berlicki & Heinzel 2004). But the slowly varying response of the chromosphere to continuum heating processes has not been studied in detail so far. Our present analysis can give some new constraints for energy transport modelling.
Acknowledgements
The authors are grateful to Dr. B. Dennis for his fruitful advices on RHESSI spectral analysis and valuable comments on the manuscript. We thank N. Vilmer, L. Sui, and P. Mein for their help and discussion on the RHESSI and THEMIS/MSDP data processing and analysis. We also wish to thank A. Poland for improving the language of this paper. We are also grateful to the RHESSI Team for free access to the RHESSI data and the development of the software, and the THEMIS team which operates the telescope at Tenerife. SOHO is a joint project of ESA and NASA, and THEMIS is a French-Italian telescope operated on the island of Tenerife by the CNRS-CNR in the Spanish Observatorio del Teide of the Instituto de Astrofísica de Canarias. The magnetic field extrapolations used in this paper were obtained from the code base FRench Online MAGnetic Extrapolations (FROMAGE). FROMAGE is a joint project between LESIA (Observatoire de Paris), CPhT (École Polytechnique), and the Centre National d'Études Spatiales (CNES). The work of HL was supported by the National Natural Science Foundation of China (NSFC, grant number 10273023 and 10333040) and National Basic Research Priorities Project (G2000078402) of China, and that of AB and BS by the European Commission through the RTN programme (European Solar Magnetism Network, contract HPRN-CT-2002-00313). This work was supported by the French-Chinese contract (CNRS-CAS No. 16304).
- Alissandrakis, C.
E. 1981, A&A, 100, 197 [NASA ADS] (In the text)
- Antiochos, S.,
& Sturrock, P. 1978, ApJ, 220, 1137 [NASA ADS] [CrossRef]
- Berlicki, A., &
Heinzel, P. 2004, A&A, 420, 319 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Berlicki, A.,
Schmieder, B., Vilmer, N., Aulanier, G., & Del Zanna, G. 2004,
A&A, 423, 1119 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Brown, J. C.
1971, Sol. Phys., 18, 489 [NASA ADS] [CrossRef] (In the text)
- Brown, J. C.,
Melrose, D. B., & Spicer, D. S. 1979, ApJ, 228, 592 [NASA ADS] [CrossRef] (In the text)
- Canfield,
R. C., & Gunkler, T. A. 1985, ApJ, 288, 353 [NASA ADS] [CrossRef] (In the text)
- David, K. H.
1961, ZAp, 53, 37 [NASA ADS] (In the text)
- Delaboudinière,
J.-P., Artzner, G. E., Brunaud, J., et al. 1995, Sol. Phys., 162,
291 [NASA ADS] [CrossRef] (In the text)
- Démoulin, P.,
Hénoux, J. C., Priest, E. R., & Mandrini, C. H. 1996,
A&A, 308, 643 [NASA ADS] (In the text)
- Démoulin, P.,
Bagala, L. G., Mandrini, C. H., Hénoux, J. C., & Rovira,
M. G. 1997, A&A, 325, 305 [NASA ADS] (In the text)
- Domingo, V., Fleck,
B., & Poland, A. I. 1995, Sol. Phys., 162, 1 [NASA ADS] [CrossRef] (In the text)
- Emslie, A. G.
1983, ApJ, 271, 367 [NASA ADS] [CrossRef]
- Emslie, A. G.,
Kucharek, H., Dennis, B. R., et al. 2004, J. Geophys. Res., 109,
A10104 [CrossRef] (In the text)
- Gallagher, P. T.,
Dennis, B. R., Krucker, S., Schwartz, R. A., & Tolbert, A. K.
2002, Sol. Phys., 210, 341 [NASA ADS] [CrossRef] (In the text)
- Hagyard, M. J.,
Teuber, D., West, E. A., & Smith, J. B. 1984, Sol. Phys., 91,
115 [NASA ADS]
- Hawley, S. L.,
& Fisher, G. H. 1994, ApJ, 426, 387 [NASA ADS] [CrossRef] (In the text)
- Heinzel, P., &
Karlický, M. 1992, Proc. of the First SOHO Workshop: Coronal
Streamers, Coronal Loops, and Coronal and Solar Wind Composition,
237
(In the text)
- Hudson, H. S.,
& Canfield, R. C. 1978, Sol. Phys., 60, 137 [NASA ADS] [CrossRef] (In the text)
- Ji, H., Wang, H.,
Schmahl, E. J., Qiu, J., & Zhang, Y. 2004, ApJ, 605, 938 [NASA ADS] [CrossRef] (In the text)
- Kasparova, J., &
Heinzel, P. 2002, A&A, 382, 688 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Leka, K., &
Barnes, G. 2003a, ApJ, 595, 1277 [NASA ADS] [CrossRef] (In the text)
- Leka, K., &
Barnes, G. 2003b, ApJ, 595, 1296 [NASA ADS] [CrossRef]
- Li, H., Fan, Z., &
You, J. Q. 1999, Sol. Phys., 185, 67 [NASA ADS] (In the text)
- Li, H., Sakurai, T.,
Ichimoto, K., & Ueno, S. 2000, PASJ, 52, 483 [NASA ADS] (In the text)
- Li, H., You, J. Q., Wu,
Q. D., & Yu, X. F. 2002, Chin. Phys. Lett., 19, 742 [NASA ADS]
- Li, H., You, J. Q., Du,
Q. S., & Yu, X. F. 2005, Sol. Phys., 225, 75 [NASA ADS] (In the text)
- Lin, R. P., Dennis,
B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [NASA ADS] [CrossRef] (In the text)
- Linsky, J. L.,
Teske, R. G., & Wilkinson, C. W. 1970, Sol. Phys., 11, 374 [NASA ADS] [CrossRef] (In the text)
- Liu, W., Jiang, Y.,
Liu, S., & Petrosian, V. 2004, ApJ, 611, L53 [NASA ADS] [CrossRef] (In the text)
- Mariska, J.
T., & Zarro, D. M. 1991, ApJ, 381, 572 [NASA ADS] [CrossRef] (In the text)
- McDonald, L.,
Harra-Murnion, L. K., & Culhane, J. L. 1999, Sol. Phys., 185,
323 [NASA ADS] [CrossRef] (In the text)
- Mein, P. 2002,
A&A, 381, 271 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Metcalf, T.
R., Jiao, L., McClymont, A. N., Canfield, R. C., & Uitenbroek,
H. 1995, ApJ, 439, 474 [NASA ADS] [CrossRef] (In the text)
- Sakurai, T.
1982, Sol. Phys., 76, 301 [NASA ADS] (In the text)
- Scherrer, P. H.,
Bogart, R. S., Bush, R. I., et al. 1995, Sol. Phys., 162, 129 [NASA ADS] [CrossRef] (In the text)
- Schmieder, B.,
Heinzel, P., Wiik, J. E., et al. 1995, Sol. Phys., 156, 337 [NASA ADS] [CrossRef]
- Trottet, G., Rolli,
E., Magun, A., et al. 2000, A&A, 356, 1067 [NASA ADS] (In the text)
- Wülser,
J., Canfield, R. C., Acton, L. W., et al. 1994, ApJ, 424, 459 [NASA ADS] [CrossRef] (In the text)
- Zarro, D. M.,
& Canfield, R. C. 1989, ApJ, 338, L33 [NASA ADS] [CrossRef] (In the text)
- Zharkova,
V., Benkhalil, A., Zharkova, S., & Ipson, S. 2005, Adv. Space
Res., in press
(In the text)
Copyright ESO 2005
![\begin{figure}
\par\includegraphics[width=8.6cm,clip]{2128f01a.eps}\hspace*{4mm}
\includegraphics[width=8.4cm,clip]{2128f01b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg17.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f02.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg18.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f03.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg19.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2128f04a.eps}\hspace*{3mm}
\...
...4c.eps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{2128f04d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg20.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f05.eps}\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg22.gif)
![\begin{figure}
\par\includegraphics[width=17cm,clip]{2128f06.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg23.gif)
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2128f07a.eps}\hspace*{3mm}
\...
...7c.eps}\hspace*{3mm}
\includegraphics[width=7cm,clip]{2128f07d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg24.gif)
![\begin{figure}
\par\includegraphics[width=6cm,clip]{2128f08a.ps}\hspace*{3mm}
\i...
...e*{4cm}\includegraphics[width=6cm,clip]{2128f08c.ps}\hspace*{4cm}}\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg28.gif)
![\begin{figure}
\par\includegraphics[width=17.4cm,clip]{2128f09.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2128f10.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=13.8cm,clip]{2128f11a.eps}\par\vspace*...
...\par\vspace*{3mm}
\includegraphics[width=13.8cm,clip]{2128f11d.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg35.gif)
![\begin{figure}
\par\includegraphics[width=7.9cm,clip]{2128f12a.eps}\includegraphics[width=8.3cm,clip]{2128f12b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg36.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2128f13a.eps}\hspace*{4mm}
\includegraphics[width=7.5cm,clip]{2128f13b.eps}
\end{figure}](/articles/aa/full/2005/28/aa2128-04/Timg39.gif)