A&A 437, 1159-1167 (2005)
DOI: 10.1051/0004-6361:20052662
C. Beck1 - W. Schmidt1 - T. Kentischer1 - D. Elmore2
1 - Kiepenheuer-Institut für Sonnenphysik,
Schöneckstr. 6, 79104 Freiburg, Germany
2 - High Altitude Observatory, National Center for Atmospheric Research![]() , 3450 Mitchell Lane, Boulder, Colorado 80301, USA
, 3450 Mitchell Lane, Boulder, Colorado 80301, USA
Received 10 January 2005 / Accepted 5 April 2005
Abstract
We present first measurements and the calibration procedure for the Polarimetric Littrow Spectrograph (POLIS) operated at the Vacuum Tower Telescope on Tenerife, together with a brief summary of the technical characteristics of the instrument. In its present configuration, we achieve a polarimetric accuracy of about
![]() in the visible channel
(630 nm) of the instrument. The accuracy is limited by cross talk among the different polarization states. The detection limit for polarized light is about
in the visible channel
(630 nm) of the instrument. The accuracy is limited by cross talk among the different polarization states. The detection limit for polarized light is about
![]() for a 7 s exposure. Polarimetric measurements in the blue channel (Ca II H line, 396.7 nm) are strongly limited by the low photon flux. At this wavelength we present Stokes-V maps with a spatial resolution of about 0.5 arcs.
The polarimetric quality of any spectropolarimeter is limited by the precision of the instrument calibration. We present a new method for self-calibration that reduces cross talk among the polarization components to 0.1%. This improvement results from a measurement of the retardance of the calibration waveplate with an accuracy of 0.1
for a 7 s exposure. Polarimetric measurements in the blue channel (Ca II H line, 396.7 nm) are strongly limited by the low photon flux. At this wavelength we present Stokes-V maps with a spatial resolution of about 0.5 arcs.
The polarimetric quality of any spectropolarimeter is limited by the precision of the instrument calibration. We present a new method for self-calibration that reduces cross talk among the polarization components to 0.1%. This improvement results from a measurement of the retardance of the calibration waveplate with an accuracy of 0.1![]() .
We demonstrate the capability of the simultaneous use of POLIS and the Tenerife Infrared Polarimeter which is integrated in the main spectrograph of the Vacuum Tower Telescope.
.
We demonstrate the capability of the simultaneous use of POLIS and the Tenerife Infrared Polarimeter which is integrated in the main spectrograph of the Vacuum Tower Telescope.
Key words: Sun: magnetic fields - instrumentation: polarimeters
![\begin{figure}
\par\includegraphics[width=14.7cm,clip]{2662fig1.eps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg13.gif) |
Figure 1: Optical layout of POLIS. Light enters the instrument at top right. F denotes the telescope focal plane. A collimator mirror forms an image of the entrance pupil near the rotating modulator, RM, and the scan mirror, SM. An imaging mirror re-images the solar image at F to the entrance slit, S, of the spectrograph. Slit jaw images are recorded from the reflective slit jaws of the entrance slit. The collimator re-images the entrance pupil to the grating, G. The dispersed beams are then re-imaged to the focal plane detectors, CCD 1 and CCD 2. A small pickoff mirror close the focal plane reflects the blue beam to CCD 2. Diffraction orders are isolated with narrow-band filters placed in front of each detector. Polarizing beam splitters placed directly in front of the CCDs separate the orthogonally polarized beams. |
| Open with DEXTER | |
This paper presents first scientific observations with POLIS and demonstrates the capability of the simultaneous use of POLIS and TIP. The calibration procedure of the spectropolarimeter is described. First, we present the main characteristics of the new instrument. Section 3 deals with the important topic of polarimetric calibration of the instrument. In that section we also describe a method to characterize the calibration unit itself. First observational results are presented in Sect. 4. The appendices provide important background material about the polarimeter response functions.
POLIS measures the Stokes vector (I,Q,U,V) simultaneously in two wavelength
regimes on two CCD cameras. One CCD records the polarization in two
photospheric Fe I lines at 630.15 nm and
630.25 nm (in the following called red channel). The second
camera records the line core and the blue wing of the Ca II H
line at 396.8 nm (blue channel). The CCDs are back-side
illuminated 14-bit PLUTO cameras from Pixel Vision, with a full detector size
of
![]() pixel, and a pixel size of
pixel, and a pixel size of
![]() .
The data can be binned internally over CCD columns and rows to
increase the signal level. A slit jaw camera takes broad band images of
the reflective front side of the slit. The wavelength of the slit jaw
images is selected by means of an interference filter.
.
The data can be binned internally over CCD columns and rows to
increase the signal level. A slit jaw camera takes broad band images of
the reflective front side of the slit. The wavelength of the slit jaw
images is selected by means of an interference filter.
The red and the blue branches of the instrument are dual beam systems with polarizing beam splitters in front of each CCD camera. The optical layout of POLIS is displayed in Fig. 1. The instrument consists of three major parts:
POLIS uses a single rotating retarder as polarization modulator that modulates the polarization signals in both wavelength bands with high efficiency. The modulator is a zero-order waveplate, equipped with a wedge to eliminate spectral fringes. A new (patented) design for the rotating waveplate has been developed (Schmidt & Kentischer 2003), which completely avoids any beam wobble caused by the rotating wedge. The wedge is compensated by two glass wedges in front and behind the retarder. The compensation of the beam displacement caused by the wedged modulator is achieved by fine-tuning of the orientation of the additional wedges. The resulting accuracy of the angular displacement compensation is much higher than the manufacturing tolerances of the wedges themselves, resulting in a wobble-free image. In addition, the final configuration has no parallel glass surfaces and therefore eliminates problems associated with interference fringes.
Polarizing beam splitters in front of the cameras split the modulated light beam in two orthogonally polarized beams ![]() ,
imaged on a single CCD in each channel. Two types of beam splitters are available splitting the beams along the spatial or spectral axis. Since the CCD is rectangular, this allows to choose a larger spatial or spectral field of view (see Table B.1 in the Appendix).
,
imaged on a single CCD in each channel. Two types of beam splitters are available splitting the beams along the spatial or spectral axis. Since the CCD is rectangular, this allows to choose a larger spatial or spectral field of view (see Table B.1 in the Appendix).
The intensity of the individual beams ![]() as a function of the incoming Stokes vector, the modulator angular position,
as a function of the incoming Stokes vector, the modulator angular position, ![]() ,
and the retardance of the modulator,
,
and the retardance of the modulator, ![]() ,
is given by:
,
is given by:
In order to derive the values of I, Q, U, and V, the intensity signal is demodulated in real-time after 8 images, taken at the modulator positions
![]() (k=0...7), using a suitable summation scheme (Lites et al. 1993). The demodulation is expressed by an
(k=0...7), using a suitable summation scheme (Lites et al. 1993). The demodulation is expressed by an ![]() matrix, applied to the 8 intensity images. The demodulation can be reversed again by the calculation of the inverse matrix by a singular value decomposition. In this paper, we do not use this option, but it would allow to perform additional corrections, e.g., dark current subtraction, on the single images, if necessary.
matrix, applied to the 8 intensity images. The demodulation can be reversed again by the calculation of the inverse matrix by a singular value decomposition. In this paper, we do not use this option, but it would allow to perform additional corrections, e.g., dark current subtraction, on the single images, if necessary.
The total integration time can be varied by changing the modulator rotation frequency,
![]() ,
or by accumulating the demodulated Stokes vectors,
,
or by accumulating the demodulated Stokes vectors,
![]() :
:
The scan unit is located in front of the entrance slit and allows to take raster images with a range of about ![]() 100 arcs around the center position of the scan mirror. The smallest step width is
0.1 arcs.
100 arcs around the center position of the scan mirror. The smallest step width is
0.1 arcs.
Table B.1 lists the spectral and spatial properties of the two CCD cameras for the two possible orientation of the polarizing beam splitters. The observable spectral lines in the wavelength intervals are listed in Table B.2.
For the calibration of the instrument, an Instrument Calibration Unit (ICU) has been installed near the prime focus of the telescope. The ICU consists of a linear polarizer and a zero order quartz retarder. The optical elements of the ICU are mounted on a motorized stage and are moved in the beam together. The retarder and the polarizer can be rotated independently around the optical axis. The angular position accuracy is better than 0.1![]() .
.
The derivation of ![]() is described in Sect. 3.2 while the limitations in its determination are discussed separately in Sect. 4 because they restrict the final accuracy of the polarization measurement.
is described in Sect. 3.2 while the limitations in its determination are discussed separately in Sect. 4 because they restrict the final accuracy of the polarization measurement.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2662fig2.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg37.gif) |
Figure 2:
Example of the gain table correction for the red channel, using data from August 2003. Image size
|
| Open with DEXTER | |
The next step toward the construction of the gain table is the removal of the spectral line information from the flat-field images. The compact design with a short focal length of the spectrograph leads to a curvature of the spectral lines along the slit (variation of the line core position of ![]() 3 pixel). Additionally, intensity gradients along the slit, and at the borders of the beams are present. This requires the application of a rather complicated procedure for the removal of the spectral information. The spectra are divided in a number of stripes along the slit. Within these stripes, the line curvature is removed, and the mean line profile is derived by averaging along the slit. The mean line profiles from the stripes are normalized to each other to remove the intensity variation along the slit. The gain table for each stripe is then obtained by dividing the spectrum by the averaged line profile.
3 pixel). Additionally, intensity gradients along the slit, and at the borders of the beams are present. This requires the application of a rather complicated procedure for the removal of the spectral information. The spectra are divided in a number of stripes along the slit. Within these stripes, the line curvature is removed, and the mean line profile is derived by averaging along the slit. The mean line profiles from the stripes are normalized to each other to remove the intensity variation along the slit. The gain table for each stripe is then obtained by dividing the spectrum by the averaged line profile.
The two beams are treated separately, and then normalized in intensity to each other as last step of the gain correction. Figure 2 displays an example of the gain table used for data of August 2003, and a spectrum before and after the gain correction. The gaintable takes into account only pixel-to-pixel variations of the intensity response. Intensity gradients in wavelength direction (cf. the profiles in Fig. 2) are not corrected for because they were found to depend on the polarization state.
The orientation of the axes has been measured in the laboratory using standard techniques with an accuracy of ![]() 0.1
0.1![]() for the polarizer, and
for the polarizer, and ![]() 1
1![]() for the retarder. The retardance value has been measured with
an indirect method, described later in Sect. 4, as (
for the retarder. The retardance value has been measured with
an indirect method, described later in Sect. 4, as (
![]() at 630 nm. The measurement of the retardance at 400 nm was not successful in the laboratory, due to the low light level of the lamp used. We therefore measured the retardance at several wavelengths and extrapolated a value of 114.5
at 630 nm. The measurement of the retardance at 400 nm was not successful in the laboratory, due to the low light level of the lamp used. We therefore measured the retardance at several wavelengths and extrapolated a value of 114.5![]() for 400 nm.
for 400 nm.
From the measured angular orientation of the elements, and modeling the ICU elements as ideal polarizer and non-ideal retarder (cf. Eq. (A.1)), we compute the polarization state of the beam that passes the ICU. A comparison with the actually measured Stokes vector yields the polarimeter response function.
Although we use solar light from nonmagnetic regions, the light incident on the ICU is already partially polarized by oblique reflections in the telescope. These effects are taken into account by the application of the telescope Mueller matrix, ![]() ,
to the solar illumination, like in Eq. (3).
,
to the solar illumination, like in Eq. (3).
Thus, the general equation between the solar input,
(I0 0 0 0 )T, and measured output,
![]() ,
during the calibration is given by:
,
during the calibration is given by:
A standard calibration data set consists of one half rotation of the
retarder in 5![]() -steps. The calibration input for
-steps. The calibration input for
![]() is thus given by:
is thus given by:
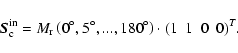 |
(6) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2662fig3.eps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg55.gif) |
Figure 3:
Stokes vector (I,Q,U,V) of a calibration measurement in the red channel. Solid: calibration input vector, calculated from the retarder and polarizer position angles. Squares: measured Stokes vector. Dash-dotted: Computed output vector
|
| Open with DEXTER | |
The polarimeter response function is derived from the measurements after arranging the Stokes vectors into ![]() matrices by a solution of the linear problem
matrices by a solution of the linear problem
In addition to the 16 elements of X, there are two free parameters:
The response function and the free parameters are measured for typically 4-8
intervals along the slit, in order to account for a possible variation of the instrument properties in the spatial direction. A typical result for the red channel is:
The total efficiency, ei, for measuring a Stokes parameter is derived from the corresponding column of the response function by
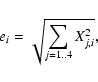 |
(10) |
For the blue channel, the simultaneously taken data have a very low light level that does not allow to derive a reliable response function. Results for the calibration of the blue channel of POLIS from another data set with longer integration time are shown in Appendix A.3.
The absolute error of the matrix inversion (cf. Appendix A)
is below
![]() for the matrix derived above. This contribution can be neglected, since the magnitude of the fit error does only reflect the value of
for the matrix derived above. This contribution can be neglected, since the magnitude of the fit error does only reflect the value of ![]() from Eq. (8) which due to the number of "free'' parameters always is very small.
from Eq. (8) which due to the number of "free'' parameters always is very small.
The main contribution to the calibration error - and hence to the quality of the calibrated data - stems from the poorly known retardance of the calibration waveplate.
We had measured the retardance directly, with the retarder placed between crossed polarizers, and found a value of 63.5
![]()
![]() which was not accurate enough for our needs. The polarimeter calibration procedure itself offers a second method with a much higher sensitivity and accuracy. Since the reference system for the Stokes vectors is fixed in space, the result of the response function must not depend on the actual orientation of the polarizer during the calibration measurement. Therefore we carried out several calibration measurements with the polarizer angle increased in 10
which was not accurate enough for our needs. The polarimeter calibration procedure itself offers a second method with a much higher sensitivity and accuracy. Since the reference system for the Stokes vectors is fixed in space, the result of the response function must not depend on the actual orientation of the polarizer during the calibration measurement. Therefore we carried out several calibration measurements with the polarizer angle increased in 10![]() -steps. The evaluation of the data using different retardance values showed that the value of the matrix elements varied with the polarizer orientation, except for a retardance value of 61.5
-steps. The evaluation of the data using different retardance values showed that the value of the matrix elements varied with the polarizer orientation, except for a retardance value of 61.5![]() .
The effect is most pronounced in the first column of X. Figure 4 displays the effect of retardance changes on the matrix element
.
The effect is most pronounced in the first column of X. Figure 4 displays the effect of retardance changes on the matrix element
![]() ,
,
![]() .
Other matrix elements (e.g.
.
Other matrix elements (e.g.
![]() and
and
![]() )
show a similar behavior, consistent with a retardance of 61.5
)
show a similar behavior, consistent with a retardance of 61.5![]() .
.
The indirect method described above allows to determine the retardance of a waveplate with an accuracy of 0.1![]() .
This is much better than typical manufacturing tolerances that are in the order of 1
.
This is much better than typical manufacturing tolerances that are in the order of 1![]() .
The accuracy of 0.1
.
The accuracy of 0.1![]() leads to a polarimetric accuracy of
leads to a polarimetric accuracy of
![]() (cf. the differences of the curves for 61.5
(cf. the differences of the curves for 61.5![]() and 61.4
and 61.4![]() in Fig. 4). From measurements in different seasons it was found that the actual retardance value of the ICU retarder depends slightly on the light level in the telescope, i.e. due to the increased illumination in summer - and thus a higher temperature of the retarder due to absorption - the retardance is then smaller by about 0.2
in Fig. 4). From measurements in different seasons it was found that the actual retardance value of the ICU retarder depends slightly on the light level in the telescope, i.e. due to the increased illumination in summer - and thus a higher temperature of the retarder due to absorption - the retardance is then smaller by about 0.2![]() -0.4
-0.4![]() .
Taking this temperature effect into account the effective error limit should be around
.
Taking this temperature effect into account the effective error limit should be around
![]() .
Note that this is the error in the determination of the relative cross-talk, not of the absolute accuracy of the measurements.
.
Note that this is the error in the determination of the relative cross-talk, not of the absolute accuracy of the measurements.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2662fig4.eps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg74.gif) |
Figure 4:
Derivation of the retardance of the calibration waveplate. The matrix element
|
| Open with DEXTER | |
Two observing campaigns were carried out in 2003. The first one was used to obtain calibration data for telescope and polarimeter, and to test the possibility of simultaneous observations with the Tenerife Infrared Polarimeter (TIP). In the second campaign we explored the capabilities and limitations of polarimetric measurements in the Ca II H line. Additionally, some simultaneous maps with TIP were taken.
Figure 7 displays the result of a short scan of two small pores. Data were taken with an exposure time of 26.7 s and a slit width of 0.48 arcs. The 50-50-beamsplitter was exchanged with a flat mirror. The chromospheric calcium line is in emission for most of the surroundings of the pores, with two separate emission peaks outside and a single emission peak inside the pores. The line core of calcium shows a sign reversal in Stokes V in the center of the pores.
Figure 8 displays an example of such co-spatial line profiles at 630 nm and at 396.7 nm, taken from an individual resolution element of
![]() /0.145 arcs2 for the blue/red channel. The noise rms of the red channel has decreased to about
/0.145 arcs2 for the blue/red channel. The noise rms of the red channel has decreased to about
![]() through the longer exposure time. The emission core of the calcium line at 396.88 nm shows a pronounced Stokes-V signal with the opposite sign compared to the photospheric absorption lines in the wing of the calcium line or in the red channel. The light level was insufficient to detect any clear Stokes Q or U signal in the calcium line core. It will require further technical improvements of the telescope and the instrument to increase the light level by a factor of, say, four, to allow for "true'' Stokes vector measurements in the blue channel of POLIS.
through the longer exposure time. The emission core of the calcium line at 396.88 nm shows a pronounced Stokes-V signal with the opposite sign compared to the photospheric absorption lines in the wing of the calcium line or in the red channel. The light level was insufficient to detect any clear Stokes Q or U signal in the calcium line core. It will require further technical improvements of the telescope and the instrument to increase the light level by a factor of, say, four, to allow for "true'' Stokes vector measurements in the blue channel of POLIS.
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{2662fig5.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg79.gif) |
Figure 5: Intensity map of sunspot NOAA 0425, observed on 9.8.2003, between 7:40 and 7:52 UT. Tick marks correspond to 1 arcs. Scan direction left to right, step width 0.35 arcs, 120 steps. The intensity gradient in scan direction is caused by the increase of intensity in the early morning. White crosses indicate the spatial positions of the profiles shown in Fig. 6. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15.5cm,clip]{2662fig6.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg80.gif) |
Figure 6:
Stokes profiles measured in the red channel, top to bottom: I, Q, U, V each normalized to continuum intensity, |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2662fig7.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg81.gif) |
Figure 7: Scan of a small pore, observed on 15 Oct. 2003. Top to bottom: Stokes components I, Q, U and V. Left column: spectra of Fe I 630.15 and Fe I 630.25 nm, single scan step. Middle column: wavelength integrated maps of Stokes I, Q. U and V around 630.2 nm. The vertical black bar in I indicates the scan position of the spectra shown. Tick marks correspond to 1 arcs. Right column: spectra of the Ca II H line. The horizontal bar in the Stokes V spectrum marks the position of the profiles displayed in Fig. 8. Only the co-spatial field-of-view of blue and red channel is shown. The red channel has been rescaled to have the same spatial sampling of 0.29 arcsec per pixel. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2662fig8.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg82.gif) |
Figure 8: Co-spatial profiles in red ( left column) and blue ( right column) channel of POLIS, top to bottom: Stokes I, Q, U and V. Data were taken on 15 Oct. 2003 at 15:30 UT, scan of a small pore. Note the opposite sign of the Stokes V signal in the calcium line core, compared to that of the photospheric lines in the wing of the calcium line or in the red channel. The apparent reversal is due to the emission profile in the calcium core that changes the sign of the circular polarization. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{2662fig9.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg84.gif) |
Figure 9:
Simultaneous data from TIP and POLIS, showing part of active region NOAA 0484, observed on 20 Oct. 2003 at 10:11 UT at the VTT Tenerife. Tick marks are 1 arcs. Bottom row, left to right: intensity maps in Fe I 1565 nm (integrated over the line), continuum at 630.3 nm, and in the blue wing of the Ca II H 396.5 nm line.
Top row, left to right: total circular polarization
|
| Open with DEXTER | |
Figure 9 displays simultaneous data from TIP and POLIS of a scan over a part of the active region NOAA 0484, taken on 20.10.2003 at 10:11 UT. The exposure time was again 26.7 s per scan step. This spot group was connected with X-ray emission and flare activity throughout its disk passage. The profiles of the blue channel in Fig. 10 show very strong emission in the calcium line in part of the area.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2662fi10.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg86.gif) |
Figure 10: Intensity spectrum of the blue channel corresponding to the strongest emission observed in the map of Fig. 9. Thin grey line: Liège atlas profile (Delbouille et al. 1973). |
| Open with DEXTER | |
We have developed a powerful method to calibrate the retardance of our calibration waveplate with an accuracy of 0.1![]() .
The value of this retardance affects directly the polarimetric accuracy, since it determines the cross-talk correction.
.
The value of this retardance affects directly the polarimetric accuracy, since it determines the cross-talk correction.
With the present light level, we are able to measure Stokes V in Ca II H profiles, with a spatial resolution of about 0.5 arcs and an exposure time of ![]() 27 s.
27 s.
This is quite unsatisfactory, and additional efforts are planned to further increase the light level. If photons were the only criterion, one could more or less easily switch to one of the infrared calcium lines around 850 nm. One of the important criterions to choose the Ca II H line in the first place was the availability of magnetically sensitive lines in the wings of the line. The simultaneous measurement of chromospheric and photospheric lines at the same wavelength guarantees that the information is indeed taken at exactly the same loaction on the sun. Otherwise, one has to measure or compute the differential refraction effects with great care.
An IDL-based software package has been developed for all steps of the photometric and polarimetric calibration. This software is available to all users of POLIS. A software code for simultaneous observations with the TIP has been implemented at the control computers.
First observations with this instrument have demonstrated that it is a very powerful tool for the investigation of the solar magnetic field at different heights in the solar atmosphere, especially in combination with the TIP to cover the deep photospheric layers. A new beamsplitter is available in the meantime which splits the light around 800 nm, i.e. all wavelengths below are reflected to POLIS while the rest is transmitted to TIP. This will increase the light level in both instruments and allow for shorter exposure times with a signal-to-noise ratio still better than in the present setup.
Acknowledgements
We thank Manolo Collados, Thomas Keller and Kim Streander for their support during the observations, and Luis Bellot Rubio, Rolf Schlichenmaier and the referee for useful comments. This work was supported by the Deutsche Forschungsgemeinschaft under grant Schl 514/2-1.
The polarimeter RF can be derived from a calibration data set by
arranging the input,
![]() (=A), and output,
(=A), and output,
![]() (=y), into
(=y), into ![]() -matrices. The
resulting linear problem
-matrices. The
resulting linear problem
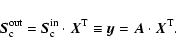 |
(A.2) |
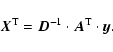 |
(A.3) |
For calibration of the calcium channel usually a separate data set is taken with longer exposure time. A data set from 27.09.2004 with a rotation frequency of the modulator of
![]() Hz and 16 accumulations of the Stokes vector (total integration time 27 s) yielded the following polarimeter response function:
Hz and 16 accumulations of the Stokes vector (total integration time 27 s) yielded the following polarimeter response function:
 |
(A.6) |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2662App1.ps}
\end{figure}](/articles/aa/full/2005/27/aa2662-05/Timg105.gif) |
Figure A.1:
Same as Fig. 3 for the blue channel, Stokes vector (I,Q,U,V) during the calibration. Solid: calibration input vector. Squares: measured Stokes vector.
Dash-dotted: Computed output vector
|
The corresponding curve of the Stokes vector during the calibration is displayed in Fig. A.1. The observed polarization level in QUV had to be increased by a factor of 10 to make the shape of the curve visible at all. The intensity is about 380 counts, while the maximum of, e.g., Stokes Q, does not exceed 9 counts. The smoothness of the curves results from the fact that each value of QUV for each calibration step is an average over 150 (in wavelength) ![]() 40 (along slit) = 6000 pixels.
40 (along slit) = 6000 pixels.
The concern about the correct retardance value mentioned in Sect. 4 of course also applies for the blue channel. Due to the lack of suitable data we had to use the extrapolated value of 114.5![]() retardance without the possibility to confirm it by another method.
retardance without the possibility to confirm it by another method.
Table B.1: Spectral and spatial properties of POLIS data for the two types of polarizing beam splitters in the red channel.
Table B.2:
Observable spectral lines in red and blue channel. aWavelengths, Pierce & Breckenridge (1974). b Effective Landé
factor, Solanki et al. (1987). c Height of line core formation above
![]() .
d all values in this section from J. Bruls
(personal note). e Values from H. Schleicher (personal note). f Nave et al. (1994).
.
d all values in this section from J. Bruls
(personal note). e Values from H. Schleicher (personal note). f Nave et al. (1994).