A&A 437, 1047-1054 (2005)
DOI: 10.1051/0004-6361:20042578
G. P. Chernov1,2,![]() -
Y. H. Yan1 -
Q. J. Fu1 -
Ch. M. Tan1
-
Y. H. Yan1 -
Q. J. Fu1 -
Ch. M. Tan1
1 - National Astronomical Observatory, Chinese Academy of Science,
20A, Datun Road, Beijing, 100012, PR China
2 -
Izmiran, Troitsk, Moscow region, 142190, Russia
Received 20 December 2004 / Accepted 13 February 2005
Abstract
A comparative analysis of two recent solar radio outbursts around
3 GHz with zebra structures and fiber bursts in their dynamical
radio spectra is carried out using all available ground-based and
satellite data (SOHO, TRACE, RHESSI). The latest theoretical models
of the zebra pattern are critically discussed.
New data on microwave zebra structures and fiber bursts suggests
that they are analogous to similar structures observed at meter
wavelengths. It was discovered that in the 2,6-3,8 GHz frequency
band more than 34 zebra stripes can appear simultaneously, and
some isolated fiber bursts can continuously be transformed into
zebra stripes. This fact indicates a single origin for both
structures. The zebra pattern was observed when the signs of
magnetic reconnections were revealed in images of 195 Å UV lines, and radio sources coincided with positions of some new sources in hard X-rays. All the main properties of the
stripes in emission and absorption can be explained if they are
associated with interactions between electrostatic plasma waves
and whistlers, taking into account the quasi-linear diffusion of
fast particles with the loss-cone distribution on whistlers. In
this model it is possible to obtain realistic values for the
magnetic field strength of
![]() at the plasma level
of about 3 GHz. The double plasma resonance model for the zebra
pattern based on the known realistic dependences of electron
density and magnetic field yields a frequency dependence for the
frequency separation between stripes that does not agree with the
observations.
at the plasma level
of about 3 GHz. The double plasma resonance model for the zebra
pattern based on the known realistic dependences of electron
density and magnetic field yields a frequency dependence for the
frequency separation between stripes that does not agree with the
observations.
Key words: Sun: flares - Sun: radio radiation - Sun: activity - Sun: UV radiation
Stripes in emission and absorption called zebra pattern structure (ZS) and fiber-bursts (FB) (or bursts with intermediate frequency drift) are well-known fine structures seen in the meter and decimeter continuum emission of type IV solar radio bursts (Elgarøy 1959; Slottje 1972; Kuijpers 1975; Slottje 1981; Elgarøy 1982). High time and frequency resolution data have improved our studies of similar fine structures in star flares. Some recent observations with a time resolution of 0.1 s, using Ondrejov radio spectrographs in the 0.8-4 GHz range, have allowed us to find new properties of zebra structures and to verify theoretical models (Ledenev et al. 2001; Karlicky et al. 2001; Sawant et al. 2002). The new microwave spectrometers of NAOC (Huairou station, China) with higher resolution (10 MHz and 5-8 ms) (Fu et al. 1995) can observe detailed zebra patterns and fiber bursts at high frequencies, 2.6-7.6 GHz (Chernov et al. 2001, 2003). The same variety of fine structure is observed in the microwave range.
In the course of development of the interpretation of such fine
structures, the theory always lagged behind the observational data
obtained (Kuijpers 1980). The interaction of plasma electrostatic
waves ![]() with whistler waves
with whistler waves ![]() (generated by
the same fast particles with loss-cone anisotropy) is a
well-accepted emission mechanism for fiber bursts:
(generated by
the same fast particles with loss-cone anisotropy) is a
well-accepted emission mechanism for fiber bursts:
![]() with freely escaping electromagnetic waves
with freely escaping electromagnetic waves ![]() in the ordinary (O) mode (Kuijpers 1975). A more detailed
analysis of the interaction
in the ordinary (O) mode (Kuijpers 1975). A more detailed
analysis of the interaction
![]() was made
in Fomichev & Fainstein (1988), where it was shown that the
observed fiber radio fluxes are explained in the framework of weak
plasma turbulence.
was made
in Fomichev & Fainstein (1988), where it was shown that the
observed fiber radio fluxes are explained in the framework of weak
plasma turbulence.
Zebra patterns are more complicated structures,
and many mechanisms have been proposed to explain them (Kuijpers
1975; Zheleznykov & Zlotnik 1975a,b; Chernov 1976; Mollwo 1983,
1988; Winglee & Dulk 1986). The majority are based on electrostatic
emission at double plasma resonance (DPR):
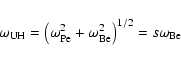 |
(1) |
However, some difficulties remain
with all these versions: the frequency separation between zebra
stripes
![]() must comprise a certain portion of the electron
cyclotron frequency (depending on the relationships of the height
scales of density and magnetic field in the corona), and this is
hard to reconcile with its often irregular variation with
frequency; the magnetic field deduced from
must comprise a certain portion of the electron
cyclotron frequency (depending on the relationships of the height
scales of density and magnetic field in the corona), and this is
hard to reconcile with its often irregular variation with
frequency; the magnetic field deduced from
![]() seems too
low for the flare region and we are faced with the difficulty of
having plasma
seems too
low for the flare region and we are faced with the difficulty of
having plasma
![]() (a well-accepted
value for magnetic traps in active regions). Practically all
models explain only stripes in emission, although the stripes
are sometimes observed predominantly in absorption. An
important property of the loss-cone distribution was missed in
all models: it also generates whistlers, and interaction of
whistlers with fast particles radically changes the velocity
distribution function when the transverse anisotropy decreases,
but a beam on the longitudinal velocities appears (Chernov 1996, 2005).
(a well-accepted
value for magnetic traps in active regions). Practically all
models explain only stripes in emission, although the stripes
are sometimes observed predominantly in absorption. An
important property of the loss-cone distribution was missed in
all models: it also generates whistlers, and interaction of
whistlers with fast particles radically changes the velocity
distribution function when the transverse anisotropy decreases,
but a beam on the longitudinal velocities appears (Chernov 1996, 2005).
Difficulties with interpretation of ZS within the framework of DPR continue to stimulate the development of new theories. Because sometimes a large number of ZS stripes is observed, it is of interest to examine the theory proposed in LaBelle et al. (2003). This model is based on the radiation mechanism of auroral "choruses'' - magnetospheric bursts observed at ground stations at frequencies of 2-4 MHz, with a fine structure similar to ZS. It is supposed that the Z-mode is radiated by the cyclotron maser mechanism (by analogy with Weengle & Dulk 1986). Although the Z-mode at the upper hybrid frequency does not escape from the source, it can be transformed into the ordinary (O) mode at discrete frequencies (quasi-harmonics or eigenmodes) with the presence of density enhancements with the appropriate scales.
In Sect. 2 the latest theoretical models of zebra patterns based on DPR are discussed critically. In Sect. 3, new observations of ZS around 3 GHz are presented. For the analysis of two events, October 29, 2000 and April 21, 2002, all accessible ground-based (spectrometers of NAOC (China) 2,6-3,8 GHz) and satellite observational data are used (SOHO, TRACE, RHESSI). Section 4 is devoted to a discussion of these data in different models of ZS.
In two papers, Aurass et al. (2003) (I. Observations) and Zlotnik et al. (2003) (II. Source model, theory), the DPR mechanism was used for the interpretation of the short type IV burst with ZS that occurred on October 25, 1994. In the first article, the results of the force-free extrapolated magnetic field of AR 7792 in the corona are presented. The extrapolated magnetic force line starting from the head spot and used in Paper II is not connected to the radio source of ZS, since the positions of the fine structure radio sources are far to the NE of AR 7792.
The authors of Paper II do not address the conclusion of Paper I (at the end of Sect. 3.2.2) that particle acceleration took place most likely above the NE part of the loop LS1, instead of the SW part. The statement about the position of particle acceleration in the SW part of the loop LS1, made in II, contradicts Fig. 5 in (I) where it is shown that the radio sources of type III bursts at 164 MHz are far to the NE of the bright area in which the main flare took place. The positions of radio sources of type III bursts and ZS coincided, therefore particles responsible for type III bursts should move upwards on the NE part of the loop LS1 and those responsible for ZS should move downwards in the same part of the loop.
In Paper II, the opposite problem is solved: using multiple crossings of the
calculated cyclotron harmonics with the fixed frequencies of
ZS stripes (at a fixed time point) a dependence
![]() is constructed (Fig. 5).
The authors have considered an arbitrary selected force line in the
center of the coronal loop LS1. They assert that the
electron density over height follows a barometric law.
is constructed (Fig. 5).
The authors have considered an arbitrary selected force line in the
center of the coronal loop LS1. They assert that the
electron density over height follows a barometric law.
From Fig. 5 in Paper II it is visible that for the extrapolated magnetic force line
the cyclotron frequency drops approximately 4 times faster than the
plasma frequency (for example, for the gyroharmonic number s = 15). More precisely,
the scale height for the magnetic field
![]() appears to be
4 times lower than the scale height for the electron density
appears to be
4 times lower than the scale height for the electron density
![]() .
Thus, these relations satisfy a condition
for realization of DPR with a large number of harmonics
.
Thus, these relations satisfy a condition
for realization of DPR with a large number of harmonics
![]() .
However, it does not satisfy a condition for the separation of
zebra stripes on the continuum background, namely
.
However, it does not satisfy a condition for the separation of
zebra stripes on the continuum background, namely
![]() ,
at least for the nonrelativistic case.
,
at least for the nonrelativistic case.
In Appendix A, B of Paper II the main formulae for the theory of
growth rates for DPR instability are presented with some newer
details than Zheleznyakov & Zlotnik (1975a) and Zheleznyakov (1995).
In particular, these authors voice two objections, relating to Winglee & Dulk (1986).
First, the dispersive curves of longitudinal electrostatic
waves at the frequency of DPR (shown in Fig. A1 in II)
![]() are valid only inside the hybrid band. This cannot be extended to the band
adjacent to the hybrid band from above, as done by Winglee & Dulk (1986).
Furthermore, in the footnote of Appendix A (in II) it is noted that
Winglee & Dulk (1986) considered only the first order of the
small parameters
are valid only inside the hybrid band. This cannot be extended to the band
adjacent to the hybrid band from above, as done by Winglee & Dulk (1986).
Furthermore, in the footnote of Appendix A (in II) it is noted that
Winglee & Dulk (1986) considered only the first order of the
small parameters
![]() in the "thermal'' dielectric
tensor. That corresponds to neglecting the important resonance
term. However, they do not discuss to what inaccuracies this leads
in the final analysis. Thus, the main result, represented in Fig. 2
in Winglee & Dulk (1986) is inaccurate: a paling or comb of harmonics
cannot be equal in intensity for s = 6-20.
in the "thermal'' dielectric
tensor. That corresponds to neglecting the important resonance
term. However, they do not discuss to what inaccuracies this leads
in the final analysis. Thus, the main result, represented in Fig. 2
in Winglee & Dulk (1986) is inaccurate: a paling or comb of harmonics
cannot be equal in intensity for s = 6-20.
However, in II, all formulae for similar estimations (after (B.7))
show only the qualitative behaviour of the growth rate of
upper hybrid waves in DPR conditions. If we choose (in
more detail) the optimal value of the wave number
![]() (where the growth rates are maximal) for the velocity of fast
particles
(where the growth rates are maximal) for the velocity of fast
particles
![]() and if we take
into account the velocity dispersion
and if we take
into account the velocity dispersion
![]() we obtain the relative bandwidth of the maximum growth rate
inside the hybrid band
we obtain the relative bandwidth of the maximum growth rate
inside the hybrid band
![]() approximately equal to the
frequency separation between stripes
approximately equal to the
frequency separation between stripes
![]() .
According Stepanov et al.
(1999), the frequency interval of a plasma wave excited in DPR conditions also occupies about 0,3-0,5 of the distance
.
According Stepanov et al.
(1999), the frequency interval of a plasma wave excited in DPR conditions also occupies about 0,3-0,5 of the distance ![]() between the adjacent harmonics. The value of
between the adjacent harmonics. The value of
![]() (see Fig. B1b in II) is obtained only for an
unrealistically narrow velocity dispersion
(see Fig. B1b in II) is obtained only for an
unrealistically narrow velocity dispersion
![]() ,
since in
the expression (B15) the term
,
since in
the expression (B15) the term
![]() is omitted (i.e. as the infinitesimal).
is omitted (i.e. as the infinitesimal).
Thus, for the calculated magnetic force line, the ZS stripes in Fig. 5 (in II) should merge in a continuum, and the plotting of the dependence f(h) becomes almost arbitrary. The authors of II discuss merging of zebra-stripes in a continuum (in Sect. 4.2.), but do not check this condition further in the construction of Fig. 5.
Therefore the explanation of frequency drift of stripes due to a
change of magnetic field and temperature cannot be accurate.
The barometric formula:
![]() (the formula (10) in II) is written by analogy to
formula (3.9) in Priest (1982) for constant temperature, thus
it is impossible to define from it a change of T. The real
dependence on T is given by the much more complex expression (3.8)
in Priest (1982). Heating and cooling of plasma are slow
processes (in the coronal loop they last some minutes), therefore
it is impossible to explain a change of frequency drift of stripes
on time intervals of less than 1 s by these processes.
The authors in II have obtained an underestimated electron
concentration of almost two orders relative to any other
model (
(the formula (10) in II) is written by analogy to
formula (3.9) in Priest (1982) for constant temperature, thus
it is impossible to define from it a change of T. The real
dependence on T is given by the much more complex expression (3.8)
in Priest (1982). Heating and cooling of plasma are slow
processes (in the coronal loop they last some minutes), therefore
it is impossible to explain a change of frequency drift of stripes
on time intervals of less than 1 s by these processes.
The authors in II have obtained an underestimated electron
concentration of almost two orders relative to any other
model (
![]() for h = 0), and the footnote on this
account (that in the base of a corona other temperatures could exist)
only aggravates this question, since the local parameters will not be
coordinated with the global parameters for the entire corona. The
authors were forced to make this assumption because of the
unrealistically calculated magnetic force line.
for h = 0), and the footnote on this
account (that in the base of a corona other temperatures could exist)
only aggravates this question, since the local parameters will not be
coordinated with the global parameters for the entire corona. The
authors were forced to make this assumption because of the
unrealistically calculated magnetic force line.
Thus, it was necessary to determine to what other density distributions the fitting corresponds better (for example, to the Newkirk model). If it is possible to choose any force line and to vary s, this method is not suitable for the solution of such a problem.
Smooth changes of frequency drift are explained by a movement of fronts of fast particles at various angles to the magnetic force lines (Mollwo 1983, 1988). Thus, a certain restriction is imposed for the cross-section size of these fronts, so that the stripes are not merged into the continuum.
In the recent paper devoted to perfection of the DPR model of Yasnov &
Karlicky (2004), the calculations of the growth rates of the upper hybrid
waves are carried out for various velocities of fast particles and
various temperatures of the background plasma. From Fig. 5 in Yasnov &
Karlicky (2004), it is seen that the large width of the maximum
of the growth rates does not satisfy the same condition
![]() ,
so
that the zebra-stripes would not merge in the continuum.
,
so
that the zebra-stripes would not merge in the continuum.
In II the question of real absorption of the background continuum in dark ZS stripes is in no way discussed, although Zheleznyakov & Zlotnik (1975a,b) relate absorptions to the negative relativistic growth rates of cyclotron waves in the hybrid band at the low frequency edge of the positive growth rates. Winglee & Dulk (1986) do not discuss this at all due to the too large differences of the values, since the scale of negative values is about two orders less than that of the positive ones. Winglee & Dulk (1986) conclude that in most cases the emitted harmonics overlap in the continuum radiation and zebra stripes can appear only if the maser instability is not at saturation, if the fast electrons have a loss-cone distribution and their velocities are close to 0.1 c.
Concerning the result of Zlotnik et al. (2003), namely the finding
of a barometric model for the plasma frequency from the
observations of the ZS, it is possible to
construct a similar graph, utilizing no calculated magnetic
force lines (Fig. 1). It is possible to take the known model of the
magnetic field in the corona, obtained from numerous radio data
(McLean & Dulk 1978),
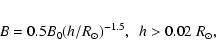
![\begin{figure}
\par\includegraphics[width=7.3cm,clip]{2578Fig1.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg41.gif) |
Figure 1:
Frequency (Hz) against height in the corona h (cm).
A grid of gyroharmonics (s = 2-22...) is plotted using the magnetic
field model of Dulk & McLean (1978). The inclined curve is
the barometric plasma frequency dependence on height:
|
| Open with DEXTER | |
If the model of the field of McLean & Dulk (1978)
is accurate (it is based on a lage amount of radio data), the distribution of
concentration according to the barometric formula cannot be used in the magnetic
loops with plasma
![]() ,
since this formula gives the distribution of
density in the gravitational field with constant temperature and without taking
into account the magnetic field.
The general consideration of a model with whistlers and
an alternative interpretation of the zebra pattern in the
event of October 25, 1994 is presented
in Chernov (2005). There it is shown that the model
with whistlers makes it possible to explain both the general parameters
(frequency band, connection with III type bursts) and all fine
effects of the behavior of the ZS on the spectrum and space drift
of radio sources.
,
since this formula gives the distribution of
density in the gravitational field with constant temperature and without taking
into account the magnetic field.
The general consideration of a model with whistlers and
an alternative interpretation of the zebra pattern in the
event of October 25, 1994 is presented
in Chernov (2005). There it is shown that the model
with whistlers makes it possible to explain both the general parameters
(frequency band, connection with III type bursts) and all fine
effects of the behavior of the ZS on the spectrum and space drift
of radio sources.
The analysis of many cases of ZS near 3 GHz in some events
shows the full variety of fine structure similar to that seen in the metric
range. In the event of October 29, 2000, for about 20 min ZS
and fiber bursts (FB) were followed by intermittent pulses of some seconds.
An example of ZS evolution is shown in Fig. 2. This event was
connected to the
![]() 2B M4.4 flare in AR NOAA 9209, located at S25E35. The ZS shows different frequency drifts: slow negative, positive or switches between the two. The FB
often overlap the zebra pattern, and the emission frequency band is
about the same for both structures. After some fluctuations of ZS a
strong series of FB with different periodicity and a
constant frequency drift of -240 MHz/s was observed. The FB and ZS have
about the same spectral parameters, e.g. the frequency bandwidth
of emission stripes
2B M4.4 flare in AR NOAA 9209, located at S25E35. The ZS shows different frequency drifts: slow negative, positive or switches between the two. The FB
often overlap the zebra pattern, and the emission frequency band is
about the same for both structures. After some fluctuations of ZS a
strong series of FB with different periodicity and a
constant frequency drift of -240 MHz/s was observed. The FB and ZS have
about the same spectral parameters, e.g. the frequency bandwidth
of emission stripes
![]() and the
frequency separation between emission lines is 50-80 MHz in the range
2.6-2.8 GHz.
and the
frequency separation between emission lines is 50-80 MHz in the range
2.6-2.8 GHz.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2578Fig2.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg45.gif) |
Figure 2: Radio spectrograms of zebra patterns and fiber bursts during the evolution of the event of 29 October 2000 between 02:19-02:28 UT in right polarization recorded by the spectrometer of NAOC (2.6-3.8 GHz). The frequency difference between the 5 regular zebra stripes in the top panel depends weakly on the frequency. |
| Open with DEXTER | |
A detailed analysis of the multi-channel time profiles (see
Fig. 3 in Chernov et al. 2001b) shows that the intensity level in
the black stripes (between emission stripes) could be lower than the
emission level of the main continuum (without ZS). Thus, the black
zebra-stripes are visible not due to the absence of bright
stripes, but due to an absorption of the main continuum emission
(a modulation effect). In this connection the main parameter of ZS
and FB is not frequency separation between emission stripes
(
![]() MHz on an average), but the frequency
separation between the emission and the adjacent low frequency
absorption with a mean value
MHz on an average), but the frequency
separation between the emission and the adjacent low frequency
absorption with a mean value
![]() MHz.
Therefore we can assume that both of the fine structures have
the same origin.
MHz.
Therefore we can assume that both of the fine structures have
the same origin.
The eruptive long duration X1.5 class flare event of April 21, 2002 occurred in AR 9906 close to the western solar limb (S14W84) between 00:43 and 02:38 UT. Images of TRACE data in the EUV 195 Å line show the formation of a bright post-flare arcade in the flare site (Gallagher et al. 2002). From 01:34 to at least 02:15, dark matter is seen falling onto the arcade from above. The dark matter apparently occults bright arcade loops.
The entire prolonged event was divided into two phases in the radio data and in hard X-rays: in the growing flow of soft X-rays (GOES) there was a first maximum in hard X-rays (about 01:15-01:18 UT, MTI/HXRS) and in the radio range (near 01:30 UT). In this phase the maximum energy release occurred in the decimeter wave band, which indicates magnetic reconnection at heights of the decimeter range. According to the data of radio-spectrographs (Hiraiso and IRS, Korea (Cho, personal communication)) high flux levels were recorded in the meter range (between 01:18-01:30), possibly with fine structure.
In the microwave range the maximum of the first phase was above that of the second phase. However, no fine structure in the first phase was registered around 3 GHz. The arcade of loops began to form only after approximately 01:30 UT.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{2578Fig3.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg48.gif) |
Figure 3: Top: the hard X-ray burst in the 44-67 keV channel of the HXRS during the period of ZS in 2.6-3.8 GHz. The Huairou radio profiles at 2.84 and 3.44 GHz showing the radio flux intensity (I = L + R) and the polarization component (V = L - R) are indicated by solid and dashed lines respectively. |
| Open with DEXTER | |
The ZS are observed only during the second phase, between 01:44 and 02:05 UT, during the second phase of the HXR (MTI, HXRS) burst presented in Fig. 3. In the loop arcade we see during this phase two new bright centers as X-points of magnetic reconnection (see top left panel in Fig. 4). During the interval 01:51-01:53 UT the ZS was very weak. At this time in the TRACE 195 Å image some bright centers disappeared (see right top panel in Fig. 4). The difference image between 01:50:57 and 01:48:16 shows many bright loops (middle left panel in Fig. 4), where the radio sources of ZS could be located. At the same time three new sources of HXR (RHESSI, Gallagher 2002) appeared under the mentioned two X-points of the magnetic reconnection visible in the bottom left panel of Fig. 4. Such a proposal is confirmed by radio source positions with SSRT data at 5.7 GHz for polarized emission (the parameter V, see two centers shown by isolines in the bottom right panel in Fig. 4). White and black contours in the bottom left panel of Fig. 4 show source positions of RHESSI/HXR energy channels respectively at 50-100 and 12-25 Kev (Gallagher 2002). Radio sources of continuum emission in intensity with SSRT data (parameter I) have approximately the same positions (the lower and upper sources shown by the grey and black background in the bottom right panel of Fig. 4).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2578Fig4.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg49.gif) |
Figure 4: The evolution of the flare of April 21, 2002 with TRACE data in EUV line 195 Å and RHESSI HXR data. The difference image between 01:50:57 and 01:48:16 UT (middle left panel) shows many bright loops, where the radio sources of ZS could be located. The bottom left panel shows three new sources (white points) of HXR (RHESSI, Gallagher 2002). The bottom right panel shows radio source positions with SSRT data at 5.7 GHz (courtesy of R. Sych) in intensity (parameter I, shown by the grey and black background) and in polarization (parameter V shown by contours). |
| Open with DEXTER | |
After 02:09 UT the arcade of bright loops in the line 195 Å rose to high altitudes (middle right panel in Fig. 4), and the maximum of activity was displaced into the decimeter range.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2578Fig5.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg50.gif) |
Figure 5: Zebra structure in the event of April 21, 2002. The two upper panels show the Huairou radio spectrograms in the 2.6-3.8 GHz range in the left and right polarization components with a zebra pattern at 01:48:18-01:48:38 UT, in which 34 stripes can be distinguished and whose frequency separation grows smoothly with frequency. The lower panel shows profiles of the intensities at four fixed frequencies. The profiles confirm the spike-like structure of each zebra stripe in emission. The dark stripes do not contain a spike-like structure, and the radiation level proves to be lower than the average level of continuum, shown by the straight line at a frequency of 3.13 GHz. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{2578Fig6.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg51.gif) |
Figure 6: Zebra structure in the event of April 21, 2002 at 02:00:43-02:01:03 UT. The zebra stripes on the high-frequency edge of the spectrum are more similar to isolated fibers without any strict periodicity. The multichannel time profiles ( in the bottom panel) show stripes in emission consisting of spikes as before. However, in the dark stripes the residual emission remains at a fixed level. |
| Open with DEXTER | |
All series of the ZS in this event represented zebra stripes with
negative frequency drift, which is more inherent to fibers.
In Figs. 5 and 6 two intervals with the most pronounced ZS are shown, taken with
the NAOC spectrometer at 2.6-3.8 GHz. In the first fragment of 20 s duration
from 01:48:18 UT 34 zebra stripes are counted in the range 2.6-3.8 GHz
with a barely noticeable increase in frequency separation between
stripes from 27 MHz at 2.8 GHz to 43 MHz at 3.7 GHz. It is remarkable
that the relative value of the frequency separation proves to be about the same
as in the meter range
![]() .
.
The frequency drift of zebra stripes was negative and almost
constant ![]()
![]() between 3.8-3.4 GHz, which is more
characteristic of fibers. At the low frequency part of the
spectrum a small deceleration of the frequency drift is observed.
However, each 1-2 s, stripes undergo failures and jumps of
frequency drift, covering several adjacent stripes with a
small time delay. Sometimes shifts in the frequency lead to
merging or splitting of stripes. Such effects are well known in
the meter wave band. In the bottom of Fig. 5 a short fragment
of intensity time profiles of about 3 s duration is shown at four frequencies. A detailed analysis of multichannel time profiles shows that each zebra stripe in emission has a spike-like
structure. In the dark stripes (between the bright zebra stripes)
the emission level can be lower than the level of burst background
(lower than the average level of continuum, shown by a
straight line at 3.12 GHz). Thus the presence of dark
stripes is connected not with the absence of bright stripes (in
emission), but with an absorption of background microwave
emission. The polarization degree was weakly left-handed. We
propose that two polarized radio sources at 5.7 GHz were
located above the leading spot (the left polarized source) and above
the tail spot (the right source in the bottom right panel of Fig. 4).
Therefore due to the limb position of the AR it is difficult to
precisely define the magnetic polarity of the corresponding radio
sources to define the type of radio wave.
between 3.8-3.4 GHz, which is more
characteristic of fibers. At the low frequency part of the
spectrum a small deceleration of the frequency drift is observed.
However, each 1-2 s, stripes undergo failures and jumps of
frequency drift, covering several adjacent stripes with a
small time delay. Sometimes shifts in the frequency lead to
merging or splitting of stripes. Such effects are well known in
the meter wave band. In the bottom of Fig. 5 a short fragment
of intensity time profiles of about 3 s duration is shown at four frequencies. A detailed analysis of multichannel time profiles shows that each zebra stripe in emission has a spike-like
structure. In the dark stripes (between the bright zebra stripes)
the emission level can be lower than the level of burst background
(lower than the average level of continuum, shown by a
straight line at 3.12 GHz). Thus the presence of dark
stripes is connected not with the absence of bright stripes (in
emission), but with an absorption of background microwave
emission. The polarization degree was weakly left-handed. We
propose that two polarized radio sources at 5.7 GHz were
located above the leading spot (the left polarized source) and above
the tail spot (the right source in the bottom right panel of Fig. 4).
Therefore due to the limb position of the AR it is difficult to
precisely define the magnetic polarity of the corresponding radio
sources to define the type of radio wave.
The fragment in Fig. 6 shows some changes of ZS properties: the polarization degree becomes stronger and it grows with time and frequency; the frequency drift almost stops in the low-frequency part of the spectrum (sometimes the stripes are almost parallel to the time axis); however, in the high-frequency part of the band they are more similar to isolated fibers with a negative frequency drift (there is no strict periodicity). The multichannel time profiles (in the bottom panel of Fig. 6) show that stripes in emission consist as before of spikes, however, in the dark stripes, deep dips in emission are not observed; the residual emission remains at a fixed level.
ZS was also observed in the pulsating regime, but almost all series of ZS were prolonged; in the examples in Figs. 5 and 6 the duration exceeded 1 min. The evolution of zebra stripes in several series began from a cloud of millisecond spikes with the gradual shaping of zebra stripes, as is shown in Fig. 7.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2578Fig7.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg55.gif) |
Figure 7: Some series of ZS began from a cloud of millisecond spikes with gradual formation of zebra stripes. |
| Open with DEXTER | |
The relative frequency parameters of
ZS in microwave and meter wave bands appear identical.
This testifies to the similar nature of the
formation of fine structure in different frequency ranges.
Since ZS and FB display similar spectral characteristics,
we will consider both structures to be
manifestations of whistlers in the radio source, due to their
interactions with electrostatic plasma waves:
![]() ,
with both waves being excited by the same fast
particles in hot flare loops, which have an anisotropic loss-cone
distribution. The computations of Yasnov et al. (2000) show a growth in the
whistler increment with temperature of the background plasma
in the flare region, with the growth in cyclotron decay being
compensated by the decrease in the whistler frequency with a
maximum increment at
,
with both waves being excited by the same fast
particles in hot flare loops, which have an anisotropic loss-cone
distribution. The computations of Yasnov et al. (2000) show a growth in the
whistler increment with temperature of the background plasma
in the flare region, with the growth in cyclotron decay being
compensated by the decrease in the whistler frequency with a
maximum increment at
![]() .
The mean duration of a
series of zebra structures and fiber bursts was about two seconds,
and the propagation of whistlers without damping over this time
places a constraint on the whistler increment of <
.
The mean duration of a
series of zebra structures and fiber bursts was about two seconds,
and the propagation of whistlers without damping over this time
places a constraint on the whistler increment of <
![]() .
This constraint can be used to estimate the magnetic field
strength in the region in which the flare is generated. Electron
temperatures in the range 2-20 MK yield magnetic fields of B = 125-190 G for regions in which the electron density is
.
This constraint can be used to estimate the magnetic field
strength in the region in which the flare is generated. Electron
temperatures in the range 2-20 MK yield magnetic fields of B = 125-190 G for regions in which the electron density is
![]() .
.
These rough estimates coincide with estimates derived from the
frequency drift rate of the fiber bursts observed at the same time
at these same frequencies, based on the formula
![]() (Elgarøy 1982), which was obtained for a 60-fold
Newkirk model and a whistler frequency of
(Elgarøy 1982), which was obtained for a 60-fold
Newkirk model and a whistler frequency of
![]() .
In the model with the whistlers we can also verify the
obtained values of B using the frequency separation between the
maximum in the emission and the adjacent minimum in the absorption (
.
In the model with the whistlers we can also verify the
obtained values of B using the frequency separation between the
maximum in the emission and the adjacent minimum in the absorption (
![]() ). This value must be equal to the frequency of whistlers, which is selected to be equal to 0.1 of the cyclotron frequency (at which the increment of whistlers is maximum). Thus,
). This value must be equal to the frequency of whistlers, which is selected to be equal to 0.1 of the cyclotron frequency (at which the increment of whistlers is maximum). Thus,
![]() and for the observed value
and for the observed value
![]() MHz we can estimate
MHz we can estimate
![]() .
This value is close to the values of the field, obtained above by
two other methods, which confirms the reliability of the
determination of the magnetic field in the model with whistlers.
.
This value is close to the values of the field, obtained above by
two other methods, which confirms the reliability of the
determination of the magnetic field in the model with whistlers.
If we estimate the magnitude of B in the new model of LaBelle et al. (2003), assuming that
![]() ,
we obtain for
,
we obtain for
![]() MHz implausibly high values of
MHz implausibly high values of
![]() ,
close to photosphere values.
,
close to photosphere values.
The alternative model based on the generation of plasma waves at
the upper-hybrid frequency
![]() under the conditions
appropriate for DPR was also considered. In the DPR- model all
estimations of the field depend strongly (even for the order of magnitude)
on the unknown relationship between the height scales in the
corona of the density and magnetic field. We can see from Fig. 8 that
the main inadequacy of this model is associated with the increase
in the frequency separation of the emission stripes
under the conditions
appropriate for DPR was also considered. In the DPR- model all
estimations of the field depend strongly (even for the order of magnitude)
on the unknown relationship between the height scales in the
corona of the density and magnetic field. We can see from Fig. 8 that
the main inadequacy of this model is associated with the increase
in the frequency separation of the emission stripes
![]() with increasing frequency: the model predicts an increase from 60 MHz at 2.7 GHz to
with increasing frequency: the model predicts an increase from 60 MHz at 2.7 GHz to ![]() 450 MHz at 3.8 GHz, which is not generally observed. Usually, the frequency separation only
slightly increases with frequency.
450 MHz at 3.8 GHz, which is not generally observed. Usually, the frequency separation only
slightly increases with frequency.
![\begin{figure}
\par\includegraphics[width=7cm,clip]{2578Fig8.eps} \end{figure}](/articles/aa/full/2005/27/aa2578-04/Timg71.gif) |
Figure 8:
Dependences of upper hybrid and cyclotron frequencies on
the height in the corona in the magnetic field model of Dulk &
McLean (1978), which is derived from radio data (B(G) =
|
| Open with DEXTER | |
The conditions of DPR are probably realized rarely in the flare region with a set of thin magnetic loops, in which the magnetic field and density change insignificantly with the height along the loops (Aschwanden et al. 1999; Aschwanden 2002). However, if they fall in a stable magnetic trap, one may expect the stable emission of stripes, most likely during the entire event. Such stable stripes in emission were observed, for example, in the decimeter range in the event of February 17, 1992 (Chernov et al. 1998, evolving emission lines, EEL). The EEL with slow wave frequency drift of one or three harmonics during more than 2 h satisfies the mechanism for DPR.
Figures 3 and 4 show the main flare moments at which a zebra pattern appears.
First, the interval of a zebra pattern synchronizes precisely with an HXR burst
(44-67 keV, HXRS). Second, the two most powerful series of ZS
represented in Figs. 5 and 6 coincide in time with the appearance of
two new HXR sources (RHESSI data in the lower left panel of Fig. 4), whose positions coincide with two maximum radio sources (SSRT data) in the polarized radiation. Thus, the formation of zebra stripes is related to the presence of fast particles in the loop
arcade, including two bright nodes in the formation X-points of
magnetic reconnection, seen in the difference image in
Fig. 4. The emission in the FeXII line at 195 Å shows
only bright loops with a temperature of 1.8 ![]() 106 K,
but radio sources at 5.7 GHz (SSRT) and 17 GHz (Nobeyama) in the
polarized radiation were located near two bright nodes, in
which the bright intersecting loops had a configuration of
the form of singular X-points.
106 K,
but radio sources at 5.7 GHz (SSRT) and 17 GHz (Nobeyama) in the
polarized radiation were located near two bright nodes, in
which the bright intersecting loops had a configuration of
the form of singular X-points.
The dark material on top is probably overheated flare plasma (to 50 MK) ejected from the region of maximum energy release at heights in the decimeter range. This prolonged flow of overheated plasma (from 01:34 through 02:15 UT)likely served as the source of heating of the entire arcade (not only the mentioned nodes with the X-points), since the duration of its precipitation tightly covered the interval of fine structure excitation.
It would be natural to connect radio sources with these bright loops. However, the large number of loops with bright apexes in a narrow height interval casts doubt on the possibility of realization of DPR-conditions in a wide interval of heights. In this connection, the example of the zebra structure shown in Fig. 5 is noteworthy since it shows that the DPR-model is not able to explain the presence of simultaneous emission in 34 zebra stripes with virtually identical intensities in the range 2.6-3.8 GHz.
At the same time, this situation is realistic in a whistler model, where strict periodicity of the stripes is specified by the whistler excitation mechanism itself (fluctuations in the instability under the action of quasi-linear effects, independent of the models for density and magnetic field in the corona) (Chernov 2005). Frequently the zebra stripes are more similar to isolated fibers, as, for example, on the high-frequency edge of the spectrum in Fig. 6. Therefore we could consider both fine structures in a unique model as manifestations of the whistler mechanism. The isolated packages of whistlers are excited more effectively below, near magnetic mirrors, and they propagate upward along the magnetic loops. Approaching the singular points (X-points), whistlers gradually fill the entire radio source with almost standing periodic wave packets, that also explain the presence of stripes barely drifting in frequency at the low-frequency edge of the spectrum in Fig. 6.
The new model of LaBelle et al. (2003) can theoretically explain all the parameters of zebra structures and as well as the large number of zebra pattern stripes originating from a point radio source. However, the stable appearance of series of zebra structures in a pulsating regime cannot be understood since this model predicts a strong dependence of the frequency separation and the number of zebra stripes on the parameters of the inhomogeneities, while we observe only a very small growth in the frequency separation with increasing frequency. The parameters of inhomogeneities such as propagating ion-sound waves cannot remain so similar over a wide range of frequencies (interval of heights) and over extended periods of time. Furthermore, we need to explain the large intensity of all zebra stripes from numerous point radio sources, exciting the total (incoherent) emission i.e., the spectrum of the stripes would be expected to blend into the continuum.
The frequency profiles in Figs. 5 and 6 demonstrate rapid pulsations in the bright zebra-pattern stripes with a well-defined period of 30 ms. Thus, these new observations support the conclusions of Chernov et al. (2003) that the ZS at centimeter wavelengths always have a fine spike-like structure, which can be explained by whistler models for zebra structure.
Figure 7 shows that zebra stripes are gradually formed in a cloud of spikes. Therefore it is possible to assume that the emission of spikes is a primary process. In the dm- range the analogous conversion was observed by Kuijpers et al. (1981). They assumed that spikes and zebra patterns can be excited by the same mechanism. On the basis of our previous results (Chernov et al. 2003), we can assume that near the flare region spikes can be excited by the nonlinear mechanism of interaction of plasma Langmuir waves with ion-sound waves. The ionic sound can be always present in shock wave fronts, departing from regions of magnetic reconnection (Chernov et al. 2001a). However, zebra stripes appear with the excitation of whistlers by fast particles with a loss-cone distribution, forming only after the reflection of particles from the magnetic mirrors. Thus, a certain delay is permissible.
If we determine the magnetic field strength of the frequency
separation between the maxima in emission and absorption in one stripe (
![]() ), for the moment 01:48:34 UT, we obtain a small value of
), for the moment 01:48:34 UT, we obtain a small value of
![]() .
.
After 02:00 UT we do not have the possibility to estimate B, since the zebra stripes did not show noticeable absorption, even in the single stripes at the HF edge. A decrease in the intensity of plasma waves due to scattering of fast particles on the whistlers in the periodic wave packets is the basic reason for absorptions. Therefore assume that in this case the particles and waves diverged in space, which is allowed with rapid particle injection and the emission of whistlers with the normal Doppler effect (in a regime of weak diffusion). It is not excluded that the large number of stripes with a narrow frequency separation is the result of the imposition of emission from the different loops due to the observation of the projection of radio sources at the solar limb. In this case the polarization will most likely be determined by the propagation conditions of radio emission perpendicular to the magnetic field.
Thus, new data on zebra structure and fiber bursts at centimeter
wavelengths show that they have similar structures to those
observed at meter wavelengths. ZS was not observed at frequencies
higher than 5.5-6 GHz. The radiation of electrostatic plasma waves
at higher frequencies is probably suppressed in the dense flare
plasma. A unified model for zebra structure and fiber bursts
involving whistlers can yield realistic values for the magnetic
field strength,
![]() ,
at a plasma level of about 3 GHz. Using realistic dependences for the electron density and magnetic field, the DPR-model for zebra structure predicts a frequency dependence of the frequency separation between stripes
that is much stronger than is observed.
,
at a plasma level of about 3 GHz. Using realistic dependences for the electron density and magnetic field, the DPR-model for zebra structure predicts a frequency dependence of the frequency separation between stripes
that is much stronger than is observed.
Acknowledgements
This research was supported by the Russian Foundation of Basic Research, grants No. 02-02-16201, 04-02-39015. G.P.Ch. thanks Dr. L.V. Yasnov for the help in some calculations. G.P.Ch. is grateful also for the support of the Chinese Academy of Sciences and NSF of China that enabled him to work with colleagues at NAOC. The Chinese authors acknowledge support of NSFC and Ministry of Sciences and Technology of China (G2000078403). The TRACE and RHESSI data were obtained from the TRACE and RHESSI databases.